化学反应工程(第三版)陈甘棠主编

格式：ppt
大小：1.24 MB
文档页数：90

下载文档原格式

化学反应工程陈甘棠第二章第三节共23页

29.11.2019
集总法 : 将性质近似的反应组分进行合并，把它当作一个反应组分看待，然后研究这些合并后的虚拟组分间的动力学关系，这种处理方法称为集总法。
例如：
最简单的催化裂化反应模型为：
重质油
汽油
焦炭+轻质气体
29.11.2019
谢谢！
cp0ek2t cA 0
29.11.2019
根据物料衡算有：
c A 0 c A (c p c p 0 ) (c s c s0 )
c s c s 0 c A 0 1 e k 1 t
k 1 c A 0e k 1 t e k 2 t k 2 k 1
k2cA
29.11.2019
反应物A总的反应速率-rA为：
AA 1(A 2)k1c Ak2cA
瞬时收率为：
p

dc p dcA

dc p dt dcA dt
p A

p A1
k
1
c
A
k
1
c
A

k
2
c
A
p
1
A1
1
当Cp取得最大时，反应时间t*
dpc /d tk k 2 1c A k 01k2e k2tk1e k1 t 0
则
kek2t 2
k1ek1t
29.11.2019
CA0 Cp,max
0
topt
29.11.2019
CS CP CA
t
解得：
1
t* k 2 k 1 1
2）得率XP : 生成的目的产物P的摩尔数与着眼组分A的起始摩尔数之比

化学反应工程陈甘棠第二章第一节-31页文档资料

2、化学计量方程
a 1 A 1 a 2A 2 a sA s 0
几点说明：
s
ai Ai 0
i 1
➢ 产物的计量系数为正，反应物的计量系数为负
➢ 计量方程式仅仅表示反应物间的质量变化，与反应历程无关。
05.04.2020
s
➢计量方程的写法统乘以非零因子都成立，即： ai Ai 0 i 1
➢为了消除计量系数在数值上的不确定性，规定计量系数里不含公因子
即：
k
k0
exp
E RT
式中：k0——指前因子或频率因子，反应了反应中分子碰撞
几率大小，与分子热运动有关。
05.04.2020
E——活化能，
物理意义：把反应分子激发到可进行反应的活化状态时
说明：
所需要的能量
活化能大小直接反映了反应进行的难易程度。代表了反应速率对温度的敏感程度。E越大k对T就越敏感。活化能E 越大，所需的反应温度就越高。
3 (1 3 1 0.4)源自4 1 (2) 3 1 0.4
4
0.5625
05.04.2020
5、反应速率方程
反应速率方程：在溶剂及催化剂和压力一定的情况下，定量描述反应速率与温度及反应物系的组成的关系式
双曲线型：由所假定的反应机理推导而得均相反应速率方程
幂函数型：依据质量作用定律
基元反应 rAkcAcB
n k 0之
组分反应掉的摩尔数 xk 组分的起始摩尔数
2）反应程度
nk0 nk nk 0
各组分在反应前后摩尔数变化与其计量系数的比值，
用ξ表示
05.04.2020
0 n1n10 1
nini
i
nk nk 0

化学反应工程(第三版)陈甘棠主编第八章气液两相反应器PPT课件

（8-14）
定常态操作时，单位界面上反应量等于扩散通量，即
NA(rA )d SA n dtD LA ddA czz0
将A的浓度分布对z求导后代入上式得
式中，
N A( rA )D L LA cA 1 i b D L L D c B c B A AL i kLc A Ai
k LA
DLA L
，称为液膜传质系数。
（8-16）
1 DLBcBL bDLAcAi
，称为瞬间反应的增强系数。物理意义是气
液反应条件下组分A的消失速率与最大物理吸收速率 kLAcAi 之比。 13
式（8-15）中cAi是界面浓度，难以测定，工程设计中通常将其换算为容易测量的pA来表示的反应速率。因为，
N AkG(A p Ap A)i( rA )kLc A A 1 ib D L L D c c B B A A L i
第八章气液两相反应器
1
整体概况
概况一
点击此处输入相关文本内容
01
概况二
点击此处输入相关文本内容
02
概况三
点击此处输入相关文本内容
03
2
8.1 概述
气-液相反应是一类重要的非均相反应。主要分为二种类型：（1）化学吸收：原料气净化、产品提纯、废气处理等。（2）制取化工产品
a.
b.
c.
（淤浆床）
A ( g b) l) B P(( r A ) k A c B c
定常态条件下，在单位面积的液膜中取一厚度为dz的微元层，对组分
A作物料衡算：
D Ld A dAc z( rA )d z D Ld A d c zAd dAc d z z
整理得
DLAdd2cz2A kcAcB 0

化学反应工程(第三版)陈甘棠主编_第五章_催化剂与催化动力学基础

Ki 称为吸附平衡常数，是i组分吸附速率常数与脱附速率常数之比。式（5-28）即为过程的总速率方程。由该式的分母可知，反应物和产物均被吸附。分母的方次表明该反应是在A、B两个活性中心之间进行的。
若控制步骤为可逆反应过程总速率：
Aσ + Bσ
k1
k2
Rσ + Sσ
r k k A 1 A B 2 R S
第五章催化剂与催化动力学基础
5.1 催化剂
能够改变化学反应速率而本身在反应前后不发生组成变化的物质。（1）类型金属（良导体）、金属氧化物和硫化物（半导体）以及盐类和酸性催化剂（大多数是绝缘体）（2）载体活性炭、硅胶、活性白土、硅藻土、沸石（分子筛）、骨架Ni、活性Al2O3、 Fe等（3）性能要求活性好、选择性高、寿命长。（4）结构
k k K K 1 A B
K
k1K A KB k2 KR KS
比较式（5-28）和式（5-30）可见，表面反应为控制步骤时，可逆反应与不可逆反应速率式的分母相同，区别在于分子。可逆反应的分子上有两项，不可逆反应只有一项。
A在吸附时解离 A + 2σ B + σ 2A1/2σ + Bσ Rσ Sσ 按上述方法可得到
几种常用催化剂的结构
无定形颗粒球形柱形长柱形三叶草形
环形
多孔柱形车轮形
比表面积
破碎强度
压降
独石形
金属独石形
Foam
（5）制备方法
① 混合法
② 浸渍法 ③ 沉淀法或共沉淀法 ④ 共凝胶法 ⑤ 喷涂法及滚涂法 ⑥ 溶蚀法 ⑦ 热熔法
5.3 气固相催化反应动力学
气-固相反应速率的定义式

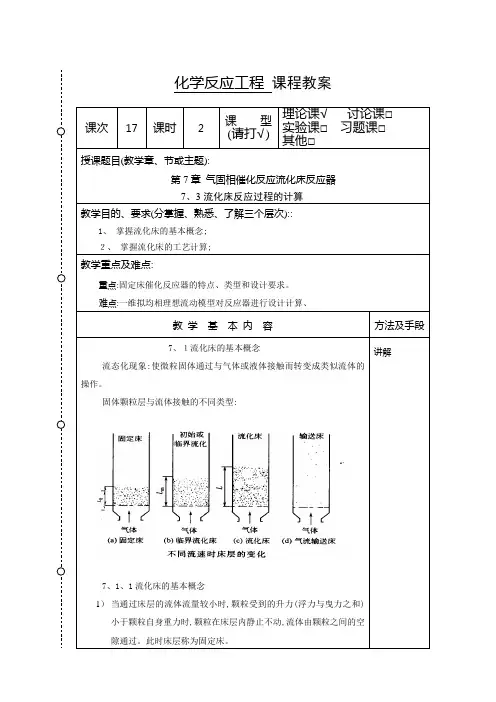
化学反应工程教案

化学反应工程课程教案课次17课时 2 课型(请打√)理论课√讨论课□实验课□习题课□其他□授课题目(教学章、节或主题):第7章气固相催化反应流化床反应器7、3流化床反应过程的计算教学目的、要求(分掌握、熟悉、了解三个层次)::1、掌握流化床的基本概念;２、掌握流化床的工艺计算;教学重点及难点:重点:固定床催化反应器的特点、类型和设计要求。

难点:一维拟均相理想流动模型对反应器进行设计计算、教学基本内容方法及手段7、１流化床的基本概念流态化现象:使微粒固体通过与气体或液体接触而转变成类似流体的操作。

固体颗粒层与流体接触的不同类型:7、1、1流化床的基本概念1）当通过床层的流体流量较小时,颗粒受到的升力(浮力与曳力之和)小于颗粒自身重力时,颗粒在床层内静止不动,流体由颗粒之间的空隙通过。

此时床层称为固定床。

讲解2）随着流体流量增加,颗粒受到的曳力也随着增大、若颗粒受到的升力恰好等于自身重量时,颗粒受力处于平衡状态,故颗粒将在床层内作上下、左右、前后的激烈运动,这种现象被称为固体的流态化,整个床层称为流化床、曳力(表面曳力、形体曳力)曳力是流体对固体的作用力,而阻力是固体壁对流体的作用力,两者是作用力与反作用力的关系。

表面曳力由作用在颗粒表面上的剪切力引起,形体曳力由作用在颗粒表面上的压强力扣除浮力部分引起、３)。

流化床类似液体的性状(a) 轻的固体浮起;(b)表面保持水平;(c)固体颗粒从孔中喷出;(d)床面拉平;(ｅ)床层重量除以截面积等于压强流化床的优点(1) 颗粒流动类似液体,易于处理、控制;(2) 固体颗粒迅速混合,整个床层等温;(3) 颗粒能够在两个流化床之间流动、循环,使大量热、质有估计在床层之间传递;(4) 宜于大规模操作;(５) 气体和固体之间的热质传递较其它方式高;(6) 流化床与床内构件的给热系数大、浓相段和稀相段(P18５-１86)1)、当流体通过固体床层的空塔速度值高于初始流化速度但低于逸出速度(p188),颗粒在气流作用下悬浮于床层中,所形成的流固混合物称为浓相段。

陈甘棠主编化学反应工程第六章

转化的多段绝
热反应器，段间引入冷空气
进行冷激。
对于这类可逆放热反应过
程，通过段间换热形成先高后低的温度变化，提高转化率和反应速率。
总之，不论是吸热或放热的反应，绝热床的应用是相当广泛的，特别对于大型的，高温或高压的反应器，希望结构简单，同样大小的装置内能容纳尽可能多的催化剂以增加生产能力（少加换热空间），而绝热床正好能符合这种要求。但绝热床的温度变化总是较大的，由于温度对反应的影响同样不可忽视，故要综合分析并根据实际情况来决定。
体积：(非球形颗粒折合成同体积的球形颗粒应当具有的直径）
球形体积： VP

6
d3
6VP
1
3
dV
外表面积： (非球形颗粒折合成相同外表面积的球形颗粒应当具有的直径）
球形外表面积： p d 2 a
ap

1
2
da
d 6 球形比表面积： V S 3 VS d d
6.2.2床层压降
气体流动通过催化剂床层的空隙形成的通道时，与孔道皱襞摩擦将产生压降。厄根（Ergun）方程：
2 um 1 B dP 150 R 1.75 3 d dL em B s

式中：Rem : 修正的雷诺数，Rem u m：平均流速空塔气速 d s : 颗粒当量直径
ap 6 VS 6 dS 6 SV ap
比表面积： (非球形颗粒折合成相同比表面积的球形颗粒应当具有的直径） 2
混合粒子的平均直径：（各不同粒径的粒子直径的加权平均）
1 dm xi d i
xi - 直径等于d i的颗粒占的分数

陈甘棠主编化学反应工程第五章

⑵选择性指？
高选பைடு நூலகம்性可节约原料、减化工艺。
影响选择性的因素很多，有物理的和化学的。
就催化剂的构造而言，主要有：活性组分在
表面上的定位和分布、微晶粒度大小、载体的孔结构、孔径和孔容等。
当遇到转化率和选择性的要求不能同时满
足时： a：如果反应原料昂贵或者产物和副产物分离困难时，宜采用高选择性的催化系统 b：若原料价格便宜，且产物与副产物分离不困难，则采用高转化率操作。

（4）共凝胶法
与沉淀法类似，将两种溶液混合生成凝胶。如合成分子筛就是将水玻璃（硅酸钠）与铝酸钠的水溶液与浓氢氧化钠溶液混合，在一定的温度和强烈搅拌下生成凝胶，再静臵相当长时间使之晶化、然后过滤、水洗、干燥得到。得到的分子筛表面含有大量的正离子，部分是容易解离的，则可与过渡金属离子（镁离子、钙离子、锂离子）等进行交换，在硅酸盐表面形成具有高活性、高选择性的交换型分子筛，并有良好的抗毒性和耐热性。在炼油工业中用量很多。
法。均匀沉淀法是首先使待沉淀溶液与沉淀剂母体充分混合，形成十分均匀的体系，然后调节温度使沉淀剂母体加热分解转化为沉淀剂，从而使金属离子产生均匀沉淀，比如尿素。采用此方法得到的沉淀物，由于过饱和度在整个溶液中都比较均匀，所以，沉淀颗粒粗细较一致而且致密，便于过滤和沉淀。
沉淀法的影响因素
（3）沉淀法借助沉淀反应，用沉淀剂将可溶性的催化剂
组分转化为难溶化合物，再经分离、洗涤、干燥、焙烧、成型等工序制得成品催化剂。
沉淀法是制备固体催化剂最常用的方法之一，
广泛用于制备高含量的非贵金属、金属氧化物、金属盐催化剂或催化剂载体。
对于要求特别均匀的催化剂，可采用均匀沉淀

化学反应工程陈甘棠第五章第二节

二、催化剂颗粒中的扩散
1、孔扩散
1）催化剂中气体扩散的形式
分子扩散 λ/2ra≤10-2，分子间的碰撞
扩散
努森扩散 λ/2ra≥ 10-2，分子与孔壁的碰撞构型扩散孔半径(0.5-1.0nm)的微孔
表面扩散内表面上分子向表面浓度降低的方向移动
2024年10月20日星期日
2)分子扩散
对于反向的一维扩散，根据费克定律：
散模数φL
L L
kV
c
m1 S
De
式中：
颗粒体积 L 颗粒的扩散表面积
=
2024年10月20日星期日
片状，δ为催化剂厚度
2
R 圆柱状，R为圆柱的半径 2
R 球形颗粒 3
2 L
代表了表面反应速率与内扩散速率之比
对片、柱、球状催化剂等温物料衡算
1 ln
d dl
l n
dc rc
dl De
边界条件为：r 0 dc 0
dr
r R c cS
2024年10月20日星期日
定义：无因次内扩散模数φs（希尔模数）
S R
kV cSm1 De
——表征内扩散影响的重要参数
物理意义：
S2
kV cSm1R2 De
kV
cSm
R
2
4 3
R
De
cS
4 3
R
2024年10月20日星期日
3
输入
De
dc dr
4r
2
r r
输出
De
dc dr
4r
2
r
反应掉的量 rA 4r 2 r
kV C m 4r 2r
输入 - 输出-反应掉的量 0

《化学反应工程》第三版(陈甘堂著)课后习题答案

《化学反应工程》第三版(陈甘堂著)课后习题答案第二章均相反应动力学基础2－4三级气相反应2NO+O22NO2，在30℃及1kgf/cm2下反应，已知反应速率常数2kC=2.65×104L2/(mol2 s)，若以rA=kppApB表示，反应速率常数kp应为何值？解：原速率方程rA=dcA2cB=2.65×104cAdt由气体状态方程有cA=代入式（1）2－5考虑反应A课所以kp=2.65×104×(0.08477×303) 3=1.564后当压力单位为kgf/cm2时，R=0.08477，T=303K。

答p p 2rA=2.65×10 A B =2.65×104(RT) 3pApBRT RTp表示的动力学方程。

解：.因，wwnAp=A，微分得RTVdaw案24网pAp，cB=BRTRT3P，其动力学方程为( rA)=dnAn=kA。

试推导：在恒容下以总压VdtVδA=3 1=21dnA1dpA=VdtRTdt代入原动力学方程整理得wdpA=kpAdt设初始原料为纯A，yA0=1，总量为n0=nA0。

反应过程中总摩尔数根据膨胀因子定义δA=n n0nA0 nA若侵犯了您的版权利益，敬请来信通知我们！Y http://.cn.co（1）mol/[L s (kgf/cm2) 3]m（1）则nA=nA01(n n0)δA1(P P0)δA（2）恒容下上式可转换为pA=P0所以将式（2）和式（3）代入式（1）整理得2－6在700℃及3kgf/cm2恒压下发生下列反应：C4H10发生变化，试求下列各项的变化速率。

（1）乙烯分压；（2）H2的物质的量，mol；（3）丁烷的摩尔分数。

解：P=3kgf/cm2，（1）课MC4H10=58，（2）w.krC2H4=2( rC4H10)=2×2.4=4.8kgf/(cm2 s)PC4H10=PyC4H101 dpC4H10= P dt2.4-1==0.8 s 3w（3）nC4H10=nyC4H10=n0(1+δC4H10yC4H10,0xC4H10)yC4H10dnH2dtdnH2dt=hdaw后n0=nC4H10,0=δC4H10rC4H10=反应开始时，系统中含C4H*****kg，当反应完成50%时，丁烷分压以2.4kgf/(cm2 s)的速率dyC4H10dt答1rCH=2.4224wdnC4H10dt案116×1000=2000mol582+1 1==21网dyC4H10=n0(1+δC4H10yC4H10,0xC4H10) dt=2000×(1+2×1×0.5)×0.8=3200 mol/s若侵犯了您的版权利益，敬请来信通知我们！Y http://.cno2C2H4+H2，dP=k[(δA+1)P0 P]=k(3P0 P)dtm（3）dpA1dP= dtδAdt2－9反应APS，( r1)=k1cA , ( r2)=k2cp，已知t=0时，cA=cA0 ，cp0=cS0=0, k1/k2=0.2。

化学反应工程陈甘棠第一章-文档资料36页

Ca SCaO S2 O
硫酸生产
S O 212O2 S O 3
H2O H2SO 4
05.12.2019
低能耗制H2
1 Ca2B H r2O CaO2 H B r
2 CaO B r 2 Ca2Br12O2
700-7500c 500-6000c
3 3Fe2B 4H r2O F2O e46 H B r + H2
反应用于净化原料
银催化剂
CH2 CH2 CHCH
加氢 CH2 CH2 氧化
（微量） CH CH H2 H2CC2H H2
CHCH
O
H2C CH2
C H C H H 2O
O
用于能源过程
400c
Ca2C C l H 3OH 1400c
氯化钙·甲醇络合物
H
iC4 H8
1000c 阳离子树脂
OCCCH 3
H2 H
(MTBE)
硫酸
CH3
H2O+iC4H8
HO C C CH3
H2 H
(叔丁醇)
05.12.2019
b ：高纯硅生产
化学纯 Si
Si
光谱纯 Si
Si
SiF 4 (G ) SiF 4 (G )
SiSiF4 2SiF2
05.12.2019
三、反应工程的研究方法
1、模型化方法
参数计算式建立数学模型动力学方程式
物料、热量、动量衡算式求解数学模型的计算方法计算机软件的实现及计算结果
05.12.2019
2、试验的方法
设备传递过程模型的测定如：大型冷模测定
无法计算的参数的测定如：热力学、动力学、催化剂等的参数

陈甘棠主编化学反应工程

催化剂参与的反应称为催化反应。催化反应又分为均相催化和多相催化
反应在同一相中进行
反应在两相界面上进行
最常见的催化反应是使用固体催化剂的气、固相催化反应
固体催化剂的主要组成及基本制备方法
❖活性组分、助催化剂、载体 1.活性组分
活性组分的作用是催化作用，通常是金属或金属氧化物，例如铁、铜、铝及其氧化物。
dr
r 2 dr
De
rA
令z r , R
则dr Rdz,
dr2 R2dz2,
代入上式得
r Rz
d 2cA dz2
2 z
dcA dz
R2 De
rA
BC :
r
0, z
0, dcA dz
0
r R, z 1,cA cAS
时间t/s 0 120 240 360 480 600 720 840 960 1080
C(t)
0
t
tEtt Ett
tC(t)
0
C (t )
374.4s
0
t2
t
2 Et E t
-
t
2
30608 s2
• 解：a平推流在前，全混流在后 • 根据平推流反应器的设计方程
C A0
X A dX A 0 rA
CA0
XA
dX A
1
0 CA0（2 1 XA）2 1 XA
-1
CA2
可得 CA=0.618mol/L 由PFR设计方程
(6分)
- CA ' dCA 1 - 1 1
CA - rA CA ' CA
（8分）
CA=0.618mol/L代入可得CA’=0.382 故XA=0.618 因此，按此题的条件，平推流在前略好于全混流在前的情况。（10分

化学反应工程陈甘棠第五章第一节

微分反应器的优点 :
可以直接求出反应速率，催化剂用量少，转化率又低，容易做到等温，但分析精度对应的要高的多。
*
STEP4
STEP3
STEP2
STEP1
催化剂回转式反应器：
把催化剂夹在框架中快速回转,从而排除外扩散的影响和达到气相完全混合及反应器等温的目的。使全混流式数据的计算和处理较方便。
G
适用于：
图中
*
减小化剂颗粒的直径，可消除内扩散得影响。在恒定的质量流速下，当dp<dp*时，无内扩散的影响。
rA
dp
dp*
2)实验用反应器
实验时改变流量，测定转化率，作图可得代表反应速率的等温线。
积分反应器:
①固定床积分反应器和微分反应器
指一次通过后转化率较大(xA>25%)的情况
宏观速率 :
整个反应过程的速率
排除内外扩散影响的速率
本征动力学：
反应速率
2、吸附与脱附
1）兰格缪尔模型Langmuir型
假定：
① 催化剂表面各处的吸附能力是均一的，即均匀表面 ② 被吸附分子间的作用力可略去不计（无作用力） ③ 单分子吸附 ④ 吸附的机理均相同。
A
B
C
脱附速率为：
当吸附达到平衡时：
则：
余各其步都达到了平衡状态
控制步骤
*
令：
iii）脱附控制
若
01.
为控制步骤
02.
其余各步都达到了平衡状态
03.
*
令：
令
2）幂数型的反应速率式
控制步骤
合成氨的机理模型
01
由焦姆金德吸附等温式可知：

化学反应工程陈甘棠第五章第一节精品文档38页

05.04.2020
令：
kk1KAKB ——反应的正反应速率常数
KP
k1KAKB k2KRKS
——反应的化学平衡常数
AKAPAK kB P PB AP BK SP P K R SP P SK RPR12
05.04.2020
ii）吸附控制
A A 控制步骤
则：
AkAP a AVkAd A
余各其步都达到了平衡状态
AkRd RkRP a RV
其余各步都达到了平衡状态
AKAPAV B KBPBV
S KSPSV
R S A B
Kr
05.04.2020
R
Kr
AB S
KrKAKB KS
PPAPSBV
令：
Kr KAKB KS
KAB
AkRK dAB P P AP SB VkRP aRV
A B R S V 1
i
1
1 Ki Pi
（无解离时）
i
当被吸附的分子发生解离现象时
ka
A2 22A kd
吸附速率和脱附速率分别为：
akapA(1A)2
d kdA
吸附平衡时： a d
A
1
K A PA K A PA
05.04.2020
2）Freundlich 弗列得利希模型（经验型）
吸附速率： a kapAA
脱附速率： d kdA
Ak1 A Bk2 R S
其余步骤认为达到了平衡
kaP AAVkdAA0
AKAPAV
同理：
05.04.2020
B KBPBV R KRPRV S KSPSV
代入：
A k 1 K A P A K B P B V 2 k 2 K R P R K S P SV 2

化学反应工程陈甘棠答案

化学反应工程陈甘棠答案化学反应工程陈甘棠答案【篇一：反应工程第五章习题答案】xt>5.1乙炔与氯化氢在hgcl2-活性炭催化剂上合成氯乙烯的反应c2h2?hcl?c2h3cl (a)(b) (c)其动力学方程式可有如下种种形式：(1) r??(papb?pc/k)/(1?kapa?kbpb?kcpc) (2)r??kakbpapb/(1?kbpb?kcpc)(1?kapa) (3)r??kapapb/(1?kapa?kbpb)(4) r??kbpapb/(1?kbpb?kcpc)2试说明各式所代表的反应机理和控制步骤。

解：（1）aa?bb?a??b??c （控制步骤）c??c??（2）a??1?a?1b??2?b?2a?1?b?2?c?2??1（控制步骤）c?1?c??1（3）aa?bb?a??b?c?? （控制步骤）（4）bb?a?b??c? （控制步骤）c??c??5.2 在pd-al2o3催化剂上用乙烯合成醋酸乙烯的反应为c2h4?ch3cooh?12实验测得的初速率数据如下[功刀等，化工志，71，2007（1968）.] 115℃, pacoh?200mmhg，po?92mmhg。

2pc2h4(mmhg)r0?10(mol/hr?g催化剂)570 100 195 247 315 4653.94.4 6.0 6.6 7.255.4注：1mmhg=133.322pa如反应机理设想为acohacoh?c2h4c2h4?acoh?c2h4?hc2h4oaco2?2??2o?hc2h4oac??o??c2h3oac??h2o? (控制步骤)c2h3oac??c2h3oac??h2o? ?h2o+?试写出反应速率并检验上述部分数据能与之符合否。

解：c2h4?ch3cooh?12o2?ch2cooc2h3?h2o（a）（b）（c）（e）（f）?a?kapa?v?b?kbpb?v?c?v?f?kfpf?v ?d?ks1kakbpapb?v ?e?kep?ev?v??k2?k3par?ks2?d?c??k1pa(k2?k3pa)2r0??pa(k2?k3pa)2pc2h4(mmhg)70 100 195 247 315 465r0?10(mol/hr?g催化剂)53.94.4 6.0 6.6 7.255.41.3410?31.51 1.80 1.932.08 2.93pa作图，基本上为一直线。

化学反应工程Aspen Plus计算示例

化学反应工程三级项目学院：环境与化学工程学院专业：化工工艺**姓名：***学号： ************ **教师：***I化学反应工程三级项目任务书说明：如计算机输入，表题黑体小三号字，内容五号字。

II一、反应器选型Aspen Plus根据不同的反应器形式，提供了三大类七种不同的反应器模块。

1.生产能力类反应器：1.1化学计量反应器：按照化学反应方程式中的计量关系进行反应，有并行反应和串联反应两种方式，分别指定每一反应的转化率或产量。

用途：已知化学反应方程式和每一反应的转化率或产量，不知化学动力学关系。

1.2产率反应器：根据每一种产与输入物流间的产率关系进行反应，只考虑总质量平衡，不考虑元素平衡。

用途：只知化学反应式和各产物间的相对产率，不知化学计量关系。

2.热力学平衡类反应器：2.1平衡反应器：根据化学反应方程式进行反应，按照化学平衡关系式达到化学平衡，并同时达到相平衡。

用途：已知反应历程和平衡反应的反应方程式，不考虑动力学可行性，计算同时达到化学平衡和相平衡的结果。

2.2吉布斯反应器：根据系统的Gibbs自由能趋于最小值的原则，计算同时达到化学平衡和相平衡时的系统组成和相分布。

用途：已知化学反应式，不知道反应历程和动力学可行性，估算可能达到的化学平衡和相平衡结果。

3.化学动力学类反应器：3.1全混釜反应器：釜内达到理想混合。

可模拟单、两、三相的体系，并可处理固体。

可同时处理动力学控制和平衡控制两类反应。

用途：已知化学反应式、动力学方程和平衡关系，计算所需的反应器体积和反应时间，以及反应器热负荷。

3.2平推流反应器：反应器内完全没有返混。

可模拟单、两、三相的体系。

只能处理动力学控制反应。

可模拟换热夹套。

用途：已知化学反应式和动力学方程，计算所能达到的转化率，或所需的反应器体积，以及反应器热负荷。

3.3间歇釜反应器：间歇或半间歇操作的搅拌釜，釜内达到理想混合。

自动根据加料和辅助时间提供缓冲罐，实现与连续过程的连接。

化学反应工程第三版陈甘棠课后习题答案

化学反应工程第三版陈甘棠课后习题答案【篇一：化学反应工程教案4(化工13)-胡江良】t>12345【篇二：化学反应工程教案】程名称：化学反应工程任课教师：所属院部：教学班级：教学时间：化工1203-04 2014 —2015 学年第2学期课程基本信息1绪论第一章均相单一反应动力学和理想反应器1.1 基本概念1.2 建立动力学方程的方法一、本次课主要内容化学反应工程课程的性质、反应器的分类及操作方式、反应器设计的基本方程和工业反应器的放大方法、化学反应速率的不同表示方式及其相互关系、化学反应速率方程的变换与应用、化学反应动力学方程的计算、建立动力学方程的方法及其应用。

二、教学目的与要求了解化学反应工程的研究对象、目的，掌握化学反应工程的研究内容和研究方法，熟悉化学反应工程在工业反应过程开发中的作用。

三、教学重点难点1、化学反应工程的研究目的、内容和方法。

四、教学方法和手段课堂讲授、提问、讨论；使用多媒体教学方式。

五、作业与习题布置书后习题第3、6、7题2绪论一、化工生产中设备的分类化工产品的生产是通过一定的工艺过程实现的，工艺过程是指从原料到制得产品的全过程。

每个化工产品的工艺过程是不同的，但有共同的特点：1，工艺过程是由设备、管道、阀门和控制仪表组成的；2，化工设备分为两大类（1）不含化学反应的设备这类设备中没有发生化学反应，只改变物料的状态，物理性质，不改变其化学性质。

在鼓风机和泵中只有能量的转换，从中能转换成机械能，输送物料；在换热器和冷却塔中只改变物料的温度，物料的化学性质没有起变化；贮槽只是起贮存物料作用（2）化学反应器在这类设备中发生了化学反应，通过化学反应改变了物料的化学性质图中的一段炉、二段炉、变换炉、甲烷化炉、合成塔等都是化学反应器。

物料在反应器中发生了化学反应，物料性质起了变化。

可见，化学工业生产是由物理过程和化学反应过程组成的，其中化学反应过程是生产过程的关键。

化学反应器的任务是完成由原料转变到产物的化学反应，是化工生产的核心设备。

化学反应工程陈甘棠第五章第二节精品

T cm2 Ms
2019年8月17日星期六
4）分子扩散与努森扩散同时存在
努森：
NA

DK
P RT
dyA dl
1
dyA N A RT
dl 1
DK P
分子:
NA

DAB
P RT

dy A dl
2

yA N A

NB

dyA P N A yA N A N B
当 L 较大时，
1 L
选择性
1
s rB
rA
k1 k2 2 1 1 k1 k2 2
k2
1
k1 2
cBg c Ag
2019年8月17日星期六
而无内扩散时：
1
s
1
k2
k1
2

cBg c Ag
也需降低外扩散阻力
即内扩散的存在使反应的选择性下降
针对这种内扩散阻力大而B的选择性又低的情况，改进的方法是制造孔径较大的催化剂和使用细粒子的催化剂。
假设内扩散阻力很大， L 3
则： 1 , L
0
1
L
SA

RL AL

k1c Ag k2cRg

k2 DAe k1cAg k1DRe k2cRg
k1 cAg k2 cRg
2019年8月17日星期六
无内扩散影响时：
sA

k1c Ag k2cRg
一般 k1 k2 比较两式知，内扩散存在使反应的选择性降低
2 dT r dr

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

三、流化床反应器的重要应用
石油催化裂化丙烯-氨氧化制丙烯腈萘氧化制邻苯二甲酸酐
煤燃烧与转化金属提取和加工
7.2 流化床中的气、固运动
7.2.1 流化床的流体力学二个特征速度：临界流化速度、带出速度（1）临界流化速度（umf）刚刚能使粒子流化起来的气体空床流速。确定umf的方法 a. 实验测定
c (1 mf )
Vc Vw Vb
（7-49）
因为气泡晕中的情况与乳相相同，即相当于临界流化状态，将式（7-40）关系引入，可导得：
3umf / mf Vw c (1 mf ) 1/ 2 ( gdb ) umf / mf Vb 0.711
由带出速度的校正系数图，查得F0=1，故不需校正。
7.2.2 气泡及其行为流化床层由固体颗粒密集区域（乳化相）和固体颗粒很少
的区域（气泡相）组成，气泡的结构和行为是分析流化床特性
和建立数学模型的基础。（1）气泡的结构气泡
{ 气泡晕
气泡云
（气泡云+尾涡）
气泡晕中粒子浓度与乳化相相同，包在气泡周围，伴随着气泡一起上升。（2）气泡的速度气泡上升速度是影响气泡相与乳化相之间传质和传热的重要因素。根据不同
3 2
(二维床）
（7-39）
(三维床）
（7-40）
式中， u f umf / mf 为乳相中真实气速。注意：气泡云的实际厚度为RC－Rb。（ii）气泡中气体的穿流量
q 4umf Rb 4u f mf Rb
2 q 3umf Rb2 3u f mf Rb
(二维床）
（v）气泡占床层的体积分率假设：进入床层的气流分为两个部分，一部分是以ub流动的气泡，另一部分则以umf在乳相中流动。床层达到临界流态化以后，床层高度增加的部分完全是气泡所作的贡献。对气流进行物料衡算（7-45）
u0 ubb umf (1 b ab )
故或
（7-46）（7-47）
（ii）细颗粒床层中，气体操作流速的范围更宽。（iii）实用操作气速的确定 a. 流化数 b.
u0 1.5 ~ 10 umf
u0 0.1 ~ 0.4 ut
（3）流化床的膨胀比流化床的体积与起始流化时床层体积之比。
R Lf Lmf
mf 1 f f
1 mf
（7-20）
图 7-14 分布器的若干形式
（2）设计或选择分布板的基本要求气体分布均匀，防止积料，结构简单，材料节省，压降合理。
35cmH2O pd 10% ~ 20%pB
二、内部构件（1）种类垂直管、水平管、多孔板、水平挡网、斜片百叶窗挡板，等。（2）作用传热，控制气泡聚并，改变气-固相流动和接触状况，减少颗粒带出。
0.36
（7-61）
该式是由大量实验数据关联得到的，适用面较广，误差小于 ±50%。
（ii）关联图计算

(hwd p / ) /[(1 f )c ps p /(c p )]
1 7.5 exp[0.44( Lh / dt )(c p / c ps )
p
W Lmf (1 mf )( p ) g At
（7-1）
b. 经验关联式计算临界流态化时，对床层受力平衡分析得
p W Lmf (1 mf )( p ) g At p (1 mf )( p ) g Lmf
2
p2
Vmf (1 ) g
d pumf

3 d p ( p )g 2 33.7 0.0408 2
1/ 2
33.7
（7-6）
小颗粒，ReP<20时，欧根公式中第一项可忽略，式（7-2）简化为：
umf
2 dP ( p )g
1650
（7-7）
大颗粒，ReP>1000时，欧根公式中第二项可忽略，式（7-2）简化为： d p ( p ) g 2 （7-8） umf 24.5 应用以上各式计算时要注意：
子沉降会互相干扰，按单个粒子计
算的带出速度需校正。
ut校正 F0 ut
式中，校正系数F0可由右图查取。
讨论：流化床的操作气速（i）流化床中，气体操作流速的下限是umf，上限是ut。小颗粒大颗粒
ut 式（7 14 ） 91.6 umf 式（7 7）
ut 式（7 16 ） 8.72 umf 式（7 8）
流化床反应器
7.1 概述
流态化：固体粒子像流体一样进行流动的现象。
一、流态化的形式
气泡
图 7-1 流态化的各种形式
二、流化床反应器的特点
结构简单传热效能高，床层温度均匀
气固相间传质速率较高
催化剂粒子小，效能高有助于催化剂循环再生催化剂和设备磨损大
气流不均时气固相接触效率降低
返混大，影响产品质量均一性
整理得
（7-2）
mf 是临式中， S 是颗粒的形状系数，部分颗粒的 S 值可由手册查取。
界空隙率，其值与颗粒直径和形状等有关，也可由手册查取。若查不
到，可由以下二式估算。
1

3 S mf
14 ,
1 mf

2 S
3 mf
11
（7-5）
式（7-5）代入式（7-2）可导出
a. 对具有一定筛分的颗粒要用调和平均直径。
dp 1 xi / d pi
式中, xi——颗粒各筛分的重量百分数； dPi——颗粒各筛分的平均直径；
dPi d1 d2 或 dPi (d1 d2 ) / 2
d1，d2 ——上、下筛目的尺寸。 b. 雷诺数中特性尺寸是颗粒的直径，密度和粘度是气体的物性。 d Pumf ρ Re P μ c.计算所得到的 u mf 要代入到雷诺数中，检验选用的公式是否符合规
（7-41）（7-42）
(三维床）
（iii）尾涡的体积分率
Vw aw fw Vw Vb aw 1
式中，
（7-43）
aw Vw / Vb
由图7-11可见，fw与颗粒的粒径、形状等因素有关。
图 7-11 尾涡体积与粒径的关系
（iv）气泡云、气泡晕与气泡的体积比
ac Vc / Vb a (Vc Vw ) / Vb ac aw
流区域。
向上流区域：以umf速度向上流动的气体；回流区域：被大于umf速度向下回流的颗粒所吸附和裹夹的气体。
定常态操作时床层截面上平均上流与回流量大致恒定。当气速增
大时，回流量相应增大。当流化数u0/umf>6~11时，乳化相中气体回流量将超过上流量，净流量成为向下流动的了。
7.2.4 分布板与内部构件一、分布板（1）分布板的类型
b
u0 umf ub umf (1 a)
b
L f Lmf Lf

u0 umf ub
（4）床层中各部分的颗粒含量与气泡体积之比（i）气泡中的颗粒含量
b
全部气泡中颗粒的体积全部气泡的总体积
（7-48）
b 0.001~ 0.01, 通常可忽略。
（ii）气泡晕中的颗粒含量
定的范围。
（2）带出速度当气速增大到一定值时，流体对粒子的曳力与粒子的重力相等，则粒子将会被气流带走，此时气体的空床速度即带出速度，或称终端速度。颗粒的带出速度等于其自由沉降速度，对球形固体颗粒，可用以下公式计算：
ut
2 dp ( p ) g
18
2 2 1 3
Rep 0.4
（iii）乳相中的颗粒含量
（7-50）
e
(1 f )
b
c b
(1 mf )(1 b )
b
c b
（7-51）
7.2.3 乳相的动态乳相是指床层中气泡相之外的区域。该区域内颗粒密集，是发生化学反应的主要场所。（1）床层中颗粒的流动在上升气泡作用下，乳相中的颗粒形成上下循环和杂乱无章的随机运动。这种运动促使颗粒快速混合均匀。注意：颗粒运动规律与床层结构有关。浅床层：中心下降，外围上升。深床层：中心上升，外围下降。
hw d P c 0.16 P
0.4

d P u0
0.76
cPS p c P
0.4
u gd P
2 0
0.2
u0 umf Lmf u Lf 0
在按装挡板或挡网等内部构件的床
层中，颗粒的自由运动受到阻碍，其行程变得更加复杂。
图7-12 颗粒运动示意图
（2）粒度及粒度分布的影响根据颗粒粒度大小对床层流化性的能影响，将颗粒分为4类。 A类：细颗粒，粒度范围20~100μm。 B类：较粗颗粒，粒度范围40~500μm。 C类：易黏结颗粒，粒度范围<30μm。 D类：粗颗粒，粒度范围>600μm。
（7-29）
事实上床层内气泡大小是不均匀的，且是不断长大的，有人提出一些不同的经验式。由于气泡行为的复杂性，现有的经验公式都存在一定的局限性。
cHale Waihona Puke 气泡中气体的穿流量q 3umf Rb2
式中，Rb——气泡半径，cm。
cm3 / s
（3）气泡云与尾涡（i）气泡云相对厚度
RC R b RC R b ubr u f u u br f ubr 2u f u u br f
7.3 流化床中的传递过程
7.3.1 床层与外壁间的传热床层内传热主要包括：固体颗粒之间、颗粒与流体之间、床层与换热面之间的传热。因床内温度均一，前二项可忽略。