内切球和外接球常见解法讲课稿
- 格式：doc
- 大小：173.50 KB
- 文档页数：6
下载文档原格式
合集下载
内切球和外接球问题课件
• 结论1：正方体或长方体的外接球的球心其体对角 线的中点。
• 结论2：正棱柱的外接球的球心是上下底面中心的 连线的中点。
• 结论3：直三棱柱的外接球的球心是上下底面三角 形外心的连线的中点。
• 结论4：正棱锥的外接球的球心在其高上，具体位 置可通过计算找到。
• 结论5：若棱锥的顶点可构成共斜边的直角三角形， 则公共斜边的中点就是其外接球的球心。
正方体的内切球
例1
将棱长为2的正方体木块削成一个体积最 大的球，则这个球的表面积为 4
直棱柱的外接球
例2
已已知知直直三三棱棱柱柱AABBCCA1AB11BC11C的1的六六个个顶顶点点都在都在 球球OO的的球球面面上上,,若若AABBBCBC 1,1,ABACBC12012,0, AAAA11 22 33，，则则球球OO的的表表面面积积为为
几何体外接：一个几何体所有顶点都 在另一个几何体表面上。
正方体的内切球、棱切球、外接球
• 三、几何体的外接球与内切球问题：
• 1、外接球的问题： • 几何体外接球问题是立体几何中的难点和重要的
考点，此类问题实质是解决球的半径或确定球心0 的位置问题，其中球心的确定是关键。 • (1)由球的定义确定球心 • 在空间，如果一个定点与一个简单多面体的所有 顶点的距离都相等，那么这个定点就是该简单多 面体的外接球的球心。 • 由上述性质，可以得到确定简单多面体外接球的 球心的如下结论。
• 途径3：若已知棱锥含有线面垂直关系，则可将棱锥补成 长方体或正方体．
• 途径4：若三棱锥的三个侧面两两垂直，则可将三棱锥补 成长方体或正方体．
(3)由性质确定球心 利用球心与截面圆圆心的连线垂直于截面圆及球心与弦 中点的连线垂直于弦的性质，确定球心． 内切球的问题 对内切球有以下几点认识： 1、内切球球心到多面体各面的距离均相等，外接球球 心到多面体各顶点的距离均相等。 2、正多面体的内切球和外接球的球心重合。 3、正棱锥的内切球和外接球球心都在高线上，但不重 合。 4、基本方法：构造三角形利用相似比和勾股定理。 5、体积分割是求内切球半径的通用做法。
球的内切和外接问题课件
内切与外接问题的解题思路与方法
01
认真审题，明确题目中 的已知条件和所求目标 。
02
分析几何体的结构特征 ，确定内切或外接关系 。
03
合理利用内切或外接的 性质和定理，建立方程 或不等式求解。
04
对于复杂问题，可以采 用数形结合、分类讨论 等数学思想方法。
05
典型例题解析
简单几何体的内切与外接问题
判断一个球是否是多面体的内切球。
利用内切球的性质解决一些与多面体相关的问题，如求解多面体的体积、表面积等 。
外接球的定义与性质
定义
外接球是指一个球完全包含一个多面体，且与多面体的各个 顶点都相切。
性质
外接球的半径等于多面体外接圆半径，也等于从多面体中心 到任意一个顶点的距离。
外接球的计算方法
直接法
，也希望教师能够增加一些互动环节，提高课堂的趣味性。
对未来学习的建议与展望
加强基础知识的巩固
建议学生在课后加强对基础知识的学习和巩固，为后续的学习打下 坚实的基础。
增加实践环节
希望教师能够增加一些实践环节，如小组讨论、案例分析等，帮助 学生更好地应用所学知识解决实际问题。
拓展相关领域的学习
鼓励学生拓展相关领域的学习，如学习其他几何体的内切与外接问题 、了解相关数学史等，以拓宽视野并加深对课程内容的理解。
性质
内切球的半径等于多面体的内切圆半 径，也等于多面体各个面上的内切圆 半径的最小值。
内切球的计算方法
直接法
通过已知条件直接求出内切球的半径。
间接法
利用体积关系求出内切球的半径。对于棱锥、棱柱等多面体，可以先求出其体 积和表面积，再利用体积和表面积的关系求出内切球的半径。
高考数学一轮复习第六章专题六几何体的外接球与内切球问题课件
)
A.4 3π
B.8π
C.12π
D.20π
解析：在底面△ABC 中，由正弦定理得底面△ABC 外接圆的
半径为
r＝2sin B∠CBAC＝2sin2
3π＝ 4
2.
直三棱柱 ABC-A1B1C1 的外接球的半径 R＝ ( 2)2＋12＝ 3，
r2＋A2A12＝
则直三棱柱 ABC-A1B1C1 的外接球的体积为43πR3＝4 3π.
当
λ＝12时，cos〈E→B，E→G〉＝2
3
2 .
∴cos〈E→B，E→G〉的最大值为2
3
2 .
∵A→C＝(－1，1，0)，A→F＝(0，1，1)， ∴E→B·A→C＝E→B·A→F＝0. ∴EB⊥AC，EB⊥AF. ∵AC∩AF＝A，∴EB⊥平面 AFC. ∵E→B·E→G>0，∴cos〈E→B，E→G〉即为 EG 与平面 AFC 所成角
如图 6-7 所示，把四面体 S-ABC 补全为长方体 ABCD-SPMN， 其中 SA，AB，BC 为长方体中首尾相连且两两相互垂直的三条棱， 点 H 为 PM 中点.
图 6-7
∵GH∥AP，∴G，H 两点到平面 AEF 的距离相等.
设点 H 到平面 AEF 的距离为 d.
∵△APF 是边长为 2 2的等边三角形，
[例 1]已知一个圆锥底面半径为 1，母线长为 3，则该圆锥内
切球的表面积为( )
A.π
B.32π
C.2π
D.3π
解析：依题意，作出圆锥与球的轴截面，如图
6-1 所示.设球的半径为 r，易知轴截面三角形边 AB
上的高为 2 2，因为△SOD∽△SBE，所以SSOB＝OBED，
即2 32－r＝1r，解得 r＝ 22.所以圆锥内切球的表面
外接球与内切球讲义
A. 4π
B. 12π
C. 16π
D.
32 3
π
·8· 惊叹数学的波澜壮阔之势 赏析数学的对称和谐之美！
领悟数学的高瞻远瞩之能 铸就数学的茅塞顿开之境！
学习数学 领悟数学 满分数学
7. (2021• 咸阳模拟 ) 在直三棱柱 ABC
- A1B1C1 中，AB = BC = 2，∠ABC =
π 2
，若该直三棱柱的外接球表面积
棱锥体积的最大值为
3
3 4
，则其外接球的半径为
(
)
A. 1
B. 2
C. 3
D.
2 3
3 ，AC = 3，若该三
考点四 含二面角的外接球终极公式
双距离单交线公式：R2 =
m2 + n2 − 2mncosα sin2α
+
l2 4
如下图，若空间四边形 ABCD 中，二面角 C − AB − D 的平面角大小为 α，ABD 的外接球球心为 O1，ABC 的外
为 16π，则此直三棱柱的高为（ ）
A. 4
B. 3
C. 4 2
D. 2 2
图1
图2
8. (2021• 呼和浩特一模 ) 四面体 ABCD 的四个顶点都在球 O 上，且 AB = AC = BC = BD = CD = 4，AD =
2 6 ，则球 O 的表面积为（ ）
A.
70π 3
B.
80π 3
C. 30π
接球球心为 O2，E 为公共弦 AB 中点，则 ∠O1EO2 = α，O1E = m，O2E = n，AE =
l 2
，OA = R，由于 O、O1、E、O2
四点共球，且 OE = 2R =
球的内切与外接问题讲课
综合应用举例
例1
解
已知一个三角形的三边长度，求其内切圆 半径和外接圆半径。
首先利用海伦公式求出三角形面积，再结 合半周长计算内切圆半径。对于外接圆半 径，可以通过正弦定理或余弦定理求解。
例2
解
给定一个正多边形，求其内切圆与外接圆 的半径比。
根据正多边形的性质，其所有内角相等， 且每条边与内切圆相切。由此可推导出内 切圆半径与外接圆半径的比例关系。
体对角线的长度来求解外接球的半径。
解答
03
长方体的体对角线长为$sqrt{3^2 + 4^2 + 5^2} = sqrt{50} =
5sqrt{2}$，因此其外接球的半径为$frac{5sqrt{2}}{2}$。
典型例题分析与解答
例题2
分析
已知一个正四面体的棱长为$a$，求其 外接球的半径。
正四面体的外接球半径可以通过构造 一个包含该正四面体的正方体来求解 。
长方体的内切球半径等于长方体相邻三条棱的倒数之和的倒数的一半，即 r=1/[(1/l)+(1/w)+(1/h)]。
解答
根据内切球的定义和性质，我们知道长方体的内切球半径等于长方体相邻三条棱的倒数之 和的倒数的一半。所以，r=1/[(1/l)+(1/w)+(1/h)]。
典型例题分析与解答
例题3
分析
解答
解答
构造一个棱长为$frac{sqrt{2}}{2}a$的 正方体，则该正方体的体对角线长等 于正四面体的外接球直径，即$2R = sqrt{(frac{sqrt{2}}{2}a)^2 + (frac{sqrt{2}}{2}a)^2 + (frac{sqrt{2}}{2}a)^2} = frac{sqrt{6}}{2}a$，因此正四面体的 外接球半径为$frac{sqrt{6}}{4}a$。
内切球和外接球常见解法讲课稿
内切与外接1 球与柱体1.1 球与正方体例 1 棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上，E F ，分别是棱1AA ，1DD 的中点，则直线EF 被球O 截得的线段长为（ ）A ．22B ．1C ．212+D 21.2 球与长方体长方体各顶点可在一个球面上，故长方体存在外切球.但是不一定存在内切球.设长方体的棱长为,,,a b c 其体对角线为l .当球为长方体的外接球时，截面图为长方体的对角面和其外接圆，和正方体的外接球的道理是一样的，故球的半径2222l a b c R ++== 例 2 在长、宽、高分别为2，2，4的长方体内有一个半径为1的球，任意摆动此长方体，则球经过的空间部分的体积为( )A.10π3B.4πC.8π3D.7π31.3 球与正棱柱例3 正四棱柱1111ABCD A B C D -的各顶点都在半径为R 的球面上，则正四棱柱的侧面积有最 值，为 .2 球与锥体 规则的锥体，如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合，以外接和内切两种形态进行结合，通过球的半径和棱锥的棱和高产生联系，然后考查几何体的体积或者表面积等相关问题.2.1 球与正四面体2222233a R r a R r CE +=-=，=，解得：66,.R r ==例4 将半径都为１的四个钢球完全装入形状为正四面体的容器里，这个正四面体的高的最 小值为 ( ) A.3263+ B. 2+263 C. 4+263 D. 43263+2.2 球与三条侧棱互相垂直的三棱锥例5 在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且AM MN ⊥,若侧棱 23SA =,则正三棱锥S-ABC 外接球的表面积是______2.3 球与正棱锥球与正棱锥的组合，常见的有两类，一是球为三棱锥的外接球，此时三棱锥的各个顶点在球面上，根据截面图的特点，可以构造直角三角形进行求解.二是球为正棱锥的内切球，例如正三棱锥的内切球，球与正三棱锥四个面相切，球心到四个面的距离相等，都为球半径R ．这样求球的半径可转化为球球心到三棱锥面的距离，故可采用等体积法解决，即四个小三棱锥的体积和为正三棱锥的体积.例6 在三棱锥P －ABC 中，PA ＝3侧棱PA 与底面ABC 所成的角为60°，则该三棱锥外接球的体积为（ ）A ．π B.3π C. 4π D.43π 接球的球心,则2SC R =. 例7 矩形ABCD 中，4,3,AB BC ==沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积是( )A.π12125B.π9125C.π6125D.π3125 3 球与球对多个小球结合在一起，组合成复杂的几何体问题，要求有丰富的空间想象能力，解决本类问题需掌握恰当的处理手段，如准确确定各个小球的球心的位置关系，或者巧借截面图等方法，将空间问题转化平面问题求解.例7 在半径为R 的球内放入大小相等的4个小球，则小球半径r 的最大值为（ ）4 球与几何体的各条棱相切球与几何体的各条棱相切问题，关键要抓住棱与球相切的几何性质，达到明确球心的位 置为目的，然后通过构造直角三角形进行转换和求解.例：与正四面体各棱都相切的球的半径为棱的一半：.例8 把一个皮球放入如图10所示的由8根长均为20 cm 的铁丝接成的四篇一：程序员实习总结范文以前在校很少自己做程序,对软件工程更是一无所知.来到公司,开始接触大规模(其实现在看来实习的项目其实还是很小的)软件开发,一时真的有些迷茫.比起VSS,MVC,QA,CMMI,我对JAVA,JSP,XML的一窍不通根本不值一提.大家都不想输在起点,所以都默契地在加班,这样一直持续了实习的两个月.刚来的时候始业教育显得慢吞吞,我们还经常盘算去哪哪玩之类的.我和FLYSKY(20个新生里唯一一个南区的兄弟,软件学院的)还经常出去吃各种小吃,每到一处都尝尝本地的风味,这是他的习惯.之后开始的培训还不是很难过,JAVA,C++,ORACLE,老师们讲的很好,可以说是非常好,好得我们没有几个人能听懂.大家开始发愁,我也是每天晚上都基本看书到10点.我心说得亏哥们我还练过,来之前的2月份我就自己买了一本THINKING IN JAVA,看懂看不懂怎么说也算是准备了一下JAVA.C++虽说没去上过课,但凭我的直觉我就一下看中这东西很有用,自己也看过一阵.至于ORACLE,虽然不了解,但毕竟因为佩服云飞扬的性格和敬业精神,咱SQL选修也不是白混的.专业倒还有点基础,再加上咱这自学能力也不是吹的,基本维持.可等到后来的日语课就全迷糊了:本就没有语言天赋,再加上记忆严重欠缺,总是特别害怕去上日语课.不过特别喜欢那个老师说话的感觉,加上她一直对我都很好,所以还是很用心的学着.随着培训的收尾,我们开始正式进入项目.从需求分析,概要设计到详细设计,我们一步一步的开始接触软件开发的每个细节.最受不了的就是每天都要记周报,填写自己的劳动成果.因为这个我还被QA通报了好几次呢,真的很郁闷.其实现在我很感谢这种制度化的东西,某些情况下好习惯的养成是要靠强制来确保的.详细设计之后就是企盼已久的编码,我心想终于可以做点正事了.现在回头一看才知道,其实编码只占软件开发的整个过程劳动量的1/4左右,而且其他的环节也不是想象中的那么无足轻重.编码我其实做的很不好,主要是因为需求分析阶段就没有认真仔细的理解需求和规格说明,加上编码时一个关键时段我回校和老同学叙旧.那阵项目经理(PM)就经常和我们说,有问题自己想办法,不要经常问我.PM其实是在叫我们自己酝酿,遇到难题只有憋一憋才能有真的收获.而我不在的那三天正好是大家技术/思路上的一个跃迁,很多难题的解决方法都基本成熟,大家的编码也接近50%了,所以回来时我感觉已经掉队很多.再一个就是编码中期时机器出问题,环境搭不上了,这使我更加紧张和急躁,大大影响了我的士气.后来利用五一其间的加班我终于赶完了自己的模块,达到了第一个里程碑.其实从发现落后到加班赶完这段经历,对我来说也具有里程碑的意义.不仅考验了我自己的能力和心理素质,也证明了我对集体的责任感和合作意识.我可以叫别人来帮我做赶上进度,但那样我会错过自己学习的机会,以后再遇到难题我还是不行;我也可以硬着头皮导致项目延期,那样我以后的日子保证不好过,而且这么做也不符合我的性格.事实证明我顶住压力独立完成任务不管是对集体还是对我个人都是一件大好事.紧张的编码之后是单体测试,很多人都在继续编码,原来大家的编码都是没有完全做完.本是自己给自己挑毛病的过程,我们却都用来完成之前没有完成的任务,说来不禁可笑.。
外接球、内切球模型总结专题课件-高三数学二轮复习备考课件
∴正三棱锥 − 的三条侧棱两两互相垂直
把三棱锥补形为正方体，则正方体外接球即为三棱锥的外接球
其直径为 =
=
1
2 + 2 + 2 + 2 + 2 + 2
2
=
1
2 + 2 + 2 =
2
1
2 + 2 + 2
半径为
6
2
4
球 = ×
找三条两两垂直的线段，直接用公式 2
即2 = 2 + 2 + 2 ，求出
2
= 2 + 2 + 2 ，
例1 （1）已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的
表面积是( C )
B. 20
A.16
C. 24
D. 32
= 2 ℎ = 16
则该四面体的外接球的表面积为( D )
A. 11
B. 7
1
C.
10
3
D.
40
3
在
��
2 = 2 + 2 − 2 ⋅ ⋅ cos120∘
=7
= 7
中
的外接球直径为
7 2 7
=
2 =
=
sin∠
3
3
2
∵ ⊥平面 ∴ ⊥ ∴ ∆是直角三角形
是这个球的外切多面体，这个球是这个多面体的内切球.
把三棱锥补形为正方体，则正方体外接球即为三棱锥的外接球
其直径为 =
=
1
2 + 2 + 2 + 2 + 2 + 2
2
=
1
2 + 2 + 2 =
2
1
2 + 2 + 2
半径为
6
2
4
球 = ×
找三条两两垂直的线段，直接用公式 2
即2 = 2 + 2 + 2 ，求出
2
= 2 + 2 + 2 ，
例1 （1）已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的
表面积是( C )
B. 20
A.16
C. 24
D. 32
= 2 ℎ = 16
则该四面体的外接球的表面积为( D )
A. 11
B. 7
1
C.
10
3
D.
40
3
在
��
2 = 2 + 2 − 2 ⋅ ⋅ cos120∘
=7
= 7
中
的外接球直径为
7 2 7
=
2 =
=
sin∠
3
3
2
∵ ⊥平面 ∴ ⊥ ∴ ∆是直角三角形
是这个球的外切多面体，这个球是这个多面体的内切球.
正四面体内切球和外接球(好用).ppt.ppt
A
[题组冲关] 3．假如某爱国实业家在20世纪初需要了解全国各地商业信
息，可采用的最快捷的方式是
(
)
A．乘坐飞机赴各地了解 B．通过无线电报输送讯息 C．通过互联网 D．乘坐火车赴各地了解
解析：本题考查中国近代物质生活的变迁。注意题干信 息“20世纪初”“最快捷的方式”，因此应选B，火车速度
远不及电报快。20世纪30年代民航飞机才在中国出现，
1．李鸿章1872年在上海创办轮船招商局，“前10年盈和，成
为长江上重要商局，招商局和英商太古、怡和三家呈鼎立
之势”。这说明该企业的创办 A．打破了外商对中国航运业的垄断 B．阻止了外国对中国的经济侵略 C．标志着中国近代化的起步 ( )
D．使李鸿章转变为民族资本家
解析：李鸿章是地主阶级的代表，并未转化为民族资本家； 洋务运动标志着中国近代化的开端，但不是具体以某个企业 的创办为标志；洋务运动中民用企业的创办在一定程度上抵
(2)1924年国民党“一大”召开，标志着第 一
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应 时 代潮流 图说历史 主旨句归纳 (1)20世纪初，孙中山提出“民族、民权、 民生”三民主义，成为以后辛亥革命 的
指导思想。 (2)三民主义没有明确提出反帝要求，也 没 有提出废除封建土地制度，是一个 不彻 底的资产阶级革命纲领。
报先后发明。
(3)近代以来，交通、通讯工具的进步，推 动了经济与社会的发展。
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应 时 代潮流 图说历史 主旨句归纳 (1)1911年，革命党人发动武昌起义，辛亥
革命
爆发，随后建立了中华民国，颁布了《中 华
民国临时约法》；辛亥革命是中国近代化
[题组冲关] 3．假如某爱国实业家在20世纪初需要了解全国各地商业信
息，可采用的最快捷的方式是
(
)
A．乘坐飞机赴各地了解 B．通过无线电报输送讯息 C．通过互联网 D．乘坐火车赴各地了解
解析：本题考查中国近代物质生活的变迁。注意题干信 息“20世纪初”“最快捷的方式”，因此应选B，火车速度
远不及电报快。20世纪30年代民航飞机才在中国出现，
1．李鸿章1872年在上海创办轮船招商局，“前10年盈和，成
为长江上重要商局，招商局和英商太古、怡和三家呈鼎立
之势”。这说明该企业的创办 A．打破了外商对中国航运业的垄断 B．阻止了外国对中国的经济侵略 C．标志着中国近代化的起步 ( )
D．使李鸿章转变为民族资本家
解析：李鸿章是地主阶级的代表，并未转化为民族资本家； 洋务运动标志着中国近代化的开端，但不是具体以某个企业 的创办为标志；洋务运动中民用企业的创办在一定程度上抵
(2)1924年国民党“一大”召开，标志着第 一
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应 时 代潮流 图说历史 主旨句归纳 (1)20世纪初，孙中山提出“民族、民权、 民生”三民主义，成为以后辛亥革命 的
指导思想。 (2)三民主义没有明确提出反帝要求，也 没 有提出废除封建土地制度，是一个 不彻 底的资产阶级革命纲领。
报先后发明。
(3)近代以来，交通、通讯工具的进步，推 动了经济与社会的发展。
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应 时 代潮流 图说历史 主旨句归纳 (1)1911年，革命党人发动武昌起义，辛亥
革命
爆发，随后建立了中华民国，颁布了《中 华
民国临时约法》；辛亥革命是中国近代化
立体几何中的与球有关的内切外接问题分解课件
公式
设多边形的边数为$n$，则球的半径$r = frac{a}{2sinfrac{180^circ}{n}}$，其中$a$为多边形的外接圆半径。
球与圆柱体的内切总结词Fra bibliotek详细描述
当一个球完全内切于一个圆柱体时， 圆柱体的底面圆周和顶面圆周都与球 面相切，且圆柱的轴线通过球心。
设圆柱体的底面圆心为$O_1$，顶面 圆心为$O_2$，球心为$O$。由于球 内切于圆柱体，所以$OO_1 = OO_2 = r$，其中$r$为球的半径。同时， 圆柱体的底面圆周和顶面圆周都与球 面相切，所以底面圆心到球心的距离 等于底面圆的半径，顶面圆心到球心 的距离等于顶面圆的半径。
公式
设圆柱体的底面半径为$R_1$，顶面 半径为$R_2$，高为$h$，则球的半 径$r = frac{R_1 + R_2 + h}{2}$。
球与圆锥体的内切
总结词
当一个球完全内切于一个圆锥体时，圆锥体的底面圆周和侧面都与球面相切，且圆锥的轴 线通过球心。
详细描述
设圆锥体的底面圆心为$O_1$，球心为$O$。由于球内切于圆锥体，所以$OO_1 = r$， 其中$r$为球的半径。同时，圆锥体的底面圆周和侧面都与球面相切，所以底面圆心到球 心的距离等于底面圆的半径。
04
球的内切外接问题应用
球在几何题中的应用
球与多面体的内切和外接
在几何题目中，经常涉及到球与多面体的内切和外接问题，需要利用球心到多面 体的顶点的距离等于半径的原理来解决。
球的切线和割线定理
切线和割线定理是球在几何题中的重要应用，通过这些定理可以推导出球与其他 几何形状的位置关系。
球在物理题中的应用
02
球的内切问题
球与多边形的内切
设多边形的边数为$n$，则球的半径$r = frac{a}{2sinfrac{180^circ}{n}}$，其中$a$为多边形的外接圆半径。
球与圆柱体的内切总结词Fra bibliotek详细描述
当一个球完全内切于一个圆柱体时， 圆柱体的底面圆周和顶面圆周都与球 面相切，且圆柱的轴线通过球心。
设圆柱体的底面圆心为$O_1$，顶面 圆心为$O_2$，球心为$O$。由于球 内切于圆柱体，所以$OO_1 = OO_2 = r$，其中$r$为球的半径。同时， 圆柱体的底面圆周和顶面圆周都与球 面相切，所以底面圆心到球心的距离 等于底面圆的半径，顶面圆心到球心 的距离等于顶面圆的半径。
公式
设圆柱体的底面半径为$R_1$，顶面 半径为$R_2$，高为$h$，则球的半 径$r = frac{R_1 + R_2 + h}{2}$。
球与圆锥体的内切
总结词
当一个球完全内切于一个圆锥体时，圆锥体的底面圆周和侧面都与球面相切，且圆锥的轴 线通过球心。
详细描述
设圆锥体的底面圆心为$O_1$，球心为$O$。由于球内切于圆锥体，所以$OO_1 = r$， 其中$r$为球的半径。同时，圆锥体的底面圆周和侧面都与球面相切，所以底面圆心到球 心的距离等于底面圆的半径。
04
球的内切外接问题应用
球在几何题中的应用
球与多面体的内切和外接
在几何题目中，经常涉及到球与多面体的内切和外接问题，需要利用球心到多面 体的顶点的距离等于半径的原理来解决。
球的切线和割线定理
切线和割线定理是球在几何题中的重要应用，通过这些定理可以推导出球与其他 几何形状的位置关系。
球在物理题中的应用
02
球的内切问题
球与多边形的内切
【高中数学】立体几何中外接球内切球 专题课件 高一下学期数学人教A版(2019)必修第二册
A．4π B．3π C．2π D．π
答案 A 解析 由已知， 2R 12 12 ( 2)2 2 ， S球 4 R2 4 π．
(4)在正三棱锥 S－ABC 中，M，N 分别是棱 SC，BC 的中点，
且 AM MN ，若侧棱 SA 2 3 ，则正三棱锥 S－ABC 外接球的表面
积是________．
2
空间几何体的外接球与内切球十大模型
1．墙角模型； 2．对棱相等模型； 3．汉堡模型； 4．垂面模型； 5．切瓜模型； 6．斗笠模型； 7．鳄鱼模型； 8．已知球心或球半径模型； 9．最值模型； 10．内切球模型．
3
一、墙角模型 墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模
型，用构造法(构造长方体)解决．外接球的直径等于长方体的体对角线 长(在长方体的同一顶点的三条棱长分别为 a，b，c，外接球的半径为 R， 则 2R＝ a2＋b2＋c2．)，秒杀公式：R2＝a2＋b2＋c2。可求出球的半径
4
2
7a 2
7
， a 2
．在正四面体
A BCD 的边长为 2，外接球的半径 R
6a 4
6
2 ，外接球的体积
V 4 R3
3
6 ．
12
(5) 已 知 三 棱 锥 A BCD ， 三 组 对 棱 两 两 相 等 ， 且
AB CD 1 ， AD BC 3 ，若三棱锥 A BCD 的外接球表面
足为 BC 的中点 M．又 AM＝12BC＝52，OM＝12AA1＝6，
所以球 O 的半径 R＝OA＝
5 2
2＋62＝13． 2
另解 过 C 点作 AB 的平行线，过 B 点作 AC 的
平行线，交点为 D，同理过 C1 作 A1B1 的平行线，过 B1 作 A1C1 的 平行线，交点为 D1，连接 DD1，则 ABCD－A1B1C1D1 恰好成为球
答案 A 解析 由已知， 2R 12 12 ( 2)2 2 ， S球 4 R2 4 π．
(4)在正三棱锥 S－ABC 中，M，N 分别是棱 SC，BC 的中点，
且 AM MN ，若侧棱 SA 2 3 ，则正三棱锥 S－ABC 外接球的表面
积是________．
2
空间几何体的外接球与内切球十大模型
1．墙角模型； 2．对棱相等模型； 3．汉堡模型； 4．垂面模型； 5．切瓜模型； 6．斗笠模型； 7．鳄鱼模型； 8．已知球心或球半径模型； 9．最值模型； 10．内切球模型．
3
一、墙角模型 墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模
型，用构造法(构造长方体)解决．外接球的直径等于长方体的体对角线 长(在长方体的同一顶点的三条棱长分别为 a，b，c，外接球的半径为 R， 则 2R＝ a2＋b2＋c2．)，秒杀公式：R2＝a2＋b2＋c2。可求出球的半径
4
2
7a 2
7
， a 2
．在正四面体
A BCD 的边长为 2，外接球的半径 R
6a 4
6
2 ，外接球的体积
V 4 R3
3
6 ．
12
(5) 已 知 三 棱 锥 A BCD ， 三 组 对 棱 两 两 相 等 ， 且
AB CD 1 ， AD BC 3 ，若三棱锥 A BCD 的外接球表面
足为 BC 的中点 M．又 AM＝12BC＝52，OM＝12AA1＝6，
所以球 O 的半径 R＝OA＝
5 2
2＋62＝13． 2
另解 过 C 点作 AB 的平行线，过 B 点作 AC 的
平行线，交点为 D，同理过 C1 作 A1B1 的平行线，过 B1 作 A1C1 的 平行线，交点为 D1，连接 DD1，则 ABCD－A1B1C1D1 恰好成为球
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
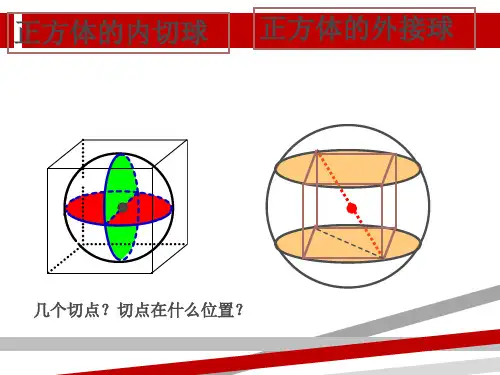
内切与外接
1 球与柱体
1.1 球与正方体
例 1 棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上，E F ，分别是棱1AA ，1DD 的中点，则直线EF 被球O 截得的线段长为（ ）
A ．22
B ．1
C ．212+
D 21.2 球与长方体
长方体各顶点可在一个球面上，故长方体存在外切球.但是不一定存在内切球.设长方体的棱长为,,,a b c 其体对角线为l .当球为长方体的外接球时，截面图为长方体的对角面和其外接圆，和正方体的外接球的道理是一样的，故球的半径222
2l a b c R ++== 例 2 在长、宽、高分别为2，2，4的长方体内有一个半径为1的球，任意摆动此长方体，则球经过的空间部分的体积为( )
A.10π3
B.4π
C.8π3
D.7π3
1.3 球与正棱柱
例3 正四棱柱1111ABCD A B C D -的各顶点都在半径为R 的球面上，则正四棱柱的侧面积有最 值，为 .
2 球与锥体 规则的锥体，如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合，以外接和内切两种形态进行结合，通过球的半径和棱锥的棱和高产生联系，然后考查几何体的体积或者表面积等相关问题.
2.1 球与正四面体
2222233a R r a R r CE +=-=，=，解得：66,.R r ==
例4 将半径都为１的四个钢球完全装入形状为正四面体的容器里，这个正四面体的高的最 小值为 ( ) A.3263+ B. 2+263 C. 4+263 D. 43263+
2.2 球与三条侧棱互相垂直的三棱锥
例5 在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且AM MN ⊥,若侧棱 23SA =,则正三棱锥S-ABC 外接球的表面积是______
2.3 球与正棱锥
球与正棱锥的组合，常见的有两类，一是球为三棱锥的外接球，此时三棱锥的各个顶点在球面上，根据截面图的特点，可以构造直角三角形进行求解.二是球为正棱锥的内切球，例如正三棱锥的内切球，球与正三棱锥四个面相切，球心到四个面的距离相等，都为球半径R ．这样求球的半径可转化为球球心到三棱锥面的距离，故可采用等体积法解决，即四个小三棱锥的体积和为正三棱锥的体积.
例6 在三棱锥P －ABC 中，PA ＝3侧棱PA 与底面ABC 所成的角为60°，则该三棱锥外接球的体积为（ ）
A ．π B.3π C. 4π D.43π 接球的球心,则2SC R =
. 例7 矩形ABCD 中，4,3,AB BC ==沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积是( )
A.π12125
B.π9125
C.π6125
D.π3
125 3 球与球
对多个小球结合在一起，组合成复杂的几何体问题，要求有丰富的空间想象能力，解决本类问题需掌握恰当的处理手段，如准确确定各个小球的球心的位置关系，或者巧借截面图等方法，将空间问题转化平面问题求解.
例7 在半径为R 的球内放入大小相等的4个小球，则小球半径r 的最大值为（ ）
4 球与几何体的各条棱相切
球与几何体的各条棱相切问题，关键要抓住棱与球相切的几何性质，达到明确球心的位 置为目的，然后通过构造直角三角形进行转换和求解.
例：与正四面体各棱都相切的球的半径为棱的一半：.
例8 把一个皮球放入如图10所示的由8根长均为20 cm 的铁丝接成的四
篇一：程序员实习总结范文
以前在校很少自己做程序,对软件工程更是一无所知.来到公司,开始接触大规模(其实现在看来实习的项目其实还是很小的)软件开发,一时真的有些迷茫.比起VSS,MVC,QA,CMMI,我对JAVA,JSP,XML的一窍不通根本不值一提.大家都不想输在起点,所以都默契地在加班,这样一直持续了实习的两个月.
刚来的时候始业教育显得慢吞吞,我们还经常盘算去哪哪玩之类的.我和FLYSKY(20个新生里唯一一个南区的兄弟,软件学院的)还经常出去吃各种小吃,每到一处都尝尝本地的风味,这是他的习惯.之后开始的培训还不是很难过,JAVA,C++,ORACLE,老师们讲的很好,可以说是非常好,好得我们没有几个人能听懂.大家开始发愁,我也是每天晚上都基本看书到10点.
我心说得亏哥们我还练过,来之前的2月份我就自己买了一本THINKING IN JAVA,看懂看不懂怎么说也算是准备了一下JAVA.C++虽说没去上过课,但凭我的直觉我就一下看中这东西很有用,自己也看过一阵.至于ORACLE,虽然不了解,但毕竟因为佩服云飞扬的性格和敬业精神,咱SQL选修也不是白混的.专业倒还有点基础,再加上咱这自学能力也不是吹的,基本维持.可等到后来的日语课就全迷糊了:本就没有语言天赋,再加上记忆严重欠缺,总是特别害怕去上日语课.不过特别喜欢那个老师说话的感觉,加上她一直对我都很好,所以还是很用心的学着.
随着培训的收尾,我们开始正式进入项目.从需求分析,概要设计到详细设计,我们一步一步的开始接触软件开发的每个细节.最受不了的就是每天都要记周报,填写自己的劳动成果.因为这个我还被QA通报了好几次呢,真的很郁闷.其实现在我很感谢这种制度化的东西,某些情况下好习惯的养成是要靠强制来确保的.详细设计之后就是企盼已久的编码,我心想终于可以做点正事了.现在回头一看才知道,其实编码只占软件开发的整个过程劳动量的1/4左右,而且其他的环节也不是想象中的那么无足轻重.
编码我其实做的很不好,主要是因为需求分析阶段就没有认真仔细的理解需求和规格说明,加上编码时一个关键时段我回校和老同学叙旧.那阵项目经理(PM)就经常和我们说,有问题自己想办法,不要经常问我.PM其实是在叫我们自己酝酿,遇到难题只有憋一憋才能有真的收获.而我不在的那三天正好是大家技术/思路上的一个跃迁,很多难题的解决方法都基本成熟,大家的编码也接近50%了,所以回来时我感觉已经掉队很多.再一个就是编码中期时机器出问题,环境搭不上了,这使我更加紧张和急躁,大大影响了我的士气.后来利用五一其间的加班我终于赶完了自己的模块,达到了第一个里程碑.其实从发现落后到加班赶完这段经历,对我来说也具有里程碑的意义.不仅考验了我自己的能力和心理素质,也证明了我对集体的责任感和合作意识.我可以叫别人来帮我做赶上进度,但那样我会错过自己学习的机会,以后再遇到难题我还是不行;我也可以硬着头皮导致项目延期,那样我以后的日子保证不好过,而且这么做也不符合我的性格.事实证明我顶住压力独立完成任务不管是对集体还是对我个人都是一件大好事.
紧张的编码之后是单体测试,很多人都在继续编码,原来大家的编码都是没有完全做完.本是自己给自己挑毛病的过程,我们却都用来完成之前没有完成的任务,说来不禁可笑.。