工程力学第8次作业解答

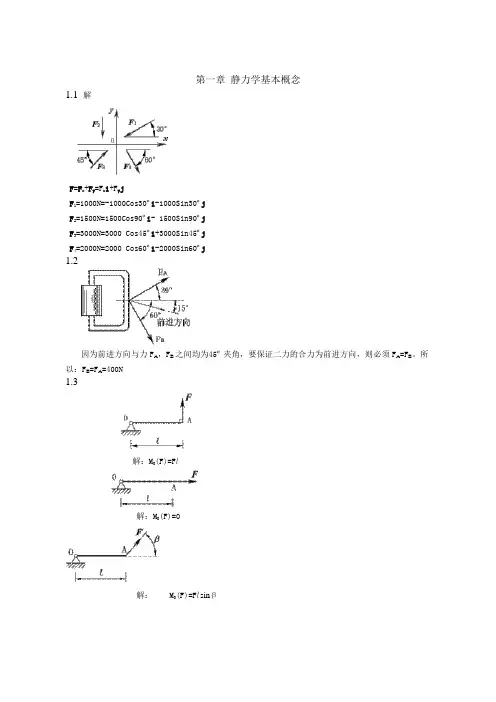
第一章静力学基本概念1.1 解F=F x+F y=F x i+F y jF1=1000N=-1000Cos30ºi-1000Sin30ºjF2=1500N=1500Cos90ºi- 1500Sin90ºjF3=3000N=3000 Cos45ºi+3000Sin45ºjF4=2000N=2000 Cos60ºi-2000Sin60ºj1.2因为前进方向与力F A，F B之间均为45º夹角，要保证二力的合力为前进方向，则必须F A=F B。

所以：F B=F A=400N1.3解：M O(F)=F l解：M O(F)=0解： M O(F)=F l sinβ解： M O(F)=F l sinθ解： M O(F)= -F a解：M O(F)= F(l＋r)解:1.4解:1.5解：1位置：M A(G)=02位置：M A(G)=-G l sinθ3位置：M A(G)=-G l1.6解：M O(F n)=-F n cosθ·D/2=-75.2N·m 1.71.8第二章平面力系2.1 力系简化解：（1）主矢大小与方位：F/R x＝∑F x＝F1cos45º+F3+F4cos60º＝100Ncos45º+200N+250cos60º＝395.7N F/R y＝∑F y＝F1sin45º-F2-F4sin60º＝100Nsin45º-150N-250sin60º＝-295.8N（2）主矩大小和转向：M O＝∑M O(F)＝M O(F1)+M O(F2)+M O(F3)+M O(F4)+m＝0-F2×0.3m+F3×0.2m+F4sin60×0.1m+F×0.1m＝0-150N×0.3m+200N×0.2m+250Nsin60×0.1m+50N×0.1m ＝21.65N·m( )向O点的简化结果如图所示。

工程力学试题八及答案一、单选题(每题3分)1. 一端固定，一端为弹性支撑的压杆如图所示，其长度系数的范围为（ ）A μ<0.7；Bμ >2；C 0.7< μ<2；D 不能确定2. 两个共点力可合成一个力，一个力也可分解为两个相交的力。

一个力分解为两个相交的力可以有（）解。

A 一个；B两个；C几个；D无穷多3. 一均质偏心轮，质量为m ，偏心距为e ，已知对转轴O 和对质心C 的转动惯量分别为J O 、J C （图示），今欲计算其动能，可采用公式（ ） A222me ω；B 22O mJ ω；C 22222C J me ωω+；D 22C mJ ω4. 用一截面将梁截为左、右两段，在同一截面上的剪力、弯矩数值是相等的，按静力学作用与反作用公理，其符号是相反的，而按变形规定，则剪力、弯矩的符号（ ）A 仍是相反的；B 是剪力相反，弯矩一致；C 总是一致；D 是剪力一致，弯矩相反5. 在圆轴扭转变形时，其它条件不变，若轴的长度增加一倍，扭转角是原来的ω（ ）。

A 1倍；B 2倍；C 3倍；D 4倍二、判断题(每题1分)1. 力的平移定理不仅适用于刚体，而且也能适用其它物体。

（ ）2. 牵连运动是动系的绝对运动。

（ ）3. 点做直线运动时，位移的大小总是等于路程。

（ ）4. 不变力矩对刚体作功的功率等于该力矩与角速度的乘积。

（ ）5. 质点运动速度很大时，受力也一定很大。

（ ）6. 矩形截面梁的纯弯曲段内，甘横截面上各点的剪应力均等于零。

（ ）7. 动点的绝对运动和相对运动都是动点的运动，只是相对的参考系不同而已。

（ ）8. 温度应力是构件在一定温度下测得的应力。

（ ）9. 用截面法求杆件的扭矩时，无论取截面以左还是以右部分来研究，按右手螺旋法则规定的扭矩正负总是相同的，从左、右两部分的作用与反作用关系看，二者方向也是相同的。

（ ）10. 梁在纯弯曲时，变形后横截面保持为平面，且其形状、大小均保持不变。

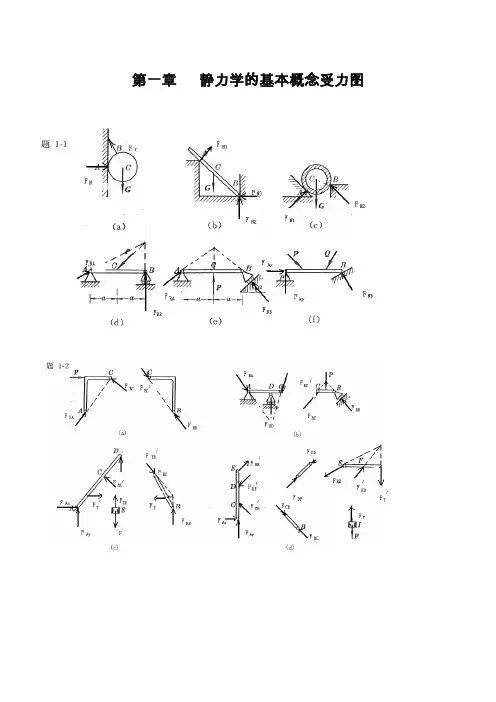
第一章静力学的基本概念受力图第二章 平面汇交力系2-1解：由解析法，23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故：22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故： 223R RX RY F F F KN=+= 方向沿OB 。

2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。

（a ） 由平衡方程有：0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=（拉力）1.155AC F W=（压力）（b ） 由平衡方程有：0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=（拉力）0.364AC F W=（压力）（c ） 由平衡方程有：0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=（压力）（d ） 由平衡方程有：0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解：（a ）受力分析如图所示：由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解：受力分析如图所示：由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式，得：22.410RA RB F KN F KN==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以：5RA F KN= （压力）5RB F KN=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解：受力分析如图所示，取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后，解得：0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得： 2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得：2.92RA F KN=1.33DC F KN=（压力）列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得： 1.67AC F KN=（拉力）1.0BC F KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得： 5RD F Q =2REF Q '=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得： 22RA F Q =2RB F Q P=+（3）取BCE 部分。

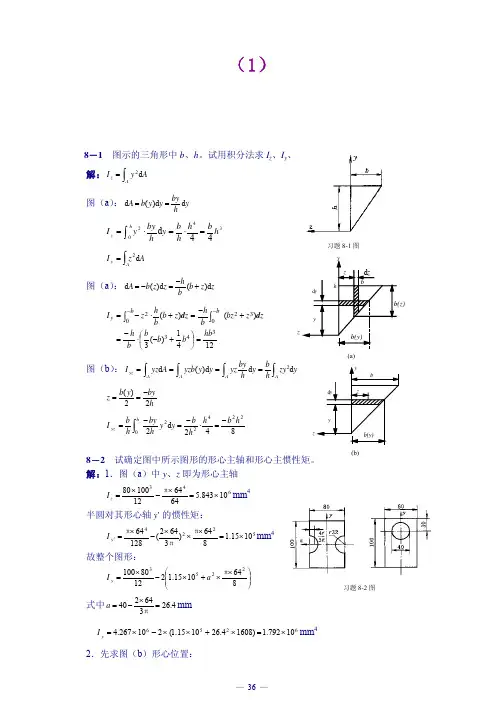
eBook工程力学习题详细解答教师用书(第8章)2011-10-1范 钦 珊 教 育 教 学 工 作 室FAN Qin-Shan ,s Education & Teaching Studio习题8－1 习题8－2 习题8－3 习题8－4 习题8－5 习题8－6 习题8－7 习题8－8 习题8－9 习题8－10 习题8－9 习题8－10习题8－11 习题8－12 习题8－13 习题8－14 习题8－15 习题8－16 习题8－17 习题8－18 习题8－19 习题8－20习题8－21工程力学习题详细解答之八第8章 弯曲强度问题8－1 直径为d 的圆截面梁，两端在对称面内承受力偶矩为M 的力偶作用，如图所示。

若已知变形后中性层的曲率半径为ρ；材料的弹性模量为E 。

根据d 、ρ、E 可以求得梁所承受的力偶矩M 。

现在有4种答案，请判断哪一种是正确的。

(A) ρ64π4d E M ＝(B) 4π64d E M ρ＝(C) ρ32π3d E M ＝(D) 3π32dE M ρ＝正确答案是 A 。

8－2 矩形截面梁在截面B 处铅垂对称轴和水平对称轴方向上分别作用有F P1和F P2，且F P1=F P2，如图所示。

关于最大拉应力和最大压应力发生在危险截面A 的哪些点上，有4种答案，请判断哪一种是正确的。

(A) +max σ发生在a 点，−max σ发生在b 点M习题8－1图A Ba b cd P2z固定端习题8－2图(B) +max σ发生在c 点，−max σ发生在d 点 (C) +max σ发生在b 点，−max σ发生在a 点 (D) +max σ发生在d 点，−max σ发生在b 点正确答案是 D 。

8－3 关于平面弯曲正应力公式的应用条件，有以下4种答案，请判断哪一种是正确的。

(A) 细长梁、弹性范围内加载；(B) 弹性范围内加载、载荷加在对称面或主轴平面内；(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内；(D) 细长梁、载荷加在对称面或主轴平面内。

第八章 直梁弯曲一、填空题1.工程中 发生弯曲 或以 弯曲变形 为主的杆件称为梁。

2.常见梁的力学模型有 简支梁 、 外伸梁 和 悬臂梁 。

3.平面弯曲变形的受力特点是 外力垂直于杆件的轴线，且外力和力偶都作用在梁的纵向对称面内 ；平面弯曲变形的变形特点是 梁的轴线由直线变成了在外力作用面内的一条曲线 ；发生平面弯曲变形的构件特征是 具有一个以上对称面的等截面直梁 。

4.作用在梁上的载荷有 集中力 、 集中力偶 和 分布载荷 。

5.梁弯曲时，横截面上的内力一般包括 剪力 和 弯矩 两个分量，其中对梁的强度影响较大的是 弯矩 。

6.在计算梁的内力时，当梁的长度大于横截面尺寸 五 倍以上时，可将剪力略去不计。

7.梁弯曲时，某一截面上的弯矩，在数值上等于 该截面左侧或右侧梁上各外力对截面形心的力矩 的代数和。

其正负号规定为：当梁弯曲成 凹面向上 时，截面上弯矩为正；当梁弯曲成凸面向上 时，截面上弯矩为负。

8.在集中力偶作用处，弯矩发生突变，突变值等于 集中力偶矩 。

9.横截面上弯矩为 常数 而剪力为 零 的平面弯曲变形称为 纯弯曲变形 。

10.梁纯弯曲变形实验中，横向线仍为直线，且仍与 梁轴线 正交，但两线不再 平行 ，相对倾斜角度θ。

纵向线变为 弧线 ，轴线以上的纵向线缩短，称为 缩短 区，此区梁的宽度 增大 ；轴线以下的纵向线伸长，称为 伸长 区，此区梁的宽度 减小 。

情况与轴向拉伸、压缩时的变形相似。

11.中性层与横截面的交线称为 中性轴 ，变形时梁的 所有横截面 均绕此线相对旋转。

12.在中性层凸出一侧的梁内各点，其正应力均为 正 值，即为 拉 应力。

13.根据弯曲强度条件可以解决 强度校核 、 截面选取 和 确定许可载荷 等三类问题。

14.产生最大正应力的截面又称为 危险截面 ，最大正应力所在的点称为 危险点 。

15.在截面积A 相同的条件下， 抗弯截面系数 越大，则梁的承载能力就越高。

第8章 压杆稳定习题：1.【解】d 图临界力最大，b 图临界力最小。

2.【解】σBC =11.25MPa <[σst ]=16.83MPa ,BC 杆满足稳定性要求3.【解】最合理的情况为AB 、BC 两杆同时失稳，此时F 最大。

()βθ22222cr cos ππcos AC AB AB l EI l EI F F === ()βθ22222cr sin ππsin AC BC BCl EI l EI F F === 两式相除得到βθ2cot tan =即()βθ2cot arctan = 4. 【解】由于杆端的约束在各个方向相同，因此，压杆将在抗弯刚度最小的平面内失稳，即杆件横截面将绕其惯性矩为最小的形心主惯性轴转动。

32123min min b bh hb AI i === 欧拉公式适用于λ≥p λ，即min i l μ≥p2πσE 由此得到 l ≥m 76.1m 10200102105.032π103032π693p =⨯⨯⨯⨯⨯=-σμE b 故此压杆适用于欧拉公式时的最小长度为1.76m 。

5. 【解】（1）F cr =329.64kN（2）n =2.29<[n st ]=2.5，结构不安全6. 【解】（1）求挺杆的柔度挺杆的横截面为圆形，两端可简化为铰支座，μ=1，i=d/4计算柔度λ=μli=4μld=4×1×0.2570.008=128.5λ1=π√EσP =π√210×109240×106=92.9挺杆是细长压杆，使用欧拉公式计算临界压力（2）校核挺杆的稳定性I=πd464=π×0.008464=2.01×10−10m4P cr=π2EI(μl)2=π2×210×109×2.01×10−10(1×0.257)2=6.31kN工作安全系数n=P crP max=6.311.76=3.59所以挺杆满足稳定性要求7. 【解】[F]=53.31kN8. 【解】（1）F cr=355.31kN（2）bℎ=0.525。

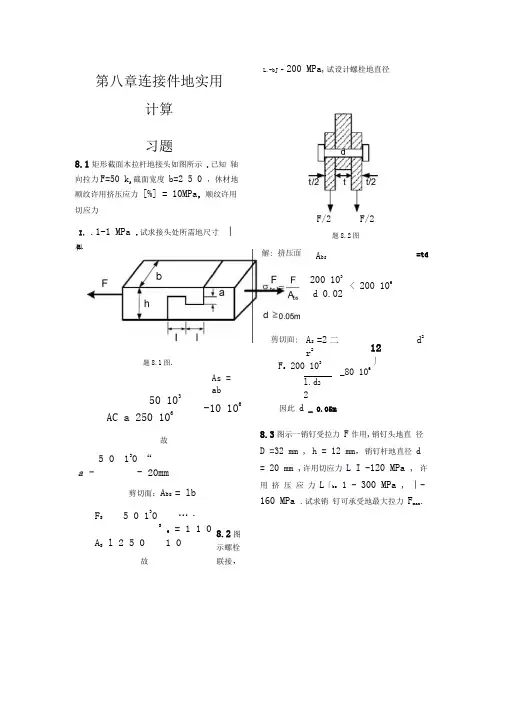
8.3图示一销钉受拉力 F 作用,销钉头地直 径D =32 mm , h = 12 mm ，销钉杆地直径 d = 20 mm ,许用切应力 L I -120 MPa , 许用 挤 压 应 力 L 「bs 1 - 300 MPa , 丨-160 MPa .试求销 钉可承受地最大拉力 F max .8.2图示螺栓联接，第八章连接件地实用计算 习题8.1矩形截面木拉杆地接头如图所示 .已知 轴向拉力F=50 k ,截面宽度 b=2 5 0 ，休材地顺纹许用挤压应力 [%] = 10MPa ，顺纹许用切应力 a . L.-bJ -200 MPa ,试设计螺栓地直径I. .1-1 MPa .试求接头处所需地尺寸 丨和 A bsd 0.02题8.1图.200 103A s =2二 r 2 As = ab50 103AC a 250 106-10 106F/2 F/2题8.2图F s 200 103l.d 2 2=td< 200 10612丿d 2_80 106因此 d _ 0.05m故5 0 130 “ a - - 20mm250 10剪切面：A bs = lbF S5 0 130 …・S6 = 1 1 0 A S l 2 5 0 1 0 故已知外力F =200 kN , 板厚度t =20 mm，板与螺栓地材料相同，其许用切应力丨.1-80 MPa ,许用挤压应力解:1 h D - I|hrZZZ/////.-d-*\\、\\题8.3图.拉杆头部地切应力拉杆头部D2 -d2F s 二A s - "：dhAs 二dh 挤压应力3.14 20 10” 12 10120 106N =90.4KN 乞F maxF =%Abs=% 兀（D2-d2）=300 心0*3.= 587.8 KN _Fmax所以应取F =90.4 KN ；F ■d 290.4 KN_3223.14 20 10 m2题8.4图.解：先考虑受剪切力时地情况，在钢板和铆钉都达到许用剪切应力时，. F S兀 2由一,A Q = na s和a s = —d 得,n =a s 2s d4将L I - 140MPa,d = 0.020m代入上式，得n 二n a s-UF S-bs3160 10兀2TT314 2 6qd _… 4 0.020 140 10A bsA bs = n a bs〉a bs = dt得_ a bs 事bs dt 竽bs _S4^再尬代入上式,得F Fa bs -上bJ dt 士bs1160"030.020 0.01 320 106由以上两式可以确定铆钉地个数为四个，下=3.64 :::=2.5 ：：3=72.0MP 确定排列方式为（n1为一行中铆钉个数）8.4图示两块钢板用直径d = 20 mm地铆钉搭接，钢板与铆钉材料相同.已知F ^1 6 0 !两板尺寸相同，厚度t =10 mm , 宽度b =1 2 0 ,m许用拉应力kr】=1 6 0 M R许a用切应力I. ）-140 MPa ,许用挤压应力L「bs丄320 MPa ,试求所需要地铆钉数，并加以排列，然后校核板地拉伸强度.F NA -山兀得，n1-l- |,A = 0.01 0.12 = 0.0012m2,a bs = 0.0002m2代入上式得160汉103 '0.0012_------ 6. 160"06£ =10.0002—1k6所以每排只排一个，共四排,在此种排列情况下,强度符合条件8.5图示直径为 30 mm 地心轴上安装着一 个手摇柄，杆与轴之间有一个键K,键长36mm,截面为正方形，边长8 mm,材料地许用切 应力LI -5 6 0 MP 锻用挤压应力L 「bs 1 = 200 MPa ,试求手摇柄右端 F 地最 大许可值.30mm解：挤压面为 傀=4 36 = 144mm 2故最大挤压应力为F bs "bs A bs =Abs bbs li 44m m 2x 20°MP a= 28.8kN剪切面为 A = 8^36=288mm 故最大剪切应力为F s= Ab 】 = 288mm 2 汉560MPa=161.28kN由于 F bs ::: Fs ,所以取 F bs 二 28.2kN , 由力矩平衡条件，得15 F bs -750 F = 0F =576N手摇柄右端F 地最大许为576N.8.6图示冲床地冲头，在F 力地作用下，冲剪 钢板，设板厚t =10 mm ，板材料地剪切强度 极限-b =360 MPq 当需冲剪一个直径 d -20 mm 地圆孔，试计算所需地冲力 F 等 于多少？解：剪切面S 二二dt由于b因此F ss ■: dt750mm题8.5图.F - ■ dt 3.14 0.02m 0.01m 360 106p a钢板。