分数指数幂及运算

分数指数幂的运算在数学中，指数是一种不同于加法、减法和乘法的特殊运算，它可以将一个数乘以多次的相同的数，即x的y指数次幂，表示为xy，这种运算被称为指数幂。

指数可以以x的y次幂，或者以a的b指数次幂的形式表示，前者表示x乘以自身y次，后者表示a乘以自身b次。

比如x2表示x 被乘以自身两次，即x×x；a3表示a被乘以自身三次，即a×a×a。

分数指数幂的运算是特殊的指数运算，它是一种将分数转换为指数的运算方式。

以x的分数指数次幂表示法来表达，即x的m/n指数次幂，表示为xm/n，m和n是整数，m≥1。

分数指数幂的运算可以用来解决大量具有指数形式的算数题目，比如求解p的1/2指数次幂，即p1/2，可以用分数指数幂运算求解。

计算分数指数幂的方法是将原式中的分数指数次幂，根据a的m/n指数次幂的形式，分解为m/n次方。

即a的m/n指数次幂等价于a的m次方的n次方根。

总的来说，分数指数幂的运算由两个步骤组成：首先将原式中的分数指数次幂分解为m/n次方，其次计算a的m次方的n次方根就可以求出结果。

分数指数幂的运算在实际中也有许多应用，例如在实际生活中，我们往往碰到如下形式的公式：a的1/4指数次幂，即a1/4。

在这种情况下，我们可以使用分数指数幂的运算计算出结果。

此外，分数指数幂可以用来解决绝对值的化简问题。

比如|x2/3|=x2/3，我们可以用分数指数的运算，将|x2/3|分解为x的4次方的3次方根，再求出结果。

从上述介绍中可以看出，分数指数幂的运算是一种非常有用且重要的数学运算。

它可以帮助我们快速求解具有分数指数形式的算数题目，同时也可以用来解决绝对值的化简问题。

因此，分数指数幂的运算在数学中占据着重要的地位，且运用起来也非常简单方便，希望读者在学习数学的过程中，能够运用分数指数幂运算，去解决各种算法题目，提高自己的数学水平。

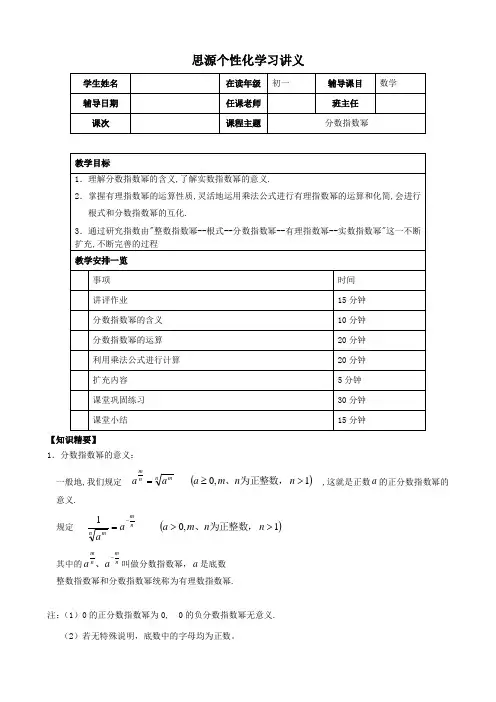
思源个性化学习讲义【知识精要】1．分数指数幂的意义： 一般地,我们规定 n m nm a a = ()1,0>≥n n m a 为正整数，、 ,这就是正数a 的正分数指数幂的意义. 规定nm n maa-=1()1,0>>n n m a 为正整数，、其中的nm nm a a -、叫做分数指数幂，a 是底数整数指数幂和分数指数幂统称为有理数指数幂.注：（1）0的正分数指数幂为0, 0的负分数指数幂无意义. （2）若无特殊说明，底数中的字母均为正数。

2. 当a >0时，整数指数幂的运算性质，对于有理指数幂也同样适用.即对于任意有理数r ,s ,均有下面的运算性质：设q p b a 、,0,0>>为有理数（1）q p q p qp q p a a a a a a -+=÷=⋅，（2）()pq qpa a =（3）()p p pp p pb a b a b a ab =⎪⎭⎫ ⎝⎛=，【热身练习】1. 把下列方根化为分数指数幂的形式（1）310 （2）32101（3）3100 （4）41002. 求值(1)21169 (2)3264 (3) 239- (4)⎪⎪⎭⎫ ⎝⎛-43256（ ）A.3B.3-C.3±D.81 4．当a _________时，式子23a 有意义 5. 若0>a ，则43a 和53-a 用根式形式表示分别为 和6.56b a 和mm 3用分数指数幂形式表示分别为 和【精解名题】 1. （1）23425-⎪⎭⎫⎝⎛= ；（2） 63125.132⨯⨯= ________2. 计算：631010⨯=__________________3.3151写成幂的形式______________4.化为分数指数幂的形式为 ___________________5. 583221)22(--化为分数指数幂得 _________________________6.式子 （ ）7. 已知32121=+-aa ，求下列各式的值。

指数运算规律一、指数法则1. 幂的乘方：(a^m)^n = a^(m×n) (m,n都是正数) ；2. 同底数幂的乘法：a^m×a^n = a^(m+n) (m,n都是正数) ；3. 同底数幂的除法：a^m / a^n = a^(m-n) (a≠0, m,n都是正数，且m>n) ；4. 幂的乘方：(a^m)^n = a^(m×n) (m,n都是正数) ；5. 积的乘方：(ab)^n = a^n×b^n (n是正整数) 。

二、指数运算性质1. 零指数幂：0^n=1 (n∈Z*)；2. 负整数指数幂：a^(-n)=1/a^n (a≠0, n∈N*)；3. 特殊值法：令字母取不同的值代入进行验证。

三、指数运算技巧1. 分散注意，将难点各个击破；2. 利用分配律简化运算；3. 利用同底数幂的乘除法法则进行简化；4. 利用幂的乘方运算法则进行简化；5. 利用积的乘方运算法则进行简化；6. 利用非零数的0次幂等于1的性质进行简化；7. 利用整体代入的思想简化运算。

四、指数运算的规律1. 负指数表示的是倒数：a^(-n) = 1/a^n2. 分数指数幂：根号[a^(2n)] = a^n，根号[a^(2n-1)] = |a|^n3. 指数为无理数时，视为实数：例如，e^(πi) + 1 = 04. 指数运算中，负数可以引入：例如，e^(-x) = 1/e^x5. 指数函数与对数函数的互为反函数：指数函数和对数函数具有反函数性质，即如果y=a^x，那么x=log_a y。

五、指数运算的应用1. 在物理学中的应用：指数函数在物理学中有广泛的应用，例如在放射性衰变、电路中的RC或LC振荡器、光的吸收和发射等过程中，都可以看到指数函数的身影。

2. 在金融学中的应用：在金融学中，复利计算就是一个典型的指数问题。

复利是指本金及其产生的利息一并计算，也就是利上有利。

复利计算的特点是：把上期末的本利和作为下一期的本金，在计算时每一期本金的数额是不同的。

指数是分数怎么算
分数为指数的运算方式是：a的x分之y次方，也就是a的y次方在开a次根号，例如a^（1/3）也就是a的1次方开3次根号。

分数指数幂是一个数的指数为分数，如2的1/2次幂就是根号2。

分数指数幂是根式的另一种表示形式，
即n次根号(a的m次幂)可以写成a的m/n次幂。

幂是指数值，如8的1/3次幂=2
一个数的b分之a次方等于b次根号下这个数的a次方
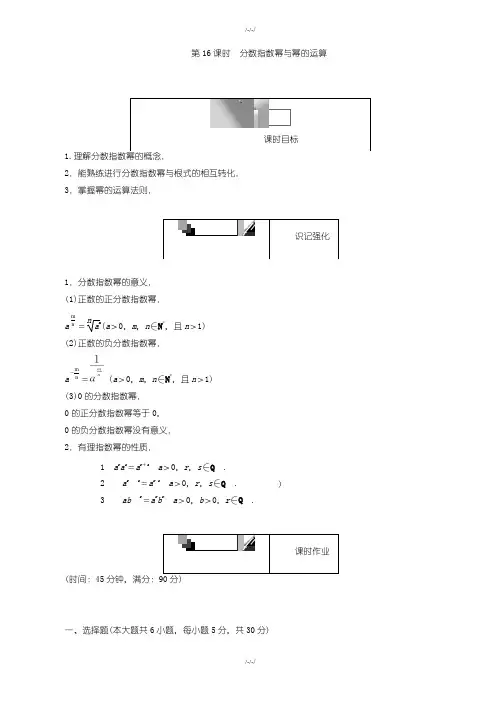
重点：
1、分数指数幂的含义的理解。

2、根式与分数指数幂的互化。

3、有理指数幂的运算性质。

难点：
1、分数指数幂概念的理解。

2、有理指数幂的运算和化简。

分数指数幂的运算法则如下：
指数相乘底数不变，幂的乘方相乘除。

指数加减底数不变，同底数幂相乘除。

积商乘方原指数，换底乘方再乘除。

负整数的指数幂，指数转正求倒数。

非零数的零次幂，常值为1不相乘除。

看到分数指数幂，底数必为非负数。

乘方指数是分子，根指数要当分母。

对于任意有理数r,s,均有下面的运算性质：
(1)ar×as=a(r+s) (a>0,r,s∈Q)。

(2) (ar)s=ars (a>0,r,s∈Q)。

(3) (ab)r=ar×br (a>0,b>0,r∈Q)。

分数指数幂的意义：
分数指数幂是一个数的指数为分数，如2的1/2次幂就是根号2。

分数指数幂是根式的另一种表示形式，即n次根号(a的m次幂)可以写成a的m/n次幂。

幂是指数值，如8的1/3次幂=2，一个数的b分之a次方等于b次根号下这个数的a次方。

正数的正分数指数幂的意义是——a的n分之m次方=n√a的m次方（a>0,m、n属于正整数，n>1），0的正分数指数幂等于0，0的负分数指数幂没有意义。

规定了分数指数幂的意义后，指数的概念就从整数指数推广到了有理数指数，那么整数指数幂的运算性质也同样可以推广到有理数指数幂。

分数指数幂的读法
摘要：
一、分数指数幂的概念
1.分数指数幂的定义
2.分数指数幂与根的关系
二、分数指数幂的性质
1.分数指数幂的乘法
2.分数指数幂的除法
3.分数指数幂的幂运算
三、分数指数幂的读法
1.常规读法
2.简化读法
四、分数指数幂的应用
1.实际问题中的应用
2.分数指数幂在数学公式中的应用
正文：
分数指数幂是数学中一种常见的概念，它涉及到指数与根的运算。

分数指数幂可以用于表示一些特殊的情况，例如，当一个数的幂等于一个分数时，我们可以使用分数指数幂来表示。

分数指数幂不仅具有自身的性质，还可以与常规的指数幂进行运算。

分数指数幂与根的关系密切，可以看作是幂与根的一种相互转换。

例如，
对于一个数a，其平方根可以表示为a^(1/2)，而a 的平方可以表示为
a^2。

这样，我们可以将幂与根相互转换，更方便地进行计算。

分数指数幂具有许多性质，可以方便地进行运算。

例如，分数指数幂的乘法可以表示为底数不变，指数相加；分数指数幂的除法可以表示为底数不变，指数相减。

此外，分数指数幂还可以进行幂运算，即一个分数指数幂的幂可以表示为底数不变，指数相乘。

在实际问题中，分数指数幂也有广泛的应用。

例如，在物理学中，电场强度E 与电荷密度ρ的关系可以表示为E = ρ^(-1/2)，这里的指数-1/2 就是一个分数指数幂。

在数学公式中，分数指数幂也有广泛的应用，例如对数函数、指数函数等。

虽然分数指数幂的概念相对复杂，但其性质和应用使其在数学领域具有重要的地位。