3.2 刚体定轴转动动力学
- 格式:ppt
- 大小:1.77 MB
- 文档页数:47








第七讲: 第3章 刚体的转动1、 刚体:在一定条件下,只考虑物体的大小、形状,而不考虑它的形变的物体。
刚体也可以看成是一个相对位置不变的质点系,可以认为是质点系的运动。
2、 刚体的基本运动可以分为刚体的平动,刚体的转动。
刚体的一般运动都可以可作是平动和转动的叠加。
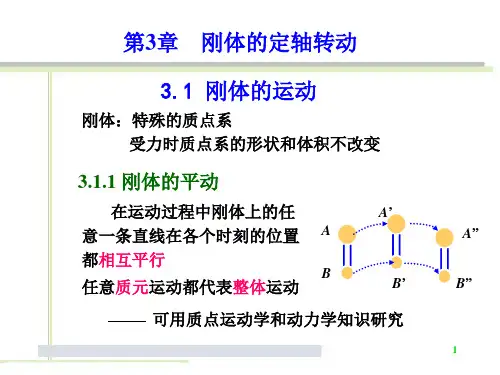
§3.1 刚体运动的描述 一、 平动和转动1、 平动:当刚体运动时,如果刚体内任何一条给定的直线在运动中始终保持的方向不变。
因为刚体的平动时,其每一点的运动规律是一样的,相当于质点的运动。
2、 转动:当刚体运动时,如果刚体的各点的在运动中都绕同一直线作圆周运动。
3、 刚体的定轴转动:绕固定轴转动的刚体。
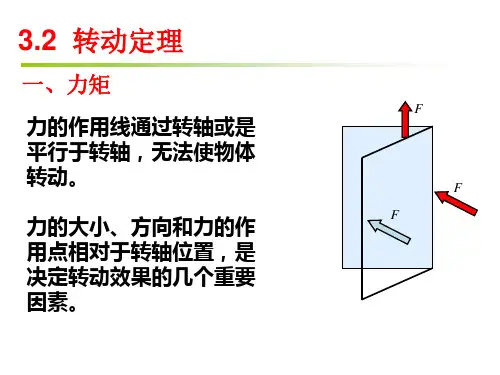
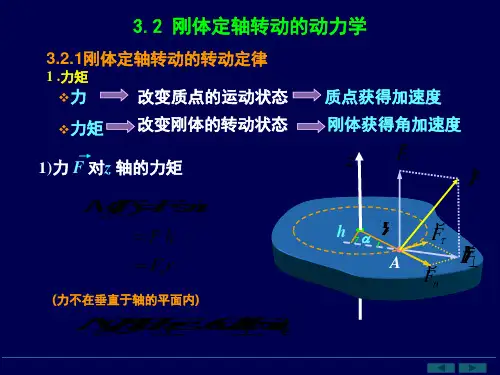
二、 定轴转动的角量描述 1、 刚体转动的角速度:dtd θω=方向满足右手螺旋法则 2、 刚体转动的角加速度:22dtd dt d θωβ== 同向为加速运动 P80 例题3-1§3.2刚体定轴转动定律 转动定律 一、 力矩:位置矢量与作用力的矢量积(叉积) 1、 矢量式:F r M ⨯= (<180°) 右手螺旋法则2、 标量式:θrFsin M =0M 0=⇒=θ 因为F 过轴,不可能驱使转盘转动。
rF M 900=⇒=θ0M 力矩驱使转盘沿转动的正方向(逆时针方向旋转) 0M 力矩驱使转盘沿转动的负方向(顺时针方向旋转)二、 转动定律 相当于牛顿第二定律的地位1、 表述:刚体定轴转动时,刚体的角加速度与它所受的合外力矩成正比;与刚体的转动惯量成反比。
2、 表达式:βββαJ M kJ M JM 1K =−−→−=⇒= J ——转动惯量,只与绕定轴转动刚体本身的性质和转轴位置有关的。
与质量的地位相同。
3、推导:应用牛顿第二定律来进行推导i i i i a m F F a m F ∆=+=⇒=‘分切向分量,法向分量βi i r m F ∑∑∑∆=+⇒'it it Fβ)()(2i i i it r r m r F i∑∑∆=−→−⨯βJ M =⇒三、 转动惯量:是描述刚体在转动中的惯性大小的物理量。