一元二次函数

一元二次函数一元二次函数是数学中常见且重要的函数类型。

它的一般形式可以表示为f(x) = ax^2 + bx + c，其中a、b、c为常数，a不为零。

在本文中，我将介绍一元二次函数的特点、图像和应用，并且探讨一些与之相关的数学概念。

特点：1. 定义域和值域：一元二次函数的定义域为实数集R，即对于任意实数x，都存在函数值。

值域则取决于函数的开口方向和导数的正负性。

2. 对称性：一元二次函数的图像关于抛物线的对称轴对称。

对称轴的横坐标可以通过满足函数为0的x解出，即x = -b / (2a)。

这一点在求解函数的最值时有重要作用。

3. 零点：一元二次函数的零点即为使函数值等于零的横坐标。

零点可以通过求解ax^2 + bx + c = 0的根来获得，其中根的个数取决于判别式的值。

图像：一元二次函数的图像是一个抛物线。

抛物线的开口方向由二次项系数a的正负性决定。

当a大于零时，抛物线开口向上；当a小于零时，抛物线开口向下。

抛物线的顶点坐标为(-b / (2a), f(-b / (2a)))，其中f(-b/ (2a))表示在对称轴上的函数值。

应用：1. 物理学：一元二次函数可以用来描述抛体运动、自由落体等物理现象。

例如，抛出物体的高度与时间的关系就可以建模为一元二次函数。

2. 经济学：一元二次函数可以用来建立成本、收益、利润等经济指标之间的关系模型，帮助决策者做出更准确的经济预测和决策。

3. 工程学：一元二次函数在工程领域中也有广泛的应用。

例如，在建筑设计中，可以利用一元二次函数来确定柱状物体的最佳高度；在电路设计中，可以利用一元二次函数来描述电流、电压等变量之间的关系。

数学概念：1. 判别式：一元二次函数的判别式决定了根的情况。

判别式的表达式为Δ = b^2 - 4ac，其中Δ大于零时，方程有两个不等的实根；Δ等于零时，方程有两个相等的实根；Δ小于零时，方程没有实根。

2. 最值：由于一元二次函数的图像是一个抛物线，它在对称轴上有一个极值点。

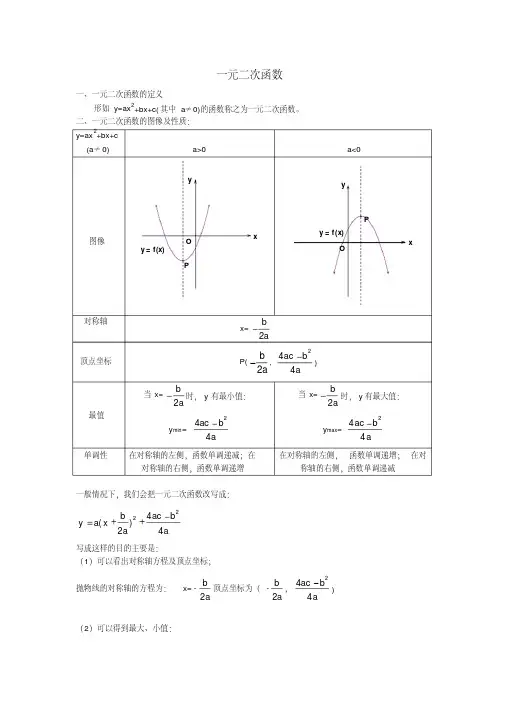
一元二次函数的图象一、 定义：一般地，如果c b a c bx ax y ,,(2++=是常数，)0≠a ，那么y 叫做x 的一元二次函数. 其中，x 是自变量，a,b,c 分别是函数表达式的二次项系数、一次项系数和常数项。

二、一元二次函数y ＝ax ²＋bx ＋c ﹙a ≠0﹚的图象(其中a,b,c 均为常数)1.当a ＞0时 函数图象开口向上；对称轴为x ＝﹣2a ／b ，有最小值且为﹙4ac －b ²﹚／4a ； 当x ∈﹙﹣∞,﹣2a ／b]时递减；当x ∈[﹣2a ／b,﹢∞﹚时递增；2.当a ＜0时函数图象开口向下；对称轴为x ＝﹣2a ／b ，有最大值且为﹙4ac －b ²﹚／4a ； 当x ∈﹙﹣∞,﹣2a ／b]时递增；当x ∈[﹣2a ／b,﹢∞﹚时递减；2.△＝b ²－4ac当△＞0时，函数图象与x 轴有两个交点； 当△＝0时，函数图象与x 轴只有一个交点； 当△＜0时，函数图象与x 轴没有交点。

(如下图所示)三、抛物线c bx ax y ++=2中，c b a ,,的作用(1) a 决定开口方向及开口大小，这与2ax y =中的a 完全一样.例1：画出212y x =- 2y x =- 22y x =-的图象212y x =- 22y x =- 2y x =-归纳：一般地，抛物线2y ax =的对称轴是y 轴，顶点是原点，当0a >时，抛物线的开口向上，顶点是抛物线的最低点，a 越大，抛物线的开口越小；当0a <时，抛物线的开口向下，顶点是抛物线的最高点，a 越大，抛物线的开口越大。

(2)b 和a共同决定抛物线对称轴的位置例2：画出二次函数21(1)2y x =-+，211)2y x =--（的图象，考虑他们的开口方向、对称轴和顶点。

21(1)2y x =-+ 211)2y x =--（可以看出，抛物线21(1)2y x =-+的开口向下，对称轴是进过点（-1,0）且与x 轴垂直的直线，记为x=-1，顶点是（-1,0）；抛物线211)2y x =--（的开口向下，对称轴是x=1，顶点是（1,0）。

1. 一元二次函数函数 2y ax bx c =++ (0)a ¹叫做一元二次函数，其中,,a b c 是常数 一般式2y ax bx c =++ ( 0a ¹)顶点式 ()2y a x h k =-+ (0a ¹),其中(),h k 为抛物线顶点坐标两点式()()12y a x x x x =-- ( 0a ¹), 其中12,x x 是抛物线与x 轴交点的横坐标。

1.1一元二次函数的基本性质1.1.1一元二次函数的定义域和值域 一元二次函数2y ax bx c =++ ，(0)a ¹的R一元二次函数2y ax bx c =++ ，(0)a ¹ 的值域是0a >时一元二次函数的值域是24,4ac ba 轹-÷ê÷+ ÷ê÷øë 0a <时一元二次函数的值域是24,4acb a 纟-çú- ççúèû1.1.2一元二次函数的单调性1. 2y ax bx c =++ ， ()0a > 在区间,2ba 纟çú-?ççúèû上为单调减函数 ，在区间,2ba 轹÷ê-+ ÷÷êøë上为单调增函数 。

当2b x a=-时 2min 44ac b y a-=， m ax y =无2. 2y ax bx c =++ ()0a <在区间,2ba 纟çú-?ççúèû上为单调增加函数，在区间,2ba轹÷ê-+ ÷÷êøë上为单调减函数 。

一元二次函数的三种形式一元二次函数，这个名字听上去有点儿严肃，但其实它就像一块好吃的蛋糕，外表看起来复杂，切开之后却是简单又美味。

今天咱们就来聊聊这个数学小家伙的三种形式，别担心，我们会轻松幽默地过关，就像喝杯咖啡一样轻松。

1. 标准形式1.1 什么是标准形式首先，我们得说说标准形式，没错，就是 ( f(x) = ax^2 + bx + c ) 这位“老大”。

这里的 ( a, b, c ) 就像是蛋糕里的配料，决定了我们的蛋糕到底好不好吃。

这个形式挺常见的，大家在学校的时候都学过。

如果你在追求直观的感觉，标准形式就是你最好的朋友。

你只要一看，就能知道二次函数的开口方向和顶点的大概位置。

1.2 这个形式的好处用这个标准形式，有个好处就是我们能快速判断出图像的形状。

比如说，( a ) 是正的，那图像就像一只微笑的笑脸；而如果是负的，就变成了哭泣的小眼泪。

想象一下，如果你在朋友面前用这个形式炫耀，大家都会觉得你真懂行。

不过，光有配方可不行，做蛋糕还得有点技术嘛。

2. vertex形式2.1 顶点形式的魅力接着，我们再来看看顶点形式，记住哦，它的样子是这样的： ( f(x) = a(x h)^2 +k )。

这里的 ( (h, k) ) 就是顶点的位置，仿佛是蛋糕上那颗樱桃，闪闪发光，诱人得不得了。

通过这个形式，我们能很方便地找到图像的顶点，直接说“嘿，来看看这个美丽的点儿吧！”2.2 什么时候用顶点形式顶点形式特别适合用来找最值，尤其是在求最小值或者最大值的时候，就像厨师要知道自己做的蛋糕是酥脆的还是松软的。

这种情况下，顶点就是我们的终极目标。

不过，有些人可能会觉得，这个形式看起来有点复杂，毕竟涉及到平方和加减的操作。

但没关系，只要多练习，最终会成为你的一部分，就像你对美食的热爱一样。

3. 交点形式3.1 交点形式的“明星”最后，我们来说说交点形式，形状是这样的： ( f(x) = a(x x_1)(x x_2) )。

一元二次函数的顶点公式一元二次函数，这可是咱们数学世界里相当重要的一部分。

说到一元二次函数，就不得不提到它的顶点公式，这可是解决相关问题的一把“金钥匙”。

咱先来说说一元二次函数的一般形式：y = ax² + bx + c（a ≠ 0）。

而顶点公式就是：顶点的横坐标 x = -b / (2a)，纵坐标 y = (4ac - b²) /(4a) 。

那这个顶点公式到底有啥用呢？我给您举个例子。

有一次我去菜市场买菜，看到一个摊主在卖西瓜。

他说西瓜的价格和卖出的数量之间存在一种关系，假设价格是 y 元，卖出的数量是 x 个，关系可以用一元二次函数 y = -0.1x² + 2x + 10 来表示。

这时候咱就可以用顶点公式来算出能获得最大利润时的卖出数量。

先算横坐标 x = -2 / (2×(-0.1)) = 10 ，再算纵坐标 y = (4×(-0.1)×10 - 2²) / (4×(-0.1)) = 15 。

这就说明，当卖出10 个西瓜时，能获得最大利润 15 元。

再比如，学校组织了一场义卖活动。

我们班打算卖自己制作的小手工。

假设价格定为 y 元，预计能卖出的数量是 x 个，函数关系是 y = -0.2x² + 3x + 8 。

同样用顶点公式，算出 x = -3 / (2×(-0.2)) = 7.5 ，y =(4×(-0.2)×8 - 3²) / (4×(-0.2)) = 12.25 。

由于数量得是整数，我们就可以考虑取 7 或者 8 个来定价，以获得比较高的利润。

您看，顶点公式在生活中的用处是不是还挺大的？在解题的时候，可一定要注意 a、b、c 的取值，千万别搞错啦。

有时候，粗心一点，一个正负号的错误，结果就会相差十万八千里。

而且，对于一些变形后的一元二次函数，要先把它化成一般形式，再用顶点公式。

一元二次函数的图象一、定义：一般地，如果y =ax2• bx - c（a,b,c是常数，a = 0），那么y叫做x的一元二次函数.其中，x是自变量，a,b,c分别是函数表达式的二次项系数、一次项系数和常数项。

二、一元二次函数y= ax2+ bx + c （a z 0）的图象（其中a,b,c 均为常数）1. 当a> 0时函数图象开口向上；对称轴为x =- 2a/b，有最小值且为（4ac—b2 ）/ 4a；当x €（-x，- 2a/ b]时递减；当x € [ - 2a/ b,十^）时递增；2.当a v 0时函数图象开口向下；对称轴为x =- 2a/b，有最大值且为（4ac—b2 ）/ 4a；当x €（-x，- 2a/ b]时递增；当x € [ - 2a/ b,十^）时递减;2. △= b2 —4ac当厶〉。

时，函数图象与x轴有两个交点；当4=0时，函数图象与x轴只有一个交点; 当Av O时，函数图象与x轴没有交点。

(如下图所示)归纳：一般地，抛物线y 二ax 2的对称轴是y 轴，顶点是原点，当a 0时，抛物线的开口向上，顶点是抛物线的最低点，a 越大，抛物线的开口越小；当a 0时, 抛物线的开口向下，顶点是抛物线的最高点，a 越大，抛物线的开口越大。

⑵b 和a 共同决定抛物线对称轴的位置1 1例2：画出二次函数y = ——(x ・1)2，y = ——(x-1)2的图象，考虑他们的开口方向、2 2y = _xy x y = -2x2y「1（ x—i）1 2y —扣i)21可以看出，抛物线y n-j d」）2的开口向下，对称轴是进过点（-1,0）且与x轴垂直的直线，记为x=-1，顶点是（-1,0）；抛物线y = -1（x-1）2的开口向下，对称轴是x=1，顶点是（1,0）。

1例3：画出函数y=-^（x・1）2一1的图象，指出它的开口方向、对称轴及顶点。

抛物线y = -l x2经过怎样的变换可以得到抛物线y =-l（x・1）2 -1 ？2 21抛物线y （x，1）2-1的开口方向向下、对称轴是x=-1，顶点是（-1, -1 ）。

一元二次函数定点式-概述说明以及解释1.引言1.1 概述一元二次函数是数学中常见且重要的函数类型之一，其定义为y = ax^2 + bx + c，其中a、b、c 是实数常数且a 不等于零。

一元二次函数的图像呈现出特定的形状，通常为一个开口朝上或朝下的抛物线。

在本文中，我们将重点研究一元二次函数的定点式及其含义。

定点式是一种表示函数图像上顶点坐标的方式，它提供了关于函数最高或最低点的关键信息。

通过研究函数的定点式，我们可以更深入地理解一元二次函数的性质和变化规律。

本文旨在通过对一元二次函数定点式的探讨，让读者对这一函数类型有更全面的了解，并认识到定点式在函数分析和解题过程中的重要性。

同时，我们还将展望定点式的应用领域，探索更多与一元二次函数定点式相关的实际问题，并寻找使用定点式解决这些问题的可能性。

在下一节中，我们将首先介绍一元二次函数的定义，为后续讨论奠定基础。

1.2文章结构文章结构是指文章的组织结构和框架，它决定了文章内容的组织方式和展示顺序。

一个良好的文章结构能够帮助读者更好地理解文章主题，并且使文章更加连贯和有条理。

下面将介绍关于一元二次函数定点式的文章结构打算。

在本文中，文章的结构主要分为三个部分：引言、正文和结论。

引言部分（Chapter 1）是文章的开篇，目的是引导读者进入主题，并介绍文章的背景和意义。

具体包括以下几个方面的内容：1.1 概述：介绍一元二次函数的基本概念和定义，简要说明一元二次函数在数学中的重要性。

1.2 文章结构：详细说明本文的组织结构和框架，引导读者了解文章的整体布局和内容安排。

1.3 目的：明确本文的写作目的和研究问题，阐述对一元二次函数定点式的探索和分析。

1.4 总结：对引言部分进行总结，承接下文，为读者带来连贯的阅读体验。

正文部分（Chapter 2）是文章的核心部分，通过对一元二次函数定点式的定义、图像特点和含义进行详细解析，以展现该主题的全面性和深度。

具体包括以下几个方面的内容：2.1 一元二次函数的定义：介绍一元二次函数的基本形式和表达式，解释其在数学中的重要性和应用。

一元二次函数知识点一元二次函数是数学中的重要概念，能够描述很多实际问题，并被广泛应用于数学、物理、工程等领域。

本文将介绍一元二次函数的基本定义、图像特征、性质以及应用，以帮助读者更好地理解和应用这一知识点。

首先，我们来看一元二次函数的定义。

一元二次函数是指形如y =ax^2 + bx + c的函数，其中a、b、c是常数，且a不为0。

其中，x为自变量，y为因变量，a、b、c是函数的系数。

一元二次函数的图像呈现出抛物线的形状，称为抛物线函数。

接下来，我们来探讨一元二次函数的图像特征。

对于一元二次函数y = ax^2 + bx + c而言，首先我们可以根据a的正负来确定抛物线的开口方向。

当a大于0时，抛物线开口朝上；当a小于0时，抛物线开口朝下。

此外，通过对x的取值范围的分析，可以确定抛物线的轴对称线在y轴左（右）侧，进而确定抛物线的对称中心。

对称中心的横坐标为-x轴系数b/2a。

图像的顶点就是抛物线的最高（最低）点，其纵坐标为函数的值，在对称中心对应的自变量下代入函数表达式即可求得。

一元二次函数还有一些重要的性质。

首先是零点的性质。

一元二次函数的零点是指函数的值为0的自变量取值。

对于一元二次函数y =ax^2 + bx + c，可以使用求根公式x = (-b±√(b^2-4ac))/2a来求解。

其中，b^2-4ac被称为判别式，根据判别式的值可以判断一元二次函数的零点情况。

当判别式大于0时，函数有两个不相等的实数零点；当判别式等于0时，函数有一个重根零点；当判别式小于0时，函数没有实数零点。

除了零点，一元二次函数还有极值的性质。

当抛物线开口朝上时，函数的最小值为顶点的纵坐标；当抛物线开口朝下时，函数的最大值为顶点的纵坐标。

通过求导数，可以求得函数的导函数，进而求得函数的最值点和最值。

最后，我们来了解一元二次函数的应用。

一元二次函数广泛应用于许多实际问题的建模过程中。

例如，在物理领域中，一元二次函数可以用来描述自由落体运动的轨迹、飞行物体的抛体运动等；在经济领域中，一元二次函数可以用来分析成本、利润、收益等与输出量的关系；在工程领域中，一元二次函数可以用来研究材料的强度、力学结构等。

一元二次函数的标准形式是指一元二次函数的通式，即：
y=ax^2+bx+c
其中，a、b、c是常数，x是一元二次函数的自变量。

一元二次函数的标准形式可以表示各种不同的一元二次函数，只要给定不同的常数a、b、c，就可以得到不同的一元二次函数。

例如，当a=1、b=2、c=3时，一元二次函数的标准形式就可以表示为y=x^2+2x+3。

在使用一元二次函数的标准形式表示函数时，我们需要注意几点：
1.当a=0时，一元二次函数就变成了一元一次函数。

2.当a=0、b=0时，一元二次函数就变成了常数函数。

3.当a=0、c=0时，一元二次函数就变成了一元一次函数。

4.当a>0时，一元二次函数为二次凹函数，函数图像的开口向上，且函数的最小值
为：f(x)=c-b^2/(4a)。

当a<0时，一元二次函数为二次凸函数，函数图像的开口向下，且函数的最大值为：f(x)=c-b^2/(4a)。

一元二次函数的标准形式在数学中有着广泛的应用，可以用来描述各种不同的物理现象和经济过程。

例如，可以用一元二次函数来描述自由落体运动的位移与时间的关系，或者用一元二次函数来描述消费者的收入与消费水平的关系等。