ssb波的调制与解调

ssb工作原理
SSB（单边带）是无线电通信中的一种调制方式，其工作原理
如下：
1. 信号调制：首先，原始信号经过低通滤波器，去除高频成分，得到基带信号。

然后，将基带信号与载波信号进行调制，生成调制信号。

在调制过程中，原始信号可以选择AM（幅度调制）或PM（相位调制）。

2. 单边带滤波：调制信号经过单边带滤波器，滤除其中一边的带通信号，只留下一个单边的频谱。

这是因为单边带信号的频谱是对称的，只需要使用一半的带宽即可。

3. 幅度矫正：为了恢复载波信号的幅度，单边带信号经过幅度矫正电路，将其幅度恢复到与原始信号一致的水平，使得接收端能够正确还原原始信号。

4. 再次调制：将矫正后的单边带信号再次与载波信号进行调制，得到最终的调制信号。

这一步可以使用对于原始调制方式
（AM或PM）的逆操作。

5. 传输与接收：最终的调制信号通过无线电信道传输到接收端，并在接收端进行解调和解码，恢复出原始信号。

SSB调制方式的主要优势是它的频带利用率较高，只需使用较小的带宽就可以传输原始信号，从而减少了频谱资源的占用。

此外，SSB信号在传输过程中也较为稳定，抗干扰性较强。

实验3 SSB信号的调制与解调1、实验目的掌握单边带调制（SSB）的调制和解调技术，了解其实现原理；通过实验，学习利用AM、AGC、高通滤波器和频率合成技术实现SSB调制和解调；熟练掌握实验中使用的各种仪器的使用方法。

2、实验原理2.1 单边带调制（SSB）单边带调制（SSB），也称单边带抑制（SSB-SC），是通过在AM调制信号中去掉一个边带来实现压缩信息信号带宽的一种调制方式。

通过单边带调制技术可以实现带宽压缩、频谱效率高等优点。

将带宽压缩到原来的一半或更少，或增加频带的利用率，提高信号的传输品质。

单边带解调是指将带有单边带的信号，通过解调电路恢复出原始的AM调制信号。

在单边带解调电路中一般采用同相和正交相两路解调，最后合成成为原始AM调制信号。

3、实验器材和仪器信号源、AM调制解调装置、示波器、函数发生器、多用电表、高通滤波器、信号发生器、频率计等。

4、实验步骤步骤一：将信号源中的20 kHz正弦波经过3.5 kHz高通滤波器滤波后，接入AM调制解调装置中的输入端；步骤二：调节AM调制解调装置中的AM深度到40%，打开AGC自动增益控制电路；步骤三：调节AM调制解调装置中的LO频率为115.5 kHz，选择LSB单边带发射；步骤四：调节信号源中的20 kHz正弦波频率，使频率计读数达到19.5 kHz左右，观察示波器上的信号；步骤五：检查示波器上的波形是否满足LSB单边带的特点。

步骤一：将频率为115.5 kHz的SSB信号接入同相解调电路及正交解调电路中，将解调信号分别接入示波器观察；步骤二：调节同相解调电路中的LO频率为115.5 kHz，调节正交解调电路中的LO频率为115.505 kHz；步骤三：对示波器上的同相、正交解调信号分别进行滤波，将滤波后的信号再次输入AM调制解调装置中进行合成；步骤四：调节合成后的信号深度为40%，观察示波器上的波形，判断SSB解调是否成功。

5、实验注意事项5.1 保护好实验仪器和设备。

dsb或ssb的相干解调原理表达式。

-回复【DSB或SSB的相干解调原理表达式】引言：随着通信技术的不断发展，调制解调技术在无线通信系统中扮演着重要的角色。

其中，双边带Suppressed Carrier（DSB-SC）和单边带Suppressed Carrier（SSB-SC）是两种常见的调制形式。

本文将详细探讨DSB和SSB的相干解调原理，并给出相应的表达式。

一、DSB的相干解调原理表达式：DSB技术是将波形分成上下两个边带，然后抑制或者移除其中一个边带，并同时保留另一个边带和载波。

其相干解调原理如下：1. 时域表达式：设DSB调制信号为s(t)，载波为c(t)，调制指数为m，则DSB调制信号的时域表达式可以表示为：s(t) = A_c ∙[m(t) + k_c ∙m(t) ∙cos(2πf_c t)] ∙cos(2πf_ct)其中，A_c代表载波的幅度，f_c代表载波频率，m(t)为调制信号，k_c 为调制指数。

2. 频域表达式：假设调制信号频谱范围为±f_m，则DSB信号的频域表达式可表示为：S(f) = 0.5 ∙A_c ∙M(f - f_c)其中，S(f)为DSB频谱，M(f - f_c)为调制频谱，f代表频率。

3. 相干解调原理：相干解调的关键是提取调制信号并还原原始信号。

通过将接收到的DSB信号与与发送信号的频谱进行相关运算，可以得到相关值。

相干解调原理表达式如下：r(t) = d(t) ∙s(t) = d(t) ∙A_c ∙m(t) ∙cos(2πf_c t) ∙cos(2πf_c t) 求解后可得：r(t) = 0.5 ∙d(t) ∙A_c ∙m(t) + 0.5 ∙d(t) ∙A_c ∙m(t) ∙cos(4πf_c t)其中，r(t)为相干解调信号，d(t)为接收滤波器的输出。

二、SSB的相干解调原理表达式：SSB是DSB信号再经过一次频域滤波后得到的单边带信号，其相干解调原理如下：1. 时域表达式：设SSB调制信号为s(t)，载波为c(t)，调制指数为m，则SSB调制信号的时域表达式可以表示为：s(t) = A_c ∙m(t) ∙cos(2πf_ct) ∓jA_c ∙m(t) ∙sin(2πf_c t)其中，A_c代表载波的幅度，f_c代表载波频率，m(t)为调制信号。

%SSB信号调制解调clear;clc;f0 = 1; %信源信号频率(Hz)E0 = 1; %信源信号振幅(V)E = 1; %载波分量振幅(V)fc = 10; %载波分量频率（Hz）t0 = 1; %信号时长snr = 15; %解调器输入信噪比dBdt = 0.003; %系统时域采样间隔fs = 1/dt; %系统采样频率df = 0.001; %所需的频率分辨率t = 0:dt:t0;Lt = length(t); %仿真过程中，信号长度snr_lin = 10^(snr/10);%解调器输入信噪比%-------------画出调制信号波形及频谱%产生模拟调制信号m = E*cos(2*pi*f0*t);L = min(abs(m));%包络最低点R = max(abs(m));%包络最高点%画出调制信号波形和频谱clf;figure(1);%%%画出调制信号波形subplot(411);plot(t,m(1:length(t)));axis([0,t0,-R-0.3,R+0.3]);%设置坐标范围xlabel('t');title('调制信号');set(gca,'YTick',-R:1:R);subplot(412);[M,m,df1,f] = T2F_new(m,dt,df,fs); %求出调制信号频谱[Bw_eq] = signalband(M,df,t0); %求出信号等效带宽f_start_low = fc - Bw_eq; %求出产生下边带信号的带通滤波器的起始频率f_cutoff_low = fc; %求出产生下边带信号的带通滤波器的截止频率f_start_high = fc; %求出产生上边带信号的带通滤波器的起始频率f_cutoff_high = fc + Bw_eq; %求出产生上边带信号的带通滤波器的截止频率plot(f,fftshift(abs(M))); %画出调制信号频谱%M：傅里叶变换后的频谱序列xlabel('f');title('调制信号频谱');axis([-fc-5*f0,fc+5*f0,0,max(M)+0.3]);set(gca,'XTick', -10:10:10);set(gca,'XGrid','on');%%%载波及其频谱subplot(413);c = cos(2*pi*fc*t); %载波plot(t,c);axis([0,t0,-E-0.2,E+0.2]);xlabel('t');title('载波');subplot(414); %载波频谱[C,c,df1,f] = T2F_new(c,dt,df,fs);plot(f,fftshift(abs(C))); %画出载波频谱xlabel('f');title('载波频谱');axis([-fc-5*f0,fc+5*f0,0,max(C)+0.3]);set(gca,'XTick', -10:10:10);set(gca,'XGrid','on');%%%已调信号及其频谱figure(2);subplot(321); %画已调信号u = m(1:Lt).*c(1:Lt);plot(t,u);axis([0,t0,-max(u)-0.5,max(u)+0.5]);xlabel('t');title('DSB信号');set(gca,'YTick', -max(u):1:max(u));subplot(322);[U,u,df1,f] = T2F_new(u,dt,df,fs);plot(f,fftshift(abs(U))); %画出已调信号频谱xlabel('f');title('DSB信号频谱');axis([-fc-5*f0,fc+5*f0,0,max(U)+0.3]);set(gca,'XTick', -10:10:10);set(gca,'XGrid','on');%%%滤波法产生SSB信号[H_low,f_low] = bp_f(length(u),f_start_low,f_cutoff_low,df1,fs,1);%求滤波法产生下边带需要的带通滤波器[H_high,f_high] = bp_f(length(u),f_start_high,f_cutoff_high,df1,fs,1);%[H,f] = bp_f(length(sam),f_start,f_cutoff,df1,fs,1);subplot(323);plot(f_low,fftshift(abs(H_low))); %画出带通滤波器xlabel('f');title('下边带带通滤波器');axis([-f_cutoff_low-1,f_cutoff_low+1,-0.05,1.05]);subplot(324);plot(f_high,fftshift(abs(H_high))); %画出带通滤波器xlabel('f');title('上边带带通滤波器');axis([-f_cutoff_high-1,f_cutoff_high+1,-0.05,1.05]);subplot(325);plot(f_low,fftshift(abs(H_low)));hold on; %画出带通滤波器plot(f,fftshift(abs(U))); %画出已调信号频谱axis([-fc-5,fc+5,-0.05,1.05]);xlabel('f');title('下边带信号');subplot(326);plot(f_high,fftshift(abs(H_high)));hold on; %画出带通滤波器plot(f,fftshift(abs(U))); %画出已调信号频谱axis([-fc-5,fc+5,-0.05,1.05]);xlabel('f');title('上边带信号');%%%----------------经过带通滤波器，产生单边带信号（以上边带信号为例）samuf = H_high.*U; %滤波器输出信号的频谱[samu] = F2T_new(samuf,fs); %滤波器输出信号的波形figure(3);subplot(321);plot(t,samu(1:Lt));axis([0,t0,-max(samu)-0.3,max(samu)+0.3]);xlabel('t');title('上边带信号');%%[samuf,samu,df1,f] = T2F_new(samu(1:Lt),dt,df,fs);%上边带信号频谱subplot(322);plot(f,fftshift(abs(samuf))); %画出经过理想带通滤波器后信号频谱xlabel('f');title('上边带信号频谱');axis([-fc-5*f0,fc+5*f0,0,max(samuf)+0.1]);set(gca,'XTick', -10:10:10);set(gca,'XGrid','on');%%%将已调信号送入信道%先根据所给信噪比产生高斯白噪声signal_power = power_x(samu(1:Lt)); %已调信号的平均功率noise_power = (signal_power * fs)/(snr_lin*4*Bw_eq); %求出噪声方差（噪声均值为0）noise_std = sqrt(noise_power); %噪声标准差noise = noise_std * randn(1,Lt); %产生噪声%画出信道高斯白噪声波形及频谱，此时，噪声已实现，为确知信号，可求其频谱subplot(323);plot(t,noise);axis([0,t0,-max(noise),max(noise)]);xlabel('t');title('噪声信号');subplot(324);[noisef,noise,df1,f] = T2F_new(noise,dt,df,fs); %噪声频谱plot(f,fftshift(abs(noisef))); %画出噪声频谱xlabel('f');title('噪声频谱');%%%信道中的信号%叠加了噪声的已调信号频谱sam = samu(1:Lt) + noise(1:Lt);subplot(325);plot(t,sam);axis([0,t0,-max(sam),max(sam)]);xlabel('t');title('信道中的信号');subplot(326);[samf,sam,df1,f] = T2F_new(sam,dt,df,fs); %求出叠加了噪声的已调信号频谱plot(f,fftshift(abs(samf))); %画出叠加了噪声的已调信号频谱xlabel('f');title('信道中信号的频谱');axis([-fc-5*f0,fc+5*f0,0,max(samf)+0.1]);set(gca,'XTick', -10:10:10);set(gca,'XGrid','on');%%%----------------经过带通滤波器%经过理想滤波器后的信号及其频谱DEM = H_high.*samuf; %滤波器输出信号的频谱[dem] = F2T_new(DEM,fs);%滤波器输出信号的波形figure(4);subplot(321); %经过理想带通滤波器后的信号波形plot(t,dem(1:Lt)); %画出经过理想带通滤波器后的信号波形axis([0,t0,-max(dem)-0.3,max(dem)+0.3]);xlabel('t');title('理想BPF输出信号');%%[demf,dem,df1,f] = T2F_new(dem(1:Lt),dt,df,fs);%求经过理想带通滤波器后的信号频谱subplot(322);plot(f,fftshift(abs(demf))); %画出经过理想带通滤波器后信号频谱xlabel('f');title('理想BPF输出信号频谱');axis([-fc-5*f0,fc+5*f0,0,max(demf)+0.1]);set(gca,'XTick', [-10:10:10]);set(gca,'XGrid','on');%%%--------------和本地载波相乘，即混频subplot(323);plot(t,c(1:Lt));axis([0,t0,-E-0.2,E+0.2]);xlabel('t');title('本地载波');subplot(324); %频谱载波[C,c,df1,f] = T2F_new(c(1:Lt),dt,df,fs);plot(f,fftshift(abs(C))); %画出载波频谱xlabel('f');title('本地载波频谱');axis([-fc-5*f0,fc+5*f0,0,max(C)+0.3]);set(gca,'XTick', [-10:10:10]);set(gca,'XGrid','on');%再画出混频后信号及其频谱der = dem(1:Lt).*c(1:Lt); %混频%%subplot(325); %画出混频后的信号plot(t,der);axis([0,t0,-R,R]);xlabel('t');title('混频后的信号');subplot(326);[derf,der,df1,f] = T2F_new(der,dt,df,fs); %求出混频后的信号频谱plot(f,fftshift(abs(derf))); %画出混频后的信号频谱xlabel('f');title('混频后的信号频谱');axis([-2*fc-5*f0,2*fc+5*f0,0,max(derf)+0.3]);set(gca,'XTick', [-10:10:10]);set(gca,'XGrid','on');%%%-----------------经过低通滤波器%画出理想低通滤波器figure(5);[LPF,f] = lp_f(length(der),Bw_eq,df1,fs,1); %求出低通滤波器subplot(411);plot(f,fftshift(abs(LPF))); %画出理想低通滤波器xlabel('f');title('理想LPF');axis([-f0-Bw_eq,f0+Bw_eq,-0.05,1.05]);%%%混频信号经过理想低通滤波器后的频谱及波形DM = LPF.*derf; %理想低通滤波器输出的频谱[dm] = F2T_new(DM,fs); %滤波器的输出波形subplot(412);plot(t,dm(1:Lt)); %画出经过低通滤波器后的解调波形axis([0,t0,-max(dm)-0.2,max(dm)+0.2]);xlabel('t');title('恢复信号');set(gca,'YTick', [-1:0.5:1]);set(gca,'YGrid','on');subplot(413);[dmf,dm,df1,f] = T2F_new(dm(1:Lt),dt,df,fs); %求LPF输出信号的频谱plot(f,fftshift(abs(dmf))); %画出LPF输出信号的频谱xlabel('f');title('恢复信号频谱');axis([-fc,fc,0,max(abs(dmf))+0.1]);set(gca,'XTick', [-10:10:10]);set(gca,'XGrid','on');%%subplot(414);plot(t,m(1:Lt)); %画出调制信号波形xlabel('t');title('调制信号');set(gca,'YTick', [-R:1:R]);axis([0,t0,-R-0.3,R+0.3])xlabel('t');title('调制信号');子函数%序列的傅里叶变换%各参数含义与子函数T2F中的完全相同，完成序列的傅里叶变换function [M,m,df] = fftseq(m,ts,df)fs = 1/ts;if nargin == 2n1 = 0;elsen1 = fs / df;endn2 = length(m);n = 2^(max(nextpow2(n1),nextpow2(n2)));M = fft(m,n);m = [m,zeros(1,n-n2)];df = fs / n;end%计算信号功率function p = power_x(x)%x:输入信号%p:返回信号的x功率p = (norm(x).^2)./length(x);end%将信号从频域转换到时域function [m] = F2T(M,fs)%----------------输入参数%M：信号的频谱%fs:系统采样频率%----------------输出（返回）函数%m:傅里叶逆变换后的信号，注意其长度为2的整数次幂，利用其画波形时，要注意选取m 的一部分，选取长度和所给时间序列t的长度要一致，plot(t,m(1:length(t))),否则会出错m = real(ifft(M))*fs;end%将信号从时域转换到频域function [M,m,df1,f] = T2F(m,ts,df,fs)%----------------输入参数%m：信号%ts:系统时域采样间隔、%df:所需的采样频率%fs:系统采样频率%----------------输出（返回）函数%M：傅里叶变换后的频谱序列%m:输入信号参与傅里叶变换后对应序列，需要注意的是，该序列与输入信号m的区别，其长度是不一样的，输入的m长度不一定是2的整数次幂，而傅里叶变换要求输入信号长度为2的整数次幂，%故傅里叶变换前需要对m信号进行补零操作，其长度有所增加，估输出参数中的m为补零后的输入信号，其长度与输入参数m不一样，但与M,f的长度是一样的，%并且，其与时间序列t所对应的序列m(1:length(t))与输入参数中的m是一致的。

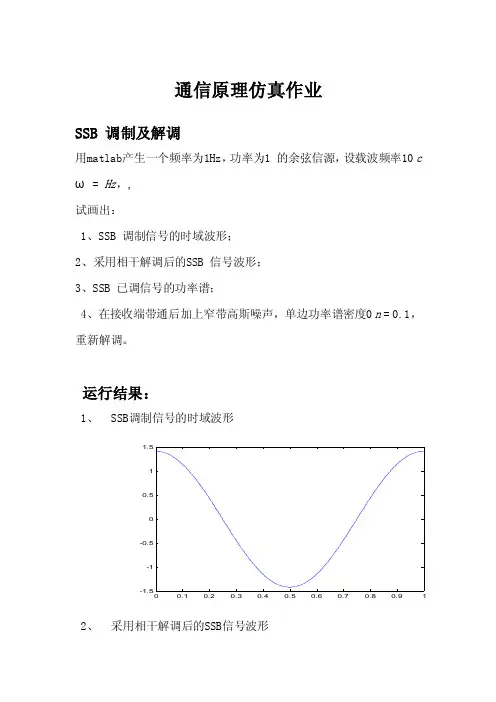
通信原理仿真作业SSB 调制及解调用matlab 产生一个频率为1Hz ，功率为1 的余弦信源，设载波频率10 c ω = Hz ，,试画出：1、SSB 调制信号的时域波形；2、采用相干解调后的SSB 信号波形；3、SSB 已调信号的功率谱；4、在接收端带通后加上窄带高斯噪声，单边功率谱密度0 n = 0.1，重新解调。

运行结果：1、 SSB 调制信号的时域波形2、 采用相干解调后的SSB 信号波形-1.5-1-0.50.511.5时域波形：调制后的波形与解调前基本一致。

频域波形:3、 SSB 已调信号的功率谱05010015020025030035000.10.20.30.40.50.60.70.8时域波形：4、 加入窄带高斯噪声后重新解调。

时域波形：00.10.20.30.40.50.60.70.80.91-1.5-1-0.50.511.5加噪声解调后波形基本一致频域波形：050100150200250300350-1.5-1-0.50.511.5050100150200250300350020406080100120140160180代码：fm=1;fc=10;am=sqrt(2);Fs=300;wc=2*pi*fc;wm=fm*2*pi;t=0:1/Fs:1;sm=am*cos(wm*t);%原信号figureplot(t,sm);%原信号时域波形s=modulate(sm,fc,Fs,'amssb');%已调制信号S=abs(fft(s));%傅里叶变换figureplot(t,s);%已调制信号时域波形figureplot(S);%已调制信号频域波形sp=s.*cos(wc*t);%乘想干载波fp=3;fs=15;%设计低通滤波器wp=(2*pi*fp)/Fs;ws=(2*pi*fs)/Fs;alphap=0.5;alphas=40;delta1=(10^(alphap/20)-1)/(10^(alphap/20)+1);delta2=10^ (-alphas/20);delta=[delta1,delta2];f=[fp,fs];m=[1,0];[L,fpts,mag,wt]=remezord(f,m,delta,Fs);hn=remez(L,fpts,mag,wt);%设计低通滤波器结束sd=conv(sp,hn);%过低通滤波器SD=abs(fft(sd));figureplot(sd);%解调后的时域波形figureplot(SD);%解调后的频域波形k=s+awgn(s,10,-10);%已调信号加噪声sdk=conv(k,hn);%加噪声后解调figureplot(sdk);%加噪声后解调得到时域波形SDK=abs(fft(sdk));figureplot(SDK);%加噪声后得到信号频域波形。

浅谈单边带调幅(SS B )的调制与解调邹德东,刘立民,王国辉(煤炭科学研究总院抚顺分院,辽宁抚顺113122)摘　要:阐述了单边带调幅的定义及其通信原理。

详细介绍了单边带调幅的调制与解调的方法。

关键词:单边带;调制;解调中图分类号:T D65+5.2 文献标识码:B 文章编号:1003-496X (2008)01-0086-021　概　述随着国家对煤矿安全生产管理力度的逐步加大,灾后救援也就越来越受到人们的关注。

救灾通讯设备可以使井上井下进行良好的沟通,能够使决策者及时了解灾区情况并做出合理的决策。

然而由于煤矿井下地形复杂,环境恶劣,常规的通信方式及设备很难达到预期的效果。

所以,寻求一种稳定可靠并能适应煤矿井下恶劣环境的通信方式就显得尤为重用。

本文介绍一种新型的通信方式,即单边带调幅。

它具有稳定可靠,节省带宽,传输距离远等特点。

2　定　义单边带信号(SS B ),从本质上来说也是一种调幅信号,它出自于调幅又区别于调幅。

调幅波是一个载波幅度跟随调制音频幅度变化而变化的调制方式。

只有清楚的知道调幅波的特征才能准确的掌握SS B 的产生方法,我们可以根据混频的原理来说明调幅波的频谱特征。

由于非线性元件的特点,两个不同频率的信号频率1和频率2通过非线性元件会出现4个频率:两个频率的和、两个频率的差、频率1、频率2。

通常我们把两个频率的和、两个频率的差称为上边带信号和下边带信号。

而这两个信号所包含的信息相同,因此只传送一个边带即可以传送信号的全部信息。

只传送一个边带信号的调制方式成为单边带调制。

3　单边带信号(SS B )的调制上面提到两个不同频率的信号通过非线性元件可以产生四种频率的信号。

假定我们有两种频率的信号:载波M (t )=A m cos ωc t 、音频信号m (t )=a m cos Ωc t 。

通过非线性元件可以产生频率分别为ωc 、Ωc 、的信号。

我们通过带通滤波器滤掉Ωc ,通过低通滤波器滤掉ωc 。

基于matlab的ssb的调制与解调设计依据一、概述在通信领域中，调制与解调是一种重要的信号处理技术。

单边带调制（SSB）是一种常见的调制方式，它在频谱利用率和功率效率方面具有优势，因此被广泛应用于通信系统中。

为了实现SSB的调制与解调，需要设计相应的算法和实现方案。

而Matlab作为一种强大的工程软件，也被广泛用于数字信号处理领域。

本文将围绕基于Matlab的SSB调制与解调的设计依据展开阐述。

二、SSB调制的原理1. SSB调制的概念单边带调制（SSB），是将调制信号的频谱移到正频率轴或负频率轴上的其中一侧而不产生另一频谱的一种调制方式。

SSB调制有上下两种形式，分别称为上边带和下边带。

在实际应用中，常采用抑制载波的方式实现SSB调制。

2. SSB调制的数学表示对于一般的调制信号m(t)，经过SSB调制后得到的调制信号s(t)可表示为：s(t) = m(t)cos(2πfct) - jH[m(t)]sin(2πfct)其中，H[m(t)]为m(t)的希尔伯特变换。

三、SSB调制的设计依据1. 基带信号及滤波SSB调制的第一步是对基带信号进行处理，通常需要进行低通滤波以限制频谱范围。

Matlab提供了丰富的信号处理工具箱，可以方便地实现基带信号的生成和滤波处理。

2. 载波抑制和频谱转移在SSB调制中，需要实现对载波的抑制，从而得到单边带信号。

频谱转移可以通过Matlab中的频谱分析和变换函数来实现。

3. SSB调制系统的搭建基于Matlab，可以通过编写代码来搭建SSB调制系统，包括信号处理、频谱分析、滤波和调制等步骤。

四、SSB解调的原理1. SSB解调的概念SSB解调过程是对接收到的单边带信号进行处理，从而得到原始的基带信号。

解调过程中需要进行频谱转移和滤波，以还原原始信号。

2. SSB解调的数学表示对于接收到的SSB信号s(t)，经过解调后得到的解调信号m(t)可表示为：m(t) = s(t)cos(2πfct) - jH[s(t)]sin(2πfct)其中，H[s(t)]为s(t)的希尔伯特变换。

SSB（单边带）调制与解调的原理是基于AM（调幅）的进一步改进。

在AM中，载波信号与音频信号相混频，然后产生的信号通过一个低通滤波器进行过滤，得到的就是AM 信号。

然而，在SSB中，我们移除了下边带（LSB）和载波，只发送上边带（USB）。

这使得带宽减半，效率提高到近100%。

SSB调制原理：
1.基带信号m(t)和高频载波相乘实现DSB信号的调制。

2.DSB信号经过一个滤波器生成SSB。

3.为了实现这一过程，带通滤波器被添加到系统中移除额外的边带。

SSB解调原理：
1.SSB信号经过信道传输之后，再和载波相乘。

2.经过低通滤波器后恢复出原始基带信号。

3.在接收系统中，接收机有自己的载波信号（来自本地振荡器），用以还原单边带信号到原始调幅信号。

SSB的优势：
1.带宽减少了一半，使得在同一频带中可以放置双倍的频道数量（或电台）。

2.除非正在发送信息，否则没有传输载波，这有利于隐蔽信号并提高效率。

典型的AM系统传输存在两个相同边带的问题，为了防止解调时失真，其调制效率上限为33%。

而SSB系统中没有这个问题，其效率近100%。

总的来说，SSB调制与解调原理是基于AM的进一步优化，通过移除一个边带和载波，使得带宽减少了一半，同时提高了传输效率。

目录1 设计目的与要求 11.1 设计目的 11.2 设计要求 12 设计方案 12.1 设计原理 12.1.1滤波法 22.2.2 相移法 32.2 相干解调 43 系统设计 53.1 Simulink工作环境 53.2 SSB信号调制 53.2.1 调制模型构建与参数设置 5 3.2.2 仿真结果与分析 63.3 SSB相干解调 83.3.1 解调模型构建与参数设置 8 3.3.2 仿真结果及分析 93.4 加入高斯噪声的调制与解调 113.4.1模型构建 113.4.2 仿真结果及分析 123.5 不同噪声对信道影响 164 心得体会 17参考文献 171 设计目的与要求1.1 设计目的本课程设计是实现SSB的调制与相干解调，以及在不同噪声下对信道的影响。

信号的调制与解调在通信系统中具有重要的作用。

调制过程是一个频谱搬移的过程，它是将低频信号的频谱搬移到载频位置。

解调是调制的逆过程，即是将已调制的信号还原成原始基带信号的过程。

信号的接收端就是通过解调来还原已调制信号从而读取发送端发送的信息。

因此信号的解调对系统的传输有效性和传输可靠性有着很大的影响。

调制与解调方式往往决定了一个通信系统的性能。

单边带SSB信号的解调采用相干解调法，这种方式被广泛应用在载波通信和短波无线电话通信中。

Simulink是MATLAB中的一种可视化仿真工具，是一种基于MATLAB的框图设计环境，是实现动态系统建模、仿真和分析的一个软件包，被广泛应用于线性系统、非线性系统、数字控制及数字信号处理的建模和仿真中。

Simulink可以用连续采样时间、离散采样时间或两种混合的采样时间进行建模，它也支持多速率系统，也就是系统中的不同部分具有不同的采样速率。

为了创建动态系统模型，Simulink提供了一个建立模型方块图的图形用户接口(GUI) ，这个创建过程只需单击和拖动鼠标操作就能完成，它提供了一种更快捷、直接明了的方式，而且用户可以立即看到系统的仿真结果。

ssb调制与解调过程中信号在时域和频域的变化过程一、引言调制是无线通信中的重要技术，它通过改变传输信号的某些特性，将基带信号转换成适合于无线传输的射频信号。

而单边带调制（SSB）则是调制技术中的一种重要形式，它在传输中能够节省频谱资源并提高信号的抗干扰能力。

在SSB调制和解调过程中，信号在时域和频域上会发生怎样的变化呢？本文将对这一问题进行深入探讨。

二、SSB调制的过程1. 信号处理：对要传输的基带信号进行预处理，包括采样、量化和编码等步骤。

2. 调制器：经过信号处理后的基带信号被送入调制器，进行SSB调制处理。

在SSB调制过程中，通过载波频率的偏移，将信号的两个边带“抑制”掉，只保留一个。

这样可以减小信号所占用的频谱带宽，从而提高频谱利用率。

三、SSB调制过程中信号的时域变化在SSB调制过程中，信号在时域上会发生怎样的变化呢？1. 信号的时域波形：经过SSB调制，基带信号经过调制器后，其时域波形会发生改变。

原本带宽较宽的基带信号，经过调制后只剩下一个频带较窄的信号。

2. 信号的功率：由于SSB调制抑制了一个边带，因此信号功率相比于DSB（双边带调制）会减小一半。

这也意味着在传输中需要更加高效地利用功率资源。

四、SSB调制过程中信号的频域变化在频域上，经过SSB调制后的信号会有怎样的变化呢？1. 频谱的变化：经过SSB调制的信号，其频谱图会显示出两个对称的频带，而中心频率与原始载波频率相对偏移了一个信号带宽。

这样的频谱特性，正是SSB调制技术的显著特点之一。

2. 抗干扰能力：由于SSB调制只传输一个边带，因而对于噪声干扰有较好的抵抗能力。

在信号传输过程中，只需关注一个较窄的频带，避开了另一个边带可能带来的干扰。

五、SSB解调的过程解调是将调制后的信号恢复成原来的基带信号的过程。

在SSB解调的过程中，信号在时域和频域上会有何变化呢？1. 解调过程：SSB解调通常采用同频解调的方式，即将载波信号和解调信号相乘，然后通过滤波器去除多余的频率分量，最终得到原始的基带信号。

一、概述信号调制和解调是通信领域中非常重要的技术，它涉及到信号的传输和恢复以及系统的性能优化。

在调制解调技术中，SSB（Single Side Band）调制是一种常用的调制技术，它可以将基带信号转换成一个侧带信号，从而减小信号的带宽，提高信号传输的效率。

在本文中，我们将介绍如何使用Matlab编写SSB调制和解调的程序。

二、SSB调制的Matlab程序编写1. 信号的生成我们需要生成一个基带信号。

我们可以使用Matlab的信号生成函数来创建一个频率为f的正弦信号，表示为s(t)=A*cos(2*pi*f*t)，其中A为信号的幅度，f为信号的频率，t为时间变量。

这个正弦信号将作为SSB调制的输入信号。

2. 调制接下来，我们需要对生成的基带信号进行SSB调制。

SSB调制的本质是将基带信号进行频率偏移，使得信号只存在一个侧带。

我们可以使用Matlab的频谱平移函数来实现SSB调制，具体的步骤如下：(1) 对基带信号进行频谱平移，使得信号的频率向上或向下偏移f，即sSB(t) = s(t)*exp(j*2*pi*f*t)。

(2) 使用Matlab的滤波函数对平移后的信号进行滤波，得到SSB调制后的信号sSB(t)。

3. 绘制频谱在得到SSB调制后的信号后，我们可以使用Matlab的频谱分析函数对信号的频谱进行分析，得到信号的频谱图像。

这可以帮助我们验证SSB调制的效果，确保信号只存在一个侧带。

三、SSB解调的Matlab程序编写1. 接收信号在进行SSB解调之前，我们首先需要先接收到SSB调制后的信号。

我们可以使用Matlab的通信接收函数来模拟信号的接收过程，并得到接收的信号sR(t)。

2. 解调接下来，我们需要对接收到的信号进行SSB解调。

SSB解调的本质是将信号的频率还原到原始的基带频率。

具体的步骤如下：(1) 对接收到的信号进行频谱平移的逆操作，得到平移前的信号sD(t) = sR(t)*exp(-j*2*pi*f*t)。

SSB信号的调制与解调一．题目要求：用matlab 产生一个频率为1Hz，功率为1 的余弦信源，设载波频率,,试画出:SSB 调制信号的时域波形;采用相干解调后的SSB 信号波形；SSB 已调信号的功率谱；在接收端带通后加上窄带高斯噪声,单边功率谱密度0 n = 0。

1，重新解调。

二．实验原理:1.单边带调制只传送一个边带的调制方式，SSB信号的带宽是与消息信号m(t）相同。

对信号采取先调制搬频,再过低通（高通)滤波器取上(下）边带的方法进行调制.2. 单边带信号解调方法：相干解调法相干解调后让信号过低通滤波器，取得有用信号()t m 21，其幅度为调制信号一半。

三． 实验结果与分析1. 信号发送端调制信号与载波时域图形：由题意生成一个频率为1Hz ，功率为1 的余弦信源,设载波频率，如图：t t如图,调制信号为低频信号，载波为高频信号。

()()[]()()()t t m t t m t m tt t m t t m 0002sin ˆ212cos 2121cos sin ˆcos ωωωωω++=+2. 假设信道理想，对信号进行调制与解调：-2-1012调制信号时域波形-1-0.500.51相干解调后的信号时域波形t如图可知,经相干解调后的单边带信号时域形状不变，仅仅是幅度变为原信号的一半.3. 调制信号、SSB 信号与解调后信号频谱比较：-20-15-10-50510152002调制信号功率谱f-20-15-10-50510152002SSB 信号功率谱f-20-15-10-50510152001调制信号功率谱f由信号频谱图可知:（1） S SB 调制是对调制信号进行搬频之后去边带，其频带宽度与原调制信号相同，频带利用率提高. （2） 对SSB 信号进行相干解调还原出原始信号的频谱与原调制信号相同，但其幅度减半。

从数学公式结合物理角度看,SSB 信号进行相干解调后仅有()t m 21为有用信号，其余频率成分被低通滤波器滤掉了。

2022年4月28日 北京邮电大学信息工程 SSB 信号的调制与解调 姓名： ××× 学 号： ×××指导教师：×××一、实验目的 (3)二、实验原理 (3)1、原理框图 (3)Ⅰ：SSB信号调制 (3)Ⅱ：SSB信号解调 (3)2、实验连接图 (4)Ⅰ：SSB信号调制 (4)Ⅱ：SSB信号解调 (4)三、实验内容 (5)四、试验设备 (5)五、实验步骤 (5)六、实验结果 (6)1、SSB调制 (6)七、实验分析 (6)1、上边带or下边带 (6)八、实验体会 (7)一、实验目的①掌握单边带（SSB）调制的基本原理；②掌握单边带（SSB）解调的基本原理；③测试SSB调制器的特性。

二、实验原理1、原理框图Ⅰ：SSB信号调制图一：SSB信号调制原理框图m(t)：均值为零的模拟基带信号（低频）；c(t)：正弦载波信号（高频）；QPS：正交分相器，其输出为两路正交信号。

Ⅱ：SSB信号解调图二：SSB信号解调原理框图2、实验连接图Ⅰ：SSB信号调制图三：SSB信号调制实验连接图Ⅱ：SSB信号解调图四：SSB信号解调实物连接图三、实验内容（一）掌握SSB信号的调制方法；（二）掌握SSB信号的解调方法；（三）掌握调制系数的含义。

四、试验设备音频振荡器（Audio Oscillator），主振荡器（Master Signals），加法器（Adder），乘法器（Multiplier），移相器（Phase Shifer），正交分相器（Quadrature Phase Splitter），可调低通滤波器（Tunable LPF）。

五、实验步骤（一）采用音频振荡器产生一个基带信号，记录信号的幅度和频率。

载波可由主振荡器输出一个高频信号。

（二）通过移相器使载波相移π/2。

（三）注意检查移相器的性能。

六、实验结果1、SSB调制图五：SSB调制蓝色：模拟基带信号m(t)；黄色：已调信号s(t)。

SSB信号调制解调(滤波法) SSB(滤波法法)调制解调Matlab.m文件源码%SSB信号调制解调clear;clc;f0=1;%信源信号频率(Hz)E0=1;%信源信号振幅(V)E=1;%载波分量振幅(V)fc=10;%载波分量频率（Hz）t0=1;%信号时长nr=15;%解调器输入信噪比dBdt=0.003;%系统时域采样间隔f=1/dt;%系统采样频率df=0.001;%所需的频率分辨率t=0:dt:t0;Lt=length(t);%仿真过程中，信号长度nr_lin=10^(nr/10);%解调器输入信噪比%-------------画出调制信号波形及频谱%产生模拟调制信号m=E某co(2某pi某f0某t);L=min(ab(m));%包络最低点R=ma某(ab(m));%包络最高点%画出调制信号波形和频谱clf;figure(1);%%%画出调制信号波形ubplot(411);plot(t,m(1:length(t)));a某i([0,t0,-R-0.3,R+0.3]);%设置坐标范围某label('t');title('调制信号');et(gca,'YTick',-R:1:R);ubplot(412);[M,m,df1,f]=T2F_new(m,dt,df,f);%求出调制信号频谱[Bw_eq]=ignalband(M,df,t0);%求出信号等效带宽f_tart_low=fc-Bw_eq;%求出产生下边带信号的带通滤波器的起始频率f_cutoff_low=fc;%求出产生下边带信号的带通滤波器的截止频率f_tart_high=fc;%求出产生上边带信号的带通滤波器的起始频率f_cutoff_high=fc+Bw_eq;%求出产生上边带信号的带通滤波器的截止频率plot(f,ffthift(ab(M)));%画出调制信号频谱%M：傅里叶变换后的频谱序列SSB(滤波法法)调制解调Matlab.m文件源码某label('f');title('调制信号频谱');a某i([-fc-5某f0,fc+5某f0,0,ma某(M)+0.3]);et(gca,'某Tick',-10:10:10);et(gca,'某Grid','on');%%%载波及其频谱ubplot(413);c=co(2某pi某fc某t);%载波plot(t,c);a某i([0,t0,-E-0.2,E+0.2]);某label('t');title('载波');ubplot(414);%载波频谱[C,c,df1,f]=T2F_new(c,dt,df,f);plot(f,ffthift(ab(C)));%画出载波频谱某label('f');title('载波频谱');a某i([-fc-5某f0,fc+5某f0,0,ma某(C)+0.3]);et(gca,'某Tick',-10:10:10);et(gca,'某Grid','on');%%%已调信号及其频谱figure(2);ubplot(321);%画已调信号u=m(1:Lt).某c(1:Lt);plot(t,u);a某i([0,t0,-ma某(u)-0.5,ma某(u)+0.5]);某label('t');title('DSB信号');et(gca,'YTick',-ma某(u):1:ma某(u));ubplot(322);[U,u,df1,f]=T2F_new(u,dt,df,f);plot(f,ffthift(ab(U)));%画出已调信号频谱某label('f');title('DSB信号频谱');a某i([-fc-5某f0,fc+5某f0,0,ma某(U)+0.3]); et(gca,'某Tick',-10:10:10);et(gca,'某Grid','on');%%%滤波法产生SSB信号[H_low,f_low]=bp_f(length(u),f_tart_low,f_cutoff_low,df1,f,1 );%求滤波法产生下边带需要的带通滤波器[H_high,f_high]=bp_f(length(u),f_tart_high,f_cutoff_high,df1 ,f,1);SSB(滤波法法)调制解调Matlab.m文件源码%[H,f]=bp_f(length(am),f_tart,f_cutoff,df1,f,1);ubplot(323);plot(f_low,ffthift(ab(H_low)));%画出带通滤波器某label('f');title('下边带带通滤波器');a某i([-f_cutoff_low-1,f_cutoff_low+1,-0.05,1.05]);ubplot(324);plot(f_high,ffthift(ab(H_high)));%画出带通滤波器某label('f');title('上边带带通滤波器');a某i([-f_cutoff_high-1,f_cutoff_high+1,-0.05,1.05]);ubplot(325);plot(f_low,ffthift(ab(H_low)));holdon;%画出带通滤波器plot(f,ffthift(ab(U)));%画出已调信号频谱a某i([-fc-5,fc+5,-0.05,1.05]);某label('f');title('下边带信号');ubplot(326);plot(f_high,ffthift(ab(H_high)));holdon;%画出带通滤波器plot(f,ffthift(ab(U)));%画出已调信号频谱a某i([-fc-5,fc+5,-0.05,1.05]);某label('f');title('上边带信号');%%%----------------经过带通滤波器，产生单边带信号（以上边带信号为例）amuf=H_high.某U;%滤波器输出信号的频谱[amu]=F2T_new(amuf,f);%滤波器输出信号的波形figure(3);ubplot(321);plot(t,amu(1:Lt));a某i([0,t0,-ma某(amu)-0.3,ma某(amu)+0.3]);某label('t');title('上边带信号');%%[amuf,amu,df1,f]=T2F_new(amu(1:Lt),dt,df,f);%上边带信号频谱ubplot(322);plot(f,ffthift(ab(amuf)));%画出经过理想带通滤波器后信号频谱某label('f');title('上边带信号频谱');a某i([-fc-5某f0,fc+5某f0,0,ma某(amuf)+0.1]);et(gca,'某Tick',-10:10:10);et(gca,'某Grid','on');SSB(滤波法法)调制解调Matlab.m文件源码%%%将已调信号送入信道%先根据所给信噪比产生高斯白噪声ignal_power=power_某(amu(1:Lt));%已调信号的平均功率noie_power=(ignal_power某f)/(nr_lin某4某Bw_eq);%求出噪声方差（噪声均值为0）noie_td=qrt(noie_power);%噪声标准差noie=noie_td某randn(1,Lt);%产生噪声%画出信道高斯白噪声波形及频谱，此时，噪声已实现，为确知信号，可求其频谱ubplot(323);plot(t,noie);a某i([0,t0,-ma某(noie),ma某(noie)]);某label('t');title('噪声信号');ubplot(324);[noief,noie,df1,f]=T2F_new(noie,dt,df,f);%噪声频谱plot(f,ffthift(ab(noief)));%画出噪声频谱某label('f');title('噪声频谱');%%%信道中的信号%叠加了噪声的已调信号频谱am=amu(1:Lt)+noie(1:Lt);ubplot(325);plot(t,am);a某i([0,t0,-ma某(am),ma某(am)]);某label('t');title('信道中的信号');ubplot(326);[amf,am,df1,f]=T2F_new(am,dt,df,f);%求出叠加了噪声的已调信号频谱plot(f,ffthift(ab(amf)));%画出叠加了噪声的已调信号频谱某label('f');title('信道中信号的频谱');a某i([-fc-5某f0,fc+5某f0,0,ma某(amf)+0.1]);et(gca,'某Tick',-10:10:10);et(gca,'某Grid','on');%%%----------------经过带通滤波器%经过理想滤波器后的信号及其频谱DEM=H_high.某amuf;%滤波器输出信号的频谱[dem]=F2T_new(DEM,f);%滤波器输出信号的波形figure(4);SSB(滤波法法)调制解调Matlab.m文件源码ubplot(321);%经过理想带通滤波器后的信号波形plot(t,dem(1:Lt));%画出经过理想带通滤波器后的信号波形a某i([0,t0,-ma某(dem)-0.3,ma某(dem)+0.3]);某label('t');title('理想BPF输出信号');%%[demf,dem,df1,f]=T2F_new(dem(1:Lt),dt,df,f);%求经过理想带通滤波器后的信号频谱ubplot(322);plot(f,ffthift(ab(demf)));%画出经过理想带通滤波器后信号频谱某label('f');title('理想BPF输出信号频谱');a某i([-fc-5某f0,fc+5某f0,0,ma某(demf)+0.1]);et(gca,'某Tick',[-10:10:10]);et(gca,'某Grid','on');%%%--------------和本地载波相乘，即混频ubplot(323);plot(t,c(1:Lt));a某i([0,t0,-E-0.2,E+0.2]);某label('t');title('本地载波');ubplot(324);%频谱载波[C,c,df1,f]=T2F_new(c(1:Lt),dt,df,f);plot(f,ffthift(ab(C)));%画出载波频谱某label('f');title('本地载波频谱');a某i([-fc-5某f0,fc+5某f0,0,ma某(C)+0.3]);et(gca,'某Tick',[-10:10:10]);et(gca,'某Grid','on');%再画出混频后信号及其频谱der=dem(1:Lt).某c(1:Lt);%混频%%ubplot(325);%画出混频后的信号plot(t,der);a某i([0,t0,-R,R]);某label('t');title('混频后的信号');ubplot(326);[derf,der,df1,f]=T2F_new(der,dt,df,f);%求出混频后的信号频谱plot(f,ffthift(ab(derf)));%画出混频后的信号频谱某label('f');title('混频后的信号频谱');a某i([-2某fc-5某f0,2某fc+5某f0,0,ma某(derf)+0.3]); SSB(滤波法法)调制解调Matlab.m文件源码et(gca,'某Tick',[-10:10:10]);et(gca,'某Grid','on');%%%-----------------经过低通滤波器%画出理想低通滤波器figure(5);[LPF,f]=lp_f(length(der),Bw_eq,df1,f,1);%求出低通滤波器ubplot(411);plot(f,ffthift(ab(LPF)));%画出理想低通滤波器某label('f');title('理想LPF');a某i([-f0-Bw_eq,f0+Bw_eq,-0.05,1.05]);%%%混频信号经过理想低通滤波器后的频谱及波形DM=LPF.某derf;%理想低通滤波器输出的频谱[dm]=F2T_new(DM,f);%滤波器的输出波形ubplot(412);plot(t,dm(1:Lt));%画出经过低通滤波器后的解调波形a某i([0,t0,-ma某(dm)-0.2,ma某(dm)+0.2]);某label('t');title('恢复信号');et(gca,'YTick',[-1:0.5:1]);et(gca,'YGrid','on');ubplot(413);[dmf,dm,df1,f]=T2F_new(dm(1:Lt),dt,df,f);%求LPF输出信号的频谱plot(f,ffthift(ab(dmf)));%画出LPF输出信号的频谱某label('f');title('恢复信号频谱');a某i([-fc,fc,0,ma某(ab(dmf))+0.1]);et(gca,'某Tick',[-10:10:10]);et(gca,'某Grid','on');%%ubplot(414);plot(t,m(1:Lt));%画出调制信号波形某label('t');title('调制信号');et(gca,'YTick',[-R:1:R]);a某i([0,t0,-R-0.3,R+0.3])某label('t');title('调制信号');SSB(滤波法法)调制解调Matlab.m文件源码子函数%序列的傅里叶变换%各参数含义与子函数T2F中的完全相同，完成序列的傅里叶变换function[M,m,df]=ffteq(m,t,df)f=1/t;ifnargin==2n1=0;elen1=f/df;endn2=length(m);n=2^(ma某(ne某tpow2(n1),ne某tpow2(n2)));M=fft(m,n);m=[m,zero(1,n-n2)];df=f/n;end%计算信号功率functionp=power_某(某)%某:输入信号%p:返回信号的某功率p=(norm(某).^2)./length(某);end%将信号从频域转换到时域function[m]=F2T(M,f)%----------------输入参数%M：信号的频谱%f:系统采样频率%----------------输出（返回）函数%m:傅里叶逆变换后的信号，注意其长度为2的整数次幂，利用其画波形时，要注意选取m的一部分，选取长度和所给时间序列t的长度要一致，plot(t,m(1:length(t))),否则会出错m=real(ifft(M))某f;end%将信号从时域转换到频域function[M,m,df1,f]=T2F(m,t,df,f)SSB(滤波法法)调制解调Matlab.m文件源码%----------------输入参数%m：信号%t:系统时域采样间隔、%df:所需的采样频率%f:系统采样频率%----------------输出（返回）函数%M：傅里叶变换后的频谱序列%m:输入信号参与傅里叶变换后对应序列，需要注意的是，该序列与输入信号m的区别，其长度是不一样的，输入的m长度不一定是2的整数次幂，而傅里叶变换要求输入信号长度为2的整数次幂，%故傅里叶变换前需要对m信号进行补零操作，其长度有所增加，估输出参数中的m为补零后的输入信号，其长度与输入参数m不一样，但与M,f的长度是一样的，%并且，其与时间序列t所对应的序列m(1:length(t))与输入参数中的m是一致的。

实验三SSB信号的调制和解调的仿真实验
实验三 SSB信号的调制和解调的仿真实验
一、实验目的
1．掌握SSB信号系统工作原理；
3．掌握SSB信号的的Matlab/Simulink仿真方法。

二、实验仪器
1．PC机
一台一套
2．Matlab软件
三、实验原理
Matlab/Simulink仿真建模的基本方法和步骤详见附录四Simulink仿真举例说明。

SSB信号调制
仿真模型如图1所示，其中常用模块的引用路径见附录四Simulink仿真举例说明，
四、实验内容
1. 进一步熟悉并掌握Matlab/Simulink基本库、通信库和DSP库中较为重要的一些功能
模块的作用以及相应功能参数的物理意义与设置方法。

2. 搭建。

SSB信号仿真模型如图1所示。

设置系统参数并调试，同时观测并记录各点
的时域波形及频域图。

3. 改变信号与载波的频率，重测图所示模型中各点的时域波形以及频域图。

五、实验报告要求
（1）SSB系统的Simulink模型；。

海南大学通信电子线路课程设计报告学院：信息科学技术学院课题名称：单边带的调制与解调专业班级：12通信工程B班姓名：学号：指导老师：黄*设计时间：2014.10——2014.12使用仪器：Multisim12同组成员：目录摘要及关键词 (1)一设计总体概述 (2)1.1 设计任务 (2)1.2.设计指标 (2)二系统框图 (2)（一）SSB调制电路 (2)（二）SSB解调电路 (3)三各单元电路图及仿真 (4)1 平衡调制器 (4)2 带通滤波器 (8)3 相乘器 (12)4.低通滤波器 (13)四总电路图 (15)五自设问题及解答 (16)六心得体会总结 (16)七所遇问题及未解决问题 (17)参考文献 (17)内容摘要本文用Multisim12设计并仿真了单边带的调制越解调，由于在调制单元，先设计一个混频器（双平衡调制器），在混频的两端通过信号发生器输入一个调制低频信号 f 和载波信号0f ，完成频谱的搬移，成为一个DSB 信号，再设计一个带通滤波器，将DSB 经过带通滤波器变成一个抑制单边带的SSB 波信号。

单边带SSB 节约频带，节省功率，具有较高的保密性。

在解调单元，将调制单元输出的SSB 和通过一个信号发生器产生的和调制单元同频同相的载波输入在相乘器（双平衡调制器）的两端，完成混频。

再设计一个低通滤波器，将相乘器输出的信号经过低通滤波器，就可恢复基带信号低频信号0f ，完成解调。

在设计单元电路时，对每部分的电路设置参数，进行仿真，调参，对结果进行分析，由于在SSB 调制时，带通滤波的带宽相对中心频率的系数太小，所以将载波设置成较低频信号。

反复调试后，得出结果和心得体会。

【关键词】：单边带 调制解调 平衡调制器 带通滤波器 低通滤波器 仿真单边带的调制与解调一、设计总体概述1.1设计任务设计单边带的调制解调电路，要求分别设计混频器、带通滤波器，和低通滤波器。

通过信号发生器产生一个调制信号和载波信号，加入混频器的两端，将调制信号搬到了高频出，再经过带通滤波器，输出抑制载波的双边带调幅波，再经过带通滤波器，产生抑制载波的单边带调幅波。

数字通信原理课程设计课题名称 单边带（SSB ）调幅与解调姓 名学 号院 系 专 业 指导教师2010年 1 月15日※※※※※※※※※ ※※ ※※ ※※※※※※※※※※※2007级学生数字通信原理课程设计一、设计任务及要求：（1）实现单边带调幅和解调。

（2）用MATLAB软件将此次设计在电脑上实现，观察输出的波形。

（3）要求有各种需要的信号波形输出，并记录。

指导教师签名：2010年 1 月15 日二、指导教师评语：指导教师签名：2010年 1 月15 日三、成绩：验收盖章2010年 1 月15 日单边带（SSB）调幅与解调0712401-19王少林（湖南城市学院物理与电信工程系通信工程专业，益阳，413000）1、设计目的1 通过本课程设计的开展，使我们能够掌握通信原理中模拟信号的调制和解调、数字基带信号的传输、数字信号的调制和解调，模拟信号的抽样、量化和编码与信号的最佳接收等原理。

2 加深对《数字通信原理与技术》及《MA TLAB》课程的认识，进一步熟悉M语言编程中各个指令语句的运用；进一步了解和掌握数字通信原理课程设计中各种原理程序的设计技巧；掌握宏汇编语言的设计方法；掌握MATLAB软件的使用方法，加深对试验设备的了解以及对硬件设备的正确使用。

加强对于电路图的描绘技能，巩固独立设计实验的实验技能。

提高实践动手能力。

2、设计的主要内容和要求1采用matlab或者其它软件工具实现对信号的单边带( SSB )调幅和解调，并且绘制相关的图形；通过编程设置，对参数进行调整，可以调节输出信号的显示效果。

所有设计要求，均必须在实验室调试，保证功能能够实现。

2系统经过的信道都假设为高斯白噪声信道。

3模拟调制要求用程序画出调制信号，载波，已调信号、解调信号的波形，数字调制要求画出误码率随信噪比的变化曲线。

3、整体设计方案单边带调制信号是将双边带信号中的一个边带滤掉而形成的。

根据方法的不同，产生SSB信号的方法有：滤波和相移法。