资料分析讲义(中公+华图深度班综合版_超级经典!超级珍藏版)

8．【答案】香港：6218007/(6218007+1881769+392425) 澳门：1881769/(6218007+1881769+392425) 台湾：392425/(6218007+1881769+392425)
9．【答案】先求 5 月的数据，再做比
10．【答案】2174629/（1+19.29%） 11．【答案】1351623/（1+22.03%）
335.6÷（1+10%）/975.5÷（1+19.5%） 22．【答案】.960.2÷（162.3÷10.5%） 23．【答案】.399.0÷（162.3÷10.5%） 24．【答案】. 960.2÷（162.3÷10.5%）-1.2% 25．【答案】. 960.2÷（1+21.9%）/[ 960.2÷（162.3÷10.5%）-1.2%] 26．【答案】.399.0÷（1+13.6%）除以（25 题结果） 27．【答案】. 162.3÷（1+24.4%） 除以（25 题结果） 28．【答案】.正确，2003 年中央财政科技拨款增长率比国家财政科技拨款的增长率高，所 以占的比重会增大。可以求解，注意列综合式，不能每一步单独计算，会增加运算的不确定 性。 29．【答案】.错误。
5 月总的入境旅游人数：10666830/(1+6.47) 两者做比 23．【答案】5 月来自欧洲的入境旅游人数：496024/(1+17.11%) 5 月总的入境旅游人数：10666830/(1+6.47) 两者做比 24．【答案】5 月来自非洲的入境旅游人数：57028/(1+15.42%) 5 月总的入境旅游人数：10666830/(1+6.47) 两者做比 25．【答案】5 月来自其他国家的入境旅游人数：233/(1+13.11%) 5 月总的入境旅游人数：10666830/(1+6.47) 两者做比 26．【答案】476486/1564539 27．【答案】476486/1564539-1 28．【答案】错，来自澳门的入境人数同比有所下降 29．【答案】徒步 30．【答案】（正确） 真题回顾 126．【答案】C。解析：A 项错，非洲的同比月增长率是最大，但是基数太小，故不能说人 数增长最多；D 项明显错误；B 项不好判断，先看 C，看游客喜欢徒步的程度只需比较，徒 步旅游人数占总人数的百分比就可以，观察图表，C 项正确，故选 C。 127．【答案】A。解析：外国五月旅游人数：2174629÷（1+19.29%）≈1822977，五月旅游 总人数=10666830÷(1+6.47%)≈10018625,那么，比值为：（10018625-1822977）÷1822977 ≈4.5,选 A。

第二、三节 速算技巧开篇第一讲我们提到行测特别是其最后一部分——资料分析部分，时间紧、任务重，如何提高答题的速度至关重要，今后两节课就来解决这样的问题。

一、估算理念开篇第一句：一切计算都要估算！！！所谓估算，是在适当的精度要求下，进行粗略估值的速算方式。

估算精度等级结合题目、选项进行分析判定。

【例1】下表显示了2007年第三季度某市各区流通部门创造产值及其所占比例：(单位：百A ．1．5B ．2．5C ．3．5D ．4．5 【答案】C【解析】845.67845.67 3.30%9.40%10 3.385.399.40%85.393.30%GDP GDP -==⨯=⨯≈+中心区1（）南区3【例2】根据下图材料，如果2006年该企业赋税增长率维持在2005年的水平上，2006年的赋税应该约为多少?( )A ．36463B ．35607C ．33895D ．32583【答案】A【解析】2005年该企业的赋税总额高于2004年，若2006年赋税增长率维持在2005年的水平上，2006年新增赋税应该多于2005年。

从2004年到2005年增长了共3000+ (千元)，按照同样的增长率，从2005年到2006年增长应该至少有3000+(千元)，选择A 。

二、直除法“直除法”是指在比较或者计算较复杂分数时，通过“直接相除”的方式得到商的首位（首一位或首两位），从而得出正确答案的速算方式。

“直除法”在资料分析的速算当中有非常广泛的用途，并且由于其“方式简单”而“极易操作”。

“直除法”从题型上一般包括两种形式：（1）比较多个分数时，在量级相当的情况下，首位最大/小的数为最大/小数；（2）计算一个分数时，在选项首位不同的情况下，通过计算首位便可选出正确答案。

“直除法”从难度深浅上来讲一般分为三种梯度：（1）简单直接能看出商的首位；（2）通过动手计算能看出商的首位；（3）某些比较复杂的分数，需要计算分数的“倒数”的首位来判定答案。

主讲教师：李委明
-1-
版权所有，盗用必究
华图教育在线

◆成数 几成相当于十分之几
【例】某单位有 300 名员工，其中有 60 人是党员，则党员占总人数的几成？ 【解】
◆折数
几折相当于十分之几
【例】某服装原件 400 元，现价 280 元，则该服装打了几折？
【解】
【注】打 N 折是指“便宜到原价的 N ”，还是“便宜原价的 N ”？
◇GDP（国内生产总值） GDP 是英文（Gross Domestic Product）的缩写，也即国内生产总值。它是指一个国家（或地区）所 有常住单位在一定时期内生产的最终产品和服务价值的总和。
◇GNP（国民生产总值） GNP 是英文（Gross National Product）的缩写，也即国民生产总值。它是指一个国家（或地区）所 有国民在一定时期内生产的最终产品和服务价值的总和。
在做题中，如果我们需要求解一串较复杂数的中位数，将其“按大小顺序排列”并 不是一个好的方法，因为这样做耗时耗力，并且容易出错。实际操作中我们可以采取“去 掉一个最大值，再去掉一个最小值”，甚至“去掉 N 个最大值，再去掉 N 个最小值”的方式， 最后留下来一个或者两个数，便可得到我们所需要的中位数。
主讲教师：李委明
-3-
版权所有，盗用必究
华图教育在线

◇环比：现在统计周期和上一个统计周期相比较，包括日环比、月环比、年环比。
【例】今年三月完成产值 2 万元，四月完成 2.2 万元，环比增长(2.2-2) ÷2×100%＝10%。
【注】环比实际上即指“与紧紧相邻的统计周期相比较”。
上证指数在2019年年内肯定超过2000点大关iiiiiivd2019年年底江苏农药价格比农资价格高题1042019年江苏农药价格下降最大的月份是a2题1052019年江苏化肥价格最高的月份是a2第三节柱状图例1根据下图回答121125题国2019年一类材料二国2019年二类材料二题121该市2019月的总保费收入比去年同期约增长了a141341题122该市2019约减少了6题123与上一年同期相比增幅最大的是月财产险保人身险保费收入题1242019健康险和意外伤害险无法判断题125根据四年来该市保费收入化可以推出1该市的收入有较大增长2人理意识不断增强例131135题国2019年一类材料四2019年部分城市日照时数题131北京的日照时数超过200小时的月份有38题133在5拉萨题134上海日照时数相差最大的两个月是10月和12上海6月份的日照时数少于北京4月份的日照时数10月份各个城市的日照时数差别最小例3根据下图回答问题2019类材料一1998用图单位

............................................................................................................................14
第四课时
..........................................................................................................................................................15
l强化练习一：国家2011年材料三.
.......................................................................................................19
l强化练习二：10-918联考材料四.
........................................................................................................20
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....

资料分析：唯一的办法就是，在正确方法的引导下进行机械化、流程式操作。

（做题顺序，排在前二或三位）主要考察应考人员对各种形式的统计资料（包括文字、图形和表格等）进行正确理解、计算、分析、比较、判断、处理的能力。

解题步骤：（1读题干（30s ）；对象“ ”；陷阱“ ”）（2）以题定位（3）准确列式 （4）合理估算计分（0.7-1），17个/20以上一、统计术语（一）掌握型术语（1）百分数<一个是量的比较>：A/B*100%。

解答与百分数有关的试题时，要明确是以什么作为标准来进行比较(和谁比，就是以谁为标准)。

如：去年的产量为a ，今年的产量为b ，今年的产量比去年高10%，则b-a=10%a （以去年的产量为标准）；去年的产量为a ，今年的产量为b ，去年的产量比今年低10%，则b-a=10%b （以今年的产量为标准）。

百分点<一个是率的比较>：以百分数的形式表示相对指标的变动幅度，没有百分号。

如：今年的产量提高了17%，去年的产量下降了12%，则今年比去年提高了29个百分点，但是不能说今年比去年提高了29%。

成数：一成即十分之一。

折数：一折即十分之一。

比重：整体中某部分所占的份额。

（2）基期、现期（报告期） 基期：作为对比基础的时期，现期：相对基期而言的一个概念。

如：“和2003年8月相比，2003年9月的某量发生的变化”，则以2003年8月为基期，2003年9月为现期。

（3）倍数：两个有联系的指标的对比。

如：去年的产量为a ，今年的产量是去年的3倍，则今年产量为3a ；去年的产量为a ，今年的产量比去年增长了3倍，则今年产量为4a 。

翻番：即数量加倍，翻一番为原来的2倍，翻两番为原来的4倍；依此类推，翻n 番为原来的2n 倍。

（4）指数 用于衡量某种要素相对变化的指标量，通常将基期的指数值定为100，其它量和基期量相比较得出的数值即为该时期的指数值。

如：a=60，b=40，若b 的指数为100，则a 的指数为150。

目录2023年度国考资料分析基础讲义 (1)第一章统计学基础概念 (1)第二章增长类公式 (6)第一节增长率 (6)第二节基量 (8)第三节增长量 (10)第四节现量 (12)第五节间隔增长率 (15)第六节乘积增长率 (16)第七节混合增长率 (17)第三章比重类公式 (18)第一节现期比重 (18)第二节现期总量 (19)第三节现期部分量 (20)第四节基期比重 (22)第五节比重变化 (23)第四章倍数 (25)第一节倍数之间的概念关系 (25)第二节量的倍数与比例间的倍数 (27)第三节基期的倍数 (28)第五章平均数 (30)第一节几个数的平均数 (30)第二节平均数的常见公式 (31)第三节求份数 (32)第三节基期的平均数 (33)第四节平均数的增长量 (35)第五节平均数的增长率 (36)第六章资料分析材料形式 (37)第一节文字类 (37)第二节表格类 (40)第三节柱形图 (44)第四节折线图 (48)第五节扇形图 (52)第六节网状图 (54)2023年度国考资料分析基础讲义第一章统计学基础概念概念一：同比和环比同比指与上年同期相比；环比指与上一个时期相比，该时期应该是最小的时间量。

环比分为日环比、周环比、月环比和年环比。

但一般在行测中出现的环比为月环比，这时因为在绝大部分统计资料中出现的最小时间往往以月为单位。

如：2021年7月的同比时期为2020年7月2021年7月的环比时期为2021年6月2021年第三季度的同比时期为2020年第三季度2021年第三季度的环比时期为2021年第二季度2009年4月份中国汽车产销数据显示，在其他国家汽车销售进一步疲软的情况下，国内乘用车销量却持续上升，当月销量已达83.1万辆，其中，轿车销量占到71%，比三月份增长8.3%，同比增长33.04%。

问题1: 2008年4月，中国轿车销量为？问题2: 2009年3月，中国轿车销量为？概念二：基量与现量、增长量和增长率统计学中一般会出现若干的时期之间的关系，一般而言：跟哪个时期相比，哪个时期就叫做基期，而在基期所体现的量值，被称为基量。

5 4.8 100% ； 4.8
5 4.6 100% 。 4.6
13.39 100% 。 41.61 13.39
中公教育学员专用资料
报名专线：400-6300-999
版权所有
翻印必究
四、年均增长
（二）例题精讲 【例 1】①【答案】C。解析：
7119 .7 3801.8 ； 5
四、比重变化量的计算
（二）例题精讲 【例 1】解析：2012 年上半年加工贸易进口额增长 0.7%，进口总额增长 6.7%，所以比重下降，所 求为
2278.8 6.7% - 0.7% （ ） ，结果读作百分点的形式。 8854.6 1 0 .7 %
中公教育学员专用资料
报名专线：400-6300-999
版权所有
翻印必究
第五节 平均量
一、平均量的基础知识
（二）例题精讲 【例 1】解析：
5729 。 15.7
二、平均量基期值的计算
（二）例题精讲 【例 1】解析：
1534.6 1777 1534.6 1.204 。 1 19.6% 1 20.4% 1777 1.196
【例 2】解析：
第一节 尾数法
二、例题精讲
【例 1】【答案】C。解析：末一位相减，结果尾数为 4，选择 C。 【例 2】【答案】A。解析：末两位相加，25+70+67，结果末两位为 62，选择 A。 【例 3】【答案】B。解析：小数点后两位相加，51+30+20，小数点后为 01，选择 B。 【例 4】【答案】A。解析：原式看成 182+420-74-153，末一位相加减，2+0-4-3，结果尾数为 5，只 有 A 满足。 【例 5】【答案】C。解析：所求等于图中所有 A 省各计划时期生产总值总量数据相加，选项末两 位各不相同，则计算时只将各项末两位相加即可。注意 16863.3=16863.30，末两位 30 参与计算。选 择 C。

资料分析讲义本讲义分为四部分，依次为：一、基本概念梳理；二、读题技巧点拨；三、计算技巧强化；四、常见陷阱剖析；以下为本讲义文档结构图：一、基本概念梳理1、同比增长与环比增长；同比与环比的区别；2007.6与2006.6；2007.6与2007.5。

2、百分数与百分点；比过去增长20％——即过去为100，现在是120；比过去降低20％——即过去是为100，现在是80；降低到原来的20％——即原来是100，现在是20。

要特别注意区分“占”、“超”、“为”、“增”的含义和用法：“占计划百分之几”指完成计划的百分之几；“超计划的百分之几”，就应该扣除原来的基数；“为去年的百分之几”就是等于或相当于去年的百分几；“比去年增长百分之几”应扣掉原有的基数。

百分点是指不同时期以百分数形式表示的相对指标，如：速度、指数、构成等的变动幅度。

它是分析百分比增减变动的一种表现形式。

百分点的计算方式与百分数有何不同？3、倍数与翻番；倍数是由两个有联系的指标对比，将对比的基数抽象化为1而计算出来的相对数,常常用于比数（分子）远大于基数（分母）的场合。

例如：某城市2000年人均住房使用面积达到14.8平方米，为1978年3.8平方米的3.9倍（14.8÷3.8=3.9倍）。

再如，甲地人均国内生产总值8000元，为乙地3000元的2.67倍（8000÷3000=2.67倍）。

翻番是指数量以2的幂次方进行翻倍，翻一番是乘以2，翻两番是乘以22，翻三番是乘以23，依此类推。

例如：十六大报告中提出的全面建设小康社会的目标，即在优化结构和提高效益的基础上，国内生产总值到2020年力争比2000年翻两番，综合国力和国际竞争力明显增强。

也就是说2020年我国的国内生产总值将是2000年的4倍。

4、平均数与中位数；平均数是指在一组数据中所有数据之和再除以数据的个数。

它是反映数据集中趋势的一项指标。

公式为：总数量和÷总份数=平均数。

【行测讲义】资料分析一、行测资料分析的特点资料分析要紧考查应试者正确理解、综合分析文字资料、图形资料和表格资料的能力，要求应试者在解读给定资料的根底上通过直截了当查寻、指标换算、计算对照、分析判定等过程，针对资料中的咨询题得出正确的结论。

文字资料:要紧考查考生对大段蕴含数字的文字的阅读、分类和提炼能力；表格资料:要紧考查考生的数学计算能力，特殊是快速计算能力；图形资料:具有直瞧形象的特点，侧重考查考生的直觉判定和估算能力。

` 针对每一个资料，都有几个咨询题，依据资料提供的信息进行分析、对照、计算处理。

然后选择最咨询题最正确的答案。

1、文字资料〔单语段或多语段〕；2、表格资料〔二维统计表〕；3、柱状图、饼图、趋势图等；4、混合资料；3.资料分析的试题难度简单题型：要紧包括直截了当查寻排序以及一步计算题。

此类试题只需通过查寻和对照、简单计算，就能够得到答案，相对简单。

中等难度：要紧包括间接查寻排序以及数据关系相对简单的计算题。

此类试题需要依据材料提供的数据求出相关数据，考查考生对数据关系的把握能力和计算能力，在资料分析中所占的比重较大．到达百分之六十以上。

难度较高：要紧包括数据关系相对复杂的多步计算以及综合判定题。

此类试题需要考生依据题干或选项查寻到材料中的相关数据之后，再进行分析、计算及对照，从而得到答案，要紧考查考生对材料的综合分析理解能力。

在考试中的比重不是非常大.4.1)．综合考查比重上升近几年资料分析靠考试数据中能够瞧出，资料分析必考文字、图形和表格三种形式，同时逐步转向对三者综合的考查。

2)．难度加大，技巧性强资料分析局部试题的计算量加大，题目的难度变大，对考生估算能力的要求越来越高；其次，对计算技巧的考查力度加大，例如一些题目假如单纯的计算会白费许多时刻，而假如熟练把握解题技巧，这些题目甚至能够变成考生“秒杀〞的对象。

3).“陷阱〞题目增多近年的行测考试中，尤其一些综合判定性题目，出现了更多类型的“陷阱〞。

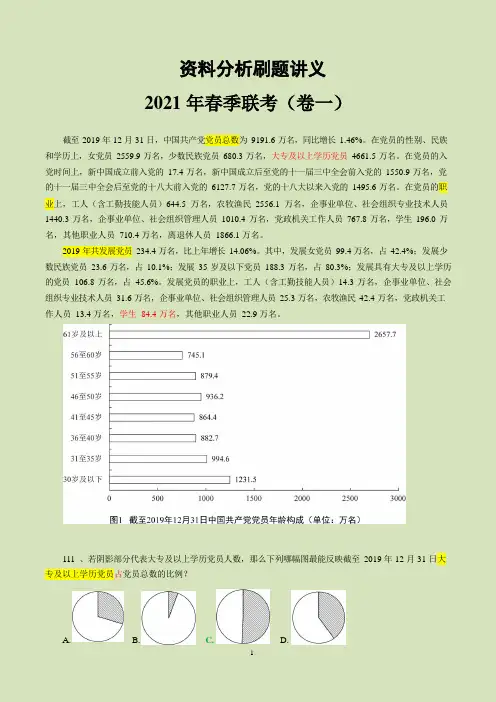
资料分析刷题讲义2021 年春季联考（卷一）截至2019 年12 月31 日，中国共产党党员总数为9191.6 万名，同比增长1.46%。

在党员的性别、民族和学历上，女党员2559.9 万名，少数民族党员680.3 万名，大专及以上学历党员4661.5 万名。

在党员的入党时间上，新中国成立前入党的17.4 万名，新中国成立后至党的十一届三中全会前入党的1550.9 万名，党的十一届三中全会后至党的十八大前入党的6127.7 万名，党的十八大以来入党的1495.6 万名。

在党员的职业上，工人（含工勤技能人员）644.5 万名，农牧渔民2556.1 万名，企事业单位、社会组织专业技术人员1440.3 万名，企事业单位、社会组织管理人员1010.4 万名，党政机关工作人员767.8 万名，学生196.0 万名，其他职业人员710.4 万名，离退休人员1866.1 万名。

2019 年共发展党员234.4 万名，比上年增长14.06%。

其中，发展女党员99.4 万名，占42.4%；发展少数民族党员23.6 万名，占10.1%；发展35 岁及以下党员188.3 万名，占80.3%；发展具有大专及以上学历的党员106.8 万名，占45.6%。

发展党员的职业上，工人（含工勤技能人员）14.3 万名，企事业单位、社会组织专业技术人员31.6 万名，企事业单位、社会组织管理人员25.3 万名，农牧渔民42.4 万名，党政机关工作人员13.4 万名，学生84.4 万名，其他职业人员22.9 万名。

111、若阴影部分代表大专及以上学历党员人数，那么下列哪幅图最能反映截至2019 年12 月31 日大专及以上学历党员占党员总数的比例？A. B. C. D.4661.5/9191.6＞1/2112、截至2019 年12 月31 日，新中国成立后至党的十八大前入党的人数是其余时间入党人数的约：A.3.8 倍B.4.1 倍C.4.6 倍D.5.1 倍=1550.9+6127.7/(9191.6-1550.9-6127.7)=7678.6/1513＞5113、截至2019 年12 月31 日，资料所列8 种党员职业类型中，党员人数占比不低于15%的有：A.3 类B.4 类C.5 类D.6 类9191.6*15%≈92*15=1380114、截至2019 年12 月31 日，55 岁以上党员人数比46 岁以下党员人数：A.多14.36%B.少14.36%C.多16.76%D.少16.76%=[(2657.7+745.1)-(864.4+882.7+994.6+1231.5)]/(864.4+882.7+994.6+1231.5)=(3402.8-3973.2)/3973.2≈-570/3973=-0.14X115、不能从上述材料中推出的是：A.2019 年发展的党员人数中，学生党员占比超过33%（84.4/234.4＞1/3）B.截至2019 年12 月31 日，55 岁以下党员占党员总数的比重不超过65%（56岁以上：3402.8/9191.6≈37%＞35%）C.截至2019 年12 月31 日，61 岁及以上的党员人数中，新中国成立前入党的不超过0.8%（17.4/2657.7＜0.8%）D.截至2019 年12 月31 日，从事农牧渔民职业的党员人数与工人（含工勤技能人员）党员人数之比超过400%（2556.1/644.5＜4）截至2019 年3 月31 日，证券业协会对证券公司2019 年第一季度经营数据进行了统计。

◆增速 增长速度=增长量¸基期量
◆增幅 增长了百分之几=增长量¸ 基期量 增长了几个百分点=增速- 基期增速 增幅和增速的关系，容易混淆，意义一样 表达的含义不同，增速表达速度，增幅表达大和小 增长了百分之几，相对；增长了几个百分点，绝对。
◆同比：与历史同期相比较 去年三月完成产值 2 万元，今年三月完成 2.2 万元，同比增长(2.2-2)¸ 2´ 100%=10%
盟，是参政党 * 合作的基本方针“长期共存，互相监督，肝胆相照，荣辱与共”。 * 八大民主党派：中国国民党革命委员会、中国民主同盟、中国民主建国会、中国民主促进
会、中国农工民主党、中国致公党、九三学社、台湾民主自治同盟 * 爱国统一战线
* 国内全体社会主义劳动者；全体用户祖国统一的爱国者 * 组织形式：政治协商制度 * 公民的基本权利（法定性、目的性、相对性和可放弃性）和义务（法定性、强制性、利他性和 不可放弃性） * 权利：法律平等、政治权利、宗教信仰权利、人身自由、社会经济权利、文化教育权利、监督 权和获取国家赔偿权、特定人的权利 * 义务：维护祖国统一和民族团结、遵守宪法和法律、维护祖国的安全荣誉和利益、保护祖国、
4
文档由风行下载 2011 正式版：/ 友情提供
依法纳税和其它义务 * 我国公民行使自由和权利的指导原则：不得损害国家的、社会的、集体的和其它公民的合法的
自由和权利 * 国家机构是国家为实现其职能而建立起来的国家机关的综合 * 我国国家机关：中央国家机关和地方国家机关 * 我国的中央国家机关：全国人民代表大会及其常务委员会、中华人民共和国主席、国务院、中
* 著作权（概念与特征、保护） * 专利权（概念、申请原则与期限、保护） * 商标权（概念与特征、取得和期限、保护） * 民事权利（概述、人身权、财产继承权） * 民事责任（概述、规则原则、方式） * 诉讼时效的概述（普通、特殊） * 诉讼时效的中止、中断与延长 * 诉讼时效的效力 * 经济法 * 经济法的概念及调整对象 * 经济法律的关系（概念、构成要素、主体） * 企业的概念及特征、种类 * 企业的分述：个人独资企业、合伙企业、公司、股份合作企业、国有国营企业 * 反不正当竞争法：概念及立法、不正当竞争行为、不正当竞争的法律责任 * 产品质量法：概念及使用范围、产品质量的监督管理、生产者销售者的产品质量义务、违反产 生质量法的法律责任 * 消费者权益保护法：消费者的权利和经营者的义务、争议的解决和法律责任 二、常识判断：政治常识 * 马克思主义哲学原理 * 哲学和哲学的基本问题、马克思主义哲学 * 马克思主义的唯物论（物质观、实践观、意识观） * 唯物辩证法（世界的普遍联系和永恒发展、世界永恒发展的一般规律） * 辩证唯物主义认识论（认识的本质、认识的辩证发展过程、认识的真理性及其检验标准） * 唯物主义历史观（社会存在和社会意识、社会基本矛盾、阶级国家和社会革命、人民群众和个 人在历史上的作用、社会进步和人的解放） * 邓小平理论及“三个代表”重要思想 * 当代中国的马克思主义（邓小平理论的形成和发展、“三个代表”重要思想是马克思主义中国 化的最新理论成果） * 社会主义初级阶段和党的基本路线（我国处在社会主义初级阶段、党在社会主义初级阶段的基 本路线） * 社会主义的根本任务和发展战略 * 建立社会主义市场经济体制 * 社会主义初级阶段的所有制结构和分配制度 * 建设社会主义的基本理论（改革、政治保证、精神文明、外交战略、和平统一“一国两制”） * 时事政治 * 国内时事：两会、台湾问题、经济发展、政治文明、三农问题、振兴东北、新农村、基础投 资、八荣八耻、西藏问题、社保体系…… * 国际时事：朝核问题、伊朗问题、中美关系、中日关系、上合组织、中梵关系、伊拉克局势、 巴勒斯坦问题、欧佩克集团、反恐合作…… * 推荐材料：《 参考消息》 、《 人民日报》

【行测资料集】：2012公务员考试【华图】名师模块班汇总讲义+练习题（全）: /source/42855/2012【华图】公务员考试【基础精讲班+强化班】资料汇总: /source/42907/华图2011公考资料大集合:/source/29711/2011【中公】公务员考试冲刺预测班行测【讲义+课件】: /source/41023/2011【中公】公务员考试冲刺预测班申论【讲义+课件】: /source/41012/2011【中公】公务员面试答题思路讲解班汇总:/source/42054/2011年【hua图】公务员面试新秀实战班MP3音频汇总: /source/42158/【华图】2011.4月24联考【蔡金龙】判断言语常识冲刺班讲义+课件:/source/40963/2011年公务员考试华图【蔡金龙】名师模块班-----判断推理讲义下载:/source/30276/2011年公务员考试华图【蔡金龙】名师模块班视频讲座-----判断推理（含讲义）: /source/30254/2011华图【魏华刚】高分技巧班-数量资料高分技巧讲义:/source/28592/2011.4.24联考【华图】公务员申论冲刺班讲义+课件（汇总）:/source/40861/2011【华图】真题+申论讲义（最新版）:/source/22509/【李进老师】2011年公务员考试秒杀系列教材行测秒杀专题-申论热点精读: /source/29959/【李进老师】2011年公务员考试秒杀系列教材行测秒杀专题-判断推理:/source/29957/【李进老师】2011公务员考试秒杀系列教材行测秒杀专题-资料分析:/source/29960/【李进老师】2011年公务员考试秒杀系列教材行测秒杀专题-数量关系: /source/29956/2011公务员【行测】【难点数量关系秒杀】----倒推-逻辑-数学归纳法:/source/28249/2011【李永新】全真模拟预测试卷行政职业能力测验12套题【国家公务员专用教材】:/source/26880/2011【华图】言语理解+数量关系+判断推理+常识讲义（新鲜出炉）:/source/22508/2011年公务员【王城】逻辑新讲义+题集:/source/29508/2011年公务员考试【秒杀系列】行测秒杀专题------判断推理（巧、快、准）: /source/29448/2011年【华图】基础班-章晓铭言语理解基础讲义:/source/28595/2011年【华图】公共基础知识-中国特色社会主义理论:/source/28594/2011年【华图】名师模块-资料分析讲义下载:/source/28593/2011华图【魏华刚】高分技巧班-数量资料高分技巧讲义:/source/28592/2011年公务员考试-----热点申论56篇（网上搜集）:/source/27752/华图2011省考新版强化提高班-行测-判断推理强化提高班汇总:/source/40892/2010年公考申论热点（不是七个怎么看，51个的）无水印清晰版:/source/29498/2010年【华图】国考冲刺班讲义[言语判断+常识+数量+申论]: /source/25453/【高清PDF扫描第4版】【华图】【伍景玉常识判断模块宝典】: /source/25456/2010【华图】国考VIP钻石笔试保过班高分技巧班讲义: /source/16867/3分钟搞定行测【数字推理】绝招（不得不看）:/source/19546/这500个常识公务员必须要了解（大家看看）：/source/24814/言语理解规律整理（总结得很不错）：/source/24815/行测中的数量关系题大全（内含答案）：/source/24818/2009年申论资料【半月谈】1-24期电子版:/source/19150/2009年公务员行测申论NO.1秘笈+面试NO.1秘笈:/source/13839/中公数学运算专项精炼200题:/source/25455/2010【中公】江苏深度班辅导【行测】内部讲义（清晰版）下载: /source/19584/2010公务员【行测】宝典打包下载（绿色破解版）:/source/22533/2010公务员【公共基础知识】宝典打包下载（绿色破解版）: /source/22534/公务员考试资料---阅读理解（行测80分高手总结经验）:/source/19680/【无密码破解版】2010年【顾菲】华图名师班-言语avi视频:/source/19859/【强烈推荐】2010公务员考试【行测+申论+面试】经典资料大放送:/source/18965/最新【华图】公务员培训申论精华资料（网络课程3小时应试技巧）:/source/19075/《2010国家公务员录用考试行政职业能力测验》专用教材配套学习软件（中共党史出版社）:/source/18631/花钱买的湖南【中公】教育资料【行测申论】都有:/source/19192/2010中公国考VIP资料+专项班答案:/source/18034/华图收费直播冲刺班讲义：钟君、李委明、顾斐:/source/17941/国家公务员考试常识888题:/source/16615/行政能力2010国考《行测》常识判断分析与预测:/source/17185/公务员考试应试要点和解题要诀55秒突破法:/source/18943/公务员考试【李委明】十大速算技巧（完整版）:/source/15240/数字推理精题例选500题及答案解析（觉得不错）:/source/17050/公务员考试【行测】法律常识部分MP3合集下载（内含华图李委明讲义的录音MP3及宋震冲刺法律真题讲解）:/source/15687/公务员考试必考常识1400题精美打印版:/source/18601/2010年华图钻石保过班和技巧提高班精华讲义:/source/16993/2010中公教育【李永新】公务员考试基础深度班视频课程-【申论篇】1.82GB: /source/18135/公务员考试【华图+中公+新东方】辅导班经典视频-音频mp3教程讲座讲义汇总: /source/18567/2010【新东方】国家公务员行政能力测试冲刺串讲mp3[共5讲]:/source/18122/2010【新东方】国家公务员考试强化精讲班视频课程【共五部分】:/source/18121/2010【新东方】国家公务员考试强化精讲班视频课程--《数量关系》:/source/18120/2010年【新东方】公务员考试经典视频资料大集合:/source/18522/2010公务员考试【李永新】行政能力测试-逻辑判断-视频教程:/source/18523/2010【最新升级版】公务员考试【行测】数学秒杀实战方法（全新快准）: /source/18528/2010【蔡金龙】华图名师模块班判断推理课件1-24+讲义:/source/17085/2010公务员考试数学运算精讲（数学运算看他就不难了）:/source/16763/2009年公务员考试备考mp3版---名师于洪泽、李委明等讲课:/source/13756/2010【华图】VIP钻石笔试保过班名师模块班讲义下载地址：/source/16948/2010年公务员考试【华图】钻石班包过班讲义:/source/16141/【华图】136天分类专项各个突破（行政+申论+模拟）内含答案:/source/16931/奇迹300分逻辑解题十八套路:/source/16128/公务员考试【华图】136天突破+李如海判断推理:/source/14376/史上最经典的【逻辑推理题】大全附答案:/source/20273/1358条公务员常识（绝对全）:/source/27546/2010年【华图】国家公务员考试钻石包过班-名师班（申论、言语、逻辑）汇总: /source/15111/2010【华图】钻石班全套视频+讲义（首发+完整版）BT下载:/source/16801/2010【华图】VIP钻石笔试保过班名师模块班讲义:/source/16948/【最新】2009年公务员考试【理论】热点面对面word 完整版:/source/16099/【版主推荐】公务员考试通关：申论+公共+行测总汇下载地址:/source/4364/2010年国家公务员考试一本通【陆玉春.夏欢.王巧芳】扫描版（完整版打包下载）:/source/18417/2010年【顾菲】华图名师班-言语avi视频（完整版打包下载）:/source/19859/2010【华图】国考VIP钻石笔试保过班高分技巧班讲义:/source/16867/2010【华图】难得的一些讲义，包括1万2钻石班的讲义:/source/16755/2010【华图】钻石保过班各模块讲义（完整版）:/source/16719/公务员冲关宝典[言语理解与表达]精美电子书090315版--【行政测试】: /source/11082/公务员行测常识txt整理版（适用手机看电子书）:/source/16996/2010【李世杰】国考速算秘诀（修订本上、中、下全套）:/source/17006/2010华图【李委明】数量关系宝典第4版PDF（完整版大小共34MB 打包下载）:/source/17341/华图【李委明】资料分析四大速算技巧:/source/16430/2010【新东方】国家公务员考试强化精讲班视频课程--《言语理解与表达》: /source/18118/2010年公务员考试--华图名师班【李委明】-资料分析:/source/12400/公务员考试【华图】培训名师模块班常识讲义:/source/16040/2010年【华图】国家公务员考试模拟题（推荐下载）:/source/17177/2010年【蔡金龙】华图名师模块班逻辑推理讲义:/source/15743/公务员考试-一个月行政能力测试高分秘诀:/source/16059/2010公务员考试常识大全+精选800例:/source/14285/公务员考试【华图+中公+新东方】辅导班经典视频-音频mp3教程讲座讲义汇总: /source/18567/公务员考试【华图】复习大全，共527页（内部资料，绝对精品）:/source/16658/2010国家公务员考试【华图】行政职业能力测试基础班讲义:2010公务员考试--【超全数学运算】强烈推荐:/source/18668/国家公务员考试【行测】出题频率最高题型大汇总:/source/18516/2010国家公务员考试基础法律常识课程讲义:/source/16464/2010年公务员考试【行测】言语理解自测题汇总:/source/14249/2010年【华图】国家公务员考试钻石包过班-名师班-言语理解与表达:/source/13838/[下载][推荐]公考常识40000题(1604页超长篇) 版主强势推荐:/source/4763/2010公务员考试【申论精华】+【新华时评】+【人民时评】+【半月评论】打包下载:2000～2009年国家公务员考试【行政职业能力】测验真题及详解:/source/16418/最为详细的【言语理解与表达题型及讲解】经典资料（推荐）:/source/16409/【华图】封闭培训班资料（朋友用3000元买来的，回报鲤鱼免费送给大家）: /source/17194/公务员考试【华图】培训班复习资料包（价值1500元资料免费赠送）: /source/17190/2010国家公务员考试资料\资料分析题目大汇总（word打印版）:/source/17142/公务员考试【行测】选择答案诀窍绝对实用:/source/17103/2009 中央国家公务员考试【行政职业能力】测试题及答案word打印版: /source/17102/行政能力【行政能力测验】言语理解与表达训练:/source/11115/申论得分技巧总结--申论78分总结得分技巧（看了至少提高5-10分）: /source/18061/2009年大笔经面试秘笈+行测申论秘笈:/source/14302/2010年【华图】国家公务员考试行测15天冲刺卷及答案解析:/source/17555/数学知识复习---奇妙数学大世界:/source/14082/逻辑解题技巧:/source/15384/牛人全面概括对言语理解的解题思路:/source/22407/【申论资料集】：2011【华图】真题+申论讲义（最新版）:/source/22509/【华图】万能申论宝典【范文+申论】（第四版电子书）随书赠送真题8套: /source/24153/2010【申论】热点总结Word版:/source/21790/2010【半月谈】半月评论1-5期:/source/21772/2009-2010.6期《半月谈》国内外大事及小测验:/source/25300/申论文章框架:/source/22722/2010【新东方】国家公务员申论冲刺串讲录音mp3+讲义:/source/18123/2007-2009年各省【申论】真题30套打印版[精心整理WORD版:/source/19536/公务员考生必看：高手教你申论如何拿满分:/source/17168/精品推荐【中公】国家公务员申论基础深度班讲义汇总（鲤鱼整理打包下载）: /source/19711/公务员考试【郭五林】教授《申论万能模板》:/source/17167/2009年【申论】华图冲刺班视频1-2+讲义（绝对精品）:/source/15406/半月谈MP3音频:/source/17145/【人民日报】【中共教育】2008冬-2009秋国内社会时政热点50条:/source/17144/公务员考试【申论】万用句型:/source/17204/公务员考试【申论】经典资料下载:/source/17203/华图【钟君】申论万能宝典3版:/source/16471/最新2010【华图】全封闭包过白金资料冲刺预测班【申论】“牛人”: /source/18258/公务员考试【申论经典背诵】142页（推荐下载）:/source/17003/公务员考试【李永新】教你十一步答好申论:/source/16566/时政申论公务员考试【李永新】老师“手把手”教你写申论:/source/14460/2010【钟君】华图申论范文宝典第4版PDF（完整版共37MB 高速下载）/source/17343/【孙景明老师】深悉2010年国考申论备战方略【共478.88MB】"/source/16793/2010【李永新】中公深度班全程申论（附件共863MB 打包下载）:/source/16802/公务员考试【申论范文】全集更新130个:/source/16357/2010【申论】高分素材十七大报告必背观点60条:/source/20436/2010年公务员考试【最具价值的申论热点】资料汇总:/source/18883/2010年国家公务员考试【申论】习题及答案（新大纲）:/source/17067/2010公务员考试【华图】冲刺班—申论MP3手机版:/source/17061/2010【高增霞主讲】公务员申论考前辅导视频讲座【共10讲】: /source/18114/公务员考试【申论】80分万能模板:/source/17055/时政申论2010【申论】答题技巧总结版:/source/18985/2010年国考深度班【李永新】申论视频下载:/source/15812/2010公务员考试【于洪泽】华图高分技巧班-申论:/source/16330/时政申论【华图】申论万能宝典第4版PDF（随书赠送8套真题）: /source/17336/2010年第一期【半月谈】评论下载:/source/19549/2010年公务员【申论】秒杀（80以上突破+）：/source/20686/2010年2月国内外【时事政治】Word版：/source/20621/2010年国务院温家宝总理政府工作报告Word版（全文）：/source/20619/【版主推荐】申论常见错误及对策:/source/22186/【真题汇总】：2010十一省公考行测真题及答案下载和申论真题解析下载: /source/23982/2000-2010年国考【行测】真题【数量关系】整理版附解析:/source/19805/2009年【天津、湖北、陕西】三省联考行测真题及参考答案:/source/22531/2009年【天津湖北陕西】三省联考申论真题及答案:/source/22532/2010【江西省】公务员考试【行测】真题及答案详解:/source/18994/2010【湖南省】公务员考试考前[行测+申论]内部押题密卷（不可外泄）: /source/21418/2010【福建省】公务员考试【行政能力测试】行测真题及解析：/source/20092/2010年【广东省】行测+申论真题及参考答案word版:/source/21848/【中公】2010【浙江省】公务员考试【行测】真题答案及解析:2001-2009【浙江省】公务员考试行测真题卷（名含答案）打包下载:/source/18310/2002-2009【福建省】公务员考试真题PDF版:/source/19518/2009年秋【福建省】公务员考试行测试卷真题及答案PDF版下载：/source/19712/2008年【浙江四川湖南上海天津等】全国十几个省历年【行测】真题及答案解析:/source/19406/2009年【四川黑龙江江苏浙江】各省公务员考试【行测】真题及答案解析: /source/19359/2010年【浙江省】公务员考试申论真题及答案（含广告）:/source/19709/2010年【浙江】公务员考试真题PDF清晰版下载（含解析）:2000-2008中央国家公务员考试【行测】真题+答案详解:/source/20173/2004-2009年【江苏】公务员考试行政能力测试试卷A、B、C类（内含答案解析）:/source/20178/2007-2010年国考【行政能力测试】行测试卷（完美解析）:/source/20179/广东公务员2002-2008真题:/source/11416/2009广东公务员行测预测题真题版（内含答案）:/source/13854/2008-2010【浙江】公务员考试行测真题附答案解析:/source/20180/2005-2009【湖南】公务员考试行测真题附答案解析:2006--2008年【上海】公务员考试行测真题下载（含答案解析）:/source/20074/2010年【浙江省】公务员考试行测+申论+综合基础知识(Word版):/source/19954/2003-2009年【山东省】公务员历年【行测】真题:/source/20432/2009年【福建省】春季公务员录用考试《行政职业能力测验》行测冲刺密卷: /source/19948/2004-2008年整理【江苏省】公务员和机关考试（公共基础知识很全）: /source/19807/2009年【重庆市福建省陕西省海南省】行测真题:/source/19409/2003--2009【云南省】公务员考试【行测】真题及详细解析：/source/20464/2008年【浙江四川湖南上海天津等】全国十几个省历年【行测】真题及答案解析:/source/19406/鲤鱼帮各位考友收集的30套各地方各省各年份的真题！内附资料分析，例题讲解真心希望大家在公务员考试里取得好成绩（互联网资料鲤鱼整理）:/source/7617/【面试资料】：公务员【哈密帮主】面试技巧全集共22MB（打包下载）:/source/16140/【哈密】面试资料mp3格式（六部分全）共90MB:/source/15998/面试小记：面试92.5分成功挑落笔试并列第一的对手:/source/17940/【经典推荐】公务员考试【面试】前突破实用资料(战术+套路+套话)附件完整版：/source/15996/行政能力公务员面试考生必看--孙景民面试经典套话:/source/11005/在特训班课堂上记的面试笔记（再经过适当整改，价格不菲）:/source/19195/公务员考试【刘彦】中公国考【面试】视频讲座下载:/source/19038/【2010新大纲版】公务员【面试】成功全程辅导600题pdf电子书:/source/19716/公务员综合精选面试1000题及答案:/source/4514/【2010新大纲版】公务员【面试】成功全程辅导600题pdf电子书免费下载:/source/19716/2010年国家各省公务员面试高分宝典【面试通关红宝书】:/source/19036/2009年华图---公务员面试应式技巧【张协云】视频资料（无密码破解版）: /source/12529/公务员考试【刘彦】中公国考【面试】视频讲座下载:/source/19038/培训班的面试材料（经典推荐）真的很好:/source/16101/公务员面试经典260题及答案+万能模板:/source/17599/更多公务员考试资料尽在鲤鱼网。

二、资料分析材料从何来 资料分析的材料一般会从各类统计公报中选取，例如国民经济和社会发展统计公报、旅游
市场统计公报等等。资料分析的材料均为真实材料，不做任何修饰与修改。 附录：中华人民共和国 2015 年国民经济和社会发展统计公报 /tjsj/zxfb/201602/t20160229_1323991.html
目录
1 资料分析总体概述...............................................................................................................2 2 资料分析基础概念...............................................................................................................3
统计图：资料分析考试中常见的统计图有两种：条形（折线）统计图、饼状图。 条形（折线）统计图：常见搭配为，条形图显示数据，折线显示增长率，数据显示较为直观， 我们需要注意各个数据间的变化趋势与大小关系；
饼状图：不仅能反应出各部分的数据，也能反应出部分与整体之间的关系，做题中我们可以根 据部分的面积大小，得出各部分的比重。
值通常作为计算过程中的除数或者减数； 本期，相对于基期而言，是当前所处的时期，该时期的数值通常作为计算过程中的被除数
或者被减数。 【注】和谁相比，谁做基期。
增长量、增长率（增长速度、增长幅度） 增长量，表示的是本期与基期之间的绝对差异，是一绝对值。 增长率，表示的是末期与基期之间的相对差异，是一相对值。
四、考试时间安排 分题型分析，文字材料：6-8 分钟；单纯统计表、统计图：5 分钟；综合题：6-8 分钟。 按照近年考试规律，一般会有四个资料分析，包含一个文字材料，两个综合题，一个单纯

【行测资料集】：【华图钻石班】全程全套包过精品笔记:/source/36675/【最新】2011公务员行测75分以上答题技巧_Word经济打印版:/source/36765/2011【中公版】公务员录用考试专项突破题库大合集:/source/37520/2011公务员考试【行测秒杀系列】汇总:/source/37658/公务员考试*行测*分项突破训练(179页打印版):/source/37407/公务员考试——行测高效复习方法:/source/37410/2011年公务员考试-行测84分珍藏国家公务员考试法律常识:/source/37411/华图2011公考资料大集合:/source/29711/绝密_2011【华图】钻石班保过资料含答案解析（内部资料）:/source/30897/2011【李委明】华图冲刺班——数量资料讲义+MP3录音:/source/34339/【高清第五版】2011公务员【华图】模块宝典高清PDF版下载（12本全）：/source/30285/2011年公务员考试华图【蔡金龙】名师模块班-----判断推理讲义下载:/source/30276/2011年公务员考试华图【蔡金龙】名师模块班视频讲座-----判断推理（含讲义）: /source/30254/2011华图【魏华刚】高分技巧班-数量资料高分技巧讲义:/source/28592/2011【华图】真题+申论讲义（最新版）:/source/22509/【李进老师】2011年公务员考试秒杀系列教材行测秒杀专题-申论热点精读:/source/29959/【李进老师】2011年公务员考试秒杀系列教材行测秒杀专题-判断推理:/source/29957/【李进老师】2011公务员考试秒杀系列教材行测秒杀专题-资料分析:/source/29960/【李进老师】2011年公务员考试秒杀系列教材行测秒杀专题-数量关系:/source/29956/2011公务员【行测】【难点数量关系秒杀】----倒推-逻辑-数学归纳法:/source/28249/2011【李永新】全真模拟预测试卷行政职业能力测验12套题【国家公务员专用教材】: /source/26880/2011【华图】言语理解+数量关系+判断推理+常识讲义（新鲜出炉）:/source/22508/2011年公务员【王城】逻辑新讲义+题集:/source/29508/2011年公务员考试【秒杀系列】行测秒杀专题------判断推理（巧、快、准）:/source/29448/2011年【华图】基础班-章晓铭言语理解基础讲义:/source/28595/2011年【华图】公共基础知识-中国特色社会主义理论:/source/28594/2011年【华图】名师模块-资料分析讲义下载:/source/28593/2011华图【魏华刚】高分技巧班-数量资料高分技巧讲义:/source/28592/2011年公务员考试-----热点申论56篇（网上搜集）:/source/27752/2010年公考申论热点（不是七个怎么看，51个的）无水印清晰版: /source/29498/2010年【华图】国考冲刺班讲义[言语判断+常识+数量+申论]:/source/25453/【吐血推荐】公务员考试模拟试卷（申论65套题+行测40套题）: /source/34566/【高清PDF扫描第4版】【华图】【伍景玉常识判断模块宝典】: /source/25456/2010【华图】国考VIP钻石笔试保过班高分技巧班讲义:/source/16867/3分钟搞定行测【数字推理】绝招（不得不看）:/source/19546/公务员**考霸心经**——原来数列题也有套路可循:/source/37339/公务员**考霸心经**——数学运算篇%2C秒杀数学运算题的无赖解法: /source/37340/这500个常识公务员必须要了解（大家看看）：/source/24814/言语理解规律整理（总结得很不错）：/source/24815/行测中的数量关系题大全（内含答案）：/source/24818/2009年公务员行测申论NO.1秘笈+面试NO.1秘笈:/source/13839/中公数学运算专项精炼200题:/source/25455/2010【中公】江苏深度班辅导【行测】内部讲义（清晰版）下载: /source/19584/2010公务员【行测】宝典打包下载（绿色破解版）:/source/22533/2010公务员【公共基础知识】宝典打包下载（绿色破解版）:/source/22534/公务员考试资料---阅读理解（行测80分高手总结经验）:/source/19680/【无密码破解版】2010年【顾菲】华图名师班-言语avi视频:/source/19859/【强烈推荐】2010公务员考试【行测+申论+面试】经典资料大放送:/source/18965/最新【华图】公务员培训申论精华资料（网络课程3小时应试技巧）:/source/19075/《2010国家公务员录用考试行政职业能力测验》专用教材配套学习软件（中共党史出版社）: /source/18631/花钱买的湖南【中公】教育资料【行测申论】都有:/source/19192/2010中公国考VIP资料+专项班答案:/source/18034/华图收费直播冲刺班讲义：钟君、李委明、顾斐:/source/17941/国家公务员考试常识888题:/source/16615/行政能力2010国考《行测》常识判断分析与预测:/source/17185/公务员考试应试要点和解题要诀55秒突破法:/source/18943/公务员考试【李委明】十大速算技巧（完整版）:/source/15240/数字推理精题例选500题及答案解析（觉得不错）:/source/17050/公务员考试【行测】法律常识部分MP3合集下载（内含华图李委明讲义的录音MP3及宋震冲刺法律真题讲解）:/source/15687/公务员考试必考常识1400题精美打印版:/source/18601/2010年华图钻石保过班和技巧提高班精华讲义:/source/16993/2010中公教育【李永新】公务员考试基础深度班视频课程-【申论篇】1.82GB:/source/18135/公务员考试【华图+中公+新东方】辅导班经典视频-音频mp3教程讲座讲义汇总:/source/18567/2010【新东方】国家公务员行政能力测试冲刺串讲mp3[共5讲]:/source/18122/2010【新东方】国家公务员考试强化精讲班视频课程【共五部分】:/source/18121/2010【新东方】国家公务员考试强化精讲班视频课程--《数量关系》:/source/18120/2010年【新东方】公务员考试经典视频资料大集合:/source/18522/2010公务员考试【李永新】行政能力测试-逻辑判断-视频教程:/source/18523/2010【最新升级版】公务员考试【行测】数学秒杀实战方法（全新快准）:/source/18528/2010【蔡金龙】华图名师模块班判断推理课件1-24+讲义:/source/17085/2010公务员考试数学运算精讲（数学运算看他就不难了）:/source/16763/2009年公务员考试备考mp3版---名师于洪泽、李委明等讲课:/source/13756/2010【华图】VIP钻石笔试保过班名师模块班讲义下载地址：/source/16948/2010年公务员考试【华图】钻石班包过班讲义:/source/16141/【华图】136天分类专项各个突破（行政+申论+模拟）内含答案:/source/16931/奇迹300分逻辑解题十八套路:/source/16128/公务员考试【华图】136天突破+李如海判断推理:/source/14376/史上最经典的【逻辑推理题】大全附答案:/source/20273/1358条公务员常识（绝对全）:/source/27546/2010年【华图】国家公务员考试钻石包过班-名师班（申论、言语、逻辑）汇总: /source/15111/2010【华图】钻石班全套视频+讲义（首发+完整版）BT下载:/source/16801/2010【华图】VIP钻石笔试保过班名师模块班讲义:/source/16948/【最新】2009年公务员考试【理论】热点面对面word 完整版:/source/16099/【版主推荐】公务员考试通关：申论+公共+行测总汇下载地址:/source/4364/2010年国家公务员考试一本通【陆玉春.夏欢.王巧芳】扫描版（完整版打包下载）: /source/18417/2010年【顾菲】华图名师班-言语avi视频（完整版打包下载）:/source/19859/2010【华图】国考VIP钻石笔试保过班高分技巧班讲义:/source/16867/2010【华图】难得的一些讲义，包括1万2钻石班的讲义:/source/16755/2010【华图】钻石保过班各模块讲义（完整版）:/source/16719/公务员冲关宝典[言语理解与表达]精美电子书090315版--【行政测试】:/source/11082/公务员行测常识txt整理版（适用手机看电子书）:/source/16996/2010【李世杰】国考速算秘诀（修订本上、中、下全套）:/source/17006/2010华图【李委明】数量关系宝典第4版PDF（完整版大小共34MB 打包下载）: /source/17341/华图【李委明】资料分析四大速算技巧:/source/16430/2010【新东方】国家公务员考试强化精讲班视频课程--《言语理解与表达》:/source/18118/2010年公务员考试--华图名师班【李委明】-资料分析:/source/12400/公务员考试【华图】培训名师模块班常识讲义:/source/16040/2010年【华图】国家公务员考试模拟题（推荐下载）:/source/17177/2010年【蔡金龙】华图名师模块班逻辑推理讲义:/source/15743/公务员考试-一个月行政能力测试高分秘诀:/source/16059/2010公务员考试常识大全+精选800例:/source/14285/公务员考试【华图+中公+新东方】辅导班经典视频-音频mp3教程讲座讲义汇总: /source/18567/公务员考试【华图】复习大全，共527页（内部资料，绝对精品）:/source/16658/2010国家公务员考试【华图】行政职业能力测试基础班讲义:/source/16587/2010公务员考试--【超全数学运算】强烈推荐:/source/18668/国家公务员考试【行测】出题频率最高题型大汇总:/source/18516/2010国家公务员考试基础法律常识课程讲义:/source/16464/2010年公务员考试【行测】言语理解自测题汇总:/source/14249/2010年【华图】国家公务员考试钻石包过班-名师班-言语理解与表达:/source/13838/[下载][推荐]公考常识40000题(1604页超长篇) 版主强势推荐:/source/4763/2010公务员考试【申论精华】+【新华时评】+【人民时评】+【半月评论】打包下载: /source/16877/2000～2009年国家公务员考试【行政职业能力】测验真题及详解:/source/16418/最为详细的【言语理解与表达题型及讲解】经典资料（推荐）:/source/16409/【华图】封闭培训班资料（朋友用3000元买来的，回报鲤鱼免费送给大家）:/source/17194/公务员考试【华图】培训班复习资料包（价值1500元资料免费赠送）:/source/17190/2010国家公务员考试资料\资料分析题目大汇总（word打印版）:/source/17142/公务员考试【行测】选择答案诀窍绝对实用:/source/17103/2009 中央国家公务员考试【行政职业能力】测试题及答案word打印版: /source/17102/行政能力【行政能力测验】言语理解与表达训练:/source/11115/申论得分技巧总结--申论78分总结得分技巧（看了至少提高5-10分）: /source/18061/2009年大笔经面试秘笈+行测申论秘笈:/source/14302/2010年【华图】国家公务员考试行测15天冲刺卷及答案解析:/source/17555/数学知识复习---奇妙数学大世界:/source/14082/逻辑解题技巧:/source/15384/牛人全面概括对言语理解的解题思路:/source/22407/【申论资料集】：2011【钟君】华图冲刺班——申论讲义+MP3录音:/source/34341/【最新】2011年国家公务员考试申论热点汇总版:/source/36766/2010年半月谈第1-24期半月评论（电子书版）:/source/36617/2011【华图】真题+申论讲义（最新版）:/source/22509/【华图】万能申论宝典【范文+申论】（第四版电子书）随书赠送真题8套: /source/24153/申论值得背诵的三篇文章:/source/36947/2010【申论】热点总结Word版:/source/21790/2010【半月谈】半月评论1-5期:/source/21772/2009-2010.6期《半月谈》国内外大事及小测验:/source/25300/申论文章框架:/source/22722/2010【新东方】国家公务员申论冲刺串讲录音mp3+讲义:/source/18123/2007-2009年各省【申论】真题30套打印版[精心整理WORD版:/source/19536/公务员考生必看：高手教你申论如何拿满分:/source/17168/精品推荐【中公】国家公务员申论基础深度班讲义汇总（鲤鱼整理打包下载）: /source/19711/公务员考试【郭五林】教授《申论万能模板》:/source/17167/2009年【申论】华图冲刺班视频1-2+讲义（绝对精品）:/source/15406/半月谈MP3音频:/source/17145/【人民日报】【中共教育】2008冬-2009秋国内社会时政热点50条:/source/17144/公务员考试【申论】万用句型:/source/17204/公务员考试【申论】经典资料下载:/source/17203/华图【钟君】申论万能宝典3版:/source/16471/最新2010【华图】全封闭包过白金资料冲刺预测班【申论】“牛人”: /source/18258/公务员考试【申论经典背诵】142页（推荐下载）:/source/17003/公务员考试【李永新】教你十一步答好申论:/source/16566/时政申论公务员考试【李永新】老师“手把手”教你写申论:/source/14460/2010【钟君】华图申论范文宝典第4版PDF（完整版共37MB 高速下载）/source/17343/【孙景明老师】深悉2010年国考申论备战方略【共478.88MB】"/source/16793/2010【李永新】中公深度班全程申论（附件共863MB 打包下载）:/source/16802/公务员考试【申论范文】全集更新130个:/source/16357/2010【申论】高分素材十七大报告必背观点60条:/source/20436/2010年公务员考试【最具价值的申论热点】资料汇总:/source/18883/2010年国家公务员考试【申论】习题及答案（新大纲）:/source/17067/2010公务员考试【华图】冲刺班—申论MP3手机版:/source/17061/2010【高增霞主讲】公务员申论考前辅导视频讲座【共10讲】:公务员考试【申论】80分万能模板:/source/17055/时政申论2010【申论】答题技巧总结版:/source/18985/2010年国考深度班【李永新】申论视频下载:/source/15812/2010公务员考试【于洪泽】华图高分技巧班-申论:/source/16330/时政申论【华图】申论万能宝典第4版PDF（随书赠送8套真题）: /source/17336/2010年第一期【半月谈】评论下载:/source/19549/2010年公务员【申论】秒杀（80以上突破+）：/source/20686/2010年2月国内外【时事政治】Word版：/source/20621/2010年国务院温家宝总理政府工作报告Word版（全文）：/source/20619/【版主推荐】申论常见错误及对策:/source/22186/【真题汇总】：【浙江省】2001-2010公务员考试行测试卷及答案解析:/source/37346/2011年国考行测真题及答案详解（完整版）:/source/36821/2011【李永新】全真模拟预测试卷行政职业能力测验12套题:2010十一省公考行测真题及答案下载和申论真题解析下载:/source/23982/2000-2010年国考【行测】真题【数量关系】整理版附解析:/source/19805/【福建省】2010年公务员考试行测真题及详细答案解析:/source/37217/【江西省】2010年度考试录用公务员申论真题及解析:/source/37219/【上海省】2010年度考试录用公务员申论真题及解析:/source/37220/【北京市】2009-2010年录用公务员考试申论真题及参考答案:/source/37222/2009年【天津、湖北、陕西】三省联考行测真题及参考答案:/source/22531/2010年[中公]公务员行政能力测试100套(含答案) :/source/36406/2009年【天津湖北陕西】三省联考申论真题及答案:/source/22532/2010【江西省】公务员考试【行测】真题及答案详解:/source/18994/2010【湖南省】公务员考试考前[行测+申论]内部押题密卷（不可外泄）: /source/21418/2010【福建省】公务员考试【行政能力测试】行测真题及解析：/source/20092/2010年【广东省】行测+申论真题及参考答案word版:/source/21848/【中公】2010【浙江省】公务员考试【行测】真题答案及解析:/source/19517/2001-2009【浙江省】公务员考试行测真题卷（名含答案）打包下载:/source/18310/2002-2009【福建省】公务员考试真题PDF版:/source/19518/2009年秋【福建省】公务员考试行测试卷真题及答案PDF版下载：/source/19712/2008年【浙江四川湖南上海天津等】全国十几个省历年【行测】真题及答案解析: /source/19406/2009年【四川黑龙江江苏浙江】各省公务员考试【行测】真题及答案解析:/source/19359/2010年【浙江省】公务员考试申论真题及答案（含广告）:/source/19709/2010年【浙江】公务员考试真题PDF清晰版下载（含解析）:/source/19676/2000-2008中央国家公务员考试【行测】真题+答案详解:/source/20173/2004-2009年【江苏】公务员考试行政能力测试试卷A、B、C类（内含答案解析）: /source/20178/2007-2010年国考【行政能力测试】行测试卷（完美解析）:/source/20179/广东公务员2002-2008真题:/source/11416/2009广东公务员行测预测题真题版（内含答案）:/source/13854/2008-2010【浙江】公务员考试行测真题附答案解析:/source/20180/2005-2009【湖南】公务员考试行测真题附答案解析:/source/20181/2006--2008年【上海】公务员考试行测真题下载（含答案解析）:/source/20074/2010年【浙江省】公务员考试行测+申论+综合基础知识(Word版):/source/19954/2003-2009年【山东省】公务员历年【行测】真题:/source/20432/2009年【福建省】春季公务员录用考试《行政职业能力测验》行测冲刺密卷:/source/19948/2004-2008年整理【江苏省】公务员和机关考试（公共基础知识很全）:/source/19807/2009年【重庆市福建省陕西省海南省】行测真题:/source/19409/2003--2009【云南省】公务员考试【行测】真题及详细解析：/source/20464/2008年【浙江四川湖南上海天津等】全国十几个省历年【行测】真题及答案解析: /source/19406/鲤鱼帮各位考友收集的30套各地方各省各年份的真题！内附资料分析，例题讲解真心希望大家在公务员考试里取得好成绩（互联网资料鲤鱼整理）:/source/7617/【面试资料】：公务员【哈密帮主】面试技巧全集共22MB（打包下载）:/source/16140/【哈密】面试资料mp3格式（六部分全）共90MB:/source/15998/面试小记：面试92.5分成功挑落笔试并列第一的对手:/source/17940/华图协议班内部绝密资料【面试】题型完全解答:/source/30421/【经典推荐】公务员考试【面试】前突破实用资料(战术+套路+套话)附件完整版：/source/15996/行政能力公务员面试考生必看--孙景民面试经典套话:/source/11005/在特训班课堂上记的面试笔记（再经过适当整改，价格不菲）:/source/19195/公务员考试【刘彦】中公国考【面试】视频讲座下载:/source/19038/【2010新大纲版】公务员【面试】成功全程辅导600题pdf电子书:/source/19716/公务员综合精选面试1000题及答案:/source/4514/【2010新大纲版】公务员【面试】成功全程辅导600题pdf电子书免费下载: /source/19716/2010年国家各省公务员面试高分宝典【面试通关红宝书】:/source/19036/2009年华图---公务员面试应式技巧【张协云】视频资料（无密码破解版）: /source/12529/公务员考试【刘彦】中公国考【面试】视频讲座下载:/source/19038/培训班的面试材料（经典推荐）真的很好:/source/16101/公务员面试经典260题及答案+万能模板:/source/17599/【经验与技巧】2011公务员考试：申论大作文写作结构如何确定:/source/37351/2011年公务员考试行测——全面复习方法与技巧:/source/37349/2011公务员招考：突破公文写作要点关为申论加分:/source/37348/公务员考试行测——10秒解题巧解数学问题:/source/30413/公务员考试申论——掌握技巧，短期奏效：/source/30406/公务员考试——六种技巧搞定你做不出来的行测题：/source/30407/公务员考试申论——申论写作之阅读篇技巧分析：/source/30408/公务员考试申论——从资料中寻找答题线索的诀窍：/source/30409/公务员考试申论——申论思维方式培养之四招：/source/30410/我的公务员考试心得体会—与大家共勉_经验交流：/source/30252/公务员考试资料---阅读理解（行测80分高手总结经验）：/source/19680/公务员考试自己总结的行测考试解题技巧和经验！！！：/source/7582/公务员考试行测——行测其实很简单——公务员考试状元心得: /source/30523/公务员考试行测——数学运算部分各种题型和思想的潜心研究: /source/30522/公务员考试行测——51.3秒决定公务员考试成败:/source/30520/公务员考试行测——言语理解与表达真题研究:/source/30519/公务员考试行测——资料分析四大速算技巧:/source/30518/。

还资料分析本来面目资料分析主要测查报考者对各种形式的文字、图表等资料的综合理解与分析加工的能力，这部分内容通常由统计性的图表、数字及文字材料构成。

针对一段资料一般有1～5个问题，报考者需要根据资料所提供的信息进行分析、比较、推测和计算，从四个备选答案中选出符合题意的答案。

思维型秒杀技巧:真题材料一：2008年全部金融机构本外存贷款情况指标年末数（亿元）比上年增长％企事业存款11490.12 9.7城乡居民储蓄存款14804.54 30短期贷款17219.69 16.0中长期贷款10742.81 19.52008年各项余额增加值最大的是：A 个事业存款B 城乡居民储蓄存款C 短期贷款D 中长期贷款14804.54/1.3*30％> 17219.69/1.16*16%材料二：2009年上半年居民现金收入情况金额（元/人同比增加（元/人同比增长％增速同比下降百分比工资性收入954 74 8.4 9.5家庭经营收入1512 79 5.5 13.4财产性收入78 7 9..9 14.1转移性收入189 45 31.4 8.7下列各项中，2008年上半年同比增加值最大的是：A 工资性收入B 家庭经营收入C 财产性收入D 转移性收入(1512-79）/1+5.5%+13.4% *(5.5%+13.4%)=1433/118.9%*18.9%今年比去年下降了13.4％，那么去年比今年就是增加了13.4％17.9 1.179 88018.9 1.189 143324 1.24 7140.1 1.401 144估算结果简易误差消除法截位算结果精确结果880*1/7= 126 167（+12）VS126(10）126+10＝136 1341433*1/6=23 200 (-11) VS239(-12) 239-12=227 22971*1/5 ＝14.2 25（-1）VS142（-0.5）142-5＝137 137144*2/7=288/7=41.14 41.21公式秒杀技巧:材料三（2009年国考真题）：全国2007年认定登记的技术合同共计220868项，同比增长7％；总成交金额2226亿元，同比增长22.44％；平均每项技术合同成交金额突破百万元大关，达到100.78万元。

/source/17067/
2010公务员考试【华图】冲刺班—申论MP3手机版:
/source/17061/
公务员考试【申论】80分万能模板:
/source/17055/
【最新】2009年公务员考试【理论】热点面对面word 完整版:
/source/16099/
【版主推荐】公务员考试通关：申论+公共+行测总汇下载地址:
/source/4364/
【孙景明老师】深悉2010年国考申论备战方略【共478.88MB】"
/source/15111/
2010【华图】钻石班全套视频+讲义（首发+完整版）BT下载:
/source/16801/
2010【华图】VIP钻石笔试保过班 名师模块班讲义:
/source/16948/
【无密码破解版】2010年【顾菲】华图名师班-言语avi视频:
/source/19859/
【强烈推荐】2010公务员考试【行测+申论+面试】经典资料大放送:
/source/18965/
最新【华图】公务员培训申论精华资料（网络课程3小时应试技巧）:
/source/18601/
2010年公务员考试【最具价值的申论热点】资料汇总:
/source/18883/
2010年华图钻石保过班和技巧提高班精华讲义:
/source/16993/
2010年国家公务员考试一本通【陆玉春.夏欢.王巧芳】扫描版（完整版 打包下载）:
/source/18417/
2010年国考深度班【李永新】申论视频下载:
/source/15812/

资料分析刷题讲义2022 年0326 联考2020 年我国数字经济规模达到39.2 万亿元，保持9.7%高位增长，占GDP 比重为38.6%，同比提升2.4 个百分点。

产业数字化发展深入推进，2020 年我国服务业、工业、农业数字经济占行业增加值比重分别为40.7%、21.0%和8.9%。

2020 年，数字经济规模超过 1 万亿元的省份有广东、江苏、山东、浙江、上海、北京、福建、湖北、四川、河南、河北、湖南和安徽；另有8 个省份超过5000 亿元；从GDP 占比看，北京、上海领先，分别达到55.9%和55.1%；从增速上看，贵州、重庆、福建数字经济增速位列前三，增速超过15%。

86 、2020 年，数字经济规模超过5000 亿元的省份有多少个？A.8B.11C.16D.21=13+8=2187、数字产业化占GDP 比重最大的年份是：A.2015 年B.2017 年C.2019 年D.2020 年备注：A*B≈[A*(1+10%)]*[B(1-10%)]=0.99AB【近似判断法】则A*B＞[A*(1+10%)]*[B(1-15%)]；A*B＜[A*(1+15%)]*[B(1-10%)]两两比较确定结果88、2015—2020 年，数字经济增速与GDP 增速之差超过8.5%的年份有多少个？A.3B.4C.5D.62015、2016、2017、201889、2020 年，产业数字化规模同比增长约：A.9.2%B.9.8%C.10%D.10.7%法一：数字经济规模同比增长率=A/B-1=9.7%结果=80.9%A/80.2%B-1=(1+9.7%)*(80.9%/80.2%)-1≈(1+9.7%)*(1+0.7%)-1=0.7%+9.79.7%+0.07%=10.47%法二：结果=39.2*80.9%/{[39.2/(1+9.7%)]*80.2%]}-1=(80.9%/80.2%)*(1+9.7%)-1（计算方法同上）90、不能从上述资料中推出的是：A.2020 年北京市数字经济规模全国领先（无法计算）B.2020 年数字经济增速是GDP 增速的3 倍多（9.7%/3%＞3）C.2020 年数字经济内部结构大约呈现“二八”比例分布（19.1%：80.9%）D.2020 年农业、工业和服务业数字经济渗透水平大约逐次倍增（8.9→21→40.7）2019 年某省规模以上企业就业人员年平均工资为62484 元，比上年增长10.1%。