数学建模预测营业额
- 格式:doc
- 大小:34.50 KB
- 文档页数:1


数学建模:利用大数据进行市场预测1. 引言1.1 概述数学建模是一种利用数学模型和方法来解决实际问题的过程。
在现代经济社会中,市场预测是企业制定发展战略、进行风险评估以及决策制定的重要依据之一。
随着大数据时代的到来,大量的市场数据变得可获取,这为我们进行精确的市场预测提供了新的机遇和挑战。
1.2 文章结构本文将分为六个主要部分进行讨论。
首先,在引言部分我们将概述本文的内容,并解释数学建模与市场预测之间的关系。
接下来,第二部分将介绍数学建模的概念与方法,并探讨大数据在市场分析中的作用。
第三部分将重点讲解数据收集与处理技术,包括大数据收集与整理方法、数据预处理技术以及数据特征提取和筛选方法。
第四部分将详细介绍市场预测模型构建与评估,包括回归分析、时间序列分析以及机器学习算法在市场预测中的应用。
在第五部分,我们将通过实际案例研究和实践经验分享来进一步加深对市场预测的理解。
最后,我们将在第六部分总结全文,并提出进一步研究的方向。
1.3 目的本文旨在探讨数学建模在市场预测中的应用,特别是利用大数据进行市场预测的方法和技术。
通过详细介绍数据收集与处理技术以及常见的市场预测模型构建方法,我们希望读者能够更加全面地了解数学建模在市场预测中的实际应用,并掌握相应的方法和技巧。
同时,通过案例研究和实践经验分享,我们将展示数学建模在不同领域、不同行业中的具体运用和效果。
最终,我们希望本文能为相关领域的专业人士和研究者提供有益的参考和启发。
2. 数学建模与市场预测2.1 数学建模的概念与方法在现代市场分析中,数学建模是一种应用数学方法和技术来描述、理解和预测市场行为的方法。
通过将实际市场问题抽象为数学对象,并运用数学公式和算法来构建模型,研究人员可以利用这些模型对市场进行定量分析和预测。
数学建模的关键步骤包括问题定义、数据收集、模型选择与建立、参数估计和验证等。
数学建模有多种方法可供选择,常见的包括回归分析、时间序列分析和机器学习算法等。

数学模型在销售预测中的应用销售预测是企业决策制定的重要组成部分,企业需要根据市场需求和自身资源来预测销售额并进行生产和营销计划。
如何精确地进行销售预测是企业发展的关键之一。
数学模型可以帮助企业进行销售预测,在决策制定、资源配置、风险控制等方面发挥着重要作用。
销售预测模型的类型在销售预测中,常用的模型包括时间序列模型、回归模型、神经网络模型等。
其中最为常见的是时间序列模型,该模型可以对未来一段时间内的销售量进行预测。
在将时间序列模型应用于销售预测中时,需要根据历史销售数据来对模型进行训练。
通过对历史数据的分析,可以确定不同时间段内销售量的分布规律,并根据规律进行预测。
回归模型则是根据市场和消费者的需求来预测销售量。
该模型需要进行数据的收集和建模,然后进行拟合和预测。
现代企业的销售预测常常会使用多个回归模型,针对不同的销售渠道和产品类型,以提高预测精确度。
神经网络模型则是根据数据进行建模,通过模拟人类的神经网络来预测销售量。
神经网络模型通常对数据要求更高,在训练和预测时需要更多的时间和计算资源。
数学模型的优势将数学模型应用于销售预测中,具有以下优势:提高预测精确度:数学模型可以对历史数据进行精确的分析,从而预测未来销售量的分布规律。
通过对模型进行不断训练和优化,可使预测精确度得到不断提高。
降低决策风险:数学模型可以帮助企业从更加科学的角度对市场和消费者的需求进行分析,较好地预测未来的市场变化趋势。
这有助于企业在生产和营销决策时降低风险,避免损失。
提升资源配置效率:数学模型可以通过数据来识别分析企业的市场和消费者需求。
根据预测结果,企业可以合理配置资源,将资源优先投入到有潜力的市场或产品上,从而提高资源利用效率,做到事半功倍。
应用现状与趋势目前,数学模型在企业销售预测中已经得到了广泛应用。
围绕销售预测的软件工具也越来越多。
例如,SAS销售预测分析软件、SAP销售预测软件、IBM Cognos销售预测软件等。

数模论文论文题目: 电子商务平台销售数据分析与预测题号 A作者电子商务平台销售数据分析与预测摘要:对电子商务平台销售数据分析与预测要建立在数据的基础上,但世界工厂分析认为,现在不是缺数据,而是数据太多。
据统计,在今天的互联网上,每秒会产生几百万次的搜索、网络上会有几十万次的内容。
稍大的电子商务公司,都会采集一些行为数据,这些数据中包含了大量对市场分析,预测有用的潜在信息,对这些信息进行深度分析,企业可以改进电子商务网站的质量并且可以提高电子商务的经营效率。
论文以购买历史数据为预测客户行为的基础数据,采用神经网络,马尔可夫链方法为建模工具,对电子商务的客户访问行为、商品销售预测等问题进行了研究。
本论文的主要工作如下:1.分析每个店铺的销售特点(包括价格,服务态度,售后服务,产品质量,优惠,日常管理等店铺政策)和其销售量的关系,可用雷达图法进行分析,建立最大利润函数模型。
2.利用效用函数对所搜集到商品信息进行数学模型,但仅仅按照两种商品进行建立,需要进一步的扩展。
3。
利用MATLAB 统计中的命令regress求解。
将回归系数的估计值带入模型中,即可预测未来两年的销售总额。
正文:问题一:搜集同一款手机(三星note3)销量前20位的店铺相关信息,把这些信息与销售量进行相关性分析,并据此对店铺如何提高销售量提出建议。
分别到京东商城,国美,苏宁,亚马逊,淘宝等相关网站了解相关的店铺的信息得到销售量前20位的店铺.分析每个店铺的销售特点(包括价格,服务态度,售后服务,产品质量,优惠,日常管理等店铺政策)和其销售量的关系。
分析用户的购买情况同等重要。
(此雷达图摘自百度文库)利用条形图进行不同的店铺之间的对比,饼状图同店铺不同要素之间的影响进行对比分析。
对每一个影响因素建立最大利润函数模型f(x)=ax2+bx+c,每一种因素分别对应x1,x2.。
.。
..。
.得到图形,利用图形对店铺进行销售建议.问题二:针对某一种类的商品(比如女式凉鞋),搜集50组店铺对应的商品信息(至少涵盖销量、价格、用户评价、品牌、样式、材质等信息),并据此建立数学模型分析用户的消费习惯。

销量预测问题一、 摘要本文通过建立微分方程模型,探讨了新产品进入市场后销售量变化的情况。
模型由简单到复杂、由理想到现实,逐步利用广告对市场的限制探讨了产品销售量变化的情况,分析了广告费问题二中,产品销售存在一定的市场容量N , 统计表明dtdx 与该产品的潜在用对销售量产生的影响,建立比较符合现实的模型。
问题一中,新产品的投入,没有市场竞争,有良好的市场环境,也有良好的口碑,故属于较为简单的微分方程模型,可直接建立模型。
容量)(t x N -成正比,故建立阻滞增长模型求解。
问题三中,则考虑了广告费用对产品销量的影响,分析了广告费用与销售速率之间的关系,建立数学微分方程模型,并运用了Matlab 软件编程求解。
二、 问题提出一种新产品问世,经营者自然要关心产品的卖出情况。
如何采取有效措施,使得产品销量大,获取更大的利润,这是每个经营者最为关注的问题。
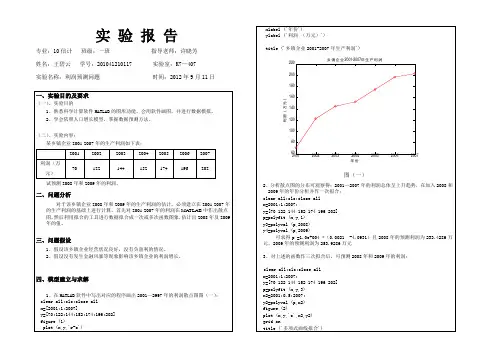
1、设t 时刻产品销量的增长率dxdt 与)(t x 成正比, 预测t 时的产品销量()t x ;2、设考虑到产品销售存在一定的市场容量N, 统计表明dt dx与该产品的潜在容量)(t x N -成正比, 预测t 时的产品销量()t x ;3、试考虑影响产品销量的广告因素,并建立模型,预测t 时的产品销量()t x .三、 模型假设与符号系统模型假设:模型基本假设:;假设1:在考虑影响商品销售的因素时,不考虑偶然因素,如经济、战争因素、政治干预等;假设2:产品的销售量符合产品的生命周期;假设3:产品为日常用品,不是耐用品,每个人都需要。
符号系统:x(t) 为t 时刻新产品的销售量a 为每件新产品的宣传效率N 为市场的销售容量b 为产品销售量的增长率与潜在容量的比例系数s(t) 为商品t 时刻的销售量(即新产品在此时刻一段时间的销售量,如七月份,八月份的销售量,而不是总销售量)M(t) 为t 时刻的广告费用θ 为销售量本身的衰减系数∂ 为广告宣传对销售速率的影响T 为商品销售速率最大的时刻四、 模型的建立与求解问题一模型的建立与求解:模型的建立:t 时刻时,新产品的销售量为x (t ),把x (t )当做连续、可微函数处理。

学号武汉理工大学数学建模与仿真课程设计设计题目专业班级姓名指导老师2011年 1 月16 日附件2:课程设计任务书学生姓名:专业班级:指导教师:工作单位:题目:初始条件:要求完成的主要任务:(包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)时间安排:指导教师签名:年月日系主任(或责任教师)签名:年月日年销售额的回归模型预测【摘要】本文首先利用题目所给数据做出散点图,分析自变量与因变量之间的线性关系,建立基本的线性回归模型t t t x y εββ++=10[1],对所建立的模型直接用MATLAB 统计工具箱[2]求解,得到的回归系数估计值及其置信区间(置信水平05.0=α)、检验统计量2R ,F ,P [3],将参数估计值代入初始模型得到t t x y 17628.04548.1+-=∧。
但是这个模型没有考虑到题目所给的数据是一个时间序列。
实际上,在对时间序列数据作回归分析时,模型的随机误差项t ε有可能存在相关性。
违背模型关于t ε(对t )相互独立的基本假设。
所以对原模型进行自相关检验,发现其随机误差存在正自相关,故对原模型作变量变换:1'--=t t t y y y ρ ,1'--=t t t x x x ρ得到新的模型:t t t u x y ++=''1'0'ββ,其中,()ρββ-=10'0,1'1ββ=。
对新的模型利用MATLAB 统计工具箱求解,并对新的模型也作一次自相关检验,即诊断随机误差t u 是否还存在自相关,经检验认为新的模型中随机误差不存在自相关。
因此经变换所得到的回归模型t t t u x y ++=''1'0'ββ是适用的。
最后,将模型t t t u x y ++=''1'0'ββ中的't y 和't x 还原为原始变量t y 和t x ,得到结果为:111099.01737.06326.03916.0--∧-++-=t t t t x x y y关键词:时间序列 回归模型 统计检验 D —W 检验一、问题重述与分析1.1、问题提出某公司(记为A)想用全行业的销售额作为自变量来预测公司的销售额,表1给出了2006年~2010年公司销售额和行业销售额的分季度数据(单位:百万元)。

在市场经济条件下,影响药品市场销售量的因素很多,如何准确预测药品销售量,对药品生产厂家来说尤为重要。
没有确切的预测数字,药品生产数量不足,会发生缺货现象,失去销售机会而减少利润;如果生产过剩,一时销售不出去,造成药品积压占用流动资金,影响资金周转,也会造成经济损失。
因此,掌握一个较为准确的预测药品销售量的方法是很重要的。
常见的定量化预测方法,大多是应用“趋势外推”的思想,当历史资料较少而预测的时间跨度又较长时,往往遇到困难。
灰色系统预测模型-GM (1,1),近年来的应用实践表明,这种预测方法有较好的准确性和适应性。
根据2012年的各个月各个销售点的需求量来预测2013年的各个销售点的月需求量问题。
模型建立假设原始数据是:0(1)(2)......()x x x n 、希望的到观测值令 00(1)(2)......x n x n ++、、令101()()ki x k x i ==∑(k=2,3,...,n),称为原始数据的一次累加生成序列。
不难理解,非负序列经多次累加后的生成数列将表现出良好的指数增长特性。
由微积分学知道,一个随时间按指数规律变化的连续变量1()y x t =可以看作下列微分方程dyay b dx+= (1) 的解: 对该方程求解,将时间t 离散化,得: 1(1)[(1)]akb bx k x eaa-+=-+(2) 由的定义求原函数列的公式为: 011(1)(1)()x k x k x k +=+- (3)取k ≥n 的正整数,即可得所求预测值0(1),(2),........x n x n ++。
上述(1)、(2)、(3)构成所谓GM (1,1)预测模型。
模型中参数a 、b 由最小二乘法原理求得:1()T T a A A A B b -⎛⎫= ⎪⎝⎭(4)其中1111111[(1)(2)]121[(2)(3)]12............1[(1)()]12x x x x A x n x n ⎛⎫-+ ⎪⎪⎪-+ ⎪= ⎪ ⎪ ⎪--+ ⎪⎝⎭000(2)(3)........()x x B x n ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭ 由(4)式求得a 、b 后,带入(2)式算出再由(3)式便可算出所求的预测值。


【数学建模】day14-建⽴GM(1,1)预测评估模型应⽤学习建⽴GM(1,1)灰⾊预测评估模型,解决实际问题:SARS疫情对某些经济指标的影响问题⼀、问题的提出 2003 年的 SARS 疫情对中国部分⾏业的经济发展产⽣了⼀定影响,特别是对部分疫情较严重的省市的相关⾏业所造成的影响是显著的,经济影响主要分为直接经济影响和间接影响。
直接经济影响涉及商品零售业、旅游业、综合服务等⾏业。
很多⽅⾯难以进⾏定量的评估,现仅就 SARS 疫情较重的某市商品零售业、旅游业和综合服务业的影响进⾏定量的评估分析。
究竟 SARS 疫情对商品零售业、旅游业和综合服务业的影响有多⼤,已知某市从 1997 年 1 ⽉到 2003 年 12 ⽉的商品零售额、接待旅游⼈数和综合服务收⼊的统计数据如下⾯三表所⽰。
试根据这些历史数据建⽴预测评估模型,评估 2003 年 SARS 疫情给该市的商品零售业、旅游业和综合服务业所造成的影响。
⼆、模型的分析与假设模型分析: 根据所掌握的历史统计数据可以看出,在正常情况下,全年的平均值较好地反映了相关指标的变化规律。
这样,对于每⼀个经济指标,考虑从两部分着⼿建⽴预测评估模型:1. 利⽤灰⾊理论建⽴GM(1,1)模型,根据1997-2002年的平均值序列,预测2003年的平均值。
2. 通过历史数据计算每⼀个⽉的指标值与全年总值之间的关系,并将此关系拓展到2003年,进⽽预测出2003年每⼀个⽉的指标值。
进⽽与真实数据值作⽐较,从⽽得出结论。
模型假设:1. 假设所有的统计数据真实可靠。
2. 假设该市SARS疫情流⾏期间和结束之后,数据的变化只与SARS疫情的影响有关,不考虑其他随机因素的影响。
三、建⽴灰⾊预测模型GM(1,1) 由已知数据,对于1997-2002年的某项指标记为A= (a ij)6*12,计算每年的平均值作为初始数列。
记为: 并要求级⽐。
对x(0)做⼀次累加得1-AGO序列: 式中: 取x(1)的加权均值序列: 式中,α是确定参数。

第六章 预测模型(Forecast Models )本讲主要内容1. 预测和预测模型2. 时间序列预测模型3. 灰色预测模型4. 数学建模案例:SARS 疫情对某些经济指标影响问题6.1预测和预测模型6.1.1 什么是预测预测作为一种探索未来的活动早在古代已经出现,但作为一门科学的预测学,是在科学技术高度发达的当今才产生的。
“预测”是来自古希腊的术语。
我国也有两句古语:“凡事预则立,不预则废”, “人无远虑,必有近忧” 。
预测的目的在于认识自然和社会发展规律,以及在不同历史条件下各种规律的相互作用,揭示事物发展的方向和趋势,分析事物发展的途径和条件,使人们尽早地预知未来的状况和将要发生的事情,并能动地控制其发展,使其为人类和社会进步服务。
因而预测是决策的重要的前期工作。
决策是指导未来的,未来既是决策的依据,又是决策的对象,研究未来和预测未来是实现决策科学化的重要前提。
预测和决策是过程的两个方面,预测为决策提供依据,而预测的目的是为决策服务,所以不能把预测模型和决策模型截然分开,有时也把预测模型称为决策模型。
20世纪以来,预测技术所以得以长足进步,一方面,与社会需求有很大关系,另一方面通过社会实践和长期历史验证,表明事物的发展是可以预测的。
而且借助可靠的数据和科学的方法,以及预测技术人员的努力,预测结果的可靠性和准确性可以达到很高的程度,这也是预测技术迅速发展的另一个重要原因。
6.1.2 预测的方法和内容为保证预测结果的精确度,预测之前的主要工作是数据的准备,数据是预测工作的前提和重要依据,预测不能是臆造和空想,任何事物的发展都有一定的规律,认真研究预测对象并充分考察预测对象所处的环境,以系统分析的方法对过去和现在的数据进行总结,从中找出规律,便可科学地推断未来。
1.数据的收集和整理 按时态分,数据可分为历史数据和现实数据;按预测对象分,可分为内部数据和外部数据;就收集的手段分,可分为第一手数据和第二手数据。
利用数据分析预测企业销售额随着科技的不断进步和数据的大规模收集,数据分析成为了各行各业中不可或缺的一部分。
企业也开始发掘数据分析的潜力,希望通过利用大数据和数据模型来预测销售额,制定更加精确的销售策略和计划。
数据分析在预测企业销售额中扮演了重要的角色。
首先,要预测企业的销售额,需要有大量的历史销售数据作为参考。
通过分析历史销售数据,我们可以找出销售额的长期趋势和季节性变化,并建立对销售额的预测模型。
这个模型可以使用各种算法,如回归分析、时间序列分析等。
通过这些模型,我们可以在一定程度上预测未来销售额的变化。
其次,了解销售数据背后的驱动因素也非常重要。
销售额可能受到多种因素的影响,如市场需求、竞争态势、营销活动等。
通过数据分析,可以找出这些影响因素与销售额之间的关联性,并探索它们对销售额的具体影响程度。
例如,通过回归分析,我们可以确定某种促销活动对销售额的直接影响,并且量化这种影响程度。
这样,企业就能更好地制定促销计划,以提高销售额。
此外,数据分析还可以帮助企业进行市场细分和客户定位。
通过对销售数据的细致分析,可以发现不同市场和客户群体之间的差异性和个性化需求。
这样,企业可以有针对性地制定不同的销售策略,以最大程度地满足不同市场和客户的需求,提高销售额。
例如,通过对销售数据的地理分析,企业可以发现不同地区的消费特点和偏好,从而针对性地调整产品定价、推广活动和分销策略。
然而,要利用数据分析预测企业销售额并不是一件容易的事情。
首先,数据质量和可靠性是一个重要的考虑因素。
如果企业的销售数据不完整或存在错误,那么建立的模型就可能失真,无法准确预测销售额。
因此,数据的采集、整理和清洗是很重要的步骤,需要保证数据的准确性和可靠性。
其次,市场环境的不确定性也是一个挑战。
企业的销售额可能受到多种外部因素的影响,如经济波动、政策变化等。
这些因素往往是难以预测和控制的,因此,在建立销售预测模型时需要考虑到这种不确定性,并增加一定的容错空间。
中国GDP 增长的分析与预测仿作于中南大学国家级精品教程 《中国GDP 上涨空间的合理性分析》摘要1978 年11月,中国经济开始改革开放,之后中国经济持续高速发展达30年之久,让全世界瞩目。
这30年中,中国经济增长成为世界第三大经济体。
国内生产总值(GDP)是现代国民经济核算体系的核心指标,是衡量一个国家综合国力的重要指标。
本文就1978年到2008年的生产总值(GDP)等相关统计数据,先建立了关于GDP 增长的回归预测模型.通过MA TLAB 编程计算, 本文判断出43295.8665x1124.7878x6564.1066x x 16126.75083967.15706ˆ+-+-=y7650.0007x 0.0880x 4.1564x -+-对现实数据的拟合效果最好,从而预测了2014年到2018年的GDP 总量,但是预测值与实际极度不符。
为了得到更好的预测结果 ,本文建立了ARIMA 模型。
通过计算自相关函数和偏相关函数,确定取d =2。
利用AIC 准则定阶,取ARIMA (1,2,2)模型。
计算得到2014年到2018年的GDP 总量,通过与2009及2010的GDP 总量比较,发现该模型短期预测精度是比较高的。
选取ARIMA 模型预测的结果进行分析,预计中国GDP 将继续保持增长,不过增长率缓慢下降。
猜想:GDP 年增长率最后将趋于稳定。
关键词:GDP ;回归预测模型;ARIMA 模型引言国内生产总值(Gross Domestic Product,简称GDP)是指在一定时期内(一个季度或一年),一个国家或地区的经济中所生产出的全部最终产品和劳务的价值,常被公认为衡量国家经济状况的最佳指标。
它不但可反映一个国家的经济表现,更可以反映一国的国力与财富。
一般来说,国内生产总值共有四个不同的组成部分,其中包括消费、私人投资、=+++。
式中:CA为消费、政府支出和净出口额。
用公式表示为:GDP CA I CB XI为私人投资、CB为政府支出、X为净出口额。
饮食行业应税营业额测算问题摘要本文研究的是饮食行业应税营业额测算问题,为了检验题目所给模型的合理性以及限制偷税问题,我们建立了灰色关联度模型、模糊聚类模型、基于时间价值的测算模型等。
针对问题一:本文建立了灰色关联度模型和模糊聚类模型,从两个角度检验题目所给模型。
一是从题目所给模型中因素对应税营业额的关联程度的角度(结果见表5-1),二是从题目所给模型的结果是否与月营业额相一致的角度(结果见表5-5),最终得出:题目所给模型考虑的因素及其结果均为合理。
针对问题二:本文建立了一个合理性评价模型,评价得出题目所给模型的系数不合理。
因此又建立了一个多目标最优化模型,求出一组合理的系数见下表1,并用合理性性评价模型进行检验,证明其合理性。
针对问题三:建立了基于熵权法的模糊聚类模型。
对地段系数序列、经营状况系数序列以及品牌系数序列进行加权求和得到一个综合评价指标,然后用模糊聚类分析求得地段系数、经营状况系数以及品牌系数的级差不够合理,级差合理性结果见表2:表2 级差合理程度针对问题四:建立了基于时间价值的测算模型,关键词:灰色关联度模糊聚类时间价值测算模型多目标最优化1.问题重述1.1问题的背景饮食行业有很多方法偷逃税款,这些方法给税务部门对饮食业纳税定额的公平、合理的核定造成了困难。
如何核定饮食业纳税定额,在典型调查的基础上,采用科学的方法,测算确定不同规模、不同地域、不同类型、不同档次、不同商誉的纳税人的生产经营情况,以共性的、起决定性的主要生产经营要素为参数,测算出月平均单位营业额(即基准营业额),再以影响纳税人个性差异的有关因素为调整系数,经过计算生成较为公平、合理的纳税定额,是税务部门必须解决的问题。
1.2问题的相关模型下面是某市税务部门为该市饮食业所建立的应税营业额计算模型:应税营业额=[单位面积营业额×营业面积×50%+单位从业人员营业额×从业人员总数×50%]×地段系数×经营状况系数×品牌系数其中:(1)单位面积营业额=272元/平米;(2)单位从业人员营业额=6635元/人(3)单位面积营业额=∑调查户营业额/∑调查户营业面积(4)单位从业人员营业额=∑调查户营业额/∑调查户从业人员数(5)经营状况系数:好(1.44)、较好(1.11)、一般(0.66)、差(0.56)(6)地段系数:一级(1.06)、二级(0.83)、三级(0.75)、四级(0.65)(7)品牌系数:强(1.2)、较强(1.1)、一般(1)1.3问题的提出问题一:利用附表一中的数据(饮食业信息采集数据)对上述模型进行检验,给出对该模型的总体看法。
公司的销售额预测一、问题重述某公司想用全行业的销售额作为自变量来预测公司的销售量,下表给出了1977—1981年公司的销售额和行业销售额的分季度数据(单位:百万元)(1)画出数据的散点图,观察用线性回归模型拟合是否合适.(2)建立公司销售额对全行业的回归模型,并用DW检验诊断随机误差项的自相关性.(3)建立消除了随机误差项自相关性之后的回归模型.二、问题分析与假设销售收入预测的方法主要有时间序列法、因果分析法和本量利分析法等.时间序列法,是按照时间的顺序,通过对过去几期实际数据的计算分析,确定预测期产品销售收入的预测值.表1 的数据是以时间顺序为序列的,称为时间序列.由于公司销售额和行业销售额等经济变量均有一定的滞后性,因此,在这样的时间序列数据中,同一变量的顺序观测值之间出现相关现象是很自然的.然而,一旦数据中存在这种自相关序列,如果仍采用普通的回归模型直接处理,将会出现不良后果,其观测也会失去意义,为此,我们必须先来检验数据是否存在自相关,一旦存在,就要考虑自相关关系,建立新的模型.定义与符号说明t x 行业销售额 t y 公司销售额 ˆt y公司销售额的估计值三、模型建立与求解一、基本统计回归模型建立以行业销售额t x 为自变量、以公司销售额t y 为因变量的散点图,其中1,220t =图1 t y 对t x 的散点图从图1可以看出,随着行业销售额的增加,公司销售额也增加,而且两者有很强的线性关系,因此可以建立线性回归模型01t t t y x ββε=++,t ε为随机误差 ()1 假设t ε与t x 是相互独立的,且t ε服从均值为零的正态分布.由表1的数据以及上述线性回归模型的假设,进行数据处理,得到回归系数估计值及其置信区间和检验统计量,见表2.参数 参数估计值 置信区间0β -1.45475 [-1.90465 -1.00485] 1β0.176283[0.173248 0.179318]21R = 14888F = 0.00000p =表2 模型()1的计算结果将参数估计值代入()1得到,ˆ 1.454750.176283t t y x =-+ ()2由表2知21R =,t y 几乎处处可由()2确定.用Matlab 作出其交互式画面,由此可以给出不同水平下的预测值及其置信区间,通过左方的Export 下拉式菜单,可以输出模型的统计结果,见图2.图2 回归分析中的交互式画面二、自相关性的判别我们可以看到模型()2的拟合度很高(21R =),即可认为t y 可由模型确定.但此模型并未考虑到我们的数据是一个时间序列.在对时间序列数据做回归分析时,模型的随机误差项可能存在相关性,违背于模型对t 独立的基本假设.现在我们考虑如下模型:011t t tt t t y x u ββεερε-=++=+ ()3其中ρ是自相关系数,1ρ≤,t u 相互独立且服从均值为0的正态分布.模型()3中,若0ρ=,则退化为普通的回归模型;若0ρ>,则随机误差t ε存在正的自相关;若0ρ<,则随机误差t ε存在负的自相关.大多数与经济有关的时间序列数据,在经济规律作用下,一般随着时间的推移有一种向上或向下的变动趋势,其随机误差表现出正相关性.D W -检验是一种常用的诊断自相关现象的统计方法.首先根据模型()2得到的残差,计算DW 统计量如下:21221()ntt t ntt e eDW e-==-=∑∑ ()4其中n 是观察值个数,残差ˆt t t e y y=-为随机误差项的估计值.当n 较大时, 122121nt t t nt t e e DW e -==⎡⎤⎢⎥⎢⎥≈-⎢⎥⎢⎥⎣⎦∑∑()5而()5式的右端1221nt t t ntt e ee-==∑∑正是自相关系数ρ的估计值ˆρ,于是 ˆ2(1)DW ρ≈- ()6 由于ˆ11ρ-≤≤,所以04DW ≤≤,并且若ˆρ在0附近时,则DW 在2附近,t ε的自相关性很弱(或不存在自相关性);若ˆρ在1±附近时,则DW 在0或4附近,t ε的自相关性很强. 要根据DW 的具体数值来确定是否存在自相关性,应该在给定的检验水平下依照样本容量和回归变量数目,查D W -分布表,得到检验的临界L d 和U d ,然后由表3中DW 所三、加入自相关后的模型根据()4式可计算出0.73465DW =,对于显著性水平0.01,20,1n q α===,查D W -分布表,得到检验的临界值0.95L d =和 1.15U d =,现在L DW d <,由表3可以认为随机误差存在正自相关,且ρ的估计值可由()6式得ˆ0.63268ρ=. 作变换,'1t t t y y y ρ-=-,'1t t t x x x ρ-=-, ()7则模型()3化为''''01t t t y x u ββ=++,其中()'001ββρ=-,'11ββ= ()8 以ρ的估计值代入()7式作变换,利用变换后的数据't y 、't x 估计模型()8的参数,得到对模型()8也做一次自相关检验,即诊断随机误差t u 是否还存在自相关,从模型()8的残差可计算出 1.65199DW =,对于显著性水平0.01,1q α==以及19n =时,检验的临界值为0.93, 1.13L U d d ==,故4U U d DW d <<-,所以可以认为随机误差不存在自相关.因此经变换()7得到的回归模型()8是适用的.最后,将模型()8中的't y 和't x 还原为原始变量t y 和t x ,得到结果为:11ˆ0.391410.632680.173740.10992t t t t yy x x --=-++- ()9 四、结果分析与预测从机理上看,对于带滞后性的经济规律作用下的时间序列数据,加入自相关的模型()9更为合理,而且在本例中,衡量与实际数据拟合程序的指标——剩余标准差从模型()2的0.081减少到0.0671.当用模型()9对公司的销售额t y 作预测时,先估计未来的全行业销售额t x ,比如,设t=21时,t x =174.1,容易由模型()9得到ˆt y=29.1860.四 、模型的评价一、模型的优点经D W -检验认为普通回归模型()1的随机误差存在自相关,由()4,()7式估计出自相关系数ρ后,采用变换()8的方法得到模型()9,成称为广义差分法.这种方法消除了原模型随机误差的自相关性,得到的()9式是一阶自相关模型.二、模型的缺点D W -检验和广义差分法在经济数据建模中有着广泛的应用,但是也存在着明显的不足:若DW 的数值落在无法确定自相关性的区间,则只能设法增加数据量,或选用其他方法;如果原始数据序列存在高阶自相关性,则需要反复使用D W -检验和广义差分,直至判定不存在自相关为止.另外,D W -分布表中数据容量n 的下限是15.参考文献[1] 徐金明,张孟喜,丁涛,《MATLAB 实用教程》,北京:清华大学出版社;北京交通大学出版社,2005.7(2007.8重印).[2]. 姜启源,谢金星、叶俊,《数学模型(第四版)》,北京:高等教育出版社,20011.1(2012.5重印).附录1.散点图的程序clear;x=[127.3 130.0 132.7 129.4 135.0 137.1 141.2 142.8 145.5 145.3 148.3 146.4 150.2 153.1 157.3 160.7 164.2 165.6 168.7 171.7]’;y=[20.96 21.40 21.96 21.52 22.39 22.76 23.48 23.66 24.10 24.0124.54 24.30 25.00 25.64 26.36 26.98 27.52 27.78 28.24 28.78]’;plot(x,y,'*')2.模型(1)的计算程序clear;x=[127.3 130.0 132.7 129.4 135.0 137.1 141.2 142.8 145.5 145.3148.3 146.4 150.2 153.1 157.3 160.7 164.2 165.6 168.7 171.7]’;y=[20.96 21.40 21.96 21.52 22.39 22.76 23.48 23.66 24.10 24.0124.54 24.30 25.00 25.64 26.36 26.98 27.52 27.78 28.24 28.78]’;x=[ones(20,1),x];[b,bint,r,rint,stats]=regress(y,x)输出结果:b =-1.454750041396340.176282811457384bint =-1.90465420468789 -1.004845878104790.173247525367995 0.179318097546773r =-0.0260518571286674-0.06201544806360460.02202096100146280.1637542388108240.0465704946494760.04637659058897010.043617063613695-0.058435434718124-0.0943990256530576-0.149142463361581-0.147990897733738-0.0530535559647056-0.02292823950276460.1058516072708220.08546379914980310.1061022401947010.02911240009385810.0423164640535205-0.0441602514643726-0.0330086858365206rint =-0.195385871759251 0.143282157501916-0.231871886037631 0.107840989910421-0.152853753861225 0.196895675864150.0131634673388031 0.314345010282846-0.128820728276878 0.22196171757583-0.130374632908482 0.223127814086423-0.135221944162416 0.222456071389806-0.236666572408848 0.119795702972601-0.26910531130757 0.0803072600014548-0.313617420748614 0.0153324940254506-0.31288219186159 0.0169003963941133-0.232314787682902 0.126207675753491-0.203701178032592 0.157844699027063-0.0664228030147936 0.278126017556437-0.0879446576592735 0.25887225595888-0.0620923905849254 0.274296870974328-0.144034956949209 0.202259757136925-0.128748679311955 0.213381607418996-0.211614739705066 0.123294236776321-0.197152337494454 0.131134965821413stats =Columns 1 through 30.998792444207198 14888.1435565111 1.01315527327091e-027Column 40.007405683407079543. 散点图的交互式程序clear;x=[127.3 130.0 132.7 129.4 135.0 137.1 141.2 142.8 145.5 145.3 148.3 146.4 150.2 153.1 157.3 160.7 164.2 165.6 168.7 171.7]’;y=[20.96 21.40 21.96 21.52 22.39 22.76 23.48 23.66 24.10 24.0124.54 24.30 25.00 25.64 26.36 26.98 27.52 27.78 28.24 28.78]’;rstool(x,y,'linear')4.模型(2)的残差x=[127.3 130.0 132.7 129.4 135.0 137.1 141.2 142.8 145.5 145.3 148.3 146.4 150.2 153.1 157.3 160.7 164.2 165.6 168.7 171.7]’;y=[20.96 21.40 21.96 21.52 22.39 22.76 23.48 23.66 24.10 24.0124.54 24.30 25.00 25.64 26.36 26.98 27.52 27.78 28.24 28.78]’;for i=1:1:20z(i)=-1.45475+0.17628*x(i);e(i)=y(i)-z(i);endze输出结果:z =Columns 1 through 320.985694 21.46165 21.937606Columns 4 through 621.355882 22.34305 22.713238Columns 7 through 923.435986 23.718034 24.19399Columns 10 through 1224.158734 24.687574 24.352642Columns 13 through 1525.022506 25.533718 26.274094Columns 16 through 1826.873446 27.490426 27.737218Columns 19 through 2028.283686 28.812526e =Columns 1 through 3-0.0256939999999979 -0.0616500000000002 0.0223940000000056 Columns 4 through 60.164118000000002 0.0469500000000025 0.0467620000000046 Columns 7 through 90.0440140000000042 -0.0580339999999993 -0.093989999999998 Columns 10 through 12-0.148733999999997 -0.147574000000002 -0.0526419999999987 Columns 13 through 15-0.0225059999999964 0.106282000000004 0.0859059999999978 Columns 16 through 180.106554000000003 0.0295740000000038 0.0427820000000025 Columns 19 through 20-0.0436859999999974 -0.03252599999999365.计算DW和e =[-0.0256939999999979-0.06165000000000020.02239400000000560.1641180000000020.04695000000000250.04676200000000460.0440140000000042-0.0580339999999993-0.093989999999998-0.148733999999997-0.147574000000002-0.0526419999999987-0.02250599999999640.1062820000000040.08590599999999780.1065540000000030.02957400000000380.0427820000000025-0.0436859999999974-0.0325259999999936];s=0;for t=2:1:20s=s+(e(t)-e(t-1))^2;endm=0;for i=1:1:20m=m+e(i)^2;endDW=s/mp=1-1/2*DW输出结果:DW =0.734645539224993p =0.6326772303875036.模型(3)中的数据变换x=[127.3 130.0 132.7 129.4 135.0 137.1 141.2 142.8 145.5 145.3 148.3 146.4 150.2 153.1 157.3 160.7 164.2 165.6 168.7 171.7]’;y=[20.96 21.40 21.96 21.52 22.39 22.76 23.48 23.66 24.10 24.0124.54 24.30 25.00 25.64 26.36 26.98 27.52 27.78 28.24 28.78]’;p=0.63268for t=1:1:19y1(t)=y(t+1)-p*y(t);x1(t)=x(t+1)-p*x(t);endy1x1输出结果:p =0.63268y1 =Columns 1 through 38.1390272 8.420648 7.6263472Columns 4 through 68.7747264 8.5942948 9.0802032Columns 7 through 98.8046736 9.1307912 8.762412Columns 10 through 129.3493532 8.7740328 9.625876 Columns 13 through 159.823 10.1380848 10.3025552 Columns 16 through 1810.4502936 10.3686464 10.6641496 Column 1910.9131168x1 =Columns 1 through 349.459836 50.4516 45.443364 Columns 4 through 653.131208 51.6882 54.459572 Columns 7 through 953.465584 55.153296 53.24506 Columns 10 through 1256.371596 52.573556 57.575648 Columns 13 through 1558.071464 60.436692 61.179436 Columns 16 through 1862.528324 61.713944 63.928192 Column 1964.9668847.模型(3)的计算结果y1 =[8.13902728.4206487.62634728.77472648.59429489.08020328.80467369.13079128.7624129.34935328.77403289.6258769.82310.138084810.302555210.450293610.368646410.664149610.9131168];x1 =[49.45983650.451645.44336453.13120851.688254.45957253.46558455.15329653.2450656.37159652.57355657.57564858.07146460.43669261.17943662.52832461.71394463.92819264.966884];x2=[ones(19,1),x1];[b,bint,r,rint,stats]=regress(y1,x2)输出结果:b =-0.3914137287916260.173739484728835bint =-0.743959505289538 -0.0388679522937137 0.167481672152938 0.179997297304732 r =-0.06268549262106760.04662674104632460.122454283086727-0.06484857214893940.005427294230647920.00983895095872533-0.0929956860946302-0.060100299345299-0.0969435599642878-0.05320511359044030.03134399898906540.01412631234283520.1251074959825240.02925880199630980.0646852421508761-0.02193146392603220.0379112976474367-0.05128780893441840.0172175781936197-0.194112737017012 0.0687417517748767-0.0885336593085636 0.1817871414012130.0161292648746043 0.228779301298849-0.201462271956211 0.0717651276583323-0.133792997199822 0.144647585661118-0.131797031575754 0.151474933493204-0.225302669864897 0.0393112976756366-0.1985101568317 0.0783095581411017-0.228268383451548 0.0343812635229727-0.192519727444524 0.0861095002636433-0.107973506382257 0.170661504360388-0.127481451736758 0.155734076422428-0.000122557504840748 0.250337549469889-0.109224013348295 0.167741617340915-0.0693312030770827 0.198701687378835-0.157373208239308 0.113510280387243-0.0980543981169386 0.173876993411812-0.181348373667138 0.0787727557983009-0.112564188002673 0.146999344389912stats =Columns 1 through 30.995069834050953 3431.159******** 4.68398711682588e-021 Column 40.004508149250504388.模型(3)的残量clear;y1 =[8.13902728.4206487.62634728.77472648.59429489.08020328.80467369.13079128.7624129.34935328.77403289.6258769.82310.138084810.302555210.450293610.368646410.664149610.9131168];x1 =[49.45983650.451645.44336453.13120851.688254.45957253.46558455.15329656.37159652.57355657.57564858.07146460.43669261.17943662.52832461.71394463.92819264.966884];for i=1:1:19z(i)=-0.39141+0.17374*x1(i);e(i)=y1(i)-z(i);endze输出结果:z =Columns 1 through 38.20174190664 8.374050984 7.50392006136Columns 4 through 68.83960607792 8.588897868 9.07039603928Columns 7 through 98.89770056416 9.19092364704 8.8593867244Columns 10 through 129.40259108904 8.74271961944 9.61178308352Columns 13 through 159.69792615536 10.10886086808 10.23790521064Columns 16 through 1810.47226101176 10.33077063056 10.71547407808Column 1910.89593642616e =Columns 1 through 3-0.0627147066400013 0.0465970159999998 0.122427138639998 Columns 4 through 6-0.0648796779199987 0.00539693200000002 0.00980716071999943 Columns 7 through 9-0.0930269641599999 -0.0601324470399991 -0.0969747244000008 Columns 10 through 12-0.0532******* 0.0313131805599998 0.0140929164799992 Columns 13 through 150.125073844640001 0.0292239319199989 0.0646499893599994 Columns 16 through 18-0.0219674117599986 0.0378757694399994 -0.0513244780799997 Column 190.01718037384000059.求模型(3)的DW值e =[-0.06271470664000130.04659701599999980.122427138639998-0.06487967791999870.005396932000000020.00980716071999943-0.0930269641599999-0.0601324470399991-0.0969747244000008-0.0532*******0.03131318055999980.01409291647999920.1250738446400010.02922393191999890.0646499893599994-0.02196741175999860.0378757694399994-0.05132447807999970.0171803738400005];s=0;for t=2:1:19s=s+(e(t)-e(t-1))^2;endm=0;for i=1:1:19m=m+e(i)^2;endDW=s/m输出结果:DW =1.6519922652328。
数学建模预测案例《数学建模预测案例:神奇的“数字魔法”》嘿,你有没有想过,就像拥有一个能预见未来的魔法水晶球一样,数学建模也可以搞预测呢!这可不是瞎忽悠的事儿。
我有个朋友小明,他在一家电商公司上班。
那公司啊,有一大堆关于销售的数据,什么不同商品的销量啊,每个月的销售额变化啊,多得像一团乱麻。
这时候,数学建模就像超级英雄登场啦。
小明跟他的团队就开始鼓捣数学建模,想预测下一个季度的销售情况。
他们首先得找各种数据之间的关系。
比如说,就像在一个复杂的拼图里找到那些关键的小块一样。
他们发现商品的价格和销量之间有个很有趣的联系。
就拿那种时尚的T恤举例吧,价格要是定高了,销量蹭蹭地往下降,就像高温下的雪人,化得特别快。
可要是价格合适呢,那销量啊,就像火箭发射一样,噌地就上去了。
然后他们用各种数学公式来构建模型。
这模型可复杂了,就像是一个超级精密的机器,每个小齿轮都得转得恰到好处。
他们把各种影响销售的因素,像季节、流行趋势、促销活动都放进去啦。
再说说我另一个朋友小美在的环保组织。
他们想用数学建模预测城市的空气质量。
这可不像电商销售数据那么直观。
小美他们就像是侦探一样,找各种线索。
比如说,汽车的排放量、周围工厂的运行情况、还有天气因素。
他们把这些的数据收集起来,然后建立模型。
这就好比盖房子,一块砖一块砖地把模型搭建起来。
然后发现,只要到了冬季,空气质量就特别容易变差,就像人在冬天更容易感冒似的。
这时候呢,如果能控制住那些工厂的排放量,就像给城市穿了一层防护服,空气质量就能好不少呢。
从这些案例来看,数学建模预测真的特别有用啊。
它能让企业提前做好准备,像是在暴风雨来临前把船帆调整好。
也能让环保组织制定策略,像给混乱的交通指挥一样,规划好改善环境的步骤。
我就觉得啊,数学建模预测就像是一把神奇的钥匙,能打开未来那扇神秘的大门,让我们不管是在商业还是环保等多个领域,充满信心地朝着正确的方向大步前进,真的是非常了不起啊。