第一章_习题课_流体流动

第一章 流体流动流体的重要性质1．某气柜的容积为6 000 m 3，若气柜内的表压力为5.5 kPa ，温度为40 ℃。

已知各组分气体的体积分数为：H 2 40%、 N 2 20%、CO 32%、CO 2 7%、C H 4 1%，大气压力为 101.3 kPa ，试计算气柜满载时各组分的质量。

解：气柜满载时各气体的总摩尔数()mol 4.246245mol 313314.860000.10005.53.101t =⨯⨯⨯+==RT pV n 各组分的质量：kg 197kg 24.246245%40%4022H t H =⨯⨯=⨯=M n m kg 97.1378kg 284.246245%20%2022N t N =⨯⨯=⨯=M n mkg 36.2206kg 284.246245%32%32CO t CO =⨯⨯=⨯=M n m kg 44.758kg 444.246245%7%722CO t CO =⨯⨯=⨯=M n m kg 4.39kg 164.246245%1%144CH t CH =⨯⨯=⨯=M n m2．若将密度为830 kg/ m 3的油与密度为710 kg/ m 3的油各60 kg 混在一起，试求混合油的密度。

设混合油为理想溶液。

解： ()kg 120kg 606021t =+=+=m m m331221121t m 157.0m 7106083060=⎪⎪⎭⎫ ⎝⎛+=+=+=ρρm m V V V 33t t m m kg 33.764m kg 157.0120===V m ρ 流体静力学3．已知甲地区的平均大气压力为85.3 kPa ，乙地区的平均大气压力为101.33 kPa ，在甲地区的某真空设备上装有一个真空表，其读数为20 kPa 。

若改在乙地区操作，真空表的读数为多少才能维持该设备的的绝对压力与甲地区操作时相同？ 解：（1）设备内绝对压力绝压=大气压-真空度= ()kPa 3.65Pa 1020103.8533=⨯-⨯（2）真空表读数真空度=大气压-绝压=()kPa 03.36Pa 103.651033.10133=⨯-⨯4．某储油罐中盛有密度为960 kg/m 3的重油（如附图所示），油面最高时离罐底9.5 m ，油面上方与大气相通。

第一章流体流动习题1. 引言本习题集旨在帮助读者巩固并深入理解流体力学中的流体流动相关知识。

通过解答各式作业题和习题，读者将能够提高对流体流动的理论知识的掌握，并能运用所学知识解决实际问题。

2. 流体等压流动2.1 定常流动1.习题1：在一水力发电站，重力因子为9.8 m/s²，一台水轮机的进口直径为10 m，出口直径为4 m，水流的速度在进口和出口处分别为12 m/s和48 m/s。

求水轮机的功率。

2.习题2：一根水平管道中水流的速度为2 m/s。

管道的截面面积为1.0 m²，密度为1000 kg/m³。

若管道上安装了一过滤器，则过滤器前后水流速度分别为2.5 m/s和1.5 m/s。

求过滤器对水流影响的大小。

2.2 无粘流动1.习题3：一个圆柱体在某无粘流体中运动，其直径为1 m，流体的密度为1 kg/m³，流速为10 m/s。

若圆柱体沿流速方向行进距离为100 m，在这一过程中流体对圆柱体所做的阻力是多少？2.习题4：一道湍流水流通过一个圆柱体。

圆柱体的直径为2 m，流速为5 m/s，流体密度为1.2 kg/m³。

若圆柱体所受到的阻力为1000 N，求流过圆柱体的湍流水流的体积流量。

3. 流体定常流动3.1 流管与元素流量1.习题5：一条河的宽度为10 m，平均流速为2 m/s。

设河水的密度为1000 kg/m³。

求河水的体积流量。

2.习题6：某水管直径为0.2 m，输送液体的流速为3 m/s。

求液体的质量流量。

3.2 动量定理与波动方程1.习题7：一个质量为1000 kg的船以速度10 m/s行驶，船上一个质量为10 kg的人以速度2 m/s从船头跳进水中。

求船在跳水后的速度。

2.习题8：一个质量为500 kg的小汽车以速度20 m/s驶入河流。

汽车下沉后速度降为8 m/s。

求汽车所受的阻力大小。

4. 流体非定常流动4.1 欧拉方程与伯努利方程1.习题9：一水管中水的流速为2 m/s。

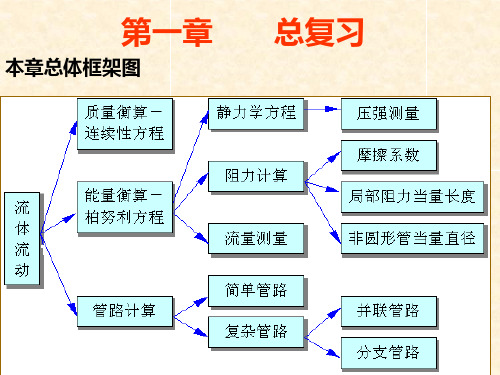
第一章：流体流动二、本章思考题1-1 何谓理想流体？实际流体与理想流体有何区别？如何体现在伯努利方程上？1-2 何谓绝对压力、表压和真空度？表压与绝对压力、大气压力之间有什么关系？真空度与绝对压力、大气压力有什么关系？1-3 流体静力学方程式有几种表达形式？它们都能说明什么问题？应用静力学方程分析问题时如何确定等压面？1-4 如何利用柏努利方程测量等直径管的机械能损失？测量什么量？如何计算？在机械能损失时，直管水平安装与垂直安装所得结果是否相同？1-5 如何判断管路系统中流体流动的方向？1-6何谓流体的层流流动与湍流流动？如何判断流体的流动是层流还是湍流？1-7 一定质量流量的水在一定内径的圆管中稳定流动，当水温升高时，将如何变化？1-8 何谓牛顿粘性定律？流体粘性的本质是什么？1-9 何谓层流底层？其厚度与哪些因素有关？1-10摩擦系数λ与雷诺数Re及相对粗糙度的关联图分为4个区域。

每个区域中，λ与哪些因素有关？哪个区域的流体摩擦损失与流速的一次方成正比？哪个区域的与成正比？光滑管流动时的摩擦损失与的几次方成正比？1-11管壁粗糙度对湍流流动时的摩擦阻力损失有何影响？何谓流体的光滑管流动？1-12 在用皮托测速管测量管内流体的平均流速时，需要测量管中哪一点的流体流速，然后如何计算平均流速？三、本章例题例1-1 如本题附图所示，用开口液柱压差计测量敞口贮槽中油品排放量。

已知贮槽直径D为3m，油品密度为900kg/m3。

压差计右侧水银面上灌有槽内的油品，其高度为h1。

已测得当压差计上指示剂读数为R1时，贮槽内油面与左侧水银面间的垂直距离为H1。

试计算当右侧支管内油面向下移动30mm后，贮槽中排放出油品的质量。

HH1DR11CEFBA10mn11-1附图解：本题只要求出压差计油面向下移动30mm时，贮槽内油面相应下移的高度，即可求出排放量。

m首先应了解槽内液面下降后压差计中指示剂读数的变化情况，然后再寻求压差计中油面下移高度与槽内油面下移高度间的关系。

1. 某设备上真空表的读数为 13.3×10 Pa,试计算设备内的绝对压强与表压强。

已知该地 区大气压强为 98.7×10 Pa 。

设备内的绝对压强P 绝 = 98.7×10 Pa -13.3×10 Pa=8.54×10 Pa设备内的表压强 P 表 = -真空度 = - 13.3×10 Pa14mm 的钢制螺钉紧固。

若螺钉材料的工作应力取为 39.23×10 Pa ，150.307×10 Nζ螺 = 39.03×10 ×3.14×0.014 ×n化工原理课后习题解答（夏清、陈常贵主编.化工原理.天津大学出版社,2005.）第一章 流体流动33解：由 绝对压强 = 大气压强 – 真空度得到：3 3332．在本题附图所示的储油罐中盛有密度为 960 ㎏/㎥ 的油品，油面高于罐底 6.9 m ，油面 上方为常压。

在罐侧壁的下部有一直径为 760 mm 的圆孔，其中心距罐底 800 mm ，孔盖用 6问至少需要几个螺钉？分析：罐底产生的压力不能超过螺钉的工作应力 即P 油 ≤ ζ螺解：P 螺 = ρgh×A = 960×9.81×(9.6-0.8) ×3.14×0.7633 22P 油 ≤ ζ螺得 n ≥ 6.23取 n min= 7至少需要 7 个螺钉3．某流化床反应器上装有两个U型管压差计，如本题附分析：根据静力学基本原则，对于右边的Ｕ管压差计，a –a 为等压面，对于左边的压差计， b –b 为另一等压面，分别列出两个等压面处的静力学基本方程求解。

a –a 处 P A + ρg gh 1 = ρ水gR 3 + ρ水银ɡR 2即：P A = 1.0 ×10 ×9.81×0.05 + 13.6×10 ×9.81×0.05= 7.16×10 Pab-b 处 P B + ρg gh 3 = P A + ρg gh 2 + ρ水银gR 1P B = 13.6×10 ×9.81×0.4 + 7.16×10=6.05×10 Pa图所示。

第一章 流体流动流体的重要性质1．某气柜的容积为6 000 m 3，若气柜内的表压力为5.5 kPa ，温度为40 ℃。

已知各组分气体的体积分数为：H 2 40%、 N 2 20%、CO 32%、CO 2 7%、C H 4 1%，大气压力为 101.3 kPa ，试计算气柜满载时各组分的质量。

解：气柜满载时各气体的总摩尔数()mol 4.246245mol 313314.860000.10005.53.101t =⨯⨯⨯+==RT pV n 各组分的质量：kg 197kg 24.246245%40%4022H t H =⨯⨯=⨯=M n m kg 97.1378kg 284.246245%20%2022N t N =⨯⨯=⨯=M n m kg 36.2206kg 284.246245%32%32CO t CO =⨯⨯=⨯=M n mkg 44.758kg 444.246245%7%722CO t CO =⨯⨯=⨯=M n m kg 4.39kg 164.246245%1%144CH t CH =⨯⨯=⨯=M n m2．若将密度为830 kg/ m 3的油与密度为710 kg/ m 3的油各60 kg 混在一起，试求混合油的密度。

设混合油为理想溶液。

解： ()kg 120kg 606021t =+=+=m m m331221121t m 157.0m 7106083060=⎪⎪⎭⎫ ⎝⎛+=+=+=ρρm m V V V 33t t m m kg 33.764m kg 157.0120===V m ρ 流体静力学3．已知甲地区的平均大气压力为85.3 kPa ，乙地区的平均大气压力为101.33 kPa ，在甲地区的某真空设备上装有一个真空表，其读数为20 kPa 。

若改在乙地区操作，真空表的读数为多少才能维持该设备的的绝对压力与甲地区操作时相同？ 解：（1）设备内绝对压力 绝压=大气压-真空度= ()kPa 3.65Pa 1020103.8533=⨯-⨯ （2）真空表读数真空度=大气压-绝压=()kPa 03.36Pa 103.651033.10133=⨯-⨯4．某储油罐中盛有密度为960 kg/m 3的重油（如附图所示），油面最高时离罐底9.5 m ，油面上方与大气相通。

第一章 流体流动习题解答1.解：（1） 1atm= Pa=760 mmHg真空度=大气压力—绝对压力，表压=绝对压力—大气压力 所以出口压差为p =461097.8)10082.0(10132576.00⨯=⨯--⨯N/m 2（2）由真空度、表压、大气压、绝对压之间的关系可知，进出口压差与当地大气压无关，所以出口压力仍为41097.8⨯Pa 2.解： T=470+273=703K ，p=2200kPa混合气体的摩尔质量Mm=28×0.77+32×0.065+28×0.038+44×0.071+18×0.056=28.84 g/mol混合气体在该条件下的密度为：ρm=ρm0×T0T×pp0=28.8422.4××.3=10.858 kg/m33.解：由题意，设高度为H 处的大气压为p ，根据流体静力学基本方程，得 dp=-ρgdH大气的密度根据气体状态方程，得 ρ=pMRT根据题意得，温度随海拔的变化关系为 T=293.15+4.81000H代入上式得ρ=pMR （293.15-4.8×10-3H ）=-dpgdh移项整理得dpp=-MgdHR293.15-4.8×10-3H对以上等式两边积分， pdpp=-0HMgdHR293.15-4.8×10-3H所以大气压与海拔高度的关系式为 lnp=7.13×ln293.15-4.8×10-3H293.15即：lnp=7.13×ln1-1.637×10-5H+11.526（2）已知地平面处的压力为 Pa ，则高山顶处的压力为 p 山顶=×=45431 Pa将p 山顶代入上式ln 45431=7.13×ln1-1.637×10-5H+11.526 解得H =6500 m ，所以此山海拔为6500 m 。

化⼯原理（上）课后习题解答-天⼤柴诚敬主编第⼀章流体流动10．有⼀装满⽔的储槽，直径1.2 m ，⾼3 m 。

现由槽底部的⼩孔向外排⽔。

⼩孔的直径为4 cm ，测得⽔流过⼩孔的平均流速u 0与槽内⽔⾯⾼度z 的关系为： zg u 262.00=试求算（1）放出1 m 3⽔所需的时间（设⽔的密度为1000 kg/m 3）；（2）⼜若槽中装满煤油，其它条件不变，放出1m 3煤油所需时间有何变化（设煤油密度为800 kg/m 3）？解：放出1m 3⽔后液⾯⾼度降⾄z 1，则 ()m 115.2m 8846.032.1785.01201=-=?-=z z由质量守恒，得21d 0d M w w θ-+=，01=w （⽆⽔补充）200000.622w u A A gzA ρρ==（为⼩孔截⾯积）AZ M ρ= (A 为储槽截⾯积) 故有 0262.00=+θρρd dz A gz A即θd AA gzdz 062.02-= 上式积分得 ))((262.022112100z z A A g -=θ ()m i n 1.2s 4.126s 115.2304.0181.9262.0221212==-??? ???=18．某液体以⼀定的质量流量在⽔平直圆管内作湍流流动。

若管长及液体物性不变，将管径减⾄原来的1/2，问因流动阻⼒⽽产⽣的能量损失为原来的多少倍？解：流体在⽔平光滑直圆管中作湍流流动时 f p ?=f h ρ∑ 或f h ∑=f p ?/ρ=λ2b 2u L d ρ∑∑f1f2hh =（2b1b22112))()(u u d d λλ式中 21d d =2 ，b2b1u u =（21d d）2 =4因此∑∑f1f2hh=221()(2)(4)λλ=3212λλ⼜由于 25.0Re316.0=λ12λλ=（25021.)Re Re =（0.251b12b2)d u d u =（2×25041.)=（0.5）0.25=0.841 故∑∑f1f2hh =32×0.84=26.919．⽤泵将2×104 kg/h 的溶液⾃反应器送⾄⾼位槽（见本题附图）。

化工原理(大题目)绪论第一章 流体流动流体的压力【1-2】某设备进、出口的表压分别为-12kPa 和157kPa ，当地大气压力为101.3kPa 。

试求此设备的进、出口的绝对压力及进、出的压力差各为多少帕。

解 进口绝对压力 ..进101312893 =-=p kPa出口绝对压力 ..出101 31572583 =+=p kPa 进、出口的压力差..p kPa p kPa ∆=--=+=∆=-=157（12）15712169 或 258 389 3169流体的密度【1-3】正庚烷和正辛烷混合液中，正庚烷的摩尔分数为0.4，试求该混合液在20℃下的密度。

解 正庚烷的摩尔质量为/kg kmol 100，正辛烷的摩尔质量为/kg kmol 114。

将摩尔分数换算为质量分数 正庚烷的质量分数 (104100)03690410006114ω⨯==⨯+⨯正辛烷的质量分数 ..2103690631ω=-=从附录四查得20℃下正庚烷的密度/kg m ρ=31684，正辛烷的密度为/kg m ρ=32703 混合液的密度 /..3169603690631684703ρ==+m kg m流体静力学【1-9】如习题1-9附图所示的测压差装置，其U 形压差计的指示液为水银，其他管中皆为水。

若指示液读数为150=R mm ，试求A 、B 两点的压力差。

解 等压面''1111，-=p p1水ρ=-A p p H g()'.1汞水05g ρρ=-+++B p p H R g R习题1-9附图由以上三式，得().汞水05ρρ-=-+A B p p R g R g已知./3汞015，13600ρ==R m kg m ，().....01513600981050151000981-=⨯⨯-+⨯⨯A B p p流量与流速【1-12】有密度为/31800kg m 的液体，在内径为60mm 的管中输送到某处。

若其流速为/0．8m s ，试求该液体的体积流量()3／m h 、质量流量()/k g s 与质量流速()/2⎡⎤⋅⎣⎦kg m s 。

化工原理练习题一（流体流动）一、填空1．用管子从高位槽放水，当管径增大一倍，则水的流量为原流量倍，假定液面高度、管长、局部阻力及摩擦系数均不变，且管路出口处的流体动能项可忽略。

2．某设备上，真空表的读数为80mmHg，其绝压＝kgf/cm2＝Pa。

该地区大气压强为720mmHg。

3．常温下水密度为1000kg／m3，粘度为1cP，在d内=100mm管内以3m/s的速度速度流动，其流动类型为。

4．12kgf·m＝J。

5．空气在标准状态下密度为1.29kg／m3，在0.25MPa下(绝压)80 ℃时的密度为。

6．20℃的水通过10m长，d内＝l 00mm的钢管，流量V0＝10m3／h，阻力系数λ＝0.02，阻力降ΔP＝。

7．常用测量流量的流量计有、、。

8．无论滞流湍流，在管道任意截面流体质点的速度沿管径而变，管壁处速度为，到管中心速度为。

滞流时，圆管截面的平均速度为最大速度的倍．9．在流动系统中，若截面上流体流速、压强、密度等仅随改变，不随而变，称为稳定流动，若以上各量既随而变又随而变，称为不稳定流动。

1０．流体在管内作湍流流动时，从中心到壁可以分、、三层。

11．流体在圆形直管中滞流流动时，平均流速增大一倍，其能量损失为原来损失的倍。

12．等边三角形边长为a，其当量直径是，长方形长2a，宽为a，当量直径是。

13．管内流体层流的主要特点是；湍流的主要特点是。

14．孔板流量计的流量系数C0的大小，主要与和有关。

当超过某一值后，C0为常数。

l 5．直管阻力的表示式hf＝。

管中流出ζ出＝，流入管内ζ入＝。

16．气体的粘度随温度的升高而，水的粘度随温度的升高而。

17．在下面两种情况下，假如流体的流量不变，而圆形直管的直径减少二分之一，则因直管阻力引起的压降损失为原来的多少倍?A)两种情况都为层流，B)两种情况都在阻力平方区。

二．某离心泵将某种石油馏分自1.5Km外的原油加工厂，经一根φ160×5mm的钢管输送到第一贮缸中，送液量为每分钟2000L。

第一章 流体流动习题解答1－1 已知甲城市的大气压为760mmHg ，乙城市的大气压为750mmHg 。

某反应器在甲地操作时要求其真空表读数为600mmHg ，若把该反应器放在乙地操作时，要维持与甲地操作相同的绝对压，真空表的读数应为多少，分别用mmHg 和Pa 表示。

[590mmHg, 7.86×104Pa]解：P （甲绝对）=760-600=160mmHg 750-160=590mmHg=7.86×104Pa1－2用水银压强计如图测量容器内水面上方压力P 0，测压点位于水面以下0.2m 处，测压点与U 形管内水银界面的垂直距离为0.3m ，水银压强计的读数R ＝300mm ，试求 （1）容器内压强P 0为多少？（2）若容器内表压增加一倍，压差计的读数R 为多少？习题1－2 附图[(1) 3.51×104N ⋅m －2 (表压)； (2)0.554m] 解：1. 根据静压强分布规律 P A ＝P 0＋g ρH P B ＝ρ，gR因等高面就是等压面，故P A ＝ P B P 0＝ρ，gR －ρgH ＝13600×9.81×0.3－1000×9.81(0.2+0.3)=3.51×104N/㎡ (表压) 2. 设P 0加倍后，压差计的读数增为R ，＝R ＋△R ，容器内水面与水银分界面的垂直距离相应增为H ，＝H ＋2R∆。

同理， ''''''02Rp gR gH gR g R gH gρρρρρρ∆=-=+∆--000p g g p p 0.254m g g 10009.81g g 136009.812R H R ρρρρρρ⨯∆⨯⨯，，，4，，－（－）－ 3.5110＝＝＝＝－－－220.30.2540.554m R R R ∆，＝＋＝＋＝1－3单杯式水银压强计如图的液杯直径D ＝100mm ，细管直径d ＝8mm 。

石油化学工程原理课后答案第一章流体流动1-1 已知油品的相对密度（即比重）为0。

9,试求其密度和比容.解:1—2 若将90kg密度为的油品与60kg密度为的油品混合，试求混合油的密度。

解：混合后各油品的重量百分比：由得：1—3 氢和氮混合气体中,氢的体积分率为0。

75。

求此混合气体在400K和的密度.解：混合气体平均分子量：1-4 如题图所示，用U形管压差计测定气体反应器进.出口处的压力，测得，，试求此反应器底部A和顶部B处的表压和绝压为多少。

当地大气压力。

解：A处的表压：A处的绝压:A、B处的压差：则B处的表压：B处的绝压：1-5 用U形管压差计测定气体管路中某两点的压力差,压差计中的指示液为水，其密度为,压差计读数为500mm.试计算两点的压力差为多少。

解：1-6 为了放大所测气体压差的读数采用如图1—10所示的斜管压差计，。

若压差计内装密度为的95％乙醇溶液，压差计读数R’为29mm。

试计算压力差，分别用SI单位和工程单位表示。

1—7 密度为的原油经过直径为的钢管流动，流速为,试求原油的体积流量、质量流量和质量流速。

解:已知1—8 比重为1.83的硫酸经由直径为和的管子串联管路,体积流量为。

试分别求硫酸在两种直径管中的质量流量、流速和质量流速。

解:1-9 如题图所示，从容器A用泵B将密度为油品输送到塔C顶部.容器内与塔顶的表压力如题图所示。

管子规格为。

油品的输送量为,输送管路的全部能量损失为，试求泵的有效功率。

解：管内流体的流速：以容器A的液面为截面1,以塔C为截面2在1-2截面间列柏努利方程：得：1-10 如题图所示，从敞口高位槽向精馏塔加料，高位槽液面维持不变，塔进料口处的压力为(表压）。

原料液的密度为，管子直径,从高位槽至塔的进料口处的阻力损失为。

试问要维持的加料量，高位槽中的液面须高出塔的进料口多少米？解:管内流体的流速：以高位槽的液面为截面1，以进料管入口为截面2在1-2截面间列柏努利方程：得:1-11 如题图所示为一由敞口高位槽的稳定供水系统，管径为.已知从高位槽液面至管出口处的能量损失为（u为管内流速）.试求水的流量为多少?欲使水量增加20％,应将高位槽水面升高多少米？解：以高位槽的液面为截面1，管出口为截面2在1—2截面间列柏努利方程：得：若使水量增大20%，则在1—2截面间列柏努利方程：得：即需要将高位槽水面升高至10。

第一章 流体流动－基本概念与基本原理一、 流体静力学基本方程式)(2112z z g p p -+=ρ或 gh p p ρ+=0注意：1、应用条件：静止的连通着的同一种连续的流体。

2、压强的表示方法：绝压—大气压=表压 表压常由压强表来测量；大气压—绝压=真空度 真空度常由真空表来测量。

3、压强单位的换算：1atm=760mmHg=10.33mH2O=101.33kPa=1.033kgf/cm2=1.033at4、应用：水平管路上两点间压强差与U 型管压差计读数R 的关系：gR p p A )(21ρρ-=-处于同一水平面的液体，维持等压面的条件必须时静止、连续和同一种液体。

二、定态流动系统的连续性方程式––––物料衡算式常数常数=====≠ρρρρuA A u A u w s A 222111,常数常数======uA A u A u V s A 2211,ρ 21221221///,d d A A u u A ===圆形管中流动常数ρ三、定态流动的柏努利方程式––––能量衡算式1kg 流体：f h u P gZ We u P gZ ∑+++=+++22222111ρρ [J/kg] 讨论点：1、流体的流动满足连续性假设。

2、理想流体，无外功输入时，机械守恒式：3、可压缩流体,当Δp/p 1<20%,仍可用上式，且ρ=ρm 。

4、注意运用柏努利方程式解题时的一般步骤，截面与基准面选取的原则。

5、流体密度ρ的计算：理想气体ρ=PM/RT 混合气体 vn n v v m x x x ρρρρ+++= 2211混合液体n wn w m w m x x x ρρρρ+++= 22112222222111u P gZ u P gZ ++=++ρρ上式中：vi x ––––体积分率；wi x ––––质量分率。

6、gz ，u 2/2，p/ρ三项表示流体本身具有的能量，即位能、动能和静压能。

∑h f 为流经系统的能量损失。

绪论1解：换算因数： 1.010********/==⋅=⋅=⋅⋅⋅⋅⋅⋅⋅⋅sm kg s m s cm g sN m scm g spa scm g∴1g ⋅cm -1⋅s -1=0.1pa ⋅s 2.解：51001325.1Paatm ⨯= 1m N Pa 2=⋅- 1m N J =⋅ 3310m L -= ∴2321001325.1m J m N m N atm L ⨯=⋅⋅⋅⋅⋅⋅-∴21001325.1J atm L ⨯=⋅以J ·mol -1·K -1表示R 的值R =0.08206×1.01325×102 J ﹒mol -1﹒K -1=8.315 J ﹒mol -1﹒K -1第一章 流体流动1. 表压=－真空度=－4.8×104Pa 绝压=5.3×104 Pa2.解：设右侧水面到B ′点高为h 3，根据流体静力学基本方程可知P B =P B ′ 则ρ油gh 2=ρ水gh 3mm mkg mmm kg h 4921000600820h 3323=⋅⨯⋅==--水油ρρ h=h 1+h 3=892mm5解:以图中截面a-a ′为等压面，则P 啊=Pa ′ρ油g(h 1+h 0)=ρ油g(h 2-R+h 0) + ρ水银gR （h 0为水银压差计高液面与容器底部的高度差） ∴ h 2=h 1 + R - ρ水银R/ρ油 = 4 +0.2-13600*0.2/860 = 1.04m6解：h=P(表压)/ ρ水g =81.9*10001000*10 =1.02 m7.解：由公式AVsu =可得 Vs=uA=u πd 2/4=0.8×π×(57-3.5×2)2×10-6/4=1.57×10-3m 3/sWs=Vs ρ=1.57×10-3×1840=2.89kg/ss m kg u AWsG ⋅=⨯===2/147218408.0ρ 9解：以地面以下的水管所在的平面为基准水平面，则：fh Pu gz u P gz ∑+++=++ρρ2222211122Z 1=9m, u 1=0, P 1=P 2=P 0 ,Z 2=4m,u 2=u∴9.81*9=9.81*4+222u +40*222u∴u=1.55m/s,Vs=uA=1.55*3.1415926*0.0252=10.95m3/h 若Vs'=Vs*(1+25%)=1.25Vs,则u'=1.25u=1.9375m/s ∴Z 1-Z 2=7.86m,即将水箱再升高7.86-5=2.86m 10解:Vs=8m3/h 时，该系统管路中水的流速为u 1=4Vs/3600πd 2=4*8/3600*3.1415926*0.0532=1.008m/s以压力表处为截面1-1'，水箱液面为截面2-2'，并以截面1-1'为基准水平面，则：f h Pu gz u P gz ∑+++=++ρρ2222211122Z2-Z1=24m P2=0 u2=0∴P1=(234.93+∑h f )*1000而3424.5001.01000*008.1*053.0Re===μρduε/d=0.2/53=0.00377查表得λ=0.0282 ∴∑h f = （h f + ξ）﹒u 12/2 =（0.0282*100/0.053 + 1）* 1.0082/2 =27.54J/Kg ∴P 1=(234.93+27.54)*1000=0.262MPa即压力表的读数为0.262MPa 时才能满足进水量为8m3/h 的需要。