正等轴测图圆画法

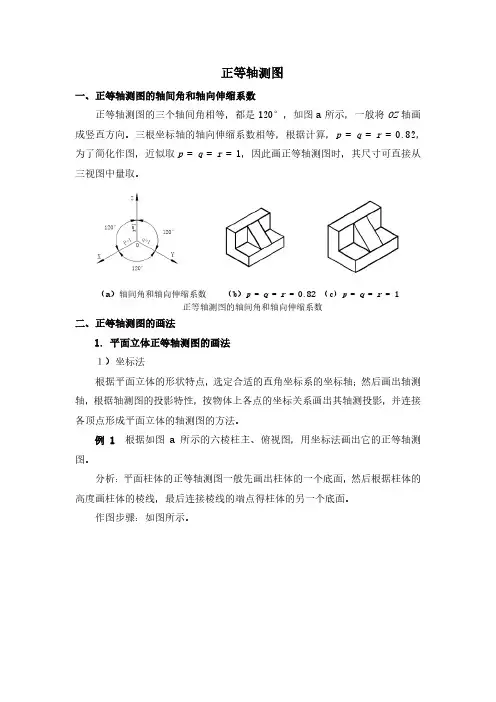
正等轴测图一、正等轴测图的轴间角和轴向伸缩系数正等轴测图的三个轴间角相等，都是120°，如图a所示，一般将OZ轴画成竖直方向。

三根坐标轴的轴向伸缩系数相等，根据计算，p = q = r = 0.82，为了简化作图，近似取p = q = r = 1，因此画正等轴测图时，其尺寸可直接从三视图中量取。

（a）轴间角和轴向伸缩系数（b）p = q = r = 0.82 （c) p = q = r = 1正等轴测图的轴间角和轴向伸缩系数二、正等轴测图的画法1. 平面立体正等轴测图的画法１）坐标法根据平面立体的形状特点，选定合适的直角坐标系的坐标轴；然后画出轴测轴，根据轴测图的投影特性，按物体上各点的坐标关系画出其轴测投影，并连接各顶点形成平面立体的轴测图的方法。

例 1 根据如图 a所示的六棱柱主、俯视图，用坐标法画出它的正等轴测图。

分析：平面柱体的正等轴测图一般先画出柱体的一个底面，然后根据柱体的高度画柱体的棱线，最后连接棱线的端点得柱体的另一个底面。

作图步骤：如图所示。

X 0′Z 0′O 0′O 0Y 0X 0XY OZ ZXY Oha 0d 0c 0b 0f 0e 01020ADⅠⅡABCD FE(a) (b) (c)ZZXXY YO OhAABBCCDDEE F F(d) (e) (f)正六棱柱的正等轴测图的画法２）切割法对于挖切形成的物体，以坐标法为基础，先用坐标法画出未切割的平面立体轴测图，然后用截切的方法逐一画出各个切割部分，这种方法称为切割法。

例 根据图 所示的切割体三视图，用切割法画出它的正等轴测图。

分析：该切割体是由基本体四棱柱切割而成的。

先用坐标法画出四棱柱基本体，再进行逐一切割即可。

作图步骤：如图所示。

Y 0X 0O 0O 0′Z 0′Z 0″X 0′Y 0″O 0″LL 2L 3BB 1B 2B 3HH 1H 2ZXYZXYHLBL 1L 1H 1H 2OO（a) （b) （c)ZZXXYYL 2B 1B 2B 3L 3OO（d) （e) （f)切割法画正等轴测图３）组合法对于叠加体，可用形体分析法将其分解成若干个基本体，然后按各基本体的相对位置关系画出轴测图，这种方法称组合法。

r=1
r=1
q=0.5
Z’
X
Y
X’
O
W
O
O’
O
1.先画没有切割前长方体的轴测图
2.画正垂面的轴测图
3.画铅垂面的轴测图
4.除掉多余的线,加粗.
X1
Y1
Z1
O
R
S
P
Q
X
Y
Z
120
120
a
b
c
d
d
c
b
a
Z
X
Y
先画前端面的投影
例3 用坐标法画圆的正等轴测图
C
Y
O
X
Y
Z
例5 带切口的直立圆柱体的轴测图
移心法 是先画出上底面圆的轴测图 ---椭圆和四段圆弧的圆心
W
ቤተ መጻሕፍቲ ባይዱ
X
O
Y1
X1
例3 用坐标法画圆的正等轴测图
O
X
Y
Z
例5 带切口的直立圆柱体的轴测图
移心法 是先画出上底面圆的轴测图 ---椭圆和四段圆弧的圆心
1.用四圆心法画圆柱上端 面的轴测图
2.将圆心Oa Oc Od沿Z轴方向向下平移W距离,得圆柱下端面轴测图的圆心.
3.画圆柱的左右素线的轴测图
四、轴测图的投影性质
平行性
等比性
X1
Y1
Z1
X
Y
Z
O
O’
A
B
C
a1
b1
c1
P
P
X’
Z’
Y’
O’
S
p=a1O’/AO
2. 轴向变形系数(p,q,r)：
§3-4-2 正等测轴测图的画法

二、正等轴测图的画法
2.圆的正等轴测投影
四心椭圆法画椭圆
——平行于XOY 坐标面的圆xyo
O
Y
X
a.定坐标原点，画轴测轴；
作图步骤：
b.画圆的外切正方形，及其轴测投影；
二、正等轴测图的画法
2.圆的正等轴测投影
作图步骤：
o
四心椭圆法画椭圆
——平行于XOY 坐标面的圆
二、正等轴测图的画法
2.圆的正等轴测投影
2.圆的正等轴测投影
正等轴测图的画法
当圆所在平面不平行于轴测投影面时,其轴测投影为椭圆。
X
P
X1
三个坐标面对轴测投影面都不平行,其轴测投影均为椭圆。
分析XOY 坐标面上圆及其轴测投影椭圆间的关系。
椭圆的长短轴方向？
二、正等轴测图的画法
2.圆的正等轴测投影
β
α
O1
Y
Z
X
O
P
X1
Z1
Y1
S
γ
椭圆的长轴方向与XOY 面内对P 面的平行线平行；
椭圆的短轴方向与XOY 面内对P 面的最大斜度线方向平行。
A
B
C
D
AB 平行P 面
CD 平行P 面最大斜度线
A1
B1
C1
D1
A1B1 = AB ---椭圆长轴
C1D1 = CD cosψ ---椭圆短轴
ψ
二、正等轴测图的画法
2.圆的正等轴测投影
β
α
O1
Y
Z
X
O
P
X1
Z1
Y1
S
γ
椭圆的长轴方向与XOY 面内对P 面的平行线平行；
椭圆的短轴方向与XOY 面内对P 面的最大斜度线方向平行。

（c） （d）
1.先在正投影图上定出原点和坐标轴的位置。考虑到作图方便， 把坐标原点选在底面上点B处，并使AB与OX轴重合。（图a） 2.画出轴测轴O1X1、O1Y1、O1Z1。 3.根据坐标关系画出底面各顶点和锥顶S1在底面的投影s1。 （图b）
4.过s1垂直于底面向上作O1Z1 的平行线，在线上量取三棱锥的 高度h，得到锥顶S1。（图c）
X
Z C M n X1 b O1
Z1
h
Z1 N O1
d X m a O
c
D
b
A
B
Y1 X1
b
Y
（a）
（b）
（c）
h
（d）
h
Y1
(1) 作图方法与步骤如图所示： 1.选定直角坐标系，以正六棱柱顶面的中点为原点（坐标系原点可 以任定，但应注意对于不同位置原点，顶面和底面各顶点的 坐标不同）。（图a） 2.画出轴测轴O1X1、O1Y1、O1Z1。 3.在O1X1 轴上量取O1M、O1N，使O1M＝OM、O1N＝ON，在O1 Y1 轴上以 尺寸b来确定A、B、C、D各点，依次连接六点即得顶面正六边 形的轴测投影。（图b） 4.过顶面正六边形各点向下作O1Z1 的平行线，在各线上量取高度h， 得到底面上各点并依次连接，得底面正六边形的轴测投影。 （图c） 5.擦去多余的图线并描深，即得到的正六棱柱体正等测图。（图 d）
四、曲面立体正轴测图的画法
1、圆柱和圆台的正等测图
如图所示，作图时，先分别作出其顶面和底面的椭圆，再作其公 切线即可。
2、圆角的正等测图
如图所示的画法，其作图步骤如下：
1.在角上分别沿轴向取一段长度等于半径R的线段，得A、A和B、B点，过A、B点 作相应边的垂线分别交于O1及O2 。 2.以O1及O2为圆心，以O1A及O2B为半径作弧，即为顶面上圆角的轴测图；（图b） 3.将O1及O2点垂直下移，取O3、、O4点，使O1 O3 =O2 O4 =h（板厚）。以O3及O4为 圆心，以O1A及O2B为半径作弧，作底面上圆角的轴测图，再作上、下圆弧的公 切线，即完成作图。（图c） 4.擦去多余的图线并描深，即得到圆角的正等测图。（图d）

Y Nhomakorabeao2
§11-2 正轴测图
二、正等轴测图的画法
2.圆的正等轴测投影
四心椭圆法画椭圆 ——平行于XOY 坐标面的圆
作图步骤： a.定坐标原点，画轴测轴；
d.定半径画4段圆弧； e.整理并描深结果。 b.画圆的外切正方形，及其轴测投影； c.在菱形对角线上定4个圆心；
x
o
o1
y
o3 o2
o4
§11-2 正轴测图
x’
z’
o’
x
o
b.圆柱顶面圆的轴测投影； c.圆柱底面圆的轴测投影； d.画公切线；e.整理、描深。
作图步骤： y
a.定坐标原点，画轴测轴；
§11-2 正轴测图
h
二、正等轴测图的画法
2.圆的正等轴测投影
圆台的正等轴测图 ——轴线垂直YOZ 坐标面
z’
h
o’ h
z”
D2
x’
D1
Z
D2
X Y
o”
作图步骤： a.定坐标原点，画轴测轴；
C1D1 = CD cosψ ---椭圆短轴
Y
§11-2 正轴测图
二、正等轴测图的画法
2.圆的正等轴测投影
椭圆的长轴方向与XOY 面内对P 面的平行线平行； 椭圆的短轴方向与XOY 面内对P 面的最大斜度线方向平行。
S
在正等轴测图中，
C
O
α＝β＝γ，
A X1 X
α
A1
D ψ O1 D1 β B1 C1
2.圆的正等轴测投影
¼ 圆角的正等轴测图 作图步骤： d.整理图形。
h
结束
§11-2 正轴测图
§11-2 正轴测图
D1

三维图中一般可见下图三个面中圆的正等轴测 图
Z1
平行于俯视面
平行于左视面
平行于主视面
X1
Y1
这节课教大家用“四心椭圆法”绘制 平行于俯视面的正等轴测圆：
步骤1：绘制圆外切正方形的正等轴测图(菱形） 步骤2：确定四个圆心和半径
步骤3：绘制四段彼此相切的圆弧 步骤4：加深四段圆弧轮廓线，呈椭圆，绘图完成
第一步： 画圆的外切菱形
e
E
B
●
●
a
b
300
300
A●
F ●
f
第二步： 确定四个圆心和半径
O● 1
E
●
●
O3
A●
●
O2
B
●
切的圆弧
O● 1
E
●
●
O3
A●
●
O2
B
●
O4 ●
F ●
第四步：加深四段圆弧轮廓线，呈椭圆圆弧
圆的正等轴测图绘制
教师：张改莉 学校：赵湾中学
教材分析
1.教材----------------------------《技术与设计1 》 2.章节-----第六章第一节 《设计图样的绘制》 3.内容--------------四心法绘制圆的正等轴测图
圆是曲面立体中最常见的图，其 轴测图画法难度较大

将组合体分解成若干 基本形体，再按其相对 位置逐个地画出各基本 形体的轴测图
2、平面体正等测画法
(１). 坐标法
例1：画四棱柱的正等轴测图
z'
z"
x'
o' o"
y"
2
o
x
3
4
y
2● X1
Z1 O1
● 4 Y1
2、平面体正等测画法
z 例2 求作图示正六棱柱的正等测图
x
z1
o1 y1
x
x1
y
2、平面体正等测画法
(1) 在视图上建立坐标系 (2) 画出正等测轴测轴 (3) 按坐标关系画出物体的轴测图
2、平面体正等测画法
正等测轴测图的基本作图方法
坐标法
切割法
叠加法
根据形体的形状特点选定 适当的坐标轴，然后将形体上 各点的坐标关系转移到轴测图 上，以定出形体上各点的轴测 投影，从而作出形体的轴测图。
对于不完整的物体， 可先按完整物体画出， 再用切割法画出其不完 整的部分
o1 y1
2、平面体正等测画法
例2 求作带切口平面立体的正等测图
z
x
o
x
o
c`
y
x1
z1
o1 y1
2、平面体正等测画法
例2 求作带切口平面立体的正等测图
z
x
o
x
o
c`
y
(3). 叠加法
2、平面体正等测画法
3、回转体正等测画法
（1） 平行于坐标面的圆的正等测图
侧平圆
Z1
水平圆
正平圆
X1
Y1
3、回转体正等测画法

⑧以E为基点，F为目标点。将平行四边形移动到 E点。
E
⑨删除和修剪掉多余的图线
⑩标注尺寸
⑾切割凹槽。在之前的图中画宽30；高10的凹槽
பைடு நூலகம்
正等轴测图
①工具—草图设置—捕捉和栅格，选中等轴 测捕捉
②用F5键切换到左轴测面，打开正交。指定一起 点，依次以长度55、50、55、50画出ABCD四边形。
③绘图—椭圆（EL）—输入I，回车—捕捉AD的 中点为圆心—输入半径（25）后回车，画出半径 为25的轴测圆；以同样的方法画出半径为12.5的 轴测圆。
④用F5键切换到右轴测main，从C点处沿X轴画出 长度为25的线段CE；以C为基点，E为目标点将大 轴测圆和直线CD沿CE方向复制。
⑤画出两个大轴测圆的外公切线
⑥用修剪、删除命令。得到下图
⑦用F5键切换到上轴测面，沿X轴、Y轴画出线段长为50的 平行四边形；切换到右轴测面，从F点沿Z轴向下画出长为 25的线段，将平行四边形向下复制，链接对应的轮廓线。

正等轴测图的分类
正等轴测图可以分为正等侧轴测 图和正等俯轴测图两种类型。
正等侧轴测图是从物体的左侧投 影，而正等俯轴测图是从物体的
顶部投影。
在实际应用中，根据需要选择不 同类型的正等轴测图来表示物体。
02
正等轴测图的绘制方法
坐标系的建立
确定原点
选择一个基准点作为原点，通常 将原点设置在图形中心或任意方
THANKS
感谢观看
添加尺寸标注
标注长度
根据需要标注图形各部分的长度，利用坐标值和单位 长度计算标注值。
标注角度
标注图形各部分之间的角度，利用坐标值和单位长度 计算标注值。
标注高度
标注立体图形的高度，利用坐标值和单位长度计算标 注值。
03
正等轴测图的绘制技巧
选择合适的视图角度
确定合适的角度
选择一个能够清晰展示物体特征的视角，使物体在正等轴测图中 呈现最佳的立体效果。
04
常见错误及纠正方法
尺寸标注不准确
总结词
在绘制正等轴测图时，尺寸标注的准确性至关重要，因为错误的尺寸会导致图 纸的误导。
详细描述
在进行尺寸标注时，要确保使用正确的测量工具，并仔细检查每个尺寸，确保 它们与实际物体或设计相符。如果发现尺寸标注错误，应及时更正，并重新测 量和标注。
投影关系不正确
绘制复杂立体图形
总结词：运用技巧
详细描述：复杂立体图形在正等轴测图中需要更高的技巧。在绘制过程中，需要 灵活运用各种绘图技巧，如旋转、缩放、镜像等，以准确表达立体图形的形状和 结构。同时，需要注意轴测投影的特性，确保图形符合视觉习惯。
绘制组合体正等轴测图
总结词：综合运用
详细描述：组合体是由多个简单立体图形组合而成的复杂物体。在绘制组合体的正等轴测图时，需要综合运用前面学到的各 种技巧和方法，根据组合体的结构特点选择合适的表达方式。同时，需要注意各部分之间的相对位置和连接关系，确保整体 效果协调一致。

第7 页
（a）
（b）
（c）
图4-30 圆木榫正等轴测图的画法
（d）
曲面立体及其轴测投影
第8 页
【例4-13】作图4-31所示圆拱门洞
的斜二等轴测图。
分析： 由图4-31所示投影图中可以看出，该 圆拱门洞左右对称，中间为拱形圆洞，左 右两侧为两个长方体，且长方体的后面与 圆洞的后面平齐，圆洞的底面与长方体的 底面平齐。为了便于画图，将坐标系设在 圆洞前端面的圆心处。
图4-31 圆拱门洞的正投影图
曲面立体及其轴测投影
第9 页
作图步骤： （1）先绘制斜二等轴测图的 轴测轴（Y轴为45°斜线），然后绘 制拱形圆洞前、后端面的轴测图， 如图4-32（a）所示。注意：前、 后端面同心圆的圆心在Y轴上的距 离为图4-31中拱形圆洞宽度的一半。 （2）绘制拱形圆洞前后端面 的切线，然后擦去被遮挡部分的轮 廓线，结果如图4-32（b）所示。 （3）先画左侧长方体的后端 面，然后在Y轴方向上截取长方体 宽度的一半，绘制左侧长方体。采 用同样的方法绘制右侧长方体，结 果如图4-32（c）所示。 （4）擦去轴测轴和被遮挡的 图线，然后加深图线，结果如图432（d）所示。
（a）
（b）
（c）
（d）
图4-27 圆柱正等轴测图的画法
第4 页
曲面立体及其轴测投影
由于圆柱体和圆锥体都是曲面立体，且其底面均为圆，因此它们 的正等轴测图的画法也基本相同。图4-28所示为圆锥体正等轴测图的画 法。
第5 页
（a）
（b）
（c）
图4-28 圆锥正等轴测图的画法
（d）
曲面立体及其轴测投影
第2 页
曲面立体及其轴测投影
第3 页
【 例 4-10 】 作 图 4-26 （ a ） 所 示 水

轴测图中画圆和圆弧的技巧摘要：在工程上，轴测图具有能同时反映形体长、宽、高三个方向的形状，立体感强，形象直观的优点，但不能确切地表达零件原来的形状与大小，且作图较复杂，因而轴测图在工程上一般仅用作辅助图样。

而如何准确、快速的画出轴测图就需要在画法技巧上找出较好的方法做指导。

关键词：轴测图;四心法在工程上，多面正投影图绘制图样，它可以较完整地确切地表达出零件各部分的形状，且作图方便，但这种图样直观性差;而轴测图能同时反映形体长、宽、高三个方向的形状，具有立体感强，形象直观的优点，但不能确切地表达零件原来的形状与大小，且作图较复杂，因而轴测图在工程上一般仅用作辅助图样。

而如何准确、快速的画出轴测图就需要在画法技巧上有所突破。

平面立体轴测图的常用画法有坐标法、切割法、叠加法;曲面立体轴测图的常用画法有针对曲面部分的坐标法和针对圆的四圆心法画法。

下面我就主要针对在轴测图上相对出现频率较高但又较难画的圆及圆弧的画法提出一些简单技巧以解决实际问题。

图a图b图1四心法1.四心法作正等测圆的方法和步骤：1.1首先测量实体上的圆的半径，且判断实体上的圆存在的平面，如图1（a）所示，这个圆存在于XY平面。

1.2在新建的轴测轴上以O为圆心，以实体圆的半径为半径在图b的X、Y、Z六个半轴上分别截取得到六个点，如图1（b）所示。

1.3利用截取的点确定两心，完成两段圆弧的连接。

由于这个圆存在于XY 平面，不关乎Z轴，所以以Z轴上截取的两点E、F分别为圆心，以与他相隔一点的点为半径画圆弧，完成两个点的连接。

如图b所示，以点E为圆心，连接EA和EC，以EA或EC为半径画圆弧，总能完成AC两点的圆弧连接。

用同样的办法可以完成图b中DB两点的圆弧连接。

1.4过点O作一条与所缺轴垂直的垂线，在这条垂线上找出另外两心并完成圆弧连接。

如图b所示，这个圆存在于XY平面，所以理解为所缺轴为Z轴，所以过点O作与Z轴垂直的垂线，分别交EA、EC于点G和点H，点G和点H即为所找的另外两个圆心。

圆的正等测图的画法教案课题：1、圆的正等测图的画法2、曲⾯⽴体的正等测图的画法课堂类型：讲授教学⽬的：1、讲解圆的正等测图的画法2、讲解曲⾯⽴体的正等测图的画法教学要求：1、掌握平⾏于投影⾯的圆的正等测图的画法2、掌握常见曲⾯⽴体的正等测图的画法3、掌握长⽴体的圆⾓的正等测图的画法教学重点：曲⾯⽴体的正等测图的画法教学难点：曲⾯⽴体的正等测图的画法中三个不同⽅向椭圆中⼼的定位和长短轴⽅向的确定教具：模型：圆柱体、圆锥体教学⽅法：曲⾯⽴体的正等测图关键在于掌握圆的画法。

⽴体上平⾏坐标⾯的圆（投影⾯上的圆），在正等测图中为椭圆，要注意平⾏不同坐标⾯的圆（各投影⾯上的圆），其长短轴⽅向是不同的。

讲课中要加强对学⽣的训练，并检查学⽣的掌握程度。

教学过程：⼀、复习旧课1、正等测图的形成、轴间⾓和轴向变形系数。

2、复习平⾯⽴体的纳正等测图的作图⽅法。

⼆、引⼊新课题绘制曲⾯⽴体的正等测图，关键是要掌握圆的的正等测图画法，平⾏于坐标⾯的圆的正等测图中为椭圆。

在曲⾯⽴体中，圆是最基本的图形，所以先来讨论圆的的正等测图。

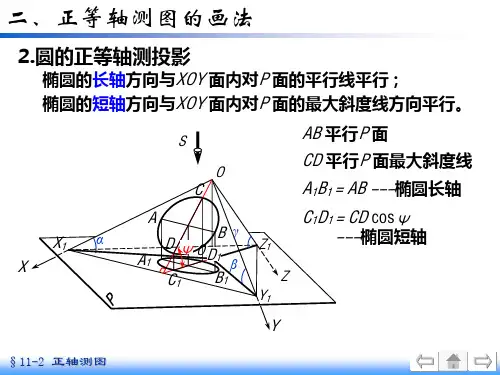
三、教学内容（⼀）圆的正轴测图的画法1、平⾏于不同坐标⾯的圆的正等测图平⾏于坐标⾯的圆的正等测图都是椭圆，除了长短轴的⽅向不同外，画法都是⼀样的。

图4－7所⽰为三种不同位置的圆的正等测图。

作圆的正等测图时，必须弄清椭圆的长短轴的⽅向。

分析图4－7所⽰的图形（图中的菱形为与圆外切的正⽅形的轴测投影）即可看出，椭圆长轴的⽅向与菱形的长对⾓线重合，椭圆短轴的⽅向垂直于椭圆的长轴，即与菱形的短对⾓线重合。

图4－7 平⾏坐标⾯上圆的正等测图通过分析，还可以看出，椭圆的长短轴和轴测轴有关，即：（1）圆所在平⾯平⾏XOY⾯时，它的轴测投影——椭圆的长轴垂直O1Z1轴，即成⽔平位置，短轴平⾏O1Z1轴；（2）圆所在平⾯平⾏XOZ⾯时，它的轴测投影——椭圆的长轴垂直O1Y1轴，即向右⽅倾斜，并与⽔平线成60°⾓，短轴平⾏O1Y1轴；（3）圆所在平⾯平⾏YOZ⾯时，它的轴测投影——椭圆的长轴垂直O1X1轴，即向左⽅倾斜，并与⽔平线成60°⾓，，短轴平⾏O1X1轴。

A为O、菱3B形为、；圆C、心D，，相作应O垂1Y线1、段O为1半X1径的画平圆行弧线；，
圆和圆角的正等轴测图 二、用“四心法”绘制圆的正等轴测图——正平圆
z'
正平圆
x'
o'
Z1 O X1
圆和圆角的正等轴测图 二、用“四心法”绘制圆正等轴测图——侧平圆侧平圆
z''
o''
y''
Z1 O
Y1
圆和圆角的正等轴测图
为简化作图，绘制圆的正 等轴测图时，一般常用“四心 法”近似画椭圆。
侧平圆的轴测图
O 正平圆的轴测图
圆和圆角的正等轴测图
二、用“四心法”绘制圆的正等轴测图——水平圆
x'
x a
z'
O'
d
O
c y
Z1Ⅰ
D
B
O1
O2
O3
X1 A
C Y1
Ⅱ b
（ （（（（（124356） ）7））））确 画 画画作作整定 圆 外轴出圆理坐 的 切测点弧图标 外 正轴O，线轴 切 方；2分、，和 正 形O别完坐方的3以成；标形轴点作原；测Ⅰ图点投。、；影I，I和作点出O点2、
o2
P
H
（（（1342）））画用 做画长“ 出圆方移 其角体心 他，顶法 图从面” 线前的画，面轴出圆的测底弧两投处面个影画圆顶；出角点公；沿切两 线边，取完距成离全R，图得。到点M、N、P、Q，分 别过个点作各边的垂线，得到点O1、O2；
谢谢观看
Thanks for looking
三、绘制圆柱体的正等轴测图
x'
z' o'
Z1 X1

2.为使图形清晰，轴测图中一般只画可见的轮廓线，避免用虚 线表达。
三、圆的正轴测图的画法
1、平行于不同坐标面的圆的正等测图
平行于坐标面的圆的正等测图都是椭圆，除了长短轴的方向不同外，画法都是 一样的。 如图所示为三种不同位置的圆的正等测图:
通过分析，还可以看出，椭圆的长短轴和轴测 轴有关，即：
1.圆所在平面平行XOY面时，它的轴测投影— —椭圆的长轴垂直O1Z1轴，即成水平位置，短 轴平行O1Z1轴；
2.圆所在平面平行XOZ面时，它的轴测投影—
—椭圆的长轴垂直O1Y1轴，即向右方倾斜，并
与水平线成60°角，短轴平行O1Y1轴；
X1
3.圆所在平面平行YOZ面时，它的轴测投
平行于YOZ坐标面
影——椭圆的长轴垂直O1X1轴，即向左方倾斜， 的圆的投影
并与水平线成60°角，，短轴平行O1X1轴。
Z1 平行于XOY坐标面 的圆的投影
5.擦去多余的图线并描深，即得到的正六棱柱体正等测图。（图 d）
3、 三棱锥的正等测图
分析：由于三棱锥由各种位置的平面组成，作图时可以先锥顶 和底面的轴测投影，然后连接各棱线即可。
作图方法与步骤如图所示 :
Z
Z1
X
a X
bO
s XS
c XC
XA Y
YS
ZS
YC
S1
B1 XA O1
YS YC
XS
X1 A1
Z1
过该角顶点的三 X 条 棱 线 为 坐 标 轴 。X 先画出轴测轴， 然后用各顶点的
O′
a
O″ O
Y a
X1 b
O1 Y1
坐标分别定出长
Y
方 体 的 八 个 顶 点 （a）