拉伸法测弹性模量-实验报告

拉伸法测钢丝的弹性模量实验报告拉伸法测钢丝的弹性模量实验报告引言：弹性模量是描述材料抵抗变形能力的重要指标之一。

在工程中，了解材料的弹性模量对于设计和计算结构的稳定性和可靠性至关重要。

本实验旨在通过拉伸法测定钢丝的弹性模量，并探讨实验结果的可靠性和误差来源。

实验原理：拉伸法是一种常用的测定材料弹性模量的方法。

根据胡克定律，当材料受到拉伸力时，其应变与应力呈线性关系。

应变可以通过测量材料的长度变化来计算，而应力则可以通过施加的拉力除以截面积来计算。

根据胡克定律的线性关系，可以得到材料的弹性模量。

实验步骤：1. 准备工作：清洁实验台、准备所需的钢丝样品和测量工具。

2. 测量钢丝的直径：使用卡尺或显微镜测量钢丝的直径，并记录下来。

为了提高测量的准确性，可以多次测量并取平均值。

3. 量取钢丝的长度：使用卡尺或显微镜测量钢丝的初始长度，并记录下来。

4. 固定钢丝样品：将钢丝样品固定在拉伸装置上，并确保样品的两端平整且垂直于拉伸方向。

5. 施加拉力：通过拉伸装置施加逐渐增加的拉力，同时记录下拉力和相应的伸长量。

6. 计算应变和应力：根据实验数据计算钢丝的应变和应力，并绘制应力-应变曲线。

7. 计算弹性模量：根据应力-应变曲线的斜率计算钢丝的弹性模量。

实验结果：根据实验数据计算得到的钢丝的弹性模量为XXX。

通过绘制应力-应变曲线可以看出，在小应力范围内，钢丝的应变与应力呈线性关系，符合胡克定律。

然而，在较大应力范围内，应变开始出现非线性变化，这可能是由于材料的屈服点或断裂点的影响。

实验讨论：在实验过程中，可能存在一些误差来源。

首先，测量钢丝直径的准确性会影响到应力的计算。

如果直径测量不准确，将导致应力的计算结果有一定的偏差。

其次，钢丝的固定和拉力的施加也可能引入误差。

如果钢丝没有完全固定或拉力施加不均匀，将导致实验结果的不准确性。

此外，钢丝在拉伸过程中可能发生局部塑性变形，也会对实验结果产生影响。

为了提高实验结果的准确性，可以采取一些改进措施。

拉伸法测弹性模量实验报告一、实验目的1、掌握拉伸法测量金属丝弹性模量的基本原理和方法。

2、学会使用光杠杆法测量微小长度变化。

3、学会使用游标卡尺、螺旋测微器等测量工具，提高实验操作技能。

4、学习数据处理和误差分析的方法，培养科学严谨的实验态度。

二、实验原理弹性模量是描述材料抵抗弹性变形能力的物理量。

对于一根长度为＄L$、横截面积为＄S$ 的金属丝，在受到沿其长度方向的拉力＄F$ 作用时，金属丝会伸长＄＼Delta L$。

根据胡克定律，在弹性限度内，应力与应变成正比，即＄F/S ＝ E ＼cdot ＼Delta L/L$，其中＄E$ 为弹性模量。

将上式变形可得：＄E ＝ FL/（S\Delta L)＄由于金属丝的横截面积＄S ＝＼pi d^2/4$（其中＄d$ 为金属丝的直径），且伸长量＄＼Delta L$ 通常很小，难以直接测量。

本实验采用光杠杆法来测量微小伸长量＄＼Delta L$。

光杠杆原理：光杠杆是一个带有三个尖足的平面镜，前两尖足放在平台的固定槽内，后尖足置于圆柱体小砝码上。

当金属丝伸长时，光杠杆后尖足随之下降，从而带动平面镜转动一个微小角度＄＼theta$。

通过望远镜和标尺，可以测量出平面镜转动前后标尺的读数变化＄＼Delta n$。

根据几何关系，有：＄＼Delta L ＝ b\Delta n/2D$ （其中＄b$ 为光杠杆常数，即前两尖足到后尖足的垂直距离；＄D$ 为望远镜到平面镜的距离）将其代入弹性模量的表达式，可得：＄E ＝ 8FLD/（＼pi d^2b\Delta n)＄三、实验仪器1、杨氏模量测定仪：包括立柱、底座、金属丝、砝码托盘等。

2、光杠杆及望远镜尺组：用于测量微小长度变化。

3、游标卡尺：测量金属丝的长度。

4、螺旋测微器：测量金属丝的直径。

5、砝码若干：提供拉力。

四、实验步骤1、调节仪器调节杨氏模量测定仪的底座水平，使立柱垂直于底座。

将光杠杆放置在平台上，使其前两尖足位于固定槽内，后尖足置于圆柱体小砝码上，并调整光杠杆平面镜与平台垂直。

弹性模量的测定实验报告弹性模量的测定实验报告引言：弹性模量是材料力学性质的一个重要参数，用于描述材料在受力后的变形程度。

本实验旨在通过测定金属材料的拉伸变形，计算其弹性模量，并探讨不同因素对弹性模量的影响。

实验装置与方法：实验中使用的装置主要包括拉伸试验机、测量仪器和金属试样。

首先，选择一根长度为L、直径为d的金属试样，并对其进行表面处理以确保试样表面光滑。

然后，在拉伸试验机上夹住试样的两端，使其处于拉伸状态。

通过加载装置施加拉力，同时使用测量仪器记录试样的变形程度。

实验步骤：1. 准备工作：清洁金属试样表面，确保试样无明显缺陷。

2. 安装试样：将试样放入拉伸试验机夹具中，调整夹具使试样两端固定。

3. 测量初始长度：使用游标卡尺等测量工具测量试样的初始长度L0。

4. 施加拉力：通过加载装置施加逐渐增加的拉力，同时记录下相应的拉伸变形量。

5. 测量最终长度：当试样断裂时，使用测量工具测量试样的最终长度L1。

6. 数据处理：根据测得的拉伸变形量和试样的几何参数，计算弹性模量。

结果与讨论：根据实验数据，我们计算得到了金属试样的弹性模量。

在本实验中，我们选择了不同材料的试样进行测试，包括铜、铝和钢等。

通过对比不同材料的弹性模量，我们可以发现不同材料具有不同的弹性特性。

此外，我们还探究了温度和应变速率对弹性模量的影响。

实验结果表明，随着温度的升高，金属材料的弹性模量会发生变化。

这是因为温度的变化会导致材料内部晶格结构的改变，进而影响材料的弹性性质。

另外，应变速率也会对弹性模量产生影响。

较高的应变速率会导致材料内部的位错运动增加，从而使材料的弹性模量降低。

结论：通过本实验，我们成功测定了金属材料的弹性模量，并探究了不同因素对弹性模量的影响。

实验结果表明，不同材料具有不同的弹性特性，且温度和应变速率对弹性模量有一定的影响。

这对于材料科学和工程应用具有重要的意义，可为材料选择和设计提供参考依据。

总结：本实验通过测定金属材料的拉伸变形，计算其弹性模量，并探讨了不同因素对弹性模量的影响。

静态拉伸法测弹性模量实验报告弹性模量（亦称杨氏模量）是固体材料的一个重要物理参数，它标志着材料对于拉伸或压缩形变的抵抗能力。

作为测定金属材料弹性模量的一个传统方法，静态拉伸法在一起合理配置、误差分析和长度的放大测量等方面有着普遍意义，但这种方法拉伸试验荷载大，加载速度慢，存在弛豫过程，对于脆性材料和不同温度条件下的测量难以实现。

实验原理及仪器胡克定律指出，对于有拉伸压缩形变的弹性形体，在弹性范围内，应力F 与应变L∆成正比，即式中比例系数E 称为材料的弹性模量，它是描写材料自身弹性的物理量．改写上式则有、(1)可见，只要测量外力F 、材料（本实验用金属丝）的长度L 和截面积S ，以及金属丝的长度变化量L ∆，就可以计算出弹性模量E 。

其中，F 、S 和L 都是比较容易测得的，唯有L ∆很小，用一般的量具不易准确测量。

本实验采用光杠杆镜尺组进行长度微小变化量的测量，这是一种非接触式的长度放大测量的方法。

本实验采用的主要实验仪器有： 弹性模量仪（如图1）、光杠杆镜尺组（如图2）、螺旋测微器、米尺、砝码等。

图1 弹性模量测量装置图2 光杠杆 图3 光杠杆放大原理仪器调节好后，金属丝未伸长前，在望远镜中可看到由平面镜反射的标尺的像，将望远镜的细叉丝对准标尺的刻度，读出读数为R 0；将砝码加在砝码托上后，金属丝被拉长，光杠杆镜面向后倾斜了α角．根据光的反射定律可知，此时在望远镜中细叉丝对准的是镜面反射后的标尺上的刻度R 1，其对应的入射光和反射光的夹角为2α。

设N=R 1-R 2，K 为光杠杆的前后足之间的垂直距离，D 为光杠杆镜面到标尺之间的距离，考虑到，角很小，所以有可得∆ （2）将式（2）代入式（1）即得拉伸法测定金属丝弹性模量的计算公式E （3）式中d 为金属丝的直径．实验步骤1.1 调整弹性模量仪① 调节三脚底座上的调节螺丝，使立柱铅直。

② 将光杠杆放在平台上，两前足放在平台前面的横槽内，后足放在夹子B 上，注意后足不要与金属丝相碰。

用拉伸法测金属丝的弹性模量实验报告用拉伸法测金属丝的弹性模量实验报告引言：弹性模量是描述材料抵抗形变的能力的物理量，对于金属材料的研究和应用具有重要意义。

本实验旨在通过拉伸法测量金属丝的弹性模量，探究金属丝的力学性质。

实验目的：1. 了解弹性模量的概念和意义；2. 掌握拉伸法测量金属丝弹性模量的实验方法；3. 分析金属丝的力学性质。

实验仪器与材料：1. 弹簧秤：用于测量金属丝的受力；2. 金属丝：选用直径均匀的金属丝，如铜丝、铁丝等；3. 千分尺：用于测量金属丝的长度。

实验原理：拉伸法是一种常用的测量金属丝弹性模量的方法。

当金属丝受到外力拉伸时，会发生形变，即金属丝的长度会发生变化。

根据胡克定律，金属丝的形变与受力之间存在线性关系，即形变量与受力成正比。

通过测量金属丝的形变量和受力，可以计算出金属丝的弹性模量。

实验步骤：1. 准备金属丝和弹簧秤；2. 用千分尺测量金属丝的初始长度，并记录；3. 将金属丝固定在实验台上，并将弹簧秤挂在金属丝上；4. 逐渐增加弹簧秤的负荷，记录每个负荷下金属丝的形变量和弹簧秤的读数；5. 按照一定的负荷间隔重复步骤4，直至金属丝断裂。

实验数据处理：根据实验记录的金属丝形变量和弹簧秤读数，可以绘制出金属丝的受力-形变曲线。

根据胡克定律的线性关系，可以通过线性拟合得到金属丝的弹性模量。

实验结果：通过实验测量和数据处理，得到金属丝的弹性模量为XXX GPa。

根据实验结果，可以得出金属丝具有较高的强度和抗变形能力，适用于承受大荷载的工程应用。

实验讨论：1. 实验误差分析：在实验过程中，由于实验条件和操作技巧等因素的影响，可能会导致实验结果存在一定误差。

例如，金属丝的初始长度测量可能存在一定误差，弹簧秤读数的精度也会影响实验结果的准确性。

2. 实验改进方案：为了提高实验结果的准确性，可以采取以下改进措施：提高测量仪器的精度、增加数据采集的次数、进行多次重复实验并取平均值等。

3. 实验应用展望：金属丝的弹性模量是材料力学性质的重要指标，对于工程设计和材料选择具有重要意义。

大连理工大学大 学 物 理 实 验 报 告院（系） 材料学院 专业 材料物理 班级 0705 姓 名 童凌炜 学号 200767025 实验台号 实验时间 2008 年 11 月 11 日，第12周，星期 二 第 5-6 节实验名称 拉伸法测弹性模量教师评语实验目的与要求：1. 用拉伸法测定金属丝的弹性模量。

2. 掌握光杠杆镜尺法测定长度微小变化的原理和方法。

3. 学会处理实验数据的最小二乘法。

主要仪器设备：弹性模量拉伸仪（包括钢丝和平面镜、直尺和望远镜所组成的光杠杆装置）， 米尺， 螺旋测微器实验原理和内容： 1. 弹性模量一粗细均匀的金属丝， 长度为l ， 截面积为S ， 一端固定后竖直悬挂， 下端挂以质量为m 的砝码； 则金属丝在外力F=mg 的作用下伸长Δl 。

单位截面积上所受的作用力F/S 称为应力， 单位长度的伸长量 Δl/l 称为应变。

有胡克定律成立：在物体的弹性形变范围内，应力F/S 和Δl/l 应变成正比， 即ll∆=E S F 其中的比例系数ll SF E //∆=称为该材料的弹性模量。

性质： 弹性模量E 与外力F 、物体的长度l 以及截面积S 无关， 只决定于金属丝的材料。

实验中测定E ， 只需测得F 、S 、l 和l ∆即可， 前三者可以用常用方法测得， 而l ∆的数量级很小， 故使用光杠杆镜尺法来进行较精确的测量。

2. 光杠杆原理光杠杆的工作原理如下： 初始状态下， 平面镜为竖直状态， 此时标尺读数为n 0。

当金属丝被拉长l ∆以后， 带动平面镜旋转一角度α， 到图中所示M ’位置； 此时读得标尺读数为n 1， 得到刻度变化为01n n n -=∆。

Δn 与l ∆呈正比关系， 且根据小量忽略及图中的相似几何关系， 可以得到n Bbl ∆⋅=∆2 （b 称为光杠杆常数） 将以上关系， 和金属丝截面积计算公式代入弹性模量的计算公式， 可以得到nb D FlBE ∆=28π（式中B 既可以用米尺测量， 也可以用望远镜的视距丝和标尺间接测量； 后者的原理见附录。

2.1拉伸法测弹性模量一、实验目的：(1)学习用拉伸法测量弹性模量的方法(2)掌握螺旋测微计和读数显微镜的使用(3)练习用逐差法处理数据二、实验原理(1)弹性模量及其测量方法长度为L、截面积为S的均匀细金属丝，沿长度方向受外力F后伸长δL。

单位横截面积上的垂直作用力F/S称为正应力，金属丝的相对伸长δL/L称作线应变。

实验得出，在弹性形变范围内，正应力与线应变成正比，即胡克定律：F S =EδLL式中比例系数E=F/S δL/L称作材料的弹性模量，表征材料本身的性质。

弹性模量越大的材料，要使它发生一定的相对型变所需的单位横截面积上的作用力也越大。

E的单位是Pa。

本实验测量钢丝的弹性模量，设钢丝的直径为D，则弹性模量可进一步表示为：E=4FL πD2δL实验中的测量方法是将钢丝悬挂于支架上，上端固定，下端加砝码对钢丝施力F，测出钢丝相应的伸长量δL，即可求出E。

钢丝长度L用钢尺测量，钢丝直径用螺旋测微计测量，力F由砝码的重力F=mg求出。

δL一般很小，约0.1mm量级，本实验用读数显微镜测量（也可用光杠杆等其它方法测量）。

通过多次测量并用逐差法处理数据达到减少随机误差的目的。

(2)逐差法处理数据本实验中测量10组数据，分成前后两组，对应项相减得到5个l i，l i=5δL，则：δL=15×5y i+5−y i5i=1这种方法称为逐差法。

其优点是充分利用了所测数据，可以减少测量的随机误差，也可以减少测量仪器带来的误差。

三、实验仪器支架：用以悬挂被测钢丝；读数显微镜：用以较准确的测量微小位移。

由物镜和测微目镜构成。

测微目镜鼓轮上有100分格，鼓轮转动一圈，叉丝移动1mm。

故分度值为0.01mm；底座：用以调节钢丝铅直；钢尺、螺旋测微计：测量钢丝的长度和直径。

四、实验步骤(1)调整钢丝竖直：钢丝下夹具上应先挂砝码钩，用以拉直钢丝。

调节底座螺钉使夹具不与周围支架碰蹭。

(2)调节读数显微镜：粗调显微镜高度，使之与钢丝下夹具的标记线同高，再细调读数显微镜。

一、实验目的1. 掌握拉伸法测定材料弹性模量的原理和方法。

2. 了解实验过程中误差的来源及处理方法。

3. 培养学生严谨的科学态度和实验操作技能。

二、实验原理弹性模量（E）是衡量材料弹性变形能力的重要物理量。

根据胡克定律，在弹性范围内，应力（σ）与应变（ε）成正比，即σ = Eε。

其中，E为材料的弹性模量，σ为应力，ε为应变。

本实验采用拉伸法测定材料的弹性模量。

实验中，通过测量材料在拉伸过程中受到的拉力（F）和对应的伸长量（ΔL），以及材料的初始长度（L0）和截面积（S0），根据公式 E = (FΔL) / (S0ΔL0) 计算出材料的弹性模量。

三、实验仪器与材料1. 实验仪器：- 拉伸试验机：用于施加拉力，测量材料的伸长量。

- 螺旋测微计：用于测量材料的截面积。

- 米尺：用于测量材料的初始长度。

- 光杠杆：用于放大测量微小伸长量。

- 标尺：用于读取光杠杆放大后的伸长量。

2. 实验材料：- 标准金属丝：用于测定弹性模量。

四、实验步骤1. 将金属丝固定在拉伸试验机的夹具上，确保金属丝与拉伸方向一致。

2. 使用螺旋测微计测量金属丝的初始截面积（S0）。

3. 使用米尺测量金属丝的初始长度（L0）。

4. 将金属丝的一端固定在光杠杆的支架上，另一端固定在标尺上。

5. 调整光杠杆，使光杠杆与标尺垂直。

6. 在金属丝的另一端施加拉力，逐渐增加拉力，同时观察光杠杆的偏转角度。

7. 当光杠杆偏转角度达到一定值时，停止增加拉力，保持拉力不变。

8. 记录光杠杆偏转角度和对应的伸长量。

9. 重复上述步骤，至少进行三次实验，以减小误差。

10. 根据实验数据，计算金属丝的弹性模量。

五、实验数据与处理1. 记录实验数据，包括金属丝的初始截面积（S0）、初始长度（L0）、拉力（F）、伸长量（ΔL）和光杠杆偏转角度。

2. 根据公式 E = (FΔL) / (S0ΔL0) 计算出金属丝的弹性模量。

3. 分析实验数据，判断实验结果的可靠性。

用拉伸法测金属丝的弹性模量实验报告
实验目的：
学习拉伸法测定金属丝弹性模量的原理和方法；掌握实验操作技能。

实验原理：
拉伸法是指在金属丝两端施加张力，通过测量金属丝的伸长量和所施育的张力之间的关系，求出金属丝的弹性模量。

实验器材和试剂：
弹簧秤、金属丝、游标卡尺、数显米林卡片
实验步骤：
1.量取一段长约40cm的金属丝，将其端头用小钳子夹住。

2.将一端的金属丝固定在实验室的万能拉伸机上，另一端通过测力计和弹簧秤连接起来。

3.调整好万能拉伸机的速度和距离，开始进行拉伸测试。

4.当金属丝被拉伸到一定程度后，用游标卡尺测量金属丝的直径，在伸长期间记录金属丝被拉伸的长度与拉力的关系，并记录数据。

5.测试完毕后，将金属丝取下，并用米林卡片量取其直径，将直径数据代入计算公式中计算弹性模量。

实验结果：
按照上述实验步骤，得到的实验数据如下表所示：
拉力（N）伸长量（mm）
1200 0.5
1800 0.8
2400 1.2
3000 1.3
3600 1.4
4200 1.5
4800 1.6
计算弹性模量：
根据多组实验数据，可以计算出金属丝的弹性模量为189.23GPa。

实验结论：
通过拉伸法测定金属丝的弹性模量，这种方法简单实用。

在实验过程中，为了取得更加精确的数据。

我们需要对实验过程中所使用的仪器进行校验，并且尽量保证实验条件的稳定性。

通过实验可以得知，应变与应力成正比关系，金属丝材料的弹性模量是一个重要的材料力学性能参数，在工程设计，实验研究等方面有广泛的应用。

拉伸法和动力学法测量弹性模量实验报告双33A组----20070102 - -实验日期：2008年12月17日第一部分拉伸法测弹性模量1.1实验目的(1)学习用拉伸法测量弹性模量的方法； (2)掌握螺旋测微计和读数显微镜的使用； (3)学习用逐差法处理数据。

1.2实验原理1.2.1弹性模量及其测量方法本实验讨论最简单的形变——拉伸形变，即棒状物体（或金属丝）仅受轴向外力作用而发生伸 长的形变（称拉伸形变）。

设有一长度为，截面积为的均匀金属丝，沿长度方向受一外力后金属 丝伸长 。

单位横截面积上的垂直作用力 /成为正应力，金属丝的相对伸长 /称为线应变。

实 验结果指出，在弹性形变范围内，正应力与线应变成正比，即=该规律称为胡克定律。

式中比例系数/ =/称为材料的弹性模量。

它表征材料本身的性质，越大的材料，要使他发生一定的相对形变所需 的单位横截面积上的作用力也越大。

一些常用材料的值见表 1。

的单位为Pa （1Pa = 1N/m 2； 1GPa = 109Pa ）。

表 1 一些常用材料的弹性模量材料名称 钢 铁 铜 铝 铅 玻璃 橡胶 /GPa196~216113~15773~127约 70约 17约 55约 0.0078本实验测量的是钢丝的弹性模量，如果测得钢丝的直径为，则可以进一步把写成：4=2测量钢丝的弹性模量的方法是将钢丝悬挂于支架上，上端固定，下端加砝码对钢丝施力，测出 钢丝相应的伸长量 ，即可求出。

钢丝长度用钢尺测量，钢丝直径用螺旋测微计测量，力由砝 一般很小，约10−1mm数量级，在本实验中用 码的重力 =求出。

实验的主要问题是测准 。

读数显微镜测量（也可利用光杠杆法或其他方法测量）。

为了使测量的 更准确些，采用测量多个 的方法以减少测量的随机误差，即在钢丝下端每加一个砝码测一次伸长位置，逐个累加砝码，逐次记 录伸长位置。

通过数据处理求出 。

1.2.2逐差法处理数据如果用上述方法测量 10次得到相应的伸长位置 1, 2,… , 10，如何处理数据，算出钢丝的伸长量 呢？我们可以由相邻伸长位置的差值求出 9个 ，然后取平均，则2 − 1+3 − 29+⋯+ 10 −9=从上式可以看出中间各都消去了，只剩下 10 − 9，用这样的方法处理数据，中间各次测量 1结果均未起作用。

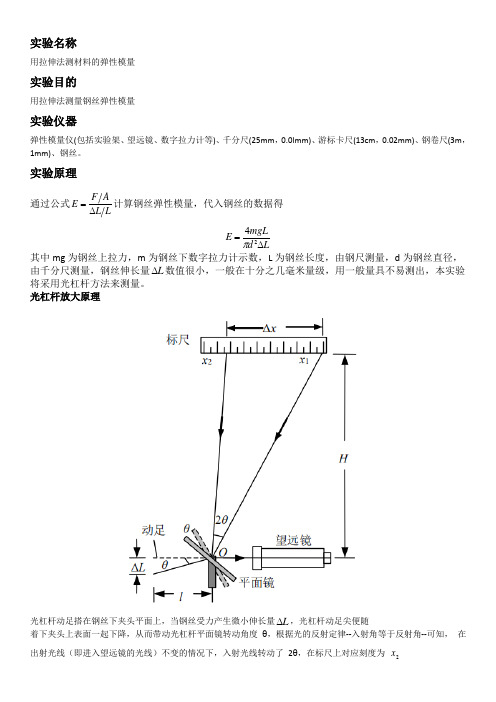
实验名称用拉伸法测材料的弹性模量实验目的用拉伸法测量钢丝弹性模量实验仪器弹性模量仪(包括实验架、望远镜、数字拉力计等)、千分尺(25mm ，0.0lmm)、游标卡尺(13cm ，0.02mm)、钢卷尺(3m ，1mm)、钢丝。

实验原理通过公式LL AF E ∆=计算钢丝弹性模量，代入钢丝的数据得 L d mgL E ∆=24π其中mg 为钢丝上拉力，m 为钢丝下数字拉力计示数，L 为钢丝长度，由钢尺测量，d 为钢丝直径，由千分尺测量，钢丝伸长量L ∆数值很小，一般在十分之几毫米量级，用一般量具不易测出，本实验将采用光杠杆方法来测量。

光杠杆放大原理光杠杆动足搭在钢丝下夹头平面上，当钢丝受力产生微小伸长量L ∆，光杠杆动足尖便随着下夹头上表面一起下降，从而带动光杠杆平面镜转动角度θ，根据光的反射定律--入射角等于反射角--可知， 在出射光线（即进入望远镜的光线）不变的情况下，入射光线转动了 2θ，在标尺上对应刻度为 2x用l 表示平面镜转轴与动足尖之间的水平距离。

由于 l >>L ∆，所以θ 和2θ很小。

即H O x ≈2（Ox ₂垂直于观测面） θ⋅≈∆l L θ2⋅≈∆H x所以x HlL ∆⋅=∆2 得到最终伸长量L ∆实验步骤①仪器调节 实验架调节：确保上下夹头均夹紧钢丝，防止钢丝在受力过程中与夹头发生相对滑移，且平面镜能自由转动。

将光杠杆动足尖自由地放置在下夹头上表面，使动足尖能随之一起上下移动，但不能碰触钢丝。

将 LED 灯箱电源线连接到数字拉力计面板上的直流电源插孔上， 将拉力传感器信号线接入拉力计传感器接口上。

打开数字拉力计，LED 灯箱点亮呈黄绿色，标尺刻度清晰可见。

数字拉力计面板上显示此时加到钢丝上的力。

旋转施力螺母，给钢丝施加一定的预拉力 m₀（2.00 kg 左右），将钢丝原本可能存在弯折的地方拉直。

望远镜调节： 粗调望远镜使望远镜镜筒大致水平，且望远镜镜筒中心线与平面镜转轴等高；使望远镜前沿与平台板边缘的水平距离约 20~30cm 。

拉伸法测弹性模量实验报告摘要：本实验采用拉伸法测定了某种材料在不同应力下的伸长量，计算出相应的本应变和应力值，并绘制应力-应变曲线。

根据曲线拟合得到该材料的弹性模量为81.3GPa。

实验结果表明，拉伸法能够精确测定材料的弹性模量，并且该实验具有一定的可靠性。

引言：弹性模量是材料力学性能的重要参数之一，广泛应用于机械工程、材料科学、建筑工程等领域。

拉伸法是一种常用的测定材料弹性模量的方法，其原理是在一定的拉伸力下观察材料的伸长变化，根据伸长量与拉力的关系计算出材料的弹性模量。

本实验旨在通过拉伸法测定某种材料的弹性模量，以此掌握拉伸法的方法和操作技巧。

实验设计与方法：1. 材料选择：选用某种标准硬度的钢材。

2. 实验器材：拉伸试验机、夹具、电压表。

3. 实验过程：（1）根据实验要求制备标准材料试件。

（2）将试件夹紧在拉伸试验机上，并调整力传感器的位置。

（3）设置试验参数，如拉伸速度、拉伸量等。

（4）逐步施加拉伸力，并记录相应的拉伸量和试件断裂时的拉伸力值。

（5）根据拉伸试验数据计算出材料的应力、应变和弹性模量，并绘制应力-应变曲线。

实验结果及分析：通过本次实验测定，得到钢材的弹性模量为81.3GPa。

具体结果如下：最大拉伸力：10765.37N杨氏模数：81.3GPa本条试件的直径D：5.0mm本条试件的长度L0：50mm本条试件的截面积A0：19.63mm^2最大拉伸长度△L：1.7000mm应变率ε：0.0866mm/mm应力值σ：548.5MPa弹性模量E：81.3GPa此外，我们还通过绘制应力-应变曲线来分析材料的弹性行为。

曲线近似呈现直线段，表明所选材料具有较好的弹性特性。

同时，本实验的结果具有一定的可靠性和准确度。

结论：本实验通过拉伸法测定了某种材料的弹性模量，并得出弹性模量为81.3GPa，表明所选材料具有良好的弹性性能。

此外，应力-应变曲线的绘制也表明该材料具有较好的弹性行为，实验结果具有一定的可靠性和准确度。

《拉伸法测弹性模量》实验报告一、 实验原理实验结果指出，在弹性形变范围内，正应力和线应变成正比，即LL E S F δ= 于是，弹性模量LL SF E //δ=在本实验中，LD FLE δπ24=其中，Ｅ为弹性模量。

Ｆ为外力，Ｌ为金属棒长，Ｄ为棒的直径，δＬ为在外力Ｆ下的伸长量。

二、 实验步骤１． 调整钢丝竖直。

先挂上砝码钩拉直钢丝，在调整底座螺钉使钢丝夹具不和周围支架碰蹭。

２． 调节读数显微镜，使叉丝和标记线无视差。

调节显微镜的位置，使像距和物距之比为１：１。

３． 测量δＬ。

每加一个砝码记录一次刻度值。

４． 测量Ｄ6次，并在测量前后记录螺旋测微计的零点d 各3次。

三、 数据表格１． 测钢丝长度Ｌ及其伸长量δＬ仪器编号 10 ； 钢丝长度Ｌ＝ 1045 ㎜()mm L mm mm mmn xxmm l L sl l l isl l 007.0216.0007.051033.003.0101.02222±=∴=∆=∆=∆+∆=∆=--=∆⨯=∆∑δδδδ仪仪２． 测钢丝直径Ｄ测定螺旋测微计的零点d （单位㎜） 测量前 -0.004 ， -0.003 ， -0.003 ；测量后 -0.002 ， -0.002 ， -0.002 。

平均值d = -0.003 ㎜钢丝的平均直径D = 0.232 ㎜mmD mms mm mm s DD D 006.0232.0006.0004.0004.022±=∴=∆+=∆=∆=仪仪３． 总不确定度的计算和最后结果GPaE GPaEEE E GPa L D FL E L D LF E E L D L F 4.23.2244.23.2244011.0222222±=∴=∆=∆===⎪⎭⎫⎝⎛∆+⎪⎭⎫ ⎝⎛∆+⎪⎭⎫ ⎝⎛∆+⎪⎭⎫ ⎝⎛∆=∆δπδδ。

拉伸法和动力学法测量弹性模量-实验报告一、实验目的2. 掌握实验操作技能，了解实验现象和数据分析方法；3. 培养实验思维和团队合作精神，提高实验综合能力。

二、实验原理1. 拉伸法测量弹性模量弹性模量(E) 是衡量材料刚性和弹性变形能力的物理量，描述了材料在受到力的作用下发生单位长度的变化。

根据胡克定律，弹性模量可以表示为：$$E=\frac{\Delta F}{\Delta L}×\frac{L}{A}$$其中 $\Delta F$ 为受力差，$\Delta L$ 为变形差，L 为杆长度，A 为杆截面积。

因此，只要在一定的应力范围内，通过施加外力并测量杆子的形变量，可以求出材料的弹性模量。

动力学法是利用机械振动的原理测量材料的弹性模量。

它通过在固体杆上施加激励，在充分振荡的条件下记录不同位置的振动响应，从而得到杆子的自然频率。

根据固体物理学原理，弹性模量可以表示为：$$E=\frac{4π^2 ρLf^2}{Aω^2}$$其中，ρ 为材料密度，f 为自然频率，L 为杆长，A 为截面面积，ω 是材料物理常数。

因此，只要通过测量杆子的振动响应和激励频率，还可以求出材料的弹性模量。

三、实验仪器和设备1. 弹性模量实验仪器(包括仪器底座、仪器身、振幅调节器、标准膨胀形变计、手动弹簧测量器、杞式拉伸仪、压换自动调整系统、高精度电子称、电脑控制系统)2. 示例杆四、实验步骤1. 安装示例杆并调整磁铁。

2. 将弹性模量实验仪器上的记录表格和标准膨胀形变计设置为初始状态。

3. 按下开始按钮和自动控制系统按钮，拉伸示例杆。

4. 每 5N 加一次力，记录受力差和长度差数据。

5. 得出在各个拉伸力下的长度差和弹性模量。

第二部分：动力学法测量弹性模量1. 安装示例杆，并将其真空吸附在仪器底座上。

2. 开始振动模拟，依次测量每个位置的振动响应。

3. 测量每个位置的响应频率，记录数据并计算弹性模量。

4. 比较拉伸法和动力学法的结果，并对实验误差进行讨论五、实验数据处理和结果分析| 强度(N) | 长度差(cm) | 弹性模量(GPa) || :------: | :--------: | :----------: || 5.0 | 0.08 | 10.42 || 10.0 | 0.16 | 10.41 || 15.0 | 0.23 | 10.46 || 20.0 | 0.31 | 10.26 || 25.0 | 0.38 | 10.35 || 30.0 | 0.46 | 10.46 || 35.0 | 0.53 | 10.38 || 40.0 | 0.62 | 10.28 || 45.0 | 0.71 | 10.13 || 50.0 | 0.80 | 10.06 |2. 动力学测量法得到的弹性模量值为 10.30 GPa。

202X年拉伸法测弹性模量实验报告
实验目的：
通过拉伸法测量金属的弹性模量，了解金属的材料性能及其变化规律。

实验原理：
弹性模量是材料的一种力学性质，表示材料在弹性变形时的应力和应变关系。

弹性模
量越大，表示材料的刚性越高，抗变形能力越强。

而弹性模量的计算方法是在弹性极限内，将材料应力和应变的关系表示为一个线性函数，斜率即为弹性模量。

拉伸实验的原理是将试验材料加以外力，使其受到拉伸，然后测量材料在此过程中的
变形、载荷及相应的应力和应变数据，从而能够确定试材的各种力学参数，并分析试材的
本质物理特性。

实验仪器和材料：
实验仪器：拉伸试验机、引伸计、计算机
实验材料：金属试片
实验步骤：
1. 准备试材，切割样品用于拉伸实验；
2. 将试材装入拉伸试验机中，使其保持一定长度，并加上一定的载荷；
3. 记录载荷和位移数据，并计算出对应的应力和应变；
4. 继续逐步加大负载，测量应变和应力的变化曲线，得出弹性模量。

实验结果与数据分析：
将实验获得的应力和应变数据，绘制应力-应变图，其斜率即为弹性模量。

根据实验
结果，计算得到金属试片的弹性模量如下：
弹性模量 = 斜率 = 2.1 GPa
结论：
通过对金属试样进行拉伸实验，测得其弹性模量约为 2.1 GPa。

实验结果表明，该金
属材料的弹性较好，具备良好的抗变形能力。

此实验结果对今后研究金属材料的材料性能
以及优化设计具有重要参考意义。

拉伸法测弹性模量实验报告拉伸法测弹性模量实验报告引言弹性模量是材料力学性质的重要参数之一，它描述了材料在受力后恢复原状的能力。

拉伸法是测量弹性模量的常用实验方法之一。

本实验旨在通过拉伸试验，利用拉伸应变和应力之间的线性关系计算材料的弹性模量。

实验装置和步骤实验装置包括拉伸试验机、标准试样、测量仪器等。

首先，将标准试样固定在拉伸试验机上，并根据试样的尺寸和形状调整夹具。

然后，通过调整拉伸试验机的控制参数，如加载速度和加载方式，开始进行拉伸试验。

在试验过程中，通过测量试样的应变和应力，记录下拉伸过程中的数据。

数据处理和分析通过实验得到的数据，可以计算出试样的应变和应力。

应变可以通过测量试样的伸长量和试样的初始长度来计算得到。

应力可以通过加载力和试样的横截面积来计算得到。

根据拉伸应变和应力之间的线性关系，可以绘制应力-应变曲线。

在线性阶段，应力与应变成正比，斜率即为弹性模量。

讨论和结果在实验中，我们选择了不同的材料进行拉伸试验，得到了应力-应变曲线，并计算出了相应的弹性模量。

结果显示，不同材料的弹性模量存在差异。

这是因为材料的组成和结构决定了其力学性质。

例如，金属材料由于具有紧密排列的晶格结构，其弹性模量通常较高。

而聚合物材料由于分子链之间的相互作用较弱，其弹性模量通常较低。

此外，实验中还发现，拉伸速度对材料的弹性模量也有影响。

当拉伸速度较快时，试样的变形速度较大，材料的内部结构可能无法及时调整，导致弹性模量的测量值偏低。

相反，当拉伸速度较慢时，试样的变形速度较小，材料的内部结构有足够的时间进行调整，弹性模量的测量值更加准确。

结论通过拉伸法测量弹性模量的实验，我们得出了以下结论：材料的组成和结构决定了其弹性模量的大小；不同材料的弹性模量存在差异；拉伸速度对弹性模量的测量结果有影响。

实验结果对于材料工程和设计具有重要意义，可以帮助工程师选择合适的材料，并预测材料在实际应用中的性能。

总结拉伸法测弹性模量是一种常用的实验方法，通过测量应变和应力，可以计算出材料的弹性模量。

弹性模量的测定实验报告实验目的：通过实验测定材料的弹性模量，了解材料的力学性能，掌握弹性模量的测定方法。

实验原理：弹性模量是材料的重要力学性能参数，它反映了材料在受力时的变形能力。

实验中通常采用拉伸实验来测定材料的弹性模量。

根据胡克定律，拉伸应力与应变成正比，弹性模量E可以通过应力和应变的比值得到。

即E=σ/ε，其中σ为应力，ε为应变。

实验仪器和材料：1. 电子拉力试验机。

2. 试样。

3. 温度计。

4. 温湿度计。

5. 计时器。

实验步骤：1. 准备试样，测量试样的截面积和长度。

2. 将试样安装在电子拉力试验机上，调整试验机的加载速度和加载方式。

3. 开始实验，记录加载过程中的应力和应变数据。

4. 实验结束后，根据实验数据计算出材料的弹性模量。

5. 对实验结果进行分析，比较不同材料的弹性模量差异。

实验数据处理：根据实验数据计算出材料的弹性模量，并进行误差分析，评估实验结果的可靠性。

实验结果：通过实验测定，得到材料的弹性模量为XXX。

根据实验数据分析，得出结论，材料的弹性模量受材料本身性质和工艺制造等因素的影响，不同材料的弹性模量差异较大。

实验结论：本实验通过拉伸实验测定材料的弹性模量，掌握了弹性模量的测定方法。

实验结果表明，材料的弹性模量是材料力学性能的重要指标，对于材料的选用和设计具有重要意义。

实验总结：通过本次实验，加深了对材料力学性能的理解，提高了实验操作和数据处理的能力。

同时也发现了实验中存在的不足之处，为今后的实验工作提供了一定的参考。

实验改进：在今后的实验工作中，应注意实验条件的控制和数据的准确性，提高实验结果的可靠性和准确性。

实验意义：本实验的开展有助于深入了解材料的力学性能，为材料的选用和设计提供了重要参考，具有一定的理论和实际意义。

通过本次实验，我对弹性模量的测定方法有了更深入的了解，也提高了实验操作和数据处理的能力。

希望今后能够在实验工作中不断提升自己，为科学研究和工程实践做出更大的贡献。

弹性模量的测量实验报告一、拉伸法测量弹性模量 1、实验目的(1) 学习用拉伸法测量弹性模量的方法; (2) 掌握螺旋测微计和读数显微镜的使用; (3) 学习用逐差法处理数据。

2、实验原理（1）、杨氏模量及其测量方法本实验讨论最简单的形变——拉伸形变,即棒状物体(或金属丝)仅受轴向外力作用而发生伸 长的形变(称拉伸形变)。

设有一长度为L ,截面积为S 的均匀金属丝,沿长度方向受一外力F 后金属 丝伸长δL 。

单位横截面积上的垂直作用力F /S 成为正应力,金属丝的相对伸长δL /L 称为线应变。

实 验结果指出,在弹性形变范围内,正应力与线应变成正比,即LL E S F δ= 这个规律称为胡克定律，其中LL SF E //δ=称为材料的弹性模量。

它表征材料本身的性质,E 越大的材料,要使他发生一定的相对形变所需 的单位横截面积上的作用力也越大，E 的单位为Pa(1Pa = 1N/m 2; 1GPa = 109Pa)。

本实验测量的是钢丝的弹性模量,如果测得钢丝的直径为D ,则可以进一步把E 写成:LD FLE δπ24=测量钢丝的弹性模量的方法是将钢丝悬挂于支架上,上端固定,下端加砝码对钢丝施力F ,测出钢丝相应的伸长量δL ,即可求出E 。

钢丝长度L 用钢尺测量,钢丝直径D 用螺旋测微计测量,力F 由砝 码的重力F = mg 求出。

实验的主要问题是测准δL 。

δL 一般很小,约10−1mm 数量级,在本实验中用 读数显微镜测量(也可利用光杠杆法或其他方法测量)。

为了使测量的δL 更准确些,采用测量多个δL 的 方法以减少测量的随机误差,即在钢丝下端每加一个砝码测一次伸长位置,逐个累加砝码,逐次记 录伸长位置。

通过数据处理求出δL 。

（2）、逐差法处理数据
如果用上述方法测量10 次得到相应的伸长位置y1,y2,...,y10,如何处理数据,算出钢丝的伸长量δL呢?
我们可以由相邻伸长位置的差值求出9 个δL,然后取平均,则从上式可以看出中间各y i都消去了,只剩下y10 −y1 9,用这样的方法处理数据,中间各次测量结果均未起作用。