高中数学循环结构

高中数学循环结构教案
教学内容：循环结构
教学目标：
1. 理解循环结构的概念；
2. 掌握循环结构的基本语法和用法；
3. 能够编写简单的包含循环结构的程序。

教学重点：
1. 循环结构的概念；
2. for循环和while循环的语法和用法。

教学难点：
1. 循环结构的灵活应用；
2. 循环条件的控制和终止。

教学准备：
1. 讲义；
2. 计算机或编程软件。

教学过程：
一、导入（5分钟）
教师引入课题，向学生介绍循环结构的概念，以及循环结构在程序设计中的重要性。

二、讲解循环结构（15分钟）
1. 讲解for循环和while循环的语法和用法；
2. 分别给出for循环和while循环的例子，让学生理解循环结构的基本原理。

三、练习编程（25分钟）
1. 让学生自行编写包含循环结构的程序，并进行调试；
2. 指导学生如何控制循环条件和终止循环。

四、总结（5分钟）
教师对本节课的内容进行总结，强调循环结构在程序设计中的重要性，并鼓励学生进行更
多的实践和练习。

五、课堂作业（5分钟）
布置作业，让学生练习编写更复杂的包含循环结构的程序，并在下节课上进行展示和讨论。

教学反思：
本节课主要介绍了循环结构的基本概念和用法，并通过实践锻炼学生的编程能力。

在教学
过程中，应注重引导学生灵活运用循环结构，并注重对学生的实际动手操作。

同时，要及
时发现学生在编程过程中的问题，并引导他们进行解决和总结。

循环结构
1．循环结构
【知识点的认识】
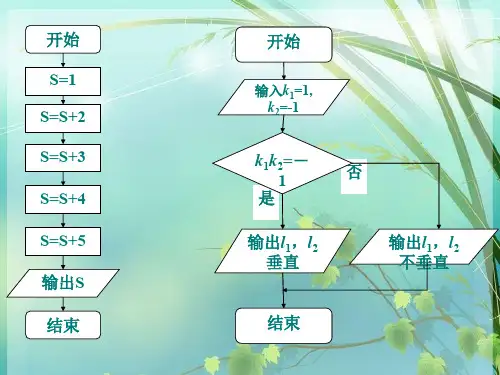
1．循环结构：需要重复执行同一操作的结构称为循环结构，即从某处开始，按照一定的条件反复执行某一处理步骤，反复执行的处理步骤称为循环体．
2．两种循环结构：
【命题方向】
掌握循环结构的功能特点，注意与其他算法结构的区分．理解“当型”和“直到型”两种循环结构的含义、作用，尤其注意区分两者区别．题目多以应用计算为主，考查纯概念性问题较少，解题时要留意题目所给条件，细心作答．
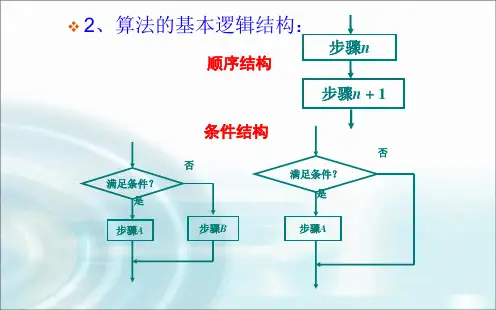
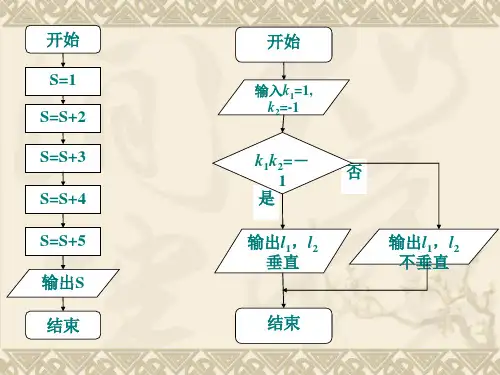
例：若执行如图所示的程序框图，输出S 的值为 3，则判断框中应填入的条件是（）
1/ 2
A．k＜6？B．k＜7？C．k＜8？D．k＜9？
分析：根据程序框图，写出运行结果，根据程序输出的结果是S＝3，可得判断框内应填入的条件．
解答：根据程序框图，运行结果如下：
S k
第一次循环 log23 3
第二次循环 log23•log34 4
第三次循环 log23•log34•log45 5
第四次循环 log23•log34•log45•log56 6
第五次循环 log23•log34•log45•log56•log67 7
第六次循环 log23•log34•log45•log56•log67•log78＝log28＝3 8
故如果输出S＝3，那么只能进行六次循环，故判断框内应填入的条件是k＜8．
故选：C．
点评：本题考查程序框图，尤其考查循环结构，对循环体每次循环需要进行分析并找出内在规律，属于基础题．
2/ 2。

1。

2。

3循环结构［学习目标]1。

掌握两种循环结构的流程图的画法，能进行两种循环结构流程图间的转化.2.掌握画流程图的基本规则，能正确画出流程图．知识点一循环结构的含义1．循环结构的定义在算法中,需要重复执行同一操作的结构称为循环结构．2．循环结构的特点（1）重复性：在一个循环结构中，总有一个过程要重复一系列的步骤若干次，而且每次的操作完全相同．(2）判断性:每个循环结构都包含一个判断条件，它决定这个循环的执行与终止．（3）函数性：循环变量在构造循环结构中起了关键作用，蕴含着函数的思想．知识点二两种循环结构的比较1．常见的两种循环结构2。

设计一个算法的流程图的步骤（1）用自然语言表述算法步骤；(2)确定每一个算法步骤所包含的基本结构，并用相应的流程图表示,得到该步骤的流程图；（3)将所有步骤的流程图用流程线连接起来，并加上起止框，得到表示整个算法的流程图．［思考］（1）循环结构的流程图中一定含有判断框吗？（2）任何一个算法的流程图中都必须含有三种基本结构吗？答(1)循环结构的流程图中一定含有判断框．(2)不一定．但必须会有顺序结构．题型一当型循环结构与直到型循环结构例1设计一个计算1＋2＋…＋100的值的算法，并画出流程图．解方法一S1i←1，S←0。

S2若i≤100成立，则执行S3；否则，输出S，结束算法；S3S←S＋i；S4i←i＋1，转S2。

流程图:方法二S1i←1,S←0。

S2S←S＋i。

S3i←i＋1。

S4若i＞100不成立，则执行S2；否则，输出S,结束算法．流程图：反思与感悟当型循环结构与直到型循环结构的联系和区别（1)联系：①当型循环结构与直到型循环结构可以相互转化；②循环结构中必然包含选择结构,以保证在适当的时候终止循环；③循环结构只有一个入口和一个出口;④循环结构内不存在死循环，即不存在无终止的循环．（2）区别:直到型循环结构是先执行一次循环体，然后再判断是否继续执行循环体,当型循环结构是先判断是否执行循环体；直到型循环结构是在条件不满足时执行循环体，当型循环结构是在条件满足时执行循环体．要掌握这两种循环结构,必须抓住它们的区别．跟踪训练1设计一个算法，求13＋23＋33＋…＋1003的值，并画出流程图．解算法如下：S1S←0；S2I←1;S3S←S＋I3；S4I←I＋1;S5若I＞100，则输出S，算法结束;否则，执行S3。

高中数学知识点总结：循环语句循环语句循环结构是由循环语句来实现的。

对应于程序框图中的两种循环结构，一般程序设计语言中也有当型（WHILE 型）和直到型（UNTIL 型）两种语句结构。

即WHILE 语句和UNTIL 语句。

1、WHILE 语句（1）WHILE 语句的一般格式是（2）当计算机遇到WHILE 语句时，先判断条件的真假，如果条件符合，就执行WHILE 与WEND 之间的循环体；然后再检查上述条件，如果条件仍符合，再次执行循环体，这个过程反复进行，直到某一次条件不符合为止。

这时，计算机将不执行循环体，直接跳到WEND 语句后，接着执行WEND 之后的语句。

因此，当型循环有时也称为“前测试型”循环。

2、UNTIL 语句（1）UNTIL 语句的一般格式是 对应的程序框图是（2）直到型循环又称为“后测试型”循环，从UNTIL 型循环结构分析，计算机执行该语句时，先执行一次循环体，然后进行条件的判断，如果条件不满足，继续返回执行循环体，然后再进行条件的判断，这个过程反复进行，直到某一次条件满足时，不再执行循环体，跳到LOOP UNTIL 语句后执行其他语句，是先执行循环体后进行条件判断的循环语句。

分析：当型循环与直到型循环的区别：（先由学生讨论再归纳） （1） 当型循环先判断后执行，直到型循环先执行后判断；在WHILE 语句中，是当条件满足时执行循环体，在UNTIL 语句中，是当条件不满足时执行循环例题： . 99...531 的一个算法设计计算⨯⨯⨯⨯（见课本21P ）Sint Pr End I S S 2 Step 99 T o 3 From I 1For For S ⨯←←Sint Pr hile End I S S 2I I97 I hile 11W W I S ⨯←+←≤←←Sint Pr hile End 2I I I S S 99 I hile 11W W I S +←⨯←≤←←◆ ♦Sint Pr ) 99 I ( 001 I 2I I I S S o11>≥+←⨯←←←或者Until Loop D I S Sint Pr99 I I S S 2I I o11≥⨯←+←←←Until Loop D I S⌧ ⍓Sint Pr 2I I I S S ) 100 I ( 99 I While o 11Loop D I S +←⨯←<≤←←或者 Sint Pr I S S 2I I ) 99 I ( 97 I While o 11Loop D I S ⨯←+←<≤←←或者。

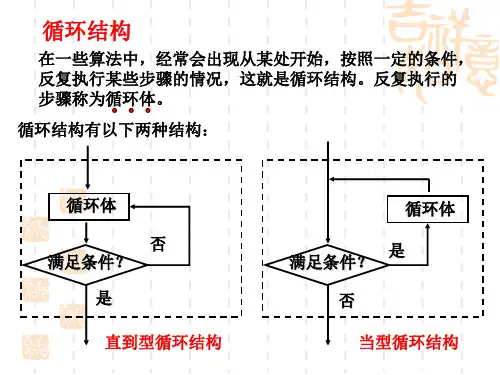
两种循环结构精析循环结构也叫重复结构，即从某处开始，按照一定条件，反复执行某几个步骤．反复执行的这几个步骤称为循环体，在循环结构中，通常都有一个起到循环计数作用的变量，这个变量称为计数变量，它的取值一般都含在执行或中止循环体的条件中，其作用是用来确定什么时候循环结束．一、两种循环结构根据执行情况和循环结束条件的不同可以分为当型循环结构〔也称为while型结构〕和直到型循环结构〔也你为until型结构〕．两种循环的结构图如下：当型循环结构执行过程：当计算机遇到当型循环时先对循环条件的真假进行判断，如果条件满足就执行循环体，然后再检查循环条件，如果条件仍然符合，再次执行循环体，这个过程反复进行，直到某一次条件不满足为止，这时，计算机将不再执行循环体，而是直接跳到循环结构下面的结构．在使用当型循环时，应注意务必使“条件〞最终变为“假〞，这样才能终止循环，否那么循环将无休止地进行下去。

WHILE的汉语意思是“当…时候〞，所以当型循环结构可以理解为“当条件成立时就循环〞．直到型循环结构执行过程：先执行一次循环体，再对循环条件进行判断，如果条件不成立，就继续执行循环体，再判断条件，直到某一次条件满足时，就退出循环，继续执行下面的结构，所以直到型循环可以理“做循环体，直到…条件为止〞．二、两种循环结构的比较〔1〕循环体执行的先后顺序不同．当型循环结构是先判断条件，假设条件成立再执行循环体；而直到型结构是先执行一次，再去判断条件．〔2〕执行的次数不一样．当型循环结构是先判断条件，当条件成立时才执行循环体内语句，假设循环条件一开始就不成立，就直接退出循环；而直到型循环是先执行一次循环体，再判断条件；这就是说当型循环可能一次也不执行，而直到型循环至少执行一次．〔3〕退出循环的条件不同．当型循环结构是当条件成立时循环，当条件不成立时退出循环；而直到型循环结构正好相反，当条件不成立时执行循环，当条件成立时退出循环．〔4〕两种循环结构的联系：当型循环结构和直到型循环结构可以相互转换的．转换时，循环体可以相同，但是循环条件必须是不同的，一般地说来，这两个条件是“互补〞的．三、用两种循环结构表达算法，关键要做好三点：〔1〕确定循环变量和初始值；〔2〕确定循环体；〔3)确定循环中止条件．四．典例精析例1．设计一个计算1×3×5×…×99的算法，画出程序框图．分析：由于乘数较多，采用逐个相乘的方法程序太长，是不可取的，因此我们应采用引入变量应用循环的办法，可用当型循环和直到型循环．解析：方法一：当型循环程序框图〔如右图上〕方法二：直到型循环程序框图〔如右图下〕误区警示：用当型循环结构和直到型循环结构描述算法时，一定要注意两种结构中判断框里的条件是相反的.例2．例下面的流程图中算法的功能是分析：功能是求积为624的相邻两个偶数．但是本流程图中的循环结构是错误的，出现了当型与直到型的混用、错用．如果是当型循环结构，应该是在满足条件时，执行循环体，而本图却是在不满足条件时执行了循环体，这与当型循环结构要求矛盾；本流程图如果采用的是直到型循环结构，那么应该先执行一次循环体，然后再对控制条件进行判断，而此题却是先判断，后执行循环体，这与直到型循环结构也是不相适应的。