聚类分析例题及解答

5.2酿酒葡萄的等级划分5.2.1葡萄酒的质量分类由问题1中我们得知，第二组评酒员的的评价结果更为可信，所以我们通过第二组评酒员对于酒的评分做出处理。

我们通过excel计算出每位评酒员对每支酒的总分，然后计算出每支酒的10个分数的平均值，作为总的对于这支酒的等级评价。

通过国际酿酒工会对于葡萄酒的分级，以百分制标准评级，总共评出了六个级别（见表5）。

在问题2的计算中，我们求出了各支酒的分数，考虑到所有分数在区间[61.6，81.5]波动，以原等级表分级，结果将会很模糊，不能分得比较清晰。

为此我们需要进一步细化等级。

为此我们重新细化出5个等级，为了方便计算，我们还对等级进行降序数字等级（见表6）。

通过对数据的预处理，我们得到了一个新的关于葡萄酒的分级表格（见表7）：考虑到葡萄酒的质量与酿酒葡萄间有比较之间的关系，我们将保留葡萄酒质量对于酿酒葡萄的影响，先单纯从酿酒葡萄的理化指标对酿酒葡萄进行分类，然后在通过葡萄酒质量对酿酒葡萄质量的优劣进一步进行划分。

5.2.2建立模型在通过酿酒葡萄的理化指标对酿酒葡萄分类的过程，我们用到了聚类分析方法中的ward 最小方差法，又叫做离差平方和法。

聚类分析是研究分类问题的一种多元统计方法。

所谓类，通俗地说，就是指相似元素的集合。

为了将样品进行分类，就需要研究样品之间关系。

这里的最小方差法的基本思想就是将一个样品看作P 维空间的一个点，并在空间的定义距离，距离较近的点归为一类；距离较远的点归为不同的类。

面对现在的问题，我们不知道元素的分类，连要分成几类都不知道。

现在我们将用SAS 系统里面的stepdisc 和cluster 过程完成判别分析和聚类分析，最终确定元素对象的分类问题。

建立数据阵，具体数学表示为：1111...............m n nm X X X X X ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦（5.2.1） 式中，行向量1(,...,)i i im X x x =表示第i 个样品；列向量1(,...,)'j j nj X x x =’，表示第j 项指标。

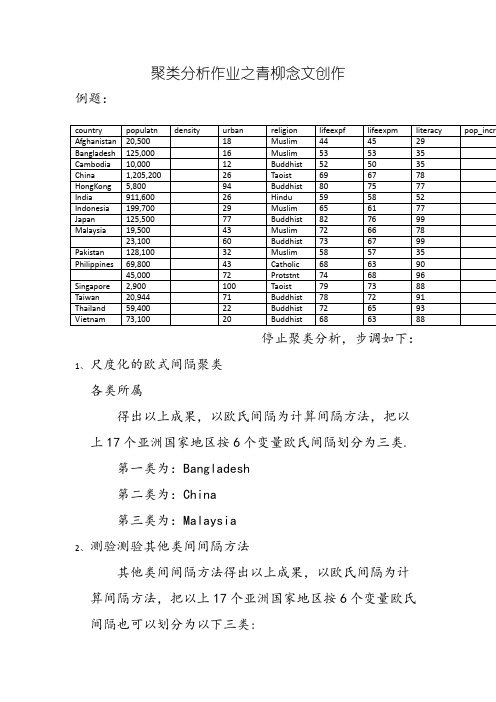
聚类分析作业之青柳念文创作
例题：
停止聚类分析，步调如下：
1、尺度化的欧式间隔聚类
各类所属
得出以上成果，以欧氏间隔为计算间隔方法，把以
上17个亚洲国家地区按6个变量欧氏间隔划分为三类.
第一类为：Bangladesh
第二类为：China
第三类为：Malaysia
2、测验测验其他类间间隔方法
其他类间间隔方法得出以上成果，以欧氏间隔为计
算间隔方法，把以上17个亚洲国家地区按6个变量欧氏
间隔也可以划分为以下三类:
第一类为：Bangladesh
第二类为：China
第三类为：Malaysia
3、用样本主成分画图
由图可知，所聚成的3类中:
第1类有5个样本，类间间隔较接近，效果较好；第2类有6个样本，类间间隔较接近，效果次之；第3类有6个样本.类间间隔较团圆，效果最差.。

一、填空题1.EM算法中，E代表期望，M代表（）。

正确答案：最大化2.无监督学习中除了聚类，另一种是（）。

正确答案：建模3.我们将一个数据可以属于多个类（概率）的聚类称作（）。

正确答案：软聚类二、判断题1.聚类算法中的谱聚类算法是一种分层算法。

正确答案：×解析：聚类算法中的谱聚类算法是一种扁平算法。

2.两个向量之间的余弦距离等于1减这两个向量的余弦相似度。

正确答案：√3.K-均值++算法能够克服最远点不能处理离群值的问题。

正确答案：√4.K-means和EM聚类之间的主要区别之一是EM聚类是一种“软”聚类算法。

正确答案：√5.监督学习的训练集时有标签的数据。

正确答案：√6.在文本聚类中，欧氏距离是比较适合的。

正确答案：×三、单选题1.以下哪些方法可以确定K-均值算法已经收敛？（）A.划分不再改变B.聚类中心不再改变C.固定次数的迭代D.以上三种均是正确答案：D2.以下哪些算法可以处理非高斯数据？（）A.K-means算法B.EM算法C.谱聚类算法D.以上三种算法都可以正确答案：C四、多选题1、无监督学习可以应用于哪些方面？（）A.图像压缩B.生物信息学：学习基因组C.客户细分（即分组）D.学习没有任何标签的聚类/群组正确答案：A、B、C、D2、以下哪些选项是K-均值聚类面临的问题？（）A.K的选择具有挑战性B.硬聚类并不总是正确的C.贪婪算法存在的问题D.关于数据的球形假设（到聚类中心的距离）正确答案：A、B、C、D3、聚类可以应用于哪些方面？（）A.基因表达数据的研究B.面部聚类C.搜索结果聚类D.新闻搜索正确答案：A、B、C、D4、在K-均值算法中，以下哪些方法可以用于随机种子的选择？（）A.随机选择数据作为中心B.空间中的随机位置作为中心C.尝试多个初始起点D.使用另一个聚类方法的结果进行初始化正确答案：A、B、C、D5、EM算法可以应用于以下哪些方面？（）A.学习贝叶斯网络的概率B.EM-聚类C.训练HMMD.学习微信好友网络正确答案：A、B、C、D。

例题1：下表是我国16个地区农民在1982年支出情况的抽样调查数据的汇总资料，每个地区都调查了反映每人平均生活消费支出情况的六个指标。

试利用调查资料对16个地区进行分类。

地区食品衣着燃料住房生活用品及其他文化生活服务支出北京190.33 43.77 9.73 60.54 49.01 9.04 天津135.2 36.4 10.47 44.16 36.49 3.94 河北95.21 22.83 9.3 22.44 22.81 2.8 山西104.78 25.11 6.4 9.89 18.17 3.25 内蒙古128.41 27.63 8.94 12.58 23.99 3.27 辽宁145.68 32.83 17.19 27.29 39.09 3.47 吉林159.37 33.38 18.37 11.81 25.29 5.52 黑龙江116.22 29.57 13.24 13.76 21.75 6.04 上海221.11 38.64 12.53 115.65 50.82 5.89 江苏144.98 29.12 11.67 42.6 27.3 5.74 浙江169.92 32.75 12.72 47.12 34.35 5安徽153.11 23.09 15.62 23.54 18.18 6.39 福建144.92 21.26 16.96 19.52 21.75 6.73 江西140.51 21.5 17.64 19.19 15.97 4.94 山东115.84 30.26 12.2 33.61 33.77 3.85 河南101.18 23.26 8.46 20.2 20.5 4.3下面用统计学软件 SAS(Statistical Analysis System) data dfdf;input city $ x1 x2 x3 x4 x5 x6;cards;beijing 190.33 43.77 9.73 60.54 49.01 9.04tianjing 135.20 36.40 10.47 44.16 36.49 3.94hebei 95.21 22.83 9.30 22.44 22.81 2.80shanxi 104.78 25.11 6.40 9.89 18.17 3.25 neimenggu 128.41 27.63 8.94 12.58 23.99 3.27 liaoning 145.68 32.83 17.19 27.29 39.09 3.47jilin 159.37 33.38 18.37 11.81 25.29 5.22 heilongjiang 116.22 29.57 13.24 13.76 21.75 6.04 shanghai 221.11 38.64 12.53 115.65 50.82 5.89 jiangsu 144.98 29.12 11.67 42.60 27.30 5.74 zhejiang 169.92 32.75 12.72 47.12 34.35 5.00anhui 153.11 23.09 15.62 23.54 18.18 6.39fujian 144.92 21.26 16.96 19.52 21.75 6.73jiangxi 140.54 21.50 17.64 19.19 15.97 4.94 shandong 115.84 30.26 12.20 33.61 33.77 3.85henan 101.18 23.26 8.46 20.20 20.50 4.30;run;proc cluster data=dfdf std outtree=tree method=ave pesudo rsq;id city;run; /*ward离差平方和法 war; 类平均法 ave; 重心法 cen;最长距离法 com;中间距离法 med; 最短距离法 sin;密度估计法 den;极大似然法 eml; 可变类平均 fle;相似分析法 mcq; 两阶段密度估计 two; */proc tree data=tree out=new graphics horizontal；id city;run;Cluster HistoryNormRMS NCL Clusters Joined--- FREQ SPRSQ RSQ PSF PST2 Dist 15 anhui fujian 2 0.0025 0.998 28.7 . 0.193 14 hebei henan 2 0.0055 0.992 19.1 . 0.2869 13 CL14 shanxi 3 0.0068 0.985 16.7 1.2 0.3116 12 CL15 jiangxi 3 0.0099 0.975 14.4 4 0.3481 11 jiangsu zhejiang 2 0.0089 0.966 14.4 . 0.366 10 CL13 neimengg 4 0.0106 0.956 14.4 1.7 0.3692 9 tianjing shandong 2 0.0092 0.947 15.5 . 0.3711 8 CL9 CL11 4 0.0237 0.923 13.7 2.6 0.4957 7 liaoning jilin 2 0.0189 0.904 14.1 . 0.5329 6 heilongj CL12 4 0.0267 0.877 14.3 4.3 0.5463 5 CL8 CL7 6 0.0528 0.824 12.9 3.5 0.6681 4 CL5 CL6 10 0.1269 0.698 9.2 6.6 0.7823 3 CL4 CL10 14 0.1955 0.502 6.6 7.8 0.8751 2 beijing shanghai 2 0.0562 0.446 11.3 . 0.91841CL2 CL3 16 0.4458 0 . 11.3 1.5454（1）2R 统计量（列标题为RSQ ）用于评价每次合并成NCL 个类时的聚类效果。

第三章 聚类分析一、填空题1.在进行聚类分析时，根据变量取值的不同，变量特性的测量尺度有以下三种类型： 间隔尺度 、 顺序尺度 和 名义尺度 。

2．Q 型聚类法是按___样品___进行聚类，R 型聚类法是按_变量___进行聚类。

3．Q 型聚类统计量是____距离_，而R 型聚类统计量通常采用_相似系数____。

4．在聚类分析中，为了使不同量纲、不同取值范围的数据能够放在一起进行比较，通常需要对原始数据进行变换处理。

常用的变换方法有以下几种：__中心化变换_____、__标准化变换____、____规格化变换__、__ 对数变换 _。

5．距离ij d 一般应满足以下四个条件：对于一切的i,j ，有0≥ij d 、 j i =时，有0=ij d 、对于一切的i,j ，有ji ij d d =、对于一切的i,j,k ，有kj ik ij d d d +≤。

6.相似系数一般应满足的条件为： 若变量i x 与 j x 成比例，则1±=ij C 、 对一切的i,j ，有1≤ij 和 对一切的i,j ，有ji ij C C =。

7.常用的相似系数有 夹角余弦 和 相关系数 两种。

8.常用的系统聚类方法主要有以下八种： 最短距离法 、最长距离法、中间距离法、重心法、类平均法、可变类平均法、可变法、离差平方和法。

9．快速聚类在SPSS 中由__K-mean_____________过程实现。

10.常用的明氏距离公式为：()qpk q jk ik ij x x q d 11⎥⎦⎤⎢⎣⎡-=∑=，当1=q 时，它表示 绝对距离 ；当2=q 时，它表示 欧氏距离 ；当q 趋于无穷时，它表示 切比雪夫距离 。

11．聚类分析是将一批 样品 或 变量 ，按照它们在性质上 的 亲疏、相似程度 进行分类。

12．明氏距离的缺点主要表现在两个方面：第一 明氏距离的值与各指标的量纲有关 ，第二 明氏距离没有考虑到各个指标（变量）之间的相关性 。

1、设有20个土壤样品分别对5个变量的观测数据如下表所示，试利用二种聚类法对其进行样品聚类分析。

解：首先将16组的异常有机物值修改为3.33.通过SPss软件进行K-均值检验，得到：由上表可见三组的聚类中心。

可认为：第一组含沙量低，淤泥含量高，黏土含量高，有机物含量中等，PH值中等。

第二组含沙量高，淤泥含量低，黏土含量低，有机物含量较低，PH值中等。

第三组含沙量中等，淤泥含量中等，黏土含量中等，有机物含量较高，PH值中等迭代两次后得到结果。

具体分组如下运用层次聚类法：首先将数据标准化，然后使用标准化后数据组别解释如下：一组：含沙量低，淤泥含量中等，黏土含量高，有机物含量高，PH值中等；二组：含沙量高，淤泥含量低，黏土含量中等，有机物含量中等，PH值较高；三组：含沙量高，淤泥含量高，黏土含量低，有机物含量高，PH值较低；但是考虑到数据可能具有相关性，我们在matlab中使用马氏距离clearclcX=importdata('lunwen.txt');normplot(X(:,5))figurenormplot(X(:,2))figurenormplot(X(:,3))figurenormplot(X(:,4))服从正态分布，使用马氏距离clearclcX=[77.30 13.00 9.70 1.50 6.40;82.50 10.00 7.50 1.50 6.50;66.90 20.00 12.50 2.30 7.00;47.20 33.30 19.00 2.80 5.80;65.30 20.50 14.20 1.90 6.90;83.30 10.00 6.70 2.20 7.00;81.60 12.70 5.70 2.90 6.70;47.80 36.50 15.70 2.30 7.20;48.60 37.10 14.30 2.10 7.20;61.60 25.50 12.60 1.90 7.30;58.60 26.50 14.90 2.40 6.70;69.30 22.30 8.40 4.00 7.00;61.80 30.80 7.40 2.70 6.40;67.70 25.30 7.00 4.80 7.30;57.20 31.20 11.60 2.40 6.30;67.20 22.70 10.10 33.3 6.20;59.20 31.20 9.60 2.40 6.00;80.20 13.20 6.60 2.00 5.80;82.20 11.10 6.70 2.20 7.20;69.70 20.70 9.60 3.10 5.90];%x=zscore(X);corrcoef(X)Y=pdist(X,'mahal');Z=linkage(Y,'average');T=cluster(Z,3);[H,T]=dendrogram(Z);可知，部分变量之间具有相关性，因此得到谱系图认为组一：含沙量中等偏低，淤泥含量低，黏土含量低，有机物含量低，PH偏酸性；认为组二：含沙量中等，淤泥含量低，黏土含量中等偏低，有机物含量高。

聚类分析期末试题及答案聚类分析被广泛应用于数据挖掘和统计分析领域，用于将一组样本根据相似性分为不同的群组。

本文将提供一些聚类分析的期末试题，并给出相应的答案。

通过阅读本文，您将对聚类分析的原理和应用有更深入的了解。

试题一：1. 请简要说明聚类分析的定义和作用。

2. 聚类分析有哪些常用的算法？3. 请解释层次聚类分析和划分聚类分析的区别。

4. 在聚类分析中，如何确定最佳聚类数目？答案一：1. 聚类分析是一种无监督学习方法，将一组样本划分为不同的群组，使得同一个群组内的样本相似度较高，而不同群组之间的相似度较低。

其作用在于揭示数据内在的结构和模式，发现数据集中的潜在规律和相似性。

2. 常用的聚类算法包括K均值聚类、层次聚类、密度聚类等。

K均值聚类是一种基于中心点的划分聚类算法，层次聚类将样本逐步合并或分割以构建树状结构，密度聚类基于样本之间的密度连接关系进行聚类划分。

3. 层次聚类分析和划分聚类分析的主要区别在于划分聚类将样本直接划分为不同的群组，而层次聚类分析构建样本之间的树状结构，通过剪枝步骤来确定最终的聚类结果。

4. 在确定最佳聚类数目时，可以使用肘部法则、轮廓系数、间隔统计量等方法。

肘部法则通过绘制聚类数目和聚类准则的关系图，选择“肘部”对应的聚类数目作为最佳聚类数目。

轮廓系数衡量了聚类结果的紧密度和分离度，数值越接近1表示聚类质量越好。

间隔统计量是一种基于距离度量的方法，选择统计量较大的聚类数目作为最佳聚类数目。

试题二：1. 请简要说明K均值聚类的原理和步骤。

2. 什么是初始聚类中心？如何确定初始聚类中心的位置？3. K均值聚类算法的优缺点是什么？4. 请论述层次聚类分析的原理和步骤。

答案二：1. K均值聚类是一种划分聚类算法，其原理是将样本划分为K个独立的群组，使得每个样本到其所属群组的质心的距离最小化。

步骤如下：a. 随机确定初始聚类中心。

b. 计算每个样本到各个聚类中心的距离，将其归类到最近的聚类中心所属群组。

练习：今有6个铅弹头，用“中子活化”方法测得7种微量元素的含量数据，如下表：⑴试用多种系统聚类法对6个弹头进行分类，并比较分类结果；⑵试用多种方法对7种微量元素进行分类.第一问：解：此题可用多种系统聚类法进行分析，共采用五种聚类方法：类平均法、重心法、密度估计法、最小距离法和Ward法。

（1）类平均法可采用以下SAS程序．该程序第一步建立名为bom的数据集，此数据集包括1-6个弹头的资料。

紧接着的proc cluster 语句调用cluster过程用来对数据集bom进行聚类,method=average表示采用类平均法,其中语句var x1 x2 x3 x4 x5 x6 x7表明对x1 x2 x3 x4 x5 x6 x7这7种元素进行聚类分析。

Id number；表明用弹头样品号区分聚类的观测．类平均法的输出如下由上图（Cluster History）给出了用类平均法聚类的结过程，每行指出新聚类的弹头样品号．各行为：1）分成五类{2 6}，{1}，{3}，{4}，{5}．2）分成四类{1 2 6}，{3}，{4}，{5}．3）分成三类{1 2 6 }，{3 5}，{4}．4）分成二类{1 2 4 6}，{3 5}．5）分成一类{1 2 3 4 5 6 }(2)使用重心法，重心法得出的输出结果如下：上图中（Cluster History）给出了用重心法聚类的过程，每行指出新聚类的弹头样品号．各行为：各行为：1）分成五类{2 6}，{1}，{3}，{4}，{5}．2）分成四类{1 2 6}，{3}，{4}，{5}．3）分成三类{1 2 6 }，{3 5}，{4}．4）分成二类{1 2 4 6}，{3 5}．5）分成一类{1 2 3 4 5 6 }⑶使用密度法使用密度法得到的输出结果如下：上图中（Cluster History）给出了用密度法聚类的过程，每行指出新聚类的弹头样品号．各行为：1）分成五类{2 6}，{1}，{3}，{4}，{5}．2）分成四类{1 2 6}，{3}，{4}，{5}．3）分成三类{1 2 6 4}，{3}，{5}．4）分成二类{1 2 34 6}，{5}．5）分成一类{1 2 3 4 5 6 }（4）使用最短距离法：使用最短距离法得到的输出结果如下：上图中（Cluster History）给出了用最短距离法聚类的过程，每行指出新聚类的弹头样品号．各行为：1）分成五类{2 6}，{1}，{3}，{4}，{5}．2）分成四类{1 2 6}，{3}，{4}，{5}．3）分成三类{1 2 6 4}，{3}，{5}．4）分成二类{1 2 4 6}，{3 5}．5）分成一类{1 2 3 4 5 6 }（5）使用ward法使用ward法得到的输出结果如下上图中（Cluster History）给出了用最短距离法聚类的过程，每行指出新聚类的弹头样品号．各行为：1）分成五类{2 6}，{1}，{3}，{4}，{5}．2）分成四类{1 2 6}，{3}，{4}，{5}．3）分成三类{1 2 6 }，{4}，{3 5}．4）分成二类{1 2 4 6}，{3 5}．5）分成一类{1 2 3 4 5 6 }对上述五种方法的结果进行分析:我们看一下分成三类，则上述方法的分析结果为：类平均法：{1 2 6 }，{3 5}，{4}．重心法{1 2 6 }，{3 5}，{4}．密度法．{1 2 6 4}，{3}，{5}．最小距离法{1 2 6 4}，{3}，{5}．Ward法{1 2 6 }，{4}，{3 5}．由以上结果可见用不同的方法进行聚类其结果是有差异的。