当前位置：文档之家 › 第3章词法分析与有穷自动机汇编

第3章词法分析与有穷自动机汇编

  • 格式：ppt
  • 大小：840.00 KB
  • 文档页数：98

下载文档原格式

  / 98

合集下载

编译原理第三章

编译原理第三章


例3.4 Z→ A→ B→
有正规文法G： 0A 0A | 0B 1A | ε
例3.5 A→ B→ C→
有正规文法G： aB | bB aC | a | b aB
例3.6 Z→ U→ V→
有正规文法G： Z=0(0|01)*0 U0 | V1 A=(a|b)(aa)*(a|b) Z1 | 1 Z=(10|01)(10|01)* Z0 | 0
A
B
r2 ε
A C
A
B
ε
B
r1
④R为复合正规式？
例3.12 3.13 P41
教学进度
3.4.4 NFA确定化为DFA
方法（子集法） 1、改造M为M’： ①引进新的初态结点X、终态结点Y； ②对M的状态转换图实施分裂（替换）
计算机科学与工程系
2、将M’进一步变换为DFA :
①状态子集T的闭包_CLOSURE(T) ②定义状态集Ta = _CLOSURE(J) ③从DFA的初态_CLOSURE({X})开始计算状态转换矩阵；直到 不再产生新的状态子集为止。
第三章
• • • • • •
词法分析与有穷自动机
计算机科学与工程系
词法分析器的功能与输出 单词符号的两种定义方式 正规表达式与有穷自动机 正规文法与有穷自动机 词法分析器的设计 词法分析程序自动构造工具LEX简介
教学进度
3.1 词法分析器的功能

计算机科学与工程系
词法分析：对字符串表示的源程序进行从左到右的扫描和 分解，根据语言的词法规则识别出一个个具有独立意义的 单词符号。
教学进度
3.3 单词符号的两种定义方式
单词符号结构的描述方法：
计算机科学与工程系
正规文法（３型文法）(regular grammar)
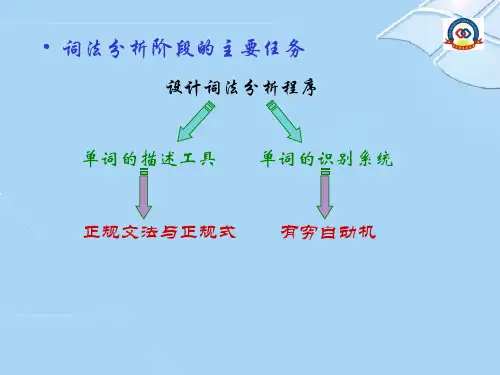
第三章 词法分析和有穷自动机

第三章 词法分析和有穷自动机


ε
ε
2
ε
6 b
ε
f
3.4.5 DFA的最小化（化简）
• 最少状态DFA 对于一个DFA M，存在一个最少状态DFA M’， 使得L(M’)=L(M)。 (a)没有多余状态 (b)没有两个状态是互相等价的 结论： 一个NFA 对应的DFA不惟一 但它对应的最小化DFA不计同构是惟一的
• 多余状态的例子 a
例
正规式 φ
ε
a a|b ab (a|b)(a|b) a* ba* (a|b)*
正规集 φ {ε } {a} L(a|b)=L(a) ∪ L(b)={a,b} L(ab)=L(a)L(b)={ab} {aa,ab,ba,bb} { ε ,a,aa,aaa,…} {b,ba,baa,baaa,…} {所有由a和b组成的字}
• 例 DFA M=({0,1,2,3},{a,b}, f ,0,{3}) 其中 f 为： f (0,a)=1 f (0,b)=2 f (1,a)=3 f (1,b)=2 f (2,a)=1 f (2,b)=3 f (3,b)=3 f (3,a)=3
3.4.1 确定有穷自动机(DFA) • DFA的表示方法 两种：矩阵和图形的方式 矩阵称为状态转换矩阵 图形称为状态转换图
• NFA M所接受字符串的集合称为NFA M所能 识别的语言，记为L(M)。 • NFA的确定化 DFA是NFA的特例
NFA M存在与之等价的DFA M’,L(M)=L(M’) 与某一NFA等价的DFA不惟一 正规式 NFA 正规文法 DFA
3.4.4 NFA 确定化
• 状态集合I的空闭包：ε -closure(I) 它是一个状态集合，包含 ： ♠ I中任何状态q ♠ I中任何状态q经任意条空弧到达的任何状态 • 状态集合I的a弧转换：Ia 定义一个状态集J，J是I中所有状态经一条a 弧到达的状态的全体 Ia＝ε -closure(J)
编译原理第三章_有穷自动机

编译原理第三章_有穷自动机

5
例 过河问题 分析（续）
初始状态：MWGC-φ；终止状态：φ-MWGC。 g
MWGC-φ
WC-MG
问题：
6
例 过河问题 状态转换图
起始 g
MWGC-φ g
g φ-MWGC
g
7
WC-MG
m
m MWC-G
w
w
c
C-MWG
c W-MGC
g
g
MGC-W c
MG-WC
w
m
c G-MWC
m
gg MWG-C
+dd. ddd;
输入符号串
数字 数字
SB
.
数字
+
A
H
-.
数字
.G
接收：若扫描完输入串， 且在一个终止状态上结 束。
数字 阻塞：若扫描结束但未 停止在终止状态上；或 者为能扫描完输入串 （如遇不合法符号）。
不完全描述：某些状态 对于某些输入符号不存 在转换。
练习：+34.567 .123 3.4.5
w
有穷自动机（FA）
数字系统：可以从一个状态移动到另一个状态；每次 状态转换，都上由当前状态及一组输入符号确定的；可以 输出某些离散的值集。
FA：一个状态集合；状态间的转换规则；通过读头来 扫描的一个输入符号串。
读头：从左到右扫描符号串。移动（扫描）是由状态 转换规则来决定的。
8
读头
一个FA的例子
(3)运行： 串f(，Q,且t1tt21)∈= Σf(，f(Qt1,t2t1∈), Σt2*)，其中Q∈K， t1t2为输入字符
17
例３
题：试证abba可为例1的DFA M所识别（所接受）。
sun编译原理第3章词法分析与有穷自动机第4 8讲 优质课件

sun编译原理第3章词法分析与有穷自动机第4 8讲 优质课件


={a,b}*{aa,bb}{a,b}*
练习：若S=a|bb，则L((a|bb)*)=？
2019/11/24
信息学院 孙丽云
5
第3章 词法分析与有穷自动机
■正规式中运算的优先级
括号优先，* 次之，•（连接）再次之，| 最后 例：a|bc* ≌ a|(b(c*))
ab|c*d ≌ (ab)|((c*)d)
其中 U、W∈N t∈T 其中 U、W∈N t∈T
2019/11/24
信息学院 孙丽云
8
第3章 词法分析与有穷自动机
■正规文法到正规式的转换
(1)将正规文法中的每个非终结符表示成关于它的一 个正规式方程，获得一个联立方程组。 (2)依照求解规则:
若x=αx|β(或x=αx+β)，则解为x=α*β; 若x=xα|β(或x=xα+β)，则解为x=βα*; 以及正规式的分配律、交换律和结合律求关于文法 开始符号的正规式方程组的解. 这个解是关于该文法开始符号S的一个正规式，显然 它表示了由该正规文法所描述的语言。
信息学院 孙丽云
2
第3章 词法分析与有穷自动机
3.3 语言单词符号的两种定义方式 多数程序设计语言的单词符号都能用正规文法或正规 式来定义。
■ 正规式与正规集
设有字母表={a1，a2，…，an}，在字母表上的正 规式和它所表示的正规集可用如下规则定义： （1） Φ是上的正规式，它所表示的正规集是Φ， 即空集{} （2）ε是上的正规式，它所表示的正规集是{ε} （3）ai是上的正规式，它所表示的正规集由单个符 号ai组成，即{ai}
③ (e1)*是上的一个正规式，它所表示的正规集为 L((e1)*) =L((e1))*
正规式描述了单词符号的构成规则，正规集是正规 式能描述的所有的单词的集合。
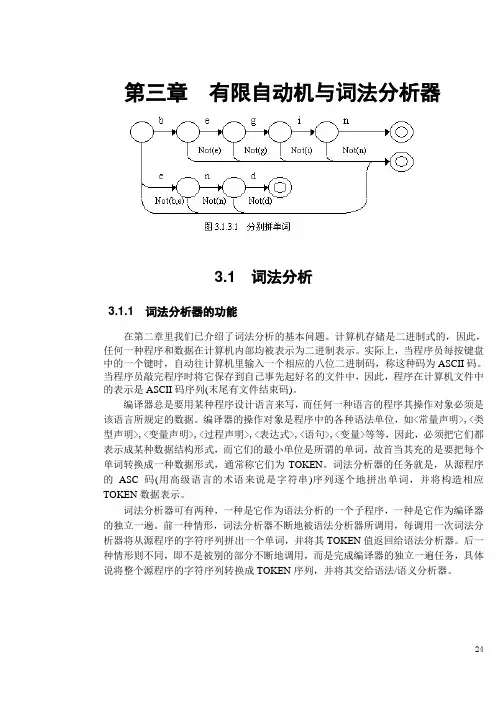
编译原理 第三章 有限自动机与词法分析器

编译原理 第三章 有限自动机与词法分析器

第三章有限自动机与词法分析器3.1词法分析3.1.1词法分析器的功能在第二章里我们已介绍了词法分析的基本问题。

计算机存储是二进制式的，因此，任何一种程序和数据在计算机内部均被表示为二进制表示。

实际上，当程序员每按键盘中的一个键时，自动往计算机里输入一个相应的八位二进制码，称这种码为ASCII码。

当程序员敲完程序时将它保存到自己事先起好名的文件中，因此，程序在计算机文件中的表示是ASCII码序列(末尾有文件结束码)。

编译器总是要用某种程序设计语言来写，而任何一种语言的程序其操作对象必须是该语言所规定的数据。

编译器的操作对象是程序中的各种语法单位，如<常量声明>,<类型声明>,<变量声明>,<过程声明>,<表达式>,<语句>,<变量>等等，因此，必须把它们都表示成某种数据结构形式，而它们的最小单位是所谓的单词，故首当其充的是要把每个单词转换成一种数据形式，通常称它们为TOKEN。

词法分析器的任务就是，从源程序的ASC码(用高级语言的术语来说是字符串)序列逐个地拼出单词，并将构造相应TOKEN数据表示。

词法分析器可有两种，一种是它作为语法分析的一个子程序，一种是它作为编译器的独立一遍。

前一种情形，词法分析器不断地被语法分析器所调用，每调用一次词法分析器将从源程序的字符序列拼出一个单词，并将其TOKEN值返回给语法分析器。

后一种情形则不同，即不是被别的部分不断地调用，而是完成编译器的独立一遍任务，具体说将整个源程序的字符序列转换成TOKEN序列，并将其交给语法/语义分析器。

实际的编译器一般都采用子程序方式，但是为了独立地介绍词法分析、语法分析和语义分析的概念和技术，我们将词法分析部分分离出来即作为独立一遍的词法处理器来介绍。

从实际的角度来说，这种方法有以下缺点:一是因为它要生成TOKEN列，自然多占用空间；二是因为要保存所有的TOKEN，需要耗费更多的时间。

第3章 词法分析(3)

第3章 词法分析(3)


3.4 正规式与有穷自动机的等价性
1. NFA M正规式R
在消结过程中,逐步用正规式来标记弧, 规则如下:
1.对于
1
2.对于
R1
2
R2
代之为
3
1
R1 R2
3
代之为 R1 R1| R2 1 2 1 2 R2 R2 3.对于 代之为 R1R2﹡R3 R 1 R 3 1 3 1 2 3
例如：有NFA M如图3.14，求其等价的正规式R。
a,b a 3
x ε 0 b 1 a|b a|b x ε 0
aa
a
4
ε
b
y (a|b)*(aa|bb)(a|b)* x y ε 2 a,b a|b aa(a|b) * y bb(a|b) *
4
ε y x
bb
2
ε
a|b
ε
0
3.4 正规式与有穷自动机的等价性
课堂练习 求以下NFA的正规式 a a 3 a 1 2 b
第一步
a
5 6 b
b
4
b
a
a
3
a
a
s

1 2
b
5 b
4 b

6 b

z
3.4 正规式与有穷自动机的等价性
第二步
a|b s 1 2
aa bb aa|bb 5
a|b
6

z
第三步
s
第四步
（a|b）*
2
5
（a|b）*
z
s
(a|b)*(aa|bb)(a|b)*
z
课堂讲解
• 【例5.12】第72页 • 【例5.13】第73页
编译原理 第3章 词法分析与有穷自动机(第5-8讲)

编译原理 第3章 词法分析与有穷自动机(第5-8讲)


它所对应的状态表如图：
状态 0 1 2 3 a 1 3 1 3 后继 状态 b 2 2 3 3
输入字符 接受 否 否 否 是
式的转化
22
第3章 词法分析与有穷自动机
■DFA所识别的语言
给定DFA M，对于字符c1,c2,…,cn,当以下条件成立时， 称M接受由c1,c2,…,cn组成的字符串c1c2…cn： 存在状态序列s0,s1,s2,…,sn,使得s1=f(S,c1), s2=f(s1,c2),…,sn=f(sn-1,cn)，且sn∈Z。 由DFA M接受的语言L(M)是所有M接受的字符串组成的集 合。
25
第3章 词法分析与有穷自动机
判断下图是DFA还是NFA的状态转换图，并 写出其他2种表示形式
26
第3章 词法分析与有穷自动机
■由正规表达式R构造NFA
1.基本正规表达式 (a)对于正规式φ,所构造NFA: (b)对于正规式ε,所构造NFA: (c)对于正规式a,a∈Σ,则 NFA:
x ε y
练习：若S=a|bb，则L((a|bb)*)=？
5
第3章 词法分析与有穷自动机
■正规式中运算的优先级
括号优先，* 次之，•（连接）再次之，| 最后 例：a|bc* ≌ a|(b(c*)) ab|c*d ≌ (ab)|((c*)d)
■ 正规式与正规集举例
L(a|bc*)=L(a)∪L(bc*) 思考：L(ab|c*d)=？ =L(a)∪L(b)L(c*) =L(a)∪L(b)(L(c))* ={a}∪{b}{ε,c,cc,ccc……} ={a,b,bc,bcc,bccc,……}
17
第3章 词法分析与有穷自动机
■有穷自动机的状态转移图表示方法
第3章词法分析与有穷自动机20090319

第3章词法分析与有穷自动机20090319


单词的种类 （1）关键字：if、for、while （2）标识符： （3） 常数： （4） 运算符：+、-、* （5）分界符：, 、;、(、)
编译原理
2013年8月27日
词法分析程序的输出形式-----二元式
单词类别 单词的属性值
单词类别可以用整数编码表示:一类一种或一字一种
单词类别 关键字 标识符 常数 运算符 分界符
编译原理
2013年8月27日
【例3．9】将描述标识符的正规式R=l(l∣d)*转换 成相应的正规文法。
• 令S为文法的开始符号， 根据规则（2） 有 • S→l(l∣d)* • 根据规则（3）变换为： • S→lA • A→(l∣d)* • 根据规则（4）变换为： • S→lA • A→(l∣d)A∣ε •
有穷自动机的作用
实质上是提供了一种逻辑的探测方式,去探测一 些输入串是否属于某种语言,即: 它可以作为一种 语法检查器。
编译原理
2013年8月27日
3.4.1
确定的有穷自动机（DFA）
M=(Σ, Q, f,S, Z)
Σ：有穷字母表，它的每个元素称为一个输入符号 Q：有穷状态集，它的每个元素称为一个状态 S∈K，是唯一的初态
运算符的优先级： 先*, 后 • , 最后 | • 在正规式中可以省略.
正规式相等 这两个正规式表示的语言相等
编译原理
2013年8月27日
正规式举例
• 例：设有字母表 ∑={a,b}，根据正规式与正规集的定义，有以 下的正规式和正规集 正规式 正规集 a {a} a∣b {a,b} ab {ab} ( a∣b)( a∣b) {aa,ab,ba,bb} a* {ε,a,aa,aaa,…,任意个a的串} （a∣b）* {ε，a,b,aa,ab,ba,bb,…所有a,b组成的串} (a︱b) *(aa︱bb) (a︱b) * ∑*上所有含两个连续的a 或两 个连续的b组成的串
《编译原理实践及应用》第3章词法分析—DFA与NFA

《编译原理实践及应用》第3章词法分析—DFA与NFA


其中 Κ ={ S 0 ,S1 ,S 2 } Σ ={a,b}
Ѕ={ S 0 , S1 } ( S0 ,a)={ S1 }
F={ S 2 }
( S 0 ,b)={ S 0 ,S 2 }
( S1 ,a)= Φ
(S1 ,b)={S 2 }
( S 2 ,a)= Φ
(S 2 ,b)={S1 }
②以每个非终结符号做其它状态
③对于形如Q→q的规则,
q
S
Q
对于形如Q→Rq的规则,
Rq Q
④以文法开始符号为终止状态。
例3-1： 文法G[Z]： Z→Za|Aa|Bb
aA
a
A→Ba|a B→Ab|b
Sb a
Za
b
Bb
2.应用状态转换图识别句子
识别句子：从开始状态到终止状态经过的边上的符号序列。 识别句子的步骤： ①从开始状态出发，以欲识别符号串的最左字符开始，寻找标
Z→Cb C→b|Bb B→Ab A→a|Ba
有限自动机(FA)
FA可看作一个机器模型，由一个带读头的有限控制器和 一条字符输入带组成。
#
a b a ba
…
输入带
控制器
工作原理：读头从左到右扫描输入带，读到一个字符，状态改
变，同时读头右移一个字符，…，直到读头读到
“#”，状态进入终止状态。
控制器中包括有限个状态，读入一个字符形成状态转换。
( S1 ,a)= S0 ( S1 ,c)= S3 ( S 2 ,b)= S1
( S3 ,b)= S3
a
b
S2 a
S0 a S1
ba
C
S3 b
定义: 所接收的语言（正则集）
L( AD)={β | S β S, S∈ F },
第3章 词法分析与有穷自动机PPT课件

第3章 词法分析与有穷自动机PPT课件


或作为一个联合
typedef struct {
TokenType tokenval;
unon { char* stringval;
int numval; } attribute;
} TokenRecord;
10
【例】试给出程序段 if (a>1) b = 100;输出 的单词符号串。
假定基本字、运算符和界符都是一符一种，标识符自身 的值是字符串，常数是二进制值。
(2,)
基本字 if
(29,)
左括号 (
(10,‘a’)
标识符 a
(23,)
大于号 >
(11,‘1’的二进制)
常数 1
(30，)
右括号 )
(10,‘b’)
标识符 b
(17,)
赋值号 =
(11,‘100’的二进制) 常数 100
(26,)
分号 ;
11
【例】考虑下述 C++ 代码段：
另一种 表示
while ( i >= j ) i--;
第三章 词法分析
人们理解一篇文章（或一个程序）起码是在单 词的级别上来思考的。同样，编译程序也是在单 词的级别上来分析和翻译源程序的。词法分析的 任务是：从左至右逐个字符地对源程序进行扫描， 产生一个个的，把作为字符串的源程序改造成为 单词符号串的中间程序。因此，词法分析是编译 的基础。
执行词法分析的程序称为词法分析器。本章讨 论词法分析程序的手工构造方法和自动构造方法。
将字符组合成记号与在一个英语句子中将字母构成单词 并确定单词的含义很相像，此时的任务很像拼写。
5
程序语言的单词符号一般可分为下列五种：
1) 关键字：是由程序语言定义的具有固定意义的标识符， 也称保留字或基本字。如Pascal中的 begin、end、 if、integer等，C 中的if、else、do、while， C++ 中的class、int、switch、break等都是保 留字，它们一般不用作一般标识符。
编译原理-第3章 词法分析--习题答案

编译原理-第3章 词法分析--习题答案

第3章词法分析习题答案1．判断下面的陈述是否正确。

（1）有穷自动机接受的语言是正规语言。

(√)（2）若r1和r2是Σ上的正规式，则r1|r2也是Σ上的正规式。

(√)（3）设M是一个NFA，并且L(M)={x,y,z}，则M的状态数至少为4个。

(× )（4）设Σ={a,b}，则Σ上所有以b为首的符号串构成的正规集的正规式为b*(a|b)*。

(× )（5）对任何一个NFA M，都存在一个DFA M'，使得L(M')=L(M)。

(√)（6）对一个右线性文法G，必存在一个左线性文法G'，使得L(G)=L(G')，反之亦然。

(√) （7）一个DFA，可以通过多条路识别一个符号串。

(× )（8）一个NFA，可以通过多条路识别一个符号串。

(√)（9）如果一个有穷自动机可以接受空符号串，则它的状态图一定含有 边。

(× )（10）DFA具有翻译单词的能力。

(× )2.指与出正规式匹配的串.（1)(ab|b)*c 与后面的那些串匹配？ababbc abab c babc aaabc（2）ab*c*(a|b)c 与后面的那些串匹配？ acac acbbc abbcac abc acc（3）(a|b)a*(ba)* 与后面的那些串匹配? ba bba aa baa ababa答案（1) ababbc c babc（2) acac abbcac abc（3) ba bba aa baa ababa3. 为下边所描述的串写正规式，字母表是{0, 1}.（1)以01 结尾的所有串（2)只包含一个0的所有串（3) 包含偶数个1但不含0的所有串（4)包含偶数个1且含任意数目0的所有串（5)包含01子串的所有串（6)不包含01子串的所有串答案注意 正规式不唯一（1)(0|1)*01（2)1*01*（3)(11)*（4)(0*10*10*)*（5)(0|1)*01(0|1)*（6)1*0*4.请描述下面正规式定义的串. 字母表{x, y}.（1) x(x|y)*x（2)x*(yx)*x*（3) (x|y)*(xx|yy) (x|y)*答案（1)必须以 x 开头和x结尾的串（2)每个 y 至少有一个 x 跟在后边的串 （3)所有含两个相继的x或两个相继的y的串5．处于/* 和 */之间的串构成注解，注解中间没有*/。

编译原理：第3章 有穷自动机

编译原理第3章内容简介学习目标第3章有穷自动机3.1 有穷自动机的形式定义3.1 有穷自动机的形式定义DFA的表示举例——状态转换表DFA的表示举例——状态转换图 3.13.1 FA的形式定义有穷自动机识别的符号串举例DFA A3.1 有穷自动机的形式定义 3.1 有穷自动机的形式定义NFA举例 3.13.1用NFA识别符号串yFA的构造FA的构造举例—1FA的构造举例—2FA的构造举例—3请构造一个有穷自动机FA的构造举例—4 3.1请构造一个有穷自动机FA的等价性举例3.2 NFA到DFA的转换 3.2 NFA到DFA的转换—NFA确定化3.2 NFA到DFA的转换3.2 NFA到DFA的转换—NFA确定化——ε闭包状态子集I的ε闭包——举例状态子集I的状态子集I的ε闭包——举例状态子集I的——Ia 子集3.2 NFA到DFA的转换Ia子集——举例Ia子集——举例 3.2 NFA到DFA的转换NFA到DFA的转换——子集法NFA=（Q NFA到DFA的转换——举例1aNFA到DFA的转换——举例2NFA DFA DFA NFA DFA DFADFA化简举例1DFA化简——注意NFA到最小化DFA的转换——举例33.3 正规文法与FA3.3 正规文法与FAFA⇒右线性正规文法FA⇒右线性正规文法——举例1y3.4 正规表达式RE与FA 正规表达式与有穷自动机3.4 RE与FA——RE的性质 3.4 RE与FA—RE⇒FARE⇒FA举例1RE⇒FA举例23.4 RE与FA——FA⇒RE FA⇒REFA⇒RE FA⇒RE举例FA⇒RE举例正规文法到正规表达式正规文法到正规表达式DFA的程序实现DFADFA的程序实现DFA DFA的程序实现lDFA的程序实现l第3章内容小结第3章内容小结参考文献。

编译原理第二版第3章词法分析

一、正规式与正规集的递归定义
1. ε和φ都是∑上的正规式，它所表示的正规集分
别为｛ε｝和Ф； 2. 任何ａ∈∑，ａ是∑上的正规式，它所表示的正 规集为｛ａ｝； 3. 假定ｅ1和ｅ2都是∑上的正规式，他们所表示的 正规集分别为Ｌ(ｅ1)和Ｌ(ｅ2)，那么，以下也 都是正规式和他们所表示的正规集；
一、正规式与正规集的递归定义
3.2 单词符号及输出单词的形式
单词自身值
对常数，基本字，运算符，界符就是他们本 身的值 对标识符，将标识符的名字登记在符号表中， ‚自身值‛是指向该标识符所在符号表中位 置的指针。
假定基本字、运算符和界符都是一符一种 例：if(a>1) b=100; 词法分析后输出的单词序列是: (2, ) if (29, ) ( (10,‘a’) a (23, ) > (11,‘1’) 1 (30, ) ) (10,’b’) b (17, ) = (11,‘100’) 100 (26, ) ;
4. 仅由有限次使用上述三步定义的表达式才是∑上的 正规式，仅由这些正规式所表示的字集才是∑上 的正规集。
重点回顾
四、将正规文法转换成正规式 求非终结符的正规式 将正规文法中的每个非终结符表示成关 于它的一个正规式方程，获得一个联立 方程组 用代入法解正规式方程组 最后只剩下一个开始符号定义的正规式, 其中不含非终结符
3.3 语言单词符号的两种定义方式
作用: 描述单词的构成规则,基于这类描 述工具建立词法分析技术,进而实现词法 分析程序的自动构造。 工具有: 正规文法 正规式(Regular Expression)
多数程序设计语言的单词符号都能用正 规文法或正规式来定义。
3.3.1 正规文法
多数程序设计语言单词的语法都能用正 规文法(3型文法)描述 正规文法回顾 文法的任一产生式α →β 的形式都为 A→aB或A→a，其中A ，B∈VN ，a∈VT A→Ba或A→a，其中A ，B∈VN ，a∈ VT 正规文法描述的是VT*上的正规集

第三章有穷自动机


C
01 S0 S1 S5 0 S1 S2 S7 1 S2 S2 S5 1 S3 S5 S7 0 S5 S3 S1 0 S7 S0 S1 1
3.2.3 合并等价状态
等价状态
若s和t是M的两个不同状态，称s和t等 价：如果从状态s出发能读出某个字而停 于终态，同样从t 出发也能读出同一个字 而停于终态；反之若从t 出发能读出某个字 而停于终态，则从s出发也能读出同一个 字而停于终态。
第三章 有穷自动机
本章介绍有关有穷自动机的基本概念和 理论以及正规文法、正规表达式与有穷自动 机之间的相互关系。
§3.1 有穷自动机的形式定义
有穷状态自动机(Finite-state Automata 或简称FA)在识别功能上与正 规文法类等价，而且也等价于一个特殊类 型的语言产生器——正规表达式(Regular Expression)。因此许多简单的程序语言 都可由FA所识别。事实上，它是描述词法 的有效工具，也是进行词法分析的主要理 论基础。
消除多余状态
多余状态是指从该自动机的开始状态出发， 任何 0 S1 S2 S7 1 S2 S2 S5 1 S3 S5 S7 0 S4 S5 S6 0 S5 S3 S1 0 S6 S8 S0 1 S7 S0 S1 1 S8 S0 S6 0
B
01 S0 S1 S5 0 S1 S2 S7 1 S2 S2 S5 1 S3 S5 S7 0 S5 S3 S1 0 S6 S8 S0 1 S7 S0 S1 1 S8 S0 S6 0
l, d
l, d
l
q0
q1
l q0
q1
q2
非 l,d
图(a)
图(b)
如果赋予状态q0、q1与q2一定的操作，则

第3章有穷自动机(胡)


(4) (a | b)* 是正规式 , 则相应正规集为 L((a | b)*)=(L(a | b))*= { a, b }*={ε,a,b,ab,ba, …} (5) ba* 是正规式 , 则相应正规集为 L(ba*)=L(b)L(a*)={b,ba,baa,baaa,…} (6) (a | b)*(aa | bb ) (a | b)*是正规式 , 则相应正规集为 L((a | b)*(aa | bb ) (a | b)*) =L((a | b)*)L(aa | bb ) L((a | b)*) ={a,b}*{aa,bb}{a,b}*
注意： 1）对于 关键字、运算符和界符 种别码是一字一 符。可以完全代表它自己。也就不用写自身值。 2）对于标识符和常数就必须依赖自身值来区分。 标识符自身值是它自己的字符串。 常数自身值是常数本身的二进制数值。 我们可以用指向标识符表或常数表的入口指针作 为它们的自身值
下表是简单语言单词符号的内部表示：
3.4 有穷自动机
自动机是一种能进行运算并实现自我控制的装置，
计算机就是一部自动机。自动机是描述符号串处理的强
有力的工具。因而自动机成为研究词法分析器的重要基
础。在识别功能上与正规文法类和正规表达式等价。 下面介绍有关有穷自动机的基本概念和理论以及正 规文法、正规表达式与有穷自动机之间的相互关系。
例题1 （右线性） 给定文法G[Z]： Z→0A A→0A|0B B→1A| ε 解：首先改为正规方程组： Z=0A A=0A+0B B=1A+ε 联立求解：3）代入2） A = 0A+01A+0 = (0+01)A+0 其次应用求解规则得 A =(0+01)*0 代入1）中 Z = 0 (0+ 01)*0 正规式为 = 0 ( 0 | 01 )* 0

编译原理 第03章 词法分析与有穷自动机


3.2 单词符号及输出单词的形式 if (a＞1) b =100；经词法分析后，输出 的单词符号串是：
（2， ） （29， ） 基本字if （30， ） 右括号 ) 左括号 ( （10，‘b’） 标识符 （17， ） 赋值号 = （10，‘a’） 标识符 b a （23， ） 大于号 ＞ （11，100）常数 100 （11，1） 常数 1 （26, ） 分号 ；
语 法 分 析 器
3.2 单词符号及输出单词的形式 语言的单词符号是指语言中具有独立 意义的最小语法单位。
关键字 也称基本字，例如，C语言中 的if，else，while, do等。
标识符 表示各种名字，如变量名、常 量名、数组名和函数名等。
3.2 单词符号及输出单词的形式 常数 整型常数125、实型常数0.718、 布尔型常数TRUE等 。
例如，(a|b)*=(a*b*)* ;
3.3.1 正规式和正规集
正规式具有如下性质 : 令A , B 和 C 均为正规式，则 1．A | B = B | A (交换律) 2．A | ( B | C) = (A | B) | C (结合律) 3．A(BC) = (AB)C (结合律) 4．A(B | C) = AB | AC (分配律) 5．(A | B)C = AC | BC (分配律) 6． Aε | εA = A 7． A* = AA* | ε = A | A* = (A | ε )* 8． (A* )* = A*
3.3.1 正规式和正规集 运算符的优先级：闭包“*” > 连 接“· ” > 或“|” 。连结符“· ”一般可省略不 写。 运算符均是左结合的。
3.3.1 正规式和正规集 例1 设有字母表Σ={a,b} ，有：
1. a 和 b是正规式，相应正规集为 L(a)={a} , L(b)={b} 2. a | b 是正规式，相应正规集为 L(a | b )=L(a)∪L(b)={a ,b} 3. ab 是正规式，相应正规集为 L(ab)=L(a)L(b)={a}{b}={ab}
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.词法分析单独作为一遍
第一遍 S.P.(字符串) 词法分析 单词串 S.P.(符号串) 第二遍 语法分析
2.词法分析程序作为单独的子程序
取单词 S.P.(字符串) 词法分 析程序 单词
优点: 结构清晰、各遍功能单一 缺点：效率低
语法分 析程序
编译原理
2018年12月6日3.2词法分析程序的输出形式
所有以a为首的符号串
所有以abb为尾的a，b符号串 所有含有两个连续的a或两个连续的b的符号串
(aa|ab|ba|bb) *
(a|b)(a|b)(a|b) *
空串和任何长度为偶数的符号串
任何长度大于等于2的符号串
编译原理
2018年12月6日
【例】使用正规式来表示程序设计语言中的相应单词符号。
<标识符>→字母 | <标识符>字母 | <标识符>数字） <无符号整数>→数字 | <无符号整数>数字 <单界符>→+ | * |< |, | ; <双界符>→<=
编译原理
2018年12月6日
【例】Σ={d,· ,e,+，-} 则Σ上的正规式
d *( · dd*∣ε)(e(+∣- ∣ε)dd*∣ε)表示的是实数。 其中d为0～9中的数字。比如：2，12.59,3.6e2和 471.88e-1等等都是该正规集所表示集合中的元素。
【例】设Σ={a,b,c},则aa*bb*cc*是Σ上的一个正规式,
运算符的优先级： 先*, 后 • , 最后 | • 在正规式中可以省略.
正规式相等 这两个正规式表示的语言相等
编译原理
2018年12月6日
正规式举例
• 例：设有字母表 ∑={a,b}，根据正规式与正规集的定义，有以 下的正规式和正规集 正规式 正规集 a {a} a∣b {a,b} ab {ab} ( a∣b)( a∣b) {aa,ab,ba,bb} a* {ε,a,aa,aaa,…,任意个a的串} （a∣b）* {ε，a,b,aa,ab,ba,bb,…所有a,b组成的串} (a︱b) *(aa︱bb) (a︱b) * ∑*上所有含两个连续的a 或两 个连续的b组成的串
第 3章
词法分析
教学目标
1. 本章介绍编译第一个阶段词法分析的设计原理和 设计方法，要求明确此阶段的任务。 2. 理解通常的单词分类和构词规则。 3. 会使用单词的描述和识别机制。 4. 要求掌握正规文法、状态图、DFA、NFA、正规式 和正规集的基本概念和它们之间的关系。 5. 掌握词法分析程序的手工实现方法。
编译原理
编码
1 2 3 4 5
2018年12月6日
• 单词符号属性的值：
单词自身符号的机内编码。 关键字、运算符、界符：只输出其种别码即可。 标识符：自身字符串的值，长度受限制。 常数：本身的值。字符型输出字符串本身，数值型，输出其自 身的二进制。 • 对于标识符和常数，若要建符号表，则输出其在符号表的入口地 址。
和L(e2), 那么e1|e2, e1 • e2和e1*也都是 上的正规式, 它们所表
示的正规集分别为L(e1)∪L(e2)、 L(e1) • L(e2)和(L(e1))* 4. 任何 上的正规式和正规集均由1、2和3产生。
编译原理
2018年12月6日
正规式中的运算符： | -----或（选择） • ----连接 * 或 { } ---重复 （） ----括号
单词的种类 （1）关键字：if、for、while （2）标识符： （3） 常数： （4） 运算符：+、-、* （5）分界符：, 、;、(、)
编译原理
2018年12月6日
词法分析程序的输出形式-----二元式
单词类别 单词的属性值
单词类别可以用整数编码表示:一类一种或一字一种
单词类别 关键字 标识符 常数 运算符 分界符
（5）建立符号表。
编译原理
2018年12月6日
main( )/*ADD*/ {int x=10,y=20,sum; sum=x+y; }
词法分析
main、(、)、{、int、x、 =、10、,、y、=、20、,、 sum、;、sum、=、x、+、 y、;、}
编译原理
2018年12月6日
实现方案：基本上有两种
编译原理
2018年12月6日
3.5 3.3.1 正规式与正规集
字母表, 定义在 上的正规式和正规集递归定义如下: 1. 和都是 上的正规式, 它们所表示的正规集分别为:{}和;
2. 任何a , a是 上的正规式,它所表示的正规集为:{a};
3. 假定e1和e2是 上的正规式, 它们所表示的正规集分别记为L(e1)
它所表示的正规集 L={abc,aabc,abbc,abcc,aaabc,...}={a mbncl∣m,n,l≥1}
编译原理
2018年12月6日
【例】设Σ={a,b}
正规式 ba* 正规集 所有以b为首后跟任意多个a的符号串
a(a|b)*
(a|b)*abb (a|b)*(aa|bb) (a|b)*
标识符： 无符号整数： 单界符： 双界符：
a(a|d) * dd* + | * |< |, | ; <=
编译原理
2018年12月6日
教学内容
1 2 3 4 5 6 词法分析程序的功能 词法分析程序的输出形式 程序设计语言单词的定义 正规式与有穷自动机 正规文法与有穷自动机 词法分析程序的编写方法
编译原理
2018年12月6日
3.1
词法分析程序的功能
（1）分析和识别单词及属性，
包括识别语言的关键字、标识符、常数、运算符等； （2）跳过各种分隔符，如空格，回车，制表符等； （3）删除注释； （4）进行词法检查，报告所发现的错误；
编译原理
2018年12月6日
表3.1
int x=10,y=20,sum;词法分析的结果
单词的属性值 int 指向x的符号表入口指针 = 10 , 指向y的符号表入口指针 = 20 , 指向sum的符号表入口指针 ;
2018年12月6日
单词类别 1 2 4 3 5 2 4 3 5 2 5
编译原理
3.3语言单词符号的两种定义方式 • 文法定义: 标识符的定义：标识符是以字母开头的、字母数字的组合 . I → aB|a 右线性文法 B →aB| dB| a |d I → a| Ia| Id 左线性文法 • 正规式定义: 字母(字母∣数字)* a(a ∣d)*