第五章例题

【例题1 •多选题】下列各项中，工业企业应计入其他业务成本的有（）。

（2011年）A. 销售材料的成本B. 单独计价包装物的成本C. 出租包装物的成本D. 经营租赁出租设备计提的折旧【答案】ABCD【解析】四个选项全部计入其他业务成本。

【例题2 •多选题】下列各项中，应列入利润表“营业成本”项目的有（）。

（2010年）A. 出售商品的成本B. 销售材料的成本C.出租非专利技术的摊销额D.以经营租赁方式出租设备计提的折旧额【答案】ABCD【解析】营业成本项目包含主营业务成本和其他业务成本。

选项 A 计入主营业务成本；选项B、C D计入其他业务成本。

【例题3 •单选题】下列各项中，应计入其他业务成本的是（）。

（2008年）A. 库存商品盘亏净损失B. 经营租出固定资产折旧C.向灾区捐赠的商品成本D.火灾导致原材料毁损净损失【答案】 B 【解析】库存商品盘亏净损失，属于一般经营损失的部分，计入管理费用，非正常损失的部分计入到营业外支出；向灾区捐赠的商品成本和火灾导致原材料毁损净损失均计入到营业外支出。

【例题4 •单选题】2010年5月，甲公司销售商品实际应交增值税38万元，应交消费税20万元，提供运输劳务实际应交营业税15万元；适用的城市维护建设税税率为7%，教育费附加为3%。

假定不考虑其他因素，甲公司当月应列入利润表“营业税金及附加”项目的金额为（）万元。

（2011 年）A．7．3 B ．38．5 C ．42．3 D ．80．3【答案】C【解析】禾U润表“营业税金及附加”项目的金额=20+15+ （38+20+15）X（7%+3%=42.3（万元）。

【例题5 •多选题】下列各项中，应计入营业税金及附加的有（）。

（2010年）A. 处置无形资产应交的营业税B. 销售商品应交的增值税C. 销售应税产品的资源税D. 销售应税消费品应交的消费税【答案】CD【解析】营业税金及附加科目核算企业经营活动发生的营业税、消费税、城市维护建设税、资源税和教育费附加等相关税费。

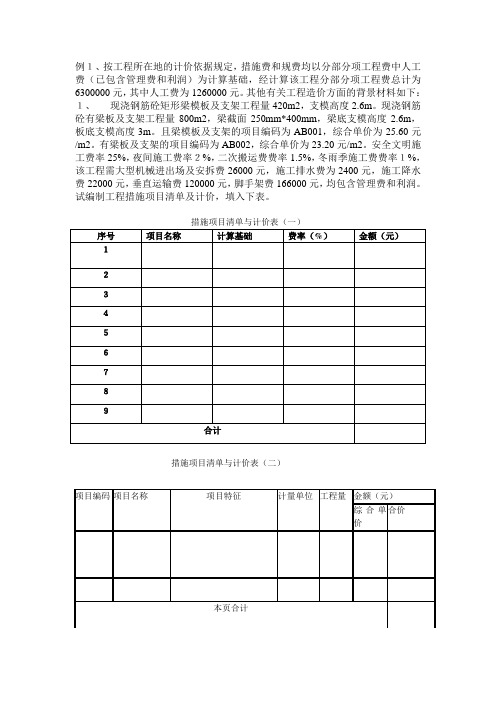
例１、按工程所在地的计价依据规定，措施费和规费均以分部分项工程费中人工费（已包含管理费和利润）为计算基础，经计算该工程分部分项工程费总计为6300000元，其中人工费为1260000元。

其他有关工程造价方面的背景材料如下：１、现浇钢筋砼矩形梁模板及支架工程量420m2，支模高度2.6m。

现浇钢筋砼有梁板及支架工程量800m2，梁截面250mm*400mm，梁底支模高度2.6m，板底支模高度3m。

且梁模板及支架的项目编码为AB001，综合单价为25.60元/m2。

有梁板及支架的项目编码为AB002，综合单价为23.20元/m2。

安全文明施工费率25%，夜间施工费率２%，二次搬运费费率1.5%，冬雨季施工费费率１%，该工程需大型机械进出场及安拆费26000元，施工排水费为2400元，施工降水费22000元，垂直运输费120000元，脚手架费166000元，均包含管理费和利润。

试编制工程措施项目清单及计价，填入下表。

措施项目清单与计价表（二）２、已知该工程暂列金额330000元，材料暂估价100000元，计日工费用20000元，总承包服务费20000元，则其他项目费为多少？３、社会保障费中养老保险费率为16%,失业保险费费率２%，医疗保险费费率６%；住房公积金费率６%；危险作业意外伤害保险费率0.48%。

税金费率为3.41%。

则该工程的招标控制价为多少？答案：１、措施项目清单与计价表（二）2、其他项目费＝330000+20000+20000=370000元（材料暂估价不列入总价中）３、规费＝1260000*(16%+2%+6%+6%+0.48%)=384048.00元税金＝（分部分项工程费+措施项目费+其他项目费+规费）*3.41%=265688.79❖例２、根据某基础工程工程是和《全国统一建筑工程基础定额》消耗指标，进行工料分析计算得出各项资源消耗及该地区相应的市场价格，如表所示。

纳税人所在地为城市，按照建标[2003]206号关于建安工程费的组成和规定取费，各项费用的费率为：措施费率为8%，间接费率为10%，利润率为4.5%.❖问题：１.计算该工程应纳的综合税率。

第五章电缆敷设工程定额计量与计价【例题1】直埋电缆时，沟的开挖平均宽度为500mm，电缆埋深900mm，埋4根电缆时，电缆沟长度为100m,则土方量为多少? 铺沙盖板工程量？【例题2】某电气工程，室内配电箱离地0.2米，离内墙0.2米，箱尺寸为W*H*D*（800*1850*600），进户电源采用VV22-3*95+1*50电缆，穿建筑物处设有电缆保护管G100，埋深0.8米，保护管算至外墙1.5米，室内外高差0.6米，计算保护管工程量？【例题3】某电缆敷设工程，采用直埋敷设4根电缆VV22-3*35+1*16，进建筑物及配电室均采用RC50镀锌钢管埋地保护，电缆室外水平距离为100米，进入1号车间后10米到配电柜，配电室的配电柜到外墙距离为5米，电缆保护管做到外墙1米，埋深0.8米，室内外高差600mm，配电柜安装高度均离地0.2米，试计算①钢管及电缆工程量？②电缆保护管挖填土方，直埋电缆挖填土方及铺沙盖板工程量？（RC50管子外径60mm)③电缆终端头制作安装工程量？【例题4】【例题5】某氮气站动力平面图1）PD1、PD2均为定型动力配电箱，落地式安装，基础型钢用10#槽钢制作，其重量为10kg/m。

2）PD1至PD2电缆沿桥架敷设，其余电缆均穿钢管敷设，埋地钢管标高为-0.2m，埋地钢管至动力配电箱出口处高出地坪+0.1m。

3）4台设备基础标高均为+0.3m，至设备电机处的配管管口高出基础面0.2m，均连接1根长0.8m同管径金属软管。

4）计算电缆长度时不计算电缆敷设驰度、波形弯度和交叉的附加长度，连接电机处，出管口后电缆的预留长度为1m，电缆头为户内干包式，其附加长度不计。

5）电缆桥架（200*100）的水平长度为22m。

【例题6】某室外总体电缆施工说明：1）某工厂有五个车间，动力配电箱电源均从1#配电间低压配电柜引来，室外电缆敷设均采用直埋敷设电缆埋深为0.9米，室内采用穿钢管敷设口径为50mm。

[例1] 在终端接负载的BJ-32波导终测得行波系数为0.29，第一个电场波腹点距负载5.7cm ，工作波长为10cm ，今用螺钉匹配，求螺钉的位置和归一化导纳值。

解：本题实质上就是讨论利用单螺钉调匹配的方法。

首先将波导等效为传输线，螺钉等效为电抗元件，利用传输线理论求得波导上任一点的归一化导纳，求出实部为1的位置即为调配螺钉的位置，此时归一化导纳虚部取反即为螺钉的归一化电纳值。

查教材附录得BJ-32波导的尺寸为04.3414.72mm b a ⨯=⨯由矩形波导中的10TE 模和20TE 模的截止波长分别为cm a cTE 428.14210==λ cm a cTE 214.720==λ 而信号的工作波长为10cm ，因此矩形波导中只能传输10TE 主模。

波导波长为 cm a g 873.13)2(12=-=λλλ根据测得的行波系数可求得波导中的驻波比为448.329.011===K ρ 因此，反射系数的模值为55.0111=+-=Γρρ再根据第一个电场波腹点的位置可算得负载处反射系数的相位1φ，即7.54876.134111max ===φπφπλg lπφ643.11=πφ643.11155.01j j e e =Γ=Γ在Smith 原图上查得5566.03918.0111j jb g y +=+=448.3=ρ的等驻波比圆与1=G 的圆相交3173.11j y in += cm d 14.1=设螺钉的归一化电纳为b ，当满足1=+jb y in 时负载是匹配的，因此螺钉的归一化电纳为373.1-=b[例2] 有一个三端口元件，测得其[S]矩阵为[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=001.000995.01.0995.00S 问：此元件有哪些性质?它是一个什么样的微波元件？ 解： 从此三端口的[S]矩阵可看出此元件有下列性质：1) 由0332211===S S S 知此元件的三个端口均是匹配的；2) 由03223==S S 知此元件的端口②和端口③是相互隔离的；3) 由)3,2,1,(==j i S S ji ij 知此元件是互易的；4) 由332211S S S ==知此元件是对称的；5) 由][][][I S S ≠+知此元件是有耗元件。

全国通用2023高中生物第5章细胞的能量供应和利用典型例题单选题1、下图为荒漠地区种植的胡杨分别在7月24号和8月26号两天测得的净光合速率日变化曲线图。

据图判断，下列相关分析正确的是（）A．这两天胡杨均在7点开始进行光合作用B．有机物的日合成量7月24号大于8月26号C．净光合速率日变化曲线走势主要受土壤含水量影响D．8月26号曲线双峰的形成与温度和光照等因素有关时刻答案：D分析：分析曲线：荒漠地区种植的胡杨在8月26号在中午时气孔关闭，导致光合速率减慢。

A、这两天胡杨均在7点时净光合速率为0，说明7点之前已经开始进行光合作用，A错误；B、由曲线走势可以看出，除21点到22点之外，26号净光合速率均大于24号，故有机物的日合成量7月24号小于8月26号，B错误；C、由曲线图可以得出，净光合速率日变化曲线走势主要光照强度影响，C错误；D、8月26号曲线双峰的形成与温度和光照等因素有关，D正确。

故选D。

2、高等植物细胞中，下列过程只发生在生物膜上的是（）A．光合作用中的光反应B．光合作用中CO2的固定C．ATP的合成过程D．氨基酸脱水缩合形成多肽链的过程答案：A分析：1 .植物在光照条件下进行光合作用，光合作用分为光反应阶段和暗反应阶段，光反应阶段在叶绿体的类囊体薄膜上进行水的光解，产生ATP和[H]，同时释放氧气，ATP和[H]用于暗反应阶段三碳化合物的还原，暗反应在叶绿体基质中进行。

2 .有氧呼吸包括三个阶段，第一阶段：这一阶段不需要氧的参与，是在细胞质基质中进行的，葡萄糖分解为两分子丙酮酸，4[H]，释放少量的能量；第二阶段：丙酮酸进入线粒体的基质中，这一阶段也不需要氧的参与，丙酮酸和水反应产生二氧化碳和[H]，释放少量的能量，第三阶段：在线粒体的内膜上，这一阶段需要氧的参与，是在线粒体内膜上进行的前两个阶段产生的[H]和氧气反应生成水，释放大量的能量。

A、高等植物细胞内光反应阶段在叶绿体的类囊体薄膜上进行水的光解，只发生在生物膜上，A正确；B、光合作用中CO2的固定发生在叶绿体基质中，不在生物膜上，B错误；C、ATP的合成过程可发生在细胞质基质和线粒体基质中，C错误；D、氨基酸脱水缩合发生在核糖体上，核糖体无膜，D错误。

1、（2013单选）为反映现时资本成本水平，计算平均资本成本最适宜采用的价值权数是（）。

A.账面价值权数B.目标价值权数C.市场价值权数D.历史价值权数【参考答案】C【参考解析】市场价值权数以各项个别资本的现行市价为基础计算资本权数，确定各类资本占总资本的比重。

其优点是能够反映现时的资本成本水平，有利于进行资本结构决策。

2、（2013单选）甲企业本年度资金平均占用额为3 500万元，经分析，其中不合理部分为500万元。

预计下年度销售增长5%，资金周转加速2%，则下年度资金需要量预计为（）万元。

A.3 000B.3 087C.3 150D.3 213【参考答案】B【参考解析】本题考核资金需要量预测的因素分析法。

资金需要量=（基期资金平均占用额-不合理资金占用额）×（1±预测期销售增减率）×（1-预测期资金周转速度增长率）=（3500-500）×（1+5%）×（1-2%）=3087（万元）。

3、（2013判断）在企业承担总风险能力一定且利率相同的情况下，对于经营杠杆水平较高的企业，应当保持较低的负债水平，而对于经营杠杆水平较低的企业，则可以保持较高的负债水平。

（）【参考答案】正确【参考解析】在总杠杆系数（总风险）一定的情况下，经营杠杆系数与财务杠杆系数此消彼长。

4、（2013计算）乙公司是一家上市公司，适用的企业所得税税率为25%，当年息税前利润为900万元，预计未来年度保持不变。

为简化计算，假定净利润全部分配，债务资本的市场价值等于其账面价值，确定债务资本成本时不考虑筹资费用。

证券市场平均收益率为12%，无风险收益率为4%，两种不同的债务水平下的税前利率和β系数如表1所示。

公司价值和平均资本成本如表2所示。

表1 不同债务水平下的税前利率和β系数表2 公司价值和平均资本成本注：表中的“×”表示省略的数据。

要求：（1）确定表2中英文字母代表的数值（不需要列示计算过程）。

(名师选题)人教高中数学必修一第五章三角函数经典大题例题单选题1、若扇形周长为20，当其面积最大时，其内切圆的半径r 为（ ） A ．5−1sin1B ．1sin1+32C ．5sin11+sin1D ．5+51+sin1 答案：C分析：先根据扇形周长求解出面积取最大值时扇形的圆心角和半径，然后根据图形中的内切关系得到关于内切圆半径r 的等式，由此求解出r 的值.设扇形的半径为R ，圆心角为α，面积为S ，因为2R +αR =20， 所以S =12αR 2=(10−R )R ≤(10−R+R 2)2=25，取等号时10−R =R ，即R =5，所以面积取最大值时R =5,α=2， 如下图所示：设内切圆圆心为O ，扇形过点O 的半径为AP ，B 为圆与半径的切点， 因为AO +OP =R =5，所以r +rsin∠BPO =5，所以r +rsin1=5， 所以r =5sin11+sin1，故选：C.2、函数f(x)=sin (2x −π3)的一个对称中心的坐标是（ ） A ．(0,0)B ．(0,−√32)C ．(π2,0)D ．(π6,0) 答案：D分析：解方程2x −π3=kπ,k ∈Z 即得解.解：令2x −π3=kπ,k ∈Z,∴x =12kπ+π6， 令k =0,∴x =π6，所以函数f(x)=sin (2x −π3)的一个对称中心的坐标是(π6,0). 故选：D3、《掷铁饼者》取材于希腊的现实生活中的体育竞技活动，刻画的是一名强健的男子在掷铁饼过程中具有表现力的瞬间（如图）．现在把掷铁饼者张开的双臂近似看成一张拉满弦的“弓”，掷铁饼者的手臂长约为π4m ，肩宽约为π8m ，“弓”所在圆的半径约为54m ，则掷铁饼者双手之间的距离约为（参考数据：√2≈1.414，√3≈1.732）（ ）A ．1.012mB ．1.768mC ．2.043mD ．2.945m 答案：B分析：由题意分析得到这段弓形所在的弧长，结合弧长公式求出其所对的圆心角，双手之间的距离，求得其弦长，即可求解.如图所示，由题意知“弓”所在的弧ACB⌢ 的长l =π4+π4+π8=5π8，其所对圆心角α=5π854=π2，则两手之间的距离|AB |=2|AD |=2×54×sin π4≈1.768(m )． 故选：B ．4、筒车是我国古代发明的一种水利灌溉工具，因其经济又环保，至今还在农业生产中得到应用.假定在水流稳定的情况下，筒车上的每一个盛水筒都做匀速圆周运动.如图，将筒车抽象为一个几何图形（圆），筒车半径为4m，筒车转轮的中心O到水面的距离为2m，筒车每分钟沿逆时针方向转动4圈.规定：盛水筒M对应的点P从水中浮现（即P0时的位置）时开始计算时间，且以水轮的圆心O为坐标原点，过点O的水平直线为x轴建立平面直角坐标系xOy.设盛水筒M从点P0运动到点P时所经过的时间为t（单位：s），且此时点P距离水面的高度为h（单位：m），则点P第一次到达最高点需要的时间为（）s.A．2B．3C．5D．10答案：C分析：设点P离水面的高度为ℎ(t)=Asin(ωt+φ)+2，根据题意求出A,ω,φ，再令ℎ(t)=6可求出结果.设点P离水面的高度为ℎ(t)=Asin(ωt+φ)+2，依题意可得A=4，ω=8π60=2π15，φ=−π6，所以ℎ(t)=4sin(2π15t−π6)+2，令ℎ(t)=4sin(2π15t−π6)=6，得sin(2π15t−π6)=1，得2π15t−π6=2kπ+π2，k∈Z，得t=15k+5，k∈Z，因为点P 第一次到达最高点，所以0<t <2π2π15=15，所以k =0,t =5s . 故选：C5、已知sinθ=45，则sin (π−θ)cos(π2+θ)cos (π+θ)sin(π2−θ)=（ ）A ．−169B ．169C ．−43D ．43 答案：B分析：由诱导公式和同角关系sin (π−θ)cos(π2+θ)cos (π+θ)sin(π2−θ)可化为sin 2θcos 2θ，再由同角关系由sinθ求出cos 2θ，由此可得结果.∵ sinθ=45，∴ cos 2θ=1−sin 2θ=925则sin (π−θ)cos(π2+θ)cos (π+θ)sin(π2−θ)=sinθ(−sinθ)(−cosθ)cosθ=sin 2θcos 2θ=169，故选：B.6、若函数f(x)=sinωx (ω>0)，在区间[0,π3]上单调递增，在区间[π3,π2]上单调递减，则ω=（ ）．A ．1B ．32C ．2D ．3 答案：B分析：根据f (π3)=1以及周期性求得ω.依题意函数f(x)=sinωx (ω>0)，在区间[0,π3]上单调递增，在区间[π3,π2]上单调递减， 则{f (π3)=sin π3ω=1T 2=πω≥π3 ， 即{π3ω=2kπ+π2,k ∈Z 0<ω≤3 ，解得ω=32.故选：B7、f(x)=−sinx−xcosx+x 2在[−π,π]的图象大致为（ ）A ．B ．C ．D ．答案：C分析：先由函数为奇函数可排除A ，再通过特殊值排除B 、D 即可. 由f(−x)=−sin (−x )+x cosx+x 2=−−sinx−xcosx+x 2=−f (x )，所以f (x )为奇函数，故排除选项A. 又f (π)=−sinπ−πcosπ+π2=−ππ2−1<0，则排除选项B,D故选：C8、sin1860°等于（ ） A ．12B ．-12C ．√32D ．-√32答案：C分析：用诱导公式先化简后求值.sin1860°=sin (5×360°+60°)=sin60°=√32, 故选: C9、已知α ∈(0,π)，且3cos 2α−8cos α=5，则sin α=（ ） A ．√53B ．23 C ．13D ．√59 答案：A分析：用二倍角的余弦公式，将已知方程转化为关于cosα的一元二次方程，求解得出cosα，再用同角间的三角函数关系，即可得出结论.3cos2α−8cosα=5，得6cos2α−8cosα−8=0，即3cos2α−4cosα−4=0，解得cosα=−23或cosα=2（舍去），又∵α∈(0,π),∴sinα=√1−cos2α=√53.故选：A.小提示：本题考查三角恒等变换和同角间的三角函数关系求值，熟记公式是解题的关键，考查计算求解能力，属于基础题.10、将函数f(x)=2cosx的图象先向右平移φ(0<φ<π)个单位长度，再把所得函数图象的横坐标变为原来的1ω(ω>0)倍，纵坐标不变，得到函数g(x)的图象，若对g(x)满足|g(x1)−g(x2)|=4，有|x1−x2|min=π4恒成立，且g(x)在区间(π6，π3)上单调递减，则φ的取值范围是（）A．[π12，π3]B．[π3，π2]C．(π3，2π3]D．[π3，2π3]答案：D分析：可得g(x)=2cos(ωx−φ)，根据题意可求出最小正周期，得出ω，求出g(x)的单调递减区间，根据包含关系可求出.由题可得g(x)=2cos(ωx−φ)，若满足|g(x1)−g(x2)|=4，则x1和x2必然一个极大值点，一个极小值点，又|x1−x2|min=π4，则T2=π4，即T=π2，所以ω=2πT=4，令2kπ≤4x−φ≤2kπ+π，可得kπ2+φ4≤x≤kπ2+π4+φ4，即g(x)的单调递减区间为[kπ2+φ4,kπ2+π4+φ4],k∈Z，因为g(x)在区间(π6，π3)上单调递减，所以(π6，π3)⊆[kπ2+φ4,kπ2+π4+φ4],k∈Z，则{kπ2+φ4≤π6kπ2+φ4+π4≥π3，解得−2kπ+π3≤φ≤−2kπ+2π3,k∈Z，因为0<φ<π，所以可得π3≤φ≤2π3.故选：D. 填空题11、函数f (x )=2tan (kx +π3)的最小正周期T 满足1<T <2，则自然数k 的值为_______． 答案：2或3分析：由正切型函数的最小正周期可构造不等式，结合k 为自然数可求得结果. ∵f (x )的最小正周期T =π|k |，∴1<π|k |<2，又k 为自然数，∴k <π<2k ， 解得：π2<k <π，∴k =2或3.所以答案是：2或3.12、已知△ABC 的内角A,B,C 的对边分别为a,b,c .若cosA (sinC −cosC )=cosB, a =2,c =√2，则角C 大小为_____. 答案：π6解析：根据三角形内角和以及诱导公式将B 转化为A,C ，利用两角和公式，可求出A ，再用正弦定理，即可求解.因为cosA (sinC −cosC )=cosB, 所以cosA (sinC −cosC )=−cos (A +C ),所以cosAsinC =sinAsinC,所以sinC (cosA −sinA )=0, 因为C ∈(0,π),∴sinC ≠0，所以cosA =sinA ， 则tanA =1，所以A =π4，又a sinA =√2sinC ，则sinC =12，因为c <a ，所以0<C <π4，故C =π6. 故答案为:π6.小提示：本题主要考查解三角形、三角恒等变换等基础知识，属于基础题. 13、已知sin α−3cos α=0，则sin 2α+sin2α=__________. 答案：32##1.5分析：首先根据同角三角函数的基本关系求出tanα，再利用二倍角公式及同角三角函数的基本关系将弦化切，最后代入计算可得；解：因为sinα−3cosα=0，所以tanα=sinαcosα=3，所以sin2α+sin2α=sin2α+2sinαcosα=sin2α+2sinαcosαsin2α+cos2α=tan2α+2tanαtan2α+1=32+2×332+1=32所以答案是：3214、若sin(θ+π8)=13，则sin(2θ−π4)＝________.答案：−79分析：由题知2(θ+π8)−π2=(2θ−π4)，进而根据诱导公式与二倍角公式求解即可.解：因为2(θ+π8)−(2θ−π4)=π2，所以sin(2θ−π4)=sin[2(θ+π8)−π2]=−cos[2(θ+π8)]=2sin2(θ+π8)−1=2×(13)2−1=−79．所以答案是：−7915、若cosα=−35,α为第二象限的角，则sin(π−α)=__________．答案：45分析：先根据同角三角函数的关系求出sinα，再结合诱导公式即可求出sin(π−α).∵cosα=−35,α为第二象限的角，∴sinα=√1−cos2α=45，∴sin(π−α)=sinα=45.所以答案是：45.小提示：本题考查同角三角函数的关系以及诱导公式的应用，属于基础题.解答题16、函数f(x)=A sin(ωx+φ)+B的部分图象如图所示，其中A>0，ω>0，|φ|<π2.（Ⅰ）求函数y=f(x)解析式；（Ⅱ）求x∈[0,π2]时，函数y=f(x)的值域.答案：（Ⅰ）f(x)=2sin(2x+π6)+2；（Ⅱ）[1,4].解析：（Ⅰ）由函数的图象的顶点坐标求出A，由周期求出ω，由f(π6)=4求出φ的值，可得函数的解析式；（Ⅱ）由已知可求范围2x+π6∈[π6,7π6]，利用正弦函数的图象和性质可得sin(2x+π6)∈[−12,1]，即可求解.（Ⅰ）根据函数f(x)=Asin(ωx+φ)+B的一部分图象，其中A>0，ω>0，|φ|<π2，可得A=4−2=2，B=2，T4=14⋅2πω=5π12−π6，∴ω=2.又f(π6)=4，得2sin(2×π6+φ)+2=4，∴π3+φ=2kπ+π2，即φ=2kπ+π6，∵|φ|<π2，∴φ=π6，∴f(x)=2sin(2x+π6)+2；（Ⅱ）∵x∈[0,π2]，∴2x+π6∈[π6,7π6]，∴sin(2x+π6)∈[−12,1]，∴y=2sin(2x+π6)+2∈[1,4].小提示：本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式、正弦函数的定义域和值域及正弦函数的单调性，考查了学生的计算能力，培养了学生分析问题与解决问题的能力，属于中档题.17、已知1|sinα|=−1sinα，且lgcosα有意义．(1)试判断角α是第几象限角；(2)若角α的终边上有一点M (35,m)，且OM =1（O 为坐标原点），求实数m 的值及sinα的值．答案：(1)角α是第四象限角 (2)m =−45，sinα=−45分析：（1）根据已知分别确定sinα,cosα的正负，再三角函数值符号得象限角的结论 （2）由余弦函数定义求出m ，再由正弦函数定义求得结论． （1） ∵1|sinα|=−1sinα，∴sinα<0， ∴角α是第三或第四象限角或终边在y 轴的负半轴上的角． 由lgcosα有意义，可知cosα>0，∴角α是第一或第四象限角或终边在x 轴的正半轴上的角． 综上，角α是第四象限角 （2）∵OM =1，∴(35)2+m 2=1，解得m =±45． 又角α是第四象限角，故m <0，∴m =−45．∴sinα=−451=−45．18、已知函数f(x)=2cos 2x +2√3sinxcosx . (1)若x ∈R ，求f （x ）的单调递增区间；(2)若f （x ）在[0，m ]上的最小值为2，求实数m 的取值范围. 答案：(1)[−π3+kπ,π6+kπ]（k ∈Z ） (2)(0,π3]分析：（1）先化简得到f(x)=2sin (2x +π6)+1，利用复合函数单调性“同增异减”列不等式求出f （x ）的递增区间；.（2）利用单调性实数m的取值范围.(1)f(x)=2cos2x+2√3sinxcosx=cos2x+√3sin2x+1=2sin(2x+π6)+1.令−π2+2kπ≤2x+π6≤π2+2kπ，（k∈Z）解得−π3+kπ≤x≤π6+kπ，（k∈Z）∴f（x）的递增区间为[−π3+kπ,π6+kπ]（k∈Z）.(2)x∈[0,m]，得2x+π6∈[π6,π6+2m].∵f（x）在[0,m]上的最小值为2，∴π6+2m≤5π6，解得m∈(0,π3].。