(完整word版)计量经济学(第四版)习题及参考答案详细版
- 格式:doc
- 大小:571.00 KB
- 文档页数:25

第三章练习题及参考解答3.1进入21世纪后,中国的家用汽车增长很快。
家用汽车的拥有量受到经济增长、公共服务、市场价格、交通状况、社会环境、政策因素,都会影响中国汽车拥有量。
为了研究一些主要因素与家用汽车拥有量的数量关系,选择“百户拥有家用汽车量”、“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量,2016年全国各省市区的有关数据如表3.5。
表3.5 2016年各地区的百户拥有家用汽车量等数据资料来源:中国统计年鉴2017.中国统计出版社1)建立百户拥有家用汽车量计量经济模型,估计参数并对模型加以检验,检验结论的依据是什么?。
2)分析模型参数估计结果的经济意义,你如何解读模型估计检验的结果? 3) 你认为模型还可以如何改进?【练习题3.1 参考解答】:1)建立线性回归模型: 1223344t t t t t Y X X X u ββββ=++++ 回归结果如下:由F 统计量为14.69998, P 值为0.000007,可判断模型整体上显著, “人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量联合起来对百户拥有家用汽车量有显著影响。
解释变量参数的t 统计量的绝对值均大于临界值0.025(27) 2.052t =,或P 值均明显小于0.05α=,表明在其他变量不变的情况下,“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”分别对百户拥有家用汽车量都有显著影响。
2)X2的参数估计值为4.8117,表明随着经济的增长,人均地区生产总值每增加1万元,平均说来百户拥有家用汽车量将增加近5辆。
由于城镇公共交通的大力发展,有减少家用汽车的必要性,X3的参数估计值为-0.4449,表明随着城镇化的推进,“城镇人口比重”每增加1%,平均说来百户拥有家用汽车量将减少0.4449辆。
汽车价格和使用费用的提高将抑制家用汽车的使用, X4的参数估计值为-5.7685,表明随着家用汽车使用成本的提高, “居民消费价格指数”每增加1个百分点,平均说来百户拥有家用汽车量将减少5.7685辆。
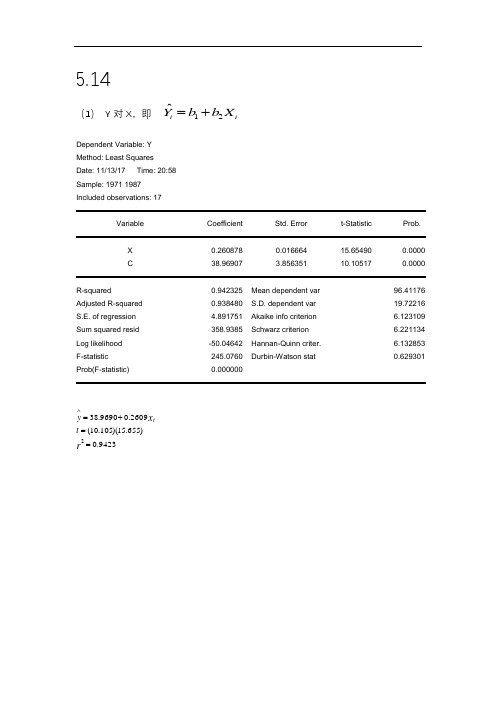
5.14(1) Y 对X ,即12ˆi iY b b X =+Dependent Variable: Y Method: Least Squares Date: 11/13/17 Time: 20:58 Sample: 1971 1987 Included observations: 17VariableCoefficient Std. Error t-Statistic Prob.X 0.260878 0.016664 15.65490 0.0000 C38.969073.85635110.10517 0.0000R-squared0.942325 Mean dependent var 96.41176 Adjusted R-squared 0.938480 S.D. dependent var 19.72216 S.E. of regression 4.891751 Akaike info criterion 6.123109 Sum squared resid 358.9385 Schwarz criterion 6.221134 Log likelihood -50.04642 Hannan-Quinn criter. 6.132853 F-statistic 245.0760 Durbin-Watson stat 0.629301Prob(F-statistic) 0.0000009423.0)655.15)(105.10(2609.09690.382==+=∧r x t y t(2)InY 对InX ,即 12ˆi iInY b b InX =+9642.0)090.20)(954.8(ln 5890.04041.1ln 2==+=∧r x t y tDependent Variable: LNY Method: Least Squares Date: 11/13/17 Time: 21:40 Sample: 1971 1987 Included observations: 17Variable Coefficient Std. Error t-Statistic Prob.C 1.404051 0.156813 8.953649 0.0000 LNX0.5889650.02931720.08981 0.0000R-squared0.964166 Mean dependent var 4.547848 Adjusted R-squared 0.961777 S.D. dependent var 0.213165 S.E. of regression 0.041675 Akaike info criterion -3.407698 Sum squared resid 0.026052 Schwarz criterion -3.309673 Log likelihood 30.96543 Hannan-Quinn criter. -3.397954 F-statistic 403.6007 Durbin-Watson stat 0.734161Prob(F-statistic)0.000000(3)InY 对X ,即 12ˆi iInY b b X =+Dependent Variable: LNY Method: Least Squares Date: 11/13/17 Time: 21:42 Sample: 1971 1987 Included observations: 17Variable Coefficient Std. Error t-Statistic Prob.C 3.931578 0.046430 84.67764 0.0000 X0.0027990.00020113.94972 0.0000R-squared0.928433 Mean dependent var 4.547848 Adjusted R-squared 0.923662 S.D. dependent var 0.213165 S.E. of regression 0.058896 Akaike info criterion -2.715956 Sum squared resid 0.052031 Schwarz criterion -2.617930 Log likelihood 25.08562 Hannan-Quinn criter. -2.706212 F-statistic 194.5946 Durbin-Watson stat 0.529132Prob(F-statistic) 0.0000009284.0)950.13)(678.84(0028.09316.3ln 2==+=∧r X t y t(4)Y 对InX ,即 12ˆi iY b b InX =+Dependent Variable: Y Method: Least Squares Date: 11/13/17 Time: 21:43 Sample: 1971 1987 Included observations: 17Variable Coefficient Std. Error t-Statistic Prob.C -192.9661 16.38000 -11.78059 0.0000 LNX54.212573.06227817.70335 0.0000R-squared0.954325 Mean dependent var 96.41176 Adjusted R-squared 0.951280 S.D. dependent var 19.72216 S.E. of regression 4.353186 Akaike info criterion 5.889824 Sum squared resid 284.2535 Schwarz criterion 5.987849 Log likelihood -48.06350 Hannan-Quinn criter. 5.899568 F-statistic 313.4086 Durbin-Watson stat 0.610822Prob(F-statistic) 0.0000009542.0)703.17)(781.11(ln 2126.549661.1922=-=+-=∧r X t Y t解:1.XY∆∆=1ˆβ斜率说明X 每变动一个单位,Y 的绝对变动量;2. E XX Y Y =∆∆=//ˆ1β斜率便是弹性系数; 3. XY Y ∆∆=/ˆ1β斜率表示X 每变动一个单位,Y 的均值的瞬时增长率; 4,. XX Y/ˆ1∆∆=β斜率表示X 的相对变化对Y 的绝对量的影响。

计量经济学(第四版)习题参考答案第一章 绪论1.1 一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析1.2 我们在计量经济模型中列出了影响因变量的解释变量,但它(它们)仅是影响因变量的主要因素,还有很多对因变量有影响的因素,它们相对而言不那么重要,因而未被包括在模型中。
为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4 估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y 就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2 NS S x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
2.3 原假设 120:0=μH备择假设 120:1≠μH 检验统计量()10/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即此样本不是取自一个均值为120元、标准差为10元的正态总体。

伍德里奇-计量经济学(第4版)答案计量经济学答案第二章2.4 (1)在实验的准备过程中,我们要随机安排小时数,这样小时数(hours )可以独立于其它影响SAT 成绩的因素。
然后,我们收集实验中每个学生SAT 成绩的相关信息,产生一个数据集{}n i hours sat i i ,...2,1:),(=,n 是实验中学生的数量。
从式(2.7)中,我们应尽量获得较多可行的i hours 变量。
(2)因素:与生俱来的能力(天赋)、家庭收入、考试当天的健康状况①如果我们认为天赋高的学生不需要准备SAT 考试,那天赋(ability )与小时数(hours )之间是负相关。
②家庭收入与小时数之间可能是正相关,因为收入水平高的家庭更容易支付起备考课程的费用。
③排除慢性健康问题,考试当天的健康问题与SAT 备考课程上的小时数(hours )大致不相关。
(3)如果备考课程有效,1β应该是正的:其他因素不变情况下,增加备考课程时间会提高SAT 成绩。
(4)0β在这个例子中有一个很有用的解释:因为E (u )=0,0β是那些在备考课程上花费小时数为0的学生的SAT平均成绩。
2.7(1)是的。
如果住房离垃圾焚化炉很近会压低房屋的价格,如果住房离垃圾焚化炉距离远则房屋的价格会高。
(2)如果城市选择将垃圾焚化炉放置在距离昂贵的街区较远的地方,那么log(dist)与房屋价格就是正相关的。
也就是说方程中u包含的因素(例如焚化炉的地理位置等)和距离(dist)相关,则E(u︱log(dist))≠0。
这就违背SLR4(零条件均值假设),而且最小二乘法估计可能有偏。
(3)房屋面积,浴室的数量,地段大小,屋龄,社区的质量(包括学校的质量)等因素,正如第(2)问所提到的,这些因素都与距离焚化炉的远近(dist,log(dist))相关2.11(1)当cigs(孕妇每天抽烟根数)=0时,预计婴儿出生体重=110.77盎司;当cigs(孕妇每天抽烟根数)=20时,预计婴儿出生体重(bwght)=109.49盎司。

第四章练习题及参考解答4.1 假设在模型i i i i u X X Y +++=33221βββ中,32X X 与之间的相关系数为零,有人建议你分别进行如下回归:1221i i i Y X u αα=++ 1332i i i Y X u γγ=++(1) 是否存在3322ˆˆˆˆβγβα==且?为什么? (2) 1ˆβ会等于1ˆα或1ˆγ或者两者的某个线性组合吗? (3) 是否有()()22ˆˆVar Var βα=且()()33ˆˆVar Var βγ=?【练习题4.1参考解答】(1) 存在2233ˆˆˆˆαβγβ==且 。
因为 ()()()()()()()2233232ˆi iii ii iy x x y x x x-∑∑∑∑资料来源:《中国统计年鉴2017》考虑建立模型: i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
(2)你认为数据中有多重共线性吗?(3)进行以下回归:121ln ln t t i Y A A GDP v =++ 122ln ln t t i Y B B CPI v =++ 123ln ln t t i GDP C C CPI v =++ 根据这些回归你能对多重共线性的性质有什么认识?(4)假设经检验数据有多重共线性,但模型中32ˆˆββ和在5%水平上显著,并且F 检验也显著,你对此模型的应用有何建议?【练习题4.2参考解答】建立模型: i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
(2)你认为数据中有多重共线性吗?其中居民消费价格指数CPI 对商品进口额影响为负,与预期不符合,可能存在多重共线性。
(3)分别进行以下回归:1)作回归121ln ln t t i Y A A GDP v =++说明GDP 的确对商品进口额有正的影响,是重要变量。

计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间NSS x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间NS S x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
第三章练习题及参考解答3.1进入21世纪后,中国的家用汽车增长很快。
家用汽车的拥有量受到经济增长、公共服务、市场价格、交通状况、社会环境、政策因素,都会影响中国汽车拥有量。
为了研究一些主要因素与家用汽车拥有量的数量关系,选择“百户拥有家用汽车量”、“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量,2016年全国各省市区的有关数据如表3.5。
表3.5 2016年各地区的百户拥有家用汽车量等数据资料来源:中国统计年鉴2017.中国统计出版社1)建立百户拥有家用汽车量计量经济模型,估计参数并对模型加以检验,检验结论的依据是什么?。
2)分析模型参数估计结果的经济意义,你如何解读模型估计检验的结果? 3) 你认为模型还可以如何改进?【练习题3.1 参考解答】:1)建立线性回归模型: 1223344t t t t t Y X X X u ββββ=++++ 回归结果如下:由F 统计量为14.69998, P 值为0.000007,可判断模型整体上显著, “人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量联合起来对百户拥有家用汽车量有显著影响。
解释变量参数的t 统计量的绝对值均大于临界值0.025(27) 2.052t =,或P 值均明显小于0.05α=,表明在其他变量不变的情况下,“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”分别对百户拥有家用汽车量都有显著影响。
2)X2的参数估计值为4.8117,表明随着经济的增长,人均地区生产总值每增加1万元,平均说来百户拥有家用汽车量将增加近5辆。
由于城镇公共交通的大力发展,有减少家用汽车的必要性,X3的参数估计值为-0.4449,表明随着城镇化的推进,“城镇人口比重”每增加1%,平均说来百户拥有家用汽车量将减少0.4449辆。
汽车价格和使用费用的提高将抑制家用汽车的使用, X4的参数估计值为-5.7685,表明随着家用汽车使用成本的提高, “居民消费价格指数”每增加1个百分点,平均说来百户拥有家用汽车量将减少5.7685辆。
第四章练习题及参考解答4.1 假设在模型i i i i u X X Y +++=33221βββ中,32X X 与之间的相关系数为零,有人建议你分别进行如下回归:1221i i i Y X u αα=++ 1332i i i Y X u γγ=++(1) 是否存在3322ˆˆˆˆβγβα==且?为什么? (2) 1ˆβ会等于1ˆα或1ˆγ或者两者的某个线性组合吗? (3) 是否有()()22ˆˆVar Var βα=且()()33ˆˆVar Var βγ=?【练习题4.1参考解答】(1) 存在2233ˆˆˆˆαβγβ==且 。
因为 ()()()()()()()22332322222323ˆi iii ii iiii iy x x y x x x x x x x β-=-∑∑∑∑∑∑∑当23X X 与 之间的相关系数为零时,离差形式的230i ix x =∑有 ()()()()223222222223ˆˆi i ii i iiiy x x y x xx x βα===∑∑∑∑∑∑ 同理有: 33ˆˆγβ= (2)会的。
(3) 存在 ()()()()2233ˆˆˆˆvar var var var βαβγ==且 因为 ()()2222223ˆvar 1ix r σβ=-∑当 230r = 时, ()()()22222222223ˆˆvar var 1iix x r σσβα===-∑∑ 同理,有 ()()33ˆˆvar var βγ=4.2 表4.4给出了1995—2016年中国商品进口额Y 、国生产总值GDP 、居民消费价格指数CPI 的数据。
表4.4 中国商品进口额、国生产总值、居民消费价格指数资料来源:《中国统计年鉴2017》考虑建立模型: i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
(2)你认为数据中有多重共线性吗?(3)进行以下回归:121ln ln t t i Y A A GDP v =++ 122ln ln t t i Y B B CPI v =++ 123ln ln t t i GDP C C CPI v =++ 根据这些回归你能对多重共线性的性质有什么认识?(4)假设经检验数据有多重共线性,但模型中32ˆˆββ和在5%水平上显著,并且F 检验也显著,你对此模型的应用有何建议?【练习题4.2参考解答】建立模型: i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
第七章练习题及参考解答7.1 表7.4中给出了1981-2015年中国城镇居民人均年消费支出(PCE)和城镇居民人均可支配收入(PDI)数据。
表7.4 1981-2015年中国城镇居民消费支出(PCE)和可支配收入(PDI)数据 (单位:元)估计下列模型:tt t t tt t PCE B PDI B B PCE PDI A A PCE υμ+++=++=-132121(1) 解释这两个回归模型的结果。
(2) 短期和长期边际消费倾向(MPC )是多少?分析该地区消费同收入的关系。
(3) 建立适当的分布滞后模型,用库伊克变换转换为库伊克模型后进行估计,并对估计结果进行分析判断。
【练习题7.1参考解答】(1) 解释这两个回归模型的结果。
Dependent Variable: PCE Method: Least Squares Date: 03/10/18 Time: 09:12 Sample: 1981 2005Variable Coefficient Std. Error t-Statistic Prob.C 149.0975 24.56734 6.068933 0.0000R-squared 0.998965 Mean dependent var 2983.768Adjusted R-squared 0.998920 S.D. dependent var 2364.412S.E. of regression 77.70773 Akaike info criterion 11.62040Sum squared resid 138885.3 Schwarz criterion 11.71791Log likelihood -143.2551 F-statistic 22196.24Durbin-Watson stat 0.531721 Prob(F-statistic) 0.000000收入跟消费间有显著关系。
计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间NSS x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
2.3 25个雇员的随机样本的平均周薪为130元,试问此样本是否取自一个均值为120元、标准差为10元的正态总体? 原假设 120:0=μH备择假设 120:1≠μH 检验统计量()10/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即 此样本不是取自一个均值为120元、标准差为10元的正态总体。
2.4 某月对零售商店的调查结果表明,市郊食品店的月平均销售额为2500元,在下一个月份中,取出16个这种食品店的一个样本,其月平均销售额为2600元,销售额的标准差为480元。
试问能否得出结论,从上次调查以来,平均月销售额已经发生了变化? 原假设 : 2500:0=μH备择假设 : 2500:1≠μH()00)100/120.83ˆX X t μσ-==== 查表得 131.2)116(025.0=-t 因为t = 0.83 < 131.2=c t , 故接受原假 设,即从上次调查以来,平均月销售额没有发生变化。
第三章 双变量线性回归模型3.1 判断题(说明对错;如果错误,则予以更正) (1)OLS 法是使残差平方和最小化的估计方法。
对(2)计算OLS 估计值无需古典线性回归模型的基本假定。
对(3)若线性回归模型满足假设条件(1)~(4),但扰动项不服从正态分布,则尽管OLS 估计量不再是BLUE ,但仍为无偏估计量。
错只要线性回归模型满足假设条件(1)~(4),OLS 估计量就是BLUE 。
(4)最小二乘斜率系数的假设检验所依据的是t 分布,要求βˆ的抽样分布是正态分布。
对(5)R 2=TSS/ESS 。
错R 2 =ESS/TSS 。
(6)若回归模型中无截距项,则0≠∑t e 。
对(7)若原假设未被拒绝,则它为真。
错。
我们可以说的是,手头的数据不允许我们拒绝原假设。
(8)在双变量回归中,2σ的值越大,斜率系数的方差越大。
错。
因为∑=22)ˆ(tx V ar σβ,只有当∑2t x 保持恒定时,上述说法才正确。
3.2设YX βˆ和XYβˆ分别表示Y 对X 和X 对Y 的OLS 回归中的斜率,证明 YX βˆXYβˆ=2r r 为X 和Y 的相关系数。
证明:22222222ˆˆ()ˆˆi ii ii i YXXYiiii i YX XYi i x y y x x yxyyx y x yr x y ββββ===⎛⎫⋅===∑∑∑∑∑∑∑∑∑3.3证明:(1)Y 的真实值与OLS 拟合值有共同的均值,即Y nY nY ==∑∑ˆ;(2)OLS 残差与拟合值不相关,即 0ˆ=∑tt eY 。
(1),得两边除以,=n ˆ0ˆ)ˆ(ˆ∑∑∑∑∑∑∑∑=∴+=⇒+=⇒+=tt t tt t t tt t t t YY e e Y Y e YY e Y YY nY nY ==∑∑ˆ,即Y 的真实值和拟合值有共同的均值。
(2)的拟合值与残差无关。
,=,即因此,(教材中已证明),由于Y 0ˆˆ),ˆ(0ˆ0,0e ˆˆ)ˆˆ(ˆ22t∑∑∑∑∑∑∑∑∑∑====+=+=tttt tttt tt tt ttttt eY e Y e Y Cov e Ye X eX e e X e Y βαβα 3.4证明本章中(3.18)和(3.19)两式:(1)∑∑=222)ˆ(tt x n X Var σα(2)∑-=22)ˆ,ˆ(txX Cov σβα(1)222222222221112222222ˆˆ,ˆˆ()ˆˆˆ2u()()ˆ()2()()()()ˆ2()()ˆ2()iit tti n n n t ii j i ii j i ji j i jtY X Y X u u X u X X u u x uX X nn xu u u x u x u X X nn x uu u x ux x u u X nn x αβαβααββααββββββββββ≠≠=+=++-=---=--+-=-⋅⋅+-++=-⋅+-+++=-⋅+-∑∑∑∑∑∑∑∑∑∑∑()2X2222222222222222()ˆˆ2E()1(()2())()2i i j i i i j i j i j i j t i i j i j i i j i j i i i j i j i jt u u u x u x x u u E E XE X n n x u u u E E u E u u n n n nx u x x u u XE n x ααββσσ≠≠≠≠≠⎛⎫⎡⎤+++ ⎪⎢⎥-=-⎪⎢⎥ ⎪⎢⎥⎝⎭⎣⎦⎛⎫+ ⎪=+==⎪⎪⎝⎭++∑∑∑∑∑∑∑∑∑∑∑∑两边取期望值,有:()-+等式右端三项分别推导如下:22222222222222222222212(()()())200ˆE()()ˆ[]0ii i i j i j ii jt t t t tt tt x Xx E u x x E u u Xx n x n x X X x x nX X X E n x n x n x σσββσσσσαα≠⎛⎫ ⎪ ⎪⎪⎝⎭=++==-=+-=-+==∑∑∑∑∑∑∑∑∑∑∑∑∑(=)因此()∑∑=222)ˆ(tt x n X Var σα即(2)2222ˆˆ,ˆˆ()ˆˆˆˆˆˆ(,)[()][(())()]ˆˆ[(()][()]ˆ0()01ˆ()t Y X Y X u u X Cov E E u X E u XE XE XVar X x αβαβααββαβααβββββββββββββσ=+=++-=--=--=---=---=--=-=-∑()(第一项为的证明见本题())3.5考虑下列双变量模型: 模型1:i i i u X Y ++=21ββ模型2:i i i u X X Y +-+=)(21αα(1)β1和α1的OLS 估计量相同吗?它们的方差相等吗? (2)β2和α2的OLS 估计量相同吗?它们的方差相等吗?(1)X Y 21ˆˆββ-=,注意到 nx n x x x n x Var x n X Var Y x Y x x X X x ii i i ii i i i 22222221222121)()ˆ()ˆ(ˆˆ,0,0,σσσασβαα==-==-==-=∑∑∑∑∑∑∑==则我们有从而由上述结果,可以看到,无论是两个截距的估计量还是它们的方差都不相同。
(2)∑∑∑∑∑∑∑==---==222222222)ˆ()ˆ()())((ˆ,ˆiiiiiiiiii xVar Var xyx x x Y Y x x xy x σαβαβ=容易验证,这表明,两个斜率的估计量和方差都相同。
3.6有人使用1980-1994年度数据,研究汇率和相对价格的关系,得到如下结果:)333.1()22.1(:528.0318.4682.6ˆ2Se R X Yt t =-=其中,Y =马克对美元的汇率X =美、德两国消费者价格指数(CPI )之比,代表两国的相对价格 (1)请解释回归系数的含义; (2)X t 的系数为负值有经济意义吗?(3)如果我们重新定义X 为德国CPI 与美国CPI 之比,X 的符号会变化吗?为什么?(1)斜率的值 -4.318表明,在1980-1994期间,相对价格每上升一个单位,(GM/$)汇率下降约4.32个单位。
也就是说,美元贬值。
截距项6.682的含义是,如果相对价格为0,1美元可兑换6.682马克。
当然,这一解释没有经济意义。
(2)斜率系数为负符合经济理论和常识,因为如果美国价格上升快于德国,则美国消费者将倾向于买德国货,这就增大了对马克的需求,导致马克的升值。
(3)在这种情况下,斜率系数被预期为正数,因为,德国CPI 相对于美国CPI 越高,德国相对的通货膨胀就越高,这将导致美元对马克升值。
3.7随机调查200位男性的身高和体重,并用体重对身高进行回归,结果如下:)31.0()15.2(:81.031.126.76ˆ2Se R Height eight W =+-=其中Weight 的单位是磅(lb ),Height 的单位是厘米(cm )。
(1)当身高分别为177.67cm 、164.98cm 、187.82cm 时,对应的体重的拟合值为多少?(2)假设在一年中某人身高增高了3.81cm ,此人体重增加了多少? (1)78.16982.187*31.126.76ˆ86.13998.164*31.126.76ˆ49.15667.177*31.126.76ˆ=+-==+-==+-=eight Weight Weight W(2)99.481.3*31.1*31.1ˆ==∆=∆height eight W3.8设有10名工人的数据如下: X 10 710 5886 7910Y11 10 12 6 10 7 910 11 10其中 X=劳动工时, Y=产量(1)试估计Y=α+βX + u (要求列出计算表格); (2)提供回归结果(按标准格式)并适当说明; (3)检验原假设β=1.0。