简单几何体的结构特征(好的)讲解
- 格式:pdf
- 大小:6.00 MB
- 文档页数:35



了解几何体的特征和分类在数学中,几何体是指具有形状和结构的三维物体。
几何体是几何学的重要研究对象之一,通过了解几何体的特征和分类,我们可以深入了解它们的属性和性质。
本文将介绍几何体的特征以及常见的分类。
一、几何体的特征几何体具有以下几个特征:1. 三维性:几何体是三维物体,即具有长度、宽度和高度三个维度。
相比于平面图形的二维性,几何体在空间中具有更为丰富的形状和结构。
2. 表面和体积:几何体具有表面和体积。
表面是几何体外部的边界,而体积则是几何体所占据的空间大小。
3. 定点和边:几何体由一系列顶点(点)和边(线段)构成。
顶点是几何体上的特定位置,而边则是相邻顶点之间的连接线。
4. 无空隙:几何体内部没有空隙或空洞,它们是紧凑而连续的。
二、几何体的分类根据几何体形状和性质的不同,可以将几何体分为以下几类:1. 立体(三维)几何体:立体几何体是在三维空间中存在的几何体,如球体、立方体、棱柱、棱锥等。
它们具有体积和表面积,可视作围绕其内部点旋转而得。
2. 平面(二维)几何体:平面几何体是在二维空间中存在的几何体,如矩形、三角形、圆形等。
它们只具有面积,没有体积,无法在空间中实体存在。
3. 多面体:多面体是指由多个多边形组成的几何体。
常见的多面体有四面体、六面体、八面体等。
多面体的边和顶点数目是通过多边形不同的组合方式得到的。
4. 曲面体:曲面体是指具有呈曲面形状的几何体,如圆柱体、圆锥体、球体等。
它们具有弯曲的表面,没有边缘。
5. 半曲面体:半曲面体是指由一个平面和一个曲面组成的几何体,如半球体、半圆柱体等。
它们只有一部分是曲面,其他部分是平面。
三、几何体的应用了解几何体的特征和分类对于很多领域都有广泛的应用,包括建筑、工程、计算机图形学等。
在建筑和工程领域,几何体的特征和分类用于设计和计算建筑物的结构,例如在建造建筑物时,需要考虑立体几何体的体积、面积和形状,以确保建筑物的稳定性和安全性。
此外,对曲面体和半曲面体的研究也有助于设计出更加流畅和美观的建筑结构。

第38讲 空间几何体的结构特征及表面积与体积(讲)思维导图知识梳理1.简单几何体(1)多面体的结构特征名称棱柱棱锥棱台图形底面 互相平行且相等 多边形互相平行且相似 侧棱 互相平行且相等相交于一点,但不一定相等延长线交于一点侧面形状 平行四边形三角形梯形①特殊的四棱柱 四棱柱――→底面为平行四边形 平行六面体――→侧棱垂直于底面直平行六面体――→底面为矩形长方体――→底面边长相等正四棱柱――→侧棱与底面边长相等正方体 ②多面体的关系:棱柱――――――→一个底面退化为一个点棱锥―――――――→用平行于底面的平面截得棱台 (2)旋转体的结构特征名称圆柱圆锥圆台球▲图形母线互相平行且相等,垂直于底面长度相等且相交于一点 延长线交于一点轴截面 全等的矩形全等的等腰三角形全等的等腰梯形圆侧面展开图 矩形扇形扇环2.直观图(1)画法:常用斜二测画法. (2)规则:①原图形中x 轴、y 轴、z 轴两两垂直,直观图中,x ′轴、y ′轴的夹角为45°(或135°),z ′轴与x ′轴和y ′轴所在平面垂直.②原图形中平行于坐标轴的线段,直观图中仍平行于坐标轴.平行于x 轴和z 轴的线段在直观图中保持原长度不变,平行于y 轴的线段长度在直观图中变为原来的一半.3.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧=2πrlS 圆锥侧=πrlS 圆台侧=π(r +r ′)l4.空间几何体的表面积与体积公式名称几何体 表面积体积柱体(棱柱和圆柱) S 表面积=S 侧+2S 底 V =Sh 锥体(棱锥和圆锥)S 表面积=S 侧+S 底V =13Sh台体(棱台和圆台) S 表面积=S 侧+S 上+S 下 V =13(S 上+S 下+S 上S 下)h球S =4πR 2V =43πR 3题型归纳题型1 空间几何体的结构特征【例1-1】给出下列命题:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥;③棱台的上、下底面可以不相似,但侧棱长一定相等.其中正确命题的个数是()A.0B.1C.2 D.3【解析】①不一定,只有当这两点的连线平行于轴时才是母线;②不一定,当以斜边所在直线为旋转轴时,其余两边旋转形成的面所围成的几何体不是圆锥,如图所示,它是由两个同底圆锥组成的几何体;③错误,棱台的上、下底面相似且是对应边平行的多边形,各侧棱延长线交于一点,但是侧棱长不一定相等.【答案】A【跟踪训练1-1】下列命题正确的是()A.两个面平行,其余各面都是梯形的多面体是棱台B.两个面平行且相似,其余各面都是梯形的多面体是棱台C.直角梯形以一条直角腰所在的直线为旋转轴,其余三边旋转形成的面所围成的旋转体是圆台D.用平面截圆柱得到的截面只能是圆和矩形【解析】如图所示,可排除A、B选项.对于D选项只有截面与圆柱的母线平行或垂直,截得的截面才为矩形或圆,否则截面为椭圆或椭圆的一部分,故选C.【答案】C【跟踪训练1-2】(多选)给出下列命题,其中真命题是()A.棱柱的侧棱都相等,侧面都是全等的平行四边形B.若三棱锥的三条侧棱两两垂直,则其三个侧面也两两垂直C.在四棱柱中,若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱D.存在每个面都是直角三角形的四面体【解析】A不正确,根据棱柱的定义,棱柱的各个侧面都是平行四边形,但不一定全等;B正确,若三棱锥的三条侧棱两两垂直,则三个侧面构成的三个二面角都是直二面角;C正确,因为两个过相对侧棱的截面的交线平行于侧棱,又垂直于底面;D正确,如图,正方体ABCDA1B1C1D1中的三棱锥C1ABC,四个面都是直角三角形.【答案】BCD【名师指导】辨别空间几何体的2种方法题型2 空间几何体的表面积【例2-1】(1)(2019·四川泸州一诊)在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2.将梯形ABCD 绕AD所在的直线旋转一周而形成的曲面所围成的几何体的表面积为()A.(5+2)πB.(4+2)πC .(5+22)π D.(3+2)π(2)(2020·河南周口模拟)如图,在三棱柱ABC A 1B 1C 1中,AA 1⊥底面ABC ,AB ⊥BC ,AA 1=AC =2,直线A 1C 与侧面AA 1B 1B 所成的角为30°,则该三棱柱的侧面积为( )A .4+42B .4+43C .12D.8+42[解析] (1)∵在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2,∴将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体是一个底面半径为AB =1,高为BC =2的圆柱挖去一个底面半径为AB =1,高为BC -AD =2-1=1的圆锥,∴该几何体的表面积S =π×12+2π×1×2+π×1×12+12=(5+2)π.故选A.(2)连接A 1B .因为AA 1⊥底面ABC ,则AA 1⊥BC ,又AB ⊥BC ,AA 1∩AB =A ,所以BC ⊥平面AA 1B 1B ,所以直线A 1C 与侧面AA 1B 1B 所成的角为∠CA 1B =30°.又AA 1=AC =2,所以A 1C =22,BC = 2.又AB ⊥BC ,则AB =2,则该三棱柱的侧面积为22×2+2×2=4+4 2.[答案] (1)A (2)A【跟踪训练2-1】在如图所示的斜截圆柱中,已知圆柱底面的直径为40 cm ,母线长最短50 cm ,最长80 cm ,则斜截圆柱的侧面面积S =________cm 2.【解析】将题图所示的相同的两个几何体对接为圆柱,则圆柱的侧面展开图为矩形.由题意得所求侧面展开图的面积S =12×(50+80)×(π×40)=2 600π(cm 2).【答案】2 600π 【名师指导】求解几何体表面积的类型及求法求多面体的表面积 只需将它们沿着棱“剪开”展成平面图形,利用求平面图形面积的方法求多面体的表面积求旋转体的表面积 可以从旋转体的形成过程及其几何特征入手,将其展开后求表面积,但要搞清它们的底面半径、母线长与对应侧面展开图中的边长关系求不规则几何体的表面积时 通常将所给几何体分割成基本的柱体、锥体、台体,先求出这些基本的柱体、锥体、台体的表面积,再通过求和或作差,求出所给几何体的表面积题型3 空间几何体的体积【例3-1】(2019·江苏南通联考)已知正三棱柱ABC A 1B 1C 1的各棱长均为2,点D 在棱AA 1上,则三棱锥D BB1C 1的体积为________.[解析] 如图,取BC 中点O ,连接AO .∵正三棱柱ABC A 1B 1C 1的各棱长均为2,∴AC =2,OC =1,则AO = 3.∵AA 1∥平面BCC 1B 1,∴点D 到平面BCC 1B 1的距离为 3. 又S △BB 1C 1=12×2×2=2,∴V D BB 1C 1=13×2×3=233.[答案]233【例3-2】(1)(2019·全国卷Ⅲ)学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体ABCD A 1B 1C 1D 1挖去四棱锥O EFGH 后所得的几何体.其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,AB =BC =6 cm ,AA 1=4 cm.3D 打印所用原料密度为0.9 g/cm 3,不考虑打印损耗,制作该模型所需原料的质量为________g.(2)如图,在多面体ABCDEF 中,已知四边形ABCD 是边长为1的正方形,且△ADE ,△BCF 均为正三角形,EF ∥AB ,EF =2,则该多面体的体积为________.[解析] (1)由题知挖去的四棱锥的底面是一个菱形,对角线长分别为6 cm 和4 cm , 故V 挖去的四棱锥=13×12×4×6×3=12(cm 3).又V 长方体=6×6×4=144(cm 3),所以模型的体积为V 长方体-V 挖去的四棱锥=144-12=132(cm 3), 所以制作该模型所需原料的质量为132×0.9=118.8(g).(2)如图,分别过点A ,B 作EF 的垂线,垂足分别为G ,H ,连接DG ,CH ,BF ,易求得EG =HF =12,AG =GD =BH =HC =32,则△BHC 中BC 边的高h =22.∴S △AGD =S △BHC =12×22×1=24,∴V 多面体=V E ADG+V F BHC +V AGD BHC =2V E ADG +V AGD BHC =13×24×12×2+24×1=23.[答案] (1)118.8 (2)23【例3-3】如图所示,已知三棱柱ABC A 1B 1C 1的所有棱长均为1,且AA 1⊥底面ABC ,则三棱锥B 1ABC 1的体积为( )A.312B.34C.612D.64[解析] 易知三棱锥B 1ABC 1的体积等于三棱锥A B 1BC 1的体积,又三棱锥A B 1BC 1的高为32,底面积为12,故其体积为13×12×32=312. [答案] A【跟踪训练3-1】如图,正四棱锥P ABCD 的底面边长为2 3 cm ,侧面积为8 3 cm 2,则它的体积为________cm 3.【解析】记正四棱锥P ABCD 的底面中心为点O ,棱AB 的中点为H ,连接PO ,HO ,PH ,则PO ⊥平面ABCD ,因为正四棱锥的侧面积为8 3 cm 2,所以83=4×12×23×PH ,解得PH =2,在Rt △PHO 中,HO=3,所以PO =1,所以V P ABCD =13·S 正方形ABCD ·PO =4 cm 3.【答案】4【跟踪训练3-2】如图,已知体积为V 的三棱柱ABC A 1B 1C 1,P 是棱B 1B 上除B 1,B 以外的任意一点,则四棱锥P AA 1C 1C 的体积为________.【解析】如图,把三棱柱ABC A 1B 1C 1补成平行六面体A 1D 1B 1C 1ADBC .设P 到平面AA 1C 1C 的距离为h ,则V P AA 1C 1C =13S AA 1C 1C ·h =13V AA 1C 1C DD 1B 1B =13·2V ABC A 1B 1C 1=2V3.【答案】2V3【名师指导】求空间几何体的体积的常用方法公式法 对于规则几何体的体积问题,可以直接利用公式进行求解割补法把不规则的图形分割成规则的图形,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算其体积 等体积法一个几何体无论怎样转化,其体积总是不变的.如果一个几何体的底面面积和高较难求解时,我们可以采用等体积法进行求解.等体积法也称等积转化或等积变形,它是通过选择合适的底面来求几何体体积的一种方法,多用来解决有关锥体的体积,特别是三棱锥的体积题型4 与球有关的切、接问题【例4-1】(2019·全国卷Ⅲ)已知三棱锥P ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°,则球O 的体积为( )A .86πB .46π C .26πD.6π[解析] 法一:∵E ,F 分别是P A ,AB 的中点,∴EF ∥PB . ∵∠CEF =90°,∴EF ⊥EC ,∴PB ⊥EC ,又∵三棱锥P ABC 为正三棱锥,∴PB ⊥AC ,从而PB ⊥平面P AC ,∴三条侧棱P A ,PB ,PC 两两垂直. ∵△ABC 是边长为2的正三角形,∴P A =PB =PC =2, 则球O 是棱长为2的正方体的外接球,设球O 的半径为R , 则2R =3×2,R =62,∴球O 的体积V =43πR 3=6π.故选D. 法二:令P A =PB =PC =2x (x >0),则EF =x ,连接FC ,由题意可得FC = 3.在△P AC 中,cos ∠APC =4x 2+4x 2-42×4x 2=2x 2-12x 2.在△PEC中,EC 2=PC 2+PE 2-2PC ·PE cos ∠EPC =4x 2+x 2-2×2x ·x ·2x 2-12x 2=x 2+2,在△FEC 中,∵∠CEF =90°,∴FC 2=EF 2+EC 2,即x 2+2+x 2=3,∴x =22,∴P A =PB =PC =2x = 2. ∵AB =BC =CA =2,∴三棱锥P ABC 的三个侧面为等腰直角三角形,∴P A ,PB ,PC 两两垂直,故球O 是棱长为2的正方体的外接球,设球O 的半径为R ,则2R =3×2,R =62,∴球O 的体积V =43πR 3=6π.故选D. [答案] D【例4-2】(1)如图,在圆柱O 1O 2内有一个球O ,该球与圆柱的上、下底面及母线均相切.记圆柱O 1O 2的体积为V 1,球O 的体积为V 2,则V 1V 2的值是________.(2)已知正三棱锥的高为1,底面边长为23,内有一个球与四个面都相切,则棱锥的内切球的半径为________.[解析] (1)设圆柱内切球的半径为R ,则由题设可得圆柱O 1O 2的底面圆的半径为R ,高为2R ,故V 1V 2=πR 2·2R 43πR 3=32. (2)如图,过点P 作PD ⊥平面ABC 于点D ,连接AD 并延长交BC 于点E ,连接PE ,∵△ABC 是正三角形,∴AE 是BC 边上的高和中线,D 为△ABC 的中心.∵AB =23,∴S △ABC =33,DE =1,PE = 2.∴S 表=3×12×23×2+33=36+3 3. ∵PD =1,∴三棱锥的体积V =13×33×1= 3. 设球的半径为r ,以球心O 为顶点,三棱锥的四个面为底面把正三棱锥分割为四个小棱锥,则r =3336+33=2-1. [答案] (1)32(2)2-1 【跟踪训练4-1】(2019·四川成都一诊)如图,在矩形ABCD 中,EF ∥AD ,GH ∥BC ,BC =2,AF =FG =BG =1.现分别沿EF ,GH 将矩形折叠使得AD 与BC 重合,则折叠后的几何体的外接球的表面积为( )A .24πB .6π C.163π D.83π 【解析】 由题意可知,折叠后的几何体是底面为等边三角形的三棱柱,底面等边三角形外接圆的半径为23×12-⎝⎛⎭⎫122=33.因为三棱柱的高为BC =2,所以其外接球的球心与底面外接圆圆心的距离为1,则三棱柱外接球的半径为R =⎝⎛⎭⎫332+12=233,所以三棱柱外接球的表面积S =4πR 2=16π3.故选C. 【答案】C 【跟踪训练4-2】(2019·广东中山一中七校联合体联考)在四棱锥P ABCD 中,底面ABCD 是边长为2a 的正方形,PD ⊥底面ABCD ,且PD =2a .若在这个四棱锥内放一球,则此球的最大半径为________.【解析】由题意知,当球与四棱锥各面均相切,即内切于四棱锥时球的半径最大.作出其侧视图,如图所示.易知球的半径r =(2-2)a .【答案】(2-2)a【名师指导】解决与球有关的切、接问题,其通法是作截面,将空间几何问题转化为平面几何问题求解,其解题的思维流程是:。
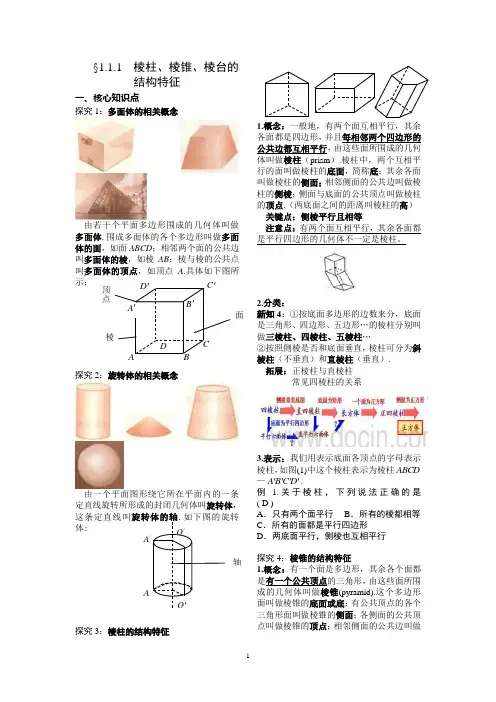
§1.1.1 棱柱、棱锥、棱台的结构特征一、核心知识点探究1:多面体的相关概念由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面,如面ABCD;相邻两个面的公共边叫多面体的棱,如棱AB;棱与棱的公共点叫示:探究2:旋转体的相关概念由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体叫旋转体,这条定直线叫体:探究3:棱柱的结构特征1.概念:一般地,有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱(prism).棱柱中,两个互相平行的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧面与底面的公共顶点叫做棱柱的顶点.(两底面之间的距离叫棱柱的高)关键点:侧棱平行且相等注意点:有两个面互相平行,其余各面都是平行四边形的几何体不一定是棱柱。
2.分类:新知4:①按底面多边形的边数来分,底面是三角形、四边形、五边形…的棱柱分别叫做三棱柱、四棱柱、五棱柱…②按照侧棱是否和底面垂直,棱柱可分为斜棱柱(不垂直)和直棱柱(垂直).拓展:正棱柱与直棱柱常见四棱柱的关系3.表示:我们用表示底面各顶点的字母表示棱柱,如图(1)中这个棱柱表示为棱柱ABCD—A B C D''''.例 1.关于棱柱,下列说法正确的是( D )A.只有两个面平行B.所有的棱都相等C.所有的面都是平行四边形D.两底面平行,侧棱也互相平行探究4:棱锥的结构特征1.概念:有一个面是多边形,其余各个面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥(pyramid).这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱.顶点到底面的距离叫做棱锥的高;关键点:侧棱交于一点2.分类:棱锥也可以按照底面的边数分为三棱锥(四面体)、四棱锥…等等。





高中数学必修二空间几何体的结构特征空间几何体是高中数学学习阶段的重点知识,下面是店铺给大家带来的高中数学必修二空间几何体的结构特征,希望对你有帮助。
高中数学空间几何体的结构特征1.多面体的结构特征(1)棱柱有两个面相互平行,其余各面都是平行四边形,每相邻两个四边形的公共边平行。
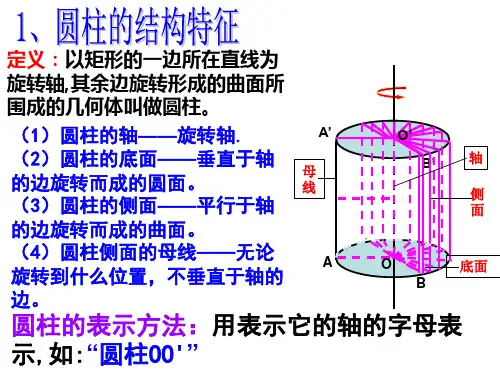
正棱柱:侧棱垂直于底面的棱柱叫做直棱柱,底面是正多边形的直棱柱叫做正棱柱.反之,正棱柱的底面是正多边形,侧棱垂直于底面,侧面是矩形.(2)棱锥的底面是任意多边形,侧面是有一个公共顶点的三角形.正棱锥:底面是正多边形,顶点在底面的射影是底面正多边形的中心的棱锥叫做正棱锥.特别地,各棱均相等的正三棱锥叫正四面体.反过来,正棱锥的底面是正多边形,且顶点在底面的射影是底面正多边形的中心.(3)棱台可由平行于底面的平面截棱锥得到,其上下底面是相似多边形.2.旋转体的结构特征(1)圆柱可以由矩形绕一边所在直线旋转一周得到.(2)圆锥可以由直角三角形绕一条直角边所在直线旋转一周得到.(3)圆台可以由直角梯形绕直角腰所在直线旋转一周或等腰梯形绕上下底面中心所在直线旋转半周得到,也可由平行于底面的平面截圆锥得到.(4)球可以由半圆面绕直径旋转一周或圆面绕直径旋转半周得到.3.空间几何体的三视图空间几何体的三视图是用平行投影得到,这种投影下,与投影面平行的平面图形留下的影子,与平面图形的形状和大小是全等和相等的,三视图包括正视图、侧视图、俯视图.三视图的长度特征:“长对正,宽相等,高平齐”,即正视图和侧视图一样高,正视图和俯视图一样长,侧视图和俯视图一样宽.若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,要注意实、虚线的画法.4.空间几何体的直观图空间几何体的直观图常用斜二测画法来画,基本步骤是:(1)画几何体的底面在已知图形中取互相垂直的x轴、y轴,两轴相交于点O,画直观图时,把它们画成对应的x′轴、y′轴,两轴相交于点O′,且使∠x′O′y′=45°或135°,已知图形中平行于x轴、y轴的线段,在直观图中平行于x′轴、y′轴.已知图形中平行于x轴的线段,在直观图中长度不变,平行于y轴的线段,长度变为原来的一半.(2)画几何体的高在已知图形中过O点作z轴垂直于xOy平面,在直观图中对应的z′轴,也垂直于x′O′y′平面,已知图形中平行于z轴的线段,在直观图中仍平行于z′轴且长度不变.高空间几何体的结构考点要求1.几何体的展开图、几何体的三视图仍是高考的热点.2.三视图和其他的知识点结合在一起命题是新教材中考查学生三视图及几何量计算的趋势.3.重点掌握以三视图为命题背景,研究空间几何体的结构特征的题型.4.要熟悉一些典型的几何体模型,如三棱柱、长(正)方体、三棱锥等几何体的三视图.。