解一元一次方程导学案

一元一次方程导学案【学习目标】1、知道什么是方程，会判断一个数学式子是算式还是方程；2、能根据简单的实际问题列一元一次方程，并了解其步骤；3、会判断方程的解。

【学习重点】一元一次方程的含义。

【学习难点】根据简单的实际问题列一元一次方程。

课前自主学习(查阅教材和相关资料,完成下列内容)考点一.方程的概念1、含有的等式叫方程。

考点二.一元一次方程的概念1.只含有个未知数，未知数的次数都是次的方程，叫做一元一次方程。

考点三.列方程遇到实际问题时,要先设字母表示 ,然后根据问题中的 ,最后写出含有未知数的 ,就能列出方程.归纳:列方程解实际问题的步骤:第一步: ,第二步: ,第三步: .考点四.解方程及方程的解的含义解方程就是求出使方程中等号左右两边的的值,这个值就是方程的 .【重要思想】1.类比思想:算式与方程的对比2.转化思想:把实际问题转化为数学问题,特别是方程问题.学练提升问题1:判断下列数学式子X+1, 0.5x-x, 2x-3=7, 3x+2=2x-5 , 2x2+3x-8=0,x+2y=7.是方程有 ,是一元一次方程有【规律总结】【同步测控】1.自己编造两个方程: , .2.自己编造两个一元一次方程: , .问题2.根据问题列方程:1.用一根长24cm的铁丝未成一个正方形,正方形的变长是多少?2.一台计算机已使用1700小时,预计每月再使用150小时,经过多少月这台计算机的使用时间他到规定的检修时间2450小时?【规律总结】【同步测控】根据下列问题,设未知数,列出方程1.环形跑道一周长400m,沿跑道跑多少周,可以跑3000m?2.甲种铅笔每只0.3元,乙种铅笔铅笔每只0.6元,用9元钱买了两种铅笔共20支,两种铅笔各买了多少支?【规律总结】【同步测控】1.一个梯形的下底比上底多2cm,高是5cm,面积是40cm2,求上底.2.x的2倍于10的和等于18;3.比b的一半小7的数等于a与b的和;4.把1400元奖学金按照两种奖项将给22名学生,其中一等奖每人200元,二等奖每人50元,获得一等奖的学生多少人?问题三、判断方程的根1.判断下列各数X=1,x=2,x=-1,x=0.5.那个是方程2x+3=5x-3的解?2.当x= 时,方程3x-5=1 两边相等?等式性质导学案【学习目标】1、了解等式的两条基本性质，并会用数学式子表示；2、能利用等式的基本性质解简单的方程； 【学习重点】理解等式的两条基本性质。

6.2.2解一元一次方程导学案一、学习目标：1、进一步经历运用方程解决实际问题的过程，发展应用数学的意识，体会方程是刻画现实世界的数学模型。

2、学会列一元一次方程解决有关的实际问题，进一步理解运用方程解决实际问题的一般步骤。

3、通过列一元一次方程解决实际问题，经历思考、探究、交流等活动过程，提高分析问题、解决问题的能力。

【重点难点】：根据应用题题意列出方程。

关键在于弄清题意，找出能够表示应用题全部含义的相等关系。

一．课前准备列一元一次方程解应用题的步骤如下：1）审题。

弄清题意，找出已知量、未知量。

2）设未知数。

对所求的未知量用设未知数表示。

3）列方程。

根据题中的等量关系列出方程。

4）解方程。

解所列的方程。

5）检验解。

检验解出的未知数值是否符合题意。

6）答题。

回答题中的问题。

简记为：______________________________________复习引入：（1）校团委有65名新团员，男同学为X人，女同学有__________人。

（2）甲、乙两班共90人，期中考试后，由甲班转入乙班4人，这时甲班人数和乙班人数相等，问期中考试前两班各有多少人？分析：设期中考试前甲班有X人，根据题意列表找等量关系_______________=______________解：二，探究活动例7、学校团委组织65名团员为学校建花坛搬砖.女同学每人搬6块,男同学每人搬8块,每人各搬4次。

总共搬了1800块.问这些新团员中有多少名男同学?分析：1、题目中告诉了我们哪些数量关系？__________+__________=________________________+__________=__________________________________________________2、设: 新团员中有x名男同学, 根据题意列表如下：找等量关系____________+_____________=________________ 解：三．归纳：用方程解实际问题的过程:解答分析和抽象过程包括（1）_____________________________________________（2）_____________________________________________（3）_____________________________________________课堂检测1.学校田径队的小刚在400米跑测试时,先以6米／秒的速度跑完了大部分路程,最后以8米／秒的速度冲刺到达终点,成绩为1分零5秒,问小刚在冲刺阶段花了多少时间?分析：设小刚在冲刺阶段的时间为X秒，根据题意列表找等量关系_____________+______________=______________解：2. 足球的表面是由一些呈多边形的黑、白皮块缝而成的,共计有32块,已知黑色皮块比白色皮块数的一半多2,问两种皮块各有多少?找等量关系: _____________+______________=______________找等量关系___________________=_____________________分析：如果设黑色块为X块，可以用哪些关系表示白色块？如果设白色块为X块，可以用哪些关系表示黑色块？你想出了几种解题方法？四．谈谈本节课收获及困惑。

___ 年___ 月____日 组长检查： 教师评价：学习内容：3.2.2解一元一次方程（2）移项学习目标：求解数字系数的一元一次方程，经历和体会解一元一次方程中“转化”的思想方法。

学习重点：学会解一元一次方程学习难点：移项学习过程：（阅读教材第88至90页，并完成学前准备的内容）一．学前准备：1．把方程的某一项 后。

从方程的一边移到另一边，这种变形叫做 。

2．移项的理论根据是 ，即在方程的两边同时减去 ，相当于把 ，改变符号后从方程的一边移到另一边。

3．方程2x -5=3x+3变形为2x+3x=3-5的错误原因是 。

4．将方程4x=2x -2，移项，得 ，合并，得 ，方程两边同除以 ，得x= 。

5．将方程2y -11=5，移项，得 ，合并，得 ，方程两边同除以 ，得y= 。

6．将方程2x -1=1-3x ，移项，得 ，合并，得 ，方程两边同除以 ，得x= 。

7．方程2x -4=3x+8移项后正确的是A ． 2x+3x=8+4B ． 2x -3x=-8+4C ． 2x -3x=8+4D ． 2x+3x=8-4二．新知探究：8．解方程（1）32x+4=0 （2）31x+23=0(3) 2x -19=7x+31 (4) 10-2x=x -19．根据下列条件求x 的值。

（1） 25与x 的差是-8； (2) x 的53与8的和是2；10．x 取何值时，4x+2与3x -1的值：（1）相等？（2）互为相反数？三．拓展与应用11．解方程：(1) 6x=24-2x (2) 5.19217-=+x x (3) 6y+7=12y -5-3y(4) 759272911-=+z z (5) 317192+=-m m (6) 3134334-=-x x四．课后巩固：12．若对任意有理数a ，b ，c ，d 规定c ad b =ad-bc ，当3x 42--=2-x 时，求x 。

13．体育馆的某个区域的座位，第一排是20个座位，以后每增加一排，座位就增加2个．如果用字母a n表示每排的座位数，用n表示排数．请填写表格，并回答问题：（2）第10排有_______个座位；（3）第n排有多少个_____________座位；（4）其中某一排的座位是118个，那么它是第几排？五、总结反思。

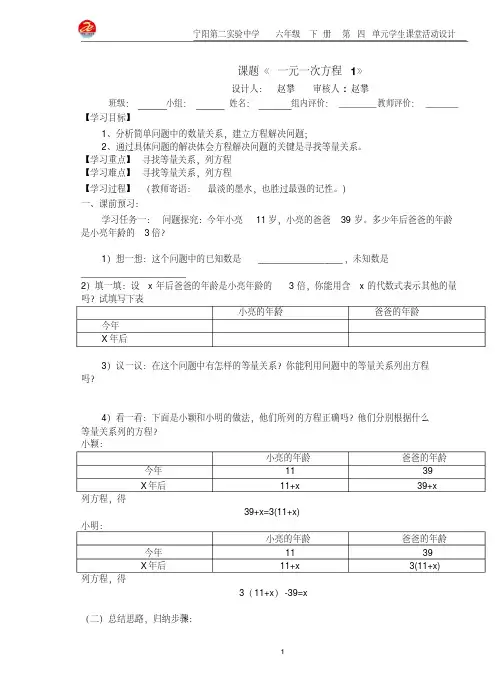
课题《一元一次方程1》设计人：赵攀审核人: 赵攀班级：小组：姓名：组内评价：________教师评价：_______【学习目标】1、分析简单问题中的数量关系，建立方程解决问题；2、通过具体问题的解决体会方程解决问题的关键是寻找等量关系。

【学习重点】寻找等量关系，列方程【学习难点】寻找等量关系，列方程【学习过程】（教师寄语：最淡的墨水，也胜过最强的记性。

）一、课前预习：学习任务一：问题探究：今年小亮11岁，小亮的爸爸39岁。

多少年后爸爸的年龄是小亮年龄的3倍？1）想一想：这个问题中的已知数是_________________，未知数是_____________________2）填一填：设x年后爸爸的年龄是小亮年龄的3倍，你能用含x的代数式表示其他的量吗？试填写下表小亮的年龄爸爸的年龄今年X年后3）议一议：在这个问题中有怎样的等量关系？你能利用问题中的等量关系列出方程吗？4）看一看：下面是小颖和小明的做法，他们所列的方程正确吗？他们分别根据什么等量关系列的方程？小颖：小亮的年龄爸爸的年龄今年11 39X年后11+x 39+x列方程，得39+x=3(11+x)小明：小亮的年龄爸爸的年龄今年11 39X年后11+x 3(11+x)列方程，得3（11+x）-39=x（二）总结思路，归纳步骤：理解题意，寻找等量关系，设未知数，列方程，解方程，作答。

【我的疑惑】____________________________________________________ 二、合作探究：探究一：1）在上面的问题中，多少年前，小亮的年龄是爸爸的51？2）经过若干年后，小亮的年龄能等于爸爸年龄的54吗？3）小川今年6岁，他的祖父72岁，几年后小川的年龄是他祖父年龄的414）某造纸厂为节约木材，大力扩大再生纸的生产，这家工厂前年和去年共生产再生纸3000吨，去年比前年生产量的2倍还多150吨，它去年生产再生纸多少吨？三、拓展提升（教师寄语：：读一书，增一智。

一元一次方程复习导学案一、教学目标：1、理解一元一次方程概念，掌握等式性质及一元一次方程的解法。

2、能列出一元一次方程解应用题，提高分析问题、解决问题的能力。

二、教学重点：等式性质及一元一次方程的解法.三、教学难点：用一元一次方程解决实际问题。

四、教学过程：<考点一> 一元一次方程的定义与等式性质1、下列方程中，是一元一次方程的是( )A 、()232x x x x +-=+B 、()40x x +-=C 、1x y +=D 、10x y+= 2、如果21m x -+8=0是一元一次方程，则m=3、下列变形正确的是( )A 4x －5＝3x ＋2变形得4x －3x ＝－2＋5B 6x ＝2变形得x ＝3C 3(x －1)＝2(x ＋3)变形得3x －1＝2x ＋6D 23 x －1＝12x+3变形得4x －6＝3x ＋18 4、下列等式变形中，正确的是（ ）<考点二> 解一元一次方程()()()y y y -=---161432 ()[]()x x x -=--121231411012=---x x 421312+-=-x x21132x x +--= 52221+-=--y y y4131312--=--n n nm m m 3213123+-=--1359232+-=-+x x x257352+-=--y y y3.07416.015x x --=- x x 23231423=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-<考点三> 一元一次方程变式训练1、若()01222=++-y x ，则y x += 。

2、单项式4124192b a b a x x -+-与是同类项，则x =3、对于非零的两个实数a 、b ，规定a ⊗b =3a －b ，若1)1(1=+⊗x ，则x 的值为 。

4、若y=1是方程12()23m y y --=的解，则关于x 的方程(4)2(3)m x mx +=+的解是 。

一元一次方程导学案【学习目标】1、知道什么是方程，会判断一个数学式子是算式还是方程；2、能根据简单的实际问题列一元一次方程，并了解其步骤；3、会判断方程的解。

【学习重点】一元一次方程的含义。

【学习难点】根据简单的实际问题列一元一次方程。

课前自主学习(查阅教材和相关资料,完成下列内容)考点一.方程的概念1、含有的等式叫方程。

考点二.一元一次方程的概念1.只含有个未知数，未知数的次数都是次的方程，叫做一元一次方程。

考点三.列方程遇到实际问题时,要先设字母表示 ,然后根据问题中的 ,最后写出含有未知数的 ,就能列出方程.归纳:列方程解实际问题的步骤:第一步: ,第二步: ,第三步: .考点四.解方程及方程的解的含义解方程就是求出使方程中等号左右两边的的值,这个值就是方程的 .【重要思想】1.类比思想:算式与方程的对比2.转化思想:把实际问题转化为数学问题,特别是方程问题.学练提升问题1:判断下列数学式子X+1, 0.5x-x, 2x-3=7, 3x+2=2x-5 , 2x2+3x-8=0,x+2y=7.是方程有 ,是一元一次方程有【规律总结】【同步测控】1.自己编造两个方程: , .2.自己编造两个一元一次方程: , .问题2.根据问题列方程:1.用一根长24cm的铁丝未成一个正方形,正方形的变长是多少?2.一台计算机已使用1700小时,预计每月再使用150小时,经过多少月这台计算机的使用时间他到规定的检修时间2450小时?【同步测控】根据下列问题,设未知数,列出方程1.环形跑道一周长400m,沿跑道跑多少周,可以跑3000m?2.甲种铅笔每只0.3元,乙种铅笔铅笔每只0.6元,用9元钱买了两种铅笔共20支,两种铅笔各买了多少支?【规律总结】【同步测控】1.一个梯形的下底比上底多2cm,高是5cm,面积是40cm2,求上底.2.x的2倍于10的和等于18;3.比b的一半小7的数等于a与b的和;4.把1400元奖学金按照两种奖项将给22名学生,其中一等奖每人200元,二等奖每人50元,获得一等奖的学生多少人?问题三、判断方程的根1.判断下列各数X=1,x=2,x=-1,x=0.5.那个是方程2x+3=5x-3的解?2.当x= 时,方程3x-5=1 两边相等?等式性质导学案【学习目标】1、了解等式的两条基本性质，并会用数学式子表示；2、能利用等式的基本性质解简单的方程； 【学习重点】理解等式的两条基本性质。

5.2解方程（第一课时）导学案主备人：审核人：时间：学习目标:1、会说出移项的依据及注意事项。

2、会使用移项的方法解一元一次方程。

学习重难点:1重点是正确掌握移项的方法求方程的解2 难点是采用移项方法解一元一次方程学习过程一:忆一忆1、上节课我们学习了等式的基本性质，你能说出来吗？2、你能利用等式的性质解下列方程吗?5X－2＝8二：自学提纲一1、任务：自学课本135页内容，并完成以下检测。

2、要求：把不懂的地方用红笔标记，如有疑问可小组交流。

然后由小组派代表在全班展示，每题答对加3分。

3、时间共计15分钟。

自学检测一：1、从原方程5X－2=8演变为5X＝8+2，等号两边的项有否发生变化？若有变化，是如何变化的？请将你发现的结论说出来与大家交流。

2、把方程中的某一项后，从方程的一边移到方程的另一边，这种变形叫“”.3、下面的移项对不对？如果不对，应如何改正？（1）从x＋5＝7，得到x＝7＋5（2）从5x＝2x－4，得到5x－2x＝4（3）从8＋x＝－2x－1到x＋2x＝－1－84、上述例子告诉我们，“移项”要注意什么？移项时，移动的项变号，不移动的项变号.(填“要”或“不要”)5、尝试用移项的方法解下列方程（1）2x ＋ 4＝1 （2）3x＋3＝x＋7三：归纳总结: 1、解一元一次方程移项的依据是什么？2、移项时应注意哪些问题？四:练一练:学生独立练习6分钟后小组交流，同时两人板演，小组点评。

用移项的方法解下列方程（1）14 X= —12 X + 3 (2) 2x －1=－x +5 (3)1—23x=25四 达标检测：独立练习6分钟后交流点评。

1.如果2x =5－3x ,那么2x +________=5..2.解下列方程(1) 2x +3=x －1 (2) 10x-3=7x+8(3) x=23x+16五：目标回顾:本节课你有何收获？移项时应注意哪些问题？五 拓展延伸.已知x=2是关于x 的方程3m+8x= 5 +x 的解，求关于x 的方程m+2x=2m －3x 解。

第四章《解一元一次方程（1）》导学案性质解简单的一元一次方程.过程与方法：经历数值代入计算的过程，领会方程的解和解方程的意义.知道求方程的解就是将方程变形为x=a的形式.情感、态度与价值观：强调检验的重要性，养成检验反思的好习惯.二、重、难点：比较方程的解和解方程的异同；归纳等式的性质；利用性质解方程.三教学过程：（一）、学前探究x= 时方程分别把0、1、2、3、4代入下列方程，哪一个值可以使方程两边相等？（1）2x-1=5 (2)3x-2=4x-3归纳：（1）方程的解：(2)解方程：（二）、新知研讨上一节课我们学习了列方程解简单的应用题，列出的方程有的我们不会解，我们知道解方程就是把方程变形成x＝a形式，本节课，我们将学习如何将方程变形。

测量一些物体的质量时，我们将它放在天平的左盘内，在右盘内放上砝码，当天平处于平衡状态时，显然两边的质量相等。

如果我们在两盘内同时加入相同质量的砝码，这时天平仍然平衡，天平两边盘内同时拿去相同质量的砝码，天平仍然平衡。

如果把天平看成一个方程，你能从天平上砝码的变化联想到方程的变形吗?让同学们观察P95图的最上面的天平；天平的左盘内有两个相同的小球和一个1g的小砝码，右盘上有5个1g的小砝码，天平平衡，表示左右两盘的质量相等。

如果我们用x表示小球的质量，1表示小砝码的质量，那么可用方程2x＋1=5表示天平两盘内物体的质量关系。

问：中间的天平内的砝码是怎样由上边天平变化而来的?它所表示的方程是什么？如何由方程2 x＋1=5变形得到的?问：下面的天平内的砝码是怎样由中间天平变化而来的?它所表示的方程是什么？学生回答后，教师归纳：方程两边都减去同一个数，方程的解不变。

问：若把方程两边都加上同一个数，方程的解有没有变?如果把方程两边都加上(或减去)同一个整式呢?让同学们看P96图。

左天平两盘内的砝码的质量关系可用方程表示为3x＝2x+3，右边的天平内的砝码是怎样由左边天平变化而来的?把天平两边都拿去2个球，相当于把方程3x＝2x+2两边都减去2x，得到的方程的解变化了吗?由可归结为；方程两边都加上或都减去同一个数或同一个整式，方程的解不变。

课题： 去分母解一元一次方程导学案学习目标：1、会用去分母的方法准确求解一元一次方程。

2、掌握解一元一次方程的一般步骤及考前须知。

3、会根据一元一次方程的特点灵活处理解方程的步骤，化为x=a 的形式。

学习重点：会用去分母的方法准确求解一元一次方程。

学习过程：一、问题式探究。

1、解方程 问题1：这个方程应该怎么解？它有什么特点？2、解方程问题2：这个方程该怎样去分母转化成整系数方程呢？解: 去分母(方程两边同乘以 〕,得 × ×3、解方程解: 去分母(方程两边同乘以 〕,得 × ×1233x x +=1223x x +=12x +=23x 12123x x+=+12x +=2x 13+4、问题3： 将3题的方程变换一下，还能用刚刚的方法解吗？ 试试看！ 解方程启示：二、依葫芦画瓢——去分母解以下方程阅读例题，观察比拟，思考问题4：你认为哪种方法更简便呢？解方程21132x x +-=34123x x -+=（）2x-1x+2=-134（2）11(x+14)=(x+20)74（3）111(15)(7)523x x +=--三、题后归纳、反思、总结。

学生活动：小组交流、合作思考答复以下问题:问题5：解一元一次方程一般有哪些步骤？问题六：解一元一次方程是否必须严格遵循上面的步骤呢？问题7： 〔1〕怎样去分母？〔2〕去分母的依据是什么？〔3〕去分母时注意些什么？〔4〕你收获了怎的什么数学思想？四、及时稳固练习1下面的解方程的过程是否正确？不正确的请改正。

(1) 〔2〕 去分母, 得 4(2X+3) - 9X+5 =0 去分母，得 2(X-1)-3(5X+1)=1(3)去分母，得 6x - 2 = x+2 - 6322136x x -+=-2151164x x -+-=2395028x x ++-=解方程〔1〕 〔2〕五、学习总结解一元一次方程方法步骤汇总：六、拓展延伸—— 如何解这样子的方程？11(1)2(2)25x x -=-+61132x x --=21(1)30.20.5x x -+-=31(2)50.50.7x x --=。