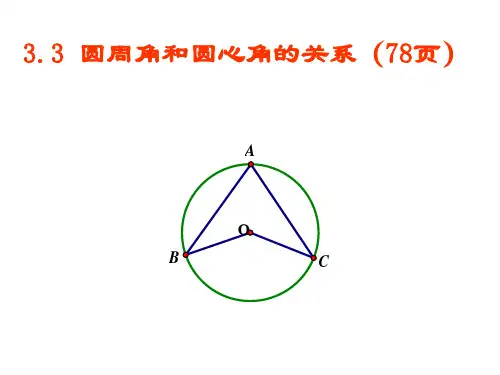
A C
∠ABC = 1∠AOC.
2
A
C
A C
●O
●O
●O
B
B B
1.如图,在⊙O中, ∠BAC=32º,则
∠BOC=__6_4_º____。
2、如图,⊙O中, ∠ACB = 130º,则
∠AOB=_1_0_0_º__。
A OB
C
O AC
练习:如图,圆O中,AB是直径,半径CO⊥AB,D是 CO的中点,DE∥AB,求∠ABE的度数.
使AC=AB,BD与CD的大小有什么关系?为什么?
A
解:BD=CD. 理由是:
连接AD.
●O
∵AB是⊙O的直径
∴∠ADB=90°
即AD⊥BD
C D B 又∵AC=AB ∴BD=CD
拓展 化心动为行动
7.在⊙O中,∠A=50°,求∠C的大小.
A
定理:
B
●O D 圆内接四边形的对角互补。
C
例题精解
8. 如图,AD是△ABC的高,AE是△ABC的外接圆直
∴∠ABE=90°
∵AD是△ABC的高 ∴∠ADC=∠ABE=90°
B
O DC
∵∠C=∠E
E
∴△ADC∽ △ABE 1、证明题的思路寻找方法;
∴ AC AD AE AB
∴ AB ·AC = AE ·AD
2、等积式的证明方法; 3、辅助线的思考方法。
拓展 化心动为行动
9.如图,圆O中,AB是直径,半径CO⊥AB,D是 CO的中点,DE∥AB,求∠ABE的度数.
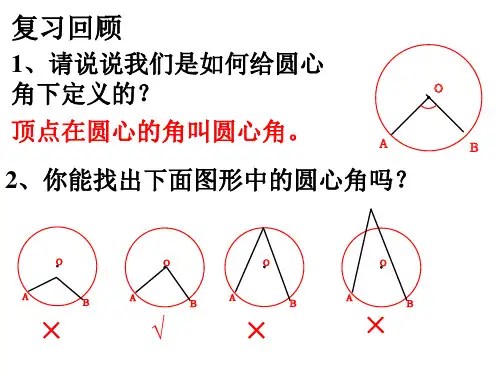
在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
为了解决这个问题,我们先探究一条弧所对的圆周 角和圆心角之间有的关系.