高中数学练习:圆锥曲线的综合问题
- 格式:doc
- 大小:330.98 KB
- 文档页数:8

1. 平面上一点向二次曲线作切线得两切点,连结两切点的线段我们称切点弦.设过抛物线22x py =外一点00(,)P x y 的任一直线与抛物线的两个交点为C 、D ,与抛物线切点弦AB的交点为Q 。
(1)求证:抛物线切点弦的方程为00()x x p y y =+; (2)求证:112||||PC PD PQ +=.2. 已知定点F (1,0),动点P 在y 轴上运动,过点P 作PM 交x 轴于点M ,并延长MP 到点N ,且.||||,0PN PM PF PM ==⋅ (1)动点N 的轨迹方程;(2)线l 与动点N 的轨迹交于A ,B 两点,若304||64,4≤≤-=⋅AB OB OA 且,求直线l 的斜率k 的取值范围.3. 如图,椭圆134:221=+y x C 的左右顶点分别为A 、B ,P 为双曲线134:222=-y x C 右支上(x 轴上方)一点,连AP 交C 1于C ,连PB 并延长交C 1于D ,且△ACD 与△PCD 的面积相等,求直线PD 的斜率及直线CD 的倾斜角.4. 已知点(2,0),(2,0)M N -,动点P 满足条件||||22PM PN -=.记动点P 的轨迹为W .(Ⅰ)求W 的方程;(Ⅱ)若,A B 是W 上的不同两点,O 是坐标原点,求OA OB ⋅的最小值.5. 已知曲线C 的方程为:kx 2+(4-k )y 2=k +1,(k ∈R) (Ⅰ)若曲线C 是椭圆,求k 的取值范围;(Ⅱ)若曲线C 是双曲线,且有一条渐近线的倾斜角是60°,求此双曲线的方程; (Ⅲ)满足(Ⅱ)的双曲线上是否存在两点P ,Q 关于直线l :y=x -1对称,若存在,求出过P ,Q 的直线方程;若不存在,说明理由。
6. 如图(21)图,M (-2,0)和N (2,0)是平面上的两点,动点P 满足: 6.PM PN +=(1)求点P 的轨迹方程; (2)若2·1cos PM PN MPN-∠=,求点P 的坐标.7. 已知F 为椭圆22221x y a b +=(0)a b >>的右焦点,直线l 过点F 且与双曲线1222=-b y a x 的两条渐进线12,l l 分别交于点,M N ,与椭圆交于点,A B . (I )若3MON π∠=,双曲线的焦距为4。

题组:圆锥曲线综合大题练题型1:定点问题1.椭圆C:x 2a2+y2b2=1(a>b>0)的离心率为12,其左焦点到点P(2,1)的距离为√10.(Ⅰ)求椭圆C的标准方程;(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求出该定点的坐标.2.已知抛物线C:y2=2px经过点M(2,2),C在点M处的切线交x轴于点N,直线l1经过点N且垂直于x轴.(Ⅰ)求线段ON的长;(Ⅱ)设不经过点M和N的动直线l2:x=my+b交C于点A和B,交l1于点E,若直线MA、ME、MB的斜率依次成等差数列,试问:l2是否过定点?请说明理由.3.已知椭圆C:2222=1x ya b(a>b>0),四点P1(1,1),P2(0,1),P3(–1,32),P4(1,32)中恰有三点在椭圆C上.(1)求C的方程;(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.4.如图,椭圆E:x 2a2+y2b2=1(a>b>0)的左焦点为F1,右焦点为F2,离心率e=12.过F1的直线交椭圆于A、B两点,且∆ABF2的周长为8.(Ⅰ)求椭圆E的方程.(Ⅱ)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.5.如图,已知椭圆Γ:x 2b2+y2a2=1(a>b>0)的离心率e=√22,短轴右端点为A,M(1.0)为线段OA的中点.(Ⅰ)求椭圆Γ的方程;(Ⅱ)过点M任作一条直线与椭圆Γ相交于P,Q两点,试问在x轴上是否存在定点N,使得∠PNM=∠QNM,若存在,求出点N的坐标;若不存在,说明理由.题型2:定值问题1.已知椭圆C :22221+=x y a b (0a b >>)的离心率为 32 ,(,0)A a ,(0,)B b ,(0,0)O ,OAB ∆的面积为1.(1)求椭圆C 的方程;(2)设P 的椭圆C 上一点,直线PA 与y 轴交于点M ,直线PB 与x 轴交于点N.求证:BM AN ⋅为定值.2.如图, 在平面直角坐标系中, 抛物线的准线与轴交于点,过点的直线与抛物线交于两点, 设到准线的距离. (1)若,求抛物线的标准方程;(2)若,求证:直线的斜率的平方为定值.xOy ()220y px p =>l x M M ,A B ()11,A x y l ()20d p λλ=>13y d ==0AM AB λ+=AB3.椭圆C:x 2a2+y2b2=1(a>b>0)的离心率√22,点(2,√2)在C上.(1)求椭圆C的方程;(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与l的斜率的乘积为定值.4.已知椭圆C:x 2a2+y2b2=1(a>b>0)的离心率√22,的离心率为,点A(1,√32)在椭圆C上,O为坐标原点.(Ⅰ)求椭圆C的方程;(Ⅱ)设动直线l与椭圆C有且仅有一个公共点,且l与圆x2+y2=5的相交于不在坐标轴上的两点P1,P2,记直线OP1,OP2的斜率分别为k1,k2,求证:k1∙k2为定值.5.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率√22,若圆x 2+y 2=a 2被直线x − y −√2=0截得的弦长为2。

高中生圆锥曲线练习题及讲解圆锥曲线是高中数学中的一个重要概念,通常包括椭圆、双曲线和抛物线。
下面是一些圆锥曲线的练习题以及相应的讲解。
### 练习题1:椭圆的标准方程给定一个椭圆的两个焦点距离为2c,且长轴长度为2a,求椭圆的标准方程。
解答步骤:1. 根据椭圆的性质,我们知道长轴和短轴的关系为 \( a^2 = b^2 +c^2 \)。
2. 题目给出 \( 2c \) 和 \( 2a \),可以求出 \( c \) 和 \( a \) 的值。
3. 将 \( c \) 和 \( a \) 的值代入上述公式,求出 \( b \) 的值。
4. 最终,椭圆的标准方程为 \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \)。
### 练习题2:双曲线的渐近线已知双曲线的方程为 \( \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \),求其渐近线方程。
解答步骤:1. 双曲线的渐近线方程可以通过 \( \frac{x^2}{a^2} -\frac{y^2}{b^2} = 0 \) 得到。
2. 将上述方程简化,得到 \( y = \pm \frac{b}{a}x \)。
3. 这就是双曲线的渐近线方程。
### 练习题3:抛物线的焦点和准线给定抛物线的方程 \( y^2 = 4ax \),求其焦点和准线。
解答步骤:1. 抛物线的焦点位于 \( (a, 0) \)。
2. 准线方程为 \( x = -a \)。
3. 焦点和准线是抛物线的重要特征,可以通过方程直接得出。
### 练习题4:圆锥曲线的参数方程已知椭圆的参数方程为 \( x = a \cos(\theta) \) 和 \( y = b\sin(\theta) \),求其标准方程。
解答步骤:1. 将参数方程中的 \( \cos(\theta) \) 和 \( \sin(\theta) \) 替换为 \( x/a \) 和 \( y/b \)。

圆锥曲线中综合问题【考情分析】1.圆锥曲线的综合问题是高考考查的重点内容,常见的热点题型有:范围、最值问题,定点、定值问题,探索型问题等.2.以解答题的压轴题形式出现,难度较大,重在提升逻辑推理、直观想象、数学运算的核心素养.【题型一】圆锥曲线中的最值、范围问题【典例分析】1.(2021·山东滕州一中高三模拟)已知椭圆22:143x y C +=的左顶点为A ,过其右焦点F 作直线交椭圆C 于D ,E (异于左右顶点)两点,直线AD ,AE 与直线:4l x =分别交于M ,N ,线段MN 的中点为H ,连接FH .(1)求证:FH DE ⊥;(2)求DEH △面积的最小值.【解析】(1)由已知得(1,0)F ,设()11,D x y ,()22,E x y ,直线DE 的方程为1x my =+,与椭圆方程联立得()2234690m y my ++-=,122634m y y m +=-+,122934y y m =-+设直线AD 的方程为11(2)2y y x x =++,与直线:4l x =联立得1164,2y M x ⎛⎫⎪+⎝⎭,同理可得2264,2y N x ⎛⎫⎪+⎝⎭,则()()()12121221212123233323339M N H my y y y y y y y y m my my m y y m y y ++⎛⎫+==+==- ⎪+++++⎝⎭,(4,3)H m ∴-,3041FH m k m --==--,当0m =时,显然DE FH ⊥;当0m ≠时,()11DE FH k k m m⨯=⨯-=-时,DE FH ⊥,综上,可得DE FH ⊥.(2)12234y y m -===+()2122121||34m DE y y m +=-=+,H 到直线DE的距离d ==(221811||234DFHm S DE d m +=⨯=+△,设2211t m t =≥⇒=-,()3322()(1)31314t t f t t t t ==≥+-+,()422233'()031t t f t t +=>+()f t ∴在[1,)+∞上单调递增,min 1()(1)4f t f ==,当1t =,即0m =时取得最小值.DEH ∴ 面积的最小值是92.2.(2021·山东省实验中学高三模拟)已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为1F ,2F ,点P 是椭圆C上位于第二象限的任一点,直线l 是12F PF ∠的外角平分线,直线2PF 交椭圆C 于另一点Q ,过左焦点1F 作l 的垂线,垂足为N ,延长1F N 交直线2PF 于点M ,||2ON =(其中O 为坐标原点),椭圆C 的离心率为12.(1)求椭圆C 的标准方程;(2)求1PF Q 的内切圆半径r 的取值范围.【解析】(1)由题意可得1||||F N NM =,且1||||PF PM =,所以1222||||||||||2PF PF PM PF MF a +=+==,因为O ,N 分别为线段12F F ,1F M 的中点,所以ON 为12MF F △的中位线,所以2//ON MF 且21||||22ON MF a ===,由12c a =,222a b c =+得23b =,所以椭圆C 的标准方程为22143x y +=.(2)由(1)知2(1,0)F ,设直线2PF 的方程为1(0)x my m =+≠,由点P 在第二象限求得33m <.设11(,)P x y ,22(,)Q x y ,由221143x my x y =+⎧⎪⎨+=⎪⎩得22(34)690m y my ++-=,由根与系数的关系得122634m y y m +=-+,122934y y m =-+,所以12212121212211121||||2()42234PF Q m S F F y y y y y y m +=⋅⋅-=⨯+-+△,令2231()3t m t =+>,则221m t =-,所以12212121213(1)4313PF Q t t S t t t t===-+++△,因为13y t t=+在233t >时单调递增,所以15332y t t =+>所以11283153PF Q S t t=∈+△,又11111(||||||)4422PF Q S PF PQ QF r a r r =++⋅=⋅⋅=△,所以83045r <<,即305r <<,所以1PF Q 内切圆半径r 的取值范围是23)5.【提分秘籍】求解圆锥曲线中最值、范围问题的主要方法(1)几何法:若题目中的条件和结论能明显体现几何特征和意义,则考虑利用图形性质数形结合求解.(2)代数法:若题目中的条件和结论能体现一种明确的函数关系,或者不等关系,或者已知参数与新参数之间的等量关系等,则利用代数法求参数的范围.【变式演练】1.(2021·辽宁本溪高级中学高三模拟)已知点F 为椭圆2222:1(0)x y C a b a b+=>>的右焦点,椭圆上任意一点到点F 距离的最大值为3,最小值为1.(1)求椭圆C 的标准方程;(2)若M 为椭圆C 上的点,以M 为圆心,MF 长为半径作圆M ,若过点(1,0)E -可作圆M 的两条切线,EA EB (,A B 为切点),求四边形EAMB 面积的最大值.【解析】(1)根据题意椭圆上任意一点到点F 距离的最大值为3,最小值为1.所以31a c a c +=⎧⎨-=⎩,解得2,1a c ==,所以b =因此椭圆C 的标准方程为22143x y +=(2)由(1)知,()1,0E-为椭圆的左焦点,根据椭圆定义知,||||4ME MF +=,设|r MF MB ==|,∵点E 在圆M 外,∴||4ME r r =->,∴12r ≤<所以在直角三角形MEB 中,||EB ==1||||2MEB S EB MB =⋅= ,由圆的性质知,四边形EAMB面积22MEB S S == ,其中12r ≤<.即)12S r =≤<.令()322412y r r r =-+≤<,则2682(34)y r r r r '=-+=--当413r <<时,0y '>,3224y r r =-+单调递增;当423r <<时,0y '<,3224y r r =-+单调递减.所以,在43r =时,y 取极大值,也是最大值此时maxS ==2.在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的两焦点与短轴的一个端点的连线构成等边三角形,直线10x y ++-=与以椭圆C 的右焦点为圆心,椭圆C 的长半轴长为半径的圆相切.(1)求椭圆C 的方程;(2)BMN △是椭圆C 的内接三角形,若坐标原点O 为BMN △的重心,求点B 到直线MN 距离的取值范围.【解析】(1)设椭圆2222:1x y C a b+=的右焦点()2,0F c ,则以椭圆C 的右焦点为圆心,椭圆C 的长半轴长为半径的圆:()222x c y a -+=,所以圆心到直线10x y ++=的距离d a ==,又椭圆的两焦点与短轴的一个端点的连线构成等边三角形,所以2,a c b ==,解得:2,1a b c ===,所以椭圆的标准方程为22143x y +=;(2)设(),B m n ,设,M N 的中点为D ,直线OD 与椭圆交于A,B 两点,因为O 为BMN △的重心,则2BO OD OA ==,所以,22m n D ⎛⎫-- ⎪⎝⎭即B 到直线MN 的距离是原点O 到直线MN 距离的3倍.当MN 的斜率不存在时,点D 在x 轴上,所以此时B 在长轴的端点处.由2OB =得:1OD =,则O 到直线MN 距离为1,B 到直线MN 距离为3;当MN 的斜率存在时,设()()1122,,,M x y N x y ,则有:22112222143143x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩两式相减得:()()()()12121212043x x x x y y y y +-+-+=,因为D 为,M N 的中点,所以1212,x x m y y n +=-+=-,所以121234y y mk x x n-==--,所以直线MN 的方程为3242n m m y x n ⎛⎫+=-+ ⎪⎝⎭,即2268430mx ny n m +++=,所以原点O 到直线MN距离22d =.因为22143m n +=,所以223124m n =-,所以22d ===因为203n <≤,所以3<≤13≤<,所以332d ≤<综上所述,33332d ≤≤.即点B 到直线MN 距离的取值范围33,32⎡⎤⎢⎥⎣⎦.【题型二】圆锥曲线中的定点、定值问题【典例分析】1.(2021浙江镇海中学高三模拟)已知()0,1F 且满足1PF x =+的动点(),P x y 的轨迹为C.(1)求曲线C 的轨迹方程;(2)如图,过点()1,0-T 的斜率大于零的直线与曲线C 交于D ,M 两点,()1,1Q -,直线DQ 交曲线C 于另外一点N ,证明直线MN 过定点.【解析】(1)∵1PF x =+,1x ≥-1x =+,等式两边平方整理得24y x =.(2)证明:设()11,M x y ,()22,N x y ,()33,D x y .由21123344y x y x ⎧=⎨=⎩两式相减得1313134DM y y k x x y y -==-+.所以直线DM 的方程为()11134y y x x y y -=-+,整理得()13134y y y x y y +=+(*).因为点T 在直线上,所以134y y =①,同理直线DN 的方程为()23234y y y x y y +=+,因为点Q 在直线上,所以()23234y y y y -+=+②.由①②两式得2211444y y y y ⎛⎫-+=+⋅ ⎪⎝⎭,整理得()121244y y y y =-+-.由(*)式同理知直线MN 的方程为()12124y y y x y y +=+,所以()()1212124444y y y x y y x y y +=+=-+-,整理得直线MN 的方程为()()()12441y y y x ++=-,所以直线MN 过定点()1,4-.2.(2021·天津八中高三模拟)已知椭圆C :2221(0)6x y b b+=>的左、右焦点分别为()1,0F c -和()2,0F c ,P 为椭圆C 上任意一点,三角形12PF F 面积的最大值是3.(Ⅰ)求椭圆C 的方程;(Ⅱ)若过点()2,0的直线l 交椭圆C 于A ,B 两点,且9,04Q ⎛⎫⎪⎝⎭,证明:QA QB ⋅ 为定值.【解析】(Ⅰ)由题意知226c b =-,当P 点位于椭圆C 短轴端点时,三角形12PF F 的面积S 取最大值,此时max 1232S c b bc =⨯⨯==.所以229b c =,即()2269bb -=,解得23b=.故椭圆C 的方程为22163x y +=.(Ⅱ)(方法1)当直线l 的斜率不为0时,设直线l :2x my =+交椭圆于()()1122,,,A x y B x y .由22226x my x y =+⎧⎨+=⎩消去x 得,()222420m y my ++-=.则12122242, 22m y y y y m m +=-=-++.而112299,,,44QA x y QB x y ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭ ,所以()()2121212129911144416QA QB x x y y m y y m y y ⎛⎫⎛⎫⋅=--+=+-++ ⎪⎪⎝⎭⎝⎭()222222141211512421621616m m m m m m m --⎛⎫⎛⎫=+---+=+=- ⎪ ⎪+++⎝⎭⎝⎭.当直线l 的斜率为0时,(A B ,则998115,0,06441616QA QB ⎫⎛⎫⋅=⋅=-+=-⎪ ⎪⎭⎝⎭ .故QA QB ⋅ 为定值,且为1516-.(方法2)当直线l 的斜率存在时,设直线l :()2y k x =-交椭圆于()()1122,,,A x y B x y .由22(2)26y k x x y =-⎧⎨+=⎩消去y 得,()2222218860k x k x k +-+-=.则2122821k x x k +=+,21228621k x x k -=+.而112299,,,44QA x y QB x y ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭.所以()()222121212129998112444416QA QB x x y y k x x k x x k ⎛⎫⎛⎫⎛⎫⋅=--+=+-++++ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭ ()22222228698811242142116k k k k k k k -⎛⎫=+⋅-+⋅++⎪++⎝⎭22126818115621161616k k --=+=-+=-+.当直线l 的斜率不存在时,可求得()()2,1,2,1A B -,则991152,12,11441616QA QB ⎛⎫⎛⎫⋅=-⋅--=-=- ⎪ ⎪⎝⎭⎝⎭ .故QA QB ⋅ 为定值,且为1516-.【提分秘籍】1.求定值问题的思路方法(1)思路:求解定值问题的基本思路是使用参数表示要解决的问题,然后证明与参数无关,这类问题选择消元的方向是非常关键的.(2)方法:从特殊入手,求出定值,再证明这个值与变量无关;直接推理、计算,并在计算推理的过程中消去变量,从而得到定值.2.求定点问题的解题方法(1)动直线l 过定点问题:设动直线方程(斜率存在)为y=kx+t,由题设条件将t 用k 表示为t=mk,得y=k(x+m),故动直线过定点(-m,0).(2)动曲线C 过定点问题:引入参变量建立曲线C 的方程,再根据其对参变量恒成立,令其系数等于零,得出定点.【变式演练】1.(2021·广东华南师范大学附属中学高三模拟)设A ,B 为双曲线2222:1x y C a b-=(0,0)a b >>的左、右顶点,直线l 过右焦点F 且与双曲线C 的右支交于M ,N 两点,当直线l 垂直于x 轴时,AMN 为等腰直角三角形.(1)求双曲线C 的离心率;(2)已知直线AM ,AN 分别交直线2ax =于,P Q 两点,当直线l 的倾斜角变化时,以PQ 为直径的圆是否过定点,若过定点,求出定点的坐标;若不过定点,请说明理由.【解析】(1)由l x ⊥轴时,AMN 为等腰直角三角形,可得||||||AF NF MF ==,所以2ba c a+=,即2220c ac a --=,故220e e --=,结合1e >,解得2e =.故双曲线C 的离心率为2.(2)因为2c e a ==,所以双曲线:C 222213x y a a-=,显然直线l 的斜率不为0,设直线:2l x my a =+,11(,)M x y ,22(,)N x y ,联立直线l 与双曲线C 的方程得2222213x my a x y a a=+⎧⎪⎨-=⎪⎩,化简得222(31)1290m y amy a -++=,根据根与系数的关系,得2121222129,3131am a y y y y m m +=-⋅=--,①所以121224()431ax x m y y a m -+=++=-,②222221212122342()431a m a x x m y y am y y a m --⋅=⋅+++=-,③设直线:AM 11()y y x a x a =++,直线:AN 22()y y x a x a=++,令2ax =,可得121233(,),(,)22()22()ay ay a a P Q x a x a ++,设()G x y ,是以PQ 为直径的圆上的任意一点,则0PG QG ⋅=,则以PQ 为直径的圆的方程为2121233()[][]022()2()ay ay a x y y x a x a -+--=++,由对称性可得,若存在定点,则一定在x 轴上,令0y =,可得2121233()022()2()ay ay a x x a x a -+⋅=++,即2212212129()024[()]a y y a x x x a x x a -+=+++,将①②③代入,可得22222222229931()034424()3131a a a m x a m a a a a m m ⋅--+=---+⋅+--,即229(24a x a -=,解得x a =-或2x a =,所以以PQ 为直径的圆过定点(,0)a -,(2,0)a .2.(2021·山师大附中高三模拟)已知圆(22:12C x y +=,动圆M过点)D且与圆C 相切.(1)求动圆圆心M 的轨迹E 的方程;(2)假设直线l 与轨迹E 相交于A ,B 两点,且在轨迹E 上存在一点P ,使四边形OAPB 为平行四边形,试问平行四边形OAPB 的面积是否为定值?若是,求出此定值;若不是,请说明理由.【解析】(1)因为CD =<,所以点D 在圆内.又因为圆M 过点D 且与圆C相切,所以MC MD =,所以MC MD CD +=>.即点M 的轨迹是以C ,D 为焦点的椭圆.则2a =,即a =又因为222a b -=,所以21b =.故动圆圆心M 的轨迹E 的方程为:2213x y +=.(2)当直线AB 的斜率不存在时,可得直线AB 的方程为32x =±,此时32A y =,所以四边形OAPB 的面积32S =.当直线AB 的斜率存在时,设直线AB 的方程为y kx m =+,由22,13y kx m x y =+⎧⎪⎨+=⎪⎩整理得,()()222316310k x kmx m +++-=.因为直线l 与轨迹E 相交于A ,B 两点,所以()()()222222361231112310k m k m k m =-+-=-+>△.设()11,A x y ,()22,B x y ,则122631kmx x k +=-+,()21223131m x x k -=+.所以()121222231my y k x x m k +=++=+.设AB 的中点为Q ,则Q 的坐标为223,3311km m k k ++⎛⎫-⎪⎝⎭.因为四边形OAPB 为平行四边形,所以22622,3131km m OP OQ k k ⎛⎫==- ⎪++⎝⎭,所以点P 的坐标为2262,3131km m k k ⎛⎫-⎪++⎝⎭.又因为点Р在椭圆上,所以222262311331km m k k ⎛⎫- ⎪+⎛⎫⎝⎭+= ⎪+⎝⎭.整理得,22431m k =+.又因为12223131AB x k k =-==++,原点О到直线AB的距离为d =所以平行四边形OAPB的面积322AOBS S AB d ==⋅== .综上可知,平行四边形OAPB 的面积为定值32.1.(2021·江苏南京师范大学附属中学高三模拟)已知抛物线2:2(0)C y px p =>,满足下列三个条件中的一个:①抛物线C 上一动点Q 到焦点F 的距离比到直线:1m x =-的距离大1;②点(2,3)A 到焦点F 与到准线:2pl x =-的距离之和等于7;③该抛物线C 被直线:20n x y --=所截得弦长为16.请选择其中一个条件解答下列问题.(1)求抛物线C 的标准方程;(2)O 为坐标原点,直线l 与抛物线C 交于M ,N 两点,直线OM 的斜率为1k ,直线ON 的斜率为2k ,当124k k ⋅=-时,求OMN 的面积的最小值.【解析】(1)若选择①,则抛物线C 上一动点Q 到焦点F 的距与到直线:2m x =-的距离相等,故22p=,故4p =,所以抛物线的方程为28y x =.2=72p +,解得4p =,故抛物线的方程为28y x =.若选择③,则由222y x y px=-⎧⎨=⎩可得2240y py p --=,16=,解得4p =,故抛物线的方程为28y x =.(2)设:MN x my n =+,()11,M x y 、()22,N x y ,因为MN 与抛物线C 相交于M 、N ,所以将:MN x my n =+代28y x =消去x 得:2880y my n --=,则264640m n ∆=+>且128y y m +=,128y y n ⋅=-,由题意可知111y k x =,222y k x =,所以1212122212121264644888y y y y k k y y x x y y n ⋅⋅=⋅====-⋅-⋅,所以2n =,所以OMN的面积1212122S y y y y =⨯⨯-=-=≥,当且仅当0m =时等号成立,所以OMN的面积的最小值为2.(2021·重庆第一中学高三模拟)已知A ,B 分别为椭圆()2222:10x y C a b a b+=>>的左、右顶点,F 为右焦点,点P 为C 上的一点,PF 恰好垂直平分线段OB (O 为坐标原点),32PF =.(1)求椭圆C 的方程;(2)过F 的直线l 交C 于M ,N 两点,若点Q 满足OQ OM ON =+(Q ,M ,N 三点不共线),求四边形OMQN面积的取值范围.【解析】(1)由题意可知(),0F c ,(),0B a ,∵PF 恰好垂直平分线段OB ,∴2a c =,令x c =,代入22221x y a b +=得:2b y a =±,∴232b a =,∴2222232a cba abc =⎧⎪⎪=⎨⎪=+⎪⎩,解得21a b c =⎧⎪=⎨⎪=⎩,∴椭圆C 的方程为:22143x y +=.(2)由题意可知直线l 的斜率不为0,设直线l 的方程为:1x my =+,设()11,M x y ,()22,N x y ,联立方程221431x y x my ⎧+=⎪⎨⎪=+⎩,消去x 得:()2234690m y my ++-=,∴()223636340m m ∆=++>,∴122634m y y m -+=+,122934y y m -=+,设MN 的中点为E ,则2OQ OM ON OE =+=,∴MN 与OQ 互相平分,四边形OMQN 为平行四边形,∴OMQN S 平行四边形2OMN S =△12122OF y y =⨯⨯⨯-12y y =-==212134m=+,令1t =≥,则()2121211313OMQN t S t t t t==≥++平行四边形,∵11333y t t t t ⎛⎫ ⎪=+=+ ⎪ ⎪ ⎪⎝⎭在[1,)+∞上单调递增,∴134t t+≥,∴(]120,313t t∈+,∴03OMQN S <≤平行四边形.综上所述,四边形OMQN 面积的取值范围为(0,3].3.(2021·浙江杭州高级中学高三模拟)已知抛物线2:2(0)C x py p =>的焦点为F ,点P 为抛物线C 上一点,点P 到F 的距离比点P 到x 轴的距离大1.过点P 作抛物线C 的切线,设其斜率为0k .(1)求抛物线C 的方程;(2)直线:l y kx b =+与抛物线C 相交于不同的两点A ,B (异于点P ),若直线AP 与直线BP 的斜率互为相反数,证明:00k k +=.【解析】(1)解:设点()00,P x y ,由点P 到F 的距离比点P 到x 轴的距离大1,可得01PF y =+,即0012py y +=+,所以2p =,即抛物线C 的方程为24x y =.(2)证明:设()11,A x y ,()22,B x y ,直线AP 的斜率为AP k ,直线BP 的斜率为BP k ,则()101010AP y y k x x x x -=≠-,()202020BP y yk x x x x -=≠-.因为直线AP 与直线BP 的斜率互为相反数,所以AP BP k k =-,即10201020y y y y x x x x --=---,又点()11,A x y ,()22,B x y 均在抛物线上,可得222200211020444x x x x x x x x --=---,化简可得1202x x x +=-,因为2114x y =,2224x y =,所以()2212124x x y y -=-,即1212124y y x x x x -+=-,故012122x y y k x x -==--,因为24x y =,所以214y x =,所以1 2y x '=,则0012k x =,故00k k +=.4.(2021·湖南长沙长郡中学高三模拟)已知椭圆E :()222210x y a b a b+=>>上有一点A ,点A 在x 轴上方,1F ,2F分别为E 的左,右焦点,当△12AF F 121sin 2AF F ∠=.(Ⅰ)求E 的标准方程;(Ⅱ)若直线l 交E 于P ,Q 两点,设PQ 中点为M ,O 为坐标原点,2PQ OM =uu u r uuu r,作ON PQ ⊥,求证:ON为定值.【解析】(Ⅰ)由椭圆的性质知,△12AF F 的面积取最大时,A 为椭圆的上顶点,即(0,)A b ,而12||2F F c =,∴12121||||2AF F S F F OA bc =⋅== 121sin 2b AF F a ∠==,又222a bc =+,∴24a =,21b =,可得E 的标准方程2214x y +=.(Ⅱ)由题意,2PQ OM =uu u r uuu r且PQ 中点为M ,易得90POQ ∠=︒,即OP OQ ⊥,若直线l 斜率不存在时,P ,Q 关于x 轴对称,2PQ OM =uu u r uuu r知:横纵坐标的绝对值相等,不妨假设P 在第一象限,则(,)P m m ,(,)Q m m -在椭圆上,∴255m =,此时,M N 两点重合,即255ON =;若直线l 斜率为0时,同理可得255ON =,若直线l 斜率存在且不为0时,设直线l 为(0)y kx b b =+≠,11(,)P x y ,22(,)Q x y ,则11(,)OP x y = ,22(,)OQ x y =,且12120x x y y +=,联立椭圆与直线得:222(41)84(1)0k x kbx b +++-=且2216(41)0k b ∆=-+>,∴122841kb x x k +=-+,21224(1)41b x x k -=+,即2222222221212122224(1)84()414141k b k b b k y y k x x kb x x b b k k k --=+++=-+=+++,∴222222224(1)45440414141b b k b k k k k ----+==+++,即||b =.∴||5ON==,为定值.5.(2021·天津南开中学高三模拟)已知点A,B分别为椭圆2222:1(0)x yE a ba b+=>>的左顶点和上顶点,且坐标原点O到直线AB 的距离为61313,椭圆E的离心率是方程2650x-+=的一个根.(1)求椭圆E的标准方程;(2)若(3,0)P,过P作斜率存在的两条射线PM,PN,交椭圆E于M,N两点,且PM PN⊥,问:直线MN经过定点吗?若经过,求出这个定点坐标;若不经过,说明理由.【解析】(1)因为椭圆E的离心率是方程2650x-+=的一个根,所以2e=或3e=.因为椭圆E的离心率(0,1)e∈,所以53e=.因为3ca=,所以2295a c=,所以222245b ac c=-=,因为点A,B分别为椭圆E的左顶点和上顶点,所以||AB===.因为坐标原点O到直线AB 的距离为61313,所以11||22ab AB=,=⨯,所以c=,所以29a=,24b=,所以椭圆E的标准方程为22194x y+=.(2)当直线MN的斜率存在时,设MN:y=kx+m,由22194y kx mx y=+⎧⎪⎨+=⎪⎩,消元并化简得222(49)189360k x kmx m+++-=,设1122(,),(,)M x y N x y ,则1221849km x x k +=-+,212293649m x x k-=+,又(3,0)P ,PM PN ⊥,所以1212133y yx x ⋅=---,所以1212123()9()()0x x x x kx m kx m -+++++=,即221212(1)(3)()(9)0k x x km x x m ++-+++=,所以2222293618(1)(3)(9)04949m kmk km m k k--++-++=++,所以2222(1)(936)(3)(18)(9)(49)0k m km km m k +-+--+++=,即224554130k km m ++=,所以30k m +=或15130k m +=,当30k m +=时,(3)y k x =-,此时M ,N ,P 重合,舍去.当15130k m +=时,15(13y k x =-,恒过点15(,0)13.当直线MN 的斜率不存在时,MN ⊥x 轴,设(),3M t t -,则()223194t t -+=,解得1513t =,所以此时直线MN 也过点15(,0)13.所以直线MN 恒过定点15(,0)13.6.(2021·湖南长郡中学高三模拟)已知抛物线2:4C x y =的焦点为F ,准线为l .设过点F 且不与x 轴平行的直线m 与抛物线C 交于A ,B 两点,线段AB 的中点为M ,过M 作直线垂直于l ,垂足为N ,直线MN 与抛物线C 交于点P .(1)求证:点P 是线段MN 的中点.(2)若抛物线C 在点P 处的切线与y 轴交于点Q ,问是否存在直线m ,使得四边形MPQF 是有一个内角为60︒的菱形?若存在,请求出直线m 的方程;若不存在,请说明理由.【解析】(1)证明:由题意知直线m 的斜率存在且不为0,故设直线m 的方程为1(0)y kx k =+≠,代入24x y =,并整理得2440x kx --=.所以216160k ∆=+>,设()11,A x y ,()22,B x y ,则124x x k +=,124x x =-.设()00,M x y ,则12022x x x k +==,200121y kx k =+=+,即()22,21M k k +.由MN l ⊥,得(2,1)N k -,所以MN 中点的坐标为()22,k k.将2x k =代入24x y =,解得2y k =,则()22,P k k ,所以点P 是MN 的中点.(2)由24x y =,得24x y =,则'2x y =,所以抛物线C 在点()22,P k k的切线PQ 的斜率为k ,又由直线m 的斜率为k ,可得m PQ ∥;又M N y ∥轴,所以四边形MPQF 为平行四边形.而||MF ==()222||211MP k k k =+-=+,由||||MF MP =,得21k =+,解得3k =±,即当3k =±时,四边形MPQF 为菱形,且此时2||1||||PF k MP MF ==+==,所以60PMF ∠=︒,直线m 的方程为13y x =±+,2即0x +=或0x +=,所以存在直线m ,使得四边形MPQF 是有一个内角为60︒的菱形.。

圆锥曲线综合训练题一、求轨迹方程:1、(1)已知双曲线1C 与椭圆2C :2213649x y +=有公共的焦点,并且双曲线的离心率1e 与椭圆的离心率2e 之比为73,求双曲线1C 的方程. (2)以抛物线28y x =上的点M 与定点(6,0)A 为端点的线段MA 的中点为P ,求P 点的轨迹方程. (1)解:1C 的焦点坐标为(0,13).±213e =由1273e e =得113e =设双曲线的方程为22221(,0)y x a b a b -=>则2222213139a b a b a ⎧+=⎪⎨+=⎪⎩ 解得229,4a b == 双曲线的方程为22194y x -= (2)解:设点00(,),(,)M x y P x y ,则00622x x y y +⎧=⎪⎪⎨⎪=⎪⎩,∴00262x x y y =-⎧⎨=⎩.代入2008y x =得:2412y x =-.此即为点P 的轨迹方程.2、(1)ABC ∆的底边16=BC ,AC 和AB 两边上中线长之和为30,建立适当的坐标系求此三角形重心G 的轨迹和顶点A 的轨迹.(2)△ABC 中,B(-5,0),C(5,0),且sinC-sinB=53sinA,求点A 的轨迹方程.解: (1)以BC 所在的直线为x 轴,BC 中点为原点建立直角坐标系.设G 点坐标为()y x ,,由20=+GB GC ,知G 点的轨迹是以B 、C 为焦点的椭圆,且除去轴上两点.因10=a ,8=c ,有6=b ,故其方程为()013610022≠=+y y x .设()y x A ,,()y x G '',,则()013610022≠'='+'y y x . ①由题意有⎪⎪⎩⎪⎪⎨⎧='='33yy x x ,代入①,得A 的轨迹方程为()0132490022≠=+y y x ,其轨迹是椭圆(除去x 轴上两点).(2)分析:由于sinA 、sinB 、sinC 的关系为一次齐次式,两边乘以2R (R 为外接圆半径),可转化为边长的关系. 解:sinC-sinB=53sinA 2RsinC-2RsinB=53·2RsinA ∴BC AC AB 53=- 即6=-AC AB (*)∴点A 的轨迹为双曲线的右支(去掉顶点) ∵2a=6,2c=10 ∴a=3, c=5, b=4所求轨迹方程为116922=-y x (x>3) 点评:要注意利用定义直接解题,这里由(*)式直接用定义说明了轨迹(双曲线右支) 3、如图,两束光线从点M (-4,1)分别射向直线y = -2上两点P (x 1,y 1)和Q (x 2,y 2)后,反射光线恰好通过椭圆C :12222=+by a x (a >b >0)的两焦点,已知椭圆的离心率为21,且x 2-x 1=56,求椭圆C 的方程. 解:设a =2k ,c =k ,k ≠0,则b =3k ,其椭圆的方程为1342222=-ky k x . 由题设条件得:114)2(120x x k ----=--+, ①224)2(120x x k ----=--+, ②x 2-x 1=56, ③ 由①、②、③解得:k =1,x 1=511-,x 2=-1,所求椭圆C 的方程为13422=+y x . 4、在面积为1的PMN ∆中,21tan =M ,2tan -=N ,建立适当的坐标系,求出以M 、N 为焦点且过P 点的椭圆方程.∴所求椭圆方程为1315422=+y x 解:以MN 的中点为原点,MN 所在直线为x 轴建立直角坐标系,设),(y x P .则⎪⎪⎪⎩⎪⎪⎪⎨⎧==+-=-.1,21,2cy c x yc x y∴⎪⎪⎩⎪⎪⎨⎧===233435c c y c x 且即)32,325(P ∴⎪⎪⎩⎪⎪⎨⎧=-=+,43,13412252222b a ba 得⎪⎩⎪⎨⎧==.3,41522b a (1)求线段PQ 的中点的轨迹方程;(2)设∠POQ 的平分线交PQ 于点R (O 为原点),求点R 的轨迹方程.解:(1)设线段PQ 的中点坐标为M (x ,y ),由Q (4,0)可得点P (2x -4,2y ),代入圆的方程x 2+y 2=4可得(2x -4)2+(2y )2=4,整理可得所求轨迹为(x -2)2+y 2=1.(2)设点R (x ,y ),P (m ,n ),由已知|OP |=2,|OQ |=4,∴21||||=OQ OP ,由角平分线性质可得||||||||RQ PR OQ OP ==21,又∵点R 在线段PQ 上,∴|PR |=21|RQ |,∴点R 分有向线段PQ 的比为21,由定比分点坐标公式可得⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+⨯+=+=+⨯+=32211021342211421n n y m m x ,即⎪⎪⎩⎪⎪⎨⎧=-=23243y n x m ,∴点P 的坐标为⎪⎭⎫ ⎝⎛-23 ,243y x ,代入圆的方程x 2+y 2=4可得42324322=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-y x , 即234⎪⎭⎫ ⎝⎛-x +y 2=916(y ≠0). ∴点R 的轨迹方程为234⎪⎭⎫ ⎝⎛-x +y 2=916(y ≠0).6、已知动圆过定点()1,0,且与直线1x =-相切.(1) 求动圆的圆心轨迹C 的方程;(2) 是否存在直线l ,使l 过点(0,1),并与轨迹C 交于,P Q 两点,且满足0OP OQ ⋅=uu u v uuu v若存在,求出直线l 的方程;若不存在,说明理由.解:(1)如图,设M 为动圆圆心, F ()1,0,过点M 作直线1x =-的垂线,垂足为N ,由题意知:MF MN =, 即动点M 到定点F 与定直线1x =-的距离相等,由抛物线的定义知,点M 的轨迹为抛物线,其中()1,0F 为焦点,1x =-为准线, ∴ 动点R 的轨迹方程为x y 42=(2)由题可设直线l 的方程为(1)(0)x k y k =-≠, 由2(1)4x k y y x=-⎧⎨=⎩得2440y ky k -+=△216160k =->,11k k <->或设),(11y x P ,),(22y x Q ,则124y y k +=,124y y k =由0OP OQ ⋅=u u u r u u u r ,即 ()11,OP x y =u u u r ,()22,OQ x y =u u u r,于是12120x x y y +=,即()()21212110ky y y y --+=,2221212(1)()0k y y k y y k +-++=,2224(1)40k k k k k +-+=g ,解得4k =-或0k =(舍去),又41k =-<-, ∴ 直线l 存在,其方程为440x y +-=7、设双曲线y ax 22231-=的两个焦点分别为F F 12、,离心率为2.(I )求此双曲线的渐近线l l 12、的方程;(II )若A 、B 分别为l l 12、上的点,且2512||||AB F F =,求线段AB 的中点M 的轨迹方程,并说明轨迹是什么曲线;(III )过点N ()10,能否作出直线l ,使l 与双曲线交于P 、Q 两点,且OP OQ →→=·0.若存在,求出直线l 的方程;若不存在,说明理由.解:(I )Θe c a =∴=2422, Θc a a c 22312=+∴==,,∴-=双曲线方程为y x 2231,渐近线方程为y x =±334分(II )设A x y B x y ()()1122,,,,AB 的中点()M x y ,[]Θ2552522101033332233333331012121221221122121212121212122122||||||||()()()()()()AB F F AB F F c x x y y y x y x x x x y y y y y x x y y x x y y x x =∴==⨯=∴-+-===-=+=+∴+=--=+∴+++⎡⎣⎢⎤⎦⎥=又,,,, ∴+=+=321321007532512222()()y x x y ,即则M 的轨迹是中心在原点,焦点在x 轴上,长轴长为103,短轴长为1033的椭圆.(9分) (III )假设存在满足条件的直线l设l y k x l P x y Q x y :,与双曲线交于,、,=-()()()11122[]ΘOP OQ x x y y x x k x x x x k x x x x i →→=∴+=∴+--=∴+-++=·00110101212122121221212()()()()由得则,y k x y x k x k x k x x k k x x k k ii =--=⎧⎨⎪⎩⎪--+-=+=-=--()()()13131633063133312222212221222由(i )(ii )得k 230+= ∴k 不存在,即不存在满足条件的直线l .8、设M 是椭圆22:1124x y C +=上的一点,P 、Q 、T 分别为M 关于y 轴、原点、x 轴的对称点,N 为椭圆C 上异于M 的另一点,且MN⊥MQ,QN 与PT 的交点为E ,当M 沿椭圆C 运动时,求动点E 的轨迹方程.解:设点的坐标112211(,),(,)(0),(,),M x y N x y x y E x y ≠则111111(,),(,),(,),P x y Q x y T x y ----……1分221122221,(1)124 1.(2)124x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩L L L L L L L L ………3分 由(1)-(2)可得1.3MN QN k k •=-…6分又MN⊥MQ,111,,MN MQ MN x k k k y ⋅=-=-所以11.3QN y k x =直线QN 的方程为1111()3yy x x y x =+-,又直线PT 的方程为11.x y x y =-从而得1111,.22x x y y ==-所以112,2.x x y y ==-代入(1)可得221(0),3x y xy +=≠此即为所求的轨迹方程. 9、已知:直线L 过原点,抛物线C 的顶点在原点,焦点在x 轴正半轴上。


如皋市名师教育培训学校高中数学圆锥曲线专项训练材料(名校经典题型附答案)1、(省启东中学高三综合测试二)已知动圆过定点P(1,0),且与定直线L:x=-1相切,点C在l上.(1)求动圆圆心的轨迹M的方程;错误!未找到引用源。
(i)问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由(ii)当△ABC为钝角三角形时,求这种点C的纵坐标的取值围.解:(1)依题意,曲线M是以点P为焦点,直线l为准线的抛物线,所以曲线M的方程为y2=4x.错误!未找到引用源。
错误!未找到引用源。
假设存在点C(-1,y),使△ABC为正三角形,则|BC|=|AB|且|AC|=|AB|,即错误!未找到引用源。
因此,直线l上不存在点C,使得△ABC是正三角形.(ii)解法一:设C(-1,y)使△ABC成钝角三角形,错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
∠CAB为钝角.错误!未找到引用源。
错误!未找到引用源。
错误!未找到引用源。
错误!未找到引用源。
.该不等式无解,所以∠ACB不可能为钝角.因此,当△ABC为钝角三角形时,点C的纵坐标y的取值围是:错误!未找到引用源。
.解法二:以AB为直径的圆的方程为:错误!未找到引用源。
.错误!未找到引用源。
当直线l上的C点与G重合时,∠ACB为直角,当C与G 点不重合,且A,B,C三点不共线时,∠ACB为锐角,即△ABC中∠ACB不可能是钝角.因此,要使△ABC为钝角三角形,只可能是∠CAB或∠CBA为钝角.错误!未找到引用源。
.错误!未找到引用源。
.错误!未找到引用源。
A,B,C三点共线,不构成三角形.因此,当△ABC为钝角三角形时,点C的纵坐标y的取值围是:错误!未找到引用源。
2、(省启东中学高三综合测试三)(1)在双曲线xy=1上任取不同三点A、B、C,证明:⊿ABC的垂心H 也在该双曲线上;(2)若正三角形ABC的一个顶点为C(―1,―1),另两个顶点A、B在双曲线xy=1另一支上,求顶点A、B的坐标。

高中数学组卷圆锥曲线练习一.解答题(共50小题)1.(2017秋•仙游县期末)设椭圆+=1(a>2)的离心率为,斜率为k的直线l过点E(0,1)且与椭圆交于C,D两点.(1)求椭圆的方程;(2)若直线l与x轴相交于点G,且=,求k的值;(3)设点A为椭圆的下顶点,k AC,k AD分别为直线AC,AD的斜率,证明:对任意的k,恒有k AC•k AD=﹣2.2.(2018•河南模拟)如图,椭圆W:+=1(a>b>0)的焦距与椭圆Ω:+y2=1的短轴长相等,且W与Ω的长轴长相等,这两个椭圆的在第一象限的交点为A,直线l经过Ω在y轴正半轴上的顶点B且与直线OA(O为坐标原点)垂直,l与Ω的另一个交点为C,l 与W交于M,N两点.(1)求W的标准方程:(2)求.3.(2018•株洲一模)已知椭圆与直线l:bx﹣ay=0都经过点.直线m与l平行,且与椭圆C交于A,B两点,直线MA,MB与x轴分别交于E,F两点.(1)求椭圆C的方程;(2)证明:△MEF为等腰三角形.4.(2018•河南模拟)已知抛物线E:y2=2px(p>0),斜率为k且过点M(3,0)的直线l 与E交于A,B两点,且,其中O为坐标原点.(1)求抛物线E的方程;(2)设点N(﹣3,0),记直线AN,BN的斜率分别为k1,k2,证明:为定值.5.(2018•资阳模拟)已知椭圆C:的离心率,且过点.(1)求椭圆C的方程;(2)过P作两条直线l1,l2与圆相切且分别交椭圆于M,N 两点.①求证:直线MN的斜率为定值;②求△MON面积的最大值(其中O为坐标原点).6.(2018•黄浦区一模)已知椭圆Γ:+=1(a>b>0),过原点的两条直线l1和l2分别与Γ交于点A、B和C、D,得到平行四边形ACBD.(1)当ACBD为正方形时,求该正方形的面积S;(2)若直线l1和l2关于y轴对称,Γ上任意一点P到l1和l2的距离分别为d1和d2,当d12+d22为定值时,求此时直线l1和l2的斜率及该定值.(3)当ACBD为菱形,且圆x2+y2=1内切于菱形ACBD时,求a,b满足的关系式.7.(2018•玉溪模拟)已知椭圆(a>b>0)的离心率为、F2分别为椭圆C的左、右焦点,过F2的直线l与C相交于A、B两点,△F1AB的周长为.(I)求椭圆C的方程;(II)若椭圆C上存在点P,使得四边形OAPB为平行四边形,求此时直线l的方程.8.(2018•淮南一模)椭圆C:=1(a>b>0)的左顶点为A,右焦点为F,上顶点为B,下顶点为C,若直线AB与直线CF的交点为(3a,16).(1)求椭圆C的标准方程;(2)点P(m,0)为椭圆C的长轴上的一个动点,过点P且斜率为的直线l交椭圆C于S,T两点,证明:|PS|2+|PT|2为定值.9.(2018•杨浦区一模)设直线l与抛物线Ω:y2=4x相交于不同两点A、B,O为坐标原点.(1)求抛物线Ω的焦点到准线的距离;(2)若直线l又与圆C:(x﹣5)2+y2=16相切于点M,且M为线段AB的中点,求直线l的方程;(3)若,点Q在线段AB上,满足OQ⊥AB,求点Q的轨迹方程.10.(2018•陕西一模)已知椭圆+=1(a>b>0)的左右焦点分别为F1和F2,由4个点M(﹣a,b)、N(a,b)、F2和F1组成了一个高为,面积为3的等腰梯形.(1)求椭圆的方程;(2)过点F1的直线和椭圆交于两点A、B,求△F2AB面积的最大值.11.(2018•重庆一模)如图,A,B是椭圆长轴的两个端点,P,Q是椭圆C 上都不与A,B重合的两点,记直线BQ,AQ,AP的斜率分别是k BQ,k AQ,k AP.(1)求证:;(2)若k AP=4k BQ,求证:直线PQ恒过定点,并求出定点坐标.12.(2018•榆林一模)已知抛物线E:y2=2px(p>0)的准线与x轴交于点k,过点k做圆C:(x﹣5)2+y2=9的两条切线,切点为.(1)求抛物线E的方程;(2)若直线AB是讲过定点Q(2,0)的一条直线,且与抛物线E交于A,B两点,过定点Q作AB的垂线与抛物线交于G,D两点,求四边形AGBD面积的最小值.13.(2018•南充模拟)已知椭圆+=1(a>b>0)的左右焦点分别为F1、F2,左顶点为A,若|F1F2|=2,椭圆的离心率为e=(Ⅰ)求椭圆的标准方程.(Ⅱ)若P是椭圆上的任意一点,求•的取值范围.14.(2018•闵行区一模)已知椭圆的右焦点是抛物线Γ:y2=2px的焦点,直线l 与Γ相交于不同的两点A(x1,y1)、B(x2,y2).(1)求Γ的方程;(2)若直线l经过点P(2,0),求△OAB的面积的最小值(O为坐标原点);(3)已知点C(1,2),直线l经过点Q(5,﹣2),D为线段AB的中点,求证:|AB|=2|CD|.15.(2018•恩施州一模)设直线l的方程为x=m(y+2)+5,该直线交抛物线C:y2=4x于P,Q两个不同的点.(1)若点A(5,﹣2)为线段PQ的中点,求直线l的方程;(2)证明:以线段PQ为直径的圆M恒过点B(1,2).16.(2018•凉山州模拟)若A(x1,y1),B(x2,y2)是椭圆E:+y2=1上位于x轴上方两点,且x1+x2=2.(1)若y1+y2=1,求线段AB的垂直平分线的方程;(2)求直线AB在y轴上截距的最小值.17.(2018•东莞市模拟)已知椭圆C:的离心率为,且过点A(2,1).(Ⅰ)求椭圆C的方程;(Ⅱ)若P,Q是椭圆C上的两个动点,且使∠PAQ的角平分线总垂直于x轴,试判断直线PQ的斜率是否为定值?若是,求出该值;若不是,说明理由.18.(2018•化州市二模)已知椭圆C:+=1(a>b>0)的焦距为2,设右焦点为F,过原点O的直线l与椭圆C交于A,B两点,线段AF的中点为M,线段BF的中点为N,且•=.(1)求弦AB的长;(2)当直线l 的斜率k=,且直线l′∥l 时,l′交椭圆于P,Q,若点A在第一象限,求证:直线AP,AQ与x轴围成一个等腰三角形.19.(2018•遂宁模拟)设椭圆+=1(a>b>0)的离心率e=,左焦点为F,右顶点为A,过点F的直线交椭圆于E,H两点,若直线EH垂直于x轴时,有|EH|=(1)求椭圆的方程;(2)设直线l:x=﹣1上两点P,Q关于x轴对称,直线AP与椭圆相交于点B(B异于点A),直线BQ与x轴相交于点D.若△APD的面积为,求直线AP的方程.20.(2018•张掖一模)已知椭圆的左右焦点分别为F1,F2,上顶点为M,若直线MF1的斜率为1,且与椭圆的另一个交点为N,△F2MN的周长为.(1)求椭圆的标准方程;(2)过点F1的直线l(直线l的斜率不为1)与椭圆交于P,Q两点,点P在点Q的上方,若,求直线l的斜率.21.(2018•浙江模拟)已知曲线C:y2=4x,M:(x﹣1)2+y2=4(x≥1),直线l与曲线C相交于A,B两点,O为坐标原点.(Ⅰ)若,求证:直线l恒过定点,并求出定点坐标;(Ⅱ)若直线l与曲线M相切,求的取值范围.22.(2018•松江区一模)已知椭圆E:=1(a>b>0)经过点,其左焦点为,过F点的直线l交椭圆于A、B两点,交y轴的正半轴于点M.(1)求椭圆E的方程;(2)过点F且与l垂直的直线交椭圆于C、D两点,若四边形ACBD的面积为,求直线l的方程;(3)设,,求证:λ1+λ2为定值.23.(2018•全国I模拟)设O为坐标原点,椭圆C:+=1,斜率为k的动直线l(l不经过O)与C交于P,Q两点,M为线段PQ的中点.(1)设直线OM的斜率为k1,求k1k的值;(2)若l经过点(0,),求k的取值范围,并求△OPQ的面积的最大值.24.(2018•佛山一模)已知椭圆的右顶点与抛物线的焦点重合,椭圆C1的离心率为,过椭圆C1的右焦点F且垂直于x 轴的直线截抛物线所得的弦长为4.(1)求椭圆C1和抛物线C2的方程;(2)过点A(﹣2,0)的直线l与C2交于M,N两点,点M关于x轴的对称点为M',证明:直线M'N恒过一定点.25.(2018•一模拟)已知椭圆C:+=1(a>b>0)的左、右焦点为F1,F2,离心率为,点P在椭圆C上,且△PF1F2的面积的最大值为2.(1)求椭圆C的方程;(2)已知直线l:y=kx+2(k≠0)与椭圆C交于不同的两点M,N,若在x轴上存在点G,使得|GM|=|GN|,求点G的横坐标的取值范围.26.(2018•顺德区一模)已知椭圆C的中心在原点,焦点在x轴上,离心率等于,它的一个顶点恰好是抛物线x2=﹣4y的焦点.(Ⅰ)求椭圆C的标准方程;(Ⅱ)若圆O:x2+y2=r2与椭圆C交于A,B,C,D四点,当半径r为多少时,四边形ABCD 的面积最大?并求出最大面积.27.(2018•武侯区校级模拟)已知A(x0,0),B(0,y0)两点分别在x轴和y轴上运动,且|AB|=1,若动点P(x,y)满足.(1)求出动点P的轨迹对应曲线C的标准方程;(2)直线l:x=ty+1与曲线C交于A、B两点,E(﹣1,0),试问:当t变化时,是否存在一直线l,使△ABE得面积为?若存在,求出直线l的方程;若不存在,说明理由.28.(2018•沈阳一模)设O为坐标原点,动点M在椭圆上,过M作x轴的垂线,垂足为N,点P满足.(Ⅰ)求点P的轨迹方程E;(Ⅱ)过F(1,0)的直线l1与点P的轨迹交于A、B两点,过F(1,0)作与l1垂直的直线l2与点P的轨迹交于C、D两点,求证:为定值.29.(2018•曲靖一模)如图,已知椭圆的左焦点为F(﹣1,0),过点F做x轴的垂线交椭圆于A,B两点,且|AB|=3.(1)求椭圆C的标准方程:(2)若M,N为椭圆上异于点A的两点,且直线AM,AN的倾斜角互补,问直线MN的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.30.(2018•一模拟)已知椭圆C:的离心率为,且以两焦点为直径的圆的内接正方形面积为2.(1)求椭圆C的标准方程;(2)若直线l:y=kx+2与椭圆C相交于A,B两点,在y轴上是否存在点D,使直线AD与BD的斜率之和k AD+k BD为定值?若存在,求出点D坐标及该定值,若不存在,试说明理由.31.(2018•茂名一模)已知椭圆C1以直线所过的定点为一个焦点,且短轴长为4.(Ⅰ)求椭圆C1的标准方程;(Ⅱ)已知椭圆C2的中心在原点,焦点在y轴上,且长轴和短轴的长分别是椭圆C1的长轴和短轴的长的λ倍(λ>1),过点C(﹣1,0)的直线l与椭圆C2交于A,B两个不同的点,若,求△OAB的面积取得最大值时直线l的方程.32.(2018•拉萨一模)已知椭圆的长轴长是短轴长的倍,且过点.(1)求椭圆的标准方程;(2)若△OAB的顶点A、B在椭圆上,OA所在的直线斜率为k1,OB所在的直线斜率为k2,若,求的最大值.33.(2018•玉溪模拟)已知点M(4,0)、N(1,0),若动点P满足.(1)求动点P的轨迹C;(2)在曲线C上求一点Q,使点Q到直线l:x+2y﹣12=0的距离最小.34.(2018•沈阳一模)已知椭圆的左、右焦点分别为F1、F2,点在椭圆上,且有.(1)求椭圆C的标准方程;(2)过F2的直线l与椭圆交于A、B两点,求△AOB面积的最大值.35.(2018•佛山一模)已知椭圆的焦点与抛物线的焦点F重合,且椭圆C1的右顶点P到F的距离为;(1)求椭圆C1的方程;(2)设直线l与椭圆C1交于A,B两点,且满足PA⊥PB,求△PAB面积的最大值.36.(2018•甘肃一模)已知椭圆C:=1(a>b>0)的离心率为,以椭圆长、短轴四个端点为顶点的四边形的面积为4.(Ⅰ)求椭圆C的方程;(Ⅱ)如图所示,记椭圆的左、右顶点分别为A、B,当动点M在定直线x=4上运动时,直线AM、BM分别交椭圆于P、Q两点,求四边形APBQ面积的最大值.37.(2018•淮南一模)已知椭圆的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线x+y+1=0与以椭圆C的上焦点为圆心,以椭圆的长半轴长为半径的圆相切.(1)求椭圆C的方程;(2)设P为椭圆C上一点,若过点M(0,2)的直线l与椭圆C相交于不同的两点S和T,满足(O为坐标原点),求实数t的取值范围.38.(2018•安阳一模)如图,在平面直角坐标系xOy中,直线l1:y=x与直线l2:y=﹣x之间的阴影部分记为W,区域W中动点P(x,y)到l1,l2的距离之积为1.(Ⅰ)求点P的轨迹C的方程;(Ⅱ)动直线l穿过区域W,分别交直线l1,l2于A,B两点,若直线l与轨迹C有且只有一个公共点,求证:△OAB的面积恒为定值.39.(2018•淮北一模)已知椭圆C:+=1(a>b>0),其左右焦点为F1,F2,过F1直线l:x+my+=0与椭圆C交于A,B两点,且椭圆离心率e=;(Ⅰ)求椭圆C的方程;(Ⅱ)若椭圆存在点M,使得2=+,求直线l的方程.40.(2018•资阳模拟)已知椭圆C:的离心率,且过点.(1)求椭圆C的方程;(2)过P作两条直线l1,l2与圆相切且分别交椭圆于M,N 两点,求证:直线MN的斜率为定值.41.(2018•浙江模拟)已知椭圆.(1)若椭圆C的一个焦点为(1,0),且点在C上,求椭圆C的标准方程;(2)已知椭圆C上有两个动点A(x1,y1),B(x2,y2),O为坐标原点,且OA⊥OB,求线段|AB|的最小值(用a,b表示).42.(2018•江苏一模)如图,在平面直角坐标系xOy中,椭圆C:(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点()处时,点Q的坐标为().(1)求椭圆C的标准方程;(2)设直线MN交y轴于点D,当点M,N均在y轴右侧,且=2时,求直线BM的方程.43.(2018•南充模拟)已知椭圆的左焦点为F,左顶点为A.(1)若P是椭圆上的任意一点,求的取值范围;(2)已知直线l:y=kx+m与椭圆相交于不同的两点M,N(均不是长轴的端点),AH⊥MN,垂足为H且,求证:直线l恒过定点.44.(2018•茂名一模)已知椭圆C1:((a>b>0))的一个焦点为F1,且经过点P.(I)求椭圆C1的标准方程;(II)已知椭圆C2的中心在原点,焦点在y轴上,且长轴和短轴的长分别是椭圆C1的长轴和短轴的长的λ倍(λ>1),过点C(﹣1,0)的直线l与椭圆C2交于A,B两个不同的点,若,求△OAB 面积取得最大值时直线l的方程.45.(2018•化州市二模)如图,已知椭圆C:,其左右焦点为F1(﹣1,0)及F2(1,0),过点F1的直线交椭圆C于A,B两点,线段AB的中点为G,AB的中垂线与x 轴和y轴分别交于D,E两点,且|AF1|、|F1F2|、|AF2|构成等差数列.(1)求椭圆C的方程;(2)记△GF1D的面积为S1,△OED(O为原点)的面积为S2.试问:是否存在直线AB,使得S1=S2?说明理由.46.(2018•徐汇区一模)已知椭圆E:(a>b>0)的左,右焦点分别为F1,F2,且F1,F2与短轴的一个端点Q构成一个等腰直角三角形,点P()在椭圆E上,过点F2作互相垂直且与x轴不重合的两直线AB,CD分别交椭圆E于A,B,C,D且M,N 分别是弦AB,CD的中点(1)求椭圆的方程(2)求证:直线MN过定点R(,0)(3)求△MNF2面积的最大值.47.(2018•普陀区一模)设点F1、F2分别是椭圆(t>0)的左、右焦点,且椭圆C上的点到点F2的距离的最小值为,点M、N是椭圆C上位于x轴上方的两点,且向量与向量平行.(1)求椭圆C的方程;(2)当时,求△F1MN的面积;(3)当时,求直线F2N的方程.48.(2018•历城区校级一模)已知抛物线y2=4x,直线l:x+2y﹣2b=0与抛物线交于A,B两点.(Ⅰ)若以AB为直径的圆与x轴相切,求该圆的方程;(Ⅱ)若直线l与y轴负半轴相交,求△AOB(O为坐标原点)面积的最大值.49.(2018•崇明县一模)在平面直角坐标系中,已知椭圆C:+y2=1 (a>0,a≠1)的两个焦点分别是F1,F2,直线l:y=kx+m(k,m∈R)与椭圆交于A,B两点.(1)若M为椭圆短轴上的一个顶点,且△MF1F2是直角三角形,求a的值;(2)若k=1,且△OAB是以O为直角顶点的直角三角形,求a与m满足的关系;(3)若a=2,且k OA•k OB=﹣,求证:△OAB的面积为定值.50.(2018•玉溪模拟)已知F(1,0),P是平面上一动点,P到直线l:x=﹣1上的射影为点N,且满足(Ⅰ)求点P的轨迹C的方程;(Ⅱ)过点M(1,2)作曲线C的两条弦MA,MB,设MA,MB所在直线的斜率分别为k1,k2,当k1,k2变化且满足k1+k2=﹣1时,证明直线AB恒过定点,并求出该定点坐标.。

专题15 圆锥曲线的综合应用基础巩固一、选择题1.“35m -<<”是“方程22153x y m m -=-+表示双曲线”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.若抛物线()220y px p =>的焦点是双曲线2213-=x y p p的一个焦点,则p =()A .2B .4C .8D .163.过双曲线2212y x -=的右焦点F 作直线l 交双曲线于,A B 两点,若AB 4=,则这样的直线l 有( )A .1条B .2条C .3条D .0条4.设圆锥曲线C 的两个焦点分别为12,F F ,若曲线C 上存在点P 满足1122::4:3:2PF F F PF =,则曲线C 的离心率等于( )A .12或32 B . 12或23 C . 12 D .235.已知双曲线2222x y a b-=1(a >0,b >0)的两条渐近线与抛物线y 2=8x 的准线分别交于M ,N 两点,A为双曲线的右顶点,若双曲线的离心率为2,且△AMN 为正三角形,则双曲线的方程为( )A .221824x y -=B .2211648x y -=C .2212472x y -=D .22164192x y -=二、填空题6.已知椭圆221x y m n +=与双曲线()221,,,x y m n p q R p q+-=∈有共同的焦点12,F F ,P 是椭圆和双曲线的一个交点,则12=PF PF ________.7.已知圆221x y +=与抛物线2y x h =+有公共点,则实数h 的取值范围是8.已知椭圆C :22194x y +=,点M 与C 的焦点不重合,若M 关于C 的焦点的对称点分别为A ,B ,线段MN 的中点在C 上,则AN BN += .三、解答题9.已知双曲线1C,且与椭圆2C :22194x y+=有公共焦点,(1)求双曲线1C 的方程;(2)若抛物线的焦点到准线的距离等于椭圆2C 的焦距,求该抛物线方程. 10.已知C 过点(0,1)A ,圆心C 在抛物线22x y =上运动,若MN 为C 在x 轴上截得的弦,设1||=AM t ,2||=AN t .(1)当C 运动时,||MN 是否变化?证明你的结论.(2)求1212+t t t t 的最大值,并求出此时C 方程.知能提升一、选择题11.设1e ,2e 分别为具有公共焦点1F 与2F 的椭圆和双曲线的离心率,P 为两曲线的一个公共点,且满足120PF PF →→⋅=,则221211e e +的值为( ) A .12B .1C .2D .412.抛物线28y x =的焦点F 是双曲线22221(0,0)x y a b a b-=>>的一个焦点,()(),0A m n n >为抛物线上一点,直线AF 与双曲线有且只有一个交点,若||8AF =,则该双曲线的离心率为( )ABC .2D 二、填空题13.抛物线22y x =的一条弦被()4,2A平分,那么这条弦所在的直线方程是__________.14.设1e ,2e 分别为具有公共焦点1F 与2F 的椭圆和双曲线的离心率,P 为两曲线的一个公共点,且满足120PF PF ⋅=,则22124e e +的最小值为__________.三、解答题15.已知椭圆2222:1(0)x y C a b a b+=>>过点31,2⎛⎫ ⎪⎝⎭,且其离心率为12,过坐标原点O 作两条互相垂直的射线与椭圆C 分别相交于M ,N 两点.(1)求椭圆C 的方程;(2)是否存在圆心在原点的定圆与直线MN 总相切?若存在,求定圆的方程;若不存在,请说明理由.专题15 圆锥曲线的综合应用基础巩固一、选择题1.“35m -<<”是“方程22153x y m m -=-+表示双曲线”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】C【解析】可以直接求出方程22153x y m m -=-+表示双曲线的充要条件,即为(5)(3)035m m m -+>⇔-<<,因此可知条件和结论之间的关系是充要条件,故选C.2.若抛物线()220y px p =>的焦点是双曲线2213-=x y p p的一个焦点,则p =()A .2B .4C .8D .16【答案】D【解析】抛物线()220y px p =>的焦点是02p ⎛⎫ ⎪⎝⎭,,双曲线2213-=x y p p的一个焦点是(),由条件得2p=解得16p =. 故选D.3.过双曲线2212y x -=的右焦点F 作直线l 交双曲线于,A B 两点,若AB 4=,则这样的直线l 有( )A .1条B .2条C .3条D .0条【答案】C【解析】由题可知:双曲线的方程为2212y x -=所以可知:1,a b c ==)F当过焦点F 直线斜率不存在时,AB 4=,有1条 当过焦点F 直线斜率存在时,双曲线的定点距离为224a =<,有2条 故选C4.设圆锥曲线C 的两个焦点分别为12,F F ,若曲线C 上存在点P 满足1122::4:3:2PF F F PF =,则曲线C 的离心率等于( )A .12或32 B . 12或23 C . 12 D .23【答案】A【解析】设1||4PF m =,则依题有122||3,||2F F m PF m ==,当该圆锥曲线为椭圆时,椭圆的离心率1212||2312||||422F F c m e a PF PF m m ====++;当该圆锥曲线为双曲线时,双曲线的离心率为1212||2332||||422F F c m e a PF PF m m ====--;综上可知, 故选A.5.已知双曲线2222x y a b-=1(a >0,b >0)的两条渐近线与抛物线y 2=8x 的准线分别交于M ,N 两点,A为双曲线的右顶点,若双曲线的离心率为2,且△AMN 为正三角形,则双曲线的方程为( )A .221824x y -=B .2211648x y -=C .2212472x y -=D .22164192x y -=【答案】B【解析】由双曲线的离心率为2可得:2c e a ==,所以b a == 所以双曲线2222x y a b-=1(a >0,b >0)的渐近线方程为:b y x a =±=,又抛物线y 2=8x 的准线方程为:2x =-,由2y x ⎧=⎪⎨=-⎪⎩得:2y x ⎧=⎪⎨=-⎪⎩2y x ⎧=-⎪⎨=-⎪⎩(M -,(2,N -- A 为双曲线的右顶点,且△AMN为正三角形,则:2a +4a =所以b =所以双曲线的方程为2211648x y -=。

培优点十九圆锥曲线综合1.直线过定点2xxF轴的离心率为且垂直于,过左焦点例1:已知中心在原点,焦点在轴上的椭圆C2P两点,且,的直线交椭圆于.Q2?2PQ C(1)求的方程;C??22MM作椭是直线处的切线,点(2)若直线是圆上任一点,过点上的点2,28??yx ll ABMAMBAB过定点,,切点分别为,设切线的斜率都存在.求证:直线圆的切线,,C并求出该定点的坐标.22yx??.2)证明见解析,;【答案】(1)(2,11??8422yx??, 1)由已知,设椭圆的方程为【解析】(0?b??1?a C ??,不妨设点,代入椭圆方程得因为,1??22PQ?2?c,P22ba22ab22cc212222,,,所以,又因为,所以8ba??b2?4?e?cb?1??2a22b22yx所以的方程为.1??C 84??,即,(2)依题设,得直线的方程为2x???y?204?x?y?l??????,,,设yxABx,y,Mx,y210120??MA,由切线的斜率存在,设其方程为xxk?y?y?11??xxy?k??y?11???2????22,联立得,0?28y?xkx?4ky?kx?x?2k1??22yx1111?1??48???22??????22?0?8k2y?1?Δ?16kkx?ykx4?,由相切得??1111??2??2222,即,化简得4?8?y?kxk04yk?y?x?8?kx?2111111xyxyx11111MA???k?的方程为因为方程只有一解,所以,所以切线??1xx?yy???,11y21xx?2yy?8xx?2yy?8MB,同理,切线即的222yyx2?8?111x方程为,2211.8y??2yxx???0011AB的方程为,所以直线,所以又因为两切线都经过点yx,M?008y??2yxx?02208y??2yxx,00??4y??xAB的方程可化为,所以直线,又82y4?x?xx?00000??2yx2?x????,,令即,得08y?x8x?2y????00?y?881?y????AB所以直线.恒过定点2,1.面积问题222yxb??FF直线,焦距为、4例2:已知椭圆,的左、右焦点分别为0a?b?1??x?:yl 21122baclFlEAB1?与线段两点,的直线关于直线与椭圆相交于、在椭圆上.斜率为的对称点221PABD相交于点两点.,与椭圆相交于、C1)求椭圆的标准方程;()求四边形面积的取值范围.(2ACBD223232yx??,;.2)【答案】(1)(1????3948?????????EFFEF【解析】(1)由椭圆焦距为4,设,连结,,,设2,0F?2,0F21121bcb222???c??ab,,又,得则,?tan?cos?sin aacFF2csin90?1ac21,??????e???bc??b?|?|EFsin?sin??ca90EF2a?21aa22yx222a?bc?c?b?c?2a?8,所以椭圆方程为解得.,1??84????m+?y?xlyx,D,Cxy方程:、2()设直线,,22211.4?m??xx22?yx?213???1?22,所以,由,得08?x3?4mx?2m??48?28m?2??m?y??x?xx??213?222238????x?y?A6,66,?6Bl,,得:,代入椭圆得由(,1)知直线?AB????133333????44???6m?6,lPAB,得由直线相交于点与线段,??233??????2,28m4?22416m2xx?2??m?+12x2CD?x???8xx2?211221393116321??1kk?l?l,,,知与而+12mAB??S?CD??12ACBD ll291232443232163??????22?m???,06,6?m,+12m??由,得,,所以??????333993??????3232??,?.面积的取值范围四边形ACBD??93??3.参数的值与范围??????20?2px?pC:yF的上,过焦点3例:已知抛物线的焦点在抛物线,点1,2F1,0A C M,两点.交抛物线于直线NCl(1)求抛物线的方程以及的值;AF C22??xFNMF?B(2)记抛物线的准线与的值.轴交于点,,若,求40BN?BM?C2?3??2(),;1【答案】(.)22AF?x?y4????20p??2:Cypx,的焦点【解析】(1)抛物线1,0F p2;,则,抛物线方程为42p?xy4?1??2p??1,2A.点在抛物线上,C2???AF?12??????,设)依题意,(2、,设,y,MxyF1,0Nx,1?xl:my?2211.2?x4?y2x,得联立方程,消去.0my?4?y?4?1my?x??1my?4mx?y?y???1112①,且,所以??1my??4x?yy???2212???????y?y?FNMF?,即,则又,y1?x,?y,??1x2121122??4???y1?????m4y?1???2??????,则,,22?y得,代入①得,消去2?4m???21,0B?yBN?,BM?xx?1,y?121122222????2222y?x?1y?1?BM?|BN?|x?BM?BN?则2121??2222yy??2?x??2?xx?x??????2228?y?y???m4?1myy2112????4222,222111??2222y??2??2my?my?(?my?1)2?(my?1)y21112216m?16m??16m40?84?4m?m?m??18124?2?2?3.当,解得,故40?m?16?40m16?m2.弦长类问题4222xyx??2的顶点,的左右顶点是双曲线4:已知椭圆且椭圆例1?ya?b?0?:?C:?1C 2122ab33CC.的上顶点到双曲线的渐近线的距离为212C(1)求椭圆的方程;1QMCMCQ5?OQ?OQ?,求,两点,与相交于两点,且与(2)若直线,相交于l22111221的取值范围.MM??2.;(2)【答案】(1)212x1??y100,?3??2C3a?b0,)由题意可知:1(【解析】,,又椭圆的上顶点为1.3C,双曲线的渐近线为:0y?x?x?y??323?3b23x2.由点到直线的距离公式有:,∴椭圆方程1??b?1??y2232x2y并整理,代入)易知直线,消去的斜率存在,设直线(2的方程为m??kxy1?y?3得:??222,033mx???6kmx?k1?32?1?3k?02?1?3k?0??C相交于两点,则应有:,要与? ??????22222220m?3??41?3k?336k?mm?1?3k????????,设,yQxx,yQ,2112122?m3?36km则有:,.?xx???xx212122k?31k?31????????22.又m?km?m??x1?k?x?OQOQ??xx?yy?xxxkx?mxkx211121*********????????2222225?OQ?OQ?,又:,所以有:?k?5?6km?m1?331?k?m?3??212k?3122k?1?9m?,②??2222y,将,代入并整理得:,2x消去my?kx?1??y0m??x3?6kmx?1?3k33????222222.③要有两交点,则m?1?04??1?3k3k3m??Δ?36k3m12.由①②③有?0?k92?33m?6km????.有,设,、yxMMx,y,??xx??xx????2222k3413m??36k3m?414332434322k31?k31???22k31???22k?3m9??432?MM?1k?21??22k1?312k2k14422222.?k?1?kMM???1?k1?MM?k??19m代入有将.2112??22k3?12k3?1.??11??2t?0,,,,令kt?12??MM??21??29??2k1?3??t1t?1?t1??????t?0,?'tf?tf?.,令??32????9??t1t?331?11????????t??0,0,t内单调递增,内恒成立,故函数在所以在t0tff'?????99????5??????10M?0,?0,?Mft.故???2172??5.存在性问题??222yx??????A1,点例5:已知椭圆,,的左、右焦点分别为1,0?1,0FF0C:??1?ab?????21222ab??在椭圆上.C(1)求椭圆的标准方程;C M,有两个不同交点时,能在,使得当直线)是否存在斜率为2的直线与椭圆(2NCll5PM?NQP?若存在,求出直线,在椭圆上找到一点直线,满足上找到一点的Q Cl?y3方程;若不存在,说明理由.2x2;(2))不存在,见解析.【答案】(11?y?2【解析】(1)设椭圆的焦距为,则,1?cCc2??A1,,在椭圆∵上,∴??1???221AF2a??AF C 2????2222????????21222????2x22222a?1c?b?a?.的方程为,故椭圆,∴1?y?C2(2)假设这样的直线存在,设直线的方程为,t2x??y l5??????????,Pxy,xyD,xQ,x,MxyNy,,,,的中点为设,MN??3004242113??y?2x?t?22x,得由,消去,0?8?tty?9y2??22x?2y?2?yy?tt2??22,且∴,,故且123t??3??y?y?y?0t?36?Δ?4t8?012929NQ?PM为平行四边形,由,知四边形PMQNDD的中点,因此的中点,而为线段为线段PQ MN5y?t15?2t43?y?,,得∴?y 049297不在椭圆上,,可得,∴点又Q3?t??31?y???43.故不存在满足题意的直线l对点增分集训一、解答题2????2PP过点相外切,动圆圆心并且与圆1.已知动圆.的轨迹为2,0F4??x?2F:y C21的轨迹方程;(1)求曲线C1????lBA,直线、,设点与轨迹交于(2)过点两点,设直线的直线1,0F2,0?D C?xl:122ADBMM于,求证:直线经过定点.交l2y??2;(1)(2)见解析.【答案】0?1x??x3,1)由已知,【解析】(2??|PF ?|PF ?2PF| |PF2211P,,轨迹为双曲线的右支,,42c??|FF 2C2a?2?a?1c212y??2?.标准方程曲线0x???1x C3xBM必过)由对称性可知,直线(2轴的定点,31????????,MlBM1,02,?2,33BPA经过点,的斜率不存在时,,,,知直线当直线??122????????ly,By,2ky:l?x?Axx的斜率存在时,不妨设直线当直线,,,122111. ??y3y31y1??111y?,M1?AD:y?x时,,,当,直线?x????????M1?x1x?212x?22??111??2?x?y?k22k?43?4k?????2222,得,,?xx??xx0k?33?kx?4kx??4???21k?kBM,经过点,即下面证明直线,即证?1,0P 2121223k?k3?223x?y?3???3yyPBPM x?1x?121?3yx?3y?xy?yy?kx?2ky?kx?2k,即,,由2121122211??234?k22k3k4?4??4???0?5?,即整理得,045xx???4xx?????BMBM.经过点过定点即证,直线1,0P1,0223yx????1,AB分别为椭圆的左顶2211222?3?3kk?3k点、下顶点,在椭圆,上,设2.已知点0bE:??1?a???222ba??221AB.原点到直线的距离为O7E1)求椭圆的方程;(yxEPDPBPA两点,求分别交轴于在第一象限内一点,直线轴、,,(2)设为椭圆C的面积.四边形ABCD22yx23.2);)【答案】(1(1?? 4392231yx??4??1,1??)因为椭圆,有经过点,【解析】(10E:a??1b????22222baba??221ab?AB,的距离为由等面积法,可得原点到直线O722a?b22yx b?3E的方程为联立两方程解得,.,所以椭圆1??E:2a?4322xy????2200?1?0?x?P0,x,yy.,则(,即2)设点12??4x3y00000043y2y??00?2y?yPA:?x.直线,令,得0x?D x?2x?20032?x2y?2232yx?y?3300000从而有.,同理,可得?BD???AC32x?x2?y3?000.x110000所以四边形的面积为??AC?BD?2?22x3?y0022x383y3xy?12x?xy?12x?83y12?12?4?4y?12?43110000000000????223y?2y?3x?2?xy?3x?2y23x00000000 y?433xy?6x12?20000.32??3y?2xy?3x?2000032所以四边形的面积为.ABCD2??2P上,且有点的圆心,在圆的半径3.已知点为圆是圆上的动点,点Q8??yx?1CPC??0?MQ?APAPM,满足.和,上的点1,0AAM2AP?P在圆上运动时,判断(1)当点点的轨迹是什么?并求出其方程;Q22F,1)若斜率为的直线与圆中所求点的轨迹交于不同的两点相切,与((2)Q1yx??kl43H的取值范围.(其中是坐标原点),且,求kO??OFOF?542x222A)2;,长轴长为(2【答案】(1)是以点,的椭圆,为焦点,焦距为1??y C2????2233,?,?.????3223????AP的垂直平分线,)由题意是线段【解析】(1MQ所以,2?22?CAQC?QP?QC?QA?CP?22A的椭圆,为焦点,焦距为2所以点的轨迹是以点,,长轴长为Q C222a?,∴,,1ab???c1c?2x2.故点的轨迹方程是Q1??y2????,,,)设直线(2:yHy,xF,xbkx??y l2112b22221??1b?k与圆直线,,即相切,得1?xy?l21?k ??222y得:联立,消去,0?4kbx?2b??1?2k2x2??b?kx?y???????2222222,得,2?x21?y??0k?02b1?1??8?2k8??Δ16kbbk?4?1?2k22?2bkb4,,?xx?x?x?????22??2k?2b1?kb4?????222b?kb?OF?OH?xx?yy?1?kb?xx?kb?x?x∴212122k21?k21?2121212122k1?21?2k????22221k41?kk2k?2k?12?1???k?,222k1k?2k?121?22431?k112,所以,得???k?25k241?23322233,∴,解得或?k????kk???322323????2332,??,故所求范围为.????2323????22yx1??222AA,的焦距为,离心率为已知椭圆,圆,.4c??O:xy0bC:??1?a?c22122ba2ABA△AB.是椭圆的左右顶点,面积的最大值为是圆的任意一条直径,2O1的方程;1)求椭圆及圆(OC PE,求,)若为圆的任意一条切线,与椭圆的取值范围.交于两点(2PQQ Oll??2264yx223,,).;1【答案】()(21?yx?1????334??1xABB,易知当线段轴距离为,(【解析】1)设则点到h h?a2??AO??h??S2S1AAAB△OB△211?a?c??S2ycBO??h,,轴时,在AB△Amax1c1b?3,,,,,1?a?c2c?2?a??e?a222yx22.,圆的方程为所以椭圆方程为1x?y?1??432b2LL的方程为,此时)当直线2;的斜率不存在时,直线(3PQ??1x??a m221d???L,,直线为圆的切线,设直线,方程为:1?k?m?mkx?y?2k?1y?kx?m????222直线与椭圆联立,,得,0?4m?4k??3x12?8kmx22?yx??1? 43??8km?x?x??21234k????2,由韦达定理得:,判别式0?k?Δ?4823?24m?12??x?x ?212?34k?22?23?kk?43?122,,令所以弦长3?3?t?4k??xxPQ?1?k2123k?42??1624??所以;3,???3PQ?3???????t3t??????64PQ?3,,综上,??3??22yx????FF经、.如图,己知的左、右焦点,直线是椭圆51xy?k?:l01a?b?G:??2122ab 43ABF△FBA.过左焦点交,且与椭圆,的周长为两点,G21(1)求椭圆的标准方程;G △ABFI为等腰直角三角形?若存在,求出直线)是否存在直线的方程;若不,使得(2l2存在,请说明理由.??xc,故与,因为直线.轴的交点为22yx;2(1))不存在,见解析.(【答案】1??23【解析】(1)设椭圆的半焦距为1,0?1?Gcl ABF△34a?3,所以,的周长为,即又,故3?AFAB??BF4a?4222222?3?1ab??c?2.22yx因此,椭圆的标准方程为.1??G32(2)不存在.理由如下:AB不可能为底边,即.先用反证法证明BFAF?22??????,假设,,设,则由题意知BFB?x,Fy1,0,yAAFx222121222????22?1x?1?y?yx?,????222112.又得:,,代入上式,消去,?1???10?6x?x?x?xyy21122222xyxy2121213322xx?xx?x?6.轴,所以,故因为直线斜率存在,所以直线不垂直于ll2211?3xx?x?2x3?3?6矛盾)与,,(2211??2222,所以矛联立方程,得:6?x??x?0?6?3k?26x?kx?3k23?22?yx?1?2k6???1?xy?k?盾.2123k?2?故.BF?AF22AB不可能为等腰直角三角形的直角腰.再证明△ABFA为直角顶点.为等腰直角三角形,不妨设假设2??22F△AF,此方设,在中,由勾股定理得:,则m?AF m?2?AF343m?2??m2112程无解.故不存在这样的等腰直角三角形.。
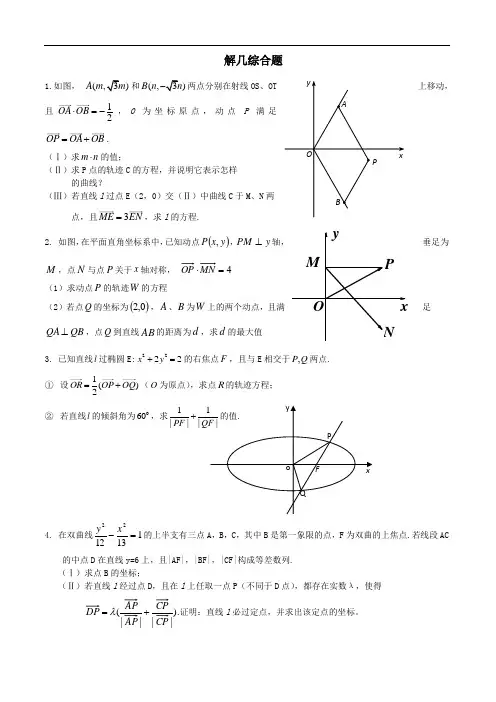
解几综合题1.如图,()A m 和(,)B n 两点分别在射线OS 、OT 上移动,且12OA OB ⋅=-,O 为坐标原点,动点P 满足OP OA OB =+.(Ⅰ)求m n ⋅的值;(Ⅱ)求P 点的轨迹C 的方程,并说明它表示怎样的曲线?(Ⅲ)若直线l 过点E (2,0)交(Ⅱ)中曲线C 于M 、N 两点,且3ME EN =,求l 的方程.2. 如图,在平面直角坐标系中,已知动点()y x P ,,y PM ⊥轴,垂足为M ,点N 与点P 关于x 轴对称, 4=⋅MN OP(1)求动点P 的轨迹W 的方程(2)若点Q 的坐标为()0,2,A 、B 为W 上的两个动点,且满足QB QA ⊥,点Q 到直线AB 的距离为d ,求d 的最大值3. 已知直线l 过椭圆E:2222x y +=的右焦点F ,且与E 相交于,P Q 两点. ① 设1()2OR OP OQ =+(O 为原点),求点R 的轨迹方程;② 若直线l 的倾斜角为060,求1||PF4. 在双曲线1131222=-x y 的上半支有三点A ,B ,C ,其中B 是第一象限的点,F 为双曲的上焦点.若线段AC 的中点D 在直线y=6上,且|AF|,|BF|,|CF|构成等差数列. (Ⅰ)求点B 的坐标;(Ⅱ)若直线l 经过点D ,且在l 上任取一点P (不同于D 点),都存在实数λ,使得 ||||(CP AP +=λ证明:直线l 必过定点,并求出该定点的坐标。
5. 如图,椭圆两焦点F 1、F 2与短轴两端B 1、B 2正好是正方形的四个顶点,且焦点到椭圆上一点最近距离为.12-(I )求椭圆的标准方程;(II )过D(0,2)的直线与椭圆交于不同的两点M 、N ,且M 在D 、N 之间,设λ=||DN DM ,求λ的取值范围.6. 已知F 1、F 2分别是椭圆)0,0(12222>>=+b a by a x 的左、右焦点,其左准线与x 轴相交于点N ,并且满足,.2||,221121==F F NF F F (1)求此椭圆的方程;(2)设A 、B 是这个椭圆上的两点,并且满足]31,51[,∈=λλ当NB NA 时,求直线AB 的斜率的取值范围.7. 已知O 为坐标原点,点E 、F 的坐标分别为(-1,0)、(1,0),动点A 、M 、N 满足||||AE m EF =(1m >),0MN AF =⋅,1()2ON OA OF =+,//AM ME .(Ⅰ)求点M 的轨迹W 的方程; (Ⅱ)点0(,)2mP y 在轨迹W 上,直线PF 交轨迹W 于点Q ,且PF FQ λ=,若12λ≤≤,求实数m 的范围.8. 已知点A (-1,0),B (1,-1)和抛物线.x y C 4:2=,O 为坐标原点,过点A 的动直线l 交抛物线C 于M 、P ,直线MB 交抛物线C 于另一点Q ,如图.(I )若△POM 的面积为25,求向量OM 与OP 的夹角; (II )试探求点O 到直线PQ 的距离是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.9. 设不等式组⎩⎨⎧x +y >0,x -y >0表示的平面区域为D .区域D 内的动点P 到直线x +y =0和直线x -y =0的距离之积为1.记点P 的轨迹为曲线C . (Ⅰ)求曲线C 的方程;(Ⅱ)过点F (2,0)的直线与曲线C 交于A ,B 两点.若以线段AB 为直径的圆与y 轴相切,求线段AB 的长.10. 如图,在△OSF 中,c OF a OS OSF ==︒=∠,,90(c a ,均为正常数),E 、P 是平面OSF内的动点,且满足0=⋅OF SE ,),(R ∈=λλ向量PE c PF a +与PE c PF a -垂 直。
课题:圆锥曲线的综合问题 【要点回顾】1.直线与圆锥曲线的位置关系判定直线与圆锥曲线的位置关系时,通常是将直线方程与曲线方程联立,消去变量y (或x )得关于变量x (或y )的方程:ax 2+bx +c =0(或ay 2+by +c =0).若a ≠0,可考虑一元二次方程的判别式Δ,有: Δ>0⇔直线与圆锥曲线相交; Δ=0⇔直线与圆锥曲线相切; Δ<0⇔直线与圆锥曲线相离.若a =0且b ≠0,则直线与圆锥曲线相交,且有一个交点. 2.圆锥曲线的弦长问题设直线l 与圆锥曲线C 相交于A 、B 两点,A (x 1,y 1),B (x 2,y 2), 则弦长|AB |=1+k 2|x 1-x 2|或 1+1k2|y 1-y 2|.【热身练习】1.(教材习题改编)与椭圆x 212+y 216=1焦点相同,离心率互为倒数的双曲线方程是( )A .y 2-x 23=1 B.y 23-x 2=1 C.34x 2-38y 2=1D.34y 2-38x 2=1 解析:选A 设双曲线方程为y 2a 2-x 2b2=1(a >0,b >0),则⎩⎪⎨⎪⎧a 2+b 2=c 2,ca =2,c =2,得a =1,b = 3.故双曲线方程为y 2-x 23=1.2.(教材习题改编)直线y =kx -k +1与椭圆x 29+y 24=1的位置关系是( )A .相交B .相切C .相离D .不确定解析:选A 由于直线y =kx -k +1=k (x -1)+1过定点(1,1),而(1,1)在椭圆内,故直线与椭圆必相交.3.过点(0,1)作直线,使它与抛物线y 2=4x 仅有一个公共点,这样的直线有( ) A .1条B .2条C .3条D .4条解析:选C 结合图形分析可知,满足题意的直线共有3条:直线x =0,过点(0,1)且平行于x 轴的直线以及过点(0,1)且与抛物线相切的直线(非直线x =0).4.过椭圆x 2a 2+y 2b2=1(a >b >0)的左顶点A 且斜率为1的直线与椭圆的另一个交点为M ,与y 轴的交点为B ,若|AM |=|MB |,则该椭圆的离心率为________.解析:由题意知A 点的坐标为(-a,0),l 的方程为y =x +a ,所以B 点的坐标为(0,a ),故M 点的坐标为⎝ ⎛⎭⎪⎫-a 2,a 2,代入椭圆方程得a 2=3b 2,则c 2=2b 2,则c 2a 2=23,故e =63.5.已知双曲线方程是x 2-y 22=1,过定点P (2,1)作直线交双曲线于P 1,P 2两点,并使P (2,1)为P 1P 2的中点,则此直线方程是________________.解析:设点P 1(x 1,y 1),P 2(x 2,y 2),则由x 21-y 212=1,x 22-y 222=1,得k =y 2-y 1x 2-x 1=x 2+x 1y 2+y 1=2×42=4,从而所求方程为4x -y -7=0.将此直线方程与双曲线方程联立得14x 2-56x +51=0,Δ>0,故此直线满足条件.答案:4x -y -7=0 【方法指导】1.直线与圆锥曲线的位置关系,主要涉及弦长、弦中点、对称、参数的取值范围、求曲线方程等问题.解题中要充分重视根与系数的关系和判别式的应用.2.当直线与圆锥曲线相交时:涉及弦长问题,常用“根与系数的关系”设而不求计算弦长(即应用弦长公式);涉及弦的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来,相互转化.同时还应充分挖掘题目中的隐含条件,寻找量与量间的关系灵活转化,往往就能事半功倍.解题的主要规律可以概括为“联立方程求交点,韦达定理求弦长,根的分布找范围,曲线定义不能忘”. 【直线与圆锥曲线的位置关系】[例1] (2012·北京高考)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的一个顶点为A (2,0),离心率为22.直线y=k (x -1)与椭圆C 交于不同的两点M ,N .(1)求椭圆C 的方程; (2)当△AMN 的面积为103时,求k 的值. [自主解答] (1)由题意得⎩⎪⎨⎪⎧a =2,c a =22,a 2=b 2+c 2,解得b =2,所以椭圆C 的方程为x 24+y 22=1.(2)由⎩⎪⎨⎪⎧y =k x -,x 24+y22=1,得(1+2k 2)x 2-4k 2x +2k 2-4=0.设点M ,N 的坐标分别为(x 1,y 1),(x 2,y 2),则y 1=k (x 1-1),y 2=k (x 2-1),x 1+x 2=4k 21+2k 2,x 1x 2=2k 2-41+2k 2,所以|MN |=x 2-x 12+y 2-y 12=+k2x 1+x 22-4x 1x 2]=2+k 2+6k21+2k2.又因为点A (2,0)到直线y =k (x -1)的距离d =|k |1+k2,所以△AMN 的面积为S =12|MN |· d =|k |4+6k 21+2k .由|k |4+6k 21+2k =103,解得k =±1. 【由题悟法】研究直线与圆锥曲线的位置关系时,一般转化为研究其直线方程与圆锥方程组成的方程组解的个数,但对于选择、填空题也可以利用几何条件,用数形结合的方法求解.【试一试】1.(2012·信阳模拟)设抛物线y 2=8x 的准线与x 轴交于点Q ,若过点Q 的直线l 与抛物线有公共点,则直线l 的斜率的取值范围是( )A.⎣⎢⎡⎦⎥⎤-12,12 B .[-2,2] C .[-1,1] D .[-4,4]解析:选C 易知抛物线y 2=8x 的准线x =-2与x 轴的交点为Q (-2,0),于是,可设过点Q (-2,0)的直线l 的方程为y =k (x +2)(由题可知k 是存在的),联立⎩⎪⎨⎪⎧y 2=8x ,y =k x +⇒k 2x 2+(4k 2-8)x +4k 2=0.当k =0时,易知符合题意;当k ≠0时,其判别式为Δ=(4k 2-8)2-16k 4=-64k 2+64≥0, 可解得-1≤k ≤1. 【最值与范围问题】[例2] (2012·浙江高考)如图,椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为12,其左焦点到点P (2,1)的距离为10.不过原点O 的直线l 与C 相交于A ,B 两点,且线段AB 被直线OP 平分.(1)求椭圆C 的方程;(2)求△ABP 面积取最大值时直线l 的方程.[自主解答] (1)设椭圆左焦点为F (-c,0),则由题意得 ⎩⎪⎨⎪⎧+c 2+1=10,c a =12,得⎩⎪⎨⎪⎧c =1,a =2.所以椭圆方程为x 24+y 23=1.(2)设A (x 1,y 1),B (x 2,y 2),线段AB 的中点为M .当直线AB 与x 轴垂直时,直线AB 的方程为x =0,与不过原点的条件不符,舍去.故可设直线AB 的方程为y =kx +m (m ≠0),由⎩⎪⎨⎪⎧y =kx +m ,3x 2+4y 2=12消去y ,整理得(3+4k 2)x 2+8kmx +4m 2-12=0, ① 则Δ=64k 2m 2-4(3+4k 2)(4m 2-12)>0,所以线段AB 的中点为M ⎝ ⎛⎭⎪⎫-4km 3+4k 2,3m 3+4k 2.因为M 在直线OP :y =12x 上,所以3m 3+4k 2=-2km3+4k 2.得m =0(舍去)或k =-32.此时方程①为3x 2-3mx +m 2-3=0,则Δ=3(12-m 2)>0,⎩⎪⎨⎪⎧x 1+x 2=m ,x 1x 2=m 2-33.所以|AB |=1+k 2·|x 1-x 2|=396·12-m 2, 设点P 到直线AB 的距离为d ,则d =|8-2m |32+22=2|m -4|13. 设△ABP 的面积为S ,则S =12|AB |·d =36·m -2-m2.其中m ∈(-23,0)∪(0,23).令u (m )=(12-m 2)(m -4)2,m ∈[-23,2 3 ],u ′(m )=-4(m -4)(m 2-2m -6)=-4(m -4)(m -1-7)(m -1+7).所以当且仅当m =1-7时,u (m )取到最大值. 故当且仅当m =1-7时,S 取到最大值. 综上,所求直线l 的方程为3x +2y +27-2=0. 【由题悟法】1.解决圆锥曲线的最值与范围问题常见的解法有两种:几何法和代数法.(1)若题目的条件和结论能明显体现几何特征和意义,则考虑利用图形性质来解决,这就是几何法; (2)若题目的条件和结论能体现一种明确的函数关系,则可首先建立起目标函数,再求这个函数的最值,这就是代数法.2.在利用代数法解决最值与范围问题时常从以下五个方面考虑: (1)利用判别式来构造不等关系,从而确定参数的取值范围;(2)利用已知参数的范围,求新参数的范围,解这类问题的核心是在两个参数之间建立等量关系; (3)利用隐含或已知的不等关系建立不等式,从而求出参数的取值范围; (4)利用基本不等式求出参数的取值范围; (5)利用函数的值域的求法,确定参数的取值范围. 【试一试】2.(2012·东莞模拟)已知抛物线y 2=2px (p ≠0)上存在关于直线x +y =1对称的相异两点,则实数p 的取值范围为( )A.⎝ ⎛⎭⎪⎫-23,0B.⎝ ⎛⎭⎪⎫0,23C.⎝ ⎛⎭⎪⎫-32,0D.⎝ ⎛⎭⎪⎫0,32 解析:选B 设抛物线上关于直线x +y =1对称的两点是M (x 1,y 1)、N (x 2,y 2),设直线MN 的方程为y =x +b .将y =x +b 代入抛物线方程,得x 2+(2b -2p )x +b 2=0,则x 1+x 2=2p -2b ,y 1+y 2=(x 1+x 2)+2b =2p ,则MN 的中点P 的坐标为(p -b ,p ).因为点P 在直线x +y =1上,所以2p -b =1,即b =2p -1.又Δ=(2b -2p )2-4b 2=4p 2-8bp >0,将b =2p -1代入得4p 2-8p (2p -1)>0,即3p 2-2p <0,解得0<p <23. 【定点定值问题】[例3] (2012·辽宁高考)如图,椭圆C 0:x 2a 2+y 2b2=1(a >b >0,a ,b 为常数),动圆C 1:x 2+y 2=t 21,b <t 1<a .点A 1,A 2分别为C 0的左,右顶点,C 1与C 0相交于A ,B ,C ,D 四点.(1)求直线AA 1与直线A 2B 交点M 的轨迹方程;(2)设动圆C 2:x 2+y 2=t 22与C 0相交于A ′,B ′,C ′,D ′四点,其中b <t 2<a ,t 1≠t 2.若矩形ABCD 与矩形A ′B ′C ′D ′的面积相等,证明:t 21+t 22为定值.[自主解答] (1)设 A (x 1,y 1),B (x 1,-y 1),又知A 1(-a,0),A 2(a,0),则直线A 1A 的方程为y =y 1x 1+a(x +a ),①直线A 2B 的方程为y =-y 1x 1-a(x -a ).② 由①②得y 2=-y 21x 21-a2(x 2-a 2).③由点A (x 1,y 1)在椭圆C 0上,故x 21a 2+y 21b2=1.从而y 21=b 2⎝ ⎛⎭⎪⎫1-x 21a 2,代入③得x 2a 2-y 2b 2=1(x <-a ,y <0). (2)证明:设A ′(x 2,y 2),由矩形ABCD 与矩形A ′B ′C ′D ′的面积相等,得4|x 1||y 1|=4|x 2|·|y 2|, 故x 21y 21=x 22y 22.因为点A ,A ′均在椭圆上,所以b 2x 21⎝ ⎛⎭⎪⎫1-x 21a 2=b 2x 22⎝ ⎛⎭⎪⎫1-x 22a 2.由t 1≠t 2,知x 1≠x 2,所以x 21+x 22=a 2,从而y 21+y 22=b 2, 因此t 21+t 22=a 2+b 2为定值. 【由题悟法】1.求定值问题常见的方法有两种(1)从特殊入手,求出表达式,再证明这个值与变量无关;(2)直接推理、计算,并在计算推理的过程中消去变量,从而得到定值. 2.定点的探索与证明问题(1)探索直线过定点时,可设出直线方程为y =kx +b ,然后利用条件建立b 、k 等量关系进行消元,借助于直线系方程找出定点;(2)从特殊情况入手,先探求定点,再证明一般情况. 【试一试】3.(2012·山东省实验中学模拟)已知抛物线y 2=2px (p ≠0)及定点A (a ,b ),B (-a,0),ab ≠0,b 2≠2pa ,M 是抛物线上的点.设直线AM ,BM 与抛物线的另一个交点分别为M 1,M 2,当M 变动时,直线M 1M 2恒过一个定点,此定点坐标为________.解析:设M ⎝ ⎛⎭⎪⎫y 202p ,y 0,M 1⎝ ⎛⎭⎪⎫y 212p ,y 1,M 2⎝ ⎛⎭⎪⎫y 222p ,y 2,由点A ,M ,M 1共线可知y 0-b y 202p-a=y 1-y 0y 212p -y 202p,得y 1=by 0-2pa y 0-b ,同理由点B ,M ,M 2共线得y 2=2pa y 0.设(x ,y )是直线M 1M 2上的点,则y 2-y 1y 222p -y 212p =y 2-y y 222p-x ,即y 1y 2=y (y 1+y 2)-2px ,又y 1=by 0-2pa y 0-b ,y 2=2pay 0, 则(2px -by )y 02+2pb (a -x )y 0+2pa (by -2pa )=0. 当x =a ,y =2pa b时上式恒成立,即定点为⎝ ⎛⎭⎪⎫a ,2pa b .答案:⎝⎛⎭⎪⎫a ,2pa b。
高考数学必做61道圆锥曲线问题——圆锥曲线性质大全.doc
高考数学必做 61 道圆锥曲线问题——圆
锥曲线性质大全
一、神奇曲线,定义统一
01. 距离和差,轨迹椭双
02. 距离定比,三线统一
二、过焦半径,相关问题
03.切线焦径,准线作法
04. 焦点切线,射影是圆
05. 焦半径圆,切于大圆
06. 焦点弦圆,准线定位
07. 焦三角形,内心轨迹
三、焦点之弦,相关问题
08.焦点半径,倒和定值
09.正交焦弦,倒和定值
10. 焦弦中垂,焦交定长
11. 焦弦投影,连线截中
12. 焦弦长轴,三点共线
13. 对焦连线,互相垂直
14. 相交焦弦,轨迹准线
15. 相交焦弦,角分垂直
16. 定点交弦,轨迹直线
17. 焦弦直线,中轴分比。
高考数学圆锥曲线典型例题(必考)9.1 椭 圆典例精析题型一 求椭圆的标准方程【例1】已知点P 在以坐标轴为对称轴的椭圆上,点P 到两焦点的距离分别为453和253,过P 作长轴的垂线恰好过椭圆的一个焦点,求椭圆的方程. 【解析】故所求方程为x 25+3y 210=1或3x 210+y 25=1.【点拨】(1)在求椭圆的标准方程时,常用待定系数法,但是当焦点所在坐标轴不确定时,需要考虑两种情形,有时也可设椭圆的统一方程形式:mx 2+ny 2=1(m >0,n >0且m ≠n );(2)在求椭圆中的a 、b 、c 时,经常用到椭圆的定义及解三角形的知识.【变式训练1】已知椭圆C 1的中心在原点、焦点在x 轴上,抛物线C 2的顶点在原点、焦点在x 轴上.小明从曲线C 1,C 2上各取若干个点(每条曲线上至少取两个点),并记录其坐标(x ,y ).由于记录失误,使得其中恰有一个点既不在椭圆C 1上,也不在抛物线C 2上.小明的记录如下:据此,可推断椭圆C 1的方程为 . x 212+y 26=1.题型二 椭圆的几何性质的运用【例2】已知F 1、F 2是椭圆的两个焦点,P 为椭圆上一点,∠F 1PF 2=60°. (1)求椭圆离心率的范围;(2)求证:△F 1PF 2的面积只与椭圆的短轴长有关.【解析】(1)e 的取值范围是[12,1).(2)21F PF S =12mn sin 60°=33b 2,【点拨】椭圆中△F 1PF 2往往称为焦点三角形,求解有关问题时,要注意正、余弦定理,面积公式的使用;求范围时,要特别注意椭圆定义(或性质)与不等式的联合使用,如|PF 1|·|PF 2|≤(|PF 1|+|PF 2|2)2,|PF 1|≥a -c . 【变式训练2】已知P 是椭圆x 225+y 29=1上的一点,Q ,R 分别是圆(x +4)2+y 2=14和圆(x -4)2+y 2=14上的点,则|PQ |+|PR |的最小值是 .【解析】最小值为9.题型三 有关椭圆的综合问题【例3】(2010全国新课标)设F 1,F 2分别是椭圆E :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,过F 1斜率为1的直线l 与E 相交于A ,B 两点,且|AF 2|,|AB |,|BF 2|成等差数列.(1)求E 的离心率;(2)设点P (0,-1)满足|PA |=|PB |,求E 的方程.(1) 22.(2)为x 218+y 29=1.【变式训练3】已知椭圆x 2a 2+y2b 2=1(a >b >0)的离心率为e ,两焦点为F 1,F 2,抛物线以F 1为顶点,F 2为焦点,P 为两曲线的一个交点,若|PF 1||PF 2|=e ,则e 的值是( )A.32B.33C.22D.63【解析】选B 题型思 有关椭圆与直线综合问题【例4】【2012高考浙江理21】如图,椭圆C :2222+1x y a b =(a >b >0)的离心率为12,其左焦点到点P (2,1)的距离为10.不过原点O 的直线l 与C 相交于A ,B 两点,且线段AB被直线OP 平分.(Ⅰ)求椭圆C 的方程;(Ⅱ) 求∆ABP 的面积取最大时直线l 的方程. .【变式训练4】【2012高考广东理20】在平面直角坐标系xOy 中,已知椭圆C 1:22221(0)x y a b a b+=>>的离心率e=23,且椭圆C 上的点到Q (0,2)的距离的最大值为3. (1)求椭圆C 的方程;(2)在椭圆C 上,是否存在点M (m,n )使得直线l :mx+ny=1与圆O :x 2+y 2=1相交于不同的两点A 、B ,且△OAB 的面积最大?若存在,求出点M 的坐标及相对应的△OAB 的面积;若不存在,请说明理由. 总结提高1.椭圆的标准方程有两种形式,其结构简单,形式对称且系数的几何意义明确,在解题时要防止遗漏.确定椭圆需要三个条件,要确定焦点在哪条坐标轴上(即定位),还要确定a 、 b 的值(即定量),若定位条件不足应分类讨论,或设方程为mx 2+ny 2=1(m >0,n >0,m ≠n )求解.2.充分利用定义解题,一方面,会根据定义判定动点的轨迹是椭圆,另一方面,会利用椭圆上的点到两焦点的距离和为常数进行计算推理.3.焦点三角形包含着很多关系,解题时要多从椭圆定义和三角形的几何条件入手,且不可顾此失彼,另外一定要注意椭圆离心率的范围.练习1(2009全国卷Ⅰ理)已知椭圆22:12x C y +=的右焦点为F ,右准线为l ,点A l ∈,线段AF 交C 于点B ,若3FA FB =u u u r u u u r ,则||AF u u u u r=( )A. 2B. 2C.3D. 3 选A.2(2009浙江文)已知椭圆22221(0)x y a b a b+=>>的左焦点为F ,右顶点为A ,点B 在椭圆上,且BF x ⊥轴,直线AB 交y 轴于点P .若2AP PB =u u u r u u u r,则椭圆的离心率是( ) A 32 C .13 D .12【答案】D3.(2009江西卷理)过椭圆22221x y a b+=(0a b >>)的左焦点1F 作x 轴的垂线交椭圆于点P ,2F 为右焦点,若1260F PF ∠=o ,则椭圆的离心率为 A .22 B .33 C .12D .13 【答案】B 4.【2012高考新课标理4】设12F F 是椭圆2222:1(0)x y E a b a b +=>>的左、右焦点,P 为直线32ax =上一点,12PF F ∆是底角为30o 的等腰三角形,则E 的离心率为( ) ()A 12 ()B 23 ()C 34 ()D 45【答案】C5【2012高考四川理15】椭圆22143x y +=的左焦点为F ,直线x m =与椭圆相交于点A 、B ,当FAB ∆的周长最大时,FAB ∆的面积是____________。
【2023届新高考必刷】圆锥曲线大题综合1.(2023春·江苏扬州·高三统考开学考试)已知AB 为抛物线G :y 2=2px (p >0)的弦,点C 在抛物线的准线l 上.当AB 过抛物线焦点F 且长度为8时,AB 中点M 到y 轴的距离为3.(1)求抛物线G 的方程;(2)若∠ACB 为直角,求证:直线AB 过定点.【答案】(1)y 2=4x(2)证明见解析【分析】(1)利用抛物线弦长公式,以及中点到y 轴的距离公式,计算出p 即可;(2)先设C -1,c ,A y 214,y 1 ,B y 224,y 2,直线AB 的方程:x =ty +n ,联立方程组,由韦达定理可得y 1+y 2=4t ,y 1y 2=-4n ,又因为∠ACB 为直角可得CA ⋅CB=0,化简求解可得n =1,所以得出直线过定点1,0 .【详解】(1)设A x A ,y A ,B x B ,y B ,则由题意得|AB |=x A +x B +p =8x A +x B 2=3,解得p =2,所以抛物线的方程为y 2=4x (2)直线AB 过定点1,0 ,证明如下:设C -1,c ,A y 214,y 1 ,B y 224,y 2,直线AB 的方程:x =ty +n ,将x =ty +n 代入y 2=4x 得y 2-4ty -4n =0,则Δ>0,得t 2+n >0,由韦达定理可得y 1+y 2=4t ,y 1y 2=-4n ,所以CA =y 214+1,y 1-c ,CB =y 224+1,y 2-c,因为∠ACB =90∘,所以CA ⋅CB =0,即y 21y 2216+y 21+y 224+1+y 1y 2-c y 1+y 2 +c 2=0,即n 2+4t 2+2n +1-4n -4tc +c 2=0,即(n -1)2+(2t -c )2=0,所以n =1,所以直线AB 过定点1,0 .2.(2023·江苏泰州·统考一模)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左顶点为A ,过左焦点F 的直线与C 交于P ,Q 两点.当PQ ⊥x 轴时,PA =10,△PAQ 的面积为3.(1)求C 的方程;(2)证明:以PQ 为直径的圆经过定点.【答案】(1)x2-y23=1(2)证明见解析【分析】(1)根据题意,可得PF=b2a,b2a2+c-a2=10212⋅2b2a⋅c-a=3c2=a2+b2,进而求解;(2)设PQ方程为x=my-2,P x1,y1,Q x2,y2,联立直线和双曲线方程组,可得3m2-1y2-12my+9 =0,以PQ为直径的圆的方程为x-x1x-x2+y-y1y-y2=0,由对称性知以PQ为直径的圆必过x轴上的定点,进而得到x2-x1+x2x+x1x2+y1y2=0,进而求解.【详解】(1)当PQ⊥x轴时,P,Q两点的横坐标均为-c,代入双曲线方程,可得y P=b2a,y Q=-b2a,即PF=b2a,由题意,可得b2a2+c-a2=10212⋅2b2a⋅c-a=3c2=a2+b2,解得a=1,b=3,c=2,∴双曲线C的方程为:x2-y23=1;(2)方法一:设PQ方程为x=my-2,P x1,y1,Q x2,y2,x=my-2 3x2-y2=3⇒3m2y2-4my+4-y2=3⇒3m2-1y2-12my+9=0,以PQ为直径的圆的方程为x-x1x-x2+y-y1y-y2=0,x2-x1+x2x+x1x2+y2-y1+y2y+y1y2=0,由对称性知以PQ为直径的圆必过x轴上的定点,令y=0,可得x2-x1+x2x+x1x2+y1y2=0,而x1+x2=m y1+y2-4=12m23m2-1-4=43m2-1,x1x2=my1-2my2-2=m2y1y2-2m y1+y2+4=-3m2-4 3m2-1,∴x2-43m2-1x+-3m2-43m2-1+93m2-1=0⇒3m2-1x2-4x+5-3m2=0⇒3m2-1x+3m2-5x-1=0对∀m∈R恒成立,∴x=1,∴以PQ为直径的圆经过定点1,0;方法二:设PQ方程为x=my-2,P x1,y1,Q x2,y2,x=my-2 3x2-y2=3⇒3m2-1y2-12my+9=0,由对称性知以PQ为直径的圆必过x轴上的定点.设以PQ 为直径的圆过E t ,0 ,∴EP ⋅EQ=0⇒x 1-t x 2-t +y 1y 2=0⇒x 1x 2-t x 1+x 2 +t 2+y 1y 2=0,而x 1x 2=my 1-2 my 2-2 =m 2y 1y 2-2m y 1+y 2 +4=m 2⋅93m 2-1-2m ⋅12m 3m 2-1+4=-3m 2-43m 2-1,x 1+x 2=m y 1+y 2 -4=12m 23m 2-1-4=43m 2-1∴-3m 2-43m 2-1-4t 3m 2-1+t 2+93m 2-1=0,3m2-1 t 2-4t +5-3m 2=0,即3m 2-1 t +3m 2-5 t -1 =0对∀m ∈R 恒成立,∴t =1,即以PQ 为直径的圆经过定点1,0 .3.(2023秋·浙江绍兴·高三期末)在平面直角坐标系xOy 中,已知点A (-2,0),B (2,0),直线PA 与直线PB 的斜率之积为-14,记动点P 的轨迹为曲线C .(1)求曲线C 的方程;(2)若直线l :y =kx +m 与曲线C 交于M ,N 两点,直线MA ,NB 与y 轴分别交于E ,F 两点,若EO=3OF ,求证:直线l 过定点.【答案】(1)x 24+y 2=1(x ≠±2)(2)证明见解析【分析】(1)设P 点坐标为(x ,y ),由y x +2⋅y x -2=-14可得结果;(2)设M x 1,y 1 ,N x 2,y 2 ,联立y =kx +m x 24+y 2=1,得x 1+x 2和x 1x 2,再求出E ,F 的坐标,根据EO =3OF得k =m ,从而可得结果.【详解】(1)设P 点坐标为(x ,y ),则y x +2⋅y x -2=-14,即x 24+y 2=1(x ≠±2),所以曲线C 的方程为x 24+y 2=1(x ≠±2).(2)设M x 1,y 1 ,N x 2,y 2 ,由y =kx +mx 24+y 2=1,消去y 并整理得4k 2+1 x 2+8km x +4m 2-4=0,由Δ=64k 2m 2-4(4k 2+1)(4m 2-4)>0,得4k 2+1>m 2,所以x 1+x 2=-8km 4k 2+1,x 1x 2=4m 2-44k 2+1.MA :y =y 1x 1+2(x +2)⇒E 0,2y 1x 1+2 ,NB :y =y 2x 2-2x -2 ⇒F 0,-2y 2x 2-2 ,因为EO =3OF ,所以-2y 1x 1+2=3⋅-2y 2x 2-2,即y 1(x 2-2)=3y 2(x 1+2),∴kx 1+m x 2-2 =3kx 2+m x 1+2 ,∴2kx 1x 2+(2k +3m )x 1+x 2 +4(k -m )x 2+8m =0,所以2k ⋅4m 2-44k 2+1+(2k +3m )⋅-8km4k 2+1+4(k -m )x 2+8m =0,所以(k -m )4km -2+4k 2+1 x 2 =0对任意x 2都成立,∴k =m ,故直线l 过定点(-1,0).4.(2023秋·浙江·高三期末)已知点A 463,233 是双曲线x 2a 2-y 2b 2=1(a >0,b >0)上一点,B 与A 关于原点对称,F 是右焦点,∠AFB =π2.(1)求双曲线的方程;(2)已知圆心在y 轴上的圆C 经过点P (-4,0),与双曲线的右支交于点M ,N ,且直线MN 经过F ,求圆C 的方程.【答案】(1)x 28-y 24=1(2)x 2+(y ±26)2=40【分析】(1)由已知条件列方程求出a ,b ,c ,即可求出双曲线的方程;(2)讨论直线MN 的斜率不存在时不满足题意;当斜率存在时设直线MN 的方程为y =kx +m ,联立双曲线的方程,由韦达定理求出MN 的中点Q 的坐标以及C 的坐标,根据勾股定理有CN 2=CP 2=CQ 2+12MN2,代入解方程即可得出答案.【详解】(1)由已知条件得:463+c ,233 ⋅463-c ,233 =0323a 2-43b 2=1a 2+b 2=c 2⇒a 2=8b 2=4c =23双曲线方程为:x 28-y 24=1.(2)若直线MN 的斜率不存在,则圆C 的圆心不在y 轴上,因此不成立.设直线MN 的方程为y =kx +m ,由y =k (x -23)x 28-y 24=1消元得:2k 2-1 x 2-83k 2x +24k 2+8 =0⇒2k 2-1≠0Δ=32k 2+1 >0x 1+x 2=83k 22k 2-1,y 1+y 2=k x 1+x 2 -43k =83k 32k 2-1-43k =43k2k 2-1∴MN 的中点Q 的坐标为43k 22k 2-1,23k2k 2-1.设C (0,m ),直线CQ :y =-1k x +m ,得C 0,63k2k 2-1,又|MN |=k 2+1⋅82⋅-8k 2+4+12k 28k 2-4 =42k 2+1 2k 2-1,根据勾股定理有CN 2=CP 2=CQ 2+12MN2∴63k 2k 2-1 2+42=43k 22k 2-1 2+23k 2k 2-1-63k 2k 2-1 2 +22k 2+1 2k 2-12.化简得2k 4-5k 2+2=0解得k 2=2或k 2=12(舍)∴C (0,±26),∴圆C 的方程为x 2+(y ±26)2=40.5.(2023春·广东揭阳·高三校考阶段练习)已知抛物线E :y 2=2px p >0 的焦点为F ,点F 关于直线y =12x +34的对称点恰好在y 轴上.(1)求抛物线E 的标准方程;(2)直线l :y =k x -2 k ≥6 与抛物线E 交于A ,B 两点,线段AB 的垂直平分线与x 轴交于点C ,若D 6,0 ,求AB CD的最大值.【答案】(1)y 2=4x(2)2915【分析】(1) 由题意得F p 2,0 ,设F 关于直线y =12x +34的对称点为F 0,m ,根据题意列出方程组,解之即可求解;(2)将直线方程与抛物线方程联立,利用韦达定理和弦长公式,并求得线段AB 的垂直平分线方程为y -2k =-1k x -2k 2+2k 2 ,进而得到AB CD=22+49t +36t-12,利用函数的单调性即可求解.【详解】(1)由题意得F p 2,0 ,设F 关于直线y =12x +34的对称点为F0,m ,则m -p 2=-2m 2=18p +34 ,解得m =p =2,∴抛物线E 的标准方程为y 2=4x .(2)由y =k x -2 y 2=4x 可得k 2x 2-4k 2+4 x +4k 2=0,设A x 1,y 1 ,B x 2,y 2 ,则x 1+x 2=4k 2+4k 2,x 1x 2=4,∴AB =1+k 2⋅x 1-x 2 =1+k 2⋅x 1+x 22-4x 1x 2=1+k 2⋅4k 2+4k 22-16=42k 4+3k 2+1k 2,y 1+y 2=k x 1+x 2 -4k =4k ,∴线段AB 的中点坐标为2k 2+2k 2,2k ,则线段AB 的垂直平分线方程为y-2k =-1k x -2k 2+2k 2 ,令y =0,得x =4+2k2,故C 4+2k 2,0 ,又D 6,0 ,得CD =4+2k 2-6=2-2k 2.∴ABCD =22k 4+3k 2+1k 2-1=22+7k 2-1k 4-2k 2+1,令t =7k 2-1k ≥6 ,则k 2=17t +1 ,t ≥41,∴AB CD=22+t 149t +1 2-27t +1+1=22+49t +36t-12,易知函数f t =t +36t在41,+∞ 上单调递增,∴当t =41时,f t 取得最小值,此时k =6,故AB CD的最大值为22+4136-12+1=2915.6.(2023·湖南邵阳·统考二模)已知双曲线C :x 2a 2-y 2b2=10<a 10,b 0 的右顶点为A ,左焦点F -c ,0 到其渐近线bx +ay =0的距离为2,斜率为13的直线l 1交双曲线C 于A ,B 两点,且AB=8103.(1)求双曲线C 的方程;(2)过点T 6,0 的直线l 2与双曲线C 交于P ,Q 两点,直线AP ,AQ 分别与直线x =6相交于M ,N 两点,试问:以线段MN 为直径的圆是否过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.【答案】(1)x 29-y 24=1(2)以线段MN 为直径的圆过定点6-23,0 和6+23,0 .【分析】(1)根据点到直线的距离公式即可求解b =2,进而联立直线与双曲线方程,根据弦长公式即可求解a =3,(2)联立直线与曲线的方程得韦达定理,根据圆的对称性可判断若有定点则在x 轴上,进而根据垂直关系得向量的坐标运算,即可求解.【详解】(1)∵双曲线C 的左焦点F -c ,0 到双曲线C 的一条渐近线bx +ay =0的距离为d =bca 2+b2=b ,而d =2,∴b =2.∴双曲线C 的方程为x 2a2-y 24=10<a <10 .依题意直线l 1的方程为y =13x -a .由x 2a 2-y 24=1,y =13x -a ,消去y 整理得:36-a 2 x 2+2a 3x -a 2a 2+36 =0,依题意:36-a 2≠0,Δ>0,点A ,B 的横坐标分别为x A ,x B ,则x A x B =a 2a 2+36a 2-36.∵x A =a ,∴x B =a a 2+36a 2-36.∴AB =1+132x A -x B =103x A -x B =8103,∴x A -x B =8.即a -a a 2+36a 2-36=8,解得a =3或a =12(舍去),且a =3时,Δ>0,∴双曲线C 的方程为x 29-y 24=1.(2)依题意直线l 2的斜率不等于0,设直线l 2的方程为x =my +6.由x =my +6,x 29-y 24=1,消去x 整理得:4m 2-9 y 2+48my +108=0,∴4m 2-9≠0,Δ1>0.设P x 1,y 1 ,Q x 2,y 2 ,则y 1+y 2=-48m 4m 2-9,y 1y 2=1084m 2-9.直线AP 的方程为y =y 1x 1-3x -3 ,令x =6得:y =3y 1x 1-3,∴M 6,3y 1x 1-3 .同理可得N 6,3y 2x 2-3.由对称性可知,若以线段MN 为直径的圆过定点,则该定点一定在x 轴上,设该定点为R t ,0 ,则RM =6-t ,3y 1x 1-3 ,RN =6-t ,3y 2x 2-3 ,故RM ⋅RN =6-t 2+9y 1y 2x 1-3 x 2-3 =6-t 2+9y 1y 2my 1+3 my 2+3 =6-t 2+9y 1y 2m 2y 1y 2+3m y 1+y 2 +9=6-t 2+9×1084m 2-9m 2×1084m 2-9-3m ×48m 4m 2-9+9=6-t 2-12=0.解得t =6-23或t =6+23.故以线段MN 为直径的圆过定点6-23,0 和6+23,0 .【点睛】关键点睛:本题解题的关键是根据圆的对称性可判断定点在坐标轴上,结合向量垂直的坐标运算化简求解就可,对计算能力要求较高.7.(2023春·湖南长沙·高三雅礼中学校考阶段练习)定义:一般地,当λ>0且λ≠1时,我们把方程x 2a 2+y 2b 2=λ(a >b >0)表示的椭圆C λ称为椭圆x 2a 2+y 2b2=1(a >b >0)的相似椭圆.(1)如图,已知F 1-3,0 ,F 23,0 ,M 为⊙O :x 2+y 2=4上的动点,延长F 1M 至点N ,使得MN =MF 1 ,F 1N 的垂直平分线与F 2N 交于点P ,记点P 的轨迹为曲线C ,求C 的方程;(2)在条件(1)下,已知椭圆C λ是椭圆C 的相似椭圆,M 1,N 1是椭圆C λ的左、右顶点.点Q 是C λ上异于四个顶点的任意一点,当λ=e 2(e 为曲线C 的离心率)时,设直线QM 1与椭圆C 交于点A ,B ,直线QN 1与椭圆C 交于点D ,E ,求AB +DE 的值.【答案】(1)x 24+y 2=1(2)5【分析】(1)由图可知OM 是△F 1NF 2的中位线,由此可得F 2N 长为定值,因为点P 在F 1N 的垂直平分线上,所以PF 1 +PF 2 =PF 2 +PN ,根据椭圆定义求解析式即可;(2)假设出点Q 坐标,表示直线QM 1与直线QN 1的斜率,并找出两斜率关系,最后表示出两直线方程,分别与椭圆C 联立方程,利用弦长公式和韦达定理求出AB +DE 的值.【详解】(1)连接OM ,易知OM ∥12F 2N 且OM =12F 2N ,∴F 2N =4,又点P 在F 1N 的垂直平分线上,∴PF 1 =PN ,∴PF 1 +PF 2 =PF 2 +PN =NF 2 =4>23,满足椭圆定义,∴a =2,c =3,b =1,∴曲线C 的方程为x 24+y 2=1.(2)由(1)知椭圆C 方程为x 24+y 2=1,则离心率e =32⇒λ=34,∴楄圆C λ的标准方程为x 23+4y 23=1,设Q x 0,y 0 为椭圆C λ异于四个顶点的任意一点,直线QM 1,QN 1斜率k QM 1,k QN 1,则k QM1⋅k QN 1=y 0x 0+3⋅y 0x 0-3=y 2x 20-3,又x 203+4y 203=1⇒y 20=143-x 20 ,∴k QM 1⋅k QN 1=-14k QM 1≠±12.设直线QM 1的斜率为k ,则直线QN 1的斜率为-14k.∴直线QM 1为y =k x +3 ,由y =k x +3 ,x 24+y 2=1,得1+4k 2 x 2+83k 2x +12k 2-4=0,设A x 1,y 1 ,B x 2,y 2 ,则x 1+x 2=-83k 21+4k 2,x 1x 2=12k 2-41+4k 2,∴AB =1+k 2x 1-x 2 =1+k 2x 1+x 2 2-4x 1x 2=41+k 21+4k 2,同理可得DE =1+16k 21+4k 2,∴AB +DE =41+k 2 1+4k 2+1+16k 21+4k 2=5.8.(2023·湖北武汉·统考模拟预测)过坐标原点O 作圆C :(x +2)2+y 2=3的两条切线,设切点为P ,Q ,直线PQ 恰为抛物E :y 2=2px ,(p >0)的准线.(1)求抛物线E 的标准方程;(2)设点T 是圆C 上的动点,抛物线E 上四点A ,B ,M ,N 满足:TA =2TM ,TB =2TN,设AB 中点为D .(i )求直线TD 的斜率;(ii )设△TAB 面积为S ,求S 的最大值.【答案】(1)y 2=2x(2)(i )0;(ii )48【分析】(1)设直线PQ 与x 轴交于P 0-p 2,0 ,由几何性质易得:CP 2=CP 0 ⋅CO ,即可解决;(2)设T x 0,y 0 ,A x 1,y 1 ,B x 2,y 2 ,(i )中,由于TA 中点M 在抛物线E 上,得y 0+y 12 2=2⋅x 0+x 12,将A x 1,y 1,B x 2,y 2 ,代入联立得D 点纵坐标为y 1+y 22=y 0,即可解决;(ⅱ)由(i )得点D 3y 20-4x 02,y 0,S =12TD ⋅y 1-y 2 =322⋅y 20-2x 03,又点T 在圆C 上,得y 20=-x 20-4x 0-1,可得:S =322⋅-x 0+32+8 3即可解决.【详解】(1)设直线PQ 与x 轴交于P 0-p2,0 .由几何性质易得:△CPP 0与△OCP 相似,所以CP CP 0=CO CP,CP2=CP 0 ⋅CO ,即:3=-p2+2 ⋅2,解得:p =1. 所以抛物线E 的标准方程为:y 2=2x .(2)设T x0,y0,A x1,y1,B x2,y2(i)由题意,TA中点M在抛物线E上,即y0+y122=2⋅x0+x12,又y21=2x1,将x1=y212代入,得:y21-2y0y1+4x0-y20=0,同理:y22-2y0y2+4x0-y20=0,有y1+y2=2y0y1y2=4x0-y20,此时D点纵坐标为y1+y22=y0,所以直线TD的斜率为0.(ⅱ)因为x1+x22=y21+y224=y1+y22-2y1y24=3y20-4x02,所以点D3y20-4x02,y0 ,此时S=12TD⋅y1-y2,TD =3y20-4x02-x0=32y20-2x0,y1-y2=y1+y22-4y1y2=8y20-2x0,所以S=322⋅y20-2x03,又因为点T在圆C上,有x0+22+y20=3,即y20=-x20-4x0-1,代入上式可得:S=322⋅-x20-6x0-13=322⋅-x0+32+83,由-2-3≤x0≤-2+3,所以x0=-3时,S取到最大价322⋅83=48.所以S的最大值为48.9.(2023·山东·潍坊一中校联考模拟预测)已知F为抛物线C:y2=2px(p>0)的焦点,O为坐标原点,M为C的准线l上的一点,直线MF的斜率为-1,△OFM的面积为1.(1)求C的方程;(2)过点F作一条直线l ,交C于A,B两点,试问在l上是否存在定点N,使得直线NA与NB的斜率之和等于直线NF斜率的平方?若存在,求出点N的坐标;若不存在,请说明理由.【答案】(1)y2=4x(2)存在,-1,0或-1,-4【分析】(1)设点M的坐标为-p 2,a,根据直线MF的斜率为-1,得到a=p,再根据△OFM的面积为1求出p,即可得解;(2)假设存在点N,使得直线NA与NB的斜率之和等于直线NF斜率的平方.设直线l 的方程为x=my+1,A x 1,y 1 ,B x 2,y 2 ,N -1,t ,联立直线与抛物线方程,消元列出韦达定理,又k NF =-t2,k NA+k NB =y 1-t x 1+1+y 2-tx 2+1,化简k NA +k NB ,即可得到方程,求出t 的值,即可得解.【详解】(1)解:由题意知F p 2,0 ,设点M 的坐标为-p2,a ,则直线MF 的斜率为a -0-p 2-p 2=-ap .因为直线MF 的斜率为-1,所以-ap =-1,即a =p ,所以△OFM 的面积S =12OF a =p 24=1,解得p =2或p =-2(舍去),故抛物线C 的方程为y 2=4x .(2)解:假设存在点N ,使得直线NA 与NB 的斜率之和等于直线NF 斜率的平方.由(1)得F 1,0 ,抛物线C 的准线l 的方程为x =-1.设直线l 的方程为x =my +1,A x 1,y 1 ,B x 2,y 2 ,N -1,t ,联立x =my +1y 2=4x得y 2-4my -4=0,所以Δ=16m 2+16>0,y 1+y 2=4m ,y 1y 2=-4.因为k NF =0-t 1+1=-t 2,k NA +k NB =y 1-t x 1+1+y 2-tx 2+1=2my 1y 2+2-tm y 1+y 2 -4t m 2y 1y 2+2m y 1+y 2 +4=2m ⋅-4 +4m 2-tm -4t -4m 2+2m ⋅4m +4=-4t m 2+14m 2+1 =-t ,所以-t =-t22,解得t =0或t =-4.故存在定点N ,使得直线NA 与NB 的斜率之和等于直线NF 斜率的平方,其坐标为-1,0 或-1,-4 .10.(2023·山东菏泽·统考一模)如图,椭圆C :x 2a 2+y 2b 2=1(a >b >0)的焦点分别为F 1-3,0,F 23,0 ,A 为椭圆C 上一点,△F 1AF 2的面积最大值为3.(1)求椭圆C 的方程;(2)若B 、D 分别为椭圆C 的上、下顶点,不垂直坐标轴的直线l 交椭圆C 于P 、Q (P 在上方,Q 在下方,且均不与B ,D 点重合)两点,直线PB ,QD 的斜率分别为k 1,k 2,且k 2=-3k 1,求△PBQ 面积的最大值.【答案】(1)x 24+y 2=1(2)12【分析】(1)根据条件,得到关于a ,b ,c 的方程,即可得到结果;(2)根据题意设直线PQ 的方程为y =kx +m ,联立直线与椭圆方程,结合韦达定理,再由k 2=-3k 1列出方程,代入计算,即可得到结果.【详解】(1)S ΔF 1AF 2=12⋅23⋅b =3,∴b =1,a =b 2+3=2,故椭圆的方程为x 24+y 2=1;(2)依题意设直线PQ 的方程为y =kx +m ,P x 1,y 1 ,Q x 2,y 2 ,联立方程组y =kx +mx 24+y 2=1,消元得:1+4k 2 x 2+8km x +4m 2-4=0,∴x 1+x 2=-8km 1+4k 2,x 1x 2=4m 2-41+4k2,Δ=64k 2m 2-41+4k 2 4m 2-4 =161+4k 2-m 2 >0,由k 2=-3k 1得:y 2+1x 2=-3⋅y 1-1x 1,两边同除x 1,y 2+1x 1x 2=-3⋅y 1-1x 21=-3⋅y 1-141-y 21 =341+y 1 ,即3x 1x 2-41+y 1 1+y 2 =0;将y 1=kx 1+m ,y 2=kx 2+m 代入上式得:3x 1x 2-41+y 1 1+y 2 =3x 1x 2-4kx 1+m +1 kx 2+m +1 =3-4k 2 x 1x 2-4k m +1 x 1+x 2 -4m +1 2=3-4k 2 4m 2-41+4k 2-4k m +1 -8km 1+4k 2 -4m +1 2=0,整理得:m 2-m -2=0所以m =2或m =-1(舍),S △PQB =12⋅1⋅x 1-x 2 =12x 1+x 2 2-4x 1x 2=12-8km 1+4k 2 2-44m 2-41+4k 2=24k 2-31+4k 2=24k 2-3+44k 2-3≤12,当k =±72时等号成立,满足条件,所以△PQB 面积的最大值为12.11.(2023·福建泉州·统考三模)已知椭圆C :x 24+y 23=1的左、右顶点分别为A ,B .直线l 与C 相切,且与圆O :x 2+y 2=4交于M ,N 两点,M 在N 的左侧.(1)若|MN |=455,求l 的斜率;(2)记直线AM ,BN 的斜率分别为k 1,k 2,证明:k 1k 2为定值.【答案】(1)k =±12;(2)证明过程见解析.【分析】(1)根据圆弦长公式,结合点到直线距离公式、椭圆切线的性质进行求解即可;(2)根据直线斜率公式,结合一元二次方程根与系数关系进行求解即可.【详解】(1)当直线l 不存在斜率时,方程为x =±2,显然与圆也相切,不符合题意,设直线l 的斜率为k ,方程为y =kx +m ,与椭圆方程联立,得x 24+y 23=1y =kx +m⇒(3+4k 2)x 2+8km x +4m 2-12=0,因为直线l 与C 相切,所以有Δ=64k 2m 2-43+4k 2 4m 2-12 =0⇒m 2=4k 2+3,圆O :x 2+y 2=4的圆心坐标为0,0 ,半径为2,圆心0,0 到直线y =kx +m 的距离为mk 2+-12,因为|MN |=455,所以有455=2×4-mk 2+-1 22⇒45=4-4k 2+3k 2+1⇒k =±12;(2)A -2,0 ,B 2,0 ,由x 2+y 2=4y =kx +m ⇒1+k 2 x 2+2km x +m 2-4=0,设M x 1,y 1 ,N x 2,y 2 ,x 1<x 2,则有x 1+x 2=-2km k 2+1,x 1x 2=m 2-4k 2+1=4k 2-1k 2+1,x 1=-km -11+k 2,x 2=-km +11+k 2,k 1k 2=y 1x 1+2⋅y 2x 2-2=kx 1+m kx 2+m x 1x 2-2x 1+2x 2-4=k 2x 1x 2+km (x 1+x 2)+m 2x 1x 2-2x 1+2x 2-4,把x 1+x 2=-2km k 2+1,x 1x 2=m 2-4k 2+1=4k 2-1k 2+1,x 1=-km -11+k 2,x 2=-km +11+k 2代入上式,得k 1k 2=k 24k 2-1k 2+1+km -2km k 2+1+m 24k 2-1k 2+1-2⋅-km -1k 2+1+2⋅-km +1k 2+1-4=m 2-4k 2m 2-4-4k2,而m 2=4k 2+3,所以k 1k 2=4k 2+3-4k 24k 2+3-4-4k 2=-3.【点睛】关键点睛:利用一元二次方程根与系数关系,结合椭圆切线的性质进行求解是解题的关键.12.(2023·江苏南通·统考模拟预测)已知A x 1,y 1 ,B x 2,y 2 ,C x 3,y 3 三个点在椭圆x 22+y 2=1,椭圆外一点P 满足OP =2AO ,BP =2CP,(O 为坐标原点).(1)求x 1x 2+2y 1y 2的值;(2)证明:直线AC 与OB 斜率之积为定值.【答案】(1)12(2)证明见解析【分析】(1)设P x ,y ,根据向量关系用x 1,x 2,y 1,y 2表示x 3,y 3,代入椭圆方程即可求解;(2)用x 1,x 2,y 1,y 2表示x 3,y 3,代入斜率公式即可求解.【详解】(1)设P x ,y ,因为OP =2AO ,所以x ,y =2-x 1,-y 1 解得x =-2x 1y =-2y 1 ,又因为BP =2CP ,所以-2x 1-x 2,-2y 1-y 2 =2-2x 1-x 3,-2y 1-y 3 解得x 3=-x 1+12x 2y 3=-y 1+12y 2,因为点C 在椭圆上,所以-x 1+12x 2 22+-y 1+12y 2 2=1⇒x 212+y 21+14x 222+y 22-12x 1x 2-y 1y 2=1,即x 1x 2+2y 1y 2=12.(2)设直线AC 与OB 斜率分别为k AC ,k OB ,k AC k OB =y 3-y 1x 3-x 1×y 2x 2=-y 1+12y 2-y 1-x 1+12x 2-x 1×y 2x 2=-2y 1y 2+12y 22-2x 1x 2+12x 22=x 1x 2-12+121-12x 22 -2x 1x 2+12x 22=x 1x 2-14x 22-2x 1x 2+12x 22=-12是定值.13.(2023·浙江嘉兴·统考模拟预测)已知抛物线C :y 2=2px p >0 ,过焦点F 的直线交抛物线C 于A ,B 两点,且AB =AF ⋅BF .(1)求抛物线C 的方程;(2)若点P 4,4 ,直线PA ,PB 分别交准线l 于M ,N 两点,证明:以线段MN 为直径的圆过定点.【答案】(1)y 2=4x (2)证明见解析【分析】(1)设AB :x =my +p2m ∈R ,联立抛物线方程,由根与系数的关系及抛物线的定义,根据AB =AF ⋅BF 建立方程求出p 得解;(2)由直线方程求出M ,N 的坐标,计算y M ⋅y N =-4,设Q x ,y 是以线段MN 为直径的圆上任意一点,根据MQ ⋅NQ=0化简0=x +1 2+y -y M y -y N ,根据对称性令y =0可得解.【详解】(1)设AB :x =my +p2m ∈R ,A x 1,y 1 ,B x 2,y 2 ,则联立y 2=2pxx =my +p 2得y 2-2pmy -p 2=0,所以Δ=4p 2m 2+4p 2>0y 1+y 2=2pm y 1y 2=-p 2,所以x 1+x 2=2m 2+1 px 1x 2=p 24,又AF =x 1+p 2,BF =x 2+p2,所以AB =AF +BF =x 1+x 2+p 由AB =AF ⋅BF 得x 1+x 2+p =x 1+p 2 x 2+p2 ,即x 1+x 2+p =x 1x 2+p 2x 1+x 2 +p 24所以2m 2+1 p +p =p 22m 2+1 p +p 22,化简得m 2+1 p p -2 =0,又p >0,所以p =2,所以抛物线C 的方程为y 2=4x .(2)由(1)知AB :x =my +1m ∈R ,A x 1,y 1 ,B x 2,y 2 ,所以y 1+y 2=4m ,y 1y 2=-4,易得x 1+x 2=4m 2+2,x 1x 2=1,由题意知AP :y -4=y 1-4x 1-4x -4 ,BP :y -4=y 2-4x 2-4x -4 ,所以令x =-1得y M =-5y 1-4 my 1-3+4,y N =-5y 2-4my 2-3+4,即M -1,-5y 1-4 x 1-4+4,N -1,-5y 2-4 x 2-4+4,所以y M ⋅y N =-5y 1-4my 1-3+4-5y 2-4 my 2-3+4=4m -5 y 1+8 4m -5 y 2+8my 1-3 my 2-3=4m -52y 1y 2+84m -5 y 1+y 2 +64m 2y 1y 2-3m y 1+y 2 +9=-44m -5 2+32m 4m -5 +64-4m 2-12m 2+9=64m 2-36-16m 2+9=-4设Q x ,y 是以线段MN 为直径的圆上得任意一点,则有MQ ⋅NQ=0,即0=x +1 2+y -y M y -y N ,由对称性令y =0得0=x +1 2+y M y N =x +1 2-4,所以x =1或x =-3所以以线段MN 为直径的圆经过定点,定点坐标为-3,0 与1,0 .【点睛】关键点点睛:求出M ,N 的点的坐标,计算出y M ⋅y N 为定值-4,是解题的关键之一,其次写出以MN 为直径的圆的方程,根据圆的方程0=x +1 2+y -y M y -y N ,由对称性,令y =0求定点是解题的关键.14.(2023·江苏连云港·统考模拟预测)已知椭圆E :x 2a 2+y 2b2=1a >b >0 的焦距为23,且经过点P -3,12 .(1)求椭圆E 的标准方程:(2)过椭圆E 的左焦点F 1作直线l 与椭圆E 相交于A ,B 两点(点A 在x 轴上方),过点A ,B 分别作椭圆的切线,两切线交于点M ,求AB MF 1的最大值.【答案】(1)x 24+y 2=1(2)2【分析】(1)由待定系数法求解析式;(2)设出直线方程,由韦达定理法及导数法求得两切线方程,即可联立两切线方程解得交点M ,再由弦长公式及两点距离公式表示出AB MF 1,进而讨论最值.【详解】(1)由题意得2c =233a 2+14b 2=1a 2=b 2+c2 ,所以a =2b =1 ,即椭圆方程为x24+y 2=1;(2)当直线l 斜率为0时,A ,B 分别为椭圆的左右顶点,此时切线平行无交点.故设直线l :x =ty -3,由x 24+y 2=1x =ty -3,得t 2+4 y 2-23ty -1=0.Δ=16t 2+16>0,y 1+y 2=23t t 2+4,y 1y 2=-1t 2+4.AB =1+t 2y 1-y 2 =1+t 2y 1+y 22-4y 1y 2=1+t212t 2t 2+42+4t 2+4=4t 2+1t 2+4不妨设A x 1,y 1 在x 轴上方,则B x 2,y 2 在x 轴下方.椭圆在x 轴上方对应方程为y =1-x 24,y =-x41-x 24,则A 处切线斜率为-x 141-x 214=-x 14y 1,得切线方程为y -y 1=-x 14y 1x -x 1 ,整理得x 1x4+y 1y =1.同理可得B 处的切线方程为x 2x4+y 2y =1.由x 1x 4+y 1y =1①x 2x 4+y 2y =1②得x M =4y 2-y 1 x 1y 2-x 2y 1=4y 2-y 1 ty 1-3 y 2-ty 2-3 y 1=4y 2-y 1 3y 1-y 2 =-433,代入①得y M =1+33x 1y 1=1+33ty 1-3 y 1=3t 3,所以M -433,3t 3.因为MF 1 =-433+3 2+t 23=1+t 23,所以AB MF 1 =4t 2+1t 2+41+t 23=43t 2+1t 2+4设m =t 2+1≥1,则t 2=m 2-1,则AB MF 1=43m m 2+3=43m +3m≤4323=2,当且仅当m 2=3,即t =±2时,ABMF 1的最大值是2.另解:当直线l 的斜率存在时,设l :y =k x +3 ,由x 24+y 2=1y =k x +3得1+4k 2 x 2+83k 2x +12k 2-4=0,所以Δ=k 2+1>0,x 1+x 2=-83k 21+4k 2,x 1x 2=12k 2-41+4k 2,AB =1+k 2x 1-x 2 =1+k 2⋅x 1+x 22-4x 1x 2=1+k 2⋅64×3k 21+4k 22-412k 2-41+4k 2=41+k 21+4k 2椭圆在x轴上方的部分方程为y=1-x24,y'=-x41-x24,则过A x1,y1y1>0的切线方程为y-y1=-x14y1x-x1,即x1x4+y1y=x214+y21=1,同理可得过B x2,y2y2<0的切线方程为x2x4+y2y=1.由x1x4+y1y=1x2x4+y2y=1得x M=4y2-y1x1y2-x2y1=4y2-y1y1k-3y2-y2k-3y1=4y2-y13y1-y2=-433设M-43 3,t,则-3x13+ty1=1-3x23+ty2=1 ,所以直线l的方程为-33x+ty=1,所以t=33k.MF1=-433+32+t2=1+k23k2,AB MF1=41+k21+4k2⋅3k21+k2=43k21+k21+4k22令n=1+4k2≥1,则k2=n-14,所以ABMF1=3-3⋅1n2+2⋅1n+1,当1n=-22×-3⇒n=3时,即k=±22时,ABMF1取得最大值,为2.【点睛】直线与圆锥曲线问题,一般设出直线,联立直线与圆锥曲线方程,结合韦达定理表示出所求的内容,进而进行进一步讨论.15.(2023春·江苏常州·高三校联考开学考试)已知点P2,-1在椭圆C:x2a2+y2b2=1(a>b>0)上,C的长轴长为42,直线l:y=kx+m与C交于A,B两点,直线PA,PB的斜率之积为14.(1)求证:k为定值;(2)若直线l与x轴交于点Q,求QA|2+QB|2的值.【答案】(1)证明见解析(2)10【分析】(1)根据题意求出椭圆方程为:x28+y22=1,将椭圆,及相关直线、点进行平移,将y1x1,y2x2看作方程8n-4X2+8t-4nX-4t+1=0的两不等实根,进而可得n=-2t,代入直线方程化简即可;(2)联立直线与椭圆方程,结合韦达定理得y3+y4=m,y3y4=m2-22,化简QA|2+QB|2=5y3+y42-2y3y4,代入韦达定理即可求解.【详解】(1)由题意知2a=424a2+1b2=1⇒a=22b=2,∴椭圆方程为:x28+y22=1.将椭圆平移至(x +2)28+(y -1)22=1即x 2+4y 2+4x -8y =0,此时P 点平移至P 0,0 ,A ,B 分别平移至A x 1,y 1 ,B x 2,y 2 ,设直线A B 方程为tx +ny =1代入椭圆⇒x 2+4y 2+4x -8y tx +ny =0,整理得8n -4 y 2+8t -4n xy -4t +1 x 2=0,两边同除以x 2⇒8n -4 ⋅y x2+8t -4n ⋅y x-4t +1 =0,∴k PA ⋅k PB=k PA ⋅k PB =14⇒y 1x 1⋅y 2x 2=14令y x =X ,则y 1x 1,y 2x 2可看作关于X 的一元二次方程,8n -4 X 2+8t -4n X -4t +1 =0的两不等实根,∴y 1x 1⋅y 2x 2=X 1X 2=-4t +1 8n -4=14,∴4t =-2n ,即n =-2t ,∴直线A B 方程为tx -2ty =1t ≠0 ,∴y =12x -12t,∴A B 的斜率为定值12,即k 的定值12.(2)设A x 3,y 3 ,B x 4,y 4 ,y =12x +m x 2+4y 2=8⇒8y 2-8my +4m 2-8=0,即2y 2-2my +m 2-2=0,Δ>0,故y 3+y 4=m ,y 3y 4=m 2-22,∴QA |2+ QB 2=1+4⋅y 3 2+1+4⋅y 4 2=5y 23+y 24 =5y 3+y 4 2-2y 3y 4=5m 2-2×m 2-22=10,∴QA |2+ QB |2=1016.(2023春·江苏苏州·高三统考开学考试)已知抛物线y 2=a 2x 的焦点也是离心率为32的椭圆x 2a2+y 2b 2=1a >b >0 的一个焦点F .(1)求抛物线与椭圆的标准方程;(2)设过F 的直线l 交抛物线于A 、B ,交椭圆于C 、D ,且A 在B 左侧,C 在D 左侧,A 在C 左侧.设a =AC ,b =μCD ,c =DB .①当μ=2时,是否存在直线l ,使得a ,b ,c 成等差数列?若存在,求出直线l 的方程;若不存在,说明理由;②若存在直线l ,使得a ,b ,c 成等差数列,求μ的范围.【答案】(1)抛物线的标准方程是y 2=12x ,椭圆的标准方程为x 212+y 23=1(2)①不存在,理由见解析;②μ∈43-12,+∞【分析】(1)根据相同焦点得到a 24=32a ,解得a =23,得到答案.(2)设l :x =my +3和各点坐标,联立方程利用韦达定理得到根与系数的关系,计算AB =12m 2+1 ,CD =43m 2+1m 2+4,根据等差数列的性质得到方程,方程无解得到答案;整理得到m 2=3+23μ-123>0,解不等式即可.【详解】(1)抛物线的焦点F a 24,0 ,椭圆的焦点F c ,0 ,由于e =c a =32,即F 32a ,0 ,则有a 24=32a ,因此a =23,c =3,b =a 2-c 2=3,故椭圆的标准方程为x 212+y 23=1,抛物线的标准方程是y 2=12x .(2)①设l :x =my +3,m ≠0 ,A x 1,y 1 ,B x 2,y 2 ,C x 3,y 3 ,D x 4,y 4 ,将直线与抛物线联立,则有y 2=12xx =my +3 ,y 2-12my -36=0,Δ=144m 2+36×4>0,则y 1+y 2=12m y 1y 2=-36,于是x 1x 2=my 1+3 my 2+3 =m 2y 1y 2+3m y 1+y 2 +9=9,将直线与椭圆联立,则有x 2+4y 2-12=0x =my +3,得到二次方程m 2+4 y 2+6my -3=0,Δ>0,则有y 3+y 4=-6m m 2+4y 3y 4=-3m 2+4,则AB =x 1-x 22+y 1-y 2 2=1+m 2⋅y 1+y 22-4y 1y 2=12m 2+1 ,CD =x 3-x 42+y 3-y 4 2=1+m 2⋅y 3+y 4 2-4y 3y 4=1+m236m 2m 2+4 2+12m 2+48m 2+42=43m 2+1 m 2+4,AC +DB =AB -CD =12m 2+1 -43m 2+1m 2+4,假设存在直线l ,使得a ,b ,c 成等差数列,即AC +DB =4CD 即有12m 2+1 -43m 2+1 m 2+4=2×2×43m 2+1m 2+4,整理得到12m 2=203-48,方程无解,因此不存在l 满足题设.②只需使得方程12m 2+1 -43m 2+1 m 2+4=2μ×43m 2+1m 2+4有解即可.整理得到m 2=3+23μ-123,故m 2=3+23μ-123>0,解得μ∈43-12,+∞【点睛】关键点睛:本题考查了抛物线和椭圆的标准方程,等差数列性质,直线和抛物线,椭圆的位置关系,意在考查学生的计算能力,转化能力和综合应用能力,其中,利用韦达定理得到根与系数的关系,根据设而不求的思想,可以简化运算,是解题的关键,需要熟练掌握.17.(2023秋·江苏无锡·高三统考期末)已知椭圆C 1:x 2a 2+y 2b 2=1a >b >0 的右焦点F 和抛物线C 2:y 2=2px p >0 的焦点重合,且C 1和C 2的一个公共点是23,263.(1)求C 1和C 2的方程;(2)过点F 作直线l 分别交椭圆于A ,B ,交抛物线C 2于P ,Q ,是否存在常数λ,使1AB -λPQ为定值?若存在,求出λ的值;若不存在,说明理由.【答案】(1)x 24+y 23=1, y 2=4x (2)存在,λ=13【分析】(1)先求出抛物线的方程,进而求出焦点,再根据椭圆的右焦点与其重合,列出方程组求解即可;(2)利用弦长公式分别表示出AB ,PQ ,然后代入1AB -λPQ ,可求出使1AB -λPQ为定值的常数λ.【详解】(1)解:由题意知2632=2p ⋅23⇒p =2,∴y 2=4x ,抛物线焦点1,0 ,∴c =149a 2+83b 2=1a 2=b 2+c2 ⇒a =2b =3 ⇒C 1方程:x 24+y 23=1,C 2方程:y 2=4x .(2)解:方法一:假设存在这样的l ,设直线l 的方程为:x =my +1,A x 1,y 1 ,B x 2,y 2 ,x =my +13x 2+4y 2=12⇒3m 2y 2+2my +1 +4y 2=12,3m 2+4 y 2+6my -9=0.Δ=36m 2+363m 2+4 =144m 2+1 ,∴AB =1+m 2⋅y 1-y 2 =1+m 2⋅144m 2+1 3m 2+4=12m 2+13m 2+4.设P x 3,y 3 ,Q x 4,y 4 ,x =my +1y 2=4x⇒y 2=4my +4,y 2-4my -4=0,Δ=16m 2+16,∴PQ =1+m 2⋅y 3-y 4=1+m 2⋅16m 2+16=4m 2+1 ,∴1AB -λPQ =3m 2+412m 2+1 -λ4m 2+1 =3m 2+4-3λ12m 2+1 为定值.∴312=4-3λ12⇒λ=13,∴存在常数λ=13使1AB -λPQ为定值14.方法二:1AB -λPQ =1-14cos 2θ3-λ1-cos 2θ4对比cos 2θ前系数λ=13.方法三:设l 倾斜角为θ,∴AB =2ab 2a 2-c 2cos 2θ=2×2×34-cos 2θ=124-cos 2θ,PQ =2p sin 2θ=4sin 2θ,∴1AB -λPQ =4-cos 2θ12-λsin 2θ4=4-3λsin 2θ-cos 2θ12为定值,∴3λ=1,λ=13,此时定值为14.18.(2023秋·江苏·高三统考期末)如图,已知椭圆x 24+y 2=1的左、右顶点分别为A ,B ,点C 是椭圆上异于A ,B 的动点,过原点O 平行于AC 的直线与椭圆交于点M ,N ,AC 的中点为点D ,直线OD 与椭圆交于点P ,Q ,点P ,C ,M 在x 轴的上方.(1)当AC =5时,求cos ∠POM ;(2)求PQ ⋅MN 的最大值.【答案】(1)-35(2)10【分析】(1)根据题意求出k AC ⋅k OD =-14,根据AC =5分析出点C 满足的方程,求出点C 坐标,进而求出cos ∠POM ;(2)利用弦长公式求出PQ 和MN ,再利用基本不等式求出最值.【详解】(1)由题知A -2,0 ,设C x 0,y 0 ,则D x 0-22,y 02,则k AC ⋅k OD =y 0x 0+2⋅y 0x 0-2=1-14x 2x 20-4=-14.因为AC =5,所以C 在圆(x +2)2+y 2=5上,又C 在椭圆x 24+y 2=1上,所以C x 0,y 0 满足(x +2)2+y 2=5x 24+y 2=1,所以(x +2)2+1-x 24=5,34x 2+4x =0,所以x 0=0或x 0=-163<-2(舍去),又C 在x 轴上方,所以C 0,1 ,所以直线AC 的斜率为12,故直线OD 的斜率为-12,所以直线AC 与直线OD 关于y 轴对称.设直线AC 的倾斜角θ,cos ∠POM =cos2π2-θ=-cos2θ=sin 2θ-cos 2θ=sin 2θ-cos 2θsin 2θ+cos 2θ=tan 2θ-1tan 2θ+1=-35(2)当直线MN 斜率为k ,k >0,则直线MN :y =kx ,直线PQ :y =-14k x ,M x 1,y 1 ,N x 2,y 2 满足y =kxx 24+y 2=1,所以4k 2+1 x 2=4,x 2=44k 2+1,所以MN 2=1+k 2 164k 2+1,同理PQ 2=1+116k 2 114k 2+1=416k 2+1 4k 2+1,所以MN 2⋅PQ 2=164k 2+4 16k 2+1 4k 2+1 2≤164k 2+4+16k 2+12 24k 2+1 2=420k 2+5 24k 2+12=100所以MN ⋅PQ ≤10,当且仅当4k 2+4=16k 2+1,即k ≤12时取“=”,所以PQ ⋅MN 的最大值为10.【点睛】方法点睛:解决直线与椭圆的综合问题时,要注意:(1)注意观察应用题设中的每一个条件,明确确定直线、椭圆的条件;(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.19.(2023·浙江·校联考模拟预测)设双曲线C :x 2a 2-y 2b 2=1的右焦点为F 3,0 ,F 到其中一条渐近线的距离为2.(1)求双曲线C 的方程;(2)过F 的直线交曲线C 于A ,B 两点(其中A 在第一象限),交直线x =53于点M ,(i )求|AF |⋅|BM ||AM |⋅|BF |的值;(ii )过M 平行于OA 的直线分别交直线OB 、x 轴于P ,Q ,证明:MP =PQ .【答案】(1)x 25-y 24=1(2)(i )1;(ii )证明见解析【分析】(1)结合点F 到其中一条渐近线的距离为2和a 2+b 2=c 2,即可求得本题答案;(2)(i )设AB 直线方程为x =my +3,A x 1,y 1 ,B x 2,y 2 ,得y M =-43m,直线方程与双曲线方程联立消x ,然后由韦达定理得y 1+y 2=-24m 4m 2-5,y 1y 2=164m 2-5,把|AF |⋅|BM ||AM |⋅|BF |逐步化简,即可求得本题答案;(ii )把QM 和OB 的直线方程分别求出,联立可得到点P 的坐标,由此即可得到本题答案.【详解】(1)因为双曲线其中一条渐近线方程为bx +ay =0,又点F 3,0 到它的距离为2,所以3b b 2+a2=3bc =2,又c =3,得b =2,又因为a 2+b 2=c 2,所以a 2=5,所以双曲线C 的方程为x 25-y 24=1.(2)(2)设AB 直线方程为x =my +3,则y M =-43m,代入双曲线方程整理得:4m 2-5 y 2+24my +16=0,设A x 1,y 1 ,B x 2,y 2 ,则y 1+y 2=-24m 4m 2-5,y 1y 2=164m 2-5,(i )|AF |⋅|BM ||AM |⋅|BF |=y 1 ⋅y 2-y M y M -y 1 ⋅y 2 =y 1y 2-y 1y My 2y M -y 2y 1 而y 1y 2-y 1y M -y 2y M -y 2y 1 =2y 1y 2-y M y 1+y 2 =324m 2-5--24m 4m 2-5⋅-43m =0,所以y 1y 2-y 1y M =y 2y M -y 2y 1,,则y 1y 2-y 1y M =y 2y M -y 2y 1 ,所以|AF |⋅|BM ||AM |⋅|BF |=1 ;(ii )过M 平行于OA 的直线方程为y +43m =y 1my 1+3x -53,直线OB 方程为y =y 2my 2+3x 与y +43m =y 1my 1+3x -53联立,得y +43m =y 1my 1+3my 2+3y 2y -53,即y 2my 1+3 y +43m my 1+3 y 2=y 1my 2+3 y -53y 1y 2,则3y 2-y 1 y =-3y 1y 2-4my 2,所以y P =-3y 1y 2-4my 23y 2-y 1 ,由y 1+y 2=-24m 4m 2-5,y 1y 2=164m 2-5两式相除得,y 1y 2y 1+y 2=2-3m ,则y 1y 2=-23m y 1+y 2 ,所以y P =-3y 1y 2-4m y 23y 2-y 1 =2m y 1+y 2 -4m y 23y 2-y 1 =2m y 1-y 2 3y 2-y 1 =-23m ,因为y Q =0,所以y P =y M +y Q2,故P 为线段MQ 的中点,所以|MP |=|PQ |.【点睛】关键点点睛:本题第二小题第一问考了|AF |⋅|BM ||AM |⋅|BF |如何用y 1,y 2,y M 表示出来,进而利用韦达定理进行化简求值,考查了学生的转化能力以及对复杂运算的求解能力20.(2023春·浙江绍兴·高三统考开学考试)在平面直角坐标系xOy 中,已知椭圆C :x 24+y 2=1,B 1,0 .(1)设P 是椭圆C 上的一个动点,求PO ⋅PB的取值范围;(2)设与坐标轴不垂直的直线l 交椭圆C 于M ,N 两点,试问:是否存在满足条件的直线l ,使得△MB N 是以B 为直角顶点的等腰直角三角形?若存在,求出直线l 的方程,若不存在,请说明理由.【答案】(1)23,6(2)y =54x -355或y =-54x +355【分析】(1)设点P (x 0,y 0),将PO ⋅PB转化为坐标表示,求取值范围;(2)设直线方程,与椭圆方程联立,设MN 中点为D ,若△MB N 是以B 为直角顶点的等腰直角三角形,则BM ⊥BN ,BD ⊥MN ,解出直线方程.【详解】(1)设点P (x 0,y 0),则x 204+y 20=1,PO ⋅PB =(-x 0,-y 0)⋅(1-x 0,-y 0)=x 0(x 0-1)+y 20=34x 0-23 2+23,因为-2≤x 0≤2,所以当x 0=-2时,PO ⋅PB max =34×-2-23 2+23=6,当x 0=23时,PO ⋅PB min =34×23-23 2+23=23,所以PO ⋅PB ∈23,6 .(2)设直线l :y =kx +m (k ≠0),M (x 1,y 1),N (x 2,y 2),y =kx +mx 24+y 2=1,消去y 得,(4k 2+1)x 2+8km x +4m 2-4=0,由题,Δ=64k 2m 2-4(4k 2+1)(4m 2-4)>0,x 1+x 2=-8km 4k 2+1,x 1x 2=4m 2-44k 2+1,y 1+y 2=kx 1+m +kx 2+m =2m 4k 2+1,y 1y 2=(kx 1+m )(kx 2+m )=m 2-4k 24k 2+1,若△MB N 是以B 为直角顶点的等腰直角三角形,则BM ⊥BN , BM ⋅BN=(x 1-1,y 1)⋅(x 2-1,y 2)=x 1x 2-(x 1+x 2)+1+y 1y 2=8km +5m 2-34k 2+1=0,所以8km +5m 2-3=0,①设MN 中点为D ,则D -4km 4k 2+1,m4k 2+1,因为BD ⊥MN ,。
高中数学高考总复习圆锥曲线的综合问题习题及详解一、选择题1.(2010·聊城模考)已知双曲线x 2a 2-y 2b 2=1的一个焦点与抛物线y 2=4x 的焦点重合,且双曲线的离心率等于5,则该双曲线的方程为( )A .5x 2-45y 2=1B.x 25-y 24=1 C.y 25-x 24=1D .5x 2-54y 2=1[答案] D[解析] 抛物线y 2=4x 焦点为(1,0),∴双曲线中c =1, 又e =c a =5,∴a =55,∴b 2=c 2-a 2=1-15=45,∴双曲线方程为x 215-y 245=1.2.(2010·山东郓城)已知对k ∈R ,直线y -kx -1=0与椭圆x 25+y 2m =1恒有公共点,则实数m 的取值范围是( )A .(0,1)B .(0,5)C .[1,5)∪(5,+∞)D .[1,5)[答案] C[解析] 直线y =kx +1过定点(0,1),只要(0,1)在椭圆x 25+y 2m =1上或共内部即可,从而m ≥1.又因为椭圆x 25+y 2m=1中m ≠5,∴m ∈[1,5)∪(5,+∞).[点评] 含参数的直线与曲线位置关系的命题方式常常是直线过定点,考虑定点与曲线位置,以确定直线与曲线的位置.3.图中的椭圆C 1、C 2与双曲线C 3、C 4的离心率分别为e 1、e 2、e 3、e 4,则它们的大小关系是( )A .e 1<e 2<e 3<e 4B .e 2<e 1<e 3<e 4C .e 1<e 2<e 4<e 3D .e 2<e 1<e 4<e 3[答案] B[解析] ∵C 1、C 2为椭圆,∴e ∈(0,1) ∵C 3、C 4为双曲线,∴e ∈(1,+∞) 比较C 1、C 2∵a 相等而C 1比C 2的短轴小, ∴C 1的焦距比C 2的焦距大,从而e 1>e 2 同理C 4的虚轴长>C 3的虚轴长,而实轴长相同 ∴C 4的焦距>C 3的焦距 ∴e 4>e 3 综上可得:e 2<e 1<e 3<e 4,选B. [点评] 对于椭圆e =ca =1-⎝⎛⎭⎫b a 2,e 越大越扁,对于双曲线e =c a=1+⎝⎛⎭⎫b a 2,e 越大开口越宽阔.4.已知以F 1(-2,0),F 2(2,0)为焦点的椭圆与直线x +3y +4=0有且仅有一个公共点,则椭圆的长轴长为( )A .3 2B .2 6C .27D .4 2[答案] C[解析] 根据题意设椭圆方程为x 2b 2+4+y 2b 2=1(b >0),则将x =-3y -4代入椭圆方程得,4(b 2+1)y 2+83b 2y -b 4+12b 2=0,∵椭圆与直线x +3y +4=0有且仅有一个公共点, ∴Δ=(83b 2)2-4×4(b 2+1)(-b 4+12b 2)=0, 即(b 2+4)(b 2-3)=0,∴b 2=3, 长轴长为2b 2+4=27,故选C.5.已知椭圆x 2a 2+y 2b 2=1(a >b >0),过椭圆的右焦点作x 轴的垂线交椭圆于A 、B 两点,若OA →·OB →=0,则椭圆的离心率e 等于( )A.-1+52B.-1+32C.12D.32[答案] A[解析] 如图,F 2(c,0)把x =c 代入椭圆x 2a 2+y 2a 2=1得A (c ,b 2a).由OA →·OB →=0结合图形分析得 |OF 2|=|AF 2|,即c =b 2a⇒b 2=ac ⇒a 2-c 2=ac⇒(c a )2+ca -1=0⇒e 2+e -1=0⇒e =5-12. 6.(2010·重庆南开中学)双曲线x 2n -y 2=1(n >1)的两焦点为F 1,F 2,点P 在双曲线上,且满足:|PF 1|+|PF 2|=2n +2,则△PF 1F 2的面积是( )A .1 B.12 C .2D .4[答案] A[解析] 由条件知⎩⎨⎧|PF 1|-|PF 2|=2n|PF 1|+|PF 2|=2n +2,∴|PF 1|=n +2+n ,|PF 2|=n +2-n 又∵|F 1F 2|=2n +1,∴|PF 1|2+|PF 2|2=|F 1F 2|2, ∴S △PF 1F 2=12|PF 1|·|PF 2|=12(n +2+n )(n +2-n )=1. 7.在同一坐标系中方程a 2x 2+b 2y 2=1与ax +by 2=0(a >b >0)的曲线大致是( )[答案] D[解析] 方程a 2x 2+b 2y 2=1,即x 21a 2+y 21b2=1,因为1a 2<1b 2,所以是焦点在y 轴上的椭圆.方程ax +by 2=0化为y 2=-abx ,为焦点在x 轴的负半轴的抛物线.8.(2010·长沙一中、雅礼中学联考)若椭圆mx 2+ny 2=1(m >0,n >0)与直线y =1-x 交于A ,B 两点,过原点与线段AB 中点的连线的斜率为12,则椭圆的离心率为( )A.12B.22C.32D.62[答案] B[解析] 设A (x 1,y 1),B (x 2,y 2),则AB 中点为⎝⎛⎭⎫x 1+x 22,y 1+y 22,mx 12+ny 12=1,mx 22+ny 22=1,两式相减得y 1+y 2x 1+x 2=-m n ×x 1-x 2y 1-y 2,∴12=-m n ×(-1),即m n =12,离心率e =1m -1n1m=1-m n =22,故选B.9.(2010·福建福州市质检)已知P 为抛物线y 2=4x 上一个动点,Q 为圆x 2+(y -4)2=1上一个动点,那么点P 到点Q 的距离与点P 到抛物线的准线距离之和的最小值是( )A .5B .8 C.17-1D.5+2[答案] C[解析] 抛物线y 2=4x 的焦点为F (1,0),圆x 2+(y -4)2=1的圆心为C (0,4),设点P 到抛物线的准线距离为d ,根据抛物线的定义有d =|PF |,∴|PQ |+d =|PQ |+|PF |,由圆的几何性质及三角形两边之和大于第三边可知,当P 、Q 、F 、C 四点共线时取最小值,故最小值为|FC |-1=17-1.10.(2010·北方四校联考)已知抛物线C :y 2=2px (p >0),过点A ⎝⎛⎭⎫p 2,0的直线与抛物线C 交于M 、N 两点,且MA →=2AN →,过点M 、N 向直线x =-p 2作垂线,垂足分别为P 、Q ,△MAP 、△NAQ 的面积分别为记为S 1与S 2,那么( )A .S 1∶S 2=2∶1B .S 1∶S 2=5∶2C .S 1∶S 2=4∶1D .S 1∶S 2=7∶1[答案] C[解析] 依题意,点A 为抛物线的焦点,直线x =-p2为抛物线的准线,则|MP |=|MA |,|NA |=|NQ |,∠PMA =π-∠QNA ,故S 1=|MP ||MA |sin ∠PMA =4|AN |2sin ∠QNA =4S 2,故选C.二、填空题11.(2010·吉林省调研)已知过双曲线x 2a 2-y 2b 2=1右焦点且倾斜角为45°的直线与双曲线右支有两个交点,则双曲线的离心率e 的取值范围是________.[答案] (1,2)[解析] 由条件知,渐近线的倾斜角小于45°,即b a <1,∴c 2-a 2a 2<1,∴c 2a 2<2,即e 2<2,∵e >1,∴1<e < 2.12.已知点M (-3,0),N (3,0),B (1,0),动圆C 与直线MN 切于点B ,过M 、N 与圆C 相切的两直线相交于点P ,则P 点的轨迹方程为________.[答案] x 2-y 28=1(x >1)[解析] 设另两个切点为E 、F ,如图所示,则|PE |=|PF |,|ME |=|MB |,|NF |=|NB |.从而|PM |-|PN |=|ME |-|NF |=|MB |-|NB |=4-2=2<|MN |,所以点P 的轨迹是以M 、N 为焦点,实轴长为2的双曲线的右支.∴a =1,c =3,∴b 2=8.故方程为x 2-y 28=1(x >1).13.(2010·平顶山市调研)在下列命题中:①方程|x |+|y |=1表示的曲线所围成区域面积为2; ②与两坐标轴距离相等的点的轨迹方程为y =±x ;③与两定点(-1,0)、(1,0)距离之和等于1的点的轨迹为椭圆;④与两定点(-1,0)、(1,0)距离之差的绝对值等于1的点的轨迹为双曲线.正确的命题的序号是________.(注:把你认为正确的命题序号都填上) [答案] ①②④[解析] 方程|x |+|y |=1与两轴交点A (-1,0),B (0,-1),C (1,0),D (0,1)组成正方形的面积S =12|AC |·|BD |=12×2×2=2,故①真;设与两坐标轴距离相等的点为P (x ,y ),则|x |=|y |,∴y =±x ,故②真;∵两点E (-1,0),F (1,0)的距离|EF |=2>1,∴到两点E 、F 距离之和等于1的点不存在,∴③错误;与两点E 、F 距离之差的绝对值等于1的点的轨迹为双曲线正确.14.(2010·安徽安庆联考)设直线l :y =2x +2,若l 与椭圆x 2+y 24=1的交点为A 、B ,点P 为椭圆上的动点,则使△P AB 的面积为2-1的点P 的个数为________.[答案] 3[解析] 设与l 平行且与椭圆相切的直线方程为y =2x +b , 代入x 2+y 24=1中消去y 得,8x 2+4bx +b 2-4=0,由Δ=16b 2-32(b 2-4)=0得,b =±22,显见y =2x +2与两轴交点为椭圆的两顶点A (-1,0),B (0,2), ∵直线y =2x +22与l 距离d =22-25,∴欲使S △ABP =12|AB |·h =52h =2-1,须使h =22-25,∵d =h ,∴直线y =2x +22与椭圆切点,及y =2x +4-22与椭圆交点均满足,∴这样的点P 有3个.三、解答题15.(2010·新课标全国)设F 1、F 2分别是椭圆E :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,过F 1斜率为1的直线l 与E 相交于A 、B 两点,且|AF 2|、|AB |、|BF 2|成等差数列.(1)求E 的离心率;(2)设点P (0,-1)满足|P A |=|PB |,求E 的方程. [解析] (1)由椭圆定义知|AF 2|+|BF 2|+|AB |=4a , 又2|AB |=|AF 2|+|BF 2|,得|AB |=43a .l 的方程为y =x +c ,其中c =a 2-b 2.设A (x 1,y 1),B (x 2,y 2),则A ,B 两点坐标满足方程组⎩⎪⎨⎪⎧y =x +c ,x 2a 2+y 2b 2=1.消去y ,整理得(a 2+b 2)x 2+2a 2cx +a 2(c 2-b 2)=0,则x 1+x 2=-2a 2c a 2+b 2,x 1x 2=a 2(c 2-b 2)a 2+b 2.因为直线AB 斜率为1,所以|AB |=2|x 2-x 1|=2[(x 1+x 2)2-4x 1x 2], 得43a =4ab 2a 2+b2,故a 2=2b 2, 所以E 的离心率e =c a =a 2-b 2a =22.(2)设AB 的中点为N (x 0,y 0),由(1)知 x 0=x 1+x 22=-a 2c a 2+b 2=-23c ,y 0=x 0+c =c3.由|P A |=|PB |得k PN =-1. 即y 0+1x 0=-1, 得c =3,从而a =32,b =3. 故椭圆E 的方程为x 218+y 29=1.16.双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,坐标原点到直线AB 的距离为32,其中A (0,-b ),B (a,0).(1)求双曲线的标准方程;(2)设F 是双曲线的右焦点,直线l 过点F 且与双曲线的右支交于不同的两点P 、Q ,点M 为线段PQ 的中点.若点M 在直线x =-2上的射影为N ,满足PN →·QN →=0,且|PQ →|=10,求直线l 的方程.[解析] (1)依题意有⎩⎨⎧ca=2,ab a 2+b2=32,a 2+b 2=c 2.解得a =1,b =3,c =2.所以,所求双曲线的方程为x 2-y 23=1.(2)当直线l ⊥x 轴时,|PQ →|=6,不合题意.当直线l 的斜率存在时,设直线l 的方程为y =k (x -2).由⎩⎪⎨⎪⎧x 2-y 23=1(x >0)y =k (x -2)得,(3-k 2)x 2+4k 2x -4k 2-3=0.①因为直线与双曲线的右支交于不同两点,所以3-k 2≠0.设P (x 1,y 1),Q (x 2,y 2),M (x 0,y 0),则x 1、x 2是方程①的两个正根,于是有⎩⎨⎧x 1+x 2=4k 2k 2-3>0,x 1x 2=4k 2+3k 2-3>0,Δ=(4k 2)2-4(3-k 2)(-4k 2-3)>0,所以k 2>3.②因为PN →·QN →=0,则PN ⊥QN ,又M 为PQ 的中点,|PQ →|=10,所以|PM |=|MN |=|MQ |=12|PQ |=5. 又|MN |=x 0+2=5,∴x 0=3,而x 0=x 1+x 22=2k 2k 2-3=3,∴k 2=9,解得k =±3.∵k =±3满足②式,∴k =±3符合题意. 所以直线l 的方程为y =±3(x -2). 即3x -y -6=0或3x +y -6=0.17.(2010·北京崇文区)已知椭圆的中心在坐标原点O ,焦点在x 轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F 与x 轴不垂直的直线l 交椭圆于P ,Q 两点.(1)求椭圆的方程;(2)当直线l 的斜率为1时,求△POQ 的面积;(3)在线段OF 上是否存在点M (m,0),使得以MP ,MQ 为邻边的平行四边形是菱形?若存在,求出m 的取值范围;若不存在,请说明理由.[解析] (1)由已知,椭圆方程可设为x 2a 2+y 2b2=1(a >b >0).∵两个焦点和短轴的两个端点恰为正方形的顶点,且短轴长为2, ∴b =c =1,a = 2. 所求椭圆方程为x 22+y 2=1.(2)右焦点F (1,0),直线l 的方程为y =x -1. 设P (x 1,y 1),Q (x 2,y 2),由⎩⎪⎨⎪⎧x 2+2y 2=2y =x -1得,3y 2+2y -1=0, 解得y 1=-1,y 2=13.∴S △POQ =12|OF |·|y 1-y 2|=12|y 1-y 2|=23.(3)假设在线段OF 上存在点M (m,0)(0<m <1),使得以MP 、MQ 为邻边的平行四边形是菱形.因为直线与x 轴不垂直,所以设直线l 的方程为y =k (x -1)(k ≠0).由⎩⎪⎨⎪⎧x 2+2y 2=2y =k (x -1)可得,(1+2k 2)x 2-4k 2x +2k 2-2=0. ∴x 1+x 2=4k 21+2k 2,x 1x 2=2k 2-21+2k 2.MP →=(x 1-m ,y 1),MQ →=(x 2-m ,y 2),PQ →=(x 2-x 1,y 2-y 1).其中x 2-x 1≠0以MP ,MQ 为邻边的平行四边形是菱形⇔(MP →+MQ →)⊥PQ →⇔(MP →+MQ →)·PQ →=0 ⇔(x 1+x 2-2m ,y 1+y 2)·(x 2-x 1,y 2-y 1)=0 ⇔(x 1+x 2-2m )(x 2-x 1)+(y 1+y 2)(y 2-y 1)=0 ⇔(x 1+x 2-2m )+k (y 1+y 2)=0 ⇔⎝⎛⎭⎫4k 21+2k 2-2m +k 2⎝⎛⎭⎫4k21+2k 2-2=0 ⇔2k 2-(2+4k 2)m =0⇔m =k 21+2k 2(k ≠0).∴0<m <12.。
冲刺2023年高考二轮 圆锥曲线的综合问题强化训练(原卷+答案)考点一 证明问题——等价转化,直击目标圆锥曲线中证明问题的两种常见类型圆锥曲线中的证明问题,主要有两类:一是证明点、直线、曲线等几何元素中的位置关系,如:某点在某直线上,某直线经过某个点、某两条直线平行或垂直等;二是证明直线与圆锥曲线中的一些数量关系(相等或不等).例 1已知椭圆E 的中心为坐标原点,对称轴为x 轴、y 轴,且过A (0,-2),B (32,-1)两点.(1)求E 的方程;(2)设过点P (1,-2)的直线交E 于M ,N 两点,过M 且平行于x 轴的直线与线段AB 交于点T ,点H 满足MT⃗⃗⃗⃗⃗⃗ =TH ⃗⃗⃗⃗⃗ .证明:直线HN 过定点.对点训练已知直线y =3与曲线C :x 2+2py =0的两个公共点之间的距离为4√6. (1)求C 的方程;(2)设P 为C 的准线上一点,过P 作C 的两条切线,切点为A ,B ,直线P A ,PB 的斜率分别为k 1,k 2,且直线P A ,PB 与y 轴分别交于M ,N 两点,直线AB 的斜率为k 0.证明:k 1·k 2为定值,且k 1,k 0,k 2成等差数列.考点二 定点问题——目标等式寻定点解析几何中的定点问题一般是指与解析几何有关的直线或圆(其他曲线过定点太复杂,高中阶段一般不涉及)过定点的问题,其实质是:当动直线或动圆变化时,这些直线或圆相交于一点,即这些直线或圆绕着定点在转动,这类问题的求解一般分为以下三步:一选:选择变量,定点问题中的定点,随某一个量的变化而固定,可选择这个量为变量(有时可选择两个变量,如点的坐标、斜率、截距等,然后利用其他辅助条件消去其中之一).二求:求出定点坐标所满足的方程,即把需要证明为定点的问题表示成关于上述变量的方程.三定点:对上述方程进行必要的化简,即可得到定点坐标. 例 2 已知椭圆M :x 2a 2+y 2b 2=1(a >b >0)的离心率为√22,AB 为过椭圆右焦点的一条弦,且AB 长度的最小值为2.(1)求椭圆M 的方程;(2)若直线l 与椭圆M 交于C ,D 两点,点P (2,0),记直线PC 的斜率为k 1,直线PD 的斜率为k 2,当1k 1+1k 2=1时,是否存在直线l 恒过一定点?若存在,请求出这个定点;若不存在,请说明理由.对点训练已知抛物线C :y 2=2px (p >0)的焦点为F ,S (t ,4)为C 上一点,直线l 交C 于M ,N 两点(与点S 不重合).(1)若l 过点F 且倾斜角为60°,|FM |=4(M 在第一象限),求C 的方程;(2)若p =2,直线SM ,SN 分别与y 轴交于A ,B 两点,且OA ⃗⃗⃗⃗⃗ ·OB ⃗⃗⃗⃗⃗ =8,判断直线l是否恒过定点?若是,求出该定点;若否,请说明理由.考点三 定值问题——巧妙消元寻定值定值问题一般是指在求解解析几何问题的过程中,探究某些几何量(斜率、距离、面积、比值等)与变量(斜率、点的坐标等)无关的问题,其求解步骤一般为:一选:选择变量,一般为点的坐标、直线的斜率等.二化:把要求解的定值表示成含上述变量的式子,并利用其他辅助条件来减少变量的个数,使其只含有一个变量(或者有多个变量,若是能整体约分也可以).三定值:化简式子得到定值.由题目的结论可知要证明为定值的量必与变量的值无关,故求出的式子必能化为一个常数,所以只需对上述式子进行必要的化简即可得到定值.例 3 已知双曲线C :x 2a2−y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1、F 2,双曲线C 的右顶点A 在圆O :x 2+y 2=3上,且AF 1⃗⃗⃗⃗⃗⃗⃗ ·AF 2⃗⃗⃗⃗⃗⃗⃗ =-1.(1)求双曲线C 的方程;(2)动直线l 与双曲线C 恰有1个公共点,且与双曲线C 的两条渐近线分别交于点M 、N ,设O 为坐标原点.求证:△OMN 的面积为定值.对点训练已知F 1(-√3,0),F 2(√3,0)分别是双曲线C :x 2a 2−y 2b 2=1(a >b >0)的左、右焦点,A 为双曲线在第一象限的点,△AF 1F 2的内切圆与x 轴交于点P (1,0).(1)求双曲线C 的方程;(2)设圆O :x 2+y 2=2上任意一点Q 处的切线l ,若l 与双曲线C 左、右两支分别交于点M 、N ,问:QM ⃗⃗⃗⃗⃗⃗ ·QN ⃗⃗⃗⃗⃗ 是否为定值?若是,求出此定值;若不是,说明理由.考点四 圆锥曲线中的最值、范围问题——巧设变量,引参搭桥圆锥曲线中的最值 (1)椭圆中的最值 F 1,F 2为椭圆x 2a2+y 2b 2=1(a >b >0)的左、右焦点,P 为椭圆上的任意一点,B 为短轴的一个端点,O 为坐标原点,则有:①|OP |∈________;②|PF 1|∈________;③|PF 1|·|PF 2|∈________;④∠F 1PF 2≤∠F 1BF 2.(2)双曲线中的最值F 1,F 2为双曲线x 2a 2−y 2b 2=1(a >0,b >0)的左、右焦点,P 为双曲线上的任一点,O为坐标原点,则有:①|OP |≥________;②|PF 1|≥________. (3)抛物线中的最值点P 为抛物线y 2=2px (p >0)上的任一点,F 为焦点,则有:①|PF |≥________;②A (m ,n )为一定点,则|P A |+|PF |有最小值;③点N (a ,0)是抛物线的对称轴上一点,则|PN |min ={|a |(a ≤p ),√2pa −p 2(a >p).例 4如图,已知椭圆x 212+y 2=1.设A ,B 是椭圆上异于P (0,1)的两点,且点Q (0,12)在线段AB 上,直线P A ,PB 分别交直线y =-12x +3于C ,D 两点.(1)求点P 到椭圆上点的距离的最大值; (2)求|CD |的最小值.对点训练已知抛物线C :x 2=2py (p >0)的焦点为F ,且F 与圆M :x 2+(y +4)2=1上点的距离的最小值为4.(1)求p ;(2)若点P 在M 上,P A ,PB 是C 的两条切线,A ,B 是切点,求△P AB 面积的最大值.[典例] 已知圆(x +√3)2+y 2=16的圆心为M ,点P 是圆M 上的动点,点N (√3,0),点G 在线段MP 上,且满足(GN⃗⃗⃗⃗⃗ +GP ⃗⃗⃗⃗⃗ )⊥(GN ⃗⃗⃗⃗⃗ −GP ⃗⃗⃗⃗⃗ ). (1)求点G 的轨迹C 的方程;(2)过点T (4,0)作斜率不为0的直线l 与轨迹C 交于A ,B 两点,点A 关于x 轴的对称点为D ,连接BD 交x 轴于点Q ,求△ABQ 面积的最大值.(1)因为(GN ⃗⃗⃗⃗⃗⃗ +GP ⃗⃗⃗⃗⃗ )⊥(GN ⃗⃗⃗⃗⃗⃗ −GP ⃗⃗⃗⃗⃗ ), 所以(GN ⃗⃗⃗⃗⃗⃗ +GP ⃗⃗⃗⃗⃗ )·(GN ⃗⃗⃗⃗⃗⃗ −GP ⃗⃗⃗⃗⃗ )=0,即GN ⃗⃗⃗⃗⃗⃗ 2-GP ⃗⃗⃗⃗⃗ 2=0, 所以|GP |=|GN |,所以|GM |+|GN |=|GM |+|GP |=|MP |=4>2√3=|MN |, 所以点G 在以M ,N 为焦点,长轴长为4的椭圆上,设椭圆的方程为x 2a 2+y 2b 2=1(a >b >0),则2a =4,2c =2√3,即a =2,c =√3,所以b 2=a 2-c 2=1, 所以点G 的轨迹C 的方程为x 24+y 2=1. (2)依题意可设直线l :x =my +4. 由{x =my +4,x 24+y 2=1消去x ,得(m 2+4)y 2+8my +12=0.设A (x 1,y 1),B (x 2,y 2),由Δ=64m 2-4×12×(m 2+4)=16(m 2-12)>0,得m 2>12. ①且y 1+y 2=-8mm 2+4,y 1y 2=12m 2+4.②因为点A 关于x 轴的对称点为D , 所以D (x 1,-y 1), 可设Q (x 0,0),所以k BD =y 2+y 1x 2−x 1=y 2+y 1m (y 2−y 1), 所以BD 所在直线的方程为y -y 2=y 2+y 1m (y2−y 1)(x -my 2-4). 令y =0,得x 0=2my 1y 2+4(y 1+y 2)y 1+y 2. ③将②代入③, 得x 0=24m−32m−8m=1, 所以点Q 的坐标为(1,0).因为S △ABQ =|S △TBQ -S △TAQ |=12|QT ||y 2-y 1|=32√(y 1+y 2)2−4y 1y 2=6√m 2−12m 2+4,令t =m 2+4,结合①得t >16, 所以S △ABQ =6√t−16t= 6√−16t 2+1t =6√−16(1t −132)2+164.当且仅当t =32,即m =±2√7时,(S △ABQ )max =34. 所以△ABQ 面积的最大值为34.参考答案考点一[例1] 解析:(1)设椭圆E 的方程为mx 2+ny 2=1(m >0,n >0,m ≠n ). 将点A (0,-2),B (32,-1)的坐标代入,得{4n =1,94m +n =1,解得{m =13,n =14. 所以椭圆E的方程为x 23+y 24=1. (2)证明:方法一 设M (x 1,y 1),N (x 2,y 2).由题意,知直线MN 与y 轴不垂直,设其方程为x -1=t (y +2).联立得方程组{x −1=t (y +2),x 23+y 24=1. 消去x 并整理,得(4t 2+3)y 2+(16t 2+8t )y +16t 2+16t -8=0,所以y 1+y 2=-16t 2+8t 4t 2+3,y 1y 2=16t 2+16t−84t 2+3.设T (x 0,y 1).由A ,B ,T 三点共线,得y 1+2x 0=y 1+1x 0−32,得x 0=32y 1+3.设H (x ′,y ′). 由MT ⃗⃗⃗⃗⃗⃗ =TH ⃗⃗⃗⃗⃗ ,得(32y 1+3-x 1,0)=(x ′-32y 1-3,y ′-y 1),所以x ′=3y 1+6-x 1,y ′=y 1, 所以直线HN 的斜率k =y 2−y ′x 2−x ′=y 2−y 1x 2+x 1−(3y 1+6)=y 2−y 1t (y 1+y 2)−3y 1+4t−4,所以直线HN 的方程为y -y 2=y 2−y 1t (y 1+y 2)−3y 1+4t−4·(x -x 2).令x =0,得y =y 2−y 1t (y 1+y 2)−3y 1+4t−4·(-x 2)+y 2=(y 1−y 2)(ty 2+2t+1)t (y 1+y 2)−3y 1+4t−4+y 2=(2t−3)y 1y 2+(2t−5)(y 1+y 2)+6y 1t (y 1+y 2)−3y 1+4t−4=(2t−3)·16t 2+16t−84t 2+3+(5−2t )·16t 2+8t4t 2+3+6y 1−t(16t 2+8t)4t 2+3−3y 1+4t−4=-2.所以直线NH 过定点(0,-2).方法二 由A (0,-2),B (32,-1)可得直线AB 的方程为y =23x -2. a .若过点P (1,-2)的直线的斜率不存在,则其直线方程为x =1.将直线方程x =1代入x 23+y 24=1,可得N (1,2√63),M (1,-2√63). 将y =-2√63代入y =23x -2,可得T (3-√6,-2√63).由MT⃗⃗⃗⃗⃗⃗ =TH ⃗⃗⃗⃗⃗ ,得H (5-2√6,-2√63). 此时直线HN 的方程为y =(2+2√63)(x -1)+2√63,则直线HN 过定点(0,-2). b .若过点P (1,-2)的直线的斜率存在,设此直线方程为kx -y -(k +2)=0,M (x 1,y 1),N (x 2,y 2).联立得方程组{kx −y −(k +2)=0,x 23+y 24=1. 消去y 并整理,得(3k 2+4)x 2-6k (2+k )x +3k (k +4)=0. 所以{x 1+x 2=6k (2+k )3k 2+4,x 1x 2=3k (4+k )3k 2+4,则{y 1+y 2=−8(2+k )3k 2+4,y 1y 2=4(4+4k−2k 2)3k 2+4, 且x 1y 2+x 2y 1=−24k3k 2+4.①联立得方程组{y =y 1,y =23x −2,可得T (3y 12+3,y 1). 由MT⃗⃗⃗⃗⃗⃗ =TH ⃗⃗⃗⃗⃗ ,得H (3y 1+6-x 1,y 1). 则直线HN 的方程为y -y 2=y 1−y 23y 1+6−x 1−x2(x -x 2). 将点(0,-2)的坐标代入并整理,得2(x 1+x 2)-6(y 1+y 2)+x 1y 2+x 2y 1-3y 1y 2-12=0.②将①代入②,得24k +12k 2+96+48k -24k -48-48k +24k 2-36k 2-48=0,显然成立.综上可得,直线HN 过定点(0,-2).对点训练解析:(1)将y =3代入x 2+2py =0,得x 2=-6p . 当p ≥0时,不合题意;当p <0时,x =±√−6p ,则2√−6p =4√6, 解得p =-4,故C 的方程为x 2=8y .(2)证明:由(1)可知C 的准线方程为y =-2, 不妨设P (m ,-2),A (x 1,y 1),B (x 2,y 2),设过点P 且与C 相切的直线l 的斜率为k ,则l :y =k (x -m )-2,且k ≠0,联立{y =k (x −m )−2,x 2=8y ,得x 2-8kx +8(km +2)=0,则Δ=64k 2-32(km +2)=0,即k 2-12mk -1=0,由题意知,直线P A ,PB 的斜率k 1,k 2为方程k 2-12mk -1=0的两根, 则k 1+k 2=m2,k 1k 2=-1,故k 1·k 2为定值. 又x 2-8kx +8(km +2)=(x -4k )2=0, 则x 1=4k 1,同理可得x 2=4k 2,则k 0=y 1−y 2x 1−x 2=18x −1218x 22x 1−x 2=x 1+x 28,因此k 0=4(k 1+k 2)8=k 1+k 22,故k 1,k 0,k 2成等差数列.考点二[例2]解析:(1)因为x 2a 2+y 2b 2=1(a >b >0)的离心率为√22,过椭圆右焦点的弦长的最小值为2b 2a=2,所以a =2,c =√2,b =√2,所以椭圆M 的方程为x 24+y 22=1. (2)设直线l 的方程为m (x -2)+ny =1,C (x 1,y 1),D (x 2,y 2),由椭圆的方程x 2+2y 2=4,得(x -2)2+2y 2=-4(x -2).联立直线l 的方程与椭圆方程,得(x -2)2+2y 2=-4(x -2)[m (x -2)+ny ], 即(1+4m )(x -2)2+4n (x -2)y +2y 2=0,(1+4m )(x−2y )2+4n x−2y+2=0, 所以1k 1+1k 2=x 1−2y 1+x 2−2y 2=-4n 1+4m=1,化简得m +n =-14,代入直线l 的方程得m (x -2)+(−14−m)y =1,即m (x -y -2)-14y =1,解得x =-2,y =-4,即直线l恒过定点(-2,-4).对点训练解析:(1)抛物线C :y 2=2px (p >0)的焦点为F (p2,0),因为l 过点F 且倾斜角为60°,所以l :y =√3(x -p2), 联立y 2=2px (p >0),可得12x 2-20px +3p 2=0,解得x =32p 或x =p6,又M 在第一象限,所以x M =32p ,因为|FM |=4,所以32p +p2=4,解得p =2,所以抛物线C 的方程为y 2=4x ;(2)由已知可得抛物线C 的方程为y 2=4x ,点S (4,4), 设直线l 的方程为x =my +n ,点M (y 12 4,y1),N (y 22 4,y2),将直线l 的方程与抛物线C :y 2=4x 联立得y 2-4my -4n =0, 所以Δ=16m 2+16n >0,y 1+y 2=4m ,y 1y 2=-4n (*),直线SM 的方程为y -4=y 1−4y 12 4-4(x -4),令x =0求得点A 的纵坐标为4y 1y 1+4,同理求得点B 的纵坐标为4y 2y2+4, 由OA ⃗⃗⃗⃗⃗ ·OB ⃗⃗⃗⃗⃗ =16y 1y 2y 1y 2+4(y 1+y 2)+16=8,化简得y 1y 2=4(y 1+y 2)+16,将上面(*)式代入得-4n =16m +16,即n =-4m -4, 所以直线l 的方程为x =my -4m -4,即x +4=m (y -4), 所以直线l 过定点(-4,4).考点三[例3] 解析:(1)不妨设F 1(-c ,0),F 2(c ,0), 因为A (a ,0), 从而AF 1⃗⃗⃗⃗⃗⃗⃗ =(−c −a ,0),AF 2⃗⃗⃗⃗⃗⃗⃗ =(c -a ,0) ,故有 AF 1⃗⃗⃗⃗⃗⃗⃗ ·AF 2⃗⃗⃗⃗⃗⃗⃗ =a 2-c 2=-1, 又因为a 2+b 2=c 2, 所以 b =1,又因为A (a ,0) 在圆 O :x 2+y 2=3 上, 所以 a =√3,所以双曲线C的标准方程为x 23-y 2=1.(2)证明:设直线l 与x 轴交于D 点,双曲线的渐近线方程为y =±√33x ,由于动直线l 与双曲线C 恰有1个公共点, 且与双曲线C 的两条渐近线分别交于点M 、N ,当动直线l 的斜率不存在时, l :x =±√3,|OD |=√3,|MN |=2,S △OMN =12×√3×2=√3,当动直线l 的斜率存在时, 且斜率k ≠±√33, 不妨设直线 l :y =kx +m,故由{y =kx +m x 23−y 2=1⇒(1-3k 2)x 2-6mkx -3m 2-3=0, 依题意,1-3k 2≠0且m ≠0,Δ=(-6mk )2-4(1-3k 2)(-3m 2-3)=0, 化简得 3k 2=m 2+1,故由{y =kx +my =√33x ⇒x M =√33−k , 同理可求,x N =-√33+k, 所以|MN |=√1+k 2|xM−x N |=2√3|m|√k 2+1|1−3k 2|,又因为原点O 到直线l :kx -y +m =0的距离d =√k 2+1,所以S △OMN =12|MN |d =√3m 2|1−3k 2|,又由3k 2=m 2+1,所以S △OMN =√3|m|√k 2+1|1−3k 2|=√3,故△OMN 的面积为定值,定值为√3.对点训练解析:(1)如图,设AF 1,AF 2与△AF 1F 2的内切圆分别交于G ,H 两点, 则2a =|AF 1|−|AF 2|=|F 1P |−|PF 2| =(1+√3)-(√3-1)=2,所以a =1,则b 2=c 2-a 2=2, 则双曲线C 的方程为x 2-y 22=1.(2)由题意得,切线l 的斜率存在.设切线l 的方程为y =kx +m ,M (x 1,y 1),N (x 2,y 2). 因为l 与圆O :x 2+y 2=2相切,所以√1+k 2=√2,即m 2=2k 2+2.联立{y =kx +m ,x 2−y 22=1,消去y 并整理得(2-k 2)x 2-2kmx -m 2-2=0, 所以x 1+x 2=2km2−k 2,x 1x 2=−m 2−22−k 2.又QM ⃗⃗⃗⃗⃗⃗ ·QN ⃗⃗⃗⃗⃗ =(QO ⃗⃗⃗⃗⃗ +OM ⃗⃗⃗⃗⃗⃗ )·(QO ⃗⃗⃗⃗⃗ +ON ⃗⃗⃗⃗⃗ ) =|QO ⃗⃗⃗⃗⃗ |2-OQ ⃗⃗⃗⃗⃗ ·ON ⃗⃗⃗⃗⃗ −OQ ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ +ON ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ =|QO ⃗⃗⃗⃗⃗ |2-|OQ ⃗⃗⃗⃗⃗ |·|ON ⃗⃗⃗⃗⃗ |cos ∠QON -|OQ ⃗⃗⃗⃗⃗ |·|OM ⃗⃗⃗⃗⃗⃗ |cos ∠QOM +ON ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ =|QO ⃗⃗⃗⃗⃗ |2-|OQ ⃗⃗⃗⃗⃗ |·|OQ ⃗⃗⃗⃗⃗ |−|OQ ⃗⃗⃗⃗⃗ |·|OQ ⃗⃗⃗⃗⃗ |+ON ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ =|QO ⃗⃗⃗⃗⃗ |2-|QO ⃗⃗⃗⃗⃗ |2-|QO ⃗⃗⃗⃗⃗ |2+ON ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ =ON ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ −|OQ ⃗⃗⃗⃗⃗ |2. 又OM ⃗⃗⃗⃗⃗⃗ ·ON ⃗⃗⃗⃗⃗ =x 1x 2+y 1y 2 =x 1x 2+(kx 1+m )(kx 2+m )=(k 2+1)x 1x 2+km (x 1+x 2)+m 2 =(k 2+1)(−m 2−2)2−k 2+2k 2m 22−k2+m 2=m 2−2k 2−22−k 2,将m 2=2k 2+2代入上式得OM ⃗⃗⃗⃗⃗⃗ ·ON ⃗⃗⃗⃗⃗ =0.所以QM ⃗⃗⃗⃗⃗⃗ ·QN ⃗⃗⃗⃗⃗ =0-|OQ ⃗⃗⃗⃗⃗ |2=-2. 综上所述,QM ⃗⃗⃗⃗⃗⃗ ·QN ⃗⃗⃗⃗⃗ 为定值,且QM ⃗⃗⃗⃗⃗⃗ ·QN ⃗⃗⃗⃗⃗ =-2.考点四(1)[b ,a ] [a -c ,a +c ] [b 2,a 2] (2)a c -a (3)p2[例4] 解析:(1)设M (2√3cos θ,sin θ)是椭圆上一点,P (0,1),则|PM |2=12cos 2θ+(1-sin θ)2=13-11sin 2θ-2sin θ=14411-11(sin θ+111)2≤14411.故|PM |的最大值为12√1111.(2)由题意,知直线AB 的斜率存在,故设直线AB 的方程为y =kx +12.将直线方程与椭圆方程联立,得{y =kx +12,x 212+y 2=1.消去y 并整理,得(k 2+112)x 2+kx -34=0. 设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=-kk 2+112,x 1x 2=-34(k 2+112).直线P A :y =y 1−1x 1x +1与直线y =-12x +3交于点C ,则x C =4x 1x1+2y 1−2=4x 1(2k+1)x 1−1. 同理可得,x D =4x 2x 2+2y 2−2=4x 2(2k+1)x 2−1,则|CD |= √1+14|x C -x D | =√52|4x1(2k+1)x1−1−4x2(2k+1)x2−1|=2√5|x 1−x 2[(2k+1)x1−1][(2k+1)x 2−1]|=2√5|x 1−x 2(2k+1)2x 1x 2−(2k+1)(x 1+x 2)+1|=3√52·√16k 2+1|3k+1|=6√55·√16k 2+1· √916+1|3k+1| ≥6√55,当且仅当k =316时等号成立.故|CD |的最小值为6√55.对点训练解析:(1)由题意知M (0,-4),F (0,p2),圆M 的半径r =1,所以|MF |-r =4,即p2+4-1=4,解得p =2.(2)由(1)知,抛物线方程为x 2=4y , 由题意可知直线AB 的斜率存在,设A (x 1,x 12 4),B (x2,x 22 4),直线AB 的方程为y =kx +b ,联立得{y =kx +bx 2=4y,消去y 得x 2-4kx -4b =0, 则Δ=16k 2+16b >0(※),x 1+x 2=4k ,x 1x 2=-4b ,所以|AB |=√1+k 2|x 1-x 2|=√1+k 2·√(x 1+x 2)2−4x 1x 2=4√1+k 2·√k 2+b . 因为x 2=4y ,即y =x 24,所以y ′=x 2,则抛物线在点A 处的切线斜率为x12,在点A 处的切线方程为y −x 12 4=x 12(x -x 1),即y =x 12x −x 12 4,同理得抛物线在点B 处的切线方程为y =x 22x −x 22 4,联立得{y =x 12x −x 124y =x22x -x 22 4,则{x =x 1+x 22=2ky =x 1x 24=−b , 即P (2k ,-b ).因为点P 在圆M 上,所以4k 2+(4-b )2=1 ①,且-1≤2k ≤1,-5≤-b ≤-3,即-12≤k ≤12,3≤b ≤5,满足(※). 设点P 到直线AB 的距离为d ,则d =2√1+k 2,所以S △P AB =12|AB |·d =4√(k 2+b )3.由①得,k 2=1−(4−b )24=−b 2+8b−154, 令t =k 2+b ,则t =−b 2+12b−154,且3≤b ≤5. 因为t =−b 2+12b−154在[3,5]上单调递增,所以当b =5时,t 取得最大值,t max =5,此时k =0,所以△P AB 面积的最大值为20√5.。