五年级下册奥数题

五年级下册数学奥数题及答案一、选择题1.下列数中，哪一个不能整除30？ A. 5 B. 6 C. 10 D. 15答案：A2.小明买了3双袜子，每双袜子花费5元，他还剩下多少元？ A. 10 B.12 C. 15 D. 18答案：C3.一个长方形的长是8cm，宽是4cm，它的面积是多少平方厘米？ A.16 B. 20 C. 30 D. 32答案：D4.下列数字中，哪一个是奇数？ A. 10 B. 15 C. 20 D. 24答案：B5.如果一个三角形的三条边长度分别是3cm、4cm和5cm，那么它是什么三角形？ A. 等边三角形 B. 直角三角形 C. 锐角三角形 D. 钝角三角形答案：B二、填空题1. 5 × 6 = ____ 答案：302.下列数字中，最小的是____ 答案：03.7 ÷ 2 = ____ 答案：3.54. 2 + 4 × 3 = ____ 答案：145.12 ÷ 3 = ____ 答案：4三、解答题1. 计算题小明在商场购买了两本数学书，每本书的价格分别是35元和20元。

他付给售货员一张50元的钞票，请问他应该找给小明多少零钱？解答：两本书的总价格：35元+ 20元= 55元小明给了售货员50元的钞票，所以需要找给小明的零钱是：50元- 55元= -5元小明应该还需要给售货员5元。

2. 推理题一辆汽车前进了200公里，然后返回原点，再往前走100公里，最后又返回原点。

请问汽车最终所在的位置与原点的位置相比，是在原点的左边还是右边？解答：汽车前进了200公里，然后返回原点，所以汽车回到了原点。

再往前走100公里，又返回原点，所以汽车依然在原点。

因此，汽车最终所在的位置与原点的位置重合，即汽车最终位置与原点相同。

四、总结本文列出了五年级下册数学奥数题及答案。

选择题包括了求除数、数字判断、图形面积、奇偶数、三角形分类等题型。

填空题涵盖了乘法、最小数、除法以及复杂的运算顺序。

五年级奥数题练习（55题）1、（1+2+8）÷（1+2+8）＝2、奥运吉祥物中的5个“福娃”取“北京欢迎您”的谐音：贝贝、京京、欢欢、迎迎、妮妮。

如果在盒子中从左向右放5个不同的“福娃”，那么，有种不同的放法。

3、有一列数：1，1，3，8，22，60，164，448……其中的前三个数是1，1，3，从第四个数起，每个数都是这个数前面两个数之和的2倍。

那么，这列数中的第10个数是。

4、有一排椅子有27个座位，为了使后去的人随意坐在哪个位置都有人与他相邻，则至少要先坐人。

5、五年级一班共有36人，每人参加一个兴趣小组，共有A,B,C,D,E五个小组，若参加A组的有15人，参加B组的仅次于A组，参加C组、D组的人数相同。

参加E组的人数最少，只有4人，那么，参加B组的有人。

6、菜地里的西红柿获得丰收，摘了全部的2/5时，装满了3筐还多16千克。

摘完其余部分后，又装满6筐，则共收得西红柿千克。

7、工程队修一条公路，原计划每天修720米，实际每天比原计划多修80米。

因而提前3天完成任务。

这条路全长千米。

8、两个完全相同长方体的长、宽、高分别是5厘米、4厘米、3厘米，把它们拼在一起可组成一个新长方体，在这些长方体中，表面积最小的是平方厘米。

9、著名的哥德巴赫猜想：“任意一个大于4的偶数都可以表示为两个质数的和”。

如6＝3+3，12＝5+7，等。

那么自然数100可以写成种两个不同质数和的形式？请分别写出来（100＝3+97和100＝97+3算作同一种形式）10、号码分别为2005、2006、2007、2008的4名运动员进行乒乓球赛，规定每2人比赛的场数是他们号码的和被4除所得的余数。

那么2008号运动员比赛了场。

11、0.15÷2.1×56=12、15+115+1115+ (1111111115)13、一个自然数除以3，得余数2，用所得的商除以4.得余数3。

若用这个自然数除以6，得余数。

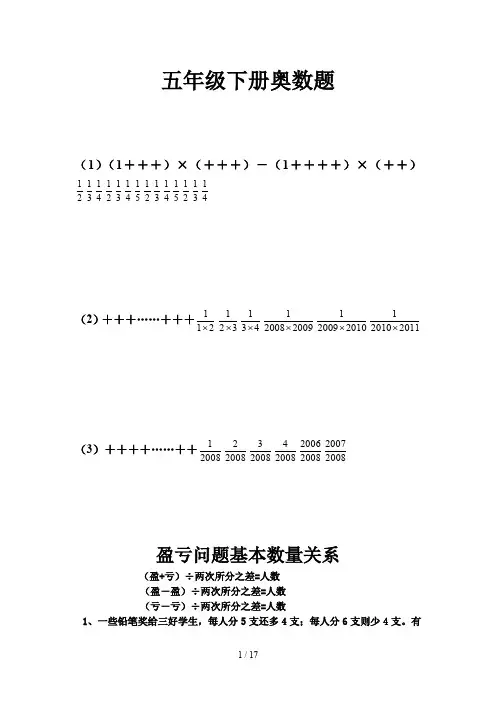
五年级下册奥数题（1）（1＋＋＋）×（＋＋＋）－（1＋＋＋＋）×（＋＋）2131412131415121314151213141（2）＋＋＋……＋＋＋211⨯321⨯431⨯200920081⨯201020091⨯201120101⨯（3）＋＋＋＋……＋＋200812008220083200842008200620082007盈亏问题基本数量关系（盈+亏）÷两次所分之差=人数（盈－盈）÷两次所分之差=人数（亏－亏）÷两次所分之差=人数1、一些铅笔奖给三好学生，每人分5支还多4支；每人分6支则少4支。

有多少个三好学生？有多少支铅笔？2、一些铅笔奖给三好学生，每人分4支还多10支；每人分6支则多2支。

有多少个三好学生？有多少支铅笔？3、一些铅笔奖给三好学生，每人分9支则少21支；每人分7支则少7支。

有多少个三好学生？有多少支铅笔？4、一筐桃子，每只猴子分6个，余12个；每只猴子分7个，少11个。

有几只猴子、几个桃子？5、一叠本子发给同学们，每人发4本还差2本，每人发6本就差20本。

求一共有多少个同学、多少个本子？6、一篮苹果分给小朋友，如果减少一人，每人正好分5个；如果增加一人，每人正好分4个。

这篮苹果一共有多少个？7、五年级同学去划船，如果增加一条船，正好每只船上坐7人；如果减少一条船，正好每只船上坐8人。

共有多少个同学？8、一个旅游团去旅馆住宿，如果6人一间，多2个房间；如果4人一间，就会少2个房间。

这个旅游团共有多少人？长方体和正方体的表面积1、有四个棱长为3分米的正方体，如果将它们拼成一个长方体，求这个长方体的表面积。

2、将一个长方体的高增加2厘米后，就成了一个正方体，且表面积比原来增加了40平方厘米，求原来长方体的表面积。

3、把三个长、宽、高分别是10厘米、8厘米、3厘米的长方体拼成一个较大的长方体，求这个长方体的表面积最小是多少平方厘米?4、一个长方体正好可以切割成3个完全一样的正方体，且没有剩余；三个正方体的表面积比原来增加了60平方厘米。

小学五年级下册奥数题精选1.小学五年级下册奥数题精选篇一1、一位少年短跑选手，顺风跑90米用了10秒钟。

在同样的风速下，逆风跑70米，也用了10秒钟。

问：在无风的时候，他跑100米要用多少秒？答案与解析：顺风时速度=90÷10=9（米/秒），逆风时速度=70÷10=7（米/秒）无风时速度=（9+7）×1/2=8（米/秒），无风时跑100米需要100÷8=12。

5（秒）2、李明、王宁、张虎三个男同学都各有一个妹妹，六个人在一起打羽毛球，举行混合双打比赛。

事先规定。

兄妹二人不许搭伴。

第一盘，李明和小华对张虎和小红；第二盘，张虎和小林对李明和王宁的妹妹。

请你判断，小华、小红和小林各是谁的妹妹。

解答：因为张虎和小红、小林都搭伴比赛，根据已知条件，兄妹二人不许搭伴，所以张虎的妹妹不是小红和小林，那么只能是小华，剩下就只有两种可能了。

第一种可能是：李明的妹妹是小红，王宁的妹妹是小林；第二种可能是：李明的妹妹是小林，王宁的妹妹是小红。

对于第一种可能，第二盘比赛是张虎和小林对李明和王宁的妹妹。

王宁的妹妹是小林，这样就是张虎、李明和小林三人打混合双打，不符合实际，所以第一种可能是不成立的，只有第二种可能是合理的。

所以判断结果是：张虎的妹妹是小华；李明的妹妹是小林；王宁的妹妹是小红。

2.小学五年级下册奥数题精选篇二1、一个长方形的周长是24厘米，长与宽的比是2：1，这个长方形的面积是多少平方厘米?2、一个长方体棱长总和为96厘米，长、宽、高的比是3∶2∶1，这个长方体的体积是多少?3、小明看一本故事书，第一天看了全书的'1/9，第二天看了24页，两天看了的页数与剩下页数的比是1：4，这本书共有多少页?4、某校参加电脑兴趣小组的有42人，其中男、女生人数的比是4∶3，男生有多少人?5、有两筐水果，甲筐水果重32千克，从乙筐取出20%后，甲乙两筐水果的重量比是4:3，原来两筐水果共有多少千克?参考答案：1、S=(2/3×24/2)×(1/3×24/2)=32平方厘米2、V=(3/6×96/4)×(2/6×96/4)×(1/6×96/4)=384立方厘米3、24÷(1/5-1/9)=45×6=270页4、男=4/7×42=24(人)5、32+32×3/4÷80%=62(千克)3.小学五年级下册奥数题精选篇三1、有一批苹果，如果每天吃掉其中的三分之一，需要几天才能吃完？2、一辆车以每小时60公里的速度行驶，行驶了5个小时后，还剩下240公里的路程，这辆车一共要行驶多少公里？3、小明有10元钱，他要买5个苹果和3个橙子，苹果每个1元，橙子每个2元，他还需要多少钱？4、一种药品的说明书上写着，每次服用2粒，每天服用3次，一盒药共有30粒，这盒药可以服用几天？5、甲、乙两人同时从A地出发，分别向B地和C地行驶，甲的速度是每小时40公里，乙的速度是每小时60公里，B、C两地的距离是120公里，甲、乙两人同时到达B、C两地，求他们出发的时间。

五年级数学下册奥数50题、附解析及参考答案一、工程问题1.甲乙两个水管单独开，注满一池水需要20小时和16小时。

丙水管单独开，排一池水要10小时。

如果水池没水，同时打开甲乙两水管，5小时后再打开排水管丙，问水池注满还需要多少小时？答：甲水管每小时注入1/20的水量，乙水管每小时注入1/16的水量，丙水管每小时排出1/10的水量。

在5小时内，甲乙两水管共注入了5/20+5/16=19/40的水量，水池中水量为19/40.再打开丙水管后，每小时水池中的水量减少1/10-1/20-1/16=3/80，所以注满整个水池还需要(1-19/40)/(3/80)=16小时。

2.修一条水渠，甲队单独修需要20天完成，乙队单独修需要30天完成。

如果两队合作，由于彼此施工有影响，他们的工作效率就要降低。

甲队的工作效率是原来的五分之四，乙队工作效率只有原来的十分之九。

现在计划16天修完这条水渠，且要求两队合作的天数尽可能少，那么两队要合作几天？答：设甲队合作x天，乙队合作XXX，则有以下两个方程：20x/(5/4)+30y/(10/9)=1.（甲、乙两队合作完成1个单位的工程）20x/(5/4)+(30-y)/(1/3)=16.（甲、乙两队合作16天完成工程）解得x=8，y=6，所以两队需要合作8天。

3.一件工作，甲、乙合做需4小时完成，乙、XXX做需5小时完成。

现在先请甲、XXX做2小时后，余下的乙还需做6小时完成。

乙单独做完这件工作要多少小时？答：设甲、乙、丙每小时完成的工作量分别为a、b、c，则有以下三个方程：2(a+c)+6b=1.（甲、乙、丙合作完成1个单位的工作）4(a+b)=1.（甲、乙合作完成1个单位的工作）5(b+c)=1.（乙、丙合作完成1个单位的工作）解得a=1/20，b=1/60，c=1/12，所以乙单独做完这件工作需要6b=6/60=1/10小时。

4.一项工程，第一天甲做，第二天乙做，第三天甲做，第四天乙做，这样交替轮流做，那么恰好用整数天完工；如果第一天乙做，第二天甲做，第三天乙做，第四天甲做，这样交替轮流做，那么完工时间要比前一种多半天。

五年级小学生奥数题3篇【篇一】五年级小学生奥数题1、有两条各长30厘米的纸条, 粘贴在一起长56厘米, 粘贴在一起的部分长（）厘米。

2、一条直线能将平面分为两部分, 两条直线最多能将平面分为4部分, 那么5条直线最多能将平面划分成（）部分。

3、小华参加数学竞赛, 共有10道赛题。

规定答对一题给十分, 答错一题扣五分。

小华十题全部答完, 得了85分。

小华答对了几题？4、图书室有连环画28本, 文艺书36本, 买来的故事书比连环画和文艺书的总和少50本。

图书室有故事书多少本？5、用数字0, 1, 2, 3, 4中的任意三个数相加可以得到多少个不同的和。

6、钟鼓楼的钟打点报时, 5点钟打5下需要4秒钟。

问中午12点是打12下需要多少秒钟？7、二（2）班有44个同学划船, 大船每条可以坐6人, 租金10元, 小船每条可以坐4人, 租金8元, 如果你是领队, 要使租金最少, 租多少条大船, 多少条小船, 租金多少元。

8、小青比小李大5岁, 小李比小风大2岁, 小风比小云小4岁, 他们4人（）, （）最小。

的比最小的大（）岁。

9、有一个卖茶叶蛋的老太太, 第一次卖去锅内茶叶蛋的一半多2个, 第二次又卖去余下的一半多2个, 锅内还有1个茶叶蛋, 这个老太太原来一共有多少个茶叶蛋？10、3个空汽水瓶可以换1瓶汽水, 小花买18瓶汽水, 可以喝到多少瓶汽水？【篇二】五年级小学生奥数题1、两组学生进行跳绳比赛, 平均每人跳152下, 甲, 组有6人, 平均每人跳140下, 乙组平均每人跳160下, 乙组有多少人？2、甲、乙、丙三人的平均年龄为22岁, 如果甲、乙的平均年龄是18岁, 乙、丙的平均年龄是25岁, 那么乙的年龄是多少岁？3、五个数排一排, 平均数是9, 如果前四个数的平均数是7, 后四个数的平均数是10, 那么, 第一个数和第五个数是多少？4、甲、乙两个码头相距144千米, 汽船从乙码头逆水行驶8小时到达甲码头, 已知汽船在静不中每小时行驶21千米。

五年级下册奥数题目录第一讲图形的变换（图形的分割与拼接）………………………………3-5第二讲因数与倍数(数的整除特征一)………………………………6-10第三讲因数与倍数（数的整除特征二）……………………………11-12第四讲因数与倍数（奇数与偶数）……………………………13-17第五讲因数与倍数（最小公倍数与最大公因数）……………………18-20第六讲因数与倍数（最小公倍数与最大公因数）……………………21-261第七讲长方体和正方体（巧算表面积）………………………………27-30 第八讲长方体和正方体（巧算体积）……………………………………31-35 第九讲分数的意义和性质……36-40 第十讲分数的加法和减法……41-44 第十一讲平均数问题……………45-49 第十二讲教学广角（追及问题）…………………………………50-54 第十三讲数学广角（还原问题）…55-58 第十四讲容斥原理………………59-62 第十五讲抽屉原理和最不利……63-67 第十六讲综合练习…………… 68-982五年级下册奥数题第一讲图形的变换（图形的分割与拼接）1、把右图分成形状、大小都相同的四块，并且每个图形中要有一个“·”。

2、把下图分成大小、形状相同的三块，使每一块都有一颗星，该怎么分割？33、下图是由一个正方形和一个等腰直角三角形组成的，请把它分成大小、形状相同的四块。

4、将下图分成大小、形状相同的四块、每块中带有一个小圆圈。

5、将图中五个图形拼成一个正方形456、将图中长方形切成两块，拼成一个正方形。

7、将下图（缺两角的长方形）分割成两块，然后拼成一个正方形。

8、将下图“T ”字剪成四块，然后拼成一个正方形。

169第二讲因数与倍数(数的整除特征一)1、五位数73（）28能被9整除，（）里应该是几？2、一梯形面积为1400平方米，高为50米，若两底的米数都是整数且可被8整除，求两底，此问题解的组数为多少？3、A8919B能被66整除，这个六位数是多少？64、期末考试六年级一班数学平均分是90分，总分是（）95（），这个班有多少名学生？5、任意一个三位数连着写两回得到一个六位数，这个六位数一定能被7，11，13整除。

最新小学五年级下册数学奥数题带答案一、拓展提优试题1．如图六角星的6个顶点恰好是一个正六边形的6个顶点，那么阴影部分面积是空白部分面积的倍．2．（15分）小吴从从家骑自行车去森林公园游玩，出发30分钟后，小吴的父亲发现小吴的钱包还在家里，于是立即开车给小吴送钱包，在距离森林公园3.5千米处追上小吴．将钱包给小吴后，父亲立即原路返回，返回家时小吴还需10分钟才能到达森林公园，若父亲开车的速度是小吴骑自行车速度的5倍，小吴家距离森林公园多少千米？3．李双骑车以320米分钟的速度从A地驶向B地，途中因自行车故障推车继续向前步行5分钟到距B地1800米的某地修车，15分钟后以原来骑车速度的1.5倍继续向前驶向B地，到达B地时，比预计时间多用17分钟，则李双推车步行的速度是米/分钟．4．如图，将一个等腰三角形ABC沿EF对折，顶点A与底边的中点D重合，若△ABC的周长是16厘米，四边形BCEF的周长是10厘米，则BC＝厘米．5．四位数的所有因数中，有3个是质数，其它39个不是质数．那么，四位数有个因数．6．（8分）6个同学约好周六上午8：00﹣11：30去体育馆打乒乓球，他们租了两个球桌进行单打比赛每段时间都有4 个人打球，另外两人当裁判，如此轮换到最后，发现每人都打了相同的时间，请问：每人打了分钟．7．（8分）图中所示的图形是迎春小学数学兴趣小组的标志，其中，ABCDEF 是正六边形，面积为360，那么四边形AGDH的面积是．8．如图，魔术师在一个转盘上的16个位置写下来了1﹣16共16个数，四名观众甲、乙、丙、丁参与魔术表演．魔术师闭上眼，然后甲从转盘中选一个数，乙、丙、丁按照顺时针方向依次选取下一个数，图示是一种可能的选取方式，魔术师睁开眼，说：“选到偶数的观众请举手．”，这时候，只有甲和丁举手，这时候魔术师就大喝一声：“我知道你们选的数了！”．你认为甲和丁选的数的乘积是．9．两个数的最大公约数和最小公倍数分别是3和135，求这两个数的差最小是．10．（8分）在如图每个方框中填入一个数字，使得乘法竖式成立．那么，两个乘数的和是．11．将100按“加15，减12，加3，加15，减12，加3，…”的顺序不断重复运算，运算26步后，得到的结果是．（1步指每“加”或“减”一个数）12．小明准备和面包饺子，他在1.5千克面粉中加入了5千克的水，发现面和得太稀了，奶奶告诉他，包饺子的面需要按照3份面，2份水和面，于是小明分三次加入相同分量的面粉，终于将面按按要求和好了，那么他每次加入了千克面粉．13．（8分）小胖把这个月的工资都用来买了一支股票．第一天该股票价格上涨，第二天下跌，第三天上涨，第四天下跌，此时他的股票价值刚好5000元，那么小胖这个月的工资是元．14．A、B两桶水同样重，若从A桶中倒2.5千克水到B桶中，则B桶中水的重量是A桶中水的重量的6倍，那么B桶中原来有水千克．15．同学们去春游，带水壶的有80人，带水果的有70人，两样都没带的有6人．若既带水壶又带水果的人数是所有参加春游人数的一半，则参加春游的同学共有人．16．如图，在△ABC中，D、E分别是AB、AC的中点，且图中两个阴影部分（甲和乙）的面积差是5.04，则S＝．△ABC17．松鼠A、B、C共有松果若干，松鼠A原有松果26颗，从中拿出10颗平分给B、C，然后松鼠B拿出自己的18颗松果平均分给A、C，最后松鼠C把自己现有松果的一半平分给A、B，此时3只松鼠的松果数量相同，则松鼠C原有松果颗．18．（7分）如图，按此规律，图4中的小方块应为个．19．（7分）对于a、b，定义运算“@”为：a@b＝（a+5）×b，若x@1.3＝11.05，则x＝．20．（8分）一个大于1的正整数加1能被2整除，加2能被3整除，加3能被4整除，加4能被5整除，这个正整数最小是．21．（8分）在长方形ABCD中，BE＝5，EC＝4，CF＝4，FD＝1，如图所示，那么△AEF的面积是；22．（15分）如图，正六边形ABCDEF的面积为1222，K、M、N分别AB，CD，EF的中点，那么三角形PQR的边长是．23．由120个棱长为1的正方体，拼成一个长方体，表面全部涂色，只有一面染色的小正方体，最多有块24．（7分）后羿朝三个箭靶分别射了三支箭，如图：他在第一个箭靶上得了29分，第二个箭靶上得了43分．请问他在第三个箭靶上得了分．25．有一行数：1，1，2，3，5，8，13，21，…，从第三个数开始，每个数都是前两个数的和，问在前2007个数中，有是偶数．26．数一数，图中有多少个正方形？27．星期天早晨，哥哥和弟弟去练习跑步，哥哥每分钟跑110米，弟弟每分钟跑80米，弟弟比哥哥多跑了半小时，结果比哥哥多跑了900米，那么，哥哥跑了米．28．小明带了30元钱去买文具，买了3个笔记本和5支笔，剩余的钱，如果再买2支笔还差0.4元，如果再买2个笔记本则还差2元，那么，笔记本每个元，笔每支元．29．某数学竞赛有10道题，规定每答对一题得5分，答错或不答扣2分．A、B 两人各自答题，得分之和是58分，A比B多得14分，则A答对道题．30．小松鼠储藏了一些松果过冬．小松鼠原计划每天吃6个松果，实际每天比原计划多吃2个，结果提前5天吃完了松果．小松鼠一共储藏了个松果．31．（12分）甲、乙两人从A地步行去B地．乙早上6：00出发，匀速步行前往；甲早上8：00才出发，也是匀速步行．甲的速度是乙的速度的2.5倍，但甲每行进半小时都需要休息半小时．甲出发后经过分钟才能追上乙．32．甲、乙两车从A城市出发驶向距离300千米远的B城市．已知甲车比乙车晚出发1小时，但提前1小时到达B城市．那么，甲车在距离B城市千米处追上乙车．33．请从1、2、3、…、9、10中选出若干个数，使得1、2、3、…、19、20这20个数中的每个数都等于某个选出的数或某两个选出的数（可以相等）的和．那么，至少需要选出个数．34．（12分）如图，C、D为AB的三等分点．8点整时甲从A出发匀速向B行走，8点12分乙从B出发匀速向A行走，再过几分钟丙从B出发匀速向A行走；甲、乙在C点相遇时丙恰好走到D点，甲、丙8：30相遇时乙恰好到A．那么，丙出发时是点分．35．某次入学考试有1000人参加，平均分是55分，录取了200人，录取者的平均分与未录取的平均分相差60分，录取分数线比录取者的平均分少4分．录取分数线是分．36．小明从家到学校去上课，如果每分钟走60米，可提前10分钟到校；如果每分钟走50米，要迟到4分钟到校．小明家到学校相距米．37．一艘船从甲港到乙港，逆水每小时行24千米，到乙港后又顺水返回甲港，已知顺水航行比逆水航行少用5小时，水流速度为每小时3千米，甲、乙两港相距千米．38．对于自然数N，如果在1﹣9这九个自然数中至少有七个数是N的因数，则称N是一个“七星数”，则在大于2000的自然数中，最小的“七星数”是．39．如图中，A、B、C、D为正六边形四边的中点，六边形的面积是16，阴影部分的面积是．40．数学家维纳是控制论的创始人．在他获得哈佛大学博士学位的授予仪式上，有人看他一脸稚气的样子，好奇地询问他的年龄．维纳的回答很有趣，他说：“我的年龄的立方是一个四位数，年龄的四次方是一个六位数，这两个数刚好把0﹣9这10个数字全都用上了，不重也不漏，”那么，维纳这一年岁，（注：数a的立方等于a×a×a，数a的四次方等于a×a×a×a）【参考答案】一、拓展提优试题1．解：根据分析，如图所示，将图进行分割成面积相等的三角形，阴影部分由18个小三角形组成，而空白部分有6个小三角形，故阴影部分面积是空白部分面积的18÷6＝3倍．故答案是：3．2．解：由题意，30÷（5﹣1）＝7.5分钟，3500÷（7.5+10）＝200（米/分），200×（30+7.5+7.5+10）＝11000米＝11千米，答：小吴家距离森林公园11千米．3．解：1800÷320﹣1800÷（320×1.5）＝5.625﹣3.75＝1.875（分钟）320×[5﹣（17﹣15+1.875）]÷5＝320×[5﹣3.875]÷5＝320×1.125÷5＝360÷5＝72（米/分钟）答：李双推车步行的速度是72米/分钟．故答案为：72．4．解：△ABC的周长是16厘米，可得△AEF的周长为：16÷2＝8 （厘米），△AEF和四边形BCEF周长和为：8+10＝18（厘米），所以BC＝18﹣16＝2（厘米），答：BC＝2厘米．故答案为：2．5．解：首先根据奇偶位数和相等一定是11的倍数．因数一共的个数是3+39＝42（个），将42分解成3个数字相乘42＝2×3×7．＝a×b2×c6．如果是11×52×26＝17600（不是四位数不满足条件）．再看一下如果这个数字最小是＝11×32×26＝6336．＝3663＝11×37×32．因数的个数共2×2×3＝12（个）．故答案为：12个．6．解：6÷2＝3（组）11时30分﹣8是＝3时30分＝210分210×2÷3＝420÷3＝140（分钟）答：每人打了140分钟．故答案为：140．7．解：根据分析，（1）△ABC面积等于六边形面积的，连接AD，四边形ABCD是正六边形面积的，故△ACD面积为正六边形面积的（2）S△ABC ：S△ACD＝1：2，根据风筝模型，BG：GD＝1：2；（3）S△BGC：S CGD＝BG：GD＝1：2，故；故AGDH面积＝六边形总面积﹣（S△ABC +S△CGD）×2＝360﹣（+40）×2＝160．故答案是：1608．解：依题意可知：2个偶数中间间隔是2个奇数．发现只有数字10，11，9，12是符合条件的数字．乘积为10×12＝120．故答案为：1209．解：因为135÷3＝45，45分解成两个互质的数有两种情况即1和45、9与5，所以差最小的是：9和5，所以这两个数分别是：9×3＝275×3＝1527﹣15＝12答：这两个数的差最小是12．故答案为：12．10．解：依题意可知：结果的首位是2，那么在第二个结果中的首位还是2．再根据第一个结果中有一个1，那么就是有和数字5相乘以后数字1的进位同时十位数字是偶数才能满足条件，第一个乘数的个位数字只能是2或者3才能满足进位是1．当第一个乘数尾数是2时，首位数字无论是哪一个偶数都不能得到200多的结果．不满足题意．当第一个乘数尾数是3时，来看看偶数的情况．23×9＝207.43，63，83无论乘以数字几都不能构成百位十位是20的结果．故是23×95＝2185，那么23+95＝118．故答案为：11811．解：每一个计算周期运算3步，增加：15﹣12+3＝6，则26÷3＝8…2，所以，100+6×8+15﹣12＝100+48+3＝151答：得到的结果是 151．故答案为：151．12．解：根据分析，因面和水的比为3：2，即每一份水需要：3÷2＝1.5份面粉，现在有5千克水，则需要面粉：5×1.5＝7.5千克，而现有面粉量为：1.5千克，故还须加：7.5﹣1.5＝6千克，分三次加入，则每次须加入：6÷3＝2千克．故答案是：2．13．解：5000÷（1﹣）÷（1+）÷（1﹣）÷（1+）＝5000××××＝5000（元）答：小胖这个月的工资是5000元．故答案为：5000．14．解：2.5×2÷（6﹣1）+2.5＝5÷5+2.5＝1+2.5＝3.5（千克）答：B桶中原来有水3.5千克．故答案为：3.5．15．解：设既带水壶又带水果的为x人，则参加春游的同学共有2x人，由题意可得：80+70﹣x+6＝2x156﹣x＝2x3x＝156x＝52则2x＝2×52＝104答：则参加春游的同学共有104人．故答案为：104．16．解：根据分析，S△BDC＝S△EBC⇒S△DOB＝S△EOC，∴S甲﹣S乙＝（S甲+S△DOB）﹣（S乙+S△EOC）＝5.04，又∵S△BDC ：S△DEC＝BC：DE＝2：1即：S△BDC＝2S△DEC∴S四边形DECB ＝3S△DEC；S△ADE＝S△DEC∴S△ABC ＝S四边形DECB+S△ADE＝4S△DEC，设S△DEC ＝X，则S△BDC＝2X，故有2X﹣X＝5.04，∴X＝5.04，S△ABC ＝4S△DEC＝4X＝4×5.04＝20.16故答案是：20.1617．解：10÷2＝5（颗）18÷2＝9（颗）此时A有：26﹣10+9＝25（颗）此时C有：25×4＝100（颗）原来C有：100﹣9﹣5＝86（颗）答：松鼠C原有松果 86颗．故答案为：86．18．解：因为图1中小方块的个数为1+2×3＝7个，图2中小方块的个数为1+（1+2）+3×4＝16个，图3中小方块的个数为1+（1+2）+（1+2+3）+4×5＝30个，所以图4中小方块的个数为1+（1+2）+（1+2+3）+（1+2+3+4）+5×6＝50个，故答案为：50．19．解：由定义可知：x@1.3＝11.05，（x+5）1.3＝11.05，x+5＝8.5，x＝8.5﹣5＝3.5故答案为：3.520．解：根据分析：这个数除以2，3，4，5均余1，那么这个数减去1后就能同时被2，3，4，5整除；2，3，4，5的最小公倍数是60，则这个数为60的倍数加1．又因为这个数大于1，所以这个数最小是61．故答案为：61．21．解：根据分析，AD＝BE+EC＝5+4＝9，AB＝1+4＝5，S△EFC＝×EC×FC＝×4×4＝8；S△ABE＝×AB×BE＝×5×5＝12.5；S△ADF＝×AD×DF＝×9×1＝4.5；S长方形ABCD＝AB×AD＝5×9＝45，要求的△AEF的面积等于整体长方形的面积减去三个三角形的面积．S△AEF＝S长方形ABCD﹣S△EFC﹣S△ABE﹣S△ADF＝45﹣8﹣12.5﹣4.5＝20．故答案是：20．22．解：如图延长BA和EF交于点O，并连接AE，由正六边形的性质，我们可知S ABCM＝S CDEN＝S EF AK＝六边形面积，根据容斥原理，重叠部分三个三角形面积和等于阴影部分面积，且因为对称，△AKP，△CMQ，△ENR三个三角形是一样的，有KP＝RN，AP＝ER，RP＝PQ，＝，则＝，＝，由鸟头定理可知道3×KP×AP＝RP×PQ，综上可得：PR ＝2KP ＝RE ，那么由三角形AEK 是六边形面积的，且S △APK ＝S △AKE ，S △APK ＝S ABCDEF ＝47，所以阴影面积为47×3＝141故答案为141．23．64[解答]设长方体的长、宽、高分别为,,l m n （不妨设l m n ≥≥），容易知道只有一面染色的小正方体只有每个面上可能有一些。

小学五年级奥数题修改版一、小数的巧算（一）填空题1. 计算 1.996+19.97+199.8=_____。

2. 计算 1.1+3.3+5.5+7.7+9.9+11.11+13.13+15.15+17.17+19.19=_____。

3. 计算 2.89⨯4.68+4.68⨯6.11+4.68=_____。

4. 计算 17.48⨯37-17.48⨯19+17.48⨯82=_____。

5. 计算 1.25⨯0.32⨯2.5=_____。

6. 计算 75⨯4.7+15.9⨯25=_____。

7. 计算 28.67⨯67+3.2⨯286.7+573.4⨯0.05=____。

（二）解答题8. 计算 172.4⨯6.2+2724⨯0.38。

9.。

10.计算 12.34+23.45+34.56+45.67+56.78+67.89+78.91+89.12+91.23。

二、数的整除性（一）填空题1. 四位数“3AA1”是9的倍数，那么A=_____。

2. 在“25□79这个数的□内填上一个数字,使这个数能被11整除,方格内应填_____。

3. 能同时被2、3、5整除的最大三位数是_____。

4. 能同时被2、5、7整除的最大五位数是_____。

5. 1至100以内所有不能被3整除的数的和是_____。

6. 所有能被3整除的两位数的和是______。

7. 已知一个五位数□691□能被55整除,所有符合题意的五位数是_____。

（二）解答题8. 173□是个四位数字，数学老师说：“我在这个□中先后填入3个数字,所得到的3个四位数,依次可被9、11、6整除。

”问：数学老师先后填入的3个数字的和是多少？9．在1992后面补上三个数字，组成一个七位数，使它们分别能被2、3、5、11整除，这个七位数最小值是多少？三质数与合数（一）填空题1. 在一位的自然数中，既是奇数又是合数的有_____；既不是合数又不是质数的有_____；既是偶数又是质数的有_____。

1一项工程，甲独做10天完成，乙独做20完成，现在甲乙合作，甲休息一天，乙休息5天，完成这项工程要多少天？解：甲休息1天，乙休息5天，相当于甲乙休息1天后，乙又休息4天那么甲4天完成甲乙的工作效率和=那么剩下的需要完成全部工程需要4+5=9天2生产一批零件，甲每小时可做18个，乙单独做要12小时成。

现在由甲乙二人合做，完成任务时，甲乙生产的数量之比是3：5，甲一共生产零件多少个？解：乙的工作效率=完成任务时乙工作了小时那么甲一共生产18×=135个3一项工作，甲乙要4小时完成，乙丙要6小时完成。

现在甲丙合作2小时，剩下的乙7小时完成。

甲乙丙单独要多久完成？解：甲丙合作2小时，乙独做7小时相当于甲乙可做2小时，乙丙合作2小时，乙独做7-2-2=3小时那么乙独做完成乙的工作效率=甲的工作效率=丙的工作效率=甲单独完成需要乙单独完成需要丙单独完成需要4服装厂接到加工一批服装的任务，王师傅每天可以制作3套服装，李师傅每天可以制作5套服装，如果王师傅单独完成制作这批服装的任务，比李师傅单独完成制作这批服装的任务要多用4天，那么，要加工的这批服装共有多少套？解答：（3×4）÷（5-3）=6（天）6×5=30（套）王王王……王王王王王李李李……李如上图，王字和李字分别代表二人一天的工作量。

王师傅在前几天一定比李师傅少加工了一部分零件，所以还需要再工作4天才和李师傅的工作量一样多。

王四天加工3×4=12（件），说明说明前几天王比李多加工12件，又由于每天多加工2件。

所以李共加工6天（12÷2），共6×5=30（套）5一项工程甲乙合做需12天完成,若甲先做3天后,再由乙工作8天,共完成这项工作的,如果这件工作由甲单独做，需多少天完成?解：甲3天乙8天看作甲乙合作3天，乙独做8-3=5天这是解决问题的关键乙独做5天完成乙的工作效率=甲的工作效率=甲单独完成需要6甲乙两人分别生产同样多的零件，各工作16天后，甲还需64个，乙还需384个才能完成，乙比甲的工作效率少40%，求甲的效率？解：设甲的工作效率为a个/天，则乙为（1-40%）a=0.6a个/天根据题意16a+64=0.6a×16+38416×0.4a=3200.4a=20a=50甲的工作效率为50个/天算术法：乙比甲每天少做40%那么16天少做384-64=320个每天少做320/16=20个那么甲的工作效率=20/40%=50个/天7有一项工程要在规定日期内完成，如果甲工程队单独做正好如期完成，如果乙工程队单独做就要超过5天才能完成。

五年级下册数学最难的奥数题1、一个筐子放进4篮苹果后，连筐共重28千克，当倒出3篮苹果后再称，连筐共重10千克，一个筐子重(4)千克2、一块正方形菜地，边长是12米。

如果要把它的面积扩大到原来的2倍，其中一条边增加4米，另一条边增长多少米?(写出过程)3、学校卖3把椅子和4张桌子共用元，未知卖2张桌子的钱可以卖5把椅子，一把椅子多少元?一张桌子多少元?(写下过程)4.一条路长米，从头到尾每隔10米栽1棵梧桐树，共栽多少棵树?5、12棵柳树排列成一排，在每两棵柳树中间种3棵桃树，共种多少棵桃树?6、一根厘米长的木条，要锯成10厘米长的小段，需要锯几次?7、.蚂蚁爬到树枝，每上时一节须要10秒钟，从第一节爬到至第13节须要多少分钟?8.在花圃的周围方式菊花，每隔1米放1盆花。

花圃周围共20米长。

需放多少盆菊花?9、从发电厂至闹市区一共存有根电线杆，每相连两根电线杆之间就是30米。

从发电厂至闹市区存有多离?10、.王老师把月收入的一半又20元留做生活费，又把剩余钱的一半又50元储蓄起来，这时还剩40元给孩子交学费书本费。

他这个月收入多少元?11.一个人沿着小骗走了全长的一半后，又跑了剩的一半，还剩1千米，问：小加全长多少千米?12.甲在加工一批零件，第一天加工了这堆零件的一半又10个，第二天又加工了剩下的一半又10个，还剩下25个没有加工。

问：这批零件有多少个?13.一条毛毛虫由幼虫短至成虫，每天短一倍，16天能长至16厘米。

反问它几天可以短至4厘米?14.一桶水，第一次倒出一半，然后倒回桶里30千克，第二次倒出桶中剩下水的一半，第三次倒出千克，桶中还剩下80千克。

桶里原来有水多少千克?15、甲、乙两书架共计图书本，甲书架的图书数比乙书架的3倍太少16本。

甲、乙两书架上各存有图书多少本?16、甲、乙、丙三人年龄之和是94岁，且甲的2倍比丙多5岁，乙2倍比丙多19岁，问：甲、乙、丙三人各多大?17.小明、小华捉住完鱼。

五年级数学下册奥数题练习班级考号姓名总分一、排列组合问题1、有五对夫妇围成一圈，使每一对夫妇的夫妻二人都相邻的排法有( )A、768种B、32种C、24种D、2的10次方种2、若把英语单词hello的字母写错了,则可能出现的错误共有( )A、119种B、36种C、59种D、48种二、容斥原理问题1、有100种赤贫.其中含钙的有68种,含铁的有43种,那么,同时含钙和铁的食品种类的最大值和最小值分别是( )A、43，25B、32，25C、32，15D、43，112、在多元智能大赛的决赛中只有三道题。

已知：(1)某校25名学生参加竞赛，每个学生至少解出一道题；(2)在所有没有解出第一题的学生中，解出第二题的人数是解出第三题的人数的2倍；(3)只解出第一题的学生比余下的学生中解出第一题的人数多1人；(4)只解出一道题的学生中，有一半没有解出第一题，那么只解出第二题的学生人数是( )A、5B、6C、7D、83、一次考试共有5道试题。

做对第1、2、3、4、5题的分别占参加考试人数的95%、80%、79%、74%、85%。

如果做对三道或三道以上为合格，那么这次考试的合格率至少是多少？三、抽屉原理、奇偶性问题1、一只布袋中装有大小相同但颜色不同的手套，颜色有黑、红、蓝、黄四种，问最少要摸出几只手套才能保证有3副同色的？2、有四种颜色的积木若干，每人可任取1-2件，至少有几个人去取，才能保证有3人能取得完全一样？3、某盒子内装50只球，其中10只是红色，10只是绿色，10只是黄色，10只是蓝色，其余是白球和黑球，为了确保取出的球中至少包含有7只同色的球，问：最少必须从袋中取出多少只球？4、地上有四堆石子，石子数分别是1、9、15、31如果每次从其中的三堆同时各取出1个，然后都放入第四堆中，那么，能否经过若干次操作，使得这四堆石子的个数都相同?（如果能请说明具体操作，不能则要说明理由）四、路程问题1、狗跑5步的时间马跑3步，马跑4步的距离狗跑7步，现在狗已跑出30米，马开始追它。

小学五年级数学下册经典奥数应用题66道（附答案）1.丽丽和家家去书店买书，他们同时喜欢上了一本书，最后丽丽用自己的钱的5分之3，家家用自己的钱的3分之2各买了一本，丽丽剩下的钱比家家剩下的钱多5块。

两人原来各有多少钱？书多少钱？2.一辆汽车每行8千米要耗油4/5千克,平均每千克汽油可行多少千米.行1千米路程要耗油多少千克?3.一辆摩托车1/2小时行30千米,他每小时行多少千米?他行1千米要多少小时?4.阅览室看书的同学中，男同学占七分之四，从阅览室走出5位男同学后，看书的同学中，女同学占二十三分之十二，原来阅览室一共有多少名同学在看书？5.红，黄，蓝气球共有62只，其中红气球的五分之三等于黄气球的三分之二，蓝气球有24只，红气球和黄气球各有多少只？6.学校阅览室有36名学生看书,其中4/9是女学生.后又来了几名女学生,这时女学生人数占看书人数的3/5,后来了几名女生?7.水结成冰后,体积要比原来膨胀11分之1,2.16立方米的冰融化成水后,体积是多少?8.甲乙的粮食560吨,如果把甲的粮食运出2/9给乙,则甲乙的粮食正好相等.原来甲的粮食有多少吨？，乙的粮食有多少吨？9.电视机降价200元.比原来便宜了2/11.现在这种电视机的价格是多少钱?10.一辆车从甲地到乙地,行了全程的2/5还多20千米,这时候离乙地还有70千米,甲乙两地相距多少千米?11.小明看一本书,第一天看了28页,第二天看了全书的1/5(5分之1),两天共看了全书的3/8(3分之8),这本书共有多少页？12.师徒二人同加工一批零件,加工一段时间后,师傅加工了84个.徒弟加工了63个.师傅比徒弟多加工的正好占全部任务的1/28.这批零件共有多少个?13.一桶油,吃了7/10后,又添进了15千克,这时桶中的油正好是一桶油的一半,这桶油重多少千克?14.一列火车从上海开往天津,行了全路程的3/5,剩下的路程,如果每小时行106千米,5小时可以到天津.上海到天津的铁路长多少千米?15.六年级参加数学兴趣小组的共有46,其中女生人数的4/5是男生人数的3/2倍,参加兴趣小组的男、女生各有多少人？16.张红抄写一份稿件,需要5小时抄完.这份稿件已由别人抄了1/3,剩下的交给张红抄,还要用几小时才能抄完?17.两列火车同时从相距600千米的两城相对开出.列火车每小时行60千米,另一列火车每小时行75千米,经过几小时两车可以相遇?18.一辆摩托车每小时行了64千米,找这样的速度,从甲到乙用了3/4小时,甲乙两地相距多少千米?19.水果店在两天内卖完一批水果,第一天卖出水果总重量的3/5,比第二天多卖了30千克,这批水果共有多少千克?20.西街小学共有学生910人,其中女生占4/7,女生有多少人?男生有多少人?21.一块长方形地,长60米,宽是长的2/5,这块地的面积是多少平方米?22.金鱼池里红金鱼与黑金鱼条数的比是7:3,黑金鱼有9条,红金鱼有多少条?23.6年级有学生132人,其中男学生与女学生人数的比是6:5,6年级男.女学生各有多少人?24.甲数和乙数的比是2:3,乙数和丙数的比是4:5.求甲数和丙数的比.25.解放路小学今年植树的棵数是去年的1.2倍.写出这个小学今年植树棵数和去年植树棵数的比.26.一个电视机厂去年彩色电视机的产量与电视机总产量的比是20分之9.去年共生产电视机250000太,其中彩色电视机有多少台?27.某工厂工人占全厂职工总数的3分之2,技术人员占全场职工总数的9分之2,其余的是干部.写出这个厂的工人,技术人员和干部人数的比.28.某班学生人数在40到50人之间,男生人数和女生人数的比是5:6.这个班的男生和女生各有多少人..29.图书馆科技书与文艺书的比是4：5，又购进300本文艺术后，科技书与文艺书的比是5：7，文艺书比原来增加了百分之几？30.100克糖水正好装满了一个玻璃杯,其中含糖10克.从杯中倒出10克糖水后,再往杯中加满水,这是被子里糖与水的比是多少?31.五、六年级只有学生175人。

五年级下册奥数题：
1.小明和小华在一个400米的环形跑道上练习跑步，两人同时从同一点出发，
同向而行，小明每秒跑3.5米，小华每秒跑5.5米。

经过多少秒，两人第三次相遇？
2.一辆公共汽车由起点站到终点站（这两站在内）共途经8个车站，已知前6
个车站共上车100人，除终点站外前面各站共下车80人，则从前六站上车而在终点站下车的乘客共有多少人。

3.在1997后面补上三个数字，组成一个七位数1997□□□，如果这七位数能
被4、5、6整除，那么补上的三个数字的和的最小可能值是多少？
4.已知两个数的最大公约数是4，最小公倍数是252，其中一个数是28，另一
个数是多少？
5.定义新运算a△b=ab-(a+b)，则(4△3)+(3△4)=多少。

五年级下册数学奥数题(含答案) 小学五年级奥数题大全及答案(更新版)-通用版1、一块草地，可以供24匹马吃6天，20匹马吃10天。

问12天时多少匹马可以吃尽这块草地？假设草地单位为“1”，所以24*6=144，20*10=200.因此每天草地长草14个单位“1”。

200-14*10=60，因此草地原有草60个单位"1"。

所以，60/12+14=19，即19匹马12天可以吃尽这块草地。

2、一块草地，可以供5只羊吃40天，6只羊吃30天。

如果4只羊吃30天后又增加2只羊一起吃，那么这块草地还可以再吃多少天？同理，40*5=200，30*6=180.因此每天草地长草2个单位“1”。

200-2*40=120是原有草。

120-（4-2）*30=60是剩余草。

因此，60/（6+2）=7.5，即再吃7.5天。

3、每小时有3000人到书店买书。

如果设一个售书口，每分钟可以让50人买完离开；如果设2个售书口，1小时后就没有人排队了。

那么如果设4个口，多长时间后就没有人排队了？每分钟有3000/60=50人来买书。

如果设一个售书口，每分钟可以卖出50本书。

因此，每分钟的人数和卖出的书数相等，不会有排队。

如果设2个售书口，每分钟可以卖出100本书。

因此，每分钟有50人来买书，需要排队等待。

但是，2个售书口可以同时处理，所以不会有排队。

同理，如果设4个售书口，每分钟可以卖出200本书。

因此，每分钟有100人来买书，需要排队等待。

但是，4个售书口可以同时处理，所以不会有排队。

4、一口井，用3部抽水机40分钟可以抽干；6部抽水机16分钟可以抽干。

那么5部同样的抽水机，多少分钟可以抽干？设5部抽水机可以在x分钟内抽干这口井。

则有3*40=6*16，即120=96.因此，每分钟5部抽水机可以抽干的水量为120/5=24.所以，用5部抽水机抽干这口井需要24x的时间。

又因为6部抽水机可以在16分钟内抽干，每分钟抽干的水量为120/16=7.5.因此，5部抽水机每分钟可以抽干的水量为7.5*5/6=6.25.所以，24x=120，即x=5，用5部抽水机可以在5分钟内抽干这口井。

五年级奥数题及答案通用13篇五年级小学生奥数题篇一1、某厂有一批煤，原计划每天烧5吨，可以烧45天。

实际每天少烧0.5吨，这批煤可以烧多少天？2、学校买来150米长的塑料绳，先剪下7.5米，做3根同样长的跳绳。

照这样计算，剩下的塑料绳还可以做多少根？3、修一条水渠，原计划每天修0.48千米，30天修完。

实际每天多修0.02千米，实际修了多少天？4、王老师看一本书，如果每天看32页，15天看完。

现在每天看40页，可以提前几天看完？5、一辆汽车4小时行驶了260千米，照这样的速度，又行了2.4小时，前后一共行驶了多少千米？（用两种方法解答）五年级小学生奥数题篇二1、快车和慢车同时从两个城市相对开出，2.5小时后相遇。

快车每小时行42千米，慢车每小时行35千米。

两个城市相距多少千米？2、甲、乙二位同学合打一份资料，甲每分打18个字，乙每分打22个字，两人用了30分打完这份资料，这份资料一共有多少个字？3、甲乙两车分别从两地同时出发，相对开来，甲车每小时行40千米，乙车每小时行50千米，3小时后两车还相距25千米，两地相距多少千米？4、两地相距628千米，甲车每小时行60千米，乙车每小时行80千米。

两车同时从两地相向而行，4小时后两车相遇了吗？两车相距多少千米？5、甲乙两人合做一批零件。

甲每小时做124个，乙每小时做136个。

他们合做了8小时，超额完成120个。

他们原来打算合做多少个零件？6、上午10时一只货船从甲港开往乙港，下午1小时一只客船从乙港开往甲港。

客船开出4小时与货船相遇。

货船每小时行18千米，客船每小时行27千米。

两港相距多远？参考答案1、（42＋35）×2.5＝192.5（千米）2、（18＋22）×30＝12003、（50＋40）×3＋25＝295（千米）4、没相遇。

（60＋80）×4＝560（千米）628－560＝68（千米）5、（124＋136）×8－120＝1960（个）6、18×3＋（18＋27）×4＝234（千米）五年级小学生奥数题篇三1、甲、乙、丙三人赛跑，同时从A地出发向B地跑，当甲跑到终点时，乙离B还有30米，丙离B还有70米；当乙跑到终点时，丙离B还有45米。

五年级奥数题100道及答案1. 小明有5个苹果，他给小华2个，自己还剩下多少个苹果？答案：小明还剩下3个苹果。

2. 一个班级有40名学生，如果每2名学生组成一个小组，可以组成多少个小组？答案：可以组成20个小组。

3. 一个数的3倍是45，这个数是多少？答案：这个数是15。

4. 一个长方形的长是15厘米，宽是10厘米，它的周长是多少？答案：周长是50厘米。

5. 一个数加上12等于36，这个数是多少？答案：这个数是24。

6. 如果一个数的一半是18，那么这个数是多少？答案：这个数是36。

7. 一个数的4倍是64，这个数是多少？答案：这个数是16。

8. 一个正方形的边长是8厘米，它的面积是多少？答案：面积是64平方厘米。

9. 一个数的5倍是100，这个数是多少？答案：这个数是20。

10. 一个班级有50名学生，如果每5名学生组成一个小组，可以组成多少个小组？答案：可以组成10个小组。

11. 一个数的6倍是72，这个数是多少？答案：这个数是12。

12. 一个数减去15得到30，这个数是多少？答案：这个数是45。

13. 一个数的7倍是49，这个数是多少？答案：这个数是7。

14. 一个数的8倍是64，这个数是多少？答案：这个数是8。

15. 一个数的9倍是81，这个数是多少？答案：这个数是9。

16. 一个数的10倍是100，这个数是多少？答案：这个数是10。

17. 一个数的11倍是121，这个数是多少？答案：这个数是11。

18. 一个数的12倍是144，这个数是多少？答案：这个数是12。

19. 一个数的13倍是169，这个数是多少？答案：这个数是13。

20. 一个数的14倍是196，这个数是多少？答案：这个数是14。

21. 一个数的15倍是225，这个数是多少？答案：这个数是15。

22. 一个数的16倍是256，这个数是多少？答案：这个数是16。

23. 一个数的17倍是289，这个数是多少？答案：这个数是17。

1一项工程,甲独做10天完成,乙独做20完成,现在甲乙合作,甲休息一天,乙休息5天,完成这项工程要多少天？解：甲休息1天,乙休息5天,相当于甲乙休息1天后,乙又休息4天那么甲4天完成甲乙的工作效率和=那么剩下的需要完成全部工程需要4+5=9天2生产一批零件,甲每小时可做18个,乙单独做要12小时成。

现在由甲乙二人合做,完成任务时,甲乙生产的数量之比是3：5,甲一共生产零件多少个？解：乙的工作效率=完成任务时乙工作了小时那么甲一共生产18×=135个3一项工作,甲乙要4小时完成,乙丙要6小时完成。

现在甲丙合作2小时,剩下的乙7小时完成。

甲乙丙单独要多久完成？解：甲丙合作2小时,乙独做7小时相当于甲乙可做2小时,乙丙合作2小时,乙独做7-2-2=3小时那么乙独做完成乙的工作效率=甲的工作效率=丙的工作效率=甲单独完成需要乙单独完成需要丙单独完成需要4服装厂接到加工一批服装的任务,王师傅每天可以制作3套服装,李师傅每天可以制作5套服装,如果王师傅单独完成制作这批服装的任务,比李师傅单独完成制作这批服装的任务要多用4天,那么,要加工的这批服装共有多少套？解答：（3×4）÷（5-3）=6（天）6×5=30（套）王王王…… 王王王王王李李李……李如上图,王字和李字分别代表二人一天的工作量。

王师傅在前几天一定比李师傅少加工了一部分零件,所以还需要再工作4天才和李师傅的工作量一样多。

王四天加工3×4=12（件）,说明说明前几天王比李多加工12件,又由于每天多加工2件。

所以李共加工6天（12÷2）,共6×5=30（套）5一项工程甲乙合做需12天完成,若甲先做3天后,再由乙工作8天,共完成这项工作的,如果这件工作由甲单独做,需多少天完成?解：甲3天乙8天看作甲乙合作3天,乙独做8-3=5天这是解决问题的关键乙独做5天完成乙的工作效率=甲的工作效率=甲单独完成需要6甲乙两人分别生产同样多的零件,各工作16天后,甲还需64个,乙还需384个才能完成,乙比甲的工作效率少40%,求甲的效率？解：设甲的工作效率为a个/天,则乙为（1-40%）a=0.6a个/天根据题意16a+64=0.6a×16+38416×0.4a=3200.4a=20a=50甲的工作效率为50个/天算术法：乙比甲每天少做40%那么16天少做384-64=320个每天少做320/16=20个那么甲的工作效率=20/40%=50个/天7有一项工程要在规定日期内完成,如果甲工程队单独做正好如期完成,如果乙工程队单独做就要超过5天才能完成。