理想变压器的电路分析

理想变压器与电路分析理想变压器是电力系统中常用的电力变换装置，它通过改变电压大小实现能量传输。

在电路分析中，理想变压器被广泛应用于电流变换、电压变换以及阻抗匹配等方面。

本文将重点探讨理想变压器的原理和在不同电路中的应用。

一、理想变压器的原理理想变压器是一种基于电磁感应原理的设备。

它由两个线圈——一侧为输入线圈，也称为初级线圈，另一侧为输出线圈，也称为次级线圈——以及一个磁心组成。

当输入线圈中通入交流电流时，它会在磁心产生一个交变磁场，进而感应次级线圈中的电动势，并从次级线圈中提取出电能。

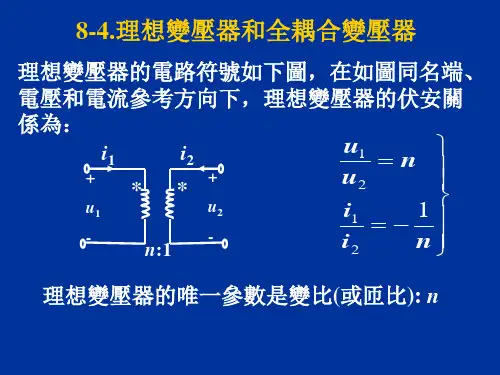
根据理想变压器的特性，可以推导出以下重要公式：1. 线圈匝数比公式：根据理想变压器的性质，我们可以得出电压和匝数的关系：\(\frac{V_1}{V_2} = \frac{N_1}{N_2}\)其中，\(V_1\)和\(V_2\)分别代表输入线圈和输出线圈的电压，\(N_1\)和\(N_2\)分别代表输入线圈和输出线圈的匝数。

2. 功率匹配公式：当变压器工作在理想状态下，输入功率等于输出功率：\(P_1 = P_2\)其中，\(P_1\)和\(P_2\)分别代表输入线圈和输出线圈的功率。

二、理想变压器在电路中的应用1. 电流变换理想变压器可以用来实现电流的变换。

根据线圈匝数比公式，当输入线圈的匝数大于输出线圈的匝数时，可以实现电流的升高。

反之，当输入线圈的匝数小于输出线圈的匝数时，可以实现电流的降低。

这种特性在电源适配器等电力设备中经常被使用。

2. 电压变换理想变压器可以用来实现电压的变换。

根据线圈匝数比公式，当输入线圈的匝数大于输出线圈的匝数时，可以实现电压的降低。

反之，当输入线圈的匝数小于输出线圈的匝数时，可以实现电压的升高。

这种特性在输电线路和变电站中被广泛应用。

3. 阻抗匹配理想变压器可以用来实现阻抗的匹配，即根据输入端和输出端的阻抗要求，选择适当的线圈匝数比以实现阻抗的变换。

这种应用在无线通信等领域中具有重要意义。

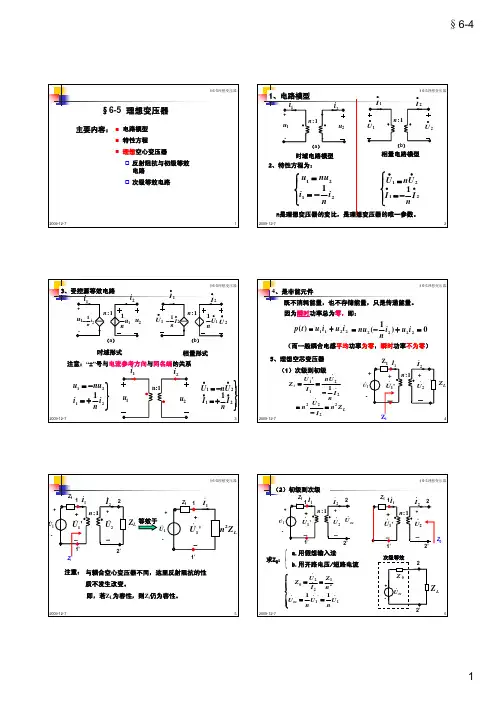
高中物理选修3-2变压器1、理想变压器（1）构造：如图所示，变压器是由闭合铁芯和绕在铁芯上的两个线圈组成的。

①原线圈：与交流电源连接的线圈，也叫初级线圈。

②副线圈：与负极连接的线圈，也叫次级线圈。

③闭合铁芯（2）原理：电流磁效应、电磁感应（3）基本公式①功率关系：P入=P出无论有几个副线圈在工作，变压器的输入功率总等于所有输出功率纸盒②电压关系：U1U2=n1n2即对同一变压器的任意两个线圈，都有电压和匝数成正比。

有多个副线圈时，U1n1=U2n2=U3n3③电流关系：只有一个副线圈时I1I2=n2n1由P入=P出及P=UI推出有多个副线圈时，U1I1=U2I2+U3I3+⋯+U n I n当原线圈中U1、I1代入有效值时，副线圈对应的U2、I2也是有效值，当原线圈中U1、I1为最大值或瞬时值时，副线圈中的U2、I2也对应最大值或瞬时值④原副线圈中通过每匝线圈的磁通量的变化率相等⑤原副线圈中电流变化规律一样，电流的周期频率一样（4）几种常用的变压器①自耦变压器-调压变压器如图是自耦变压器的示意图。

这种变压器的特点是铁芯上只绕有一个线圈。

如果把整个线圈作原线圈，副线圈只取线圈的一部分，就可以降低电压；如果把线圈的一部分作原线圈，整个线圈作副线圈，就可以升高电压。

调压变压器：就是一种自耦便要，它的构造如图所示。

线圈AB绕在一个圆环形的铁芯上。

AB之间加上输入电压U1。

移动滑动触头P的位置就可以调节输出电压U2。

②互感器{电压互感器：用来把高电压变成低电压电流互感器：用来把大电流变成低电流交流电压表和电流表都有一定的量度范围，不能直接测量高电压和大电流。

用变压器把高电压变成低电压，或者把大电流变成小电流，这个问题就可以解决了。

这种变压器叫做互感器。

a、电压互感器电压互感器用来把高电压变成低电压，它的原线圈并联在高电压电路中，副线圈接入交流电压表。

根据电压表测得的电压U2和铭牌上注明的变压比（U1U2），可以算出高压电路中的电压。

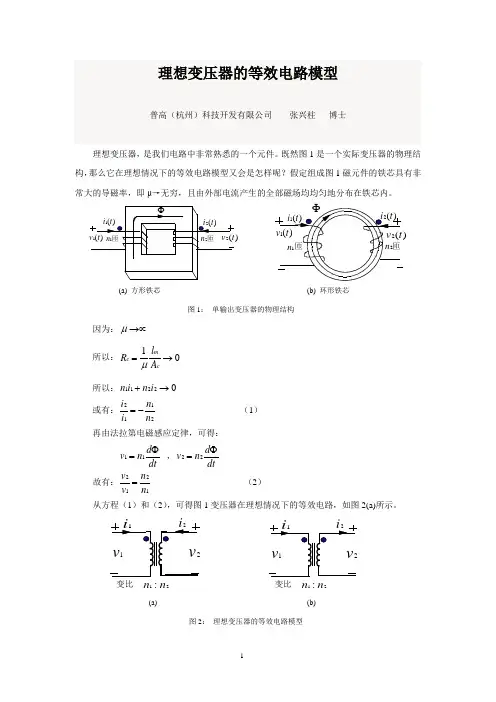
理想变压器的等效电路模型普高（杭州）科技开发有限公司 张兴柱 博士理想变压器，是我们电路中非常熟悉的一个元件。

既然图1是一个实际变压器的物理结构，那么它在理想情况下的等效电路模型又会是怎样呢？假定组成图1磁元件的铁芯具有非常大的导磁率，即μ→无穷，且由外部电流产生的全部磁场均均匀地分布在铁芯内。

(a) 方形铁芯 (b) 环形铁芯图1： 单输出变压器的物理结构因为：→∝µ 所以：01→=cmc A l R µ 所以：02211→+i n i n 或有：2112n n i i −= （1） 再由法拉第电磁感应定律，可得： dt d n v Φ=11 ，dtd n v Φ=22 故有：1212n n v v = （2） 从方程（1）和（2），可得图1变压器在理想情况下的等效电路，如图2(a)所示。

(a) (b)图2： 理想变压器的等效电路模型由于方程（1）中有一个负号，故也可采用图2(b)来表示理想变压器的等效电路模型，它与图2(a)的区别是电流i 2的参考方向，在这种参考方向下，一个理想变压器满足下列电压电流关系：2112//n n i i =1212//n n v v = （3）方程组（3）就是我们在电路中看到的关于变压器元件的电压和电流关系，通过关系，可以看出，由铁芯和两个绕组组成的单输出变压器，其绕组两端的电压之比与绕组的匝数之比成正比，绕组中流过的电流之比与绕组的匝数成反比，如果将两个绕组中的一个看成是输入绕组（或原边绕组），将绕组中的另一个看成是输出绕组（或副边绕组），那么图1的变压器和其等效电路模型就可分别用图3 (a)和图3 (b)来表示，这种变压器的表示方法已被开关电源文献和书籍中所规范，所以本文及后续要介绍的文章，也将以此来表示变压器。

原边或一次侧用下标p 表示，副边或二次侧用下标s 表示。

因此方程组（3）将变成方程组（4）：(a) 变压器结构 (b) 等效电路图3： 开关电源中规范化表示的变压器sp p s N N i i //=ps p s N N v v //= （4）当变压器的副边不止一个绕组时，该变压器就是多输出变压器，多输出变压器在理想情况下的电压电流关系可以用方程组（5）表示，其中K 为副边绕组的个数。

专题拓展课四 理想变压器的综合问题[学习目标要求] 1.综合应用变压器的原理和基本关系分析电路的动态变化。

2.能够利用变压器的基本关系和能量守恒定律分析原线圈含电阻的变压器问题。

拓展点1 理想变压器的动态电路分析1．制约关系(1)电压：原决定副根据变压器的原理可知，输入电压U 1决定输出电压U 2，U 2＝n 2n 1U 1。

当U 1不变时，不论负载电阻R 的阻值变化与否，U 2都不会改变。

(2)电流：副决定原输出电流I 2决定输入电流I 1。

当负载电阻R 的阻值增大时，I 2减小，则I 1相应减小；当负载电阻R 的阻值减小时，I 2增大，则I 1相应增大。

因此，在使用变压器时不能使变压器副线圈短路。

(3)功率：副决定原输出功率P 2决定输入功率P 1。

理想变压器的输出功率与输入功率相等，即P 2＝P 1。

在输入电压U 1一定的情况下，当负载电阻R 的阻值增大时，I 2减小，则P 2＝I 2U 2减小，P 1也将相应减小；当负载电阻R 的阻值减小时，I 2增大，P 2＝I 2U 2增大，则P 1也将增大。

利用以上关系可解决变压器的电压、电流、功率等问题。

2．常见情况(1)原、副线圈匝数比不变，分析各物理量随负载电阻变化而变化的情况，进行动态分析的顺序是R →I 2→P 2→P 1→I 1。

(2)负载电阻不变，分析各物理量随匝数比的变化而变化的情况，进行动态分析的顺序是n 1、n 2→U 2→I 2→P 2→P 1→I 1。

3．特别提醒(1)理想变压器将电能由原线圈传给副线圈时总是“量出为入”，即用户消耗多少，原线圈就提供多少，因而输出功率决定输入功率。

(2)可以把理想变压器的副线圈看作给用户供电的无阻电源，对负载电路进行动态分析时，可以参照直流电路动态的分析方法。

【例1】(2021·河北唐山市高二期末)如图是街头变压器通过降压给用户供电的示意图。

如果变压器的输入电压不变，变压器上的能量损失可以忽略，当R的滑片向下移时()A．电压表V2示数变小B．电压表V3示数变大C．电流表A2示数变大D．电流表A1示数变小答案 C解析原线圈电压不变，匝数比不变，所以副线圈电压不变，即电压表V2示数不变，A错误；当R的滑片向下移时，有效电阻减小，则副线圈电流变大，电流表A2示数变大，根据原、副线圈电流关系，电流表A1示数变大，C正确，D 错误；副线圈电流变大，则R0两端的电压增大，而副线圈两端的总电压不变，所以R两端的电压减小，即电压表V3示数变小，B错误。

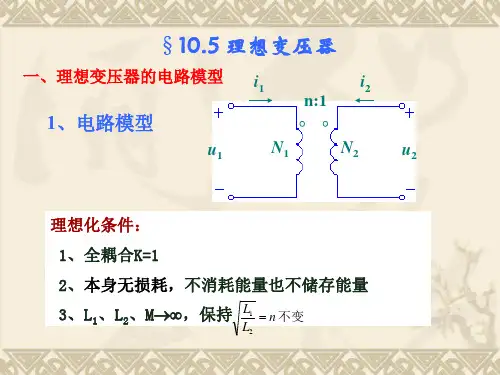
对理想变压器电路中 等效电阻 的探讨邓㊀伟(重庆市开州中学㊀４０５４９９)摘㊀要:自从新课标高考考纲中知识点 理想变压器 由 Ⅰ 级要求变为 Ⅱ 级要求后ꎬ在高考中变压器问题考查频率与难度都有所增加ꎬ有一类这样的问题(在变压器原线圈中连入电阻)在高考中频频出现ꎬ使问题变得较为复杂ꎬ如果用常规解法ꎬ计算量很大ꎬ令学生感到望而生畏.笔者在教学研究中发现这类问题如果用等效电路来分析计算ꎬ能降低难度ꎬ使问题简单明了ꎬ实现问题的 巧解 .关键词:等效电阻ꎻ理想变压器ꎻ推导ꎻ应用ꎻ化繁为简中图分类号:Ｇ６３２㊀㊀㊀㊀㊀㊀文献标识码:Ａ㊀㊀㊀㊀㊀㊀文章编号:１００８－０３３３(２０２１)１０－００９４－０２收稿日期:２０２１－０１－０５作者简介:邓伟(１９７６.１－)ꎬ男ꎬ重庆市开州人ꎬ本科ꎬ中学高级教师ꎬ从事中学物理教学研究.㊀㊀２０２０年高考ꎬ在全国Ⅲ卷第２０题㊁山东卷第５题㊁北京卷第６题等物理试题中均有与理想变压器相关的问题.理想变压器的原线圈和副线圈通过电磁感应联系在一起ꎬ互相影响ꎬ彼此制约ꎬ内部机制相当复杂.在高中阶段ꎬ当原线圈输入电压一定时ꎬ相关问题采用原副线圈电压㊁电流与匝数的关系加以分析ꎬ解决起来比较容易.而在原线圈上串联有一个定值电阻的电路中ꎬ当负载电阻改变时ꎬ副线圈中电流也改变ꎬ原线圈输入电压与电流亦随之改变ꎬ从而又引起副线圈的输出电压改变.此种情形下采用常规的电压㊁电流与匝数的关系来分析ꎬ解决起来非常繁杂.此时ꎬ将变压器问题转化为恒定电流中的等效电路来分析ꎬ可以达到化繁为简ꎬ事半功倍的效果.㊀㊀一㊁理想变压器电路问题中等效电阻公式的推导㊀㊀设理想变压器原副线圈的匝数之比为ｎ１ʒｎ２ꎬ原线圈输入电压为Ｕ１ꎬ副线圈负载电阻为Ｒꎬ如图１(１)所示ꎬ在变压器正常工作时ꎬ我们先分析一下ａ㊁ｂ间的等效电阻.先画出等效电路图如图１(２)所示ꎬ设变压器等效负载电阻为Ｒᶄ.在(１)中由变压器的分压规律:Ｕ１Ｕ２＝ｎ１ｎ２得:Ｕ２＝ｎ２ｎ１Ｕ１.方法一:用电压推导等效电阻Ｕ１＝ｎ１ｎ２Ｕ２＝ｎ１ｎ２Ｉ２Ｒ＝ｎ１ｎ２ ｎ１ｎ２Ｉ１Ｒ＝Ｉ１ ｎ２１ｎ２２Ｒ而Ｕ１＝Ｉ１Ｒᶄꎬ可得ａ㊁ｂ间的等效电阻Ｒᶄ＝ｎ２１ｎ２２Ｒ方法二:用功率推导等效电阻(略)通过分析可知:在只有一个副线圈的理想变压器电路中ꎬ原线圈的匝数为ｎ１ꎬ副线圈的匝数为ｎ２ꎬ副线圈负载电阻为Ｒꎬ则变压器的原㊁副线圈和负载电阻可以等效为一个电阻Ｒᶄ＝(ｎ１ｎ２)２Ｒ㊀(∗).以上是只有一个副线圈的情形.若在变压器中含有多个副线圈时ꎬ能否采用上述等效电阻的方法呢?作图图２所示.由等效电阻法我们可以将副线圈ｎ２ꎬ负载Ｒ１与原线圈看为整体ꎬ等效为新电阻Ｒ１ｘꎬ将副线圈ｎ３ꎬ负载Ｒ２与原线圈看为整体ꎬ等效为另一个新电阻Ｒ２ｘꎬ则Ｒ１ｘ与Ｒ２ｘ两端电压相同ꎬ均为原线圈输入电压Ｕ１.作等效电路图如图３所示.推导可知ꎬ等效电阻Ｒ１ｘ与Ｒ２ｘ的值均满足(∗)式中的规律ꎬ表明多个副线圈的变压器问题ꎬ确实可以将每个副线圈与原线圈分别看为一个整体ꎬ等效为一个新电阻ꎬ作出等效电阻的并联电路图加以分析.㊀㊀二㊁理想变压器电路问题中等效电阻公式的应用㊀㊀１.关于负载电阻一定时的计算问题４９例１㊀(２０１５年全国新课标Ⅰ卷 理综)(单选)理想变压器的原㊁副线圈的匝数比为３ʒ１ꎬ在原㊁副线圈的回路中分别接有阻值相同的电阻ꎬ原线圈一侧接在电压为２２０Ｖ的正弦交流电源上ꎬ如图４所示.设副线圈回路中电阻两端的电压为Ｕꎬ原㊁副线圈回路中电阻消耗的功率的比值为ｋꎬ则(㊀㊀).Ａ.Ｕ＝６６Ｖꎬｋ＝１９㊀㊀Ｂ.Ｕ＝２２Ｖꎬｋ＝１９Ｃ.Ｕ＝６６Ｖꎬｋ＝１３Ｄ.Ｕ＝２２Ｖꎬｋ＝１３解析㊀其等效电路图如图５所示ꎬ则Ｒｘ＝(ｎ１ｎ２)２Ｒ＝９Ｒ由于Ｒ与Ｒｘ串联ꎬ电流相等ꎬ功率㊁电压与电阻成正比所以有:ｋ＝１９ꎬＵＲｘ＝Ｕ１＝９ＵＲꎬ而ＵＲｘ＋ＵＲ＝２２０ＶꎻＵ１Ｕ＝ｎ１ｎ２ꎬ解得:Ｕ＝６６Ｖ.故答案选Ａ.２.关于负载电阻变化时的动态电路分析问题例２㊀(重庆七校联考题 理综)(单选)如图６所示是某一理想变压器所在电路的电路图ꎬ交变电源的输出电压Ｕ的有效值不变ꎬ电阻Ｒ０ꎬＲ１已知ꎬＡ１㊁Ａ２㊁Ｖ为理想交流电表ꎬ滑动变阻器总阻值为Ｒꎬ原副线圈匝数比为ｋ＝２ꎬ且Ｒ１＝Ｒ０/８ꎬＲ＝Ｒ０.当滑动变阻器的滑片Ｐ由最上端向下滑动的过程中ꎬ下列说法正确的是(㊀㊀).Ａ.电压表Ｖ的示数增大Ｂ.电流表Ａ１的示数减小Ｃ.电流表Ａ２的示数减小Ｄ.变压器副线圈输出的功率先增大后减小解析㊀作出等效电路如图７所示ꎬ由 等效电阻法 中的二级结论可知Ｒｘ＝ｎ１ｎ２æèçöø÷２Ｒ１＋Ｒ()ꎬ滑片Ｐ下移ꎬＲ减小ꎬＲｘ减小ꎬ则等效电路图中的电流Ｉ１＝ＵＲｘ增大ꎬ即电流表Ａ１的示数增大ꎬ由变压器电流关系Ｉ１ｎ１＝Ｉ２ｎ２知副线圈中电流Ｉ２即电流表Ａ２示数也增大.Ｒ０两端电压增大ꎬ而Ｒｘ两端电压ꎬ即原线圈输入电压Ｕ１＝Ｕ－Ｉ１Ｒ０ꎬ知Ｕ１减小ꎬ由电压比关系知副线圈输出电压ꎬ即电压表Ｖ示数减小ꎬ则Ａ㊁Ｂ㊁Ｃ选项均错误.滑动变阻器总阻值ＲɤＲ０ꎬ则等效电阻Ｒ０２ɤＲｘɤ９Ｒ０２ꎬ将Ｒ０看为交流电源Ｕ的内阻ꎬＲｘ看为外电阻ꎬ对理想变压器ꎬ等效电阻Ｒｘ消耗的功率Ｐ即为变压器副线圈输出的功率ꎬ由等效电路图作出Ｐ－Ｒｘ的关系如图８所示.由图可知ꎬＰ先增大后减小ꎬ正确选项为Ｄ.３.关于含多个副线圈的变压器计算问题例３㊀(模考试题 理综)(单选)如图９所示ꎬ接在理想变压器回路中的四个规格相同的灯泡都正常发光ꎬ那么ꎬ理想变压器的匝数比ｎ１ʒｎ２ʒｎ３为(㊀㊀㊀)Ａ.１ʒ１ʒ１Ｂ.３ʒ２ʒ１Ｃ.６ʒ２ʒ１Ｄ.２ʒ２ʒ１解析㊀变压器有多个副线圈ꎬ作出等效电阻的电路如图１０所示ꎬ四个灯泡电阻均相同ꎬ令其为Ｒ０ꎬ则由 等效电阻法 中的二级结论可知ＲＢＣ＝ｎ１ｎ２æèçöø÷２２Ｒ０㊀ＲＤ＝ｎ１ｎ３æèçöø÷２Ｒ０等效电阻上消耗功率即为对应负载所消耗的功率ꎬ而每个灯泡消耗的功率均相同ꎬ则ＰＢＣ＝２ＰＤ＝２ＰＡ则ＵＤ＝３ＵＡ由Ｐ＝Ｕ２Ｒ容易得到２ＲＢＣ＝ＲＤ＝９Ｒ０联立以上各式解得ｎ１ʒｎ２ʒｎ３＝３ʒ２ʒ１ꎬ选项Ｂ正确.通过以上的分析过程ꎬ在理想变压器电路问题之中ꎬ当原线圈串联有一个定值电阻时ꎬ采用电压㊁电流与匝数关系的常规解法分析时ꎬ由于原线圈中定值电阻的分压ꎬ使得采用常规法解题时往往比较繁琐.而将变压器通过等效ꎬ转化为一个简单的闭合回路后ꎬ能将问题的分析过程变得直观形象ꎬ解题变得更加的便捷ꎬ起到了化繁为简ꎬ化难为易的功效.㊀㊀参考文献:[１]李小丹.两种等效法解决变压器问题研究[Ｊ].中学物理教学参考ꎬ２０１７(０５):４１.[责任编辑:李㊀璟]５９。

理想变压器等效电路
理想变压器等效电路是电气工程中常用的一种电路模型，它是指假设变压器没有损耗，可以无限传输功率的模型。

在该模型中，变压器的输入端和输出端可以看作是独立的电路，它们之间的传输效率是完美的。

理想变压器等效电路可以简化复杂的变压器电路问题，例如在电力传输和电子设备中常见的变压器应用。

该模型利用变压器的原理，可以将输入端的电压和输出端的电压按照一定的比例转换，并且可以通过改变变压器的绕组比例来改变电压的大小。

理想变压器等效电路通常由一个电感器和多个旋变器组成，其中电感器模拟变压器的铁芯，而旋变器模拟变压器的绕组。

通过调整旋变器的匝数比例，可以使得输入端和输出端的电压比例发生变化，从而实现变压器的功能。

总之，理想变压器等效电路是电气工程中重要的一种电路模型，它可以有效地简化复杂的变压器电路问题，实现电压的转换和传输。

- 1 -。

理想变压器电压电流关系理想变压器是一种用于将交流电压从一个电平变换到另一个电平的装置。

它有一个铁心，上面有两个线圈：一个是输入线圈，一个是输出线圈。

这两个线圈被绝缘绕在铁心上，它们由相对数目的匝数组成。

当输入交流电流在输入线圈中流动时，它激励铁心中的磁通。

这个磁通被传输到输出线圈并诱导出一个输出电压。

在理想的情况下，这个变压器是不会有任何损耗的，电压和电流的变换是完全有效的。

一般情况下，变压器由一个交流电源提供输入电流。

这个电流流过变压器的输入线圈并激起一个磁场。

此磁场穿过铁心，在输出线圈中诱导出一个输出电压。

理想变压器使用的基础原理就是这些磁场的相互作用。

当输入电压在一个给定的电路条件下变化时，输出电压的大小和变化方向也会随之变化。

这个关系可以用变换比例来表示。

变压器变压比例是变压器输入电压和输出电压之间的比率。

这个比率是用变压器的绕制率来表示的。

变压器绕组是输出导线所包围的线圈或线圈部分。

变压器绕制率=变压器输出线圈绕数/变压器输入线圈绕数。

这个比例是通过物理设计来控制，根据需要进行变化。

在理想变压器中，电流的变化比电压的变化更加直接。

这是一个重要的数学关系，它可以用 Ohm's 定律来表示。

Ohm's 定律表明，电流是与电压成正比的，反比于电阻。

在变压器中，电流是由金属线到导体的移动而产生的。

这个电流的大小受到线圈中导体数量和金属线的材料、长度和宽度的影响。

变压器电压电流关系是通过调整输出端和输入端的匝数来实现的。

这个关系可以用 Ohm's 定律来表示为：V2=V1*N2/N1。

其中 V2 和 V1 分别是输出电压和输入电压，N2 和 N1 分别是输出线圈和输入线圈的匝数。

可以看出，这个公式显示了一个直接的线性关系：向输出线圈添加更多的匝数会导致电压直接变化。

除了 Ohm's 定律之外，理想变压器还遵循 Faraday's 定律。

Faraday's 定律说明在变压器线圈中的磁场变化会诱导出电势，这个电势也称为感应电压。