(完整)五年级上册求阴影部分的面积

2022-2023学年五年级数学上册典型例题系列之期中专项练习：求阴影部分的面积（解析版）一、填空题。

1．下图中阴影都分的面积是( )平方厘米。

（单位：厘米）【答案】52【分析】观察图可知：题中阴影部分的面积＝梯形面积－空白三角形的面积，根据梯形面积公式S＝（a＋b）×h÷2和三角形面积公式S＝ah÷2，代入数值计算即可。

【详解】（9＋13）×8÷2－9×8÷2＝22×8÷2－36＝88－36＝52（平方厘米）【点睛】本题考查梯形面积公式和三角形面积公式的应用，关键是熟记公式。

2．图中的ABCD是长方形，长BC＝8厘米，宽AB＝5厘米，ABDE是梯形，△BDE的面积是（）平方厘米。

【答案】20【分析】通过观察图形可知，三角形ABE与三角形AED是同底等高的三角形，所以面积相等，因此，阴影面积为长方形ABCD面积的一半，根据长方形的面积公式：S＝ab，把数据代入公式解答即可。

【详解】长方形ABCD的面积为：8×5＝40（平方厘米）三角形ABE与三角形AED是同底等高的三角形，所以面积相等，即三角形ABD 的面积等于阴影面积，因此，阴影面积为长方形ABCD面积的一半。

所以阴影部分的面积是：40÷2＝20（平方厘米）【点睛】此题解答的关键是根据同底等高的三角形的面积相等，推出三角形ABE与三角形AED相等，进而推出阴影部分的面积是长方形ABCD面积的一半。

3．下图中长方形的面积是24cm²，那么阴影部分的面积是( )cm²。

【答案】12【分析】长方形的面积＝长×宽，三角形的面积＝底×高÷2；图中长方形的长相当于三角形的底，长方形的宽相当于三角形的高，据此可知，阴影部分的面积等于长方形面积的一半；据此计算即可。

【详解】24÷2＝12（平方厘米）4．如图，平行四边形的底是12厘米，高是8厘米，图中阴影部分的面积是( )平方厘米。

五年级上册数学教案5.7 小练习（二）求阴影部分面积▏沪教版作为一名经验丰富的教师，我很高兴能分享我的教学经验。

一、教学内容今天我要分享的是五年级上册数学教案中第七章第五节的内容，主要讲解如何求阴影部分的面积。

我们会用到之前学过的平面几何知识，包括三角形、矩形和圆的面积计算公式。

二、教学目标通过本节课的学习，我希望学生能够掌握求阴影部分面积的方法，并能灵活运用到实际问题中。

三、教学难点与重点重点是让学生理解并掌握求阴影部分面积的计算方法。

难点在于如何引导学生将实际问题转化为数学问题，并运用适当的公式进行计算。

四、教具与学具准备我已经准备好了黑板、粉笔、投影仪和一些实际的阴影图形模型，以便于学生更好地理解。

五、教学过程我会通过一个实际的情景引入，比如一个矩形里面有一个圆形，让学生观察并尝试计算阴影部分的面积。

然后，我会引导学生思考如何将这个问题转化为数学问题，并引导他们运用之前学过的面积计算公式。

接着，我会给出一些例题，并引导学生一起解答。

在解答过程中，我会强调关键步骤和注意事项。

我会给出一些随堂练习题，让学生独立解答，并及时给予他们反馈和指导。

六、板书设计我会设计一个清晰的板书，包括阴影部分的图形、计算公式和相关步骤。

七、作业设计1. 一个半径为5cm的圆中，有一个直径为10cm的矩形。

2. 一个边长为8cm的正方形中，有一个边长为4cm的小正方形。

答案：1. 阴影部分面积 = 圆的面积矩形的面积= πr^2 长×宽 = 3.14×5^2 10×5 = 78.5cm^22. 阴影部分面积 = 大正方形的面积小正方形的面积 = 边长^2 小边长^2 = 8^2 4^2 = 64 16 = 48cm^2八、课后反思及拓展延伸通过本节课的教学，我发现学生们在将实际问题转化为数学问题上还存在一些困难，需要在今后的教学中加强引导和练习。

另外，学生们在解答过程中要注意细节，比如单位的转换和公式的正确运用。

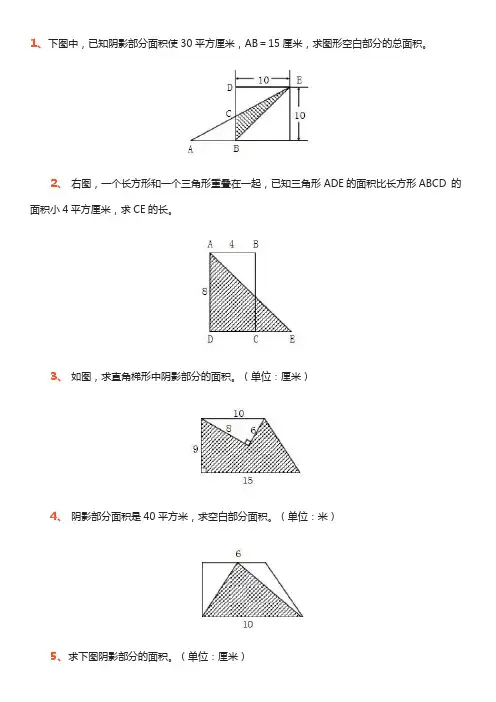
1、下图中，已知阴影部分面积使30平方厘米，AB＝15厘米，求图形空白部分的总面积。

2、右图，一个长方形和一个三角形重叠在一起，已知三角形ADE的面积比长方形ABCD 的面积小4平方厘米，求CE的长。

3、如图，求直角梯形中阴影部分的面积。

（单位：厘米）4、阴影部分面积是40平方米，求空白部分面积。

（单位：米）5、求下图阴影部分的面积。

（单位：厘米）6、右图，ABCD只直角梯形，已知AE＝EF＝FD，AB为6厘米，BC为10厘米，阴影部分面积为6平方厘米。

求直角梯形ABCD的面积。

7、下图是由一个三角形和一个梯形组成，已知三角形的面积是1平方分米，求这个图形的面积。

（单位：分米）8、如图，平行四边形面积240平方厘米，求阴影部分面积。

9、下图ABCD是梯形，它的面积是140平方厘米，已知AB＝15厘米，DC＝5厘米。

求阴影部分的面积。

10、求右面图形的面积（单位：厘米）11、如图，求长方形中的梯形面积。

（单位：厘米）12、求下图阴影部分的面积（单位：厘米）13、求梯形的面积。

（单位：厘米）14、如图，已知梯形ABCD的面积为37.8平方厘米，BE长7厘米，EC长4厘米，求平行四边形ABED的面积。

15、求空白部分面积。

（单位：厘米）16、如图，已知平行四边形ABCD中，阴影部分面积为72平方厘米，求三角形BCD的面积。

17、求梯形中阴影部分的面积。

（单位：cm）18、下图，ABCD是一个等腰梯形，ADFE是边长为4厘米的正方形，CF＝2厘米，求阴影部分的面积。

19、下图ABCD是梯形，它的面积是200平方厘米，已知AB＝20厘米，DC＝5厘米，求阴影部分的面积。

（单位：厘米）20、在平行四边形ABCD中，CE上的高是6厘米，AD＝8厘米，BE＝11厘米，求三角形ABC 的面积。

21、在下图中，已知直角梯形ABCD的面积是60平方厘米，DC长6厘米，AB长24厘米，求：三角形AED的面积。

22、如图：梯形ABCD分割成一个平行四边形，一个三角形。

小学五年级数学求阴影部分面积习题1、下图中，已知阴影部分面积是30平方厘米，AB＝15厘米，求图形空白部分的总面积。

2、下图，一个长方形和一个三角形重叠在一起，已知三角形ADE的面积比长方形ABCD 的面积小4平方厘米，求CE的长。

3、如图，求直角梯形中阴影部分的面积。

（单位：厘米）4、阴影部分面积是40平方米，求空白部分面积。

（单位：米）5、求下图阴影部分的面积。

（单位：厘米）6、下图，ABCD是直角梯形，已知AE＝EF＝FD，AB为6厘米，BC为10厘米，阴影部分面积为6平方厘米。

求直角梯形ABCD的面积。

7、下图是由一个三角形和一个梯形组成，已知三角形的面积是1平方分米，求这个图形的面积。

（单位：分米）8、如图，平行四边形面积240平方厘米，求阴影部分面积。

9、下图ABCD是梯形，它的面积是140平方厘米，已知AB＝15厘米，DC＝5厘米。

求阴影部分的面积。

10、求下面阴影部分的面积（单位：厘米）11、如图，求长方形中的梯形面积。

（单位：厘米）12、求下图阴影部分的面积（单位：厘米）13、求梯形的面积。

（单位：厘米）14、如图，已知梯形ABCD的面积为37.8平方厘米，BE长7厘米，EC长4厘米，求平行四边形ABED 的面积。

15、求空白部分面积。

（单位：厘米）16、如图，已知平行四边形ABCD中，阴影部分面积为72平方厘米，求三角形BCD的面积。

17、求梯形中阴影部分的面积。

（单位：cm）18、下图，ABCD是一个等腰梯形，ADFE是边长为4厘米的正方形，CF＝2厘米，求阴影部分的面积。

19、下图ABCD是梯形，它的面积是200平方厘米，已知AB＝20厘米，DC＝5厘米，求阴影部分的面积。

（单位：厘米）20、在平行四边形ABCD中，CE上的高是6厘米，AD＝8厘米，BE＝11厘米，求三角形ABC 的面积。

21、在下图中，已知直角梯形ABCD的面积是60平方厘米，DC长6厘米，AB长24厘米，求：三角形AED的面积。

阴影部分面积计算一、直接与间接方法求阴影部分面积例1:已知右面得两个正方形边长分别为６分米与４分米,求图中阴影部分得面积。

1、如图,ＡBDC就就是一个长１2厘米,宽5厘米得长方形,已知DE长3厘米,求阴影部分三角形ＡCE得面积。

二、等量代换法求阴影部分得面积例2:右图就就是两个相同得直角三角形叠在一起,求阴影部分得面积。

(单位：厘米)１、下图中两个完全一样得三角形重叠在一起,求阴影部分得面积。

(单位：厘米)例3：在右图中,平行四边形ＡBCD得边BＣ长10厘米，直角三角形EＣB得直角边EＣ长8厘米。

已知阴影部分得总面积比三角形EFＧ得面积大10平方厘米,求平行四边形ABCＤ得面积。

1、在右图中,三角形EDＦ得面积比三角形AＢE得面积大75平方厘米，已知正方形ABＣD得边长为１5厘米,(1)求三角形ＡCＦ得面积（2)ＤF得长就就是多少厘米?四、平移法求面积例4:右图就就是一块长方形公园绿地，绿地长24米,宽16米，中间有一条宽为2米得道路，求草地(阴影部分）得面积。

1、下图得长方形就就是一块草坪，中间有两条宽１米得走道,求植草得面积。

五、等高求面积例5:求下图中阴影部分得面积。

六、按一定得比求面积把下图三角形得底边BＣ四等分,在下面括号里填上“>”、“<”或“=”。

甲得面积( )乙得面积。

例6:（选讲）两条对角线把梯形ABＣＤ分割成四个三角形。

已知两个三角形得面积(如图所示),求另两个三角形得面积各就就是多少?(单位:平方厘米)1、如下图，图中BＯ=２ＤO，阴影部分得面积就就是4平方厘米,求梯形ABCD得面积就就是多少平方厘米?作业:1、已知正方形甲得边长就就是８厘米，正方形乙得面积就就是３6平方厘米,那么图中阴影部分得面积就就是多少？2、图中两个正方形得边长分别就就是6厘米与4厘米,求阴影部分得面积。

3、求下图长方形AＢＣD得面积（单位:厘米)。

4、图中两个正方形得边长分别就就是1０厘米与６厘米，求阴影部分得面积。

阴影图形面积应知应会基础图形的面积：【1】平行四边形的面积=底×高字母公式：S=ah÷2【2】三角形的面积=底×高字母公式：S=ah÷2【3】梯形的面积=（上底＋下底）×高÷2字母公式：s梯形=(a＋b)×h÷2a=s梯形×2÷h-bb=s梯形×2÷h-ah=s梯形×2÷(a＋b)二、求阴影图形的面积的方法（一）分析思路：计算时需转化成已学的基本图形，通过加、减进行计算。

（二）具体方法：1、分割法：将组合图形分成几个基本图形，通过加，求几个基本图形的和。

2、填补法：将组合图形补成一个基本图形，通过大面积减小面积，求两个基本图形的差。

阴影图形的面积直接计算：根据公式计算阴影三角形的面积【1】分析：图中的阴影三角形和平行四边形等底等高，因此三角形的面积等于平行四边形面积的一半。

解：S阴影三角形=底×高÷2=14×10÷2 =70（平方厘米）根据图中已知图形面积和所求图形面积之间的关系计算：S 三角形形=S 大平行四边形面积÷2【2】如图，空白部分的面积是13.5平方厘米，求平行四边形的面积是多少平方分米？ 解：S 空白部分=S 阴影三角形=平行四边形的底×高÷2 =S 平行四边形面积÷2所以S 平行四边形面积=S 空白部分×2=13.5×2=27(平方厘米） 先求出所需数据，再根据公式计算阴影三角形的面积【3】分析： 图中的阴影三角形和平行四边形等高，因此只需计算出三角形的底，再计算出三角形的面积。

解：14-10=6（厘米） S 阴影三角形=底×高÷2 =14×10÷2 =70（平方厘米）先求出所学数据，再计算梯形面积。

【4】寻找合适的条件，求出下面涂色部分的面积。

人教版五年级上册数学平面图形阴影面积计算1、下图中，大阴影三角形的面积比小阴影三角形的面积大多少平方厘米？2、下图中正方形的边长为8厘米，CE为20厘米，梯形BCDF的面积是多少平方厘米？3、下图中两个完全一样的三角形重叠在一起，求阴影部分的面积。

（单位：厘米）4、图中ABCD是长方形，AB=4厘米，BC=6厘米，三角形EFD的面积比三角形ABF的面积大6平方厘米，求ED的长。

5、如下图，正方形ABCD中，AB=4厘米，EC=10厘米，求阴影部分的面积？6、如图，ABCD是直角梯形，求阴影部分的面积和。

（单位：厘米）7、求下图中阴影部分的面积。

8、如图，平行四边形BCEF中，BC=8厘米，直角三角形中，AC=10厘米，阴影部分面积比三角形ADH的面积大8平方厘米。

求AH长多少厘米？9、下图的长方形是一块草坪，中间有两条宽1米的走道，求植草的面积。

10、求图中阴影部分的面积。

（单位：厘米）11、如图，三角形ABC的面积是40平方厘米，D、E和F分别是BC、AC和AD的中点。

求：三角形DEF 的面积。

12、在三角形ABC中，DC=2BD，CE=3AE，阴影部分的面积是20平方厘米，求三角形ABC的面积？13、如图，已知三角形ABC面积为1，延长AB至D，使BD＝AB；延长BC至E，使CE＝2BC；延长CA至F，使AF＝3AC，求三角形DEF的面积？14、如图，在三角形ABC中，BC＝8厘米，高是6厘米，E、F分别为AB和AC的中点，那么三角形 EBF 的面积是多少平方厘米？15、一个大长方形被两条平行于它的两条边的线段分成四个较小的长方形，其中三个长方形的面积如下图所求，求第四个长方形的面积？16、下面一个长方形被分成六个小长方形，其中四个长方形的面积如图所示（单位：平方厘米），求A 和B 的面积。

17、下图一个长方形被分成四个小长方形，其中三个长方形的面积分别是24平方厘米、30平方厘米和32平方厘米，求阴影部分的面积。

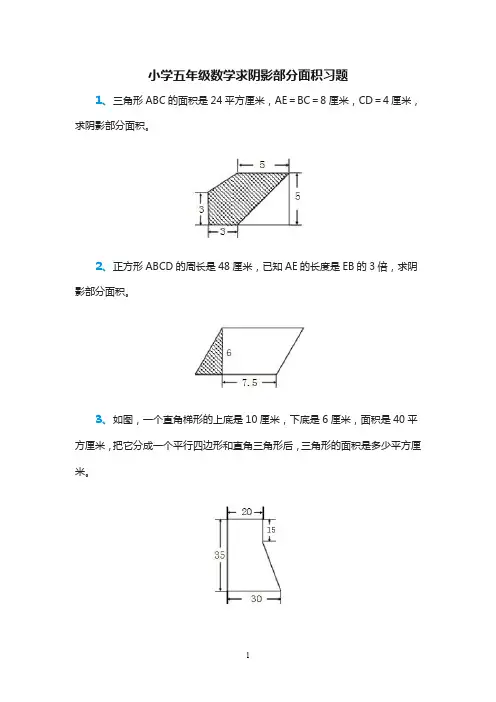
小学五年级数学求阴影部分面积习题 1、三角形ABC的面积是24平方厘米，AE＝BC＝8厘米，CD＝4厘米，求阴影部分面积。

2、正方形ABCD的周长是48厘米，已知AE的长度是EB的3倍，求阴影部分面积。

3、如图，一个直角梯形的上底是10厘米，下底是6厘米，面积是40平方厘米，把它分成一个平行四边形和直角三角形后，三角形的面积是多少平方厘米。

4、下面直角梯形的面积是49平方分米，求阴影部分的面积。

5、求整个图形的面积。

（单位：厘米） 6、下图所示梯形，如果它的上底增加4厘米，面积就增加18平方厘米，这梯形原来的面积是多少平方厘米？ 7、求下面图形中阴影部分的面积。

（单位：厘米） 8、下图由大小不等的两个正方形拼成，小正方形的边长是6厘米，阴影部分面积是60 厘米，求图中空白部分的面积。

9、求正方形中阴影部分的面积。

10、在下图中，已知平行四边形ABED的面积是30平方厘米，BE长6厘米，EC长4厘米。

求梯形ABCD的面积。

11、图中空白部分是一个面积为30平方厘米的平行四边形，求阴影部分面积。

12、如图：在直角梯形ABCD中，AB＝4分米。

CD＝9分米，空白部分面积为10平方分米，求阴影部分面积。

13、求阴影部分的面积（单位：厘米）：14、图中三角形DEC的面积是2.7平方米，AD＝4.4米，AB＝2米。

求平行四边形CDFG中阴影部分的面积。

15、如图，在梯形ABCD中，CD＝4厘米，AB＝2DC，AECD为平行四边形，已知梯形面积为66平方厘米，求阴影部分面积。

16、图中三角形ABC的面积是24平方厘米，AE＝BC＝8厘米，CD＝4厘米，求阴影部分的面积。

17、图中空白部分是一个面积为30平方厘米的平行四边形，求阴影部分面积。

18、图中，阴影部分的面积是56平方厘米，BD＝14厘米，求梯形ABCD 的面积。

19、梯形ABCD面积是96平方厘米，AB＝6厘米，中位线EF＝12厘米，求阴影部分面积。

求阴影部分的面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为 r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.1 25平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。

(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。

平面图形1、 和差法：分割、合并、倍数比2、 运动法：3、 等积变换法：等底、等高则等积；等积、等高则等底；等积、等底则等高。

例1、求阴影部分的面积。

例2、大、小两个正方形的边长分别是8厘米和6厘米， 求阴影部分的面积。

例3、两个相同的直角三角形如图重叠在一起， 求阴影部分的面积。

例4、求阴影部分面积。

例5、图中长方形ABCD 中AB=5厘米，BC=8厘米。

三角形DEF （甲）的面积 比三角形ABF （乙）的面积大8平方厘米。

求DE 的长。

3cm4cm6cm5cm2cm12cm甲ABCDEF乙AD B C 10cm 10cm24cm45° E5cm例6、在三角形ABC 中，DC=2BD ，CE=3AE ，三角形ADE 的面积是 8平方厘米。

求三角形ABC 的面积。

例7、四边形ABCD 中，AC 和BD 互相垂直，AC=20厘米，BD=15厘米。

求四边形的面积。

例8、在四边形ABCD 中，∠C=45°，∠B=90°，∠D=90°， AD=4cm ，BC=12cm 。

求四边形ABCD 的面积。

例9、AF=2cm,AB=4cm,CD=5cm,DE=8cm,∠B=∠E=90°。

求四边形ACDF 的面积。

例10、已知大正方形比小正方形边长多2厘米，大正方形比小正方形的面积大10平方厘米。

求大、小正方形的面积各数多少平方厘米。

ABCDC45°AB CDABCDEF 4cm8cm2cm练习1、图中两个正方形的边长是10厘米和7厘米，求阴影部分的面积（如图）练习2、如下图，在三角形ABC中，AD=BD,CE=3BE。

若三角形BED的面积是1平方厘米，则三角形ABC的面积是多少平方厘米？练习3、三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. A B长40厘米, BC长多少厘米.练习4、在右图中(单位:厘米),两个阴影部分面积的和是平方厘米.练习5、ABC是等腰直角三角形. D是半圆周的中点,BC是半圆的直径,已知:AB=BC=10,那么阴影部分的面积是多少?练习6、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积. C②①A B121520A10DCB练习7、右图中三角形是等腰直角三角形, 阴影部分的面积是 (平方厘米).练习8、如右图,阴影部分的面积是 .练习9、如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π练习10、ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?练习11、在四边形ABCD 中，∠C=135°，∠D=90°。

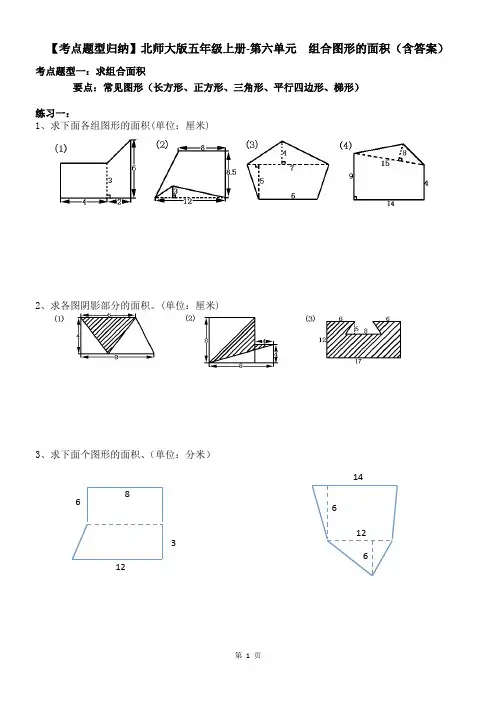
【考点题型归纳】北师大版五年级上册-第六单元 组合图形的面积（含答案）考点题型一：求组合面积要点：常见图形（长方形、正方形、三角形、平行四边形、梯形）练习一：1、求下面各组图形的面积(单位：厘米)2、求各图阴影部分的面积。

(单位：厘米)3、求下面个图形的面积、（单位：分米）812366612 14考点题型二：两个正方形要点：①阴影部分是常见图形可尝试直接求出②阴影部分切割法③整体减去部分得到阴影部分练习二：1、先观察图形特点，再求图形中阴影部分的面积．（单位：厘米）5.44.26431.52.5 82、求阴影部分的面积．（单位：厘米）3、图中两个正方形的边长分别是10厘米和6厘米，求阴影部分的面积。

4、大小正方形如图放置，阴影部分为重叠部分，求空白部分面积。

（单位：厘米）1577225、求下图阴影部分的面积（单位：厘米）考点题型三：平行四边形与三角形练习三：1、下图的平行四边形面积是40平方厘米，求阴影部分的面积.(单位：厘米)2、平行四边形的面积是320平方厘米，求梯形面积．3、已知平行四边形的面积是48平方分米，求阴影部分的面积。

3dm8dm4、如图所示，一个平行四边形被分成A、B两份，A的面积比B的面积打40平方米，A的上底是多少？B8米A5、如图，平行四边形面积240平方厘米，求阴影部分面积。

考点题型四：梯形和三角形练习四：1、阴影部分面积是40平方米，求空白部分面积。

（单位：米）2、求阴影部分的面积．（单位：厘米）3、如图所示，梯形的周长是52厘米，求阴影部分的面积。

1014164、下图直角梯形的面积是49平方分米，求阴影部分的面积。

5、图中梯形中空白部分是直角三角形，它的面积是45平方厘米，求阴影部分面积。

6、阴影部分面积是40平方米，求空白部分面积。

（单位：米）7、下图ABCD是梯形，它的面积是140平方厘米，已知AB＝15厘米，DC＝5厘米。

求阴影部分的面积。

8、求梯形的面积。

（单位：厘米）9、如图，已知梯形ABCD的面积为37.8平方厘米，BE长7厘米，EC长4厘米，求平行四边形ABED 的面积。

组合图形面积应用1．求下面图形的面积（1）（2）（1）解：8×6＋（8＋12）×3÷2=48＋20×3÷2=48＋60÷2=48＋30=78（平方米）（2）解：5.4×4.2＋5.4×6÷2=22.68＋32.4÷2=22.68＋16.2=38.88（平方厘米）2．工厂制作一些流动红旗，式样如图，制作一面流动红旗需要多少平方厘米的布料？解：60×30-30×（60-45）÷2=60×30-30×15÷2=1800-450÷2=1800-225=1575（平方厘米）答：制作一面流动红旗需要1575平方厘米的布料。

3．友谊公园的中心有一块长方形草坪，草坪里有一条宽1米的曲折小路。

草坪的实际面积有多大？解：（12-1）×（10-1）=11×9=99（平方米）答：草坪的实际面积有99平方米。

4．李叔叔家原来有一块边长12米的正方形菜地，今年他将这块菜地进行了扩建（如图中的涂色部分）。

（1）原来这块菜地的面积是多少平方米？（2）李叔叔今年扩建了多少平方米的菜地？（1）解：12×12=144（平方米）答：原来这块菜地的面积是144平方米。

（2）解：（12＋7）×（12＋2）-144=19×14-144=266-144=122（平方米）答：李叔叔今年扩建了122平方米的菜地。

5．求出下面图形的面积。

（1）如图，已知梯形的面积是60米2，那么，阴影部分（三角形）的面积是多少米"？（2）求出下面组合图形的面积。

（单位：厘米）（1）解：（60×2）÷（8＋12）=120÷20=6（米）8×6÷2=48÷2=24（平方米）答：阴影部分（三角形）的面积是24平方米。

组合图形面积应用1．求图中相连的三个正方形内阴影部分的面积(单位：厘米)。

解：15-6-4=5（厘米）（5+4）×5÷2=9×5÷2=22.5（cm2）2．一块近似平行四边形的菜地，中间有一条石子路（如图）。

这块菜地的面积多少平方米？解：20×8－8×1＝160－8＝152（平方米）答：这块菜地的面积152平方米。

3．本次簕杜鹃花展有许多展台供市民参观，其中一个展台把展区精心布置成一个如下图所示的图形。

这个展台占地面积一共有多少平方米?解：（4+6）×（8-5）÷2+5×4=10×3÷2+5×4=15+20=35（平方米）答：这个展台占地面积一共有35平方米。

4．赵小军在一张平行四边形的硬纸板上剪下了一个三角形（如下图），剩下图形的面积是多少平方分米？解：8×6－（8－3－2）×4÷2＝48－3×4÷2＝48－6＝42（平方分米）答：剩下图形的面积是42平方分米。

5．某农场开辟一块新的菜地（如图），一条水渠穿过这块菜地，若每平方米菜地一年可收入12元，那么这块菜地一年可收入多少元？解：18-3=15（米）23-3=20（米）（15＋20）×23÷2×12=402.5×12=4830（元）答：这块菜地一年可收入3360元。

6．学校修建了一个艺术广场（平面图如下），这个艺术广场的占地面积是多少平方米？解：（15+30）×8÷2+30×20=180+600=780（平方米）答：这个艺术广场的占地面积是780平方米。

7．如图是某种植果园基地的示意图。

（1）求这个果园的面积是多少m2？（2）如果每棵果树占地10m2，这个果园共有多少棵果树？（1）解：90×40÷2+90×50＝1800+4500＝6300（平方米）答：这个果园的面积是6300平方米。

五年级上册求阴影部分的面积一、求阴影面积例1、两个相同的直角三角形如图所示（单位：厘米）重叠在一起，求阴影部分的面积？巩固练习1、在图中，平行四边形ABCD的边BC 长10厘米，直角三角形ECB的直角边EC 长8厘米。

已知阴影部分的总面积比三角形EFG的面积大10平方厘米，求平行四边形ABCD面积。

例2、右图所示的等腰直角三角形中，剪去一个三角形后，剩下的部分是一个直角梯形（阴影部分）。

已知梯形的面积为36平方厘米，上底为3厘米，求下底和高？巩固练习2、如图，BD、DE、EC的长分别是2厘米，4厘米，2厘米，F是线段AE的中点，三角形ABC的高为4厘米，求三角形DEF的面积。

例3、下图中，有四条线段的长度已知，还有两个角是直角，那么四边形ABCD（阴影部分）的面积是多少？巩固练习3、在右图中，阴影部分A的面积比阴影部分B的面积大10.5平方厘米，求线段BC的长度？二、课堂练习简便计算4.4+5.6×2.5÷5.6×2.5 （3.8－7.7÷2.5）×2.81、一块长方形钢板，长截下4分米，宽截下1分米后，成了一块正方形钢板，如右图，面积比原来减少了49平方米。

原来长方形钢板的面积是多少平方米？2、在边长为6的正方形内有一个三角形BEF，线段AE＝3，DF＝2，求三角形BEF的面积。

3、在右图中，ABCD是长方形，三条线段的长度如图所示，M是线段DE的中点，求四边形ABMD（阴影部分）的面积。

家庭作业一、直接写得数1.52－（－0.48）= －1.25×6= 3.062÷3.2≈ (保留两位小数)二、解方程（带*号的要检验）6X+0.4×6=9.6 42.8+X=2.6+1.2 * 2.5X－9.4=0.5（X－4.8）三、递等式计算，能简便的用简便方法计算（7.5+7.5+7.5+7.5）×2.5 3.65×62+0.28×365+36.5（49.5÷7.5+49.5÷2.5）÷0.01 [3.25－3.25÷（10.3+2.2）]×0.1四、文字题9.1减去2.5与0.4的积所得的差除以0.9，商是多少？甲、乙两数的和是3.8，甲数比乙数的3倍多0.2，求乙数？五应用题1、小红和小明做同样多的口算题，小红每分钟做60道口算题，小明每分钟做75道口算题，当小明做完时，小红还有45道没有做，小明做了几分钟？2、红光足球俱乐部有一线队员45人，二线队员65人，二线队员要抽调多少人到一线，才能使一线队员人数是二线队员人数的1.2倍？3、两辆汽车都从A地开往B地，甲车每小时行40千米，先行2小时后，乙车才出发，经过5小时乙车追上甲车。

人教版小学数学五年级上册6.《求阴影部分面积》重点考点（含答案）五年级上册数学重点考点求阴影部分面积（知识点：平行四边形的面积三角形的面积梯形的面积组合图形的面积）1．计算下面图形的面积。

2．求下图阴影部分的面积。

（单位：厘米）3．如图是两个正方形，求阴影部分的面积（单位：厘米）。

4．将一张长方形纸如图折叠，求图中阴影部分面积。

（单位：cm）5．计算图中阴影部分的面积。

（单位：cm）6．有一张长方形纸，把纸的一角如图那样折叠，求图中阴影部分的面积。

7．寻找合适的条件，求出下图中涂色部分的面积。

（单位：cm）8．下图梯形中，阴影部分面积是24平方分米，求梯形面积。

9．求如图中阴影部分的面积。

（单位：厘米）10．已知阴影部分面积是24cm2，求梯形面积。

11．求阴影部分的面积。

（单位：米）12．计算阴影部分的面积。

（单位：dm）13．计算图形中阴影部分的面积。

14．求出阴影部分的面积。

（单位：cm）15．求涂色部分的面积。

16．计算阴影部分的面积。

（1）（2）17．求下列阴影部分的面积。

（单位：cm）18．求阴影部分面积。

19．求下面图形中阴影部分的面积。

（单位：cm）20．求阴影部分的面积。

21．求阴影部分的面积。

（单位：分米）22．求阴影部分的面积。

（单位：cm）23．求阴影部分的面积。

（单位：分米）24．求阴影部分的面积。

参考答案：1．100平方厘米【分析】要求的图形面积可以看作是一个长为15厘米，宽为10厘米的长方形面积减去两个底为5厘米，高为5厘米的三角形面积和一个边长为5厘米的正方形的面积之和，再根据长方形面积＝长×宽，正方形面积＝边长×边长，三角形面积＝底×高÷2，代入相应数值计算，即可解答。

【详解】（平方厘米）【点睛】本题主要考查的是组合图形面积的计算，解题关键是先分析都是由哪些基本图形组成，再根据相应图形面积的计算公式，代入数值计算即可。

2．144平方厘米【分析】用长方形的面积减去梯形的面积即是阴影部分的面积，分别利用长方形的面积＝长×宽和梯形的面积＝（上底＋下底）×高÷2求解。

五年级数学上册《求部分阴影面积》专项训练1．求图中阴影部分的面积．(单位：米)55×28﹣55×3﹣5×28+5×3，=1540﹣165﹣140+15，=1375﹣140+15，=1235+15，=1250(平方米)；答：图中阴影部分的面积是1250平方米．2．计算下面图形的面积．(单位：cm)3×4÷2+(3+6)×3÷2，=6+13.5，=19.5(平方厘米)；答：图形的面积是19.5平方厘米．3．有一条水渠穿过一块菜地(如图)，这块菜地的面积是多少？(40﹣5)×25，=35×25，=875(平方米)；答：这块菜地的面积是875平方米．4.如图是一块长方形草坪，长是16米，宽是10米，中间有两条小路，一条是长方形，一条是平行四边形，那么有草部分(阴影部分)的面积有多大？(单位：米)(16﹣2)×(10﹣2)，=14×8，=112(平方米)；答：阴影部分的面积是112平方米．5、如图所示是两个相同的直角梯形重叠在一起，求阴影部分的面积．(单位：厘米)(20﹣5+20)×8÷2，=35×8÷2，=280÷2，=140(平方厘米)；答：阴影部分的面积是140平方厘米．6、一条长方形毛巾，长60厘米，宽25厘米，把它的4个角折向同一面(如图)，所得的每个三角形的面积都是32平方厘米，求图中阴影部分面积．60×25﹣32×2×4，=1500﹣256，=1244(平方厘米)；答：图中阴影部分的面积是1244平方厘米．。

小学五年级语文上册求阴影部分长度习题
本文档将提供小学五年级语文上册阴影部分长度题的解答。

以下是一些示例题和对应的答案：
1. 下图中，矩形的长和宽分别是7厘米和3厘米，求阴影部分的面积。

解答：矩形的面积可以通过长度和宽度相乘来计算。

阴影部分的面积等于矩形的面积减去内部长方形的面积。

所以阴影部分的面积为 (7厘米 × 3厘米) - (5厘米 × 1厘米) = 11平方厘米。

2. 图中的长方形ABCDEF为一个立方体的一部分，已知BC的长度为10厘米，AD的长度为8厘米，求阴影部分的长度。

解答：由于长方形ABCDEF是立方体的一部分，所以阴影部分的长度即为BC的长度。

因此阴影部分的长度为10厘米。

3. 一根长度为15厘米的木棍被剪成两段，其中一段的长度为8厘米，求另一段的长度。

解答：木棍被剪成两段，其中一段的长度已知为8厘米。

所以另一段的长度等于整根木棍的长度减去已知段的长度。

因此另一段的长度为 15厘米 - 8厘米 = 7厘米。

以上是一些示例习题的解答，希望能够帮助到你。

如果有其他问题，请随时提问。