基4-FFT算法编程

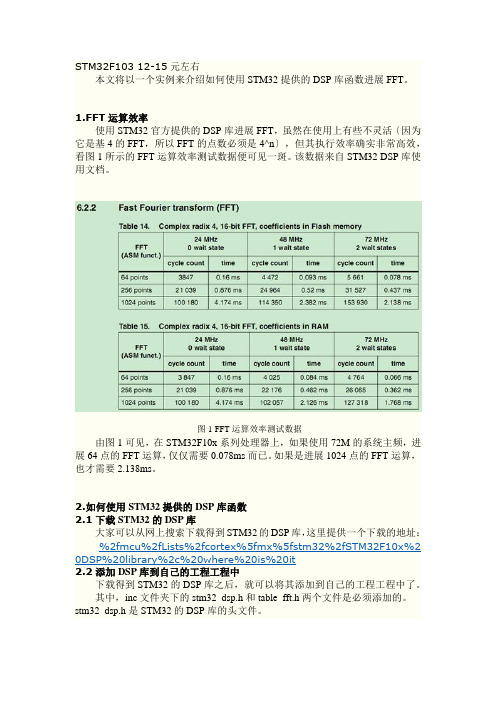
常用FFT 算法总结一、DFT 及IDFT 的定义对于N 点有限长序列)(n x ，其DFT 及IDFT 定义如下： DFT ：∑-==10)()(N n nk N W n x k XIDFT ：∑-=-=1)(1)(N k nk NWk X Nn x其中，Np j p NeW/2π-=称为旋转因子，p 称为旋转因子的指数。

二、基2-FFT 算法 设序列)(n x 的长度N 满足MN2=，M 为自然数。

1、时间域抽取FFT （DIT-FFT ） （1）算法原理按n 的奇偶把)(n x 分解为两个N/2点的子序列：)12()()2()(21+==r x r x r x r x则)(n x 的DFT 为)()()12()2()(2112/0)12(12/02k X W k X Wr x Wr x k X kN N r k r NN r rk N+=++=∑∑-=+-=其中)(1k X 和)(2k X 分别为)(1r x 和)(2r x 的N/2点DFT 。

利用)(1k X 和)(2k X 的周期性，)(k X 可以表示为⎪⎩⎪⎨⎧-=++=)()()2()()()(2121k X W k X N k X k X W k X k X kN k N 上式表明一个N 点的DFT 可以用两个N/2点的DFT 来表示。

（2）运算量 当MN2=时，共有M 级蝶形，每级N/2个蝶形，每个蝶形有1次复数乘法2次复数加法。

复数乘法：NN M N mF2log22==复数加法：NN NM a F2log==NN NN NFFT m DFT m F F 222log2log 2)()(==（3）蝶形运算⎪⎩⎪⎨⎧-=+=----)()()()()()(1111j X W k X j X j X W k X k X m pN m m m pN m m m表示第m 级迭代，k 和j 表示数据所在的行数，12-+=m k j ，m M k p -⋅=2。

FPGA FFT_IP核函数的使用说明一．基本性能特点：(1)采用基-4算法和基-4/2混合基算法；采用频域抽取方式(DIF)的FFT算法；(2)输入数据采用定点方式输入(输入数据为real、imag ，但没有exponent)，在运算过程中采用块浮点方式进行运算，使用块浮点结构能够获得最大的SNR 和最少逻辑需求之间的平衡；输出采用指数形式输出(即包含real、imag、exponent)，输出结果为：“数据”×（2^(-“指数”)）；(3)可以完成的FFT变换长度为2^m(6≤m≤14)，即64～16384点；数据位宽为8～24bits；(4)如果输入的数据向量不够N点（FFT设置中的转换长度，例如：1024等），则FFT_IP核函数会在输入数据的后面自动进行补0填充，扩展成N点的数据。

(5)输入、输出数据采用有符号复数表示，都采用自然排序方式；(6)支持单倍输出(Signal-output)和四输出(Quad-output)引擎(engine)；(7)多路I/O数据流模式：流(Streaming)、缓冲突发(Buffer Burst)、突发(Burst)；(8)Version_2.1.0版本的FFT_IP核函数采用的是Atlantic Interface接口协议；Version_7.2版本的FFT_IP核韩式采用的是Avalon Streaming(ST) Interface接口协议。

(9)Version_2.1.0版本不支持RTL级Modelsim仿真，Version_7.2版本支持。

也就是说，2.1.0版本的FFT_IP核函数不能再自己新建的工程中通过QuartusII调用Modelsim进行RTL的仿真。

二．IP_Core的参量设置：(1)Twiddle Precision表示的是旋转因子的位宽精度；Data Precision表示的是输入、输出数据位宽精度。

注意：旋转因子的位宽精度必须小于或等于数据的位宽精度；(2)在Complex Multiplier Implementation选择栏中的Structure列表中选择期望的复数乘法器结构复数乘法器可以使用4个实数乘法器和2个加法／减法器完成，或使用3个乘法器、5个加法器和一些附加的延时单元完成。

FFT 算法分析FFT 算法的基本原理是把长序列的DFT 逐次分解为较短序列的DFT 。

按照抽取方式的不同可分为DIT-FFT （按时间抽取）和DIF-FFT （按频率抽取）算法。

按照蝶形运算的构成不同可分为基2、基4、基8以及任意因子（2n,n 为大于1的整数），基2、基4算法较为常用。

基2、DIT-FFT （按时间抽取）：-1/21/212(21)/21/21/2/2()() ()()(2)(21)(2)(21)N knNn knknN Nn n N N k r k r NNr n N N kr k krN NN r n X k x n Wx n W x n W x r Wx r Wx r WWx r W ===--+==--====+=++=++∑∑∑∑∑∑∑偶数奇数000令/211/2(2)()N kr N r x r WX k -==∑，/212/2(21)()N krN r x r W X k -=+=∑，则有：1212()()()(/2)()()kN k NX k X k W X k X k N X k W X k =++=-蝶形运算单元如下所示：基2、DIF-FFT （按频率抽取）：-10/211/2/21/21(/2)/21/2/21/2()() ()()()(/2)[()(/2)](2)[()(/2)](21)[()(N knNn N N kn knNNn n N N N kn k n N NNn n N kN kn NNn N rnN n X k x n Wx n Wx n W x n Wx n N W x n Wx n N WX r x n x n N W X r x n x n N =--==--+==-=-===+=++=++=+++=-+∑∑∑∑∑∑∑00000/21/2/2)]N n rnN N n W W -=∑则有：12()()(/2)()[()(/2)]nNx n x n x n N x n x n x n N W =++=-+蝶形运算单元如下所示：由前面的分析可知，DIT （按时间抽取）算法与DIF （按频率抽取）算法没有本质上的区别，只是复数加减法与旋转因子乘法的次序有区别，两种方法的运算量是一样的。

快速傅⾥叶变换-基4时间抽取FFT算法matlab实现快速傅⾥叶变换-基4时间抽取FFT 算法matlab 实现作者姓名：李林摘要：FFT ( 快速傅⾥叶变换) 算法与DFT (离散傅⾥叶变换) 算法⽐较, 其运算量显著减少, ⽤计算机实现时速度⼤为提⾼。

但FFT 过程所需的运算量仍较可观, 常给数字信号的实时处理带来困难,理论和实践表明, 若要加快FFT 算法在计算机上的实现, 关键是得设法减少FFT 过程在乘法运算上的时间开销。

若改进算法, 减少过程中的乘法次数, 则⽆疑能加快FFT 的实现。

通常的FFT 幂法都是“基2 分解法” , 即长度为N 的DFT 序列由两个长度为2 / N 的DFT 序列的组合表⽰; ⽽这两个长度为2 / N 的DFT 序列各⾃⼜分别由两个长度为4 / N 的DFT 序列的组合表⽰ , 按照这⼀做法对序列进⾏反复分解, 直到每个序列的长度等于2为⽌。

这个分解、组合过程如同⼀棵标准⼆叉树。

按分解的逆过程进⾏组合运算便得到所要求的频谱序列)n ( F ,... , l , 0 (n ,1- N ) 整个变换过程共需要进⾏ N log 2 / N 2次复数乘法运算。

参考上述的分解、组合⽅法, 对序列进⾏“ 基4 分解” ,即长度为N 的DFT 序列由四个长度为4 / N 的DFT 序列组合表⽰。

关键词： FFT 基2分解法基4分解运算时间和精度⽬录⼀，前⾔1，实验⽬的2，题⽬要求3，考查要求⼆，基—4FFT算法原理1，基—4FFT定义：2，举例3,旋转因⼦kmW的性质N4,16点基4时间抽取FFT算法流图三，基—4FFT运算的实现1，算法分析2.算法流程图3.Matlab程序执⾏结果四，两种程序运算量分析和⽐较 1，matlab⾃带函数运算量分析2，基四FFT的运算量3，运算结果⽐较4，结果分析五，设计总结六，参考⽂献七，附录：⼀，前⾔1，实验⽬的:检查学⽣的综合应⽤能⼒。

FFT算法设计（含程序设计）简介快速傅里叶变换（FFT）是一种高效计算离散傅里叶变换（DFT）的算法，它的运算复杂度是O(nlogn)。

FFT在信号处理、图像处理、通信以及其他领域中广泛应用。

本文将介绍FFT算法的原理，并给出一个简单的FFT算法的程序设计示例。

FFT算法原理FFT算法基于DFT的性质，通过利用对称性和周期性，将一个长度为n的序列划分为多个规模较小的子序列，并对其进行逐步变换，最终得到整个序列的傅里叶变换结果。

FFT算法的核心思想是分治法，即将一个长度为n的序列划分为两个长度为n/2的子序列，然后对子序列分别进行FFT变换，再进行组合得到原序列的DFT。

具体的步骤如下：1. 如果n=1，DFT即为序列本身；2. 将长度为n的序列划分为两个长度为n/2的子序列，分别为序列A和序列B；3. 对序列A进行FFT变换得到A的傅里叶变换结果；4. 对序列B进行FFT变换得到B的傅里叶变换结果；5. 将A和B的傅里叶变换结果按照以下公式组合得到原序列的傅里叶变换结果：![FFT公式]()FFT算法程序设计示例下面是一个使用语言实现的简单FFT算法的程序设计示例：import cmathdef fft(x):N = len(x)if N <= 1:return xeven = fft(x[0::2])odd = fft(x[1::2])T = [cmath.exp(-2j cmath.pi k / N) odd[k] for k in range(N // 2)]return [even[k] + T[k] for k in range(N // 2)] + [even[k] T[k] for k in range(N // 2)]测试代码x = [1, 2, 3, 4]X = fft(x)print(X)以上代码实现了一个递归版本的FFT算法。

输入序列x为长度为2的幂次的复数序列，输出序列X为其傅里叶变换结果。

一、前言Fast Fourier Transform（FFT）是一种用来计算离散傅立叶变换（DFT）的算法。

radix-4 fft是一种基于四次根的FFT计算方法，它可以在一定程度上优化FFT的计算速度和效率。

本文将介绍radix-4 fft的计算原理，希望能够让读者对其有一个更深入的了解。

二、FFT算法概述1. DFT的定义离散傅立叶变换（DFT）是一种将离散的时域信号转换成离散的频域信号的变换方式。

它的定义如下：\[X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-j\frac{2\pi}{N}kn}\]其中，\(x[n]\)是输入的时域信号，\(X[k]\)是输出的频域信号。

2. FFT的概念FFT是一种用来加速DFT计算的算法。

它可以将DFT的复杂度从O(N^2)降低到O(NlogN)。

在很多实际应用中，FFT都被广泛应用于信号处理、通信系统等领域。

三、radix-4 fft的计算原理1. 基本思想radix-4 fft是一种基于四次根的FFT计算方法。

它的基本思想是将DFT的计算任务划分成多个子任务，然后利用四次根的性质来优化计算过程。

具体来说，它将一个长度为N的DFT计算分解成四个长度为N/4的DFT计算，然后通过一系列的旋转因子来完成计算。

2. 算法流程radix-4 fft的算法流程可以简单概括为以下几个步骤：- 将输入序列分成奇偶部分，分别进行DFT计算；- 利用四次根的性质对奇偶部分进行二次合并；- 利用旋转因子对合并后的结果进行变换；- 重复上述步骤直到计算完成。

3. 算法优化在radix-4 fft的计算过程中，有很多可以进行优化的地方。

可以利用指数函数的对称性来减少计算量；可以使用分块技术来提高内存访问效率；可以采用乘积累加技术来减少乘法运算次数等。

这些优化能够在一定程度上提高radix-4 fft的计算速度和效率。

四、结论radix-4 fft作为一种基于四次根的FFT计算方法，具有很强的计算优化能力。

7.6实验6：快速傅里叶变换-基4时间抽取FFT 算法matlab 实现7.6.1实验目的1.练习利用matlab6.5中工具箱中的信号处理函数2.熟悉快速傅里叶变换的基本原理3.熟悉基4DIT-FFT 运算的MATLAB 程序并运用7.6.2涉及函数信号处理函数X=fft(x)或者X=fft(x,N):自定义功能函数function [Xk]=DIF_FFT_4(xn,N)7.6.3实验原理与方法（基-4时域抽取算法与基-2时域抽取算法具有完全相同的实质，两者的差异仅源于基的选择不同。

）1 DIT-FFT 算法的基本原理有限长序列x (n )的N 点DFT 定义为：∑-==10 )()(N n n k N W n x k X ，式中N j N eW π2-=，其整数次幂简称为旋转因子。

N 符合2的整数幂，N 为2的几次幂，则需要进行几次分解。

碟形运算流图符号如下：2 DIT-FFT 算法的运算规律及编程思想为了编写DIT-FFT 算法的运算程序，首先要分析其运算规律，总结编程思想并绘出程序框图。

由右图可知，DIT-FFT 算法的运算过程很有规律。

2.1 原位计算对M N 2=点的FFT 共进行M 级运算，每级由N /2个蝶形运算组成。

在同一级中，每个蝶的输入数据只对本蝶有用，且输出节点与输入节点在同一水平线上，这就意味着每算完一个蝶后，所得数据可立即存入原输入数据所占用的数组元素(存储单元)，这种原位(址)计算的方法可节省大量内存。

2.2 蝶形运算实现FFT 运算的核心是蝶形运算，找出蝶形运算的规律是编程的基础。

for mm=1:m %将DFT 做m 次基2分解，从左到右，对每次分解作DFT 运算 Nmr=2^mm;u=1; %旋转因子u 初始化WN=exp(-j*2*pi/Nmr); %本次分解的基本DFT 因子WN ＝exp(-i*2*pi/Nmr)for n=1:Nmr/2 %本次跨越间隔内的各次碟形运算for k=n:Nmr:N %本次碟形运算的跨越间隔为Nmr=2^mmkp=k+Nmr/2; %确定碟形运算的对应单元下标(对称性)t=x(kp)*u; %碟形运算的乘积项x(kp)=x(k)-t; %碟形运算的加法项x(k)=x(k)+t;endu=u*WN; %修改旋转因子，多乘一个基本DFT 因子WN2.3 序列倒序为了保证运算输出的X (k )按顺序排列，要求序列x (n )倒序输入，即在运算前要先对输入的序列进行位序颠倒。