工程流体力学答案(陈卓如)第四章

第1章 绪论【1-1】500cm 3的某种液体，在天平上称得其质量为0.453kg ，试求其密度和相对密度。

【解】液体的密度3340.4530.90610 kg/m 510m V ρ-===⨯⨯ 相对密度330.906100.9061.010w ρδρ⨯===⨯ 【1-2】体积为5m 3的水，在温度不变的条件下，当压强从98000Pa 增加到4.9×105Pa 时，体积减少1L 。

求水的压缩系数和弹性系数。

【解】由压缩系数公式10-1510.001 5.110 Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 910111.9610 Pa 5.110pE β-===⨯⨯ 【1-3】温度为20℃，流量为60m 3/h 的水流入加热器，如果水的体积膨胀系数βt =0.00055K -1，问加热到80℃后从加热器中流出时的体积流量变为多少？ 【解】根据膨胀系数1t dV V dtβ=则2113600.00055(8020)6061.98 m /ht Q Q dt Q β=+=⨯⨯-+= 【1-4】用200升汽油桶装相对密度0.70的汽油。

罐装时液面上压强为98000Pa 。

封闭后由于温度变化升高了20℃，此时汽油的蒸汽压力为17640Pa 。

若汽油的膨胀系数为0.0006K -1，弹性系数为13.72×106Pa ，（1）试计算由于压力温度变化所增加的体积，（2）问灌装时汽油的体积最多不应超过桶体积的百分之多少？【解】（1）由1β=-=P pdV Vdp E可得，由于压力改变而减少的体积为6200176400.257L 13.7210⨯∆=-===⨯P p VdP V dV E 由于温度变化而增加的体积，可由1β=tt dV V dT得 0.000620020 2.40L β∆===⨯⨯=t t t V dV VdT（2）因为∆∆tp V V ，相比之下可以忽略由压力变化引起的体积改变，则由 200L β+=t V V dT得1198.8%200110.000620β===++⨯t V dT 【1-5】图中表示浮在油面上的平板，其水平运动速度为u =1m/s ，δ=10mm ，油品的粘度μ=0.9807Pa ·s ，求作用在平板单位面积上的阻力。

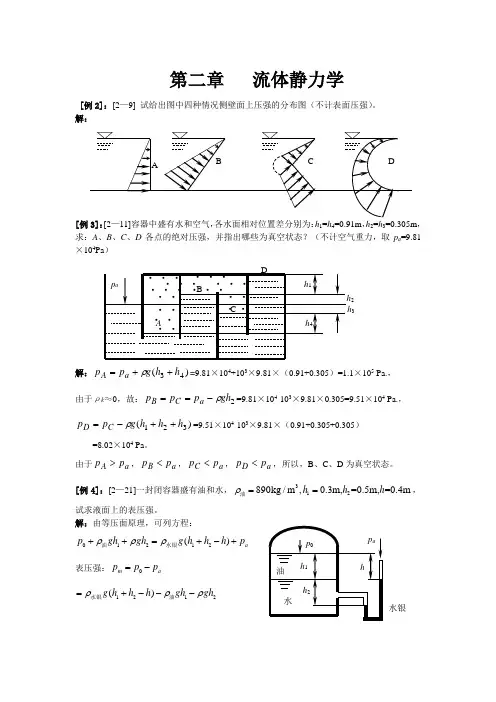
第四章 理想流体动力学和平面势流答案4－1 设有一理想流体的恒定有压管流，如图所示。

已知管径1212d d =，212d D =，过流断面1-1处压强p 1>大气压强p a 。

试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。

解：总水头线、测压管水头线，分别如图中实线、虚线所示。

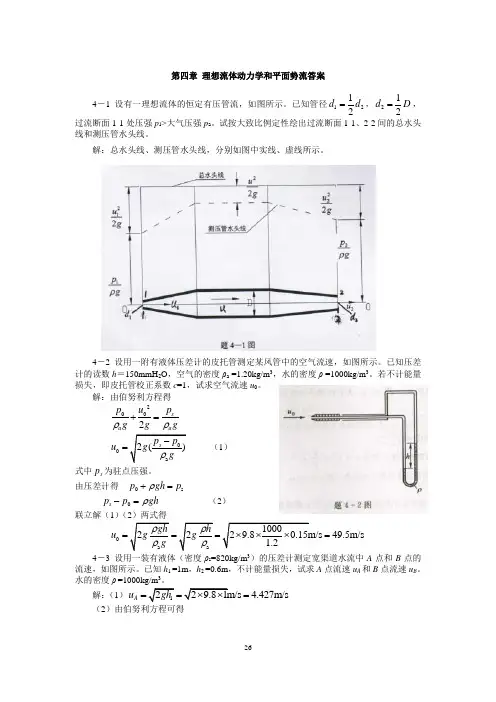
4－2 设用一附有液体压差计的皮托管测定某风管中的空气流速，如图所示。

已知压差计的读数h ＝150mmH 2O ，空气的密度ρa =1.20kg/m 3，水的密度ρ =1000kg/m 3。

若不计能量损失，即皮托管校正系数c =1，试求空气流速u 0。

解：由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=（1） 式中s p 为驻点压强。

由压差计得 0s p gh p ρ+=0s p p gh ρ-= （2）联立解（1）（2）两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4－3 设用一装有液体（密度ρs =820kg/m 3）的压差计测定宽渠道水流中A 点和B 点的流速，如图所示。

已知h 1 =1m ，h 2 =0.6m ，不计能量损失，试求A 点流速u A 和B 点流速u B 。

水的密度ρ =1000kg/m 3。

解：（1）1229.81m/s 4.427m/s A u gh ==⨯⨯= （2）由伯努利方程可得22A AA u p h g gρ+= （1）22B BB u p h g gρ+= （2）式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。

由（1）、（2）式可得2222A B A BA B p p u u h h g g gρ-=+-- （3） 由压差计得，22ρρρρ--++=A A s B B p gh gh gh gh p ，所以220.82A BA B p p h h h h gρ-=+-- (4) 由（3）式、（4）式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。

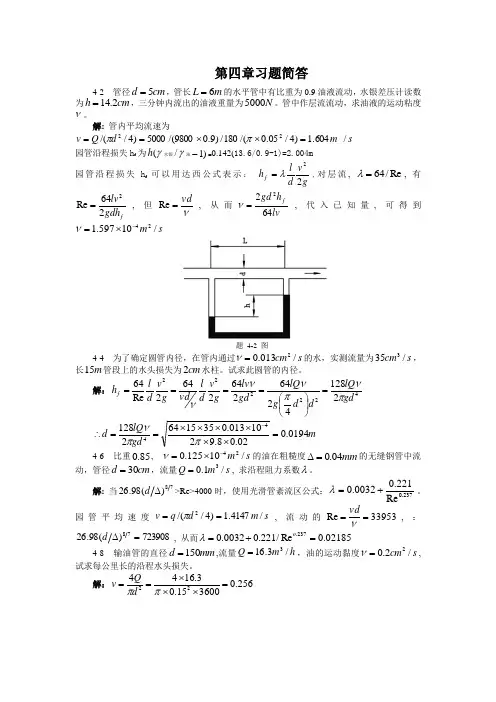
第四章习题简答4-2 管径cm d 5=，管长m L 6=的水平管中有比重为0.9油液流动，水银差压计读数为cm h 2.14=，三分钟内流出的油液重量为N 5000。

管中作层流流动，求油液的运动粘度ν。

解: 管内平均流速为s m d Q v /604.1)4/05.0/(180/)9.09800/(5000)4//(22=⨯⨯==ππ 园管沿程损失h f 为γ(h 水银γ/油)1-=0.142(13.6/0.9-1)=2.004m园管沿程损失h f 可以用达西公式表示： g v d l h f 22λ=,对层流, Re /64=λ, 有fgdh lv 264Re 2=, 但νvd =Re , 从而lv h gd f 6422=ν, 代入已知量, 可得到s m /10597.124-⨯=ν题 4-2 图4-4 为了确定圆管内径，在管内通过s cm /013.02=ν的水，实测流量为s cm /353，长m 15管段上的水头损失为cm 2水柱。

试求此圆管的内径。

解：422222212842642642642Re 64gd lQ d d g lQ gd lv g v d l vd g v d l h f πνπννν=⎪⎭⎫ ⎝⎛==== m gd lQ d 0194.002.08.9210013.0351********4=⨯⨯⨯⨯⨯⨯==∴-ππν 4-6 比重85.0s m /10125.024-⨯=ν的油在粗糙度mm 04.0=∆的无缝钢管中流动，管径cm d 30=，流量s m Q /1.03=, 求沿程阻力系数λ。

解: 当78)(98.26∆d >Re>4000时，使用光滑管紊流区公式：237.0Re221.00032.0+=λ。

园管平均速度s m d q v /4147.1)4//(2==π, 流动的33953Re ==νvd , ： 723908)(98.2678=∆d , 从而02185.0Re /221.00032.0237.=+=o λ4-8 输油管的直径mm d 150=,流量h m Q /3.163=，油的运动黏度s cm /2.02=ν,试求每公里长的沿程水头损失。

工程流体力学习题详解第一章 流体的物理性质【1－1】500cm 3的某种液体，在天平上称得其质量为0.453kg ，试求其密度和相对密度。

【解】3340.4530.90610 kg/m 510m V ρ-===⨯⨯ 330.906100.9061.010w ρδρ⨯===⨯【1－2】 体积为5m 3的水，在温度不变的条件下，当压强从98000Pa 增加到4.9×105Pa 时，体积减少1升。

求水的压缩系数和弹性系数。

【解】由压缩系数公式10510.001 5.110 1/Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 9111.9610 Pa 5.1pE β===⨯ 【1－3】温度为20℃，流量为60 m 3/h 的水流入加热器，如果水的体积膨胀系数βt =0.00055K -1，问加热到80℃后从加热器中流出时的体积流量变为多少？【解】根据膨胀系数1t dVV dtβ=则211t Q Q dt Q β=+3600.00055(8020)6061.98 m /h =⨯⨯-+=【1－4】图中表示浮在油面上的平板，其水平运动速度为u =1m/s ，δ=10mm ，油品的粘度μ=0.9807Pa·s ，求作用在平板单位面积上的阻力。

【解】根据牛顿内摩擦定律=du dy τμ则21=0.980798.07N/m 0.01τ⨯= 【1－5】已知半径为R 圆管中的流速分布为习题1-5图22=(1)r u c R-式中c 为常数。

试求管中的切应力τ与r 的关系。

【解】根据牛顿内摩擦定律=dudy τμ则2222=[(1)]d r r c c dr R Rτμμ-=-第二章 流体静力学【2－1】容器中装有水和空气，求A 、B 、C 和D 各点的表压力？【解】34342223232()()()(2)MA MB MA MC MB MD MC p g h h p p g h h h gh p p gh p p g h h g h h ρρρρρρ=+=-++=-==-=-+=-+【2－2】如图所示的U 形管中装有水银与水，试求：(1)A 、C 两点的绝对压力及表压力各为多少？ (2)求A 、B 两点的高度差h ？ 【解】(1) ()w 0.3ab A a p p g ρ=+⨯w 0.3MA p g ρ=⨯()w H 0.30.1ab C a p p g g ρρ=+⨯+⨯w H 0.30.1MC p g g ρρ=⨯+⨯(2)选取U 形管中水银的最低液面为等压面，则w H 0.3g gh ρρ⨯= 得 wH0.322 cm h ρρ⨯==【2－3】 在一密闭容器内装有水及油，密度分别为ρw 及ρo ，油层高度为h 1，容器底部装有水银液柱压力计，读数为R ，水银面与液面的高度差为h 2，试导出容器上方空间的压力p 与读数R 的关系式。

第1章 绪论【1-1】500cm 3的某种液体，在天平上称得其质量为0.453kg ，试求其密度和相对密度。

【解】液体的密度3340.4530.90610 kg/m 510m V ρ-===⨯⨯ 相对密度330.906100.9061.010w ρδρ⨯===⨯ 【1-2】体积为5m 3的水，在温度不变的条件下，当压强从98000Pa 增加到4.9×105Pa 时，体积减少1L 。

求水的压缩系数和弹性系数。

【解】由压缩系数公式10-1510.001 5.110 Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 910111.9610 Pa 5.110pE β-===⨯⨯ 【1-3】温度为20℃，流量为60m 3/h 的水流入加热器，如果水的体积膨胀系数βt =0.00055K -1，问加热到80℃后从加热器中流出时的体积流量变为多少？【解】根据膨胀系数1t dVV dtβ=则2113600.00055(8020)6061.98 m /ht Q Q dt Q β=+=⨯⨯-+= 【1-4】用200升汽油桶装相对密度0.70的汽油。

罐装时液面上压强为98000Pa 。

封闭后由于温度变化升高了20℃，此时汽油的蒸汽压力为17640Pa 。

若汽油的膨胀系数为0.0006K -1，弹性系数为13.72×106Pa ，（1）试计算由于压力温度变化所增加的体积，（2）问灌装时汽油的体积最多不应超过桶体积的百分之多少？【解】（1）由1β=-=P pdV Vdp E可得，由于压力改变而减少的体积为6200176400.257L 13.7210⨯∆=-===⨯P p VdP V dV E 由于温度变化而增加的体积，可由1β=t t dV V dT得 0.000620020 2.40L β∆===⨯⨯=t t t V dV VdT（2）因为∆∆tp VV ，相比之下可以忽略由压力变化引起的体积改变，则由 200L β+=tV V dT得1198.8%200110.000620β===++⨯t V dT 【1-5】图中表示浮在油面上的平板，其水平运动速度为u =1m/s ，δ=10mm ，油品的粘度μ=0.9807Pa ·s ，求作用在平板单位面积上的阻力。

工程流体力学课后习题答案(第二版)(总22页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章 绪论1-1．20℃的水，当温度升至80℃时，其体积增加多少 [解] 温度变化前后质量守恒，即2211V V ρρ= 又20℃时，水的密度31/23.998m kg =ρ 80℃时，水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2．当空气温度从0℃增加至20℃时，运动粘度ν增加15%，重度γ减少10%，问此时动力粘度μ增加多少（百分数）[解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了%1-3．有一矩形断面的宽渠道，其水流速度分布为μρ/)5.0(002.02y hy g u -=，式中ρ、μ分别为水的密度和动力粘度，h 为水深。

试求m h 5.0=时渠底（y =0）处的切应力。

[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =，y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4．一底面积为45×50cm 2，高为1cm 的木块，质量为5kg ，沿涂有润滑油的斜面向下作等速运动，木块运动速度u=1m/s ，油层厚1cm ，斜坡角 （见图示），求油的粘度。

[解] 木块重量沿斜坡分力F 与切力T 平衡时，等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5．已知液体中流速沿y 方向分布如图示三种情况，试根据牛顿内摩擦定律yud d μτ=，定性绘出切应力沿y 方向的分布图。

第一章[陈书1-15] 图轴在滑动轴承中转动，已知轴的直径cm D 20=，轴承宽度cm b 30=，间隙cm 08.0=δ。

间隙中充满动力学粘性系数s Pa 245.0⋅=μ的润滑油。

若已知轴旋转时润滑油阻力的损耗功率W P 7.50=，试求轴承的转速?=n 当转速min 1000r n =时，消耗功率为多少？（轴承运动时维持恒定转速）【解】轴表面承受的摩擦阻力矩为：2D M Aτ= 其中剪切应力：drdu ρντ= 表面积：Db A π=因为间隙内的流速可近似看作线性分布，而且对粘性流体，外表面上应取流速为零的条件，故径向流速梯度：δω2Ddr du = 其中转动角速度：n πω2=所以：2322nD D D nbM Db πμπμπδδ== 维持匀速转动时所消耗的功率为：3322D n bP M M n μπωπδ===所以：DbP D n μπδπ1=将： s Pa 245.0⋅=μm cm D 2.020== m cm b 3.030==m cm 410808.0-⨯==δW P 7.50=14.3=π代入上式，得：min r 56.89s r 493.1==n 当r 350min r 1000==n 时所消耗的功率为： W b n D P 83.6320233==δμπ[陈书1-16]两无限大平板相距mm 25=b 平行（水平）放置，其间充满动力学粘性系数s Pa 5.1⋅=μ的甘油，在两平板间以s m 15.0=V 的恒定速度水平拖动一面积为2m 5.0=A 的极薄平板。

如果薄平板保持在中间位置需要用多大的力？如果置于距一板10mm 的位置，需多大的力？【解】平板匀速运动，受力平衡。

题中给出平板“极薄”，故无需考虑平板的体积、重量及边缘效应等。

本题应求解的水平方向的拖力。

水平方向，薄板所受的拖力与流体作用在薄板上下表面上摩擦力平衡。

作用于薄板上表面的摩擦力为：A dz duA F uu u μτ== 题中未给出流场的速度分布，且上下两无限大平板的间距不大，不妨设为线性分布。

流体力学第四章参考答案流体力学是研究流体运动和力学性质的学科，它在工程学、物理学和地球科学等领域中具有重要的应用价值。

第四章是流体力学中的一个重要章节，主要讨论了流体的运动方程和流体的动力学性质。

在本文中，将对流体力学第四章的参考答案进行详细的论述和解释。

首先，我们来讨论流体的运动方程。

流体的运动方程是描述流体运动的基本方程，它包括连续性方程、动量方程和能量方程。

连续性方程描述了流体的质量守恒，即单位时间内通过某一截面的质量流量等于该截面内质量的减少量。

动量方程描述了流体的动量守恒，即单位时间内通过某一截面的动量流量等于该截面内动量的减少量。

能量方程描述了流体的能量守恒，即单位时间内通过某一截面的能量流量等于该截面内能量的减少量。

其次，我们来讨论流体的动力学性质。

流体的动力学性质包括粘性、密度、压力和速度等。

粘性是流体的一种性质，它描述了流体内部分子之间的摩擦力。

密度是流体的另一种性质，它描述了单位体积内的质量。

压力是流体的一种性质，它描述了单位面积上受到的力的大小。

速度是流体的运动状态，它描述了单位时间内流体通过某一截面的体积。

在解答流体力学问题时，我们需要根据具体情况选择合适的运动方程和动力学性质。

首先，我们可以根据问题中给出的条件和要求选择适当的运动方程。

例如，如果问题中要求求解流体的速度分布，则我们可以选择动量方程。

其次，我们可以根据问题中给出的条件和要求选择适当的动力学性质。

例如，如果问题中给出了流体的密度和压力分布，则我们可以选择密度和压力作为动力学性质。

在解答流体力学问题时，我们还需要运用一些基本的解题方法和技巧。

首先，我们可以利用物理规律和数学方法建立数学模型。

例如，我们可以利用连续性方程、动量方程和能量方程建立流体的运动方程。

其次，我们可以利用数学工具和计算方法求解数学模型。

例如，我们可以利用微积分和偏微分方程求解流体的运动方程。

最后，我们可以利用实验和观测数据验证数学模型和解题结果。

第一章 流体及其主要物理性质1-1.轻柴油在温度15ºC 时相对密度为0.83，求它的密度和重度。

解：4ºC 时所以，33/8134980083.083.0/830100083.083.0mN m kg =⨯===⨯==水水γγρρ1-2.甘油在温度0ºC 时密度为1.26g/cm3，求以国际单位表示的密度和重度。

333/123488.91260/1260/26.1m N g m kg cm g =⨯==⇒==ργρ 1-3.水的体积弹性系数为1.96×109N/m 2，问压强改变多少时，它的体积相对压缩1％？M P aPa E E VVVV p p6.191096.101.07=⨯==∆=∆=∆β 1-4.容积4m 3的水，温度不变，当压强增加105N/m 2时容积减少1000cm 3，求该水的体积压缩系数βp 和体积弹性系数E 。

解：1956105.2104101000---⨯=⨯--=∆∆-=Pa p V V p β Pa E p89104105.211⨯=⨯==-β 1-5石油相对密度0.9，粘度28cP ，求运动粘度为多少m 2/s?()c S t St s m 3131.0/101.310009.01028253==⨯=⨯⨯==--ρμν1-6 相对密度0.89的石油，温度20ºC 时的运动粘度为40cSt ，求动力粘度为多少？ 解：89.0==水ρρd ν＝40cSt ＝0.4St ＝0.4×10-4m 2/s μ＝νρ＝0.4×10-4×890＝3.56×10-2 Pa ·s1-7 图示一平板在油面上作水平运动，已知运动速度u=1m/s ，板与固定边界的距离δ=1mm ，油的动力粘度μ＝1.147Pa ·s ，由平板所带动的油层的运动速度呈直线分布，求作用在平板单位面积上的粘性阻力为多少？解：233/10147.11011147.1m N dy du ⨯=⨯⨯==-μτ 1-8 如图所示活塞油缸，其直径D ＝12cm ，活塞直径d ＝11.96cm ，活塞长度L ＝14cm ，油的μ＝0.65P ，当活塞移动速度为0.5m/s 时，试求拉回活塞所需的力F=？解：A ＝πdL , μ＝0.65P ＝0.065 Pa ·s , Δu ＝0.5m/s , Δy=(D-d)/2()N dy du AF 55.821096.11125.010141096.1114.3065.0222=⨯-⨯⨯⨯⨯⨯⨯==---μ第二章 流体静力学2-1. 如图所示的U 形管中装有水银与水，试求：（1）A 、C 两点的绝对压力及表压各为多少？ （2）A 、B 两点的高度差为多少？解：① p A 表＝γh 水＝0.3mH 2O ＝0.03at ＝0.3×9800Pa ＝2940Pap A 绝＝p a + p A 表＝（10+0.3）mH 2O ＝1.03at ＝10.3×9800Pa＝100940Pap C 表＝γhgh hg + p A 表＝0.1×13.6m H 2O+0.3mH 2O ＝1.66mH 2O ＝0.166at＝1.66×9800Pa ＝16268Pap C 绝＝p a + p C 表＝（10+1.66）mH 2O ＝11.66 mH 2O ＝1.166at ＝11.66×9800Pa ＝114268Pa ② 30c mH 2O ＝13.6h cmH 2O ⇒h ＝30/13.6cm=2.2cm题2-22-2 今有U 形管，内装水和四氯化碳（CCl 4），如图所示。

第四章作业答案4-3水在变直径竖管中流动，已知粗管直径 d 1=300mm ，流速v 1=6m/s 。

两断面相距3m,为使两断面的压力表读值相同。

试求细管直径（水头损失不计）。

解：221122122222112222p v p v Z Z g 2g g 2gp v p v v 6 300 3 4.837m v 9.74m/sg 2g g 2g 2g 2g lh ρρρρ++=+++++=+++=+=⇒=22221121v d v d d 300235.5mm ==== 4—4变直径管段AB ，d A =0.2m,d B =0.4m ，高差△h=1.5m ，测得p A =30kPa ，p B =40kPa ，B 点处断面平均流速v B =1.5m/s ，试判断水在管中的流动方向。

解：22222220.43061.5()6m/s 0 4.900.229.8240 1.51.5 5.69m29.819.6B A A A B A A A B B B B d p H z md g g g p H Z g g υυυρυρ==⨯==++=++==++=++= H B >H A , 水由B 流向A; 水头损失5.69-4.90=0.79m4—5用水银压差计测量水管中的点流速u ，如读值 △h=60mm ，（1）求该点流速；（2）若管中流体是30.8/kg m ρ=的油，△h 不变，不计水头损失，则该点的流速是多少？解：(1) 3.85m/s u ===(2) 4.34m/s u ===4—6 利用文丘里管的喉管处负压抽吸基坑中的积水，已经知道管道直径1100d mm =，喉管直径250d mm =，2h m =，能量损失忽略不计。

试求管道中流量至少为多大，才能抽出基坑中的积水？ 解：由题意知，只有当1212()()p pz z h g gρρ+-+=时，刚好才能把水吸上来，由文丘里流量计原理有Q =，其中211d k π=，代入数据，有12.7Q l s =。

(完整版)工程流体力学习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第1章 绪论选择题【1.1】 按连续介质的概念，流体质点是指：（a ）流体的分子；（b ）流体内的固体颗粒；（c ）几何的点；（d ）几何尺寸同流动空间相比是极小量，又含有大量分子的微元体。

解：流体质点是指体积小到可以看作一个几何点，但它又含有大量的分子，且具有诸如速度、密度及压强等物理量的流体微团。

（d ）【1.2】 与牛顿内摩擦定律直接相关的因素是：（a ）切应力和压强；（b ）切应力和剪切变形速度；（c ）切应力和剪切变形；（d ）切应力和流速。

解：牛顿内摩擦定律是d d v y τμ=，而且速度梯度d d v y 是流体微团的剪切变形速度d d t γ，故d d t γτμ=。

（b ）【1.3】流体运动黏度υ的国际单位是：（a ）m 2/s ；（b ）N/m 2；（c ）kg/m ；（d ）N·s/m 2。

解：流体的运动黏度υ的国际单位是/s m 2。

（a ）【1.4】理想流体的特征是：（a ）黏度是常数；（b ）不可压缩；（c ）无黏性；（d ）符合RTp=ρ。

解：不考虑黏性的流体称为理想流体。

（c ）【1.5】当水的压强增加一个大气压时，水的密度增大约为：（a ）1/20 000；（b ）1/1 000；（c ）1/4 000；（d ）1/2 000。

解：当水的压强增加一个大气压时，其密度增大约95d 1d 0.51011020 000k p ρρ-==⨯⨯⨯=。

（a ）【1.6】 从力学的角度分析，一般流体和固体的区别在于流体：（a ）能承受拉力，平衡时不能承受切应力；（b ）不能承受拉力，平衡时能承受切应力；（c ）不能承受拉力，平衡时不能承受切应力；（d ）能承受拉力，平衡时也能承受切应力。

解：流体的特性是既不能承受拉力，同时具有很大的流动性，即平衡时不能承受切应力。

【4-4】管路阀门关闭时，压力表读数为49.8kPa ，阀门打开后，读数降为9.8kPa 。

设从管路进口至装表处的水头损失为流速水头的2倍，求管路中的平均流速。

【解】当管路阀门关闭时，由压力表度数可确定管路轴线到自由液面的高度H 49.810 5.082m1109.8p H g ρ⨯===⨯⨯当管路打开时，列1-1和2-2断面的伯努利方程，则000222p v v H g g gρ++=+++35.0821 4.082m 2v pH ggρ=-=-= 5.164m/s v【沿变截面管路排出的质量流量Qm=14kg/s ，若d1=100mm ，d2=75mm ，d3=50mm ，不计损失，求所需的水头H ，以及第二段管段中央M 点的压力，并绘制测压管水头线。

【解】列1-1和3-3断面的伯努利方程，则00002v H g ++=++4143.171m/s11000 3.140.0754ρπ⨯===⨯⨯Q v d 4147.134m/s 11000 3.140.054ρπ⨯===⨯⨯Q v d 得 7.134 2.6m229.8===⨯v H g列M 点所在断面2-2和3-3断面的伯努利方程，则7.134 3.171100020.42kPa22ρ--==⨯=v v p 【4-9】由断面为0.2m2和0.1m2的两根管子组成的水平输水管系从水箱流入大气中：（1）若不计损失，①求断面流速v1及v2；②绘总水头线及测压管水头线；③求进口A 点的压力。

（2）计入损失：第一段的水头损失为流速水头的4倍，第二段为3倍，①求断面流速v1及v2；②绘制总水头线及测压管水头线；③根据所绘制水头线求各管段中间点的压力。

【解】（1）列自由液面和管子出口断面的伯努利方程，则00002vH g ++=++29.848.854m/s⨯⨯v又由 Av A v =1 4.427m/s =v 列A 点所在断面和管子出口断面的伯努利方程，则00022p v v gg gρ++=++8.854 4.427100029.398kPa 22ρ--==⨯=v v p （2）列自由液面和管子出口断面的伯努利方程，则43222v v v H g g g =++由 1122Av A v =得3.96m/s v =、1 1.98m/s v = 细管段中点的压力为：13 3.96(3)100011.76kPa 2222ρ⨯⨯=⨯⨯=v 粗管段中点的压力为：1.98(2)(2 3.96)100033.32kPa 22ρ+=⨯+⨯=v v 【4-10】用73.5×103W 的水泵抽水，泵的效率为90％，管径为0.3m ，全管路的水头损失为1m ，吸水管水头损失为0.2m ，试求抽水量、管内流速及泵前真空表的读数。