2013-2018年上海高考试题汇编-数列(最新整理)

2013年全国各地高考数学试题及解答分类汇编大全（06数列）一、选择题：1．(2013安徽文)设n S 为等差数列{}n a 的前n 项和，8374,2S a a ==-，则9a = （A ）6- （B ）4- （C ）2- （D ）2 【答案】A 【解析】188333636978()442226a a S a a a a a a d a a d +=⇒=⇒+=∴==-=+=-【考点定位】考查等差数列通项公式和前n 项公式的应用，以及数列基本量的求解.2．(2013福建理) 已知等比数列{}n a 的公比为q ，记(1)1(1)2(1)...,n m n m n m n m b a a a -+-+-+=+++*(1)1(1)2(1)...(,),n m n m n m n m c a a a m n N -+-+-+=⋅⋅⋅∈则以下结论一定正确的是（ ）A ．数列{}n b 为等差数列，公差为m qB ．数列{}n b 为等比数列，公比为2m qC ．数列{}n c 为等比数列，公比为2m q D ．数列{}n c 为等比数列，公比为mm q【答案】C【解析】等比数列{}n a 的公比为q,2222222,m m m mm m m a a a a aa ++++=⋅=⋅112...m c a a a =⋅⋅⋅,212...,m m m m c a a a +++=⋅⋅⋅321222...,m m m m c a a a +++=⋅⋅⋅2213c c c ∴=⋅∴数列{}n c 为等比数列，2221212211212............mm m m m m m m m ma a a a a a q c q q c a a a a a a +++⋅⋅⋅⋅⋅⋅⋅====⋅⋅⋅⋅⋅⋅Q 故选C3．(2013江西理) 等比数列x,3x ＋3,6x ＋6，…的第四项等于( ) A ．－24 B ．0 C ．12 D ．24 答案 A解析 由x,3x ＋3,6x ＋6成等比数列得，(3x ＋3)2＝x (6x ＋6)． 解得x 1＝－3或x 2＝－1(不合题意，舍去)． 故数列的第四项为－24.4．(2013辽宁文、理)下面是关于公差d ＞0的等差数列{a n }的四个命题： p 1：数列{a n }是递增数列；p 2：数列{na n }是递增数列；p 3：数列⎩⎨⎧⎭⎬⎫a n n 是递增数列；p 4：数列{a n ＋3nd }是递增数列．其中的真命题为( )A ．p 1，p 2B ．p 3，p 4C ．p 2，p 3D ．p 1，p 4 答案 D解析 a n ＝a 1＋(n －1)d ，d ＞0， ∴a n －a n －1＝d ＞0，命题p 1正确．na n ＝na 1＋n (n －1)d ，∴na n －(n －1)a n －1＝a 1＋2(n －1)d 与0的大小和a 1的取值情况有关． 故数列{na n }不一定递增，命题p 2不正确．对于p 3：a n n ＝a 1n ＋n －1n d ，∴a n n －a n －1n －1＝－a 1＋dn (n －1)，当d －a 1＞0，即d ＞a 1时，数列{a nn}递增，但d ＞a 1不一定成立，则p 3不正确． 对于p 4：设b n ＝a n ＋3nd ，则b n ＋1－b n ＝a n ＋1－a n ＋3d ＝4d ＞0.∴数列{a n ＋3nd }是递增数列，p 4正确． 综上，正确的命题为p 1，p 4.【解析2】设1(1)n a a n d dn m =+-=+，所以1P 正确；如果312n a n =-则满足已知，但2312n na n n =-并非递增所以2P 错；如果若1n a n =+，则满足已知，但11n a n n=+，是递减数列，所以3P 错；34n a nd dn m +=+，所以是递增数列，4P 正确5．(2013全国大纲文、理) 已知数列{a n }满足3a n ＋1＋a n ＝0，a 2＝43-，则{a n }的前10项和等于( )． A ．－6(1－3－10) B ．19(1－310) C ．3(1－3－10) D ．3(1＋3－10) 答案：C解析：∵3a n ＋1＋a n ＝0，∴a n ＋1＝13n a -.∴数列{a n }是以13-为公比的等比数列．∵a 2＝43-，∴a 1＝4.∴S 10＝101413113⎡⎤⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦+＝3(1－3－10)．故选C.6．(2013全国新课标Ⅱ理)等比数列{a n }的前n 项和为S n ，已知S 3＝a 2＋10a 1，a 5＝9，则a 1等于( )A.13 B ．－13 C.19 D ．－19 答案 C解析 设等比数列{a n }的公比为q ，由S 3＝a 2＋10a 1得a 1＋a 2＋a 3＝a 2＋10a 1，即a 3＝9a 1，q 2＝9，又a 5＝a 1q 4＝9，所以a 1＝19.7．(2013全国新课标Ⅰ文) 设首项为1，公比为23的等比数列{}n a 的前n 项和为n S ，则（ ） （A ）21n n S a =- （B ）32n n S a =- （C ）43n n S a =- （D ）32n n S a =-答案 D解析 S n ＝a 1(1－q n)1－q ＝a 1－q ·a n1－q＝1－23a n13＝3－2a n .故选D.8、(2013全国新课标Ⅰ理) 设等差数列{a n }的前n 项和为S n ，1m S -＝－2，m S ＝0，1m S +＝3，则m ＝ ( )A 、3B 、4C 、5D 、6【命题意图】本题主要考查等差数列的前n 项和公式及通项公式，考查方程思想，是容易题. 【解析】有题意知m S =1()2m m a a +=0，∴1a =－m a =－（m S -1m S -）=－2， 1m a += 1m S +-m S =3，∴公差d =1m a +-m a =1，∴3=1m a +=－2m +，∴m =5，故选C.9、(2013全国新课标Ⅰ理)设△A n B n C n 的三边长分别为a n ,b n ,c n ，△A n B n C n 的面积为S n ，n =1,2,3,…若b 1＞c 1，b 1＋c 1＝2a 1，a n ＋1＝a n ，b n ＋1＝c n ＋a n 2，c n ＋1＝b n ＋a n2，则( )A 、{S n }为递减数列B 、{S n }为递增数列C 、{S 2n －1}为递增数列，{S 2n }为递减数列D 、{S 2n －1}为递减数列，{S 2n }为递增数列 【命题意图】 【解析】B二、填空题：10．(2013安徽理)如图，互不-相同的点12,,,n A A X K K 和12,,,n B B B K K 分别在角O 的两条边上，所有n n A B 相互平行，且所有梯形11n n n n A B B A ++的面积均相等。

专题06 数列一．基础题组1. 【2014上海,理8】 设无穷等比数列{n a }的公比为q ，若)(lim 431 ++=∞→a a a n ，则q= .【考点】无穷递缩等比数列的和.2. 【2013上海,理10】设非零常数d 是等差数列x 1，x 2，…，x 19的公差，随机变量ξ等可能地取值x 1，x 2，…，x 19，则方程Dξ＝______.【答案】30|d |　3. 【2013上海,理17】在数列{a n }中，a n ＝2n －1.若一个7行12列的矩阵的第i 行第j 列的元素c ij ＝a i ·a j ＋a i ＋a j (i ＝1,2，…，7；j ＝1,2，…，12)，则该矩阵元素能取到的不同数值的个数为( )A ．18B ．28C ．48D ．63【答案】A 4. 【2012上海,理6】有一列正方体，棱长组成以1为首项、12为公比的等比数列，体积分别记为V 1，V 2，…，V n ，…，则12lim ()n n V V V →∞+++=…__________.【答案】875. 【2011上海,理18】设{a n }是各项为正数的无穷数列，A i 是边长为a i ，a i ＋1的矩形的面积(i ＝1，2，…)，则{A n }为等比数列的充要条件是( )A ．{a n }是等比数列B ．a 1，a 3，…，a 2n －1，…或a 2，a 4，…，a 2n ，…是等比数列C ．a 1，a 3，…，a 2n －1，…和a 2，a 4，…，a 2n ，…均是等比数列D ．a 1，a 3，…，a 2n －1，…和a 2，a 4，…a 2n ，…均是等比数列，且公比相同【答案】D6. 【2010上海,理11】将直线1l ：0nx y n +-=、2l ：0x ny n +-=（*n N ∈，2n ≥）x 轴、y 轴围成的封闭图形的面积记为n S ，则lim n n S →∞= ；【答案】1【点评】本题将直线与直线的位置关系与数列极限结合，考查两直线的交点的求法、两直线垂直的充要条件、四边形的面积计算以及数列极限的运算法则，是本次考题的一个闪光点.7. (2009上海,理12)已知函数f(x)=sinx+tanx,项数为27的等差数列{a n }满足a n ∈(2π-,2π),且公差d≠0.若f(a 1)+f(a 2)+…+f(a 27)=0,则当k=__________时,f(a k )=0.【答案】148. (2009上海,理23)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分8分.已知{a n }是公差为d 的等差数列,{b n }是公比为q 的等比数列.(1)若a n =3n+1,是否存在m 、k∈N *,有a m +a m+1=a k ?说明理由;(2)找出所有数列{a n }和{b n },使对一切n∈N *,n nn b a a =+1,并说明理由;(3)若a1=5,d=4,b1=q=3,试确定所有的p,使数列{a n}中存在某个连续p项的和是数列{b n}中的一项,请证明.【答案】(1)不存在;(2) {a n}为非零常数列,{b n}为恒等于1的常数列;(3)参考解析9. 【2008上海,理14】 若数列{a n }是首项为1，公比为a －的无穷等比数列，且{a n }各项的和为a ，则a 32的值是（ ） A ．1 B ．2 C ． D ．1254【答案】B10. 【2005上海,理12】用n 个不同的实数n a a a ,,,21 可得到!n 个不同的排列，每个排列为一行写成一个!n 行的数阵。

数列一、选择题1.辽宁4、下面关于公差d>0的等差数列{}n a 的四个命题：P1：数列{}n a 是递增数列； P2：数列{}n na 是递增数列P3：数列n a n ⎧⎫⎨⎬⎩⎭是递增数列； P4：数列{}+3n a nd 是递增数列。

其中的真命题为( )A ．P1，P2 B. P3，P4 C. P2，P3 D. P1，P42.全国（3）等比数列{a n }的的前n 项和为S n ，已知S 3 = a 2 +10a 1 ，a 5 = 9，则a 1 =( )（A ）13 （B ）- 13 （C ）19 （D ）- 193.福建9. 已知等比数列{}n a 的公比为q ，记m n m n m n m n a a a b +-+-+-+⋅⋅⋅++=)1(2)1(1)1(，m n m n m n m n a a a b +-+-+-*⋅⋅⋅**=)1(2)1(1)1(，()*,N n m ∈，则以下结论一定正确的是（ ）A. 数列{}n b 为等差数列，公差为m q B. 数列{}n b 为等比数列，公比为m q 2 C. 数列{}n c 为等比数列，公比为2m q D. 数列{}n c 为等比数列，公比为m mq 4.江西3.等比数列x ，3x+3，6x+6，…的的第四项等于（ ）A.-24 B.0 C.12 D.24二、填空题5.全国（16）等差数列{a n }的前n 项和为S n ，已知S 10 = 0，S 15 = 25，则nS n 的最小值为 .6.北京10.若等比数列{a n }满足a 2＋a 4=20，a 3＋a 5=40，则公比q = ；前n 项和S n = .7.重庆（12）已知{}n a 是等差数列，11a =，公差0d ≠，n S 为其前n 项和，若1a 、2a 、5a 称等比数列，则8S = ．8.陕西14. 观察下列等式:211=22123-=-2221263+-=2222124310-+-=-…照此规律, 第n 个等式可为 .9.湖北14.古希腊毕达哥拉斯学派的数学家研究过各种多边形数.如三角形数1,3,6,10,...，第n 个三角形数为2(1)11222n n n n +=+.记第n 个k 边形数为(,)(3)N n k k ≥，以下列出了部分k 边形数中第n 个数的表达式：三角形数 211(,3)22N n n n =+， 四边形数 2(,4)N n n =，五边形数 231(,5)22N n n n =-， 六边形数 2(,6)2N n n n =-，…可以推测(,)N n k 的表达式，由此计算(10,24)N = .10.安徽（14）如图，互不相同的点12,,,n A A X 和12,,,n B B B 分别在角O 的两条边上，所有n n A B 相互平行，且所有梯形11n n n n A B B A ++的面积均相等。

（2018年全国一·文科）17．（12分）已知数列{}n a 满足11a =，()121n n na n a +=+，设nn a b n=． （1）求123b b b ，，； （2）判断数列{}n b 是否为等比数列，并说明理由； （3）求{}n a 的通项公式．（2018年全国二·文科）17．（12分） 记为等差数列的前项和，已知，． （1）求的通项公式； （2）求，并求的最小值．（2018年全国三·文科）17．（12分）等比数列中，． （1）求的通项公式；（2）记为的前项和．若，求．（2018年北京·文科）（15）（本小题13分）设{}n a 是等差数列，且123ln 2,5ln 2a a a =+=. （Ⅰ）求{}n a 的通项公式； （Ⅱ）求12e e e n a a a +++L .（2018年天津·文科）（18）（本小题满分13分）设{a n }是等差数列，其前n 项和为S n （n ∈N *）；{b n }是等比数列，公比大于0，其前n 项和为T n （n ∈N *）．已知b 1=1，b 3=b 2+2，b 4=a 3+a 5，b 5=a 4+2a 6． （Ⅰ）求S n 和T n ；（Ⅱ）若S n +（T 1+T 2+…+T n ）=a n +4b n ，求正整数n 的值．n S {}n a n 17a =-315S =-{}n a n S n S {}n a 15314a a a ==，{}n a n S {}n a n 63m S =m（2018年江苏）14．已知集合*{|21,}A x x n n ==-∈N ，*{|2,}n B x x n ==∈N ．将A B U 的所有元素从小到大依次排列构成一个数列{}n a ．记n S 为数列{}n a 的前n 项和，则使得112n n S a +>成立的n 的最小值为 ▲ ．（2018年浙江）10．已知1234,,,a a a a 成等比数列，且1234123ln()a a a a a a a +++=++．若11a >，则A ．1324,a a a a <<B ．1324,a a a a ><C ．1324,a a a a <>D ．1324,a a a a >>（2018年上海）20．（本题满分15分）已知等比数列{a n }的公比q >1，且a 3+a 4+a 5=28，a 4+2是a 3，a 5的等差中项．数列{b n }满足b 1=1，数列{（b n +1−b n ）a n }的前n 项和为2n 2+n ． （Ⅰ）求q 的值；（Ⅱ）求数列{b n }的通项公式．高考一、考试中途应饮葡萄糖水大脑是记忆的场所，脑中有数亿个神经细胞在不停地进行着繁重的活动,大脑细胞活动需要大量能量。

全国高考理科数学试题分类汇编4：数列一、选择题1 （高考上海卷（理））在数列{}n a 中,21nn a =-,若一个7行12列的矩阵的第i 行第j 列的元素,i j i j i j a a a a a =⋅++,(1,2,,7;1,2,,12i j ==)则该矩阵元素能取到的不同数值的个数为( )(A)18 (B)28 (C)48 (D)63*A.2 （大纲版数学（理）WORD 版含答案（已校对））已知数列{}n a 满足12430,3n n a a a ++==-,则{}n a 的前10项和等于(A)()10613--- (B)()101139-- (C)()10313-- (D)()1031+3-*C 3 （高考新课标1（理））设n n n A B C ∆的三边长分别为,,n n n a b c ,n n n A B C ∆的面积为n S ,1,2,3,n =,若11111,2b c b c a >+=,111,,22n n n n n n n n c a b a a a b c +++++===,则( ) A.{S n }为递减数列 B.{S n }为递增数列 C.{S 2n -1}为递增数列,{S 2n }为递减数列 D.{S 2n -1}为递减数列,{S 2n }为递增数列*B 4 （安徽数学（理）试题）函数=()y f x 的图像如图所示,在区间[],a b 上可找到(2)n n ≥个不同的数12,...,,n x x x 使得1212()()()==,n nf x f x f x x x x 则n 的取值范围是(A){}3,4 (B){}2,3,4 (C) {}3,4,5 (D){}2,3*B5 （福建数学（理）试题）已知等比数列{}n a 的公比为q,记(1)1(1)2(1)...,n m n m n m n m b a a a -+-+-+=+++*(1)1(1)2(1)...(,),n m n m n m n m c a a a m n N -+-+-+=∙∙∙∈则以下结论一定正确的是( )A.数列{}n b 为等差数列,公差为m q B.数列{}n b 为等比数列,公比为2m qC.数列{}n c 为等比数列,公比为2m qD.数列{}n c 为等比数列,公比为m m q *C 6 （新课标Ⅱ卷数学（理））等比数列{}n a 的前n 项和为n S ,已知12310a a S +=,95=a ,则=1a (A)31 (B)31- (C)91 (D)91-*C 7 （高考新课标1（理））设等差数列{}n a 的前n 项和为11,2,0,3n m m m S S S S -+=-==,则m =( ) A.3 B.4 C.5D.6*C 8 （辽宁数学（理）试题）下面是关于公差0d >的等差数列()n a 的四个命题:{}1:n p a 数列是递增数列；{}2:n p na 数列是递增数列； 3:n a p n ⎧⎫⎨⎬⎩⎭数列是递增数列； {}4:3n p a nd +数列是递增数列； 其中的真命题为(A)12,p p (B)34,p p (C)23,p p (D)14,p p *D9 （高考江西卷（理））等比数列x,3x+3,6x+6,..的第四项等于A.-24B.0C.12D.24*A二、填空题10（高考四川卷（理））在等差数列{}n a 中,218a a -=,且4a 为2a 和3a 的等比中项,求数列{}n a 的首项、公差及前n 项和.*解:设该数列公差为d,前n 项和为n s .由已知,可得 ()()()21111228,38a d a d a d a d +=+=++. 所以()114,30a d d d a +=-=, 解得14,0a d ==,或11,3a d ==,即数列{}n a 的首相为4,公差为0,或首相为1,公差为3. 所以数列的前n 项和4n s n =或232n n n s -= 11（新课标Ⅱ卷数学（理））等差数列{}n a 的前n 项和为n S ,已知10150,25S S ==,则n nS 的最小值为________.*49-12（高考湖北卷（理））古希腊毕达哥拉斯学派的数学家研究过各种多边形数.如三角形数1,3,6,10,,第n 个三角形数为()2111222n n n n +=+.记第n 个k 边形数为(),N n k ()3k ≥,。

上海市各地市2013年高考数学 最新联考试题分类汇编（4）数列一、选择题:15．（上海市八校2013届高三下学期联合调研理）设等比数列{}n a 的前n 项和为n S ，则“10a >”是“32S S >”的 （ ） （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充要条件 （D ）既不充分又不必要条件 【答案】C17、(上海市奉贤区2013年1月高考一模理)（理）已知n S 是等差数列*{}()n a n N ∈的前n项和，且675S S S >>，有下列四个命题，假命题．．．的是（ ） A ．公差0d <； B ．在所有0<n S 中，13S 最大； C ．满足0>n S 的n 的个数有11个； D ．76a a >； 【答案】C17、(上海市奉贤区2013年1月高考一模文)（文）已知n S 是等差数列*{}()n a n N ∈的前n项和，且65S S <，876S S S >=，则下列结论错误的是 （ ）A ．6S 和7S 均为n S 的最大值.B ．07=a ；C ．公差0d <；D ．59S S >； 【答案】D 二、填空题:5．（上海市八校2013届高三下学期联合调研理）已知{}n a 为等差数列，其前n 项和为n S ，若36a =，312S =，则公差d = 。

【答案】24．（上海市八校2013届高三下学期联合调研文）已知{}n a 为等差数列，其前n 项和为n S ，若36a =，312S =，则公差d = 。

【答案】214．（上海市八校2013届高三下学期联合调研理）设等差数列{}n a 满足：公差*d N ∈，*n a N ∈，且{}n a 中任意两项之和也是该数列中的一项.若513a =，则d 的所有可能取值之和为 。

【答案】3644．（上海市黄浦区2013年4月高考二模理）等差数列{}n a 的前10项和为30，则14710a a a a +++=___________.【答案】125．（上海市黄浦区2013年4月高考二模文）等差数列{}n a 的前10项和为30，则14710a a a a +++= ．【答案】186、(上海市奉贤区2013年1月高考一模文理)设无穷等比数列{}n a 的前n 项和为S n ，首项是1a ，若∞→n lim S n ＝11a ，⎪⎪⎭⎫⎝⎛∈22,01a ，则公比q 的取值范围是 ． 【答案】⎪⎭⎫⎝⎛1,2114、(上海市奉贤区2013年1月高考一模理)（理）设函数()2cos f x x x =-，{}n a 是公差为8π的等差数列，125()()()5f a f a f a π++⋅⋅⋅+=，则=-5123)]([a a a f ． 【答案】21613π三、解答题: 23．（上海市黄浦区2013年4月高考二模理）(本题满分18分) 本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分. 已知数列{}n a 具有性质：①1a 为整数；②对于任意的正整数n ，当n a 为偶数时，12n n a a +=；当n a 为奇数时，112n n a a +-=. （1）若1a 为偶数，且123,,a a a 成等差数列，求1a 的值；（2）设123m a =+(3m >且m ∈N )，数列{}n a 的前n 项和为n S ，求证：123m n S +≤+；（3）若1a 为正整数，求证：当211log n a >+(n ∈N )时，都有0n a =. 【解析】⑴设12a k =，2a k =，则：322k a k +=，30a =分两种情况： k 是奇数，则2311022a k a --===，1k =，1232,1,0a a a === 若k 是偶数，则23022a ka ===，0k =，1230,0,0a a a === ⑵当3m >时，123123423,21,2,2,m m m m a a a a ---=+=+==45122,,2,1,0m m m m n a a a a a ++-======L L∴1124223n m m m S S +≤=++++=+L⑶∵211log n a >+，∴211log n a ->，∴112n a ->由定义可知：1,212,2nn n n n na a a a a a +⎧⎪⎪=≤⎨-⎪⎪⎩是偶数是奇数 ∴112n n a a +≤ ∴1211112112n n n n n n a a a a a a a a a ----=⋅⋅⋅≤⋅L ∴111212n n n a --<⋅= ∵n a N ∈，∴0n a =，综上可知：当211log n a >+()n N ∈时，都有0n a =23．（上海市黄浦区2013年4月高考二模文）（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分．已知数列{}n a 具有性质：①1a 为整数；②对于任意的正整数n ，当n a 为偶数时，12nn a a +=； 当n a 为奇数时，112n n a a +-=． （1）若164a =，求数列{}n a 的通项公式； （2）若123,,a a a 成等差数列，求1a 的值；（3）设123m a =-（3m ≥且m ∈N ），数列{}n a 的前n 项和为n S ，求证：125m n S m +≤--．解：（1）由61642a ==，可得522a =，432a =，…，162a =，072a =，81102a -==，90a =，…， 即{}n a 的前7项成等比数列，从第8起数列的项均为0． ……………………2分故数列{}n a 的通项公式为72(17,)0,(8,)n n n n a n n -⎧≤≤∈=⎨≥∈⎩, N N ． …………………4分（2）若14()Z a k k =∈时，1222a a k ==，232aa k ==，由123,,a a a 成等差数列，可知即2(2)4k k k =+，解得0k =，故10a =； 若141()Z a k k =+∈时，12122a a k -==，232aa k ==， 由123,,a a a 成等差数列，可知2(2)(41)k k k =++，解得1k =-，故13a =-；………7分 若142()Z a k k =+∈时，12212a a k ==+，2312a a k -==， 由123,,a a a 成等差数列，可知2(21)(42)k k k +=++，解得0k =，故12a =； 若143()Z a k k =+∈时，121212a a k -==+，2312a a k -==， 由123,,a a a 成等差数列，可知2(21)(43)k k k +=++，解得1k =-，故11a =-； ∴1a 的值为3,1,0,2--． ……………………10分 （3）由123m a =-（3m ≥），可得1121222m a a --==-， 223212m a a -==-，3341212m a a --==-， 若21()N*tk a t =-∈，则k a 是奇数，从而1112112122t t k k a a -+---===-，可得当31n m ≤≤+时，121m n n a -+=-成立． ……………………13分 又01210m a +=-=，20m a +=，…故当n m ≤时，0n a >；当1n m ≥+时，0n a =． ……………………15分 故对于给定的m ，n S 的最大值为12m a a a +++L1231(23)(22)(21)(21)(21)m m m m ---=-+-+-+-++-L1211(2222)325m m m m m m --+=++++--=--L ，故125m n S m +≤--． ……………………18分23．（上海市闵行区2013年高考二模理）（本题满分18分）本题共有3个小题，第(1)小题满分4分，第(2)小题满分6分，第(3)小题满分8分．xy OP 1P 2P 3Q 1Q 3Q 2 P 4如图，过坐标原点O 作倾斜角为60o的直线交抛物线2:y x Γ=于1P 点，过1P 点作倾斜角为120o 的直线交x 轴于1Q 点，交Γ于2P 点；过2P 点作倾斜角为60o的直线交x 轴于2Q 点，交Γ于3P 点；过3P 点作倾斜角为120o的直线，交x 轴于3Q 点，交Γ于4P 点；如此下去……．又设线段112231n n OQ Q Q Q Q Q Q -，，，，，L L 的长分别为123,,,,,n a a a a L L ，11122OPQ Q P Q ∆∆，，2331n n n Q PQ Q P Q -∆∆，，，L L 的面积分别为123,,,,,,n G G G G L L 数列{}n a 的前n 项的和为n S ．（1）求12,a a ； （2）求n a ，limnn nG S →∞；（3）设(01)n an b a a a =>≠且，数列{}n b 的前n 项和为n T ，对于正整数,,,p q r s ，若p q r s <<<，且p s q r +=+，试比较p s T T ⋅与q r T T ⋅的大小．23．（上海市闵行区2013年高考二模文）（本题满分18分）本题共有3个小题，第(1)小题满分4分，第(2)小题满分6分，第(3)小题满分8分．过坐标原点O 作倾斜角为60o的直线交抛物线2:y x Γ=于1P 点，过1P 点作倾斜角为120o 的直线交x 轴于1Q 点，交Γ于2P 点；过2P 点作倾斜角为60o 的直线交x 轴于2Q 点，交Γ于3P 点；过3P 点作倾斜角为120o的直线，交x 轴于3Q 点，交Γ于4P 点；如此下去……．又设线段112231n n OQ Q Q Q Q Q Q -，，，，，L L 的长分别为123,,,,,n a a a a L L ，数列{}n a 的前n 项的和为n S ．（1）求12,a a ； （2）求n a ，n S ；xyOP 1 P 2P 3Q 1Q 3Q 2P 4又3sin 602n n y a a =⋅=o，故131112n n a S -=++ 从而21324n n n a a S --= ……① ……………………………………………2分 由①有211324n n n a a S ++-= ……②②-①得22113()2()4n n n n n a a a a a ++---=即11()(332)0n n n n a a a a +++--=，又0n a >，于是123n n a a +-= 所以{}n a 是以23为首项、23为公差的等差数，12(1)3n a a n d n =+-= …………2分 （文）1()1(1)23n n a a n S n n +==+ ………………………………文2分 （理）1()1(1)23n n a a n S n n +==+223349n n G a n ==，233lim lim 3(1)3n n n n G n S n n →∞→∞==+ ……………………理2分 法2：点1n Q -的坐标为1231(,0)n a a a a -+++⋅⋅⋅+，即点100(,0)(=0)n S Q S -点与原点重合，，所以直线1n n Q P -的方程为13()n y x S -=-或13()n y x S -=--因此，点(,)n P x y 的坐标满足213()n y x y x S -⎧=⎪⎨=-⎪⎩消去y 得213()n x S x --=，又12n n a x S -=+，所以213()22n n n a a S -=+，从而21324n n n a a S --= …① ……2分以下各步同法1法3：点1n Q -的坐标为1231(,0)n a a a a -+++⋅⋅⋅+，即点100(,0)(=0)n S Q S -点与原点重合，，所以13(,)22n nn n a a P S -+， 又13(,)22n n n n a a P S -+在抛物线2y x =上，得21342n n n a a S -=+ 即21324n n n a a S --= …………………………………………………………2分以下各步同法1（3）（文）因为2(1)231323n n n nb aa b a++==，所以数列{}n b 是正项等比数列，且公比2301q a =≠，首项2310b a q ==，2000(1)()dp p d q q q +=--22000000(1)(1)(1)(1)d p d p d d q q q q q q =--=--- …………… 2分 因为01a a >≠且，所以230001q a q =>≠且，又d 为正整数，所以0(1)d q -与20(1)dq -同号，故2000(1)(1)0---<p d dq q q ，所以，p s T T ⋅q r T T <⋅． ………………… 2分（理）因为2(1)231323n n n nb aa b a++==，所以数列{}n b 是正项等比数列，且公比2301q a =≠，首项2310b a q ==，则100(1)1p p b q T q -=-，100(1)1q q b q T q -=-，100(1)1r r b q T q -=-，100(1)1ss b q T q -=- …… 2分p s T T ⋅q r T T -⋅=21000020(1)(1)(1)(1)(1)p s q rb q q q q q ⎡⎤⋅-----⎣⎦-（注意00p s q r q q ++=） 21000020()()(1)q r p sb q q q q q ⎡⎤=⋅+-+⎣⎦- ………………………… 2分 而00000000()()()()q r p s q p s rq q q q q q q q +-+=---0000000(1)(1)(1)()p q p r s r q p p rq q q q q q q ---=---=--（注意q p s r -=-） 000000(1)(1)(1)(1)q p p r p p q p r p q q q q q q ----=--=--- ……………………… 2分因为01a a >≠且，所以230001q a q =>≠且 又,q p r p --均为正整数，所以0(1)q pq --与0(1)r pq --同号，故000(1)(1)0p q p r pq q q -----<，所以，p s T T ⋅q r T T <⋅．………………… 2分（第（3）问只写出正确结论的，给1分）22（理）解:（1）由题设，满足条件的数列5A 的所有可能情况有：（1）01210,,,,.； （2）01010,,,,.；（3）01010,,,,.-； （4）01210,,,,.---； （5）01010,,,,.-； （6）01010,,,,.--；2个起评，对2个1分，3个2分，4个3分，5个4分，6个5分（2）11k k k a a c ---=，由1)(21=--k k a a ，则11k c -=或11k c -=-（n k ≤≤2，k ∈*N ）， 6分211a a c -=， 322a a c -=， …11n n n a a c ---=，所以1121n n a a c c c -=++++L ． 7分 因为01==n a a ，所以1210n c c c -+++=L ，且n 为奇数， 8分121,,,n c c c -L 是由21-n 个1和21-n 个1-构成的数列． 9分 所以()()()121211-+++++++=m m c c c c c c A S ΛΛ12212)2()1(--+++-+-=m m c c c m c m Λ． 10分22、(上海市奉贤区2013年1月高考一模文)（文）等比数列．．．．{}n c 满足11410-+⋅=+n n n c c ，*N n ∈，数列{}n a 满足n a n c 2=11 （1）求{}n a 的通项公式；（5分）（2）数列{}n b 满足11n n n b a a +=⋅，n T 为数列{}nb 的前n 项和．求n n T ∞→lim ；（5分） （3）是否存在正整数(),1m n m n <<，使得1,,m n T T T 成等比数列？若存在，求出所有,m n的值；若不存在，请说明理由．（6分）22、解：（1）解：40,103221=+=+c c c c ，所以公比4=q 2分 10411=+c c 计算出21=c 3分 121242--=⋅=n n n c 4分 12-=∴n a n 5分（2）11122121n b n n ⎛⎫=- ⎪-+⎝⎭ 6分 于是11111112335212121n n T n n n ⎡⎤⎛⎫⎛⎫⎛⎫=-+-++-= ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎣⎦L 8分 n n T ∞→lim =21 10分。

近五年上海高考真题汇编 排列组合、二项式定理、概率、统计（2017秋2）若排列数4566⨯⨯=mP ，则____=m答案：3（2018春8）某校组队参加辩论赛，从6名学生中选出4人分别担任一、二、三、四辩．若其中学生甲必须参赛且不担任四辩，则不同的安排方法种数为__________． 答案：180（2017春11）设126a a a 、、、为123456、、、、、的一个排列，则满足1234563a a a a a a -+-+-=的不同排列的个数为______答案：48（2014年）为强化安全意识，某商场拟在未来的连续10天中随机选择3天进行紧急疏散演练，则选择的三天恰好为连续3天的概率是_____(结果用最简分数表示) 知识点：计数原理，等可能事件及其概率计算 解析：连续10天中随机选择3天的选法种数为310C 种三天恰好为连续3天的选法种数为8种，所以概率为18310115C C =（2009春10）一只猴子随机敲击只有26个小写英文字母的练习键盘. 若每敲1次在屏幕上出现一个字母，它连续敲击10次，屏幕上的10个字母依次排成一行，则出现单词“monkey”的概率为 .（结果用数值表示）答案：6265（2015理8文10）在报名的3名男老师和6名女老师中，选择5人参加义务献血，要求男、女教师都有，则不同的选取方式的种数为_______(结果用数值表示)答案：120（2011春12）2011年上海春季高考有8所高校招生，如果某3位同学恰好被其中2所高校录取，那么录取方法的种数为 .答案：第一步：从8所高校取2所高校的方法有28C 28=种，第二步：3位同学分配到2所高校的方法有2位同学被分配到同一所高校，所以有2132C C 6=种，所以录取方法的种数为286168⨯=种．（2010理14）以集合{},,,Ua b c d =的子集中选出4个不同的子集，需同时满足以下两个条件：(1),U ∅都要选出；（2）对选出的任意两个子集A 和B ，必有A B ⊆或B A ⊆，那么共有_________种不同的选法 知识：分类计数原理解：由条件（1）知，本题本质上找两个非空真子集，根据子集含元素的个数分类 A 集合含1元素，B 集合含2个元素，共114312C C =种选法 A 集合含1元素，B 集合含3个元素，共124312C C =种选法 A 集合含2元素，B 集合含3个元素，共214212C C =种选法所以由分类计数原理得共有36种选法（2010文10）从一副混合后的扑克牌（52张）中随机抽取2张，则“抽出的2张均为红桃”的概率为 .（结果用最简分数表示）答案：基本事件总数为2525251265121n C ⨯===⨯⨯，红桃共13张，抽出的2张均为红桃的事件数为213136m C ==⨯，所以“抽出的2张均为红桃”的概率为1361265117m P n ⨯===⨯ （2018秋9）有编号互不相同的五个砝码，其中5克、3克、1克砝码各一个，2克砝码两个，从中随机选取三个，则这三个砝码的总质量为9克的概率是 （结果用最简分数表示）答案：15（2016理14）如图，在平面直角坐标系xOy 中，O 为正八边形128A A A 的中心，1(1,0)A ．任取不同的两点i A 、j A ，点P 满足0i j OP OA OA ++=，则点P 落在第一象限的概率是__________．答案：528（2014年）为强化安全意识，某商场拟在未来的连续10天中随机选择3天进行紧急疏散演练，则选择的三天恰好为连续3天的概率是_____(结果用最简分数表示)知识点：计数原理，等可能事件及其概率计算解析：连续10天中随机选择3天的选法种数为310C 种三天恰好为连续3天的选法种数为8种，所以概率为18310115C C =（2013年文理）盒子中装有编号为1，2,3,4,5,6,7,8,9的九个球，从中任意取出两个，则这两个球的编号之积为偶数的概率是_________(结果用最简分数表示)答案：1318知识点：对立事件和等可能事件及其概率计算解析：从1,2,3,4,5,6,7,8,9,九个球中，任意取出两个球的取法种数为2936C =种记A ：取出的两个球的编号之积为偶数则A 的对立事件A ：取出的两个球的编号之积为奇数，相当于从编号为1,3,5,7,9,这五个球中取出2个球，取法种数为2510C =，所以()1053618P A ==，()51311818P A =-=（2012文理）三位同学参加跳高、跳远、铅球项目的比赛，若每人都选择其中两个项目，则有且仅有两人选择的项目完全相同的概率是_______________(结果用最简分数表示)知识点：分步计数原理和等可能事件的概率及其计算方法解：每个同学都有三种选择：跳高与跳远；跳高和铅球；跳远和铅球，三个同学共有33327⨯⨯=种有且仅有两人选择的项目完全相同的选取过程是 第一步从3个同学中选2个同学，即23C 种第二步从三种比赛项目组合中选一个分配给这两名同学，即13C 种 第三步从剩余的两个项目组合中选一个分配给余下的1名同学所以选取方法共有21133218C C C⨯⨯=种故有且仅有两人选择的项目完全相同的概率是182 273=故答案为：2 3试一试：（2016文11）某食堂规定，每份午餐可以在四种水果中任选两种，则甲、乙两同学各自所选的两种水果相同的概率为_____答案：1（2011理12文13）随机抽取9个同学中，至少有2个同学在同一月出生的概率是.（默认每月天数相同，结果精确到0.001）答案：0.985（2010理9）从一副混合后的扑克牌（52张）中随机抽取1张，事件A为“抽得红桃K”，事件B为“抽得黑桃”，则概率()P A B=________（结果用最简分数表示）答案：7 26（2013文19）10(1)x+的二项展开式中的一项是（）.A45x.B290x.C3120x D.4252x 答案：C+)10x的2x项1.80,1.69,1.77，则这组数据的中位数是_________（米）答案：1.76（2014年高考文5）某校高一、高二、高三分别有学生1600名、1200名、800名．为了解该校高中学生的牙齿健康状况，按各年级的学生数进行分层抽样．若高三抽取20名学生，则高一、高二共需抽取的学生数为．答案：70（2013年高考文6）某学校高一年级男生人数占该年级学生人数的40%．在一次考试中，男、女生平均分数分别为75、80，则这次考试该年级学生平均分数为.答案：78（2010年高考文5）将一个总数为A、B、C三层，其个体数之比为5:3:2.若用分层抽样方法抽取容量为100的样本，则应从C中抽取个个体.答案：20。

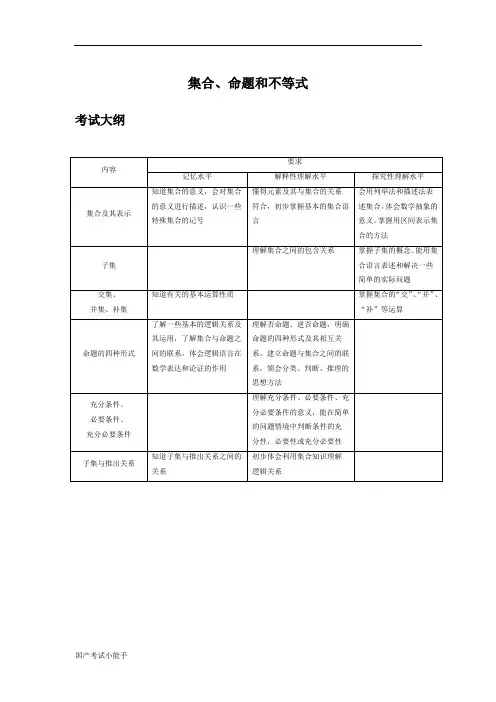
集合、命题和不等式考试大纲高考分析（1）单纯的集合交并补运算一般在填空题的前两个位置，但是集合是后面叙述函数，数列、解析几何、立体几何和排列组合的语言，所以要深刻理解集合的元素的性质，（2）逆否命题涉及到反证法，正难则反的逆向思维方法，在后面章节，尤其是计数原理、概率计算部分应用很（3）充分条件与必要条件一般在不等式、复数、数列等知识背景下的考察，需能区分充分条件与必要条件，能转化为推出关系，一般都在选择题中考一个，（4）在与数列，解析几何、立体几何等其他问题结合时要注意不等式有解，恒成立问题的识别，比如2017春18考了不等式恒成立问题，2014年理23题就是数列与不等式恒成立近五年上海高考真题汇编一、填空题（2018春1）不等式1x >的解集为__________． 答案：(,1)(1,)-∞-+∞（2018春3）设集合{|02}A x x =<<，{|11}B x x =-<<，则A B =__________．答案：(0,1)（2017秋1）已知集合}4,3,2,1{=A ，集合}5,4,3{=B ，则___=B A 答案：{}3,4（2017秋3）不等式11>-xx 的解集为_______ 答案：(),0-∞（2017秋12）如图，用35个单位正方形拼成个矩形，点4321,,,P P P P 以及四个标记为“∆”的点在正方形的顶点处，设集合{}4321,,,P P P P =Ω，点Ω∈P ，过P 作直线P l ，使得不在P l 上的“∆”的点分布在P l 的两侧；用)(1P l D 和)(2P l D 分别表示P l 一侧和另一侧的“∆”的点到P l 的距离之和；若过P 的直线P l 中有且只有一条满足)()(21P P l D l D =，则Ω中所有这样的P 为_____答案：134,,p p p 解析：证：过2P 的任意一条直线l 都满足条件四边形ABCD 为平行四边形，2P 是,AC BD 的交点，过2P 的任意一条直线l ，由5528,P P 到直线l 的距离之和等于D 到直线l 的距离的两倍；同理1241,P P 到直线l 的距离之和等于B 到直线l 的距离的两倍；而由于2P 为BD 的中点，故B D 、到直线l 的距离相等K 到直线l 的距离等于C到直线l 的距离的2倍K 到直线与L 到直线的距离之差等于C 到直线的距离的2倍（2017春1）设集合{}1,2,3A =，集合{}3,4B =，则A B =________ 答案：{}1,2,3,4（2017春2）不等式13x -<的解集为_____ 答案：()2,4-（2016理文1）设x R ∈，则不等式31x -<的解集为_______答案：()2,4（2015理1文2）设全集U R =，若集合{}{}1,2,3,4,|23A B x x ==≤<，则UAB =____ 答案：{}1,3,4(2013理12)设a为实常数，()y f x =是定义在R 上的奇函数，当0x <时，2()97a f x x x=++，若()1f x a ≥+对一切0x ≥成立，则a 的取值范围为________解析：由()y f x =是定义在R 上的奇函数知(0)0f =，01a ≥+，1a ≤-（1-1）当0x >时，()()()229797a a f x f x x x x x ⎡⎤=--=--++=+-⎢⎥-⎣⎦，2971a x a x +-≥+，2239a a x x -⨯≥+，82371,7a a a -⨯-≥+≤-（1-2） 结合（1-1）和（1-2），得88,,77a a ⎛⎤≤-∈-∞-⎥⎝⎦二、选择题（2018秋14）已知a ∈R ，则“1a >”是“11a<”的（ ）． （A ）充分非必要条件 （B ）必要非充分条件 （C ）充要条件 （D ）既非充分又非必要条件 【解析】（A ）（2018春15）记n S 为数列{}n a 的前n 项和．“{}n a 是递增数列”是“n S 为递增数列”的（ ） （A ）充分非必要条件 （B ）必要非充分条件（C ）充要条件（D ）既非充分也非必要条件答案：D（2017秋15）已知数列*2,N n c bn an x n ∈++=，使得k k k x x x +++300200100,,成等差数列的必要条件是 （ ）A. 0≥aB. 0≤bC. 0=cD. 02=+-c b a 答案：A（2017秋16）已知点P 在椭圆1436:221=+y x C ，点Q 在椭圆19:222=+x y C 上，O 为坐标原点，记OQ OP ⋅=ω，集合(){},|P Q OP OQ ω=⋅，当ω取得最大值时，集合中符合条件的元素有几个 （ ）A. 2个B. 4个C. 8个D. 无数个 答案：D（2017春14）设a R ∈，“0a >”是“10a>”的（ ）条件 A 、充分非必要 B 、必要非充分 C 、充要 D 、既非充分有非必要 答案：C（2016理15）设a R ∈，则“1a >”是“21a >”的（ ）． A 、充分非必要条件 B 、必要非充分条件C 、充要条件D 、即非充分又非必要条件 答案：A（2015理15）设12,z z C ∈，则“12z z 、中至少有一个数是虚数”是“12z z -是虚数”的（ ）． A 、充分非必要条件 B 、必要非充分条件C 、充要条件D 、即非充分又非必要条件 答案：B（2014理15）设,a b ∈R ，则“4a b +>”是“2a >且2b >”的（ ） (A) 充分条件. (B) 必要条件.(C) 充分必要条件.(D) 既非充分又非必要条件.答案：B（2013理15文16）设常数a R ∈，集合{|A x =(1)(x x -)a -0}≥，{|1}B x x a =≥-．若A B R =，则的取值范围为（ ）答案：B（2013文15理15）设常数a R ∈，集合()(){}{}10,1A x x x a B x x a =--≥=≥-，若a .A (,2)-∞.B (,2]-∞.C (2,)+∞.D [2,)+∞A B R =，则a 的取值范围为（ ）． A ．(),2-∞ B ．(],2-∞ C ．()2,+∞ D ．[)2,+∞答案：B（2013理16）钱大姐常说“便宜没好货”，她这句话的意思是：“不便宜”是“好货”的（ ）．.A 充分条件 .B 必要条件.C 充要条件 .D 既非充分也非必要条件答案：B 三、解答题（2017秋21）已知函数)(x f 满足：（1）R x ∈；（2）当21x x <时，)()(21x f x f ≤； （1）若1)(3+=ax x f ，求a 的范围；（2）若)(x f 是周期函数，求证：)(x f 是常值函数；（3）若)(x g 是R x ∈上的周期函数，且0)(>x g ，且)(x g 最大值为M ,)()()(x f x g x h ⋅=，求证：)(x h 是周期函数的充要条件是)(x f 是常值函数； 证：（3）必要性若()h x 是周期函数，记其一个周期为h T ，(){}A x g x M ==①若存在0x ，使得()00f x =，进而()00h x =，由()h x 的周期性，知()00,h h x kT k Z +=∈，而()g x 恒大于0，故()00h f x kT +=，所以对任意()00,1h h x x kT x k T ∈+++⎡⎤⎣⎦，再利用()f x 的单调增性可知，()0f x =恒成立②若存在1212,,x x x x >，使得()()120,0f x f x ><，则由题可知，12x x >，那么必然存在正整数1N 使得211k x N T x +>，∴()()211k f x N T f x +>，因为()()212k h x N T h x +=，但是()()()2121210k k k h x N T f x N T g x N T +=++>，()()()2220h x f x g x =<，矛盾综上，()0f x =恒成立或()0f x >恒成立或()0f x <恒成立③若()0f x >恒成立，第一步：任取0x A ∈，则必存在2N N ∈，使得020k g x N T x T -≤-，即[]00020,,g h x T x x N T x ⎡⎤-⊆-⎣⎦，()()()()()()000020202h h h h x g x f x h x N T g x N T f x N T ==-=--，∵()()002h g x M g x N T =≥- ，故()()002h f x f x N T ≤-， 再由单调性可知()()()0020h g f x f x N T f x T =-=-，第二步：用0g x T -代替第一步中的0x ，同理可得()()002g g f x T f x T -=-， 再用0g x T +代替第一步中的0x ，同理可得()()00+g f x T f x =，依次下去，可得()()()()()()000000322g g g g g f x T f x T f x T f x f x T f x T =-=-=-==+=+=利用单调性，可得()f x 为常数；④若()0f x <恒成立第一步：任取0x A ∈，则必存在3N N ∈，使得003g k x T x N T +≤+，即[]00002,g h x x T x x N T ⎡⎤+⊆+⎣⎦，，()()()()()()000030303h h h h x g x f x h x N T g x N T f x N T ==+=++，∵()()003h g x M g x N T =≥+ ，故()()003h f x f x N T ≥+， 再由单调性可知()()()0030h g f x f x N T f x T =+=+，第二步：用0g x T -代替第一步中的0x ，同理可得()()002g g f x T f x T +=+， 再用0g x T +代替第一步中的0x ，同理可得()()00g f x T f x -=，依次下去，可得()()()()()()000000322g g g g g f x T f x T f x T f x f x T f x T =-=-=-==+=+=利用单调性，可得()f x 为常数；（2016理23）若无穷数列{}n a 满足：只要*(,)p q a a p q N =∈，必有11p q a a ++=，则称{}n a 具有性质P .（1）若{}n a 具有性质P ，且12451,2,3,2a a a a ====，67821a a a ++=，求3a ； （2）若无穷数列{}n b 是等差数列，无穷数列{}n c 是公比为正数的等比数列，151b c ==，5181b c ==，n n n a b c =+判断{}n a 是否具有性质P ，并说明理由；（3）设{}n b 是无穷数列，已知*1sin ()n n n a b a n N +=+∈.求证：“对任意1,{}n a a 都具有性质P ”的充要条件为“{}n b 是常数列”.答案：（1）316a =；（2）由于15a a =，但26a a ≠，故{}n a 不具有性质P ；（3）证明： 必要性：若对于任意1a ，{}n a 都具有性质P ，则211sin a b a =+，设函数()()1,sin ,f x x b g x x =-= 由()(),f x g x 图像可得，对于任意的1b ，二者图像必有一个交点，所以一定能找到1a ，使得111sin a b a -=，所以2111sin a b a a =+=，所以1n n a a +=，故1211sin sin n n n n n n b a a a a b ++++=-=-=，故{}n b 是常数列（2017春18）设a R ∈，函数()221x x a f x +=+，（1）求a 的值，使得()f x 是奇函数； （2）若()22a f x +<对任意x R ∈成立，求a 的取值范围. 参考答案：（1）由()f x 的定义域为R ，且()f x 是奇函数，可得()00f =，即102a+=，解得1a =-， 此时()2121x x f x -=+，()()21122112x xx xf x f x -----===-++，即1a =-时，()f x 是奇函数；（2）()22a f x +<对任意x R ∈成立，即为22221x x a a ++<+对任意x R ∈成立， 等价于1221x a a-<+对任意x R ∈成立，（2014年理23）已知数列{}n a 满足1133n n n a a a +≤≤，*n ∈N ，11a =.(1)若2342,,9a a x a ===，求x 的取值范围； (2)设{}n a 是公比为q 的等比数列，12n n S a a a =+++. 若1133n n n S S S +≤≤，*n ∈N ，求q 的取值范围； (3)若12,,,k a a a 成等差数列，且121000k a a a +++=，求正整数k 的最大值，以及k 取最大值时相应数列12,,,k a a a 的公差.答案：（1）由条件得263x ≤≤且933xx ≤≤，解得36x ≤≤．所以x 的取值范围是[3,6]x ∈．（2）由133n n a a ≤，且110n n a a q -=≠，得0n a >，所以113n n S S +≤．又1133n n n a a a +≤≤，所以133q ≤≤．当1q =时，nS n =，11n Sn +=+，由13n n +≤得13n n S S +≤成立．当1q ≠时，13n n S S +≤．即111311n nq q q q+--≤⋅--． ① 若13q <≤，则(3)2n q q -≥．由nq q ≥，n N *∈，得(3)2q q -≥，所以12q <≤．① 若113q ≤<，则(3)2n q q -≤．由n q q ≤，n N *∈，得(3)2q q -≤，所以113q ≤<．综上，q 的取值范围为1,23⎡⎤⎢⎥⎣⎦． （3）设12,,k a a a 的公差为d ．由1133n n n a a a +≤≤，且11a =，国产考试小能手 得1[1(1)]13[1(1)]3n d nd n d +-≤+≤+-，1,2,,1n k =-．即(21)2,(23)2,n d n d +≥-⎧⎨-≥-⎩ 1,2,,1n k =-． 当1n =时，223d -≤≤； 当2,,1n k =-时，由222123n n -->+-，得221d n -≥+，所以22213d k -≥≥--． 所以()()111210002221k k k k ka d k k ---=+≥+⋅-，即2200010000k k -+≤，得1999k ≤． 所以k 的最大值为1999，1999k =时，12,,k a a a 的公差为11999-．。

数列（2018秋6）记等差数列{}n a 的前n 项和为n S ，若30a =，6714a a +=，则7S = 答案：14（2018春5）已知{}n a 是等差数列，若2810a a +=，则357a a a ++=__________．答案：1（2017秋15）已知数列*2,N n c bn an x n ∈++=，使得100200300,,k k k x x x +++成等差数列的必要条件是 （ ）A. 0≥aB. 0≤bC. 0=cD. 02=+-c b a 答案：A（2013年文22）已知函数，无穷数列满足，．（1）若，求；（2）若，且成等比数列，求的值；（3）是否存在，使得12,,,,n a a a L L 成等差数列？若存在，求出所有这样的1a ；若不存在，说明理由．解：（1）22a =，30a =，42a =．（2）21122a a a =-=-，321222a a a =-=--．① 当102a <≤时，()31122a a a =--=，所以()22112a a =-，得11a =．② 当12a >时，()311224a a a =--=-，所以()()211142a a a -=-，得12a =去）或12a =综合①②得11a =或12a =．（3）假设这样的等差数列存在，那么212a a =-，3122a a =--．由2132a a a =+得111222a a a -+-=（*）． 以下分情况讨论：()2f x x =-{}n a 1()n n a f a +=*n N ∈10a =234,,a a a 10a >123,,a a a 1a 1a① 当12a >时，由（*）得10a =，与12a >矛盾； ② 当102a <≤时，由（*）得11a =，从而1n a = ()1,2,n =L ，所以{}n a 是一个等差数列；③ 当10a ≤时，则公差()2111220da a a a =-=+-=>，因此存在2m ≥使得()1212m a a m =+->．此时120m m m m d a a a a +=-=--<，矛盾．综合①②③可知，当且仅当11a =时，123,,a a a L 构成等差数列．（2013理23）给定常数，定义函数．数列123,,,a a a L 满足，．（1）若，求及；（2）求证：对任意，；（3）是否存在，使得12,,,,n a a a L L 成等差数列？若存在，求出所有这样的；若不存在，说明理由．解：（1）232,10a a c ==+．（2）()8,33+8,8,x c f x x c x c ++⎧⎪=+⎨⎪---⎩,4,4.x c c x c x c ≥---≤<-<--当n a c ≥-时，18n n a a c c +-=+>； 当4n c a c --≤<-时，()12382438n n n a a a c c c c +-=++≥--++=；当4n a c <--时，()128248n nn a a a c c c c +-=---≥-----=．0c >()24f x x c x c=++-+1()n n a f a +=*n N ∈12a c =--2a 3a *n N ∈1n na a c +-≥1a 1a所以，对任意n N *∈，1n n a a c +-≥．方法二： 要证：24x c x c x c ++-+-≥ 24x c x c x c ++≥+++当0x c +<时，等式右边为0，不等式显然成立 当0x c +≥时，等式化为()()242x c x c ++≥+显然 （3）由（2），结合0c >得1n n a a +>，即{}n a 为无穷递增数列．又{}n a 为等差数列，所以存在正数M ，当n M >时，nac ≥-，从而，1()8n n n a f a a c +==++．由于{}n a 为等差数列，因此其公差8d c =+．① 若14a c <--，则211()8a f a a c ==---，又2118a a d a c =+=++，故1188a c a c ---=++，即18a c =--，从而20a =． 当2n ≥时，由于{}n a 为递增数列，故20naa c ≥=>-，所以，1()8n n n a f a a c +==++，而218aa c =++，故当18a c =--时，{}n a 为无穷等差数列，符合要求；② 若14c a c --≤<-，则211()338a f a a c ==++，又2118aa d a c =+=++，所以，113388a c a c ++=++，得1a c =-，舍去； ③ 若1a c ≥-，则由1n a a ≥得到1()8n n n a f a a c +==++，从而{}n a 为无穷等差数列，符合要求．综上，1a 的取值集合为[){},8c c -+∞--U ．（2015理17）记方程①：2110x a x ++=，方程②：2220x a x ++=，方程③：2340x a x ++=，其中123,,a a a 是正实数．当123,,a a a 成等比数列时，下列选项中，能推出方程③无实根的是（ ）A ．方程①有实根，且②有实根B ．方程①有实根，且②无实根C ．方程①无实根，且②有实根D ．方程①无实根，且②无实根 答案：B（2011理18）设{}n a 是各项为正数的无穷数列，i A 是边长为1,ii a a+的矩形面积（1,2,i =L ），则{}n A 为等比数列的充要条件为 （ ） A {}n a 是等比数列B 1321,,,,n a a a -L L 或242,,,,n a a a L L 是等比数列C 1321,,,,n a a a -L L 和242,,,,n a a a L L 均是等比数列D 1321,,,,n a a a -L L 和242,,,,n a a a L L 均是等比数列，且公比相同 答案：D（2016文22）对于无穷数列{}n a 与{}n b ，记*{|,}n A x x a n N ==∈，*{|,}n B x x b n N ==∈，若同时满足条件：① {}n a ，{}n b 均单调递增；② A B =∅I 且*A B N =U ，则称{}n a 与{}n b 是无穷互补数列．（1）若21n a n =-，42n b n =-，判断{}n a 与{}n b 是否为无穷互补数列，并说明理由；（2）若2n na =且{}n a 与{}nb 是无穷互补数列，求数列{}n b 的前16项的和；（3）若{}n a 与{}n b 是无穷互补数列，{}n a 为等差数列，且1636a =，求{}n a 与{}n b 的通项公式．【解】（1）因为4,4A B ∉∉，所以4A B ∉U ，从而{}n a 与{}n b 不是无穷互补数列． （2）因为416a =，所以416420b =+=． 数列{}n b 的前16项的和为：2345120(1220)(2222)20(22)1802++++-+++=⨯--=L ． （3）设{}n a 的公差为,d d N *∈，则1611536a a d =+=．由136151a d =-≥，得1d =或2． 若1d =，则121a =，20n a n =+，与“{}n a 与{}n b 是无穷互补数列”矛盾；若2d =，则16a =，24n a n =+，,525,5n n n b n n ≤⎧=⎨->⎩．综上，24na n =+，,525,5n n n b n n ≤⎧=⎨->⎩．（2014年理23）已知数列满足1133n n n a a a +≤≤，*n N ∈，11a =．（1）若2342,,9a a x a ===，求x 的取值范围；（2）设{}n a 是公比为q 的等比数列，12n n S a a a =+++L ．若1133n n n S S S +≤≤，*n N ∈，求q 的取值范围；（3）若12,,,k a a a L 成等差数列，且121000k a a a +++=L ，求正整数k 的最大值， 以及k 取最大值时相应数列12,,,k a a a L 的公差．解：（1）由条件得263x ≤≤且933xx ≤≤，解得36x ≤≤．所以x 的取值范围是[3,6]x ∈． （2）由133n n a a ≤，且110n n a a q -=≠，得0n a >，所以113n n S S +≤．又1133n n n a a a +≤≤，所以133q ≤≤．当1q =时，nS n =，11n Sn +=+，由13n n +≤得13n n S S +≤成立．当1q ≠时，13n n S S +≤．即111311n nq q q q+--≤⋅--． {}n a① 若13q <≤，则(3)2n q q -≥．由nq q ≥，n N *∈，得(3)2q q -≥，所以12q <≤．② 若113q ≤<，则(3)2n q q -≤．由n q q ≤，n N *∈，得(3)2q q -≤，所以113q ≤<．综上，q 的取值范围为1,23⎡⎤⎢⎥⎣⎦． （3）设12,,k a a a L 的公差为d ．由1133n n n a a a +≤≤，且11a =，得1[1(1)]13[1(1)]3n d nd n d +-≤+≤+-，1,2,,1n k =-L ．即(21)2,(23)2,n d n d +≥-⎧⎨-≥-⎩ 1,2,,1n k =-L ．当1n =时，223d -≤≤； 当2,,1n k =-L 时，由222123n n -->+-，得221d n -≥+，所以22213d k -≥≥--．所以()()111210002221k k k k ka d k k ---=+≥+⋅-，即2200010000k k -+≤，得1999k ≤． 所以k 的最大值为1999，1999k =时，12,,k a a a L 的公差为11999-．（2014文23）已知数列{}n a 满足1113,,13n n n a a a n N a *+≤≤∈=．（1）若1342,,9a a x a ===，求x 的取值范围；（2）设{}n a 是等比数列，且11000m a =，求正整数m 的最小值，以及m 取最小值时相应{}n a 的公比； （3）若12100,,,a a a L成等差数列，求数列12100,,,a a a L 的公差的取值范围．解：（1）由条件得263x ≤≤且933xx ≤≤，解得36x ≤≤．所以x 的取值范围是[3,6]x ∈． （2）设{}n a 的公比为q ．由133n n a a ≤，且110n n a a q -=≠，得0n a >．因为1133n n n a a a +≤≤，所以133q ≤≤．从而111111()10003m m m a q q ---==≥，131000m -≥，解得8m ≥．8m =时，1[,3]3q =．所以，m 的最小值为8，8m =时，{}n a（3）设数列12100,,a a a L 的公差为d ．由133n n n a a d a ≤+≤，223n n a d a -≤≤，1,2,,99n =L ．① 当0d >时，999821a a a a >>>>L ，所以102d a <≤，即02d <≤． ② 当0d =时，999821a a a a ====L ，符合条件． ③当d <时，999821a a a a <<<<L ，所以9999223a d a -≤≤，2(198)2(198)3d d d -+≤≤+， 又0d <，所以20199d -≤<．综上，12100,,a a a L 的公差的取值范围为2[,2]199-．（2012文14）已知，各项均为正数的数列满足，，若，则的值是 ．答案：解：由，，得， 由，得，，，，，依次类推，得全体偶数项相等， 所以 （2017春21）已知函数()21log 1xf x x+=- （1）解方程()1f x =；（2）设()()1,1,1,,x a ∈-∈+∞ 证明：()11,1ax a x-∈--，且()11ax f f x f a x a -⎛⎫⎛⎫-=- ⎪ ⎪-⎝⎭⎝⎭； 1()1f x x=+{}n a 11a =2()n n a f a +=20102012a a =2011a a +265133+11a =2()n n a f a +=312a =579112358,,,35813a a a a ====2()n n a f a +=211n n a a +=-20102012a a =2010201220101111a a a =-=-201012a -=20082010201011a a a =-=22010a a =2011813a a +==（3）在数列{}n x 中，()11,1x ∈-，()113113n n n nx x x ++-=--，n N *∈，求1x 的取值范围，使得3n x x ≥对任意n N *∈成立答案：（1）13x =； （3）11,3⎛⎤- ⎥⎝⎦；（2016理11）无穷数列{}na由k个不同的数组成，nS为{}n a的前n项和.若对任意*∈Nn，{}3,2∈n S ，则k 的最大值为______________.答案：4（2018春15）记n S 为数列{}n a 的前n 项和．“{}n a 是递增数列”是“n S 为递增数列”的（ ） （A ）充分非必要条件 （B ）必要非充分条件 （C ）充要条件（D ）既非充分也非必要条件答案：D（2015理22文23）已知数列{a n }与{b n }满足a n +1﹣a n =2（b n +1﹣b n ），n ∈N *． （1）若b n =3n+5，且a 1=1，求数列{a n }的通项公式； （2）设{a n }的第0n 项是最大项，即0n n a a ≥（n ∈N *），求证：数列{b n }的第0n 项是最大项；（3）设a 1=λ＜0，b n =λn （n ∈N *），求λ的取值范围，使得{a n }有最大值M 与最小值m ，且()2,2Mm∈-． 答案：（1）65n - ；（3）1,02⎛⎫- ⎪⎝⎭（2016年理23）若无穷数列{}n a 满足：只要*(,)pq a a p q N =∈，必有11p q a a ++=，则称{}n a 具有性质P .（1）若{}n a 具有性质P ，且12451,2,3,2a a a a ====，67821a a a ++=，求3a ；（2）若无穷数列{}n b 是等差数列，无穷数列{}n c 是公比为正数的等比数列，151b c ==，5181b c ==，n n n a b c =+判断{}n a 是否具有性质P ，并说明理由；（3）设{}n b 是无穷数列，已知*1sin ()n n n a b a n N +=+∈ .求证：“对任意1,{}n a a 都具有性质P ”的充要条件为“{}n b 是常数列”.答案：（1）316a =；（2）由于15a a =，但26a a ≠，故{}n a 不具有性质P ；（3）证明：必要性：若对于任意1a ，{}n a 都具有性质P ，则211sin a b a =+，设函数()()1,sin ,f x x b g x x =-= 由()(),f x g x 图像可得，对于任意的1b ，二者图像必有一个交点，所以一定能找到1a ，使得111sin a b a -=，所以2111sin a b a a =+=，所以1n n a a +=，故1211sin sin n n n n n n b a a a a b ++++=-=-=，故{}n b 是常数列（2013理1）计算：20lim 313n n n →∞+=+ ．答案：13（2018秋10）设等比数列{}n a 的通项公式为1n n a q -=（*n N ∈），前n 项和为n S ，若11lim2n n n S a →∞+=，则q =答案：3（2017年春 8）已知数列{}n a 的通项公式为3n n a =，则12lim nn na a a a →∞+++=L ______答案：32（2015理18文18）设是直线与圆在第一象限的交点，则极限（ ） A 、 B 、 C 、 D 、 解：当时，直线趋近于，与圆在第一象限的交点无限靠近，而可看成点与连线的斜率，其值会无限接近圆在点处的切线的斜率，其斜率为，∴ （2013文18）记椭圆221441x ny n +=+围成的区域（含边界）为(1,2,)n n Ω=L ，当点(,)x y 分别在12,,ΩΩL 上时，x y +的最大值分别是12,,M M L ，则lim n n M →∞=（ ）(),n n n P x y ()2N 1nx y n n *-=∈+222x y +=1lim1n n n y x →∞-=-1-12-12n →∞21n x y n -=+21x y -=221x y +=()1,111n n y x --(),n n n P x y ()1,1222x y +=()1,11-1lim11n n n y x →∞-=--A ． 0B ．14C ． 2D ．答案：D（2016理17）已知无穷等比数列}n a 的公比为q ，前n 项和为n S ，且S Snn =∞→lim .下列条件中，使得()*∈<N n S S n2恒成立的是（ ）（A ）7.06.0,01<<>q a （B ）6.07.0,01-<<-<q a （C ）8.07.0,01<<>q a （D ）7.08.0,01-<<-<q a 答案：B思考：1,a q 需要满足____________答案：110,0,22a q ⎛⎫⎛⎫<∈- ⎪⎪ ⎪⎝⎭⎝⎭U （2014理8文10）设无穷等比数列{}n a 的公比为q ，若()134lim n n a a a a →∞=+++L ，则q =___答案：12-知识点13：数列与函数的性质结合（2009文13）已知函数．项数为27的等差数列满足且公差． 若，则当= ．时 ．答案：14 （2015理13）已知函数()sin f x x =．若存在12,,,m x x x L 满足1206m x x x π≤<<<≤L，且()()()()()()()12231122,m m f x f x f x f x f x f x m m N *--+-++-=≥∈L ，则m 的最小值为 ．答案：8（2012文18）若（），则在中，正数的个数是（ ）x x tan sin +{}n a ⎪⎭⎫⎝⎛-∈22ππ，n a 0≠d 0)()()(2721=+⋯++a f a f a f k0)(=k a f 2sin sin...sin 777n n S πππ=+++n N *∈12100,,...,S S SA ．16B ．72C ．86D ．100 答案；C（2012理18）设，，在中，正数的个数是（ ）A ．25B ．50C ．75D ．100 答案：D（2013理17）在数列{}n a 中，21n na =-．若一个7行12列的矩阵的第i 行第j 列的元素,i j i j i j c a a a a =⋅++（1,2,,7i =L；1,2,,12j =L ），则该矩阵元素能取到的不同数值的个数为（ ）A ．18B ． 28C ． 48D ． 63 答案：A（2018秋21）给定无穷数列{}n a ，若无穷数列{}n b 满足：对任意*n N ∈，都有||1n n b a -≤，则称{}n b 与{}n a “接近”.（1）设{}n a 是首项为1，公比为12的等比数列，11n n b a +=+，*n N ∈，判断数列{}n b 是否与{}n a 接近，并说明理由；（2）设数列{}n a 的前四项为：11a =，22a =，34a =，48a =，{}n b 是一个与{}n a 接近的数列，记集合{|,1,2,3,4}i M x x b i ===，求M 中元素的个数m ；（3）已知{}n a 是公差为d 的等差数列，若存在数列{}n b 满足：{}n b 与{}n a 接近，且在21b b -，32b b -，⋅⋅⋅，201200b b -中至少有100个为正数，求d 的取值范围.解析：（1）1112n n nb a -=-≤，所以{}n b 与{}n a “接近”； （2）[]10,2b ∈，[]21,3b ∈，[]33,5b ∈，[]47,9b ∈，{}|,1,2,3,4i M x x b i ===元素个数34m =或；（3）2d =-时，10,1,2,,200k k b b k +-≤=L ，即21b b -，32b b -，…，201200b b -中没有正数；当2d >-时，存在12201,,,b b b L 使得210b b ->，320b b -<，430b b ->，540b b -<…，2001990b b ->，2012000b b -<，即有100个正数，故2d >-． 25sin 1πn n a n =n n a a a S +++=Λ2110021,,,S S S Λ（2018春21）若{}n c 是递增数列，数列{}n a 满足：对任意*n N ∈，存在*m N ∈，使得10m nm n a c a c +-≤-，则称{}n a 是{}n c 的“分隔数列”．（1）设2n c n =，1n a n =+，证明：数列{}n a 是{}n c 的“分隔数列”；（2）设4nc n =-，n S 是{}n c 的前n 项和，31n nd c -=，判断数列{}n S 是否是数列{}n d 的分隔数列，并说明理由； （3）设1n nc aq -=，n T 是{}n c 的前n 项和，若数列{}n T 是{}n c 的分隔数列，求实数a q 、的取值范围．答案：（2）不是，反例：4n =时，m 无解；（3）02a q >⎧⎨≥⎩（2017秋19）共享单车问题：每月供应量⎩⎨⎧+∞∈+-∈+=),4[47010]3,1[1554n n n n a n ，*N n ∈，每月损失量()*5N n n b n∈+=，保有量Q 为na的累计量减去n b 的累计和；（1）求第4月的保有量；（2）2(46)8800n S n =--+，记n S 为自行车停放点容纳车辆，当Q 取最大值时，停放点是否能容纳？。

历年上海高考试题(数列)班级 学号 姓名1、（98上海）在数列{a n }和{b n }中，a 1＝2，且对任意自然数n ，3a n ＋1－a n ＝0，b n 是a n 与a n ＋1的等差中项，则的各项和为____________2、（99上海）在等差数列{a n }中，满足3a 4=7a 7,，且a 1>0，若S n 取得最大值，则n=__________3、(00上海) 在等差数列{a n }中，若a 10＝0，则有等式a 1＋a 2＋……＋a n ＝a 1＋a 2＋……＋a 19－n (n ＜19，n ∈N )成立，类比上述性质，相应地，在等比数列{b n }中，若b 9＝1，则有等式______ __成立4、(01春上海)甲、乙两人于同一天分别携款1万元到银行储蓄，甲存五年期定期储蓄，年利率为2.88%。

乙存一年期定期储蓄，年利率为2.25%，并在每年到期时将本息续存一年期定期储蓄。

按规定每次计息时，储户须交纳利息的20%作为利息税，若存满五年后两人同时从银行取出存款，则甲与乙所得本息之和的差为__________元。

（假定利率五年内保持不变，结果精确到1分）。

5、(02上海)若数列}{n a 中，211,3n n a a a ==+且（n 是正整数），则数列的通项=n a6、(03上海)等差数列}{n a 中，a 5=3, a 6=－2,则a 4+a 5+…+a 10=7、(03上海)若首项为a 1,公比为q 的等比数列}{n a 的前n 项和总小于这个数列的各项和,则首项a 1,公比q 的一组取值可以是（a 1，q ）=8、(03上海)),0,24(),2,0(),2,0(nC n B n A +-其中n 的为正整数.设S n 表示 △ABC 外接圆的面积，则n n S ∞→lim = . 9、（04上海春）在数列}{n a 中，31=a ，且对任意大于1的正整数n ，点),(1-n n a a 在直线03=--y x 上，则=+∞→2)1(lim n a nn _____________.10、（04上海春）在等差数列}{n a 中，当s r a a =)(s r ≠时，}{n a 必定是常数数列。

数列一、选择题1.辽宁4、下面关于公差d>0的等差数列{}n a 的四个命题：P1：数列{}n a 是递增数列； P2：数列{}n na 是递增数列P3：数列n a n ⎧⎫⎨⎬⎩⎭是递增数列； P4：数列{}+3n a nd 是递增数列。

其中的真命题为( )A ．P1，P2 B. P3，P4 C. P2，P3 D. P1，P42.全国（3）等比数列{a n }的的前n 项和为S n ，已知S 3 = a 2 +10a 1 ，a 5 = 9，则a 1 =( )（A ）13 （B ）- 13 （C ）19 （D ）- 193.福建9. 已知等比数列{}n a 的公比为q ，记m n m n m n m n a a a b +-+-+-+⋅⋅⋅++=)1(2)1(1)1(，m n m n m n m n a a a b +-+-+-*⋅⋅⋅**=)1(2)1(1)1(，()*,N n m ∈，则以下结论一定正确的是（ ）A. 数列{}n b 为等差数列，公差为m q B. 数列{}n b 为等比数列，公比为m q 2 C. 数列{}n c 为等比数列，公比为2m q D. 数列{}n c 为等比数列，公比为m mq 4.江西3.等比数列x ，3x+3，6x+6，…的的第四项等于 （ ）A.-24B.0C.12D.24二、填空题5.全国（16）等差数列{a n }的前n 项和为S n ，已知S 10 = 0，S 15 = 25，则nS n 的最小值为 .6.北京10.若等比数列{a n }满足a 2＋a 4=20，a 3＋a 5=40，则公比q = ；前n 项和S n =.7.重庆（12）已知{}n a 是等差数列，11a =，公差0d ≠，n S 为其前n 项和，若1a 、2a 、5a 称等比数列，则8S = ．8.陕西14. 观察下列等式:211=22123-=-2221263+-=2222124310-+-=-…照此规律, 第n 个等式可为 .9.湖北14.古希腊毕达哥拉斯学派的数学家研究过各种多边形数.如三角形数1,3,6,10,...，第n 个三角形数为2(1)11222n n n n +=+.记第n 个k 边形数为(,)(3)N n k k ≥，以下列出了部分k 边形数中第n 个数的表达式： 三角形数 211(,3)22N n n n =+， 四边形数 2(,4)N n n =，五边形数 231(,5)22N n n n =-， 六边形数 2(,6)2N n n n =-，…可以推测(,)N n k 的表达式，由此计算(10,24)N = .10.安徽（14）如图，互不相同的点12,,,n A A X 和12,,,n B B B 分别在角O 的两条边上，所有n n A B 相互平行，且所有梯形11n n n n A B B A ++的面积均相等。

矩阵行列式（2013理17）在数列{}n a 中，21n n a =-，若一个7行12列的矩阵的第i 行第j 列的元素,i j i j i j a a a a a =⋅++，（1,2,,7;1,2,,12i j ==）则该矩阵元素能取到的不同数值的个数为（ ）.18A.28B .48C .63D答案：A（2017秋13）二元线性方程组⎩⎨⎧=+=+43205y x y x 的系数矩阵=D （ ）A. ⎪⎪⎭⎫ ⎝⎛4350B. ⎪⎪⎭⎫ ⎝⎛3201C. ⎪⎪⎭⎫ ⎝⎛3251D. ⎪⎪⎭⎫ ⎝⎛4201答案：C（2016春8）若线性方程组的增广矩阵为0201a b ⎛⎫ ⎪⎝⎭，解为21x y =⎧⎨=⎩，则a b +=________. 答案：2（2015理3，文5）若线性方程组的增广矩阵为122301c c ⎛⎫ ⎪⎝⎭解为35x y =⎧⎨=⎩ ，12c c -= ． 答案：16___________ 答案：18（2013文4）若2011x =，111x y =，则x y += ．答案：3 （2013理3）若2211x x x y y y =--，则x y +=．答案：0(2017春5)若关于,x y 的方程组2436x y x ay +=⎧⎨+=⎩无解，则实数a =_____答案：6（2016理10，文13）设.0,0>>b a 若关于,x y 的方程组11ax y x by +=⎧⎨+=⎩无解，则b a +的取值范围是____________答案：()2,+∞（2014理17、文18）已知111(,)P a b 与222(,)P a b 是直线1y kx =+（k 为常数）上两个不同的点，则关于x 和y 的方程组11221,1a x b y a x b y +=⎧⎨+=⎩的解的情况是 （ ） (A) 无论12,,k P P 如何，总是无解.(B) 无论12,,k P P 如何，总有唯一解. (C) 存在12,,k P P ，使之恰有两解. (D) 存在12,,k P P ，使之有无穷多解. 答案：B（2013年高考理18）在边长为1的正六边形ABCDEF 中，记以A 为起点，其余顶点为终点的向量分别为12345,,,,a a a a a ；以D 为起点，其余顶点为终点的向量分别为12345,,,,d d d d d .若,m M 分别为()()i j k r s t a a a d d d ++⋅++的最小值、最大值，其中{,,}{1,2,3,4,5}i j k ⊆,{,,}{1,2,3,4,5}r s t ⊆,则,m M 满足（ ）.(A) 0,0m M => (B) 0,0m M <>(C) 0,0m M <= (D) 0,0m M <<解答：作图知，只有0AF DE AB DC ⋅=⋅>，其余均有0i ra d ⋅≤，故选D ． （2013年高考文14）已知正方形ABCD 的边长为1．记以A 为起点，其余顶点为终点的向量分别为1a 、2a 、3a ；以C 为起点，其余顶点为终点的向量分别为1c 、2c 、3c ．若{},,,1,2,3i j k l ∈且,i j k l ≠≠，则()()i j k l a a c c +⋅+的最小值是 ． 答案：5-。

2018年高考试题分类汇编（数列）考法1 等差数列1.（2018·全国卷Ⅰ理科）记n S 为等差数列数列{}n a 的前n 项的和.若323S S =4S +，12a =,则5a =A.12-B.10-C.10D. 12 2.（2018·北京卷理科）设{}n a 是等差数列，且13a =，2536a a +=，则{}n a 的通 项公式为_____．3.（2018·上海卷）记等差数列{}n a 的前n 项和为n S ，若30a =，6714a a +=，则7S = .4.（2018·全国卷Ⅱ文理）记n S 为等差数列{}n a 的前n 项的和,已知17a =-,315S =-.（Ⅰ）求{}n a 的通项公式； （Ⅱ）求n S ，并求n S 的最小值. 考法2 等比数列1.（2018·全国卷Ⅰ理科）记n S 为数列{}n a 的前n 项的和，若21n n S a =+，则6S = .2.（2018·北京卷文理） “十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于．若第一个单音的频率为f ，则第八个单音的频率为C.D.3.（2018·上海卷）设等比数列{}n a 的通项公式为1n n a q +=（n N *∈），前n 项和为n S .若11lim2n n n S a →∞+=，则q =_______.4.（2018·浙江卷）已知1234,,,a a a a 成等比数列，且1234123ln()a a a a a a a +++=++， 若11a >，则 A.1324,a a a a <<B.1324,a a a a ><C.1324,a a a a <>D.1324,a a a a >>5.（2018·全国卷Ⅰ文科）已知数列{}n a 满足11a =， 12(1)n n na n a +=+，设nn a b n=. （Ⅰ）求1b ，2b ，3b .（Ⅱ）判断数列{}n b 是否为等比数列，并说明理由； （Ⅲ）求数列{}n a 的通项公式.6.（2018·全国卷Ⅲ文理）等比数列{}n a 中，11a =，534a a =. （Ⅰ）求数列{}n a 的通项公式；（Ⅱ）记n S 为{}n a 的前n 项的和.若63m S =，求m . 考法3 等差数列与等比数列综合1.（2018·北京卷文科）设{}n a 是等差数列，且1ln 2a =,235ln 2a a +=. （Ⅰ）求{}n a 的通项公式； （Ⅱ）求12n a a a e e e +++.2.（2018·浙江卷）已知等比数列{}n a 的公比1q >，且34528a a a ++=，42a +是3a ，5a 的等差中项．数列{}n b 满足11b =，数列{}1()n n n b b a +-的前n 项和为22n n +． （Ⅰ）求q 的值；（Ⅱ）求数列{}n b 的通项公式．3.（2018·天津卷理科）设{}n a 是等比数列，公比大于0，其前n 项和为n S （n N *∈），{}n b 是等差数列. 已知11a =，322a a =+，435a b b =+，5462a b b =+.（Ⅰ）求{}n a 和{}n b 的通项公式；（Ⅱ）设数列{}n S 的前n 项和为n T （n N *∈）， （1）求n T ；（2）证明221()22(1)(2)2n nk k k k T b b k k n ++=+=-+++∑（n N *∈）.4.（2018·天津卷文科）设{}n a 是等差数列，其前n 项和为n S （n N *∈）；{}n b 是 等比数列，公比大于0，其前的前n 项和为n T （n N *∈）．已知11b =，322b b =+，435b a a =+，5462b a a =+. （Ⅰ）求n S 和n T ； （Ⅱ）若12()4n n n n S T T T a b ++++=+，求正整数n 的值．。

2013年高考解析分类汇编5：数列一、选择题1 ．（2013年高考大纲卷（文7））已知数列{}na 满足12430,,3n n aa a ++==-则{}n a 的前10项和等于（ ）A ．()-10-61-3 B ．()-1011-39C ．()-1031-3D ．()-1031+3【答案】C由31=++n n a a ，所以311-=+n n a a ，所以qa a 12=,所以4)3(34121=-⨯-=•=q a a ，所以)31(3311])31(1[4101010-=+--=S ，故选C 。

2 ．(2013年高考安徽（文））设nS 为等差数列{}na 的前n 项和,8374,2Sa a ==-,则9a =( ）A ．6-B ．4-C ．2-D ．2【答案】A188333638()442a a S a a a a a +=⇒=⇒+=60a ∴=972,26d a a d =-=+=-，选A.3 ．（2013年高考课标Ⅰ卷（文6））设首项为1,公比为23的等比数列{}na 的前n 项和为nS ,则 ( ）A ．21nn Sa =- B ．32n n S a =- C ．43n n S a =- D ．32n n S a =-【答案】D在等比数列中,1112()3n n n a a q --==，1213322113nn n n a a qa S a q --===---，选D 。

4 ．（2013年高考辽宁卷（文4))下面是关于公差0d >的等差数列()na 的四个命题：{}1:n p a 数列是递增数列；{}2:n p na 数列是递增数列； 3:n a p n ⎧⎫⎨⎬⎩⎭数列是递增数列；{}4:3n p a nd +数列是递增数列；其中的真命题为 （ ）A ．12,p pB ．34,p p C ．23,p pD ．14,p p【答案】D设1(1)naa n d dn m =+-=+，所以1P 正确；如果312n a n =-则满足已知，但2312nna n n =-并非递增所以2P 错；如果若1n a n =+，则满足已知，但11na nn=+,是递减数列，所以3P 错;34n a nd dn m +=+，所以是递增数列，4P 正确二、填空题5 ．（2013年高考重庆卷（文12））若2、a 、b 、c 、9成等差数列，则c a -=____________. 【答案】72本题考查等差数列的基本运算与性质。

第四部 数列专题【考点1】等差数列与等比数列1. 等差数列等差数列{}n a 的通项公式：1(1)n a a n d *()n N . 等差数列{}n a 的递推公式：1n n a a d (2)n . 等差数列{}n a 的前n 项和公式：11()(1)22n n n a a n n S na d na 中. 等差数列{}n a 的性质： ① ()n m a a n m d .② 若m n p q ，则m n p q a a a a .③ k a 、k m a 、2k m a 、 成等差数列，公差为md .④ n S 、2n n S S 、32n n S S 、43n n S S 、 成等差数列，公差为2n d .⑤ 数列{}n a 成等差数列n a pn q ，112n n n a a a ，2n S An Bn .⑥ 若数列{}n a 是等差数列，则{}n ac 为等比数列，0c .⑦ n S 是前n 项和，S 奇表示奇数项的和，S 偶表示偶数项的和，则n S S S 奇偶. 当n 为偶数时，2n S S d偶奇. 当n 为奇数时，S S a 奇偶中，11S n S n 奇偶，S S n S S 奇偶奇偶. ⑧ 设n S 和n T 分别表示等差数列{}n a 、{}n b 的前n 项和，则2121n n n n a S b T. ⑨ 若p a q ，q a p ，p q ，则0p q a ，1d . 若p S q ，q S p ，p q ，则()p q S p q . 若p q S S ，p q ，则0p q S .1.（2018年6）记等差数列{}n a 的前n 项和为n S ，若30a ，6714a a ，则7S2.（2014春7）已知等差数列{}n a 的首项为1，公差为2，则该数列的前n 项和n S3.（2013春11）若等差数列的前6项和为23，前9项和为57，则数列的前n 项和n S4.（2018春5）已知{}n a 是等差数列，若2810a a ，则357a a a5.（2017春6）若等差数列{}n a 的前5项的和为25，则15a a6.（2013文2）在等差数列{}n a 中，若123430a a a a ，则23a a7.（2012春13）已知等差数列{}n a 的首项及公差均为正数，令n b （*n N ，2012n ），当k b 是数列{}n b 的最大项时，k8.（2017年15）已知a 、b 、c 为实常数，数列{}n x 的通项2n x an bn c ，*n N ， 则“存在*k N ，使得100k x 、200k x 、300k x 成等差数列”的一个必要条件是（ ） A. 0a B. 0b C. 0c D. 20a b c9.（2015春附3）已知数列{}n a 满足413n n n n a a a a ()n *N ，那么（ ）A. {}n a 是等差数列B. 21{}n a 是等差数列C. 2{}n a 是等差数列D. 3{}n a 是等差数列10.（2015春21）若无穷等差数列{}n a 的首项10a ，公差0d ，{}n a 的前n 项和为n S ， 则（ ）A. n S 单调递减B. n S 单调递增C. n S 有最大值D. n S 有最小值 2. 等比数列等比数列{}n a 的通项公式：11n n a a q*()n N .等比数列{}n a 的递推公式：1n n a a q (2)n .等比数列{}n a 的前n 项和公式：11(1)11n n n a a qa q S qq (1)q ，1n S na (1)q .等比数列{}n a 的性质： ① n mn m a a q.② 若m n p q ，则m n p q a a a a .③ k a 、k m a 、2k m a 、 成等比数列，公比为mq .④ n S 、2n n S S 、32n n S S 、43n n S S 、 成等比数列，公比为nq . ⑤ 数列{}n a 成等比数列211n n n a a a ，n n a p q ，(1)n n S A q .⑥ 若数列{}n a 是等比数列，则{log }c n a 为等差数列，0n a .⑦ n S 是前n 项和，S 奇表示奇数项的和，S 偶表示偶数项的和，则n S S S 奇偶. 当n 为偶数时，S q S 偶奇. 当n 为奇数时，1S a q S 奇偶. ⑧ 设n T 是前n 项积，T 奇表示奇数项的积，T 偶表示偶数项的积，则n T T T 奇偶. 当n 为偶数时，2n T q T 偶奇. 当n 为奇数时，T a T 奇中偶. 11.（2011春8）若n S 为等比数列{}n a 的前n 项和，2580a a ，则63S S12.（2014春22）已知数列{}n a 是以q 为公比的等比数列，若2n n b a ，则数列{}n b 是 （ ）A. 以q 为公比的等比数列B. 以q 为公比的等比数列C. 以2q 为公比的等比数列D. 以2q 为公比的等比数列13.（2011理18）设{}n a 是各项为正数的无穷数列，i A 是边长为i a 、1i a 的矩形面积 （1,2,i ），则{}n A 为等比数列的充要条件是（ ） A. {}n a 是等比数列B. 1321,,,,n a a a 或242,,,n a a a 是等比数列C. 1321,,,,n a a a 和242,,,n a a a 均是等比数列D. 1321,,,,n a a a 和242,,,n a a a 均是等比数列，且公比相同14.（2015理17）记方程①：2110x a x ；方程②：2210x a x ；方程③： 2310x a x ；其中1a 、2a 、3a 是正实数，当1a 、2a 、3a 成等比数列时，下列选项中， 能推出方程③无实数根的是（ ）A. 方程①有实根，且②有实根B. 方程①有实根，且②无实根C. 方程①无实根，且②有实根D. 方程①无实根，且②无实根15.（2014文23）已知数列{}n a 满足1133n n n a a a ，*n N ，11a .（1）若22a ，3a x ，49a ，求x 的取值范围；（2）设{}n a 是等比数列，且11000m a ，求正整数m 的最小值，以及m 取最小值时相 应{}n a 的公比；（3）若12100,,,a a a 成等差数列，求数列12100,,,a a a 的公差的取值范围.16.（2014理23）已知数列{}n a 满足1133n n n a a a ，*n N ，11a .（1）若22a ，3a x ，49a ，求x 的取值范围；（2）设{}n a 是公比为q 的等比数列，12n n S a a a ，若1133n n n S S S ，*n N ，求q 的取值范围；（3）若12,,,k a a a 成等差数列，且121000k a a a ，求正整数k 的最大值， 以及k 取最大值时相应数列12,,,k a a a 的公差.17.（2013文22）已知函数()2||f x x ，无穷数列{}n a 满足1()n n a f a ，*n N . （1）若10a ，求2a 、3a 、4a ；（2）若10a ，且1a 、2a 、3a 成等比数列，求1a 的值；（3）是否存在1a ，使得12,,,,n a a a 成等差数列？若存在，求出所有这样的1a ； 若不存在，说明理由.【考点2】数列通项与数列求和1. 求数列通项方法（1）公式法：等差数列通项1(1)n a a n d ，等比数列通项11n n a a q .（2）累加法（累乘法）：1()n n a a f n ，1()nn a f n a ，2n . （3）作差法（作商法）：若123n n S a a a a ，则1n n n a S S ，2n . 若123n n T a a a a ，则1nn n T a T，2n . （4）构造法：1n n a Aa B ，1n n a Aa Bn C ，1nn n a Aa B .1q n n a pa ，11n n n a a ka b，11n n n a pa qa ，其他类型.（5）数学归纳法：对数列通项进行归纳猜想，然后按数学归纳法步骤进行证明. 2. 数列求和方法（1）求和公式法：等差数列前n 项和公式：11()(1)22n n n a a n n S na d na中. 等比数列前n 项和公式：11(1)11n n n a a qa q S qq (1)q .22221123(1)(21)6n n n n (3333221)123(1)4n n n ….（2）倒序相加法：首尾距离相等的两项有共性或数列的通项与组合数相关联. （3）错位相减法：数列通项由等差数列与等比数列相乘构成.（4）裂项相消法：将数列中的每项进行分解，然后重新组合，达到消项的目的.111(1)1n n n n ，1111()()n n k k n n k， 1111[](1)(2)2(1)(1)(2)n n n n n n n ，1k，11(1)!!(1)!n n n n ，sin1tan(1)tan cos cos(1)n n n n.（5）分组求和法：将通项中有共同规律的部分进行分组，分别求和.（6）数学归纳法：对数列前n 项和进行归纳猜想，然后按数学归纳法步骤进行证明. 18.（2019年8）已知数列{}n a 前n 项和为n S ，且满足2n n S a ，则5S 19.（2017年10）已知数列{}n a 和{}n b ，其中2n a n ，*n N ，{}n b 的项是互不相等的正 整数，若对于任意*n N ，{}n b 的第n a 项等于{}n a 的第n b 项，则149161234lg()lg()b b b b b b b b20.（2016理11）无穷数列{}n a 由k 个不同的数组成，n S 为{}n a 的前n 项和，若对任意*N ，{2,3}n S ，则k 的最大值为21.（2013春12）36的所有正约数之和可按如下方法得到：∵223623 ，∴36所有正约 数之和22222222(133)(22323)(22323)(122)133)91 （， 参照上述方法，可求得2000的所有正约数之和为 22.（2012文14）已知函数1()1f x x，各项均为正数的数列{}n a 满足11a ， 2()n n a f a ，若20102012a a ，则2011a a 的值是23.（2013理17）在数列{}n a 中，21n n a ．若一个7行12列的矩阵的第i 行第j 列 的元素,i j c i j i j a a a a （1,2,,7i ；1,2,,12j ），则该矩阵元素能取到的不同 数值的个数为（ ）A. 18B. 28C. 48D. 6324.（2016春19）用数学归纳法证明等式2123...22n n n ()n *N 的第（ii ）步中，假设n k 时原等式成立，那么在1n k 时，需要证明的等式为（ ） A. 22123...22(1)22(1)(1)k k k k k k B. 2123...22(1)2(1)(1)k k k kC. 22123...2(21)2(1)22(1)(1)k k k k k k kD. 2123...2(21)2(1)2(1)(1)k k k k k 25.（2016春28）已知数列{}n a 是公差为2的等差数列. （1）若1a 、3a 、4a 成等比数列，求1a 的值；（2）设119a ，数列{}n a 的前n 项和为n S ，数列{}n b 满足11b ，11(2n n n b b ，记12n n n n c S b ()n *N ，求数列{}n c 的最小值0n c .（即0n n c c 对任意n *N 成立）26.（2012春22）已知数列{}n a 、{}n b 、{}n c 满足11()()n n n n n a a b b c （*n N ）. （1）设36n c n ，{}n a 是公差为3的等差数列，当11b 时，求2b 、3b 的值； （2）设3n c n ，28n a n n ，求正整数k ，使得一切*n N 均有n k b b ；（3）设2nn c n ，1(1)2nn a，当11b 时，求数列{}n b 的通项公式.27.（2011文23）已知数列{}n a 和{}n b 的通项公式分别为36n a n ，27n b n （*n N ），将集合**{|,}{|,}n n x x a n x x b n N N 中的元素从小到大依次排列， 构成数列1c ，2c ，3c ， ，n c ， .（1）求三个最小的数，使它们既是数列{}n a 中的项，又是数列{}n b 中的项； （2）数列1c ，2c ，3c ， ，40c 中有多少项不是数列{}n b 中的项？请说明理由； （3）求数列{}n c 的前4n 项和4n S （*n N ）.28.（2011理22）已知数列{}n a 和{}n b 的通项公式分别为36n a n ，27n b n （*n N ），将集合**{|,}{|,}n n x x a n x x b n N N 中的元素从小到大依次排列， 构成数列1c ，2c ，3c ， ，n c ， . （1）求1c ，2c ，3c ，4c ；（2）求证：在数列{}n c 中，但不在数列{}n b 中的项恰为2a ，4a ， ，2n a ， ； （3）求数列{}n c 的通项公式.【考点3】数列单调性常结合函数性质分析数列单调性，或根据1n n a a 的大小分析数列单调性29.（2018春15）设n S 为数列{}n a 的前n 项和，“{}n a 是递增数列”是“{}n S 是递增数列” 的（ ）A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分又非必要条件【考点4】数列极限三个常用极限：① lim n C C（C 为常数）. ② 1lim0n n. ③ 当||1q ，lim 0n n q .我们把||1q 的无穷等比数列的前n 项和n S 当n 时的极限叫做无穷等比数列各项的 和，并用符号S 表示，即11a S q(||1)q . 30.（2019春2）计算：22231lim 41n n n n n31.（2015春4）计算：223lim 2n n n n32.（2018春2）计算：31lim 2n n n33.（2013理1）计算：20lim313n n n34.（2011文2）计算3lim(13n nn35.（2017春8）已知数列{}n a 的通项公式为3nn a ，则123lim nn na a a a a36.（2016春9）无穷等比数列{}n a 的首项为2，公比为13，则{}n a 的各项和为 37.（2012理6）有一列正方体，棱长组成以1为首项、12为公比的等比数列，体积分别记为12,,,,n V V V ，则12lim()n n V V V38.（2014理8）设无穷等比数列{}n a 的公比为q ，若134lim()n n a a a a，则q39.（2018年10）设等比数列{}n a 的通项公式为1n n a q （n *N ），前n 项和为n S ， 若11lim 2n n n S a ，则q40.（2011理14）已知点(0,0)O 、0(0,1)Q 和点0(3,1)R ，记00Q R 的中点为1P ，取01Q P 和10PR 中的一条，记其端点为1Q 、1R ，使之满足11(||2)(||2)0OQ OR ，记11Q R 的中点为2P ，取12Q P 和21P R 中的一条，记其端点为2Q 、2R ，使之满足22(||2)(||2)0OQ OR 依次下去，得到12,,,,n P P P ，则0lim ||n n Q P41.（2017年14）在数列{}n a 中，1()2n n a ，*n N ，则lim n n a（ ）A. 等于12B. 等于0C. 等于12D. 不存在42.（2015年18）设(,)n n n P x y 是直线21nx y n ()n *N 与圆222x y 在第一象限 的交点，则极限1lim1n n n y x（ ） A. 1 B. 12C. 1D. 243.（2013文18）记椭圆221441x ny n围成的区域（含边界）为(1,2,)n n ，当点 (,)x y 分别在1 、2 、 上时，x y 的最大值分别是1M 、2M 、 ，则lim n n M（ ）A. 0B. 14C. 2D.44.（2016理17）已知无穷等比数列{}n a 的公比为q ，前n 项和为n S ，且lim n n S S，下列条件中，使得2n S S （n *N ）恒成立的是（ ）A. 10a ，0.60.7qB. 10a ，0.70.6qC. 10a ，0.70.8qD. 10a ，0.80.7q45.（2013春27）已知数列{}n a 的前n 项和为2n S n n ，数列{}n b 满足2n an b ，求12limn n b b b（）.46.（2019春18）已知数列{}n a 中，13a ，前n 项和为n S . （1）若{}n a 为等差数列，且415a ，求n S ；（2）若{}n a 为等比数列，且lim 12n n S，求公比q 的取值范围.【考点5】数列应用题47.（2016春附6）小明用数列{}n a 记录某地区2015年12月份31天中每天是否下过雨， 方法为：当第k 天下过雨时，记1k a ，当第k 天没下过雨时，记1k a (131)k ； 他用数列{}n b 记录该地区该月每天气象台预报是否有雨，方法为：当预报第k 天有雨时， 记1k b ，当预报第k 天没有雨时，记1k b (131)k ；记录完毕后，小明计算出1122333131...a b a b a b a b 25 ，那么该月气象台预报准确的总天数为48.（2017年19）根据预测，某地第n *()n N 个月共享单车的投放量和损失量分别为n a和n b （单位：辆），其中4515,1310470,4n n n a n n ，5n b n ，第n 个月底的共享单车的保有量是前n 个月的累计投放量与累计损失量的差.（1）求该地区第4个月底的共享单车的保有量；（2）已知该地共享单车停放点第n 个月底的单车容纳量24(46)8800n S n （单位：辆）. 设在某月底，共享单车保有量达到最大，问该保有量是否超出了此时停放点的单车容纳量？【考点6】数列新定义题型49.（2019年21）数列{}n a ()n *N 有100项，1a a ，对任意[2,100]n ，存在n i a a d ，[1,1]i n ()n *N ，若k a 与前n 项中某一项相等，则称k a 具有性质P .（1）若11a ，2d ，求4a 所有可能的值；（2）若{}n a 不是等差数列，求证：数列{}n a 中存在某些项具有性质P ；（3）若{}n a 中恰有三项具有性质P ，这三项和为c ，请用a 、d 、c 表示12100a a a .50.（2018春21）若{}n c 是递增数列，数列{}n a 满足：对任意n *N ，存在m *N ，使 得10m nm n a c a c ，则称{}n a 是{}n c 的“分隔数列”.（1）设2n c n ，1n a n ，证明：数列{}n a 是{}n c 的分隔数列；（2）设4n c n ，n S 是{}n c 的前n 项和，32n n d c ，判断数列{}n S 是否是数列{}n d 的分隔数列，并说明理由；（3）设1n n c aq ，n T 是{}n c 的前n 项和，若数列{}n T 是{}n c 的分隔数列，求实数a 、q 的取值范围.51.（2018年21）给定无穷数列{}n a ，若无穷数列{}n b 满足：对任意n *N ，都有||1n n b a ，则称{}n b 与{}n a “接近”.（1）设{}n a 是首项为1，公比为12的等比数列，11n n b a ，n *N ，判断数列{}n b 是 否与{}n a 接近，并说明理由；（2）设数列{}n a 的前四项为：11a ，22a ，34a ，48a ，{}n b 是一个与{}n a 接近的数列，记集合{|,1,2,3,4}i M x x b i ，求M 中元素的个数m ；（3）已知{}n a 是公差为d 的等差数列，若存在数列{}n b 满足：{}n b 与{}n a 接近，且在21b b ，32b b ， ，201200b b 中至少有100个为正数，求d 的取值范围.52.（2016理23）无穷数列{}n a 满足：只要p q a a （,p q *N ），必有11p q a a ， 则称{}n a 具有性质P .（1）若{}n a 具有性质P ，且11a ，22a ，43a ，52a ，67821a a a ，求3a ； （2）若无穷数列{}n b 是等差数列，无穷数列{}n c 是公比为正数的等比数列，151b c ，5181b c ，n n n a b c ，判断{}n a 是否具有性质P ，并说明理由；（3）设{}n b 是无穷数列，已知1sin n n n a b a （n *N ），求证：“对任意1a ，{}n a 都具 有性质P ”的充要条件为“{}n b 是常数列”.53.（2016文22）对于无穷数列{}n a 与{}n b ，记{|,}n A x x a n *N ，{|,}n B x x b n *N ，若同时满足条件：① {}n a ，{}n b 均单调递增；②A B 且A B *N ，则称{}n a 与{}n b 是无穷互补数列.（1）若21n a n ，42n b n ，判断{}n a 与{}n b 是否为无穷互补数列，并说明理由； （2）若2nn a 且{}n a 与{}n b 是无穷互补数列，求数列{}n b 的前16项的和；（3）若{}n a 与{}n b 是无穷互补数列，{}n a 为等差数列，且1636a ，求{}n a 与{}n b 的通 项公式.54.（2016春附7）对于数列{}n a 与{}n b ，若对数列{}n c 的每一项k c ，均有k k c a 或k k c b ，则称数列{}n c 是{}n a 与{}n b 的一个“并数列”.（1）设数列{}n a 与{}n b 的前三项分别为11a ，23a ，35a ，11b ，22b ，33b ， 若数列{}n c 是{}n a 与{}n b 的一个“并数列”，求所有可能的有序数组123(,,)c c c ； （2）已知数列{}n a 、{}n c 均为等差数列，{}n a 的公差为1，首项为正整数t ，{}n c 的前 10项和为30 ，前20项和为260 ，若存在唯一的数列{}n b ，使得{}n c 是{}n a 与{}n b 的 一个“并数列”，求t 的值所构成的集合.55.（2015理23）对于定义域为R 的函数()g x ，若存在正常数T ，使得cos ()g x 是以T 、为周期的函数，则称()g x 为余弦周期函数，且称T 为其余弦周期；已知()f x 是以T 为余 弦周期的余弦周期函数，其值域为R ，设()f x 单调递增，(0)0f ，()4f T . （1）验证()sin3xh x x 是以6 为余弦周期的余弦周期函数； （2）设a b ，证明对任意[(),()]c f a f b ，存在0[,]x a b ，使得0()f x c ； （3）证明：“0u 为方程cos ()1f x 在[0,]T 上的解”的充要条件是“0u T 为方程cos ()1f x 在[,2]T T 上的解”，并证明对任意[0,]x T 都有()()()f x T f x f T .56.（2012文23）对于项数为m 的有穷数列{}n a ，记12max{,,...,}k k b a a a（1,2,...,k m ），即k b 为12,,...,k a a a 中的最大值，并称数列{}n b 是{}n a 的控制数列， 如1、3、2、5、5的控制数列是1、3、3、5、5.（1）若各项均为正整数的数列{}n a 的控制数列为2、3、4、5、5，写出所有的{}n a ； （2）设{}n b 是{}n a 的控制数列，满足1k m k a b C （C 为常数，1,2,...,k m ）， 求证：k k b a （1,2,...,k m ）； （3）设100m ，常数1(,1)2a ，若(1)22(1)n n n a an n ，{}n b 是{}n a 的控制数列，求1122100100()()()b a b a b a .57.（2012理23）对于数集12{1,,,,}n X x x x ，其中120n x x x ，2n ，定义向量集{|(,),,}Y a a s t s X t X，若对任意1a Y ，存在2a Y ，使得120a a ，则称X 具有性质P ，例如{1,1,2} 具有性质P .（1）若2x ，且{1,1,2,}x 具有性质P ，求x 的值；（2）若X 具有性质P ，求证：1X ，且当1n x 时，11x ；（3）若X 具有性质P ，且11x 、2x q （q 为常数），求有穷数列12,,,n x x x 的 通项公式.【考点7】数列综合题型58.（2015春29）已知函数2()|22|x f x ()x R . （1）解不等式()2f x ；（2）数列{}n a 满足()n a f n ()n *N ，n S 为{}n a 的前n 项和，对任意的4n ，不等式12n n S ka恒成立，求实数k 的取值范围.59.（2019春21）若{}n a 是等差数列，公差(0,]d ，数列{}n b 满足：sin()n n b a ，n *N ，记{|,}n S x x b n *N .（1）设10a ，23d ，求集合S ； （2）设12a，试求d 的值，使得集合S 恰有两个元素；（3）若集合S 恰有三个元素，且n T n b b ，其中T 为不超过7的正整数，求T 所有可能值.60.（2017春21）已知函数21()log 1xf x x. （1）解方程()1f x ；（2）设(1,1)x ，(1,)a ，证明：1(1,1)ax a x ，且11(()()ax f f x f a xa ； （3）设数列{}n x 中，1(1,1)x ，1131(1)3n nn nx x x ，n *N ，求1x 的取值范围， 使得3n x x 对任意n *N 成立.61.（2011春23）对于给定首项0x 0a ），由递推式11(2n n x x （*n N ）得到数列{}n x ，且对于任意的*n N，都有n x，用数列{}n x的近似值.（1）取05x ，100a ，计算1x 、2x 、3x 的值（精确到0.01）， 并且归纳出n x 、1n x 的大小关系； （2）当1n 时，证明：111()2n n n n x x x x； （3）当0[5,10]x 时，用数列{}n x41||10n n x x ， 请你估计n ，并说明理由.62.（2013理23）给定常数0c ，定义函数()2|4|||f x x c x c ，数列123,,,a a a ，满足1()n n a f a ，*n N .（1）若12a c ，求2a 及3a ；（2）求证：对任意*n N ，1n n a a c ；（3）是否存在1a ，使得12,,,,n a a a 成等差数列？若存在，求出所有这样的1a ； 若不存在，说明理由.63.（2015年22）已知数列{}n a 与{}n b 满足112()n n n n a a b b ，n *N .（1）若35n b n ，且11a ，求{}n a 的通项公式；（2）设{}n a 的第0n 项是最大项，即0n n a a ()n *N ，求证{}n b 的第0n 项是最大项；（3）（文）设130a ，n n b ()n *N ，求 的取值范围，使得对任意m 、n *N ，0n a ，且1(,6)6m na a . （3）（理）设10a ，nn b ()n *N ，求 的取值范围，使得{}n a 有最大值M 与最小值m ，且(2,2)Mm.。

(直打版)2013—2018年全国高考数学1卷数列部分汇编(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(直打版)2013—2018年全国高考数学1卷数列部分汇编(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(直打版)2013—2018年全国高考数学1卷数列部分汇编(word版可编辑修改)的全部内容。

2013—2018年全国高考数学1卷集合部分汇编班级 姓名 得分一、小题部分每题5分1.(2013年7题）.设等差数列{}n a 的前n 项和为11,2,0,3n m m m S S S S -+=-==，则m = ( ）A.3B 。

4C.5D.62.（2013年12）.设n n n A B C ∆的三边长分别为,,n n n a b c ，n n n A B C ∆的面积为n S ,1,2,3,n =，若11111,2b c b c a >+=，111,,22n n nnn n n n c a b a a a b c +++++===，则( ) A.｛S n ｝为递减数列 B 。

{S n ｝为递增数列C.{S 2n －1}为递增数列，{S 2n }为递减数列D 。

{S 2n －1}为递减数列，｛S 2n }为递增数列3.(2013年14).若数列｛n a ｝的前n 项和为S n ＝2133n a +，则数列｛n a ｝的通项公式是n a =______。

5.（2016年3).已知等差数列{}n a 前9项的和为27,108a =，则100a = (A)100 (B ）99 (C ）98 （D ）976。