配合物电势计算

配位化合物研究方法配位化合物简称为配合物，有时也叫络合物，是指中心金属与可给出电子对或多个不定域电子的物种以配位键形成的化合物。

配位化合物的存在范围极为广泛，在生产生活中起着重要作用。

对它的研究，形成了无机化学的一个重要分支学科——配位化学，并成为引人瞩目的化学领域之一。

对配合物的研究，现在已经有很多方法，这里介绍常见的几种。

1..热分析技术热分析是研究物质随温度变化所发生的物理化学过程以及相应产生的状态变化的一种方法。

这种分析方法应用甚广，国际热分析学会（成立于1965年，简称IOTA ）于1977年对热分析作了如下定义：热分析是在程序控制温度下测量物质的物理性质与温度关系的一类技术。

化合物包括配合物以及材料相，在受热过程中，会发生许多物理变化，譬如熔化、升华和蒸发以及晶型转变，还会发生化合物分解等化学过程，这些过程会伴有热效应；而物理和化学过程中若产生逸出气体，则会发生质量变化。

相应就形成了热分析技术：(1). 示差扫描量热法(DSC)、(2)差热法(DTA)，(3).热重法(TG) (包括微分热重(DTG))。

因此，借助热分析技术可以获得化合物的热稳定性以及热分解反应的许多信息，包括测定熔点、沸点或升华温度，也可以测定多晶转变温度以及热分解过程的揭示。

近年来随着电子技术的发展使这个方法向微量、快速等方面发展，还形成了多种技术联用仪器，包括TG/DSC 同步仪器以及逸出气体的红外、拉曼光谱以及色谱分离联用仪器，使得应用领域逐渐扩大。

图3.1给出了同步热分析仪获得的CaC 2O 4·2H 2O 的热分析图谱，其中包括TG 、DTG 和DSC 三条曲线。

图3.1 CaC 2O 4·2H 2O 的热分析曲线(1) TG 和DTG 曲线　热重分析是在程序控制温度下，测量物质质量与温度关系的一种技术。

热重法实验得100 200 300 400 500 600 700 .800ΔE /μV3.02.5 2.0 1.5 1.0 0.5 0.0 0-2-4-6-8-10ΔG /m g DSC TG DTG到的曲线称为热重(TG)曲线。

静电场中的电势差计算静电场是由带电粒子形成的一种力场，其特征之一就是电势差的存在。

电势差可以用来描述电场中两个位置之间的电势差异。

本文将介绍如何计算静电场中的电势差。

一、电势差的概念电势差是指在静电场中，从一个点A移动到另一个点B所经历的电势变化量。

它是电场力做功的结果，可以用以下公式表示：ΔV = V_B - V_A其中，ΔV表示电势差，V_B表示点B处的电势，V_A表示点A处的电势。

二、电势差的计算方法静电场中的电势差计算可以利用电势差定义公式进行求解。

下面将介绍两种常用的计算方法。

1. 均匀电场中的电势差计算对于均匀电场中两点之间的电势差计算，可以使用以下公式：ΔV = E * d其中，ΔV表示电势差，E表示电场强度，d表示两点之间的距离。

举个例子，在一个均匀电场中，如果电场强度为E = 100 N/C，两点之间的距离为d = 2 m，那么电势差为：ΔV = 100 N/C * 2 m = 200 V2. 非均匀电场中的电势差计算对于非均匀电场中的电势差计算，可以利用积分的方法进行求解。

具体步骤如下：步骤一：选择一个参考点，将其电势定义为零点，即V_0 = 0。

步骤二：选择从参考点到目标点的路径。

步骤三：计算路径上每一点的电势。

步骤四：将计算得到的电势相加，得到电势差。

举个例子，假设有一个非均匀电场，我们需要计算两个点A和B之间的电势差。

选择一个参考点O，将其电势定义为零点。

然后选择从O到A再到B的路径。

在路径上，我们计算每一个点的电势并相加，最终得到电势差。

三、总结本文介绍了静电场中的电势差计算方法，包括均匀电场和非均匀电场中的计算方法。

对于均匀电场，可以利用电场强度和距离的关系进行计算；对于非均匀电场，则需要使用积分的方法来求解。

通过掌握这些计算方法，我们可以更好地理解和分析电场中的电势变化情况。

注意：文章中所提供的公式和计算方法仅适用于静电场中的电势差计算，实际问题中还需根据具体情况进行适当的调整和求解。

综述伏打电池的发明归功于两位意大利科学家。

一位是解剖学家和医学教授伽伐尔，一位是物理学家和化学家伏打。

1780，伽伐尼在一次做青蛙解剖时偶然发现，一只已解剖的青蛙放在一个潮湿的铁案上，当解剖刀无意中触及蛙腿上外露的神经时，青蛙腿部的肌肉立刻抽搐了一下，仿佛受到电流的刺激。

伽伐尼立即重复了这个实验，又观察到了同样的现象。

起初他以为蛙腿发生抽搐是“大气电”作用的结果。

后来他以严谨的科学态度，选择各种不同的金属，例如铜和铁或铜和银接在一起，而把另外两端分别与死蛙的肌肉和神经接触，青蛙就会不停的屈伸抽动；如果用玻璃、橡胶、松香、干木头等代替金属，就不会发生这样的现象。

作为解剖学家和医学家的伽伐尼脑子里总是想着肌肉和神经等，他猜想这是由于动物体内存在“动物电”，伽伐尼于1789 年将此实验结果写成论文《关于电对肌肉运动的作用》，并于1791年公布于学术界。

伽伐尔的实验使人们注意到运动电荷产生的现象。

意大利物理学家伏打和大家一样感到十分振奋，但他认为“动物电”的说法值得进一步研究，拒绝人云亦云。

伏打把注意点主要集中在那两根金属上，而不是青蛙的神经。

他在之前就对电学有着深刻的研究，对于伽伐尔发现的蛙腿抽搐现象，他想这可能与电有关，但是他认为青蛙的肌肉和神经中是不存在电的，他推想电的流动可能是由两种不同的金属相互接触产生的，与金属是否接触动物神经无关。

伏打用自己设计的精密验电器，对各种金属进行了许多实验，这些实验证明，只要在两种金属片间隔以用盐水或碱水浸泡过的（甚至只要是湿的）硬纸、麻布、皮革或其他海绵状的物质，并用金属线把两个金属片连接起来，不管有没有青蛙的肌肉，都会有电流通过。

这就说明电并不是从青蛙的组织中产生的，蛙腿的作用只不过是相当于一个非常灵敏的验电器而已。

在1796年的一封信中，伏打把金属（以及黄铁矿等某些矿石和木炭称为第一类导体或干导体，把酸、碱、盐等的溶液称为第二类导体或湿导体。

他指出：“把第一类导体与第二类导体相接触，就会引起电的扰动，产生电运动。

6.4.5电势的计算方法一般说来，计算电势的方法有两种。

第一种方法是由电势的定义式通过场强的线积分来计算；另一种方法是下面马上就要介绍的电势叠加原理。

对不同的带电体系，本质上讲上述两种方法都能够计算出电势，但是选择不同的方法计算的难易程度是大不相同的。

通过后面内容的学习，大家要注意对不同的带电体系选择不同的计算方法。

下面我们介绍电势迭加原理。

1、点电荷电场的电势如右图所示，一个点电荷q处于O点处。

在q所产生的电场中，距离O点为r处P点的电势，可以根据电势的定义式计算得到。

选无穷远处作为电势零点，积分路径沿O P方向由P点延伸到无穷远。

由于积分方向选取得与场强点电荷的电势的方向相同，P点电势可以很容易地计算出来此式给出点电荷电场中任意一点的电势大小，称作点电荷电势公式。

公式中视q的正负，电势V可正可负。

在正点电荷的电场中，各点电势均为正值，离电荷越远的点，电势越低，与r成反比。

在负点电荷的电场中，各点的电势均为负，离电荷越远的点，电势越高，无穷远处电势为零。

容易看出，在以点电荷为心的任意球面上电势都是相等的，这些球面都是等势面。

2、电势的叠加原理在前面的知识点中，大家学习了场强叠加原理。

该原理告诉我们，任意一个静电场都可以看成是多个或无限多个点电荷电场的叠加，即有其中E表示总电场，E1，E2，…为单个点电荷产生的电场。

根据电势的定义式，并应用场强叠加原理，电场中a点的电势可表示为上式最后面一个等号右侧被求和的每一个积分分别为各个点电荷单独存时在a点的电势。

即有式中V a i是第i个点电荷单独存在时在a点产生的电势。

显然，如果我们将带电体系分成若干部分（不一定是点电荷），上述结论仍然是正确的。

即，任意一个电荷体系的电场中任意一点的电势，等于带电体系各部分单独存在时在该点产生电势的代数和。

这个结论叫做电势叠加原理。

若一个电荷体系是由点电荷组成的，则每个点电荷的电势可以按上式进行计算，而总的电势可由电势叠加原理得到，即式中r i是从点电荷q i到a点的距离。

静电场中的电势差与电势能在物理学中，静电场是指由电荷所产生的电场，而静电场中的电势差和电势能则是描述电荷在该场中相互作用的重要概念。

本文将着重探讨静电场中的电势差与电势能，并对它们的性质和应用进行详细讨论。

一、电势差的概念及计算方法电势差是指在静电场中两点之间的电势差异或电压差异。

在电场中，电势差可以用来描述电荷在空间中移动时所受到的力及电势能的变化。

电势差的计算方法如下：假设在空间中存在电场，两个点A和B分别位于该电场中的不同位置，电势差V_AB可以通过对电场力沿路径积分来计算。

具体地，电势差V_AB等于从点A到点B沿任意路径C的路径积分，即：V_AB = ∫_C E · dl其中，E表示电场强度矢量，l表示路径C上的微元位移矢量。

二、电势差的性质及意义1. 电势差与电场强度的关系：根据电势差的定义可知，电势差与电场强度之间存在一定的关系。

在静电场中，电势差的方向与电场强度的方向相反。

当电势差为正时，电场强度朝着电势升高的方向指向；当电势差为负时，电场强度朝着电势降低的方向指向。

2. 电势差与电荷移动：电势差可以反映电荷在电场中所受到的力及其移动过程中的能量变化。

当电荷从电势较高的点向电势较低的点移动时，它会沿电场线受到电场的作用力，同时将电势能转化为动能。

3. 电势差的单位：国际单位制中，电势差的单位为伏特(V)。

1伏特等于1焦耳(C)每库仑(Coulomb)。

电势差作为静电场中的重要物理量，在电路、电容器、静电存储设备等方面有着广泛的应用。

三、电势能的概念及计算方法电势能是指电荷由于存在于电场中而具有的能量。

在静电场中，电势能可以用来描述电荷在电场中的能量状态。

电势能的计算方法如下：假设一个电荷q位于电场中的某一位置，其电势能U可以通过电荷与引入电场的体系的相互作用来计算。

具体地，电势能U等于电荷q受到电场力沿路径C的位移的负积分，即：U = -∫_C F · dl其中，F表示电场对电荷所施加的力矢量，l表示路径C上的微元位移矢量。

氧化还原与电化学实验一、实验目的1．了解电极电势与氧化还原反应的关系；2．了解氧化态或者还原态浓度变化、形成配合物对氧化还原反应及电极电势的影响；3．掌握原电池的组成和电动势的测定。

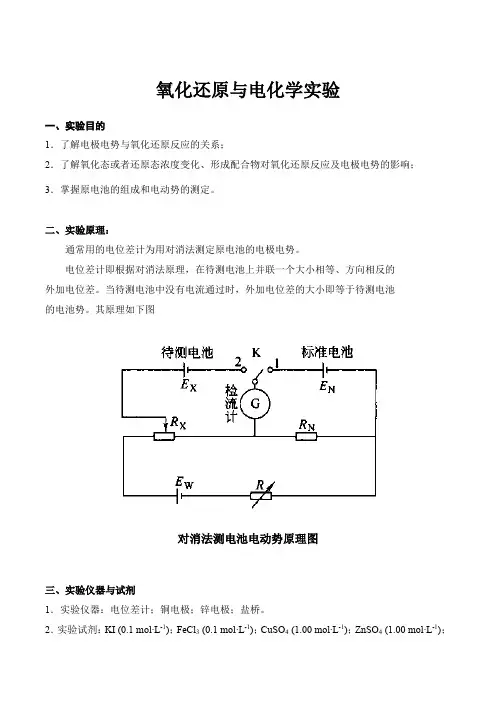
二、实验原理：通常用的电位差计为用对消法测定原电池的电极电势。

电位差计即根据对消法原理，在待测电池上并联一个大小相等、方向相反的外加电位差。

当待测电池中没有电流通过时，外加电位差的大小即等于待测电池的电池势。

其原理如下图对消法测电池电动势原理图三、实验仪器与试剂1．实验仪器：电位差计；铜电极；锌电极；盐桥。

2．实验试剂：KI (0.1 mol∙L-1)；FeCl3 (0.1 mol∙L-1)；CuSO4 (1.00 mol∙L-1)；ZnSO4 (1.00 mol∙L-1)；浓氨水。

四、实验内容1．电极电势与氧化还原反应的关系（1）将3～4滴0.1 mol∙L-1的KI溶液用蒸馏水稀释至1 mL，加入2滴0.1 mol∙L-1的FeCl3溶液，同时溶液中加入少量淀粉，振荡，观察现象。

（2）思考：如果用0.1 mol∙L-1的KBr溶液溶液代替0.1 mol∙L-1的KI溶液做同样的实验会有什么结果？2．浓度对电极电势的影响（1）在一干燥的50 mL小烧杯中加入20 mL 1.00 mol∙L-1 CuSO4溶液，将饱和甘汞电极接入电位差计的正极，铜电极接到正极上，室温下测定其电池电动势。

（2）由1.00 mol∙L-1 CuSO4溶液分别配制0.500 mol∙L-1、0.250 mol∙L-1和0.100 mol∙L-1 CuSO4溶液，用同样的方法分别测定不同浓度时的电池电动势(每次测量前均应将电极洗干净)。

由测得的各电动势数值，计算相应浓度的E(Cu2+/Cu)值。

（3）测定浓差电池的电动势设计电池如下: Cu(S)｜CuSO4(0.100mol·kg-1)‖CuSO4(1.00mol·kg-1)｜Cu(S)电池的电动势3．配合物的形成对电极电势的影响将约8 mL浓氨水溶液加入到Cu/CuSO4 (1 mol∙L-1)半电池的CuSO4溶液中，开始生成Cu(OH)2沉淀，慢慢地沉淀溶解，搅拌，待沉淀完全溶液后，与饱和甘汞电极组成原电池，测定其电动势。

二氨合亚铜离子和铜原子标准电极电势1、二氨合亚铜离子二氨合亚铜离子是一种化学物质，化学式为[Cu(NH3)2]+。

它是由铜离子与两分子氨分别形成化合物后产生。

在这种离子中，铜原子通过配位键与氨分子相连，形成了一个稳定的配合物。

2、铜原子标准电极电势铜原子标准电极电势是指在标准状态下，铜原子在溶液中发生氧化还原反应时的电势。

它是测量氧化还原反应强弱的重要指标之一。

铜原子标准电极电势的数值通常为0.34V。

3、深度评估针对二氨合亚铜离子和铜原子标准电极电势这两个主题，我们需要从化学结构、物理性质、氧化还原反应等多个方面进行深度评估。

我们可以从化学结构的角度探讨二氨合亚铜离子的形成过程，配位键的稳定性以及与其他物质的反应特性。

针对铜原子标准电极电势，我们可以探讨其在不同溶液中的变化规律，以及与其他金属原子的电势比较等内容。

4、全面评估在全面评估二氨合亚铜离子和铜原子标准电极电势时，我们还需要考虑它们在实际应用中的意义和作用。

二氨合亚铜离子在化学合成和催化反应中的应用，以及铜原子标准电极电势在电化学实验和工业生产中的重要性等方面。

5、撰写文章在本文中，我们将首先详细介绍二氨合亚铜离子和铜原子标准电极电势的相关知识，然后从化学结构、物理性质、氧化还原反应等多个角度对这两个主题进行全面评估。

我们将共享对这两个主题的个人观点和理解。

6、文章内容一、二氨合亚铜离子的结构和性质二氨合亚铜离子的化学结构和形成过程氨分子与铜离子的配位键稳定性二氨合亚铜离子的反应特性和应用领域二、铜原子标准电极电势的相关知识标准状态下铜原子的氧化还原反应铜原子标准电极电势的数值和意义铜原子标准电极电势在实际应用中的作用三、深度评估从化学结构、物理性质、氧化还原反应等多个方面对二氨合亚铜离子和铜原子标准电极电势进行深度评估四、全面评估二氨合亚铜离子和铜原子标准电极电势在实际应用中的意义和作用五、个人观点和理解对二氨合亚铜离子和铜原子标准电极电势的个人观点和理解7、总结和回顾通过对二氨合亚铜离子和铜原子标准电极电势的全面评估，我们深入了解了它们的化学结构、物理性质、氧化还原反应等方面的知识，并了解了它们在实际应用中的重要性。

电解池的电势怎么计算公式电解池是化学反应中的一种重要装置，它由两个电极和电解质溶液组成，通过电解质溶液中的离子在电极上的氧化还原反应来产生电流。

电解池的电势是指电解质溶液中的离子在电极上发生氧化还原反应时所产生的电动势，也就是电解质溶液中的离子在电极上发生氧化还原反应时所产生的电压。

电解池的电势可以通过一个简单的公式来计算，下面我们来详细介绍一下。

在电解质溶液中，离子在电极上发生氧化还原反应时，会产生电势差。

这个电势差可以通过电解质溶液中的离子浓度和标准电极电势来计算。

电解质溶液中的离子浓度可以通过离子活度系数来计算，而标准电极电势则是指在标准条件下，电极上的氧化还原反应所产生的电势。

电解质溶液中的离子浓度和标准电极电势可以通过Nernst方程来计算，Nernst方程的表达式如下：E = E0 (RT/nF) ln(Q)。

其中，E是电解质溶液中的离子在电极上发生氧化还原反应时所产生的电势，E0是标准电极电势，R是气体常数，T是温度，n是电子转移数，F是法拉第常数，Q是反应物的活度积。

通过Nernst方程，我们可以计算出电解质溶液中的离子在电极上发生氧化还原反应时所产生的电势。

在实际应用中，我们可以通过Nernst方程来计算电解质溶液中的离子在电极上发生氧化还原反应时所产生的电势。

首先，我们需要确定电解质溶液中反应物的活度积，然后通过Nernst方程进行计算。

在计算过程中，我们需要考虑到温度对电势的影响，因为温度会影响反应物的活度积，从而影响电解质溶液中的离子在电极上发生氧化还原反应时所产生的电势。

除了Nernst方程外，我们还可以通过其他方法来计算电解质溶液中的离子在电极上发生氧化还原反应时所产生的电势。

例如，我们可以通过电解质溶液中的离子浓度和标准电极电势的关系来计算电势差。

在实际应用中，我们可以根据具体的情况选择合适的方法来计算电解质溶液中的离子在电极上发生氧化还原反应时所产生的电势。

总之，电解质溶液中的离子在电极上发生氧化还原反应时所产生的电势可以通过Nernst方程来计算。

大学化学 | 配合物与配位平衡总结●7.1 配位化合物的基本概念●中心离子（或原子）：具有接受孤对电子或不定域电子的空位的原子或离子●具有9~17电子构型的d区金属离子，如Fe3+、Co3+；具有18电子构型的ds区金属离子，如Cu+、Ag+ 等；●s区金属离子如叶绿素中Mg2+、p区高氧化态的非金属元素，如BF4-中B(Ⅲ)、SiF62-中的Si(Ⅳ)、PF6-中的P(Ⅴ)；●0价金属或负价金属，金属羰基配合物Ni(CO)4、Fe(CO)5 和[Ti(CO)6]2−、[M(CO)4]2− (M = Fe, Ru, Os，氧化数-2)。

●配体：能给出孤对电子或多个不定域电子的离子或分子●单齿配体：一个分子只有一个配位原子的配体●氢氰酸：H一C≡N、异氢氰酸：H-N ≡ C●硫氰根以S为配位原子；异硫氰根以N作配位原子。

●多齿配体：含有两个或两个以上配位原子的配体，如乙二胺四乙酸根，其中含有2个N、4个O均可配位，是六齿配体，1个配体可形成多个配位键●桥联配体：如OH-、Cl-不止1对孤对电子，可提供两对电子作桥，桥联多个中心离子。

主要在多核配合物中。

●配位原子：配体中与中心离子直接键合的原子，即提供孤对电子的原子。

常见配位原子是电负性较大的非金属原子，如O、S、N、X等●配位数，C.N.：配位原子的个数●配位数一般为偶数（2、4、6、8），其中最常见的是4和6●配位数大小与中心离子的电荷、半径以及配体的电荷、半径有关●规律●中心离子电荷数越高、半径r越大：内层空轨道越多、周围能容纳的配体就越多，C.N.越大●配体半径 r 越小(在中心离子周围能容纳的配体就越多)，电荷数越少(配体之间的斥力小)， C.N.越大●配合物生成条件：配体浓度越高、温度越低， C.N.越大●●配位单元：由中心离子和配体通过配位共价键结合形成的单元，用[ ]标出●配位键：一个原子提供孤对电子，一个原子或离子的空轨道接受孤对电子形成的共价键●内界：即配位单元，由中心原子（离子）和配体构成的离子●外界：带有与内界异号电荷的离子●如：在配合物[Co(NH3)6]Cl3中，内界[Co(NH3)6]3+，外界Cl-； K4[Fe(CN)6]？中性配位单元作为配合物的[Ni(CO)4]则无外界●7.1.3配合物的命名：中文名的写法●内、外界之间先写阴离子，后阳离子。

点电荷的电势强度公式
点电荷的电势强度公式可以表示为：
\[ V = \frac{k \cdot q}{r} \]
其中，V表示电势强度，k是库仑常数，q是电荷的大小，r是距离电荷的距离。

这个公式告诉我们，电势强度与电荷大小成正比，与距离成反比。

这意味着，电荷越大，电势强度越大；而距离越远，电势强度越小。

这个公式也可以帮助我们计算电荷在空间中的电势分布。

通过测量电荷的大小和距离，我们可以计算出任意点的电势强度，从而了解电场的分布情况。

除了理论上的意义，点电荷的电势强度公式在工程和科学领域也有着广泛的应用。

例如，在电路设计中，我们可以利用这个公式来计算电荷在电路中的电势分布，从而设计出更加稳定和高效的电路。

总之，点电荷的电势强度公式是物理学中非常重要的公式之一，它帮助我们理解电荷在空间中产生的电势场，并在工程和科学领域
中有着广泛的应用。

对于配位反应已知φ0(Cu2+/ Cu )= 0.337V , K0稳[Cu (NH3)42+]=2.1×1013，求电对Cu (NH3)42+ + 2e = Cu + 4NH3的标准电极电势φ0(Cu (NH3)42+/ Cu )？解：电对Cu (NH3)42+ + 2e = Cu + 4NH3的标准态[Cu (NH3)42+]= [NH3]=1.00mol/L根据Cu (NH3)42+ = Cu2+ + 4NH3的配位解离平衡K0稳[Cu (NH3)42+] =[Cu (NH3)42+]/ [Cu2+]·[NH3] 4 =2.1×1013，解得[Cu2+] =1/ K0稳= 4.76×10-14 ( 4分)根据Cu 2+ + 2e = Cu电对的Nernst 方程φ0(Cu (NH3)42+/ Cu ) ==φ(Cu2+/ Cu )= φ0(Cu2+/ Cu )+[ 0.0592 / 2 ]log[Cu2+] = 0.337 +[ 0.0592 / 2 ]log[4.76×10-14] = －0.057V补充：根据Cu 2+ + 2e = Cu电对的Nernst 方程φ(Cu2+/ Cu ) = φ0(Cu2+/ Cu )+[ 0.0592 / 2 ]log[Cu2+]当[Cu2+]= 4.76×10-14 = K0不稳，求出的φ(Cu2+/ Cu )和电对Cu (NH3)42+ + 2e = Cu + 4NH3的标准态φ0(Cu (NH3)42+/ Cu )恰好具有相同的[Cu2+]= 4.76×10-14 = K0不稳值，所以才有等式φ0(Cu (NH3)42+/ Cu ) ==φ(Cu2+/ Cu ) = φ0(Cu2+/ Cu )+[ 0.0592 / 2 ]log[Cu2+]=φ0(Cu2+/ Cu )+[ 0.0592 / 2 ]log [K0不稳]对于沉淀反应①Ag+ +e → Ag电对ϕ(Ag+ /Ag)=ϕ0(Ag+ /Ag)+0.0592lg[Ag+]②AgCl+e→Ag+Cl-电对ϕ(AgCl/Ag)=ϕ0(AgCl/Ag)+0.0592lg{1/[Cl-]}[Cl-]=1.00M为标准态,根据沉淀溶解平衡AgCl(s)→Ag+(aq)+Cl-(aq)K sp=[Ag+][Cl-] 所以②标态[Ag+]= K sp将②标态[Ag+]= K sp带入①能斯特方程得ϕ0(AgCl/Ag)=ϕ(Ag+ /Ag) =ϕ0(Ag+ /Ag)+0.0592lg[K sp]总结:1.酸碱介质ϕB0=ϕA0+ (0.0592) lg[K w]2.弱酸HA/H2电对ϕ0HA/H=ϕA=ϕA0+ (0.0592) lg K HA氧化型金属离子被沉淀或配位时，其标准电极电势值减小。