华师大版高等数学上册第二章导数与微分
- 格式:ppt
- 大小:6.77 MB
- 文档页数:128




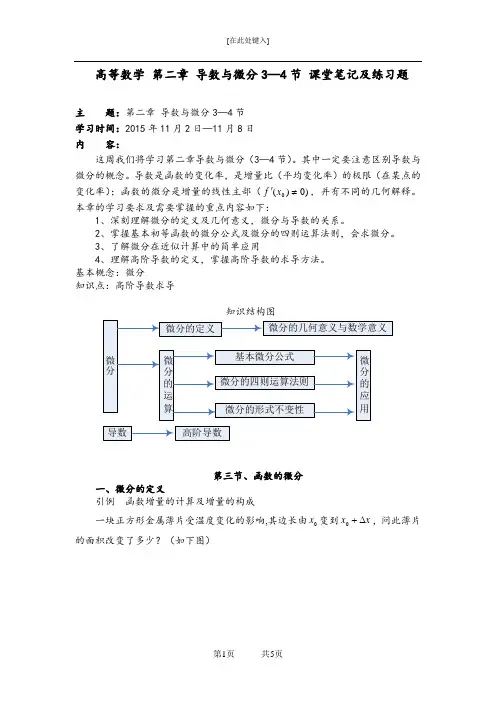
高等数学 第二章 导数与微分3—4节 课堂笔记及练习题主 题:第二章 导数与微分3—4节学习时间:2015年11月2日—11月8日内 容:这周我们将学习第二章导数与微分(3—4节)。
其中一定要注意区别导数与微分的概念。
导数是函数的变化率,是增量比(平均变化率)的极限(在某点的变化率);函数的微分是增量的线性主部()0)(0≠'x f ,并有不同的几何解释。
本章的学习要求及需要掌握的重点内容如下:1、深刻理解微分的定义及几何意义,微分与导数的关系。
2、掌握基本初等函数的微分公式及微分的四则运算法则,会求微分。
3、了解微分在近似计算中的简单应用4、理解高阶导数的定义,掌握高阶导数的求导方法。
基本概念:微分知识点:高阶导数求导知识结构图第三节、函数的微分一、微分的定义引例 函数增量的计算及增量的构成一块正方形金属薄片受温度变化的影响,其边长由0x 变到x x ∆+0,问此薄片的面积改变了多少?(如下图)设此正方形的边长为x ,面积为A ,则A 是x 的函数:2)(x x A =。
金属薄片的面积改变量为202020)(2)()(x x x x x x A ∆+∆=-∆+=∆。
几何意义:x x ∆02表示两个长为0x 宽为x ∆的长方形面积;2)(x ∆表示边长为x ∆的正方形的面积。
数学意义:当0→∆x 时,2)(x ∆是比x ∆高阶的无穷小,即)()(2x x ∆=∆ο;x x ∆02是x ∆的线性函数,它的系数02x 是函数2)(x x A =在0x 处的导数。
当||x ∆很小时,x x A A ∆'≈∆)(0。
定义:设函数)(x f y =在x 处可导,则增量)()(x f x x f y -∆+≈∆的线性主部x x f ∆')(称为)(x f 在x 处的微分,记作dy 或)(x df ,即x x f dy ∆'=)(。
注1:规定x dx ∆=,所以)(x f y =的微分记作x x f dy ∆'=)(,所以)(x f dxdy '=,因此,导数也叫做微商。

数学分析教案(华东师大版)导数和微分一、教学目标1. 理解导数的定义和几何意义;2. 掌握导数的计算法则;3. 学会应用导数解决实际问题,如求函数的极值、单调区间等;4. 理解微分的概念及其应用。
二、教学内容1. 导数的定义与几何意义引入极限的概念,说明导数是函数在某一点的切线斜率;解释导数表示函数在某一点的瞬时变化率;借助几何图形,展示导数表示切线的斜率。
2. 导数的计算法则幂函数、指数函数、对数函数的导数;三角函数的导数;复合函数的导数(链式法则);反函数的导数;高阶导数。
3. 应用导数解决实际问题求函数的极值;判断函数的单调性;求解曲线的切线方程;应用导数解决物理、经济等领域的实际问题。
4. 微分的概念与计算引入微分的概念,说明微分表示函数在某一点的增量;掌握微分的计算法则,如乘法法则、幂函数的微分等;应用微分求解函数的增量。
三、教学方法1. 采用讲授法,系统地介绍导数和微分的概念、计算法则及应用;2. 借助图形和实例,直观地展示导数和微分的几何意义;3. 引导学生通过练习,巩固所学知识,提高解题能力;4. 鼓励学生提问、讨论,提高课堂互动性。
四、教学准备1. 教案、教材、课件等教学资源;2. 投影仪、黑板、粉笔等教学工具;3. 练习题及答案。
五、教学评价1. 课堂提问:检查学生对导数和微分概念、计算法则的理解;2. 课后作业:评估学生对课堂所学知识的掌握程度;3. 章节测试:检测学生对导数和微分知识的综合运用能力。
六、教学内容5. 利用导数研究函数的极值与单调性定义极值的概念,介绍第一类和第二类极值;利用导数判断函数的单调区间;求解函数的极值点和单调区间。
6. 洛必达法则与极限的计算引入洛必达法则,解释其在极限计算中的应用;演示洛必达法则的具体操作步骤;练习使用洛必达法则计算极限。
七、教学内容7. 高阶导数与隐函数求导定义高阶导数,介绍高阶导数的计算法则;引入隐函数的概念,讲解隐函数求导的方法;举例说明隐函数求导的应用。



数学分析教案(华东师大版):导数和微分第一章:导数概念1.1 引入导数的概念解释导数的定义:函数在某一点的导数是其在该点的切线斜率。
强调导数的重要性:导数可以描述函数在某一点的局部性质,如增减性、凹凸性等。
1.2 导数的计算讲解导数的计算方法:常数函数的导数为0;幂函数的导数为其指数乘以底数的指数减1;指数函数的导数为底数;对数函数的导数为1除以函数的底数;三角函数的导数分别为各自的导数公式。
1.3 导数的应用解释导数的应用:求函数的极值:导数为0的点可能是极值点,通过二阶导数判断;求函数的单调区间:导数大于0表示函数递增,导数小于0表示函数递减;求曲线的切线方程:利用导数求出切点坐标和切线斜率,写出切线方程。
第二章:微分2.1 微分的概念解释微分的定义:微分是导数的一个局部线性逼近,表示函数在某一点的增量与自变量的增量之比。
强调微分的重要性:微分可以用来近似计算函数在某一点的增量,简化计算。
2.2 微分的计算讲解微分的计算方法:利用导数计算微分:微分等于函数在该点的导数乘以自变量的增量;微分的性质:微分是无穷小量,具有线性、齐次性和对称性。
2.3 微分的应用解释微分的应用:近似计算函数在某一点的增量:利用微分公式,将自变量的增量代入计算;求曲线的切线:利用微分求出切点坐标和切线斜率,写出切线方程;微分方程的求解:通过微分方程描述物理、化学等现象的规律,求解未知函数。
第三章:导数和微分的进一步应用3.1 洛必达法则介绍洛必达法则:当函数在某一点的导数为0时,可以通过求导数的极限来判断该点是否为极值点。
3.2 罗尔定理介绍罗尔定理:如果函数在某一区间内有两个不同的点处的导数相等,则在这两点之间存在一个点,使得函数在该点处的导数为0。
3.3 泰勒公式介绍泰勒公式:将函数在某一点附近展开为多项式,可以用来近似计算函数在该点附近的值。
第四章:高阶导数4.1 高阶导数的定义解释高阶导数的定义:函数的n阶导数是其导数的导数,即导数的导数直到第n 次。
