辽宁省铁岭市昌图县七年级数学上册第一章丰富的图形世界1.1生活中的立体图形2学案无答案新版北师大版

展开与折叠教师寄语：天才就是无止境刻苦勤奋的能力 －－卡莱尔 一、学习目标——目标明确、行动有效1. 通过展开与折叠活动，了解三棱柱、四棱柱、五棱柱、圆柱、圆锥的侧面展开图；2. 经历展开与折叠、模型制作等活动，发展空间观念，积累数学活动经验．课标要求：了解直棱柱的侧面展开图.二、温馨提示——方法得当、事半功倍 学习重点：通过活动了解棱柱、圆柱、圆锥的侧面展开图．学习难点：通过活动能感受到研究空间问题的思维方法．三、课前热身——温故而知新 将图中的棱柱沿某些棱剪开，展成一个平面图形，你能得到哪些形状的平面图形？试一试，画一画？四、课堂探究——质疑解疑、合作探究探究点1：棱柱的表面展开图以下_______图形经过折叠可以围成一个棱柱?你能将上图中不能围成棱柱的图形适当修改后使其能折叠成棱柱吗?例题：1.下面的图形中，________图形经过折叠可以围成一个棱柱？2. 哪种几何体的表面能展开成下面的图形？你能在下面写出这些几何体的名称吗？练习：1.图中的两个图形经过折叠_________能否围成棱柱？2. 哪种几何体的表面能展开成下面的平面图形？你能在下面写出这些几何体的名称吗？3．如图是一个棱柱的表面展开图，则它是______棱柱.探究点2：圆柱和圆锥的表面展开图把圆柱的侧面展开，会得到什么图形？把圆锥的侧面展开，会得到什么图形？先想一想，再画一画.结论：圆柱的侧面展开图是_________，圆锥的侧面展开图是_________.____________________________________________例题：哪种几何体的表面能展开成下面的平面图形？你能在下面写出这些几何体的名称吗？练习：下图中都是几何体的展开图，你能在下面写出这些几何体的名称吗？探究点3：利用几何体的表面展开图求几何体的体积例题：（2013黄冈）已知一个圆柱的侧面展开图为长方形，则其底面圆的面积为（ ）A ．πB ．4πC ．π或4πD ．2π或4π练习：如图，是一张纸片，尺寸如下，它能否做成一个长方体盒子？若能，求出它的体积._________ _________ __________________五、巩固提升——（有效训练、反馈矫正）1．下列立体图形中，侧面展开图是扇形的是( )2．如下图（ ）不是三棱柱的表面展开图3．下图中各图形经过折叠后不能围成一个棱柱的是（ ）4.下图是某些几何体的平面展开图,写出它们的名称.5．如图是某种几何体表面展开图的图形，这个几何体是（ ）A ．棱柱B ．球C ．圆柱D ．圆锥6.下列四个图中，是三棱锥的表面展开图的是（ ）_________ _________ _________7．如下图（）是四棱柱的侧面展开图．8．图中的两个图形_____经过折叠能否围成棱柱？9．下列几何体不能展开成平面图形的是（）A．圆锥 B．球C．圆台 D．正方体10．如图所示，沿图中虚线把圆柱的侧面展开，会得到什么图形？若圆柱的底面半径为4厘米，圆柱的高为5厘米，求侧面展开图的面积．本文档仅供文库使用。

生活中的立体图形课题§1.1生活中的立体图形〔2〕主备审阅七年级数学组时间课型新授授课教师教师寄语：世上最重要的事，不在于我们在何处，而在于我们朝着什么方向走一、学习目标——目标明确、行动有效1. 通过丰富的实例，进一步认识点、线，面、初步感受点、线、面之间的关系；2. 进一步经历从现实世界中抽象出图形的过程，从构成图形的根本元素的角度认识几何体的某些特征．课标要求：通过丰富的实例，进一步认识点、线、面.二、温馨提示——方法得当、事半功倍学习重点：认识点、线、面，初步感受点、线、面的关系．学习难点：认识“点动成线、线动成面、面动成体〞的事实．三、课前热身——温故而知新⑴你能找出图中的点、线、面吗？⑵哪些线是直的，哪些线是曲的?⑶哪些面是平的，哪些面是曲的？四、课堂探究——质疑解疑、合作探究探究点1：立体图形中的点、线、面.仔细观察，以下图形是由点、线、面构成的吗？⑴正方体是由几个面围成的？圆柱体是由几个面围成的？它们都是平的吗？⑵圆柱的侧面与底面相交成几条线？它们是直的还是曲的？⑶正方体有几个顶点？经过每个顶点有几条边？结论：图形是由、、构成的，面与面相交得到，线与线相交得到 . 例题：下面的立体图形分别是由几个面围成的,它们是平面还是曲面.练习：1．图形一般是由〔〕A．点、线、面构成 B．线和面构成 C．点和面构成 D．点和线构成2．围成圆柱的面有〔〕A．3个 B．2个 C．1个 D．多于3个3．下面几种几何图形中，含有曲面的是〔〕A.〔1〕〔3〕 B．〔1〕〔2〕 C.〔2〕〔3〕 D．〔2〕〔4〕探究点2：图形的形成观察以下图，你发现了什么？点动成，线动成，你还能举出类似以上三幅图的例子吗？例题：飞机表演“飞机拉线〞，我们用数学知识可解释为点动成线，用数学知识解释以下现象：〔1〕一只蜗牛行走留下的路线可解释为_________．〔2〕自行车辐条运动形成的图形可解释为_________．〔3〕一个圆沿着它的一条直径旋转形成图形可解释为________．练习：〔1〕假设我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了______________, 〔2〕时钟秒针旋转时,形成一个圆面,这说明了_______________,〔3〕三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了___________________.探究点3：旋转体圆柱可以看做由哪个平面图形旋转得到？球体和圆锥呢？例题：如下图，花瓶的外表可以看做由哪个平面图形绕虚线旋转一周而得到？用线连一连.练习：如下图，第二行的图形绕虚线旋转一周，便能形成第一行的某个几何体，用线连起来．五、稳固提升——〔有效训练、反应矫正〕1．围成一个三棱柱，所需平面的个数为( )A．3个 B．4个C．5个 D．6个2．六棱柱共有〔〕条棱.A.16B.17C.18D.203．正方形纸片绕它的一边旋转一周所得的几何体是( )A．正方体 B．圆锥C．圆柱 D．球4．如图，图中的图形沿虚线旋转一周所形成的几何体是( )A．圆柱 B．正方体C．长方体 D．圆锥5．用图甲的图形绕轴旋转一周，可得〔〕图形6．以下说法，不正确的选项是〔〕A. 圆锥和圆柱的底面都是圆B. 棱锥底面边数与侧棱数相等C. 棱柱的上、下底面是形状、大小相同的多边形D. 长方体是四棱柱，四棱柱是长方体7．以下几何体中有6个面的有〔〕⑴长方体⑵圆柱⑶四棱柱⑷正方体⑸三棱柱A．3个 B．2个C．1个 D．4个8．观察左图，左边的图形绕着给定的直线旋转一周后可能形成的几何体是〔〕9.以下几何体可以由平面图形绕其中一条直线旋转一周得到是___________.10.第一行的图形绕虚线转一周，能形成第二行的某个几何体，用线连起来.。

展开与折叠教师寄语：只有不断找寻机会的人才会及时把握机会一、学习目标——目标明确、行动有效1. 了解立体图形可由平面图形围成，立体图形可展开为平面图形；2. 通过展开与折叠的实践操作，在经历和体验图形的转换过程中，初步建立空间概念，发展几何直觉. 课标要求：能根据展开图判断和制作立体模型.二、温馨提示——方法得当、事半功倍 学习重点：了解正方体可以通过平面图形的折叠而得到．学习难点：正确判断哪些平面图形可以折叠为正方体．三、课前热身——温故而知新在生活中，我们经常见到正方体形状的盒子，为了设计和制作的需要，我们应了解正方体盒子展开后的平面图形.四、课堂探究——质疑解疑、合作探究探究点1：正方体的表面展开图的识别将一个正方体的表面沿某些棱剪开,能展成一个平面图形吗？你能得到下面的平面图形吗？你能得到哪些形状的平面图形？你剪开了几条棱？把展开后的图形画在下面，与同伴进行交流.小明同学得到了11种图形，你同意吗？例题：在下面的图形中，（ ）是正方体的表面展开图.练习：如图（ ）是正方体的展开图．例题：有一个正方体和四个展开的正方体表面图形，（ ）可以折成如下图的正方体．练习：将右图围成一个正方体，这个正方体应是（ ）探究点2：正方体的表面展开图的应用如图，把下面的图形折成一个正方体的盒子，折好以后，与1相邻的数是什么？相对的数是什么？ A B C DA B C DA B C D正方体的表面展开图有11种情况,你能找到所有情况相对的面吗？例题：把图中的硬纸片沿虚线折起来，便可成为一个正方体，这个正方体的2•号平面的对面是（）A．3号面B．4号面C．5号面D．6号面练习：若要使得图中平面展开图折叠成正方体后，相对面上的两个数之和为15，则 x+y+z的值为_______.五、巩固提升——（有效训练、反馈矫正）1.下图中经过折叠后不能围成正方体的是（）2.当下图的图案被折起来组成一个立方体,哪一个数字会在与5•所在的平面相对的平面上?_______ _______3.如图，有一个无盖的正方体纸盒，下底标有字母“M”，沿图中粗线将其剪开展成平面图形．想一想,这个平面图形是（）4．如图，将正方体的表面分别标示上数字1，2，3，4, 5，6使它任意两个相对面上两数和为7，将它沿某些棱剪开，能展开成下列的平面图形的是___________.5．下面四个图形每个均由六个相同的小正方形组成，折叠后能围成正方体的是（）6. （2013河南）如图是正方形的一种展开图,其中每个面上都标有一个数字,那么在原正方形中，与数字“2”相对的面上的数字是( )A．1 B.4C.5D.67．小丽制作了一个如下左图所示的正方体礼品盒，其对面图案都相同，那么这个正方体的平面展开图可能是（）8．如图是一个正方体纸盒的展开图，若在其中的三个正方形A，B，C内分别填入适当的数，使得它们折成正方体的相对的面上的两个数互为倒数，则填入正方形A，B，C内的三个数依次是_____，_____，_____.。

辽宁省铁岭市昌图县七年级数学上册第一章丰富的图形世界1.1 生活中的立体图形（1）学案（无答案）（新版）北师大版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（辽宁省铁岭市昌图县七年级数学上册第一章丰富的图形世界1.1 生活中的立体图形（1）学案（无答案）（新版）北师大版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为辽宁省铁岭市昌图县七年级数学上册第一章丰富的图形世界1.1 生活中的立体图形（1）学案（无答案）（新版）北师大版的全部内容。

生活中的立体图形教师寄语:成功与不成功之间有时距离很短只要后者再向前几步一、学习目标-—目标明确、行动有效1。

在具体的情境中，认识并能够辨别出基本的几何体；2. 能用自己的语言描述单个几何体的基本特征,并能根据几何体的某些特征将其分类． 课标要求:通过丰富的实例,进一步认识点、线、面。

二、温馨提示——方法得当、事半功倍学习重点：通过观察,讨论，思考活动，将学生生活中常见的实物模型抽象成简单的几何体． 学习难点:从具体实物中抽象出几何体的概念和动手做几何图形． 三、课前热身——温故而知新1。

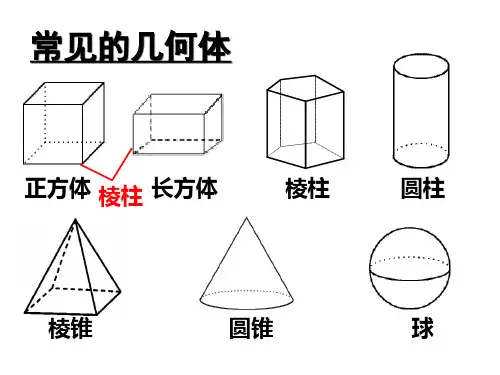
请将下面的几何体的名称填在括号内.2.你在小学还学过哪些几何体？_____________. 四、课堂探究-—质疑解疑、合作探究 探究点1:从实物中抽象出几何体课题§1.1生活中的立体图形（1）主备审阅七年级数学组时间课型 新 授 授课教师( ) ( ) ( ) ( ) ( ) ( )请参观我的简易书房.⑴在小明的书房中，哪些物品的形状与小学还学过几何体类似?______________________________。

第一章丰富的图形世界知识要点1、几何图形从实物中抽象出来的各种图形，包括立体图形和平面图形.2、点、线、面、体（1）几何图形的组成点:线和线相交的地方是点，它是几何图形中最基本的图形。

线：面和面相交的地方是线，分为直线和曲线。

面:包围着体的是面，分为平面和曲面。

体：几何体也简称体。

（2）点动成线,线动成面，面动成体。

3、生活中的立体图形圆柱柱生活中的立体图形球棱柱:三棱柱、四棱柱（长方体、正方体）、五棱柱、……(按名称分) 锥圆锥棱锥球体:由球面围成的（球面是曲面)圆柱:圆柱的表面展开图是由两个相同的圆形和一个长方形连成.圆锥：圆锥的表面展开图是由一个圆形和一个扇形连成.4、棱柱及其有关概念:棱：在棱柱中，任何相邻两个面的交线，都叫做棱。

侧棱：相邻两个侧面的交线叫做侧棱.棱柱的上、下底面的形状相同，侧面的形状都是长方形根据底面图形的边数，人们将棱柱分为三棱柱、四棱柱、五棱柱、六棱柱……它们底面图形的形状分别为三角形、四边形、五边形、六边形……长方体和正方体都是四棱柱。

n棱柱有两个底面，n个侧面，共（n+2）个面；3n条棱，n条侧棱；2n个顶点。

*5、正方体的平面展开图：11种1-4—1型:6种2—3—1型：3种2—2—2型：1种3-3型：1种6、截一个正方体：用一个平面去截一个正方体，截出的面可能是三角形，四边形，五边形,六边形。

7、三视图物体的三视图指主视图、俯视图、左视图.主视图：从正面看到的图，叫做主视图.左视图：从左面看到的图，叫做左视图.俯视图：从上面看到的图，叫做俯视图。

北师大版七年级数学上册说课稿：第一章丰富的图形世界1.1生活中的立体图形（第2课时）一. 教材分析《丰富的图形世界》是北师大版七年级数学上册第一章的内容，本章主要让学生接触和认识各种平面图形和立体图形，培养学生的空间想象能力和抽象思维能力。

1.1节生活中的立体图形，主要通过生活中的实例，让学生认识和了解常见的立体图形，如长方体，正方体，圆柱体，圆锥体等。

这些立体图形在现实生活中无处不在，本节课旨在让学生能够识别这些图形，并了解它们的特点。

二. 学情分析七年级的学生已经具备了一定的空间想象能力，他们对生活中的立体图形并不陌生。

但是，对于如何用数学的眼光去看待和理解这些立体图形，可能还存在一定的困难。

因此，在教学过程中，教师需要引导学生从生活的实例中抽象出立体图形，并了解它们的特点。

三. 说教学目标1.知识与技能目标：让学生能够识别和了解长方体，正方体，圆柱体，圆锥体等常见的立体图形，并能够描述它们的特点。

2.过程与方法目标：通过观察，操作，思考，让学生感受和体验到生活中立体图形的存在，培养学生的空间想象能力和抽象思维能力。

3.情感态度与价值观目标：让学生感受到数学与生活的紧密联系，激发学生学习数学的兴趣。

四. 说教学重难点1.教学重点：让学生能够识别和了解长方体，正方体，圆柱体，圆锥体等常见的立体图形，并能够描述它们的特点。

2.教学难点：如何引导学生从生活的实例中抽象出立体图形，并了解它们的特点。

五. 说教学方法与手段1.教学方法：采用观察，操作，思考，讨论等教学方法，让学生在活动中学习，体验学习的过程。

2.教学手段：利用多媒体课件，实物模型等教学手段，帮助学生直观地认识和理解立体图形。

六. 说教学过程1.导入：通过展示一些生活中的实物，如牙膏盒，篮球，圆柱形的饮料瓶等，让学生观察并思考这些实物是什么立体图形。

2.新课导入：介绍长方体，正方体，圆柱体，圆锥体等常见的立体图形，并通过多媒体课件展示它们的特点。

几何学起源
考古资料表明，十万年前的陶制器皿上已出现了几何图形的花纹；某些器皿、工具也都呈现了几何形状。

在中国，殷代的甲骨文(至少是公元前1200年)中，已有了“规”、“矩”二字；《周髀算经》(公元前100年前后)一书中，已明确了矩(相当于直角三角形)在测量中的作用。

一般认为，几何学起源于测地、航海、天文学，以及日常生活的测积（长度、面积、容积）与铺地板等等。

几何的第一个来源是测地。

希腊历史学家希罗多德（Herodotus, 约公元前485～425年）认为，古埃及的尼罗河常常洪水泛滥湮没田地，几乎每年都需要重新测量土地，确定其归属。

Geometry（几何学）一词就是由（Geometrein）演变而来的，其中（geo）是指土地，「metrein」是指测量。

测量土地的人叫做rope-stretchers (操绳师)，因为绳子是用来帮忙测量的工具，具有精湛的测量技术与丰富的几何知识。

几何的第二个来源是航海与天文学。

中外的天文观测可以追溯到公元前两千多年以前，这种对星空的观察逐渐抽象出点、线、三角形、多边形、圆、方向、角度、距离等几何概念，以及三角形的测量。

据公元前六世纪巴比伦的一个文件说，他们已经能够事先计算出太阳和月亮的相对位置，有可能预测日、月食了。

几何学的第三个来源是日常生活的测积。

在现存的古埃及数学的《纸草纸》书中，记载了一系列的简单平面几何图形的面积计算公式。

此外，还记载有计算容积、计算土方的公式等。

所以，几何是由天文、测地、求积等需要而产生的，几何知识是来源于生产实践又用于生产实践的。

七年级数学上册第一章丰富的图形世界1 生活中的立体图形图形是怎样构成的？素材（新版）北师大版
编辑整理：
尊敬的读者朋友们：
这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（七年级数学上册第一章丰富的图形世界1 生活中的立体图形图形是怎样构成的？素材（新版）北师大版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为七年级数学上册第一章丰富的图形世界 1 生活中的立体图形图形是怎样构成的？素材（新版）北师大版的全部内容。

图形是怎样构成的？
难易度：★★★
关键词：图形的构成
答案：
图形是由点、线、面构成的。

面与面相交成线,线与线相交得到点。

【举一反三】
典题：下列立体图形中，有五个面的是（）。

A、四棱锥
B、五棱锥
C、四棱柱
D、五棱柱
思路导引：四棱锥有五个面，五棱锥有六个面，四棱柱有6个面,五棱柱有7个面。

标准答案：选A.。