小学数学 阴影部分面积计算

4、六年级《如何巧妙的求阴影部分的面积》教学设计一等奖一、教学内容：人教版第97页平面图形的周长和面积。

二、教学目标：1、进一步理解平面图形的周长和面积的意义与区别。

使学生了解平面图形的周长和面积计算公式的推导过程，并会运用这些公式进行正确计算。

2、使学生对平面图形的周长和面积形成知识体系。

三、教学重点：复习计算公式四、难点：公式推导过程，并能熟练的应用公式进行计算。

五、教学设计：1、呈现面积计算公式我们学过这些平面图形，它们的面积公式是怎样的？如何用字母表示呢？根据学生的回答逐个出示平面图形。

2、逐个梳理推导过程这六个平面图形的面积公式是怎么推导出来的.呢？我们一起来回忆一下。

（小组讨论）学生可以相互说说，媒体演示推导过程：长方形：s=ab正方形：s=a2平行四边形：S=ah三角形：s= 1/2 ab梯形：s= （a+b）h圆：s=r23、整理完善知识结构平面图形面积计算公式是以长方形面积公式为基础推导来的：因为S长=___________，而正方形是（）和（）相等的长方形，所以S正=________；平行四边形可以割补成长方形，它的底相当于（），高相当于（），所以S平=___________；两个形状、大小相同的三角形，可以拼成一个（），所以S三=___________；两个形状、大小相同的梯形，可以拼成一个（），所以S梯=____________；圆可以割补成一个近似的长方形，这个长方形的长相当于圆的（），长方形的宽相当于圆的（），所以S圆=___________，最后推出S圆=___________。

4、练习：第97页做一做。

5、六年级《如何巧妙的求阴影部分的面积》教学设计一等奖【教学内容】北师大版小学数学第十一册第一单元P16——18圆的面积【教学目标】1、了解圆的面积的含义，经历圆面积计算公式的推导过程，掌握圆面积计算公式。

2、能正确运用圆的面积公式计算圆的面积，并能运用圆面积知识解决一些简单实际的问题。

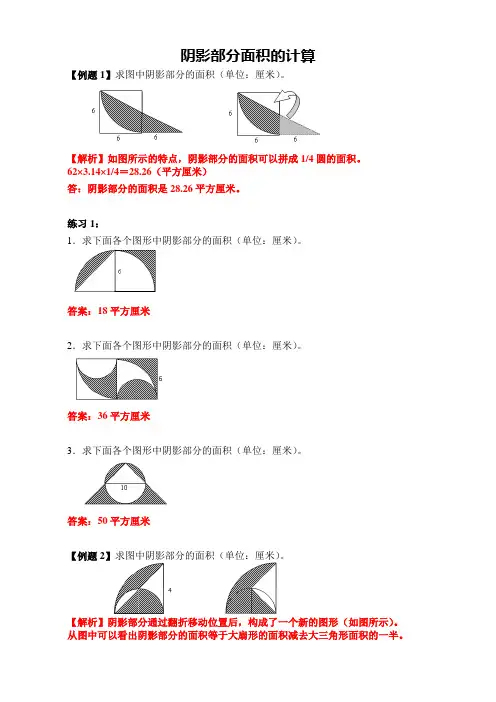
阴影部分面积的计算【例题1】求图中阴影部分的面积（单位：厘米）。

【解析】如图所示的特点，阴影部分的面积可以拼成1/4圆的面积。

62×3.14×1/4＝28.26（平方厘米）答：阴影部分的面积是28.26平方厘米。

练习1：1．求下面各个图形中阴影部分的面积（单位：厘米）。

答案：18平方厘米2．求下面各个图形中阴影部分的面积（单位：厘米）。

答案：36平方厘米3．求下面各个图形中阴影部分的面积（单位：厘米）。

答案：50平方厘米【例题2】求图中阴影部分的面积（单位：厘米）。

【解析】阴影部分通过翻折移动位置后，构成了一个新的图形（如图所示）。

从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。

3.14×4×4×1/4－4×4÷2÷2＝8.56（平方厘米）答：阴影部分的面积是8.56平方厘米。

练习2：1．计算下面图形中阴影部分的面积（单位：厘米）。

答案：8平方厘米2．计算下面图形中阴影部分的面积（单位：厘米，正方形边长4）。

答案：8平方厘米3．计算下面图形中阴影部分的面积（单位：厘米，正方形边长4）。

答案：4.56平方厘米【例题3】如图19－10所示，两圆半径都是1厘米，且图中两个阴影部分的面积相等。

求长方形ABO1O的面积。

【解析】因为两圆的半径相等，所以两个扇形中的空白部分相等。

又因为图中两个阴影部分的面积相等，所以扇形的面积等于长方形面积的一半（如图19－10右图所示）。

所以3.14×12×1/4×2＝1.57（平方厘米）答：长方形长方形ABO1O的面积是1.57平方厘米。

练习3：1．如图所示，圆的周长为12.56厘米，AC两点把圆分成相等的两段弧，阴影部分（1）的面积与阴影部分（2）的面积相等，求平行四边形ABCD的面积。

答案：12.56平方厘米2．如图所示，直径BC＝8厘米，AB＝AC，D为AC的中点，求阴影部分的面积。

计算图19-1中阴影部分面积是多少平方厘米？（圆的半径r=10厘米，∏取3.14）分析：要计算图19-1中阴影部分的面积，关键在于处理图中空白部分的面积。

利用割补进行转化，把空白部分转移到圆的边缘。

如图19-2所示，这样阴影部分面积就可以转化为41圆面积加上两个正方形的面积来计算。

解 ∏×102×41+102×2=25∏+200=78.5+200=278.5图19-3大小两圆相交部分面积是大圆面积的154，是小圆面积的53，量得小圆的半径是5厘米，问大圆的半径是多少厘米？分析：因为已知阴影部分与大圆，小圆的面积比，所以可以先求出两圆面积的比，继而求出它们的半径比。

，解 设阴影部分的面积为1.则小圆面积是415，小圆面积是35。

于是： 大圆面积：小圆面积=415：35=49=（23）2 5×23=7.5厘米如图19-4，正方形面积是8平方厘米。

求阴影部分的面积是多少平方厘米？分析：这道题按常规思路是：要求阴影部分的面积，用正方形的面积减去一个四分之一圆的面积。

因此，只要知道圆的半径，问题就得到解决了。

但是，从题中的已知条件知道，圆的半径是不可能求出的，问题难以得解。

这时，就必须改变解题思路，重新审题和分析图形，从图中不难看到，正方形的边长等于圆的半径，进而可以推出a ×a=r ×r=8平方厘米。

所以，在求四分之一圆的面积时，就不必按常规的方法，去求解圆的半径，而直接用8平方厘米代替r ×r 的面积，四分之一圆的面积是3.14×8×41=6.28平方厘米，则阴影部分的面积就是8-3.14×8×41=1.72平方厘米。

如图19-7，求空白部分的面积是正方形面积的几分之几？分析：因为圆和正方形它们的对称性，可以先画出两条辅助线帮助分析，即将正方形分成4个全等的小正方形。

先看上面的两个小正方形，从圆中可知，A=B ，C=D 。

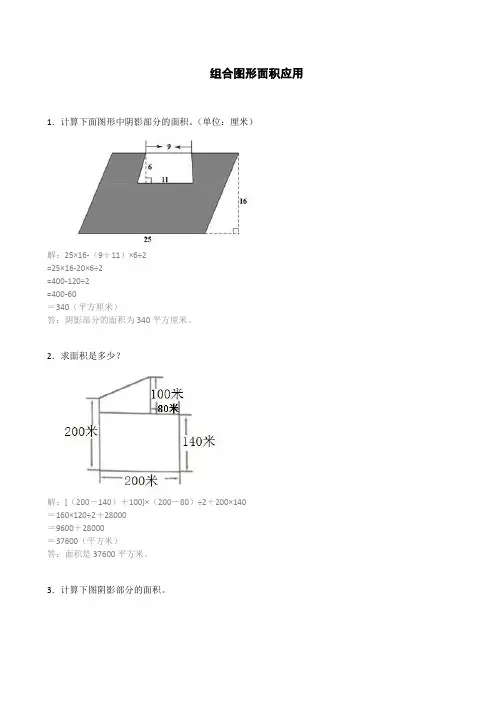
组合图形面积应用1．计算下面图形中阴影部分的面积。

（单位：厘米）解：25×16-（9＋11）×6÷2=25×16-20×6÷2=400-120÷2=400-60＝340（平方厘米）答：阴影部分的面积为340平方厘米。

2．求面积是多少？解：[（200－140）＋100]×（200－80）÷2＋200×140＝160×120÷2＋28000＝9600＋28000＝37600（平方米）答：面积是37600平方米。

3．计算下图阴影部分的面积。

解：阴影部分的面积=（10+15）×10÷2-10×10÷2 =25×10÷2-100÷2=250÷2-50=125-50=75（平方米）。

4．计算阴影部分的面积。

（单位：cm）解：60×40-60×40÷2=2400-2400÷2=2400-1200=1200（平方厘米）5．求下面组合图形的面积。

（单位：cm）解：8×4＋8×4÷2=32＋32÷2=32＋16=48（平方厘米）6．计算下面阴影部分的面积。

（1）（2）（1）解：阴影部分的面积=14×12÷2=168÷2=84（平方厘米）（2）解：阴影部分的面积=12×10-12×6÷2=120-72÷2=120-36=84（平方分米）（2）阴影部分的面积=平行四边形的面积-三角形的面积，平行四边形的底是20dm，高是10dm；三角形的底是20dm，高是6dm，再根据平行四边形的面积=底×高，三角形的面积=底×高÷2，代入数值计算即可。

7．计算下面图形的面积。

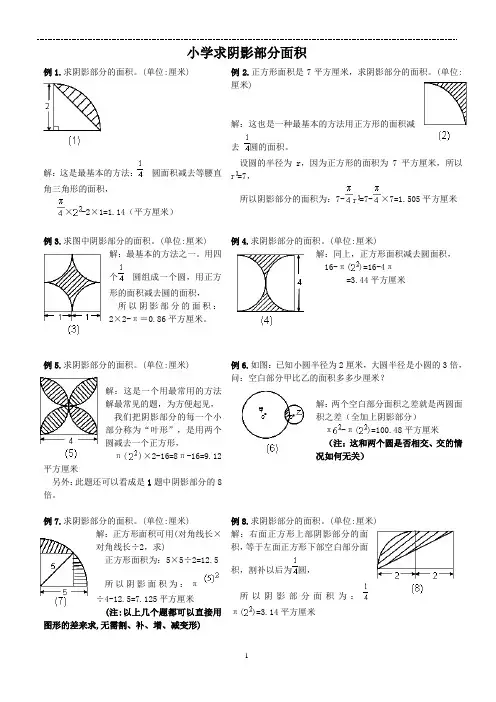
小学数学图形求阴影部分面积十大方法总结(附例题)_2023.9小学阶段的学生通常在学习上存在着总结归纳能力欠缺等问题，为了很好地帮助孩子系统地掌握小学阶段的数学知识，老师把小学求图形面积的十大方法给大家做了总结，各位家长，快给孩子收藏起来吧！我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算。

如下表：实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。

那么，不规则图形的面积及周长怎样去计算呢？我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了。

例题分析例1、如下图，甲、乙两图形都是正方形，它们的边长分别是10 厘米和12 厘米. 求阴影部分的面积。

一句话：阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形（△ABG、△BDE、△EFG）的面积之和。

例2、如下图，正方形ABCD 的边长为 6 厘米，△ABE、△ADF 与四边形AECF 的面积彼此相等，求三角形AEF 的面积。

一句话：因为△ABE、△ADF 与四边形AECF 的面积彼此相等，都等于正方形ABCD 面积的三分之一，也就是12 厘米。

解：S△ABE=S △ADF=S 四边形AECF=12在△ABE 中，因为AB=6. 所以BE=4，同理DF=4，因此CE=CF=2 ，∴△ECF 的面积为2×2÷2=2 。

所以S△AEF=S 四边形AECF-S △ECF=12-2=10 （平方厘米）。

例3、两块等腰直角三角形的三角板，直角边分别是10 厘米和 6 厘米。

如右图那样重合.求重合部分（阴影部分）的面积。

一句话：阴影部分面积=S△ABG-S △BEF，S△ABG 和S△BEF 都是等腰三角形总结：对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合，分析整体与部分的和、差关系，问题便得到解决求面积十大方法01相加法这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如：求下图整个图形的面积一句话：半圆的面积+正方形的面积=总面积02相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差. 例如：下图，求阴影部分的面积。

小学阴影面积求解技巧和方法小学阴影面积求解是数学中的一个重要内容，掌握好这个技巧和方法可以帮助我们更好地理解和应用数学知识。

下面，我将为您介绍一些小学阴影面积求解的技巧和方法。

一、认识阴影面积的概念阴影面积是指物体挡住光线后所产生的面积。

在数学中，我们通常通过几何图形的形状和位置关系去计算阴影面积。

二、常见的几何图形阴影面积计算方法1. 长方形和正方形的阴影面积计算方法：当光线垂直照射在长方形或正方形上时，阴影面积等于图形的面积，即长度乘以宽度。

2. 三角形的阴影面积计算方法：当三角形的一条边平行于光线且与地面平行时，阴影面积等于三角形的面积的一半。

阴影面积 = 三角形面积 / 23. 梯形的阴影面积计算方法：当梯形的两条平行边平行于光线且与地面平行时，阴影面积等于梯形的面积的一半。

阴影面积 = 梯形面积 / 24. 圆形的阴影面积计算方法：当光线垂直照射在圆形上时，阴影面积等于圆形的面积。

阴影面积 = 圆形面积5. 正方体和长方体的阴影面积计算方法：当正方体或长方体在某一面上完全阻挡光线时，阴影面积等于这个面的面积。

阴影面积 = 长方体面积或正方体面积三、实例分析1. 某正方形的一角被光线照射，求阴影面积。

解法：由于正方形的一角被光线照射，那么这个阴影的形状是一个直角三角形。

因此，阴影面积等于正方形面积的一半。

2. 光线从上方照射到一个梯形上，求阴影面积。

解法：由于梯形的两条平行边平行于光线且与地面平行，所以阴影面积等于梯形面积的一半。

3. 光线从侧面照射到一个直角三角形上，求阴影面积。

解法：由于光线从侧面照射，那么这个阴影的形状是一个等腰直角三角形。

根据三角形的性质可知，阴影面积等于三角形面积的一半。

四、综合运用在实际问题中，我们可能会遇到需要计算复杂几何图形的阴影面积。

此时，我们可以将复杂图形分解成基本几何图形，然后再根据基本几何图形的阴影面积计算方法进行计算。

最后，将各个部分的阴影面积相加，得到整个复杂图形的阴影面积。

250小学数学组合图形中的阴影部分面积的计算教学研究卢婵娟…（江西省宜春市上高县翰堂中心小学，江西宜春…336405）摘要：组合图形的阴影面积计算是小学数学的重点教学内容，也是以后进行复杂几何计算的入门内容，能充分培养学生的分析几何问题的思维能力，通过运用简单图形基础面积计算知识和数学方法，解决稍微复杂的几何问题。

组合图形的阴影面积的计算对于小学生而言有一定的难度，教师在教学中应该谨记将教材与现实生活联系，提前巩固学生对基础图形面积的计算公式的掌握程度，细化数学计算方法。

关键词：小学数学；组合图形；阴影面积在小学的数学学习阶段，学生对于很多基础图形如圆形、长方形、正方形等都进行了系统的学习，但一些学生仍旧没有充分掌握基础图形面积计算的知识。

而在小学六年级的教学，更加注重图形综合知识的学习，甚至涉及到一些立体几何如圆柱、圆锥的简单计算，这部分学生的学习进度便会难以跟上。

基于此，将从实际教学中遇到的问题，对组合图形的阴影部分面积计算展开教学研究。

1 巩固基础图形面积计算知识，提高学生计算效率人教版小学数学教材，依据学生的成长特性、学习能力等，将图形的学习进行循序渐进的分布在数学学习中，随着年级越高学习的图形知识越复杂，数学图形知识综合性运用也跟着层层递进。

所以学生充分掌握简单图形计算知识的基础，对于组合图形的面积计算尤为重要。

但是学生往往因为简单图形面积学习公式多且杂，出现将计算公式记混的状况，进而影响到后面的组合图形的计算学习。

数学教师在进行图形组合的相关面积计算教学中，可以带领学生进行提问及学生互动等方式，将基础的图形的面积计算知识进行回顾，提高学生的学习效率。

人教版六年级上册中关于《圆的面积》一课的学习中，教师利用多媒体电脑展示将圆形逐步分4等份、8等份直到128等份时，拼接的近乎一个长方形，教师先要带领学生回顾长方形的计算面积为长乘以宽，进而引导学生利用长方形的面积公式推导出圆的面积公式为S=πr2。

人教版小学数学五年级上册6.《求阴影部分面积》重点考点（含答案）五年级上册数学重点考点求阴影部分面积（知识点：平行四边形的面积三角形的面积梯形的面积组合图形的面积）1．计算下面图形的面积。

2．求下图阴影部分的面积。

（单位：厘米）3．如图是两个正方形，求阴影部分的面积（单位：厘米）。

4．将一张长方形纸如图折叠，求图中阴影部分面积。

（单位：cm）5．计算图中阴影部分的面积。

（单位：cm）6．有一张长方形纸，把纸的一角如图那样折叠，求图中阴影部分的面积。

7．寻找合适的条件，求出下图中涂色部分的面积。

（单位：cm）8．下图梯形中，阴影部分面积是24平方分米，求梯形面积。

9．求如图中阴影部分的面积。

（单位：厘米）10．已知阴影部分面积是24cm2，求梯形面积。

11．求阴影部分的面积。

（单位：米）12．计算阴影部分的面积。

（单位：dm）13．计算图形中阴影部分的面积。

14．求出阴影部分的面积。

（单位：cm）15．求涂色部分的面积。

16．计算阴影部分的面积。

（1）（2）17．求下列阴影部分的面积。

（单位：cm）18．求阴影部分面积。

19．求下面图形中阴影部分的面积。

（单位：cm）20．求阴影部分的面积。

21．求阴影部分的面积。

（单位：分米）22．求阴影部分的面积。

（单位：cm）23．求阴影部分的面积。

（单位：分米）24．求阴影部分的面积。

参考答案：1．100平方厘米【分析】要求的图形面积可以看作是一个长为15厘米，宽为10厘米的长方形面积减去两个底为5厘米，高为5厘米的三角形面积和一个边长为5厘米的正方形的面积之和，再根据长方形面积＝长×宽，正方形面积＝边长×边长，三角形面积＝底×高÷2，代入相应数值计算，即可解答。

【详解】（平方厘米）【点睛】本题主要考查的是组合图形面积的计算，解题关键是先分析都是由哪些基本图形组成，再根据相应图形面积的计算公式，代入数值计算即可。

2．144平方厘米【分析】用长方形的面积减去梯形的面积即是阴影部分的面积，分别利用长方形的面积＝长×宽和梯形的面积＝（上底＋下底）×高÷2求解。

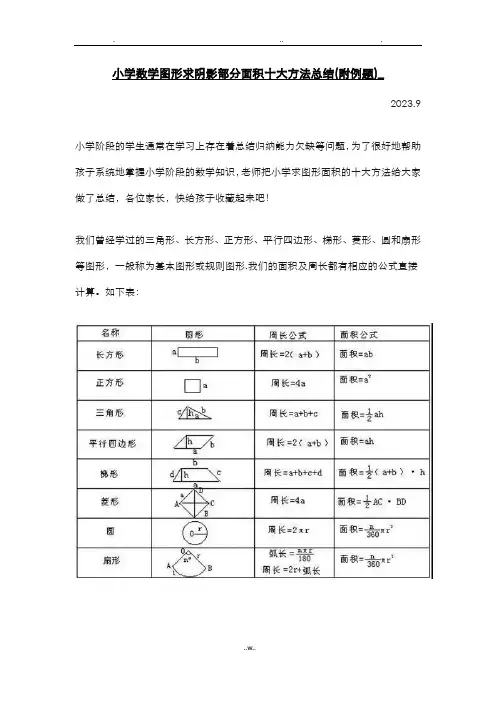
小学数学图形求阴影部分面积十大方法总结(附例题)_2023.9小学阶段的学生通常在学习上存在着总结归纳能力欠缺等问题，为了很好地帮助孩子系统地掌握小学阶段的数学知识，老师把小学求图形面积的十大方法给大家做了总结，各位家长，快给孩子收藏起来吧！我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算。

如下表：实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。

那么，不规则图形的面积及周长怎样去计算呢？我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了。

例题分析例1、如下图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米.求阴影部分的面积。

一句话：阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形（△ABG、△BDE、△EFG）的面积之和。

例2、如下图，正方形ABCD的边长为6厘米，△ABE、△ADF与四边形AECF 的面积彼此相等，求三角形AEF的面积。

一句话：因为△ABE、△ADF与四边形AECF的面积彼此相等，都等于正方形ABCD面积的三分之一，也就是12厘米。

解：S△ABE=S△ADF=S四边形AECF=12在△ABE中，因为AB=6.所以BE=4，同理DF=4，因此CE=CF=2，∴△ECF的面积为2×2÷2=2。

所以S△AEF=S四边形AECF-S△ECF=12-2=10（平方厘米）。

例3、两块等腰直角三角形的三角板，直角边分别是10厘米和6厘米。

如右图那样重合.求重合部分（阴影部分）的面积。

一句话：阴影部分面积=S△ABG-S△BEF，S△ABG和S△BEF都是等腰三角形总结：对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合，分析整体与部分的和、差关系，问题便得到解决求面积十大方法01相加法这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如：求下图整个图形的面积一句话：半圆的面积+正方形的面积=总面积02相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如：下图，求阴影部分的面积。

北师大版小学六年级上册数学计算阴影部分的面积在一个长6m、宽3m的长方形中，画一个最大的半圆。

现在需要计算图中阴影部分的面积和周长。

为了计算阴影部分的面积和周长，我们需要先确定半圆的半径。

由于半圆必须是最大的，因此我们可以将半圆的直径设置为长方形的宽度，即3m。

因此，半圆的半径为1.5m。

现在我们可以计算出半圆的面积和周长。

半圆的面积为1/2πr²，代入半径1.5m，得到半圆面积为3.53m²。

半圆的周长为πr，代入半径1.5m，得到半圆周长为4.71m。

接下来，我们需要计算出阴影部分的面积和周长。

阴影部分是由长方形和半圆组成的。

长方形的面积为长乘宽，代入长6m和宽3m，得到长方形面积为18m²。

因此，阴影部分的面积为18m²减去半圆的面积3.53m²，得到14.47m²。

阴影部分的周长由长方形和半圆的周长组成。

长方形的周长为2（长+宽），代入长6m和宽3m，得到长方形周长为18m。

半圆的周长为4.71m。

因此，阴影部分的周长为18m加上4.71m，得到22.71m。

在正方形中剪下一个面积为314厘米²的1/4圆，求阴影部分的面积。

首先，我们需要计算出这个1/4圆的半径。

我们可以使用面积公式S=1/4πr²，将已知面积314厘米²代入，得到r²=125.6，因此r=√125.6≈11.21厘米。

接下来，我们可以计算出1/4圆的面积和周长。

1/4圆的面积为1/4πr²，代入半径11.21厘米，得到1/4圆面积为98.77厘米²。

1/4圆的周长为1/2πr，代入半径11.21厘米，得到1/4圆周长为17.68厘米。

现在我们需要计算出阴影部分的面积。

阴影部分是由正方形和1/4圆组成的。

正方形的面积为边长的平方，代入已知面积16cm²，得到正方形边长为4厘米。

因此，正方形的面积为16厘米²。

1. 下图中，大小正方形的边长分别是9厘米和5厘米，求阴影部分的面积。

2.右图中，大小正方形的边长分别是12厘米和10厘米。

求阴影部分面积。

3. 求右图中阴影部分图形的面积及周长。

4. 已知右图阴影部分三角形的面积是5平方米，求圆的面积。

5.已知右图中，圆的直径是2厘米，求阴影部分的面积。

6. 求右图中阴影部分图形的面积及周长。

7. 求下图中阴影部分的面积。

（单位：厘米）8.求下图中阴影部分的面积。

9.求右图中阴影部分的面积。

10.求右图中阴影部分的面积。

3. 求下图中阴影部分的面积。

附：六年级精英班专题第三讲参考答案例1：（5+9）×5÷2+9×9÷2－（5+9）×5÷2=40.5（平方厘米）练一练1：1.（10+12）×10÷2+3.14×12×12÷4－（10+12）×10÷2=113.04（平方厘米）2. 面积：6×（6÷2）－3.14×（6÷2）×（6÷2）÷2=3.87（平方厘米）周长： 3.14×6÷2+6＋（6÷2）×2=21.42（厘米）例2：2r×r÷2=5 即r×r=5圆的面积=3.14×5=15.7（平方厘米）练一练2：1. 3.14×（2÷2）×（2÷2）－2×2÷2=1.14（平方厘米）2.面积：3.14×6×6÷4－3.14×（6÷2）×（6÷2）÷2=14.13 （平方厘米）周长：2×3.14×6÷4+3.14×6÷2+6=24.84 （厘米）3.（6+4）×4÷2－（4×4－3.14×4×4÷4）=16.56（平方厘米）例3：6×3－3×3÷2=13.5（平方厘米）练一练3：1. 8×（8÷2）÷2=16（平方厘米）2. 3.14×4×4÷4－4×4÷2=4.56（平方厘米）3. 5×5÷2=12.5（平方厘米）。

求阴影部分面积方法举例1、用替换法求面积“替换”就是等量代换。

用一种量（或一种量的一部分）来替代和它相等的另一种量（或另一种量的一部分），从而减少问题中的数量个数，降低解题难度，然后设法将这个被代换的量求出。

【例】：如图所示，正方形的面积为12平方厘米，求阴影部分的面积。

【分析】设正方形的边长为r，则r×r=r2=12，用12替换r2即可求出扇形的面积，进而求出阴影部分的面积。

列式：12－3.14×12÷4＝12－9.42＝2.58（平方厘米）同类练习：(1)如图所示，图中正方形的面积为10平方厘米，求阴影部分的面积。

(2)如图所示，三角形OAB的面积是7cm2，求图中阴影部分的面积。

(3)如图所示。

②如果环形面积是25.12cm2，求阴影部分的面积。

2、用割补法求面积（这里主要讲“补”）补一些单一图形或集合图形使之成为可以计算的形或体，再解答，这种方法称之为割补法。

【例】：求图中阴影部分面积（单位：cm）。

【分析】在原图的基础上，补上一个与原图完全相同的图形，如右图所示。

列式：10×10－3.14×（）2÷2＝100－39.25＝10.75（cm2）3、用构造法求面积在计算某些图形题时，把原来不易处理的、不规则的图形，通过平移、旋转、翻折后，重新构成一个新的更便于处理的图形来解决问题，这种方法，称之为构造法。

【例】1：求图3（1）a 中阴影部分的面积。

（单位：厘米）【分析】观察图3（1）a ，会发现阴影部分中包含了与左边空白部分完全相同的扇形，将它平移到空白部分上，恰好与所剩阴影部分构成一个正方形。

如图3（1）b 将阴影部分重新构成了一个正方形。

列式：S 阴S 正=10×10=100（平方厘米）【例】2：如图3（2）a ，用一张斜边为29厘米的红色直角三角形纸片，一张斜边为49厘米的蓝色直角三角形纸片，一张黄色的正方形纸片，拼成了一个直角三角形。