2015-2016学年新人教版三年级(上)月考数学试卷(11月份)

新人教版2015—2016学年上学期三年级数学第二次月考测试卷一、想一想、填一填。

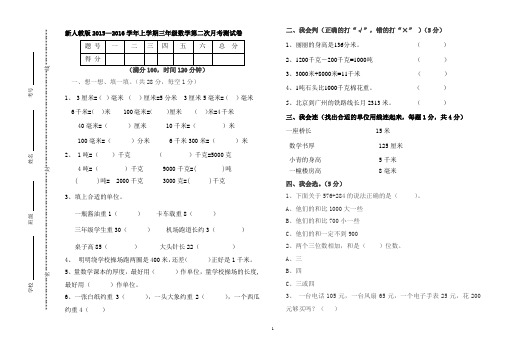
（共28分，毎空1分）1、 3厘米=（）毫米（）厘米=5分米3厘米5毫米=（）毫米6千米=（）米 100毫米=（）厘米（）米=4千米40毫米=（）厘米10千米=（）米100毫米=（）分米6千米300米=（）米2、1吨=（）千克（）千克=5000克4吨=（）千克9000千克=( )吨( )吨= 2000千克3000克=( )千克3、填上合适的单位。

一瓶酱油重1（）卡车载重8（）三年级学生重30（）机场跑道长约3（）桌子高85（）大头针长22（）4、明明绕学校操场跑两圈是400米，还差（）正好是1千米。

5、量数学课本的厚度，最好用（）作单位，量学校操场的长度,最好用（）作单位。

6、一张白纸约重3（），一头大象约重2（），一个西瓜约重4（）二、我会判（正确的打“√”，错的打“×” ）（5分）1、丽丽的身高是136分米。

（）2、1200千克－200千克=1000吨（）3、3000米+8000米=11千米（）4、1吨石头比1000千克棉花重。

（）5、北京到广州的铁路线长月2313米。

（）三、我会连（找出合适的单位用线连起来，每题1分，共4分）一座桥长 15米数学书厚 125厘米小青的身高 5千米一幢楼房高 8毫米四、我会选。

（5分）1、下面关于576+284的说法正确的是（）。

A、他们的和比1000大一些B、他们的和比700小一些C、他们的和一定不到9002、两个三位数相加，和是（）位数。

A、三B、四C、三或四3、一台电话105元，一台风扇65元，一个电子手表25元，花200元够买吗？（）1A. 不够B.不多不少，刚刚够C.够买，而且还有剩钱4、下面的结果刚好是250的是（）A、1500-500 ； B.2500-2250 C.150+150；5、564=（）－63A.501B.627C.170五、我会算。

（32分）1、估算。

三年级上册语文第四次月考试卷班级姓名成绩一、基础知识1、看拼音写词语。

hú diétuī cè xìwēi sū xǐng gù rán( ) ( ) ( ) ( ) ( )zī shì yuàn yìyōng bào shun lìzhù shì( ) ( ) ( ) ( ) ( )2、比一比，再组成词语。

胶( ) 脯( ) 绪( ) 恼( ) 精( )咬( ) 捕( ) 著( ) 脑( ) 情( )3、在括号里填上合适的词语。

( )的服装高兴地( ) 走得( ) ( )地想( )的歌声傲慢地( ) 听得( ) ( )地瞧4、给句中加点字选择正确的解释。

深：①深度②深奥③从上到下或从外到里的距离大(跟“浅”相对) ④深刻⑤感情厚⑥颜色浓⑦距离开始的时间久A、这本书内容很深，初学者不容易看懂。

( )B、夜深了，老师还在工作。

( )C、他们的感情很深。

( )D、这件事影响很深。

( )E、这件衣服是深红的。

( )F、河水有三尺深。

( )5、短语填空。

不假( ) 兴高( )烈成( )结队相( )并论千( )万( ) 大( )失( ) ( )头( )气千( )万( )今年是狗年，你能写几个带狗的短语吗？6、对对子。

天对( )，雨对( )，大陆对( )，山花对( )。

日对( )，山对( )，朝霞对( )，春华对( )。

7、照样子写词。

红通通 ( )( )( )安安静静( )( )( )自言自( )( )( )8、组词填空。

然①在这样一个小山村( )还有这么现代化的文化建设，真让人惊叹。

②从她的话里可以感觉到，这件事情她( )没有参加。

③王老师教了那么多年的语文，但( )坚持认真备课。

④天气预报说今天下午有雨，到了下午( )下起了大雨。

9、根据课文内容填空。

秋天的雨，是一把钥匙。

三年级上册数学11月质量检测题年级__________ 姓名__________ 等级_________一、口算。

（5分）29＋21= 63＋27= 24＋19= 810－170= 760＋220= 55－18= 71－34= 37－18= 231＋426= 256－134=二、填空。

（27分）1、秒针从2走到5；经过的时间是（）；分针从2走到5；经过的时间是（）；时针从2走到5；经过的时间是（）。

2、（1）5吨是（）个1000千克；也就是（）千克。

（2）鲸鱼的体重约70（）（3）长江长约6300（）。

3、直尺上1厘米的长度里有（）小格；一个小格代表（）毫米。

4、新华小学有男生697人；女生811人；女生比男生多（）人；男生和女生共有（）人。

5、如果学校操场跑道1圈是200米；跑（）圈正好是1千米。

6、甲数是386；比乙数少198；乙数是（）；列式为（）7、用6、4、8组成的三位数．．．中；最大．．的三位数和最小．．的三位数和是（）。

8、单位换算1分30秒=（）秒 2时30分=（）分 2吨=（）千克9千米=（）米 80厘米（）分米 60毫米=（）厘米9、在○里填上“>”“<”或“=”。

（6分）1分30秒秒 6600千克吨 10米＋9米6千米米 8分米厘米 5毫米厘米-2毫米三、选择。

（10分）1．看书时眼睛离书本的距离约（）。

A、30厘米B、30毫米C、10厘米2、一个鸡蛋约重（）。

A 、50千克B、5克C、50克3、估算499+201的结果大约是（）A 、500B 、700 C、6004、最小的三位数减去35；差是（）。

A、75B、135C、655、10吨与8千米相比较。

（）A、10吨多B、8千米长C、无法比较四、判断。

（10分）1、三位数的加法；要从最高位算起。

（）2、小明每步的长度是62分米。

（）3、两个三位数相减；差一定是三位数。

（）4、丽丽7：35到校；乐乐7:40到校；乐乐比丽丽晚5分钟到校。

2015-2016学年新人教版四年级（下）月考数学试卷（6月份）一、填空．（25分，每空1分）1．（7分）1370060800是位数，7在位上，表示个，万位上是，表示个．2．（2分）9080000改写成用“万”作单位的数是，省略最高位后面的尾数约是．3．（1分）□15×37，要是积是五位数，□里最小可以填．4．（2分）一本书的总字数省略万后面的尾数约是24万字，这本书最多有字，最少有字．5．（2分）100张纸大约厚1厘米．照这样推算10000张纸大约厚米，10000000张这样的纸大约厚米．6．（2分）一个双层书架，下层书的本数是上层的4倍，如果从下层搬60本到上层，那么两层书的本数正好相等．原来上层有本，下层有本．7．（1分）一节废旧电池能使周围约140平方分米的土壤受到污染，希望小学的同学在环保活动中，捡起了60节废旧电池，这样就减少了平方米的土地污染．8．（2分）从6时05分到6时20分，分钟旋转了度，如果继续旋转180度，是6时分．9．（3分）三角形有条边，个角．生活中许多物体都有三角形的结构，这是因为三角形具有性．10．（3分）最高位是千万位的数是一个位数，其中最大的一个数是，最小的一个数是．二、选择．（5分）11．（1分）有23个亿和4个百组成的数是（）A．23000400 B．2300000400C．230000000040012．（1分）由6个千万、3个十万和4个千组成的数是（）A．36004000 B．63004000 C．6340000 D．60304000 13．（1分）将绕点A逆时针旋转90°后是（）A．B．C．14．（1分）320×24的结果比320×25少（）A．1 B．24 C．320 D．2515．（1分）99×52=100×52﹣52运用了（）A．乘法交换律B．乘法分配律C．乘法结合律三、计算16．（8分）口算60×90=500×80=600÷30=20×34=13×600=75﹣18=70﹣30=8000﹣300=120÷3=45×20=210×4=70×200=25×100=75÷3=125×8=300×40=17．（18分）递等式计算．（能简算的简算）68×15﹣15×6025×441498﹣246+254199+199×99（25+125）×32518+171+482+129．四、作图题18．（4分）操作题（1）把平行四边形向右平移5格，画出平移后的图形；（2）将三角形围绕点o逆时针旋转90°，画出旋转后的图形；19．（4分）作出下列图形的高20．（3分）求出下列角的度数．（写出过程）∠1=42°，∠2=38°．求∠3的度数．五、应用题（33分）21．（4分）小军和小玲同时从学校出发，向相反方向走去．小军的速度是70米∕分，小玲的速度是55米∕分．12分钟后，小军和小玲相距多少米？22．（4分）小明和小芳一共有48本书，小明的书比小芳多12本．小明和小芳各有多少本书？（先画出线段图，再解答并检验．）解答：检验：23．（5分）哥哥和弟弟都是集邮爱好者，哥哥收集的邮票枚数是弟弟的3倍，哥哥给弟弟45枚邮票，两人的邮票枚数就同样多．他们两人原来各有多少枚邮票？（先画线段图，再解答．）24．（5分）一个宽15米的长方形花圃，由于扩建，宽增加了8米，这样花圃的面积增加了240平方米．现在这个花圃的面积是多少平方米？（先画图整理再解答）25．（5分）一辆客车和一辆货车同时从南京出发开往徐州，客车的速度是95千米∕时，货车的速度是76千米∕时，4小时后，两车相距多少千米？26．（5分）甲乙两人在一个长400米的环形跑道上从一点同时反向而行，甲每分钟走45米，乙每分钟走35米，多少分钟后两人第二次相遇？27．（5分）修一条长850米长的隧道，每天修75米，修了几天后，剩下的比已经挖的多100米．已经挖了多少天？（先画图，再解答）智力冲浪：28．张庄小学原来有一个长方形操场，长50米，宽40米．扩建校园时，操场的长增加了10米，宽增加了8米，操场的面积增加了多少平方米？（先画图，再解答）2015-2016学年新人教版四年级（下）月考数学试卷（6月份）参考答案与试题解析一、填空．（25分，每空1分）1．（7分）1370060800是10位数，7在千万位上，表示7个千万，万位上是6，表示6个万．【解答】解：1370060800是10位数，7在千万位上，表示7个千万，万位上是6，表示6个万．故答案为：10，千万，7，千万，6，6，万．2．（2分）9080000改写成用“万”作单位的数是908万，省略最高位后面的尾数约是9百万．【解答】解：9080000=908万；90805300≈9百万；故答案为：908万，9百万．3．（1分）□15×37，要是积是五位数，□里最小可以填3．【解答】解：由分析知，□15×37，把37看作40，估大了，40×3000=12000，积是五位数，所以应把□15看作300，即□里可以填3、4、5、6、7、8、9．所以□里最小填3．故答案为：3．4．（2分）一本书的总字数省略万后面的尾数约是24万字，这本书最多有244999字，最少有235000字．【解答】解：一本书的总字数省略万后面的尾数约是24万字，这本书最多有244999字，最少有235000字．故答案为：244999，235000．5．（2分）100张纸大约厚1厘米．照这样推算10000张纸大约厚1米，10000000张这样的纸大约厚1000米．【解答】解：10000÷100=100（个）100×1=100（厘米）100厘米=1米；10000000÷100=100000（个）100000×1=100000（厘米）100000厘米=1000米答：10000张纸大约厚1米，10000000张这样的纸大约厚1000米．故答案为：1，1000．6．（2分）一个双层书架，下层书的本数是上层的4倍，如果从下层搬60本到上层，那么两层书的本数正好相等．原来上层有40本，下层有160本．【解答】解：设上层有书x本，则下层有书4x本，根据题意可得方程：4x﹣60=x+603x=120x=4040×4=160（本）答：原来上层有40本，下层有160本．故答案为：40，160．7．（1分）一节废旧电池能使周围约140平方分米的土壤受到污染，希望小学的同学在环保活动中，捡起了60节废旧电池，这样就减少了84平方米的土地污染．【解答】解：140×60=8400（平方分米）8400平方分米=84平方米答：减少了84平方米土地污染．故答案为：84．8．（2分）从6时05分到6时20分，分钟旋转了90度，如果继续旋转180度，是6时50分．【解答】解：从6时05分到6时20分，分钟旋转了90度，如果继续旋转180度，是6时50分．故答案为：90，50．9．（3分）三角形有三条边，三个角．生活中许多物体都有三角形的结构，这是因为三角形具有稳定性．【解答】解：由分析可知：三角形有三条边，三个角，生活中许多物体都有三角形的结构，这是因为三角形具有稳定性；故答案为：三、三、稳定性．10．（3分）最高位是千万位的数是一个八位数，其中最大的一个数是99999999，最小的一个数是10000000．【解答】解：由分析可知：最高位是千万位的数是一个八位数，其中最大的一个数是99999999，最小的一个数是10000000；故答案为：99999999；10000000．二、选择．（5分）11．（1分）有23个亿和4个百组成的数是（）A．23000400 B．2300000400C．2300000000400【解答】解：有23个亿和4个百组成的数是2300000400．故选：B．12．（1分）由6个千万、3个十万和4个千组成的数是（）A．36004000 B．63004000 C．6340000 D．60304000【解答】解：由6个千万、3个十万和4个千组成的数是：60304000．故选：D．13．（1分）将绕点A逆时针旋转90°后是（）A．B．C．【解答】解：将绕点A逆时针旋转90°后是；故选：B．14．（1分）320×24的结果比320×25少（）A．1 B．24 C．320 D．25【解答】解：320×25=320×（24+1）=320×24+320×1=320×24+320320×24比320×24+320少320．故选：C．15．（1分）99×52=100×52﹣52运用了（）A．乘法交换律B．乘法分配律C．乘法结合律【解答】解：99×52=100×52﹣52=5200﹣52=5148运用了乘法分配律．故选：B．三、计算16．（8分）口算60×90=500×80=600÷30=20×34=13×600=75﹣18=70﹣30=8000﹣300=120÷3=45×20=210×4=70×200=25×100=75÷3=125×8=300×40=【解答】解：60×90=5400500×80=40000600÷30=2020×34=68013×600=780075﹣18=5370﹣30=408000﹣300=7700 120÷3=4045×20=900210×4=84070×200=14000 25×100=250075÷3=25125×8=1000300×40=1200017．（18分）递等式计算．（能简算的简算）68×15﹣15×6025×441498﹣246+254199+199×99（25+125）×32518+171+482+129．【解答】解：（1）68×15﹣15×60=（68﹣60）×15=8×15=120（2）25×44=25×4×11=100×11=1100（3）1498﹣246+254=1252+254=1506（4）199+199×99=199×（1+99）=199×100=19900（5）（25+125）×32=25×32+125×32=25×4×8+125×8×4=100×8+1000×4=800+4000=4800（6）518+171+482+129=（518+482）+（171+129）=1000+300=1300四、作图题18．（4分）操作题（1）把平行四边形向右平移5格，画出平移后的图形；（2）将三角形围绕点o逆时针旋转90°，画出旋转后的图形；【解答】解：（1）把平行四边形向右平移5格，画出平移后的图形（图中红色部分）：（2）将三角形围绕点o逆时针旋转90°，画出旋转后的图形（图中绿色部分）：19．（4分）作出下列图形的高【解答】解：如图：20．（3分）求出下列角的度数．（写出过程）∠1=42°，∠2=38°．求∠3的度数．【解答】解：180﹣42﹣38=138﹣38=100（度）答：∠3等于100度．五、应用题（33分）21．（4分）小军和小玲同时从学校出发，向相反方向走去．小军的速度是70米∕分，小玲的速度是55米∕分．12分钟后，小军和小玲相距多少米？【解答】解：（55+70）×12=125×12=1500（米）答：小军和小玲相距1200米．22．（4分）小明和小芳一共有48本书，小明的书比小芳多12本．小明和小芳各有多少本书？（先画出线段图，再解答并检验．）解答：检验：【解答】解：根据题意可得：；小明：（48+12）÷2=60÷2=30（本）；小芳：（48﹣12）÷2=36÷2=18（本）；检验：两人共有30+18=48（本），小明比小芳多30﹣18=12（本）．答：小明游30本，小芳有18本．23．（5分）哥哥和弟弟都是集邮爱好者，哥哥收集的邮票枚数是弟弟的3倍，哥哥给弟弟45枚邮票，两人的邮票枚数就同样多．他们两人原来各有多少枚邮票？（先画线段图，再解答．）【解答】解：根据题意可得：；（45+45）÷（3﹣1）=90÷2=45（枚）；45×3=135（枚）．答：哥哥原来有135枚，弟弟原来有45枚．24．（5分）一个宽15米的长方形花圃，由于扩建，宽增加了8米，这样花圃的面积增加了240平方米．现在这个花圃的面积是多少平方米？（先画图整理再解答）【解答】解：如图所示：（240÷8）×（15+8）=30×23=690（平方米）答：现在这个花圃的面积是690平方米．25．（5分）一辆客车和一辆货车同时从南京出发开往徐州，客车的速度是95千米∕时，货车的速度是76千米∕时，4小时后，两车相距多少千米？【解答】解：（95﹣76）×4=19×4=76（千米）答：4小时后，两车相距76千米．26．（5分）甲乙两人在一个长400米的环形跑道上从一点同时反向而行，甲每分钟走45米，乙每分钟走35米，多少分钟后两人第二次相遇？【解答】解：400×2÷（45+35）=800÷80，=10（分钟）．答：10分钟后，两人第二次相遇．27．（5分）修一条长850米长的隧道，每天修75米，修了几天后，剩下的比已经挖的多100米．已经挖了多少天？（先画图，再解答）【解答】解：（850﹣100）÷2÷75=750÷2÷75=375÷75=5（天）答：已经挖了5天．智力冲浪：28．张庄小学原来有一个长方形操场，长50米，宽40米．扩建校园时，操场的长增加了10米，宽增加了8米，操场的面积增加了多少平方米？（先画图，再解答）【解答】解：（50+10）×（40+8）﹣50×40=60×48﹣2000=2880﹣2000=880（平方米）答：操场的面积增加了880平方米．。

2015-2016学年某某省马某某市红星中学高三（上）第二次月考数学试卷（理科）一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的.1．设全集U是实数集R，M={x|y=ln（x2﹣2x） }，N={y|y=}，则图中阴影部分表示的集合是( )A．{x|﹣2≤x＜2} B．{x|1＜x≤2}C．{x|1≤x≤2}D．{x|x＜1}2．已知函数f（x）=且f（a）=﹣3，则f（6﹣a）=( ) A．﹣B．﹣C．﹣D．﹣3．给出如下命题，正确的序号是( )A．命题：∀x∈R，x2≠x的否定是：∃x0∈R，使得x02≠xB．命题：若x≥2且y≥3，则x+y≥5的否命题为：若x＜2且y＜3，则x+y＜5C．若ω=1是函数f（x）=cosωx在区间[0，π]上单调递减的充分不必要条件D．命题：∃x0∈R，x02+a＜0为假命题，则实数a的取值X围是a＞04．已知某几何体的三视图如图所示，其中，正（主）视图，侧（左）视图均是由三角形与半圆构成，俯视图由圆与内接三角形构成，根据图中的数据可得此几何体的体积为( )A．B．C．D．5．设F1、F2为椭圆+y2=1的左、右焦点，过椭圆中心任作一直线与椭圆交于P、Q两点，当四边形PF1QF2面积最大时，•的值等于( )A．0 B．2 C．4 D．﹣26．设a=log37，b=21.1，c=0.83.1，则( )A．b＜a＜c B．c＜a＜b C．c＜b＜a D．a＜c＜b7．执行如图所示的程序框图，如果输入P=153，Q=63，则输出的P的值是( )A．2 B．3 C．9 D．278．若点（16，tanθ）在函数y=log2x的图象上，则=( ) A．B．C．4 D．49．已知函数f（x）=（）x﹣log3x，若实数x0是方程f（x）=0的解，且x0＜x1，则f（x1）的值( )A．恒为负B．等于零C．恒为正D．不大于零10．已知数列{a n}的前n项和为S n，过点P（n，S n）和Q（n+1，S n+1）（n∈N*）的直线的斜率为3n﹣2，则a2+a4+a5+a9的值等于( )A．52 B．40 C．26 D．2011．函数y=e|lnx|﹣|x﹣1|的图象大致是( )A．B． C．D．12．已知定义在R上的奇函数f（x），其导函数为f′（x），对任意正实数x满足xf′（x）＞2f（﹣x），若g（x）=x2f（x），则不等式g（x）＜g（1﹣3x）的解集是( )A．（，+∞）B．（﹣∞，）C．（0，）D．（﹣∞，）∪（，+∞）二、填空题：本大题共4小题，每小题5分.13．计算：（）+lg+lg70+=__________．14．设变量x，y满足约束条件，则z=x﹣3y的最小值是__________．15．已知定义在R上的奇函数f（x）满足f（x﹣4）=﹣f（x），且在区间[0，2]上是增函数．若方程f（x）=m（m＞0）在区间[﹣8，8]上有四个不同的根x1，x2，x3，x4，则x1+x2+x3+x4=__________．16．关于函数f（x）=（x≠0），有下列命题：①f（x）的最小值是lg2；②其图象关于y轴对称；③当x＞0时，f（x）是增函数；当x＜0时，f（x）是减函数；④f（x）在区间（﹣1，0）和（1，+∞）上是增函数，其中所有正确结论的序号是__________．三、解答题：解答应写出文字说明，证明过程或演算步骤．17．已知p：|1﹣|≤2；q：x2﹣2x+1﹣m2≤0（m＞0），若￢p是￢q的必要不充分条件，某某数m的取值X围．18．已知函数f（x）=﹣x2+2ex+m﹣1，g（x）=x+（x＞0）．（1）若y=g（x）﹣m有零点，求m的取值X围；（2）确定m的取值X围，使得g（x）﹣f（x）=0有两个相异实根．19．已知函数f（x）=log a（x+1）（a＞1），若函数y=g（x）的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数f（x）的图象．（1）写出函数g（x）的解析式；（2）当x∈[0，1）时，总有f（x）+g（x）≥m成立，求m的取值X围．20．某机床厂今年初用98万元购进一台数控机床，并立即投入使用，计划第一年维修、保养费用12万元，从第二年开始，每年的维修、保养修费用比上一年增加4万元，该机床使用后，每年的总收入为50万元，设使用x年后数控机床的盈利总额y元．（1）写出y与x之间的函数关系式；（2）从第几年开始，该机床开始盈利？（3）使用若干年后，对机床的处理有两种方案：①当年平均盈利额达到最大值时，以30万元价格处理该机床；②当盈利额达到最大值时，以12万元价格处理该机床．问哪种方案处理较为合理？请说明理由．21．已知函数f（x）=+xlnx，g（x）=x3﹣x2﹣3．（1）讨论函数h（x）=的单调性；（2）如果对任意的s，t∈[，2]，都有f（s）≥g（t）成立，某某数a的取值X围．四、选做题：请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题记分．22．已知曲线C1的参数方程是（θ为参数）以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程是ρ=﹣4cosθ．（1）求曲线C1与C2交点的极坐标；（2）A、B两点分别在曲线C1与C2上，当|AB|最大时，求△OAB的面积（O为坐标原点）．23．已知不等式|2x+2|﹣|x﹣1|＞a．（1）当a=0时，求不等式的解集（2）若不等式在区间[﹣4，2]内无解．某某数a的取值X围．2015-2016学年某某省马某某市红星中学高三（上）第二次月考数学试卷（理科）一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的.1．设全集U是实数集R，M={x|y=ln（x2﹣2x） }，N={y|y=}，则图中阴影部分表示的集合是( )A．{x|﹣2≤x＜2} B．{x|1＜x≤2}C．{x|1≤x≤2}D．{x|x＜1}【考点】Venn图表达集合的关系及运算．【专题】应用题；集合思想；定义法；集合．【分析】由图知，阴影部分表示的集合中的元素是在集合N中的元素但不在集合M中的元素组成的，即N∩C U M．【解答】解：由韦恩图知阴影部分表示的集合为N∩（C U M）M={x|y=ln（x2﹣2x） }∴x2﹣2x＞0，解得x＜0，或x＞2，∴M={x|x＜0，或x＞2}，∴C U M={x|0≤x≤2}=[0，2]，N={y|y=}={y|y≥1}=[1，+∞），∴N∩（C U M）=[1，2]，故选：C【点评】本小题主要考查Venn图表达集合的关系及运算、二次不等式的解法等基础知识，属于基础题2．已知函数f（x）=且f（a）=﹣3，则f（6﹣a）=( ) A．﹣B．﹣C．﹣D．﹣【考点】分段函数的应用；函数的零点．【专题】函数的性质及应用．【分析】由f（a）=﹣3，结合指数和对数的运算性质，求得a=7，再由分段函数求得f（6﹣a）的值．【解答】解：函数f（x）=且f（a）=﹣3，若a≤1，则2a﹣1﹣2=﹣3，即有2a﹣1=﹣1＜0，方程无解；若a＞1，则﹣log2（a+1）=﹣3，解得a=7，则f（6﹣a）=f（﹣1）=2﹣1﹣1﹣2=﹣．故选：A．【点评】本题考查分段函数的运用：求函数值，主要考查指数和对数的运算性质，属于中档题．3．给出如下命题，正确的序号是( )A．命题：∀x∈R，x2≠x的否定是：∃x0∈R，使得x02≠xB．命题：若x≥2且y≥3，则x+y≥5的否命题为：若x＜2且y＜3，则x+y＜5C．若ω=1是函数f（x）=cosωx在区间[0，π]上单调递减的充分不必要条件D．命题：∃x0∈R，x02+a＜0为假命题，则实数a的取值X围是a＞0【考点】命题的真假判断与应用．【专题】计算题；规律型；简易逻辑．【分析】利用命题的否定判断A的正误；四种命题的逆否关系判断B的正误；充要条件判断C 的正误；命题的真假判断D的正误；【解答】解：对于A，命题：∀x∈R，x2≠x的否定是：∃x0∈R，使得x02≠x0，不满足命题的否定形式，所以不正确；对于B，命题：若x≥2且y≥3，则x+y≥5的否命题为：若x＜2且y＜3，则x+y＜5，不满足否命题的形式，所以不正确；对于C，若ω=1是函数f（x）=cosx在区间[0，π]上单调递减的，而函数f（x）=cosωx在区间[0，π]上单调递减的，ω≤1，所以ω=1是函数f（x）=cosωx在区间[0，π]上单调递减的充分不必要条件，正确．对于D，命题：∃x0∈R，x02+a＜0为假命题，则命题：a≥0，∀x∈R，x2+a≥0是真命题；所以，命题：∃x0∈R，x02+a＜0为假命题，则实数a的取值X围是a＞0，不正确；故选：C．【点评】本题考查命题的真假的判断与应用，基本知识的考查．4．已知某几何体的三视图如图所示，其中，正（主）视图，侧（左）视图均是由三角形与半圆构成，俯视图由圆与内接三角形构成，根据图中的数据可得此几何体的体积为( )A．B．C．D．【考点】由三视图求面积、体积．【专题】图表型．【分析】先由三视图还原成原来的几何体，再根据三视图中的长度关系，找到几何体中的长度关系，进而可以求几何体的体积．【解答】解：由三视图可得该几何体的上部分是一个三棱锥，下部分是半球，所以根据三视图中的数据可得：V=××=，故选C．【点评】本题考点是由三视图求几何体的面积、体积，考查对三视图的理解与应用，主要考查三视图与实物图之间的关系，用三视图中的数据还原出实物图的数据，再根据相关的公式求表面积与体积，本题求的是组合体的体积，一般组合体的体积要分部分来求．三视图的投影规则是：“主视、俯视长对正；主视、左视高平齐，左视、俯视宽相等”．三视图是高考的新增考点，不时出现在高考试题中，应予以重视．5．设F1、F2为椭圆+y2=1的左、右焦点，过椭圆中心任作一直线与椭圆交于P、Q两点，当四边形PF1QF2面积最大时，•的值等于( )A．0 B．2 C．4 D．﹣2【考点】椭圆的简单性质．【专题】计算题．【分析】通过题意可推断出当P、Q分别在椭圆短轴端点时，四边形PF1QF2面积最大．进而可根据椭圆的方程求得焦点的坐标和P的坐标，进而求得和，则•的值可求得．【解答】解：根据题意可知当P、Q分别在椭圆短轴端点时，四边形PF1QF2面积最大．这时，F1（﹣，0），F2（，0），P（0，1），∴=（﹣，﹣1），=（，﹣1），∴•=﹣2．故选D【点评】本题主要考查了椭圆的简单性质．考查了学生数形结合的思想和分析问题的能力．6．设a=log37，b=21.1，c=0.83.1，则( )A．b＜a＜c B．c＜a＜b C．c＜b＜a D．a＜c＜b【考点】对数值大小的比较．【专题】函数的性质及应用．【分析】分别讨论a，b，c的取值X围，即可比较大小．【解答】解：1＜log37＜2，b=21.1＞2，c=0.83.1＜1，则c＜a＜b，故选：B．【点评】本题主要考查函数值的大小比较，根据指数和对数的性质即可得到结论．7．执行如图所示的程序框图，如果输入P=153，Q=63，则输出的P的值是( )A．2 B．3 C．9 D．27【考点】程序框图．【专题】图表型；算法和程序框图．【分析】模拟执行程序，依次写出每次循环得到的R，P，Q的值，当Q=0时，满足条件Q=0，退出循环，输出P的值为3．【解答】解：模拟执行程序，可得P=153，Q=63不满足条件Q=0，R=27，P=63，Q=27不满足条件Q=0，R=9，P=27，Q=9不满足条件Q=0，R=0，P=9，Q=0满足条件Q=0，退出循环，输出P的值为9．故选：C．【点评】本题主要考查了程序框图和算法，依次写出每次循环得到的R，P，Q的值是解题的关键，属于基本知识的考查．8．若点（16，tanθ）在函数y=log2x的图象上，则=( ) A．B．C．4 D．4【考点】三角函数的化简求值．【专题】计算题；转化思想；转化法；三角函数的求值．【分析】先根据对数的运算性质求出tanθ，再化简代值计算即可．【解答】解：点（16，tanθ）在函数y=log2x的图象上，∴tanθ=log216=4，∴====，故选：B．【点评】本题考查了二倍角公式，函数值的求法，以及对数的运算性质，属于基础题．9．已知函数f（x）=（）x﹣log3x，若实数x0是方程f（x）=0的解，且x0＜x1，则f（x1）的值( )A．恒为负B．等于零C．恒为正D．不大于零【考点】函数的零点与方程根的关系．【专题】函数的性质及应用．【分析】由函数的性质可知，f（x）=（）x﹣log3x在（0，+∞）上是减函数，且可得f（x0）=0，由0＜x0＜x1，可得f（x1）＜f（x0）=0，即可判断【解答】解：∵实数x0是方程f（x）=0的解，∴f（x0）=0．∵函数y（）x，y=log3x在（0，+∞）上分别具有单调递减、单调递增，∴函数f（x）在（0，+∞）上是减函数．又∵0＜x0＜x1，∴f（x1）＜f（x0）=0．∴f（x1）的值恒为负．故选A．【点评】本题主要考查了函数的单调性的简单应用，解题的关键是准确判断函数f（x）的单调性并能灵活应用．10．已知数列{a n}的前n项和为S n，过点P（n，S n）和Q（n+1，S n+1）（n∈N*）的直线的斜率为3n﹣2，则a2+a4+a5+a9的值等于( )A．52 B．40 C．26 D．20【考点】数列的求和．【专题】等差数列与等比数列．【分析】首先根据题中的已知条件已知数列{a n}的前n项和为S n，过点P（n，S n）和Q（n+1，S n+1）（n∈N*）的直线的斜率为3n﹣2，进一步求出数列的通项公式，然后根据通项公式求出各项的值，最后确定结果．【解答】解：已知数列{a n}的前n项和为S n，过点P（n，S n）和Q（n+1，S n+1）（n∈N*）的直线的斜率为3n﹣2则：∴a n=3n﹣5a2+a4+a5+a9=40故选：B【点评】本题考查的知识点：根据点的斜率求出数列的通项公式，由通项公式求数列的项．11．函数y=e|lnx|﹣|x﹣1|的图象大致是( )A．B． C．D．【考点】对数的运算性质；函数的图象与图象变化．【分析】根据函数y=e|lnx|﹣|x﹣1|知必过点（1，1），再对函数进行求导观察其导数的符号进而知原函数的单调性，得到答案．【解答】解：由y=e|lnx|﹣|x﹣1|可知：函数过点（1，1），当0＜x＜1时，y=e﹣lnx﹣1+x=+x﹣1，y′=﹣+1＜0．∴y=e﹣lnx﹣1+x为减函数；若当x＞1时，y=e lnx﹣x+1=1，故选D．【点评】本题主要考查函数的求导与函数单调性的关系．12．已知定义在R上的奇函数f（x），其导函数为f′（x），对任意正实数x满足xf′（x）＞2f（﹣x），若g（x）=x2f（x），则不等式g（x）＜g（1﹣3x）的解集是( )A．（，+∞）B．（﹣∞，）C．（0，）D．（﹣∞，）∪（，+∞）【考点】函数奇偶性的性质．【专题】转化思想；数学模型法；函数的性质及应用；导数的综合应用．【分析】f（x）是定义在R上的奇函数，可得：f（﹣x）=﹣f（x）．对任意正实数x满足xf′（x）＞2f（﹣x），可得：xf′（x）+2f（x）＞0，由g（x）=x2f（x），可得g′（x）＞0．可得函数g（x）在（0，+∞）上单调递增．即可得出．【解答】解：∵f（x）是定义在R上的奇函数，∴f（﹣x）=﹣f（x）．对任意正实数x满足xf′（x）＞2f（﹣x），∴xf′（x）+2f（x）＞0，∵g（x）=x2f（x），∴g′（x）=2xf（x）+x2f′（x）＞0．∴函数g（x）在（0，+∞）上单调递增．又g（0）=0，g（﹣x）=x2f（﹣x）=﹣g（x），∴函数g（x）是R上的奇函数，∴g（x）是R上的增函数．由不等式g（x）＜g（1﹣3x），∴x＜1﹣3x，解得．∴不等式g（x）＜g（1﹣3x）的解集为：．故选：B．【点评】本题考查了函数的奇偶性与单调性，考查了推理能力与计算能力，属于中档题．二、填空题：本大题共4小题，每小题5分.13．计算：（）+lg+lg70+=．【考点】对数的运算性质；有理数指数幂的化简求值．【专题】计算题；函数思想；定义法；函数的性质及应用．【分析】根据对数和幂的运算性质计算即可．【解答】解：（）+lg+lg70+=+lg（）+1﹣lg3=+lg+1=+1+1=，故答案为：．【点评】本题考查了对数和幂的运算性质，关键是掌握性质，属于基础题．14．设变量x，y满足约束条件，则z=x﹣3y的最小值是﹣8．【考点】简单线性规划．【专题】不等式的解法及应用．【分析】将z=x﹣3y变形为，此式可看作是斜率为，纵截距为的一系列平行直线，当最大时，z最小．作出原不等式组表示的平面区域，让直线向此平面区域平移，可探求纵截距的最大值．【解答】解：由z=x﹣3y，得，此式可看作是斜率为，纵截距为的直线，当最大时，z最小．画出直线y=x，x+2y=2，x=﹣2，从而可标出不等式组表示的平面区域，如右图所示．由图知，当动直线经过点P时，z最小，此时由，得P（﹣2，2），从而z min=﹣2﹣3×2=﹣8，即z=x﹣3y的最小值是﹣8．故答案为：﹣8．【点评】本题考查了线性规划的应用，为高考常考的题型，求解此类问题的一般步骤是：（1）作出已知不等式组表示的平面区域；（2）运用化归思想及数形结合思想，将目标函数的最值问题转化为平面中几何量的最值问题处理．15．已知定义在R上的奇函数f（x）满足f（x﹣4）=﹣f（x），且在区间[0，2]上是增函数．若方程f（x）=m（m＞0）在区间[﹣8，8]上有四个不同的根x1，x2，x3，x4，则x1+x2+x3+x4=﹣8．【考点】奇偶性与单调性的综合；函数的周期性．【专题】数形结合．【分析】由条件“f（x﹣4）=﹣f（x）”得f（x+8）=f（x），说明此函数是周期函数，又是奇函数，且在[0，2]上为增函数，由这些画出示意图，由图可解决问题．【解答】解：此函数是周期函数，又是奇函数，且在[0，2]上为增函数，综合条件得函数的示意图，由图看出，四个交点中两个交点的横坐标之和为2×（﹣6），另两个交点的横坐标之和为2×2，所以x1+x2+x3+x4=﹣8．故答案为﹣8．【点评】数形结合是数学解题中常用的思想方法，能够变抽象思维为形象思维，有助于把握数学问题的本质；另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷．16．关于函数f（x）=（x≠0），有下列命题：①f（x）的最小值是lg2；②其图象关于y轴对称；③当x＞0时，f（x）是增函数；当x＜0时，f（x）是减函数；④f（x）在区间（﹣1，0）和（1，+∞）上是增函数，其中所有正确结论的序号是①②④．【考点】命题的真假判断与应用；奇偶性与单调性的综合．【专题】函数思想；定义法；函数的性质及应用．【分析】是结合复合函数单调性的关系进行判断．②根据基本由函数奇偶性的定义判断函数为偶函数判断；③利用对勾函数的单调性判断；④由对勾函数的最值及函数奇偶性的性质进行判断即可．【解答】解：①函数f（x）=lg，（x∈R且x≠0）．∵=2，∴f（x）=lg≥2，即f（x）的最小值是lg2，故①正确，②∵f（﹣x）==f（x），∴函数f（x）为偶函数，图象关于y轴对称，故②正确；③当x＞0时，t（x）=，在（0，1）上单调递减，在（1，+∞）上得到递增，∴f（x）=lg在（0，1）上单调递减，在（1，+∞）上得到递增，故③错误；④∵函数f（x）是偶函数，由③知f（x）在（0，1）上单调递减，在（1，+∞）上得到递增，∴在（﹣1，0）上单调递增，在（﹣∞，﹣1）上得到递减，故④正确，故答案为：①②④【点评】本题考查了命题的真假判断与应用，考查了函数奇偶性的性质，考查了复合函数的单调性，是中档题．三、解答题：解答应写出文字说明，证明过程或演算步骤．17．已知p：|1﹣|≤2；q：x2﹣2x+1﹣m2≤0（m＞0），若￢p是￢q的必要不充分条件，某某数m的取值X围．【考点】必要条件；绝对值不等式的解法．【专题】规律型．【分析】先求出命题p，q的等价条件，利用￢p是￢q的必要不充分条件转化为q是p的必要不充分条件，建立条件关系即可求出m的取值X围．【解答】解：由||=，得|x﹣4|≤6，即﹣6≤x﹣4≤6，∴﹣2≤x≤10，即p：﹣2≤x≤10，由x2+2x+1﹣m2≤0得[x+（1﹣m）][x+（1+m）]≤0，即1﹣m≤x≤1+m，（m＞0），∴q：1﹣m≤x≤1+m，（m＞0），∵￢p是￢q的必要不充分条件，∴q是p的必要不充分条件．即，且等号不能同时取，∴，解得m≥9．【点评】本题主要考查充分条件和必要条件的应用，将￢p是￢q的必要不充分条件转化为q 是p的必要不充分条件是解决本题的关键．18．已知函数f（x）=﹣x2+2ex+m﹣1，g（x）=x+（x＞0）．（1）若y=g（x）﹣m有零点，求m的取值X围；（2）确定m的取值X围，使得g（x）﹣f（x）=0有两个相异实根．【考点】函数零点的判定定理；根的存在性及根的个数判断．【专题】计算题；函数的性质及应用；导数的综合应用；不等式的解法及应用．【分析】（1）由基本不等式可得g（x）=x+≥2=2e，从而求m的取值X围；（2）令F（x）=g（x）﹣f（x）=x++x2﹣2ex﹣m+1，求导F′（x）=1﹣+2x﹣2e=（x﹣e）（+2）；从而判断函数的单调性及最值，从而确定m的取值X围．【解答】解：（1）∵g（x）=x+≥2=2e；（当且仅当x=，即x=e时，等号成立）∴若使函数y=g（x）﹣m有零点，则m≥2e；故m的取值X围为[2e，+∞）；（2）令F（x）=g（x）﹣f（x）=x++x2﹣2ex﹣m+1，F′（x）=1﹣+2x﹣2e=（x﹣e）（+2）；故当x∈（0，e）时，F′（x）＜0，x∈（e，+∞）时，F′（x）＞0；故F（x）在（0，e）上是减函数，在（e，+∞）上是增函数，故只需使F（e）＜0，即e+e+e2﹣2e2﹣m+1＜0；故m＞2e﹣e2+1．【点评】本题考查了基本不等式的应用及导数的综合应用，同时考查了函数零点的判断与应用，属于中档题．19．已知函数f（x）=log a（x+1）（a＞1），若函数y=g（x）的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数f（x）的图象．（1）写出函数g（x）的解析式；（2）当x∈[0，1）时，总有f（x）+g（x）≥m成立，求m的取值X围．【考点】求对数函数解析式；函数解析式的求解及常用方法；函数最值的应用．【专题】计算题；转化思想．【分析】（1）由已知条件可知函数g（x）的图象上的任意一点P（x，y）关于原点对称的点Q （﹣x，﹣y）在函数f（x）图象上，把Q（﹣x，﹣y）代入f（x），整理可得g（x）（2）由（1）可令h（x）=f（x）+g（x），先判断函数h（x）在[0，1）的单调性，进而求得函数的最小值h（x）min，使得m≤h（x）min【解答】解：（1）设点P（x，y）是g（x）的图象上的任意一点，则Q（﹣x，﹣y）在函数f （x）的图象上，即﹣y=log a（﹣x+1），则∴（2）f（x）+g（x）≥m 即，也就是在[0，1）上恒成立．设，则由函数的单调性易知，h（x）在[0，1）上递增，若使f（x）+g（x）≥m在[0，1）上恒成立，只需h（x）min≥m在[0，1）上成立，即m≤0．m的取值X围是（﹣∞，0]【点评】本题（1）主要考查了函数的中心对称问题：若函数y=f（x）与y=g（x）关于点M （a，b）对称，则y=f（x）上的任意一点（x，y）关于M（a，b）对称的点（2a﹣x，2b﹣y）在函数y=g（x）的图象上．（2）主要考查了函数的恒成立问题，往往转化为求最值问题：m≥h（x）恒成立，则m≥h（x）m≤h（x）恒成立，max则m≤h（x）min20．某机床厂今年初用98万元购进一台数控机床，并立即投入使用，计划第一年维修、保养费用12万元，从第二年开始，每年的维修、保养修费用比上一年增加4万元，该机床使用后，每年的总收入为50万元，设使用x年后数控机床的盈利总额y元．（1）写出y与x之间的函数关系式；（2）从第几年开始，该机床开始盈利？（3）使用若干年后，对机床的处理有两种方案：①当年平均盈利额达到最大值时，以30万元价格处理该机床；②当盈利额达到最大值时，以12万元价格处理该机床．问哪种方案处理较为合理？请说明理由．【考点】基本不等式在最值问题中的应用．【专题】计算题．【分析】（1）赢利总额y元即x年中的收入50x减去购进机床的成本与这x年中维修、保养的费用，维修、保养的费用历年成等差数增长，，（2）由（1）的结论解出结果进行判断得出何年开始赢利．（3）算出每一种方案的总盈利，比较大小选择方案．【解答】解：（1）y=﹣2x2+40x﹣98，x∈N*．（2）由﹣2x2+40x﹣98＞0解得，，且x∈N*，所以x=3，4，，17，故从第三年开始盈利．（3）由，当且仅当x=7时“=”号成立，所以按第一方案处理总利润为﹣2×72+40×7﹣98+30=114（万元）．由y=﹣2x2+40x﹣98=﹣2（x﹣10）2+102≤102，所以按第二方案处理总利润为102+12=114（万元）．∴由于第一方案使用时间短，则选第一方案较合理．【点评】考查审题及将题中关系转化为数学符号的能力，其中第二问中考查了一元二次不等式的解法，第三问中考查到了基本不等式求最值，本题是一个函数基本不等式相结合的题．属应用题中盈利最大化的问题．21．已知函数f（x）=+xlnx，g（x）=x3﹣x2﹣3．（1）讨论函数h（x）=的单调性；（2）如果对任意的s，t∈[，2]，都有f（s）≥g（t）成立，某某数a的取值X围．【考点】利用导数求闭区间上函数的最值；利用导数研究函数的单调性．【专题】综合题；导数的综合应用．【分析】（1）求导数，利用导数的正负，即可讨论函数h（x）=的单调性；（2）求出g（x）max=g（2）=1，当x∈[，2]时，f（x）=+xlnx恒成立，等价于a≥x﹣x2lnx 恒成立，然后利用导数求函数u（x）=x﹣x2lnx在区间[，2]上取得最大值，则实数a的取值X围可求．【解答】解：（1）h（x）==+lnx，h′（x）=，①a≤0，h′（x）≥0，函数h（x）在（0，+∞）上单调递增②a＞0时，h'（x）＞0，则x∈（，+∞），函数h（x）的单调递增区间为（，+∞），h'（x）＜0，则x∈（0，），函数h（x）的单调递减区间为（0，），．（2）g（x）=x3﹣x2﹣3，g′（x）=3x（x﹣），x 2g′（x）0 ﹣0 +g（x）﹣递减极小值递增 13由上表可知，g（x）在x=2处取得最大值，即g（x）max=g（2）=1所以当x∈[，2]时，f（x）=+xlnx≥1恒成立，等价于a≥x﹣x 2lnx恒成立，记u（x）=x﹣x2lnx，所以a≥u（x）max，u′（x）=1﹣x﹣2xlnx，可知u′（1）=0，当x∈（，1）时，1﹣x＞0，2xlnx＜0，则u′（x）＞0，∴u（x）在x∈（，2）上单调递增；当x∈（1，2）时，1﹣x＜0，2xlnx＞0，则u′（x）＜0，∴u（x）在（1，2）上单调递减；故当x=1时，函数u（x）在区间[，2]，上取得最大值u（1）=1，所以a≥1，故实数a的取值X围是[1，+∞）．【点评】本题考查了利用导数研究函数的单调性，考查了导数在最大值、最小值问题中的应用，考查了数学转化思想方法和函数构造法，训练了利用分离变量法求参数的取值X围，属于中档题．四、选做题：请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题记分．22．已知曲线C1的参数方程是（θ为参数）以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程是ρ=﹣4cosθ．（1）求曲线C1与C2交点的极坐标；（2）A、B两点分别在曲线C1与C2上，当|AB|最大时，求△OAB的面积（O为坐标原点）．【考点】参数的意义；简单曲线的极坐标方程．【专题】选作题；转化思想；综合法；坐标系和参数方程．【分析】（1）把参数方程和极坐标方程化为直角坐标方程，联立方程组求出交点的坐标，再把交点的直角坐标化为极坐标；（2）画出图象，由平面几何知识可知，A，C1，C2，B依次排列且共线时|AB|最大．【解答】解：（1）由（θ为参数），消去参数得：x2+（y﹣2）2=4，即x2+y2﹣4y=0；由ρ=﹣4cosθ，得ρ2=﹣4ρcosθ，即x2+y2=﹣4x．两式作差得：x+y=0，代入C1得交点为（0，0），（﹣2，2）．其极坐标为（0，0），（2，）；（2）如图，由平面几何知识可知，A，C1，C2，B依次排列且共线时|AB|最大．此时|AB|=2+4，O到AB的距离为．∴△OAB的面积为S=×（2+4）×=2+2．【点评】本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程，考查了推理能力与计算能力，属于基础题．23．已知不等式|2x+2|﹣|x﹣1|＞a．（1）当a=0时，求不等式的解集（2）若不等式在区间[﹣4，2]内无解．某某数a的取值X围．【考点】绝对值不等式的解法．【专题】不等式的解法及应用．【分析】（1）把要解的不等式等价转化为与之等价的三个不等式组，求出每个不等式组的解集，再取并集，即得所求．（2）求得f（x）=|2x+2|﹣|x﹣1|=在区间[﹣4，2]内的值域，结合|2x+2|﹣|x﹣1|＞a无解，求得a的X围．【解答】解：（1）当a=0时，不等式即|2x+2|﹣|x﹣1|＞0，可得①，或②，或③．解①求得 x＜﹣3，解②求得﹣＜x＜1，解③求得x≥1．综上可得，原不等式的解集为{x|x＜﹣3，或x＞﹣}．（2）当x∈[﹣4，2]，f（x）=|2x+2|﹣|x﹣1|=的值域为[﹣2，3]，而不等式|2x+2|﹣|x﹣1|＞a无解，故有a≤3．【点评】本题主要考查绝对值不等式的解法，体现了转化、分类讨论的数学思想；还考查了分段函数的应用，求函数的值域，属于中档题．。

2015-2016学年某某省某某一中高一（上）11月月考数学试卷（奥班）一.选择题（本大题共12小题，共12&#215;5=60分，在给出的四个选项中，只有一项是符合要求的.）1．集合A可以表示为，也可以表示为{0，|x|，x+y}，则y﹣x的值为( ) A．﹣1 B．0 C．1 D．﹣1或12．已知向量=（λ+1，1），=（λ+2，2），若（+）⊥（﹣），则λ=( )A．﹣4 B．﹣3 C．﹣2 D．﹣13．函数的图象大致是( )A．B．C．D．4．已知函数，则f（2+log23）的值为( )A．B．C．D．5．设=（cos2θ，sinθ），=（1，0），已知•=，且，则tanθ=( ) A．B． C．D．6．下列函数既是奇函数，又在区间[﹣1，1]上单调递减的是( )A． f（x）=sinx B．f（x）=﹣|x+1|C．D．7．将函数y=（sinx+cosx）（sinx﹣cosx）的图象向左平移个单位后，得到函数y=g（x）的图象，则y=g（x）的图象( )A．关于原点对称 B．关于y轴对称C．关于点（﹣，0）对称D．关于直线x=对称8．在△ABC中，cos2=，（a，b，c分别为角A，B，C的对边），则△ABC的形状为( ) A．正三角形 B．直角三角形C．等腰三角形或直角三角形D．等腰直角三角形9．已知f（x）=ln（﹣3x）+1，则f（lg3）+f（lg）等于( )A．2 B．1 C．0 D．﹣110．如图是函数f（x）=Acos（πx+φ）﹣1（A＞0，|φ|＜）的图象的一部分，则f=( )A．1 B．2 C．D．﹣311．函数y=tan（x﹣）的部分图象如图所示，则（+）=( )A．6 B．4 C．﹣4 D．﹣612．若非零不共线向量、满足|﹣|=||，则下列结论正确的个数是( )①向量、的夹角恒为锐角；②2||2＞•；③|2|＞|﹣2|；④|2|＜|2﹣|．A．1 B．2 C．3 D．4二.填空题（本大题共4小题，共4&#215;5=20分，请把正确答案填写在横线上）13．求值：=__________．14．设函数y=sinx（0≤x≤π）的图象为曲线C，动点A（x，y）在曲线C上，过A且平行于x轴的直线交曲线C于点B（A、B可以重合），设线段AB的长为f（x），则函数f（x）单调递增区间__________．15．在△ABC中，∠A=60°，M是AB的中点，若|AB|=2，|BC|=2，D在线段AC上运动，则的最小值为__________．16．已知函数f（x）=，则关于x的方程f[f（x）]+k=0给出下列四个命题：①存在实数k，使得方程恰有1个实根；②存在实数k，使得方程恰有2个不相等的实根；③存在实数k，使得方程恰有3个不相等的实根；④存在实数k，使得方程恰有4个不相等的实根．其中正确命题的序号是__________（把所有满足要求的命题序号都填上）．三.解答题（解答应写出文字说明、证明过程或演算步骤）17．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜）的图象的相邻两条对称轴的距离是，当x=时取得最大值2．（1）求函数f（x）的解析式；（2）若函数g（x）=f（x）﹣的零点为x0，求．18．已知集合A={x|x2﹣3（a+1）x+2（3a+1）＜0}，B=，（1）当a=2时，求A∩B；（2）求使B⊆A的实数a的取值X围．19．已知函数．（Ⅰ）求函数f（x）的最小正周期和单调递增区间；（Ⅱ）当时，若f（x）≥log2t恒成立，求t的取值X围．20．在△ABC中，角A，B，C的对边分别为a、b、c，tanC=．（1）求角C的大小；（2）若△ABC的外接圆直径为1，求△ABC面积S的取值X围．21．在△ABC中，A，B，C为三个内角a，b，c为相应的三条边，若，且．（1）求证：A=C；（2）若||=2，试将表示成C的函数f（C），并求f（C）值域．22．已知函数f（x）=log9（9x+1）+kx（k∈R）是偶函数．（1）求k的值；（2）若函数y=f（x）的图象与直线没有交点，求b的取值X围；（3）设，若函数f（x）与h（x）的图象有且只有一个公共点，某某数a的取值X围．2015-2016学年某某省某某一中高一（上）11月月考数学试卷（奥班）一.选择题（本大题共12小题，共12&#215;5=60分，在给出的四个选项中，只有一项是符合要求的.）1．集合A可以表示为，也可以表示为{0，|x|，x+y}，则y﹣x的值为( ) A．﹣1 B．0 C．1 D．﹣1或1【考点】集合的相等．【专题】计算题．【分析】利用集合相等的定义，紧紧抓住0这个特殊元素，结合列方程组解方程解决问题，注意集合中元素的互异性．【解答】解：∵集合A可以表示为，也可以表示为{0，|x|，x+y}∴y=0，则或解得x=0或x=±1注意到集合中元素的互异性则x=﹣1∴y﹣x=0﹣（﹣1）=1故选C．【点评】本题主要考查集合的相等，如果已知集合中有特殊元素，抓住它是简化解题的关键，还需注意集合中元素的互异性，属于基础题．2．已知向量=（λ+1，1），=（λ+2，2），若（+）⊥（﹣），则λ=( )A．﹣4 B．﹣3 C．﹣2 D．﹣1【考点】数量积判断两个平面向量的垂直关系．【专题】平面向量及应用．【分析】利用向量的运算法则、向量垂直与数量积的关系即可得出．【解答】解：∵，．∴=（2λ+3，3），．∵，∴=0，∴﹣（2λ+3）﹣3=0，解得λ=﹣3．故选B．【点评】熟练掌握向量的运算法则、向量垂直与数量积的关系是解题的关键．3．函数的图象大致是( )A．B．C．D．【考点】函数的图象．【专题】作图题．【分析】根据选项提供的信息利用函数值的符号对选项进行筛选．【解答】解：当0＜x＜1时，因为lnx＜0，所以，排除选项B、C；当x＞1时，，排除D．故选A．【点评】本题考查了函数的图象，筛选法是做选择题常用的办法．4．已知函数，则f（2+log23）的值为( )A．B．C．D．【考点】函数的值；分段函数的解析式求法及其图象的作法．【专题】计算题．【分析】先判断出2+log23＜4，代入f（x+1）=f（3+log23），又因3+log23＞4代入f（x）=，利用指数幂的运算性质求解．【解答】解：∵1＜log23＜2，∴3＜2+log23＜4，∴f（2+log23）=f（2+log23+1）=f（3+log23），∵4＜3+log23＜5，∴f（3+log23）==×=，故选A．【点评】本题的考点是分段函数求函数值，先判断自变量的X围，再代入对应的关系式，根据指数幂的运算性质进行化简求值．5．设=（cos2θ，sinθ），=（1，0），已知•=，且，则tanθ=( ) A．B． C．D．【考点】平面向量数量积的运算；三角函数中的恒等变换应用．【专题】计算题；向量法；三角函数的求值；平面向量及应用．【分析】进行数量积的坐标运算可得到cos2，这样根据二倍角的余弦公式及θ的X围便可求出sinθ，cosθ，从而可以得出tanθ．【解答】解：；∴；∵；∴，；∴．故选B．【点评】考查向量数量积的坐标运算，二倍角的余弦公式，切化弦公式，清楚正弦函数、余弦函数在各象限的符号，要熟悉正余弦函数的图象．6．下列函数既是奇函数，又在区间[﹣1，1]上单调递减的是( )A．f（x）=sinx B．f（x）=﹣|x+1|C．D．【考点】奇偶性与单调性的综合．【专题】常规题型．【分析】本题是选择题，可采用逐一检验的方法，只要不满足其中一条就能说明不正确．【解答】解：f（x）=sinx是奇函数，但其在区间[﹣1，1]上单调递增，故A错；∵f（x）=﹣|x+1|，∴f（﹣x）=﹣|﹣x+1|≠﹣f（x），∴f（x）=﹣|x+1|不是奇函数，∴故B错；∵a＞1时，y=a x在[﹣1，1]上单调递增，y=a﹣x[﹣1，1]上单调递减，∴f（x）=（a x﹣a﹣x）在[﹣1，1]上单调递增，故C错；故选 D【点评】本题综合考查了函数的奇偶性与单调性，是函数这一部分的常见好题．7．将函数y=（sinx+cosx）（sinx﹣cosx）的图象向左平移个单位后，得到函数y=g（x）的图象，则y=g（x）的图象( )A．关于原点对称 B．关于y轴对称C．关于点（﹣，0）对称D．关于直线x=对称【考点】函数y=Asin（ωx+φ）的图象变换．【专题】计算题．【分析】利用平方差公式和二倍角公式对解析式进行化简，根据左加右减求出g（x）的解析式，由正弦函数的对称性进行判断．【解答】解：y=（sinx+cosx）（sinx﹣cosx）=sin2x﹣cos2x=﹣cos2x，则由题意知，g（x）=﹣cos2（x+）=sin2x，即g（x）的图象关于原点对称．故选A．【点评】本题考查了复合三角函数图象的变换，根据平方差公式和二倍角公式对解析式进行化简，由条件和正弦函数的性质进行判断，考查了分析问题和解决问题的能力．8．在△ABC中，cos2=，（a，b，c分别为角A，B，C的对边），则△ABC的形状为( ) A．正三角形 B．直角三角形C．等腰三角形或直角三角形D．等腰直角三角形【考点】解三角形．【专题】计算题．【分析】利用二倍角公式代入cos2=求得cosB=，进而利用余弦定理化简整理求得a2+b2=c2，根据勾股定理判断出三角形为直角三角形．【解答】解：∵cos2=，∴=，∴cosB=，∴=，∴a2+c2﹣b2=2a2，即a2+b2=c2，∴△ABC为直角三角形．故选B【点评】本题主要考查了三角形的形状判断．考查了学生对余弦定理即变形公式的灵活利用．9．已知f（x）=ln（﹣3x）+1，则f（lg3）+f（lg）等于( )A．2 B．1 C．0 D．﹣1【考点】对数的运算性质．【专题】函数的性质及应用．【分析】利用f（x）+f（﹣x）=2即可得出．【解答】解：∵f（x）+f（﹣x）=++1=ln1+2=2．∴f（lg3）+f（lg）=f（lg3）+f（﹣lg3）=2．故选：A．【点评】本题考查了函数的奇偶性、对数的运算法则，属于基础题．10．如图是函数f（x）=Acos（πx+φ）﹣1（A＞0，|φ|＜）的图象的一部分，则f=( )A．1 B．2 C．D．﹣3【考点】余弦函数的图象．【专题】计算题；数形结合；数形结合法；三角函数的图像与性质．【分析】根据已知中函数f（x）=Acos（πx+φ）﹣1（A＞0，|φ|＜）的图象，求出函数的解析式，结合函数周期性可得f=f（2）=2cosπ﹣1=﹣3．【解答】解：∵函数f（x）=Acos（πx+φ）﹣1的周期T==3，函数的最大值A﹣1=1，故A=2，又由函数图象过（1，0），故2cos（π+φ）﹣1=0，即cos（π+φ）=，由|φ|＜得：φ=﹣，∴f（x）=2cos（πx﹣）﹣1∴f=f（2）=2cosπ﹣1=﹣3，故选：D【点评】本题考查的知识点是余弦型函数的图象和性质，熟练掌握余弦型函数的图象和性质，是解答的关键．11．函数y=tan（x﹣）的部分图象如图所示，则（+）=( )A．6 B．4 C．﹣4 D．﹣6【考点】向量在几何中的应用．【专题】图表型．【分析】先利用正切函数求出A，B两点的坐标，进而求出与的坐标，再代入平面向量数量积的运算公式即可求解．【解答】解：因为y=tan（x﹣）=0⇒x﹣=kπ⇒x=4k+2，由图得x=2；故A（2，0）由y=tan（x ）=1⇒x﹣=k ⇒x=4k+3，由图得x=3，故B（3，1）所以=（5，1），=（1，1）．∴（）=5×1+1×1=6．故选A．【点评】本题主要考查平面向量数量积的运算，考查的是基础知识，属于基础题．解决本题的关键在于利用正切函数求出A，B两点的坐标．12．若非零不共线向量、满足|﹣|=||，则下列结论正确的个数是( )①向量、的夹角恒为锐角；②2||2＞•；③|2|＞|﹣2|；④|2|＜|2﹣|．A．1 B．2 C．3 D．4【考点】平面向量数量积的运算．【专题】综合题．【分析】对于①，利用已知条件，推出向量、、﹣组成的三角形是等腰三角形，判定正误即可；对于②，利用数量积公式，结合已知条件，判断正误；对于③，通过平方以及向量的数量积判断正误．对于④，|2|＜|2﹣|，得到4||cos＜，＞＜||不一定成立，说明正误即可．【解答】解：①因为非零向量、满足|﹣|=||，所以由向量、、﹣组成的三角形是等腰三角形，且向量是底边，所以向量、的夹角恒为锐角，①正确；②：2||2＞•=||•||cos＜，＞⇒2||＞||cos＜，＞，而||+|﹣|=2||＞||＞||cos＜，＞，所以②正确；③：|2|＞|﹣2|⇒4||2＞|﹣2|2=||2﹣4||•||cos＜，＞+4||2⇒4||•||cos＜，＞＞||2⇒4•||cos＜，＞＞||，而2||cos＜，＞=||，所以4||cos＜，＞＞||，③正确；④：|2|＜|2﹣|⇒4||cos＜，＞＜||，而4||cos＜，＞＜||不一定成立，所以④不正确．故选C．【点评】本题考查向量的数量积的应用，向量的模的求法，考查计算能力．二.填空题（本大题共4小题，共4&#215;5=20分，请把正确答案填写在横线上）13．求值：=19．【考点】对数的运算性质；有理数指数幂的化简求值．【专题】计算题．【分析】根据式子的特点需要把底数和真数表示成幂的形式，把对数前的系数放到真数的指数位置，利用恒等式，进行化简求值．【解答】解：原式=9﹣3×（﹣3）+=18+1=19，故答案为：19．【点评】本题的考点是对数和指数的运算性质的应用，常用的方法是把（底数）真数表示出幂的形式，或是把真数分成两个数的积（商）形式，根据对应的运算法则和“”进行化简求值．14．设函数y=sinx（0≤x≤π）的图象为曲线C，动点A（x，y）在曲线C上，过A且平行于x轴的直线交曲线C于点B（A、B可以重合），设线段AB的长为f（x），则函数f（x）单调递增区间[]．【考点】正弦函数的图象；正弦函数的单调性．【专题】计算题；三角函数的图像与性质．【分析】依题意，对x∈[0，]与x∈[，π]讨论即可．【解答】解：依题意得f（x）=|AB|，（0≤|AB|≤π）．当x∈[0，]时，|AB|由π变到0，∴[0，]为f（x）单调递减区间；当当x∈[，π]时，|AB|由0变到π，∴[，π]为f（x）单调递增区间．故答案为：[，π]．【点评】本题考查正弦函数的图象与性质，考查数形结合思想与分析问题的能力，属于中档题．15．在△ABC中，∠A=60°，M是AB的中点，若|AB|=2，|BC|=2，D在线段AC上运动，则的最小值为．【考点】平面向量数量积的运算；余弦定理．【专题】平面向量及应用．【分析】把向量用，表示，可化简数量积的式子为，由余弦定理可得AC的长度，进而可得的X围，由二次函数区间的最值可得答案．【解答】解：∵=，==，故=（）•（）====，设AC=x，由余弦定理可得，整理得x2﹣2x﹣8=0，解得x=4或x=﹣2（舍去），故有∈[0，4]，由二次函数的知识可知当=时，取最小值故答案为：【点评】本题考查平面向量的数量积的运算，涉及余弦定理和二次函数的最值，属中档题．16．已知函数f（x）=，则关于x的方程f[f（x）]+k=0给出下列四个命题：①存在实数k，使得方程恰有1个实根；②存在实数k，使得方程恰有2个不相等的实根；③存在实数k，使得方程恰有3个不相等的实根；④存在实数k，使得方程恰有4个不相等的实根．其中正确命题的序号是①②（把所有满足要求的命题序号都填上）．【考点】命题的真假判断与应用；根的存在性及根的个数判断．【专题】综合题．【分析】由解析式判断出f（x）＞0，再求出f[f（x）]的解析式，根据指数函数的图象画出此函数的图象，根据方程根的几何意义和图象，判断出方程根的个数以及对应的k的X围，便可以判断出命题的真假．【解答】解：由题意知，当x≥0时，f（x）=e x≥1；当x＜0时，f（x）=﹣2x＞0，∴任意x∈R，有f（x）＞0，则，画出此函数的图象如下图：∵f[f（x）]+k=0，∴f[f（x）]=﹣k，由图得，当﹣e＜k＜﹣1时，方程恰有1个实根；当k＜﹣e时，方程恰有2个实根，故①②正确．故答案为：①②．【点评】本题考查了命题的真假判断，以及方程根的根数问题，涉及到了分段函数求值，指数函数的图象及性质应用，考查了学生作图能力和转化思想．三.解答题（解答应写出文字说明、证明过程或演算步骤）17．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜）的图象的相邻两条对称轴的距离是，当x=时取得最大值2．（1）求函数f（x）的解析式；（2）若函数g（x）=f（x）﹣的零点为x0，求．【考点】正弦函数的图象．【专题】计算题；转化思想；三角函数的求值；三角函数的图像与性质．【分析】（1）由已知求出函数的振幅，周期和初相，可得函数f（x）的解析式；（2）若函数g（x）=f（x）﹣的零点为x0，，利用诱导公式，可得答案．【解答】解：（1）由题意知，振幅A=2，周期T=，∴ω=2，∴f（x）=2sin（2x+φ）．将点代入得：，又，故．∴．（2）由函数的零点为x0知：x0是方程的根，故，得sin（2x0+）=，又（2x0+）+（﹣2x0）=，∴．【点评】本题考查的知识点是正弦型函数的图象和性质，熟练掌握正弦型函数的图象和性质，是解答的关键．18．已知集合A={x|x2﹣3（a+1）x+2（3a+1）＜0}，B=，（1）当a=2时，求A∩B；（2）求使B⊆A的实数a的取值X围．【考点】交集及其运算；集合的包含关系判断及应用．【专题】计算题．【分析】（1）把a的值分别代入二次不等式和分式不等式，然后通过求解不等式化简集合A，B，再运用交集运算求解A∩B；（2）把集合B化简后，根据集合A中二次不等式对应二次方程判别式的情况对a进行分类讨论，然后借助于区间端点值之间的关系列不等式组求解a的X围．【解答】解：（1）当a=2时，A={x|x2﹣3（a+1）x+2（3a+1）＜0}={x|x2﹣9x+14=0}=（2，7），B=={x|}=（4，5），∴A∩B=（4，5）（2）∵B=（2a，a2+1），①当a＜时，A=（3a+1，2）要使B⊆A必须，此时a=﹣1，②当时，A=∅，使B⊆A的a不存在．③a＞时，A=（2，3a+1）要使B⊆A，必须，此时1≤a≤3．综上可知，使B⊆A的实数a的X围为[1，3]∪{﹣1}．【点评】本题考查了交集及其运算，考查了集合的包含关系及其应用，考查了分类讨论的数学思想，解答此题的关键是对集合A的讨论，此题是中档题．19．已知函数．（Ⅰ）求函数f（x）的最小正周期和单调递增区间；（Ⅱ）当时，若f（x）≥log2t恒成立，求t的取值X围．【考点】两角和与差的正弦函数；函数恒成立问题；正弦函数的单调性．【专题】三角函数的图像与性质．【分析】（Ⅰ）函数解析式利用二倍角的余弦函数公式化简，整理后利用两角和与差的正弦函数公式化为一个角的正弦函数，找出ω的值，代入周期公式即可求出函数f（x）的最小正周期，根据正弦函数的单调性即可确定出f（x）的单调递增区间；（Ⅱ）由x的X围求出这个角的X围，利用正弦函数的值域确定出f（x）的最小值，根据f （x）≥log2t恒成立，得到log2t小于等于f（x）的最小值，即可确定出t的X围．【解答】解：（I）f（x）=sin2x﹣cos2x+1=2sin（2x﹣）+1，∵ω=2，∴函数f（x）最小正周期是T=π；当2kπ﹣≤2x﹣≤2π+，k∈Z，即kπ﹣≤x≤kπ+，k∈Z，函数f（x）单调递增区间为[kπ﹣，kπ+]，k∈Z；（II）∵x∈[，]，∴2x﹣∈[0，]，∴f（x）=2sin（2x﹣）+1的最小值为1，由f（x）≥log2t恒成立，得log2t≤1=log22恒成立，∴0＜t≤2，即t的取值X围为（0，2]．【点评】此题考查了两角和与差的正弦函数公式，函数恒成立问题，以及正弦函数的单调性，熟练掌握公式是解本题的关键．20．在△ABC中，角A，B，C的对边分别为a、b、c，tanC=．（1）求角C的大小；（2）若△ABC的外接圆直径为1，求△ABC面积S的取值X围．【考点】三角函数中的恒等变换应用；正弦定理．【专题】转化思想；数形结合法；三角函数的求值；解三角形．【分析】（1）先将tanC写成，再展开化为sin（C﹣A）=sin（B﹣C），从而求得A+B；（2）先用正弦定理，再用面积公式，结合A﹣B的X围，求面积的X围．【解答】解：（1）∵tanC=，∴=，即sinCcosA+sinCcosB=cosCsinA+cosCsinB，所以，sinCcosA﹣cosCsinA=cosCsinB﹣sinCcosB，因此，sin（C﹣A）=sin（B﹣C），所以，C﹣A=B﹣C或C﹣A=π﹣（B﹣C）（不成立），即2C=A+B，故C=；（2）根据正弦定理，外接圆直径2R====1，所以，a=2RsinA=sinA，b=2RsinB=sinB，而S△ABC=absinC=sinAsinB=[cos（A﹣B）﹣cos（A+B）]=[cos（A﹣B）+]，其中，A+B=，所以，A﹣B∈（﹣，），因此，cos（A﹣B）∈（﹣，1]，所以，S△ABC=∈（0，]，故△ABC面积S的取值X围为：．【点评】本题主要考查了三角函数的恒等变换，涉及同角三角函数基本关系式，两角和差的正弦公式，以及运用正弦定理解三角形和面积的求解，属于中档题．21．在△ABC中，A，B，C为三个内角a，b，c为相应的三条边，若，且．（1）求证：A=C；（2）若||=2，试将表示成C的函数f（C），并求f（C）值域．【考点】正弦定理；函数解析式的求解及常用方法；平面向量数量积的运算．【专题】计算题；转化思想；分析法；解三角形；平面向量及应用．【分析】（1）由已知及正弦定理化简可得sinB=sin2C，解得B=2C或B+2C=π，利用角C的X 围及三角形内角和定理分类讨论即可得证．（2）由B+2C=π，可得cosB=﹣cos2C．由，利用平面向量数量积的运算，结合a=c，可得，从而可求f（C）=，结合C的X围，利用余弦定理的图象和性质即可得解f（C）值域．【解答】（本小题满分12分）解：（1）由，及正弦定理有sinB=sin2C，∴B=2C或B+2C=π．…若B=2C，且，∴，B+C＞π（舍）；…∴B+2C=π，所以 A=C，…（2）∵B+2C=π，∴cosB=﹣cos2C．∵，∴a2+c2+2ac•cosB=4，…∴（∵a=c），从而 f（C）==…∵，∴，∴，∴2＜f（C）＜3，所以 f（C）值域是（2，3）…【点评】本题主要考查了正弦定理，平面向量数量积的运算，三角形内角和定理，余弦函数的图象和性质的综合应用，考查了计算能力和转化思想，属于中档题．22．已知函数f（x）=log9（9x+1）+kx（k∈R）是偶函数．（1）求k的值；（2）若函数y=f（x）的图象与直线没有交点，求b的取值X围；（3）设，若函数f（x）与h（x）的图象有且只有一个公共点，某某数a的取值X围．【考点】函数奇偶性的性质；函数与方程的综合运用．【专题】计算题．【分析】（1）因为f（x）为偶函数所以f（﹣x）=f（x）代入求得k的值即可；（2）函数与直线没有交点即无解，即方程log9（9x+1）﹣x=b 无解．令g（x）=log9（9x+1）﹣x，则函数y=g（x）的图象与直线y=b无交点．推出g（x）为减函数得到g（x）＞0，所以让b≤0就无解．（3）函数f（x）与h（x）的图象有且只有一个公共点，即联立两个函数解析式得到方程，方程只有一个解即可．【解答】解：（1）因为y=f（x）为偶函数，所以∀x∈R，f（﹣x）=f（x），即log9（9﹣x+1）﹣kx=log9（9x+1）+kx对于∀x∈R恒成立．即恒成立即（2k+1）x=0恒成立，而x不恒为零，所以．（2）由题意知方程即方程log9（9x+1）﹣x=b无解．令g（x）=log9（9x+1）﹣x，则函数y=g（x）的图象与直线y=b无交点．因为任取x1、x2∈R，且x1＜x2，则，从而．于是，即g（x1）＞g（x2），所以g（x）在（﹣∞，+∞）是单调减函数．因为，所以．所以b的取值X围是（﹣∞，0）．（3）由题意知方程有且只有一个实数根．令3x=t＞0，则关于t的方程（记为（*））有且只有一个正根．若a=1，则，不合，舍去；若a≠1，则方程（*）的两根异号或有两相等正根．由或﹣3；但，不合，舍去；而；方程（*）的两根异号⇔（a﹣1）•（﹣1）＜0，即﹣a+1＜0，解得：a＞1．综上所述，实数a的取值X围{﹣3}∪（1，+∞）．【点评】考查学生运用函数奇偶性的能力，以及函数与方程的综合运用能力．。

第1单元综合测试一．选择题1．（2019秋•汉川市期中）()时整，时针、分针、秒针重合在一处．A．9时整B．6时整C．12时整D．3时整2．（2019春•单县期末）用24时记时法，下午5时是()A．5时B．17时C．17小时3．（2019•福建模拟）当6:00时，时针和分针成()A．直角B．锐角C．平角D．钝角4．（2017春•靖州县期末）某商店的营业时间如下：8:0011:00-．这个商店一天共营业(-，13:0020:30)A．8小时30分钟B．9小时30分钟C．10小时30分钟5．（2017•长沙）时针从第一个数字到第二个数字经过的时间是()A．60秒B．60分C．2小时6．（2017春•上城区校级期末）一个门卫晚上9时上班，第二天早上7时下班，他工作的时间是() A．10小时B．9小时C．8小时二．填空题7．（2018秋•博兴县期末）小红练琴从开始，到结束，一共练了分钟．8．（2019春•英山县期末）22:009:4513:00晚上10时下午3时20分凌晨4时30分9．（2019春•营山县月考）80分=小时．10．（2016秋•青岛期中）经过了小时分钟．11．（2012秋•上海期末）上海开往某地的列车，上午6时24分开车，当天晚上8时50分到达，这列火车共行驶了小时分．12．（2010•南通校级模拟）小明每天8时半到学校上课，11时50分放学回家，他上午在校的时间是分．三．判断题（共6小题）13．（2019春•秦皇岛期末）深夜12时，用24时计时法既可以表示为今天的24时，也可以表示为明天的0时．（判断对错）14．（2019春•新田县期中）分针从数字3走到数字6，经过的时间是15分．．（判断对错）15．（2019春•宁远县期中）笑笑一秒钟可以写30个字．（判断对错）16．90分90秒．．（判断对错）17．午休时间从11:30到1:00，午休时间为2时30分．．（判断对错）18．时针指着6，分针指着12，这时是6:00．．（判断对错）四．应用题19．机灵狗从家出发去给距离22千米的森林老人送信，机灵狗平均每小时跑多少千米？20．看图回答问题．（1）3月22日下午5时爸爸开车走了这条道路，他违反交通规则了吗？（2）爸爸晚上11时下火车，要坐207路夜班车，有车吗？五．操作题21．（2017秋•新晃县期末）根据时间，在钟表内画时针和分针．22．（2016秋•济南期末）填一填，画一画．23．（2017秋•浠水县期中）24．（2016秋•宁城县期中）填一填、画一画（1）我会填（2）我会画：画一条比5厘米少20毫米的线段．25．（2015秋•成都期末）连一连六．解答题26．（2017秋•海安县校级期末）写出下列钟表的时间27．（2017秋•博兴县期末）看钟面填空（1）电影从时分放映，在时分放映结束．放映了时分．（2）李新看完电影在时分回到家里．电影院到李新家要走分钟．28．（2018春•南郊区月考）奶奶今天早上6:30去活动中心锻炼身体，比昨天提前了10分钟．她昨天什么时间去锻炼身体的？29．（2017秋•蔡甸区月考）小青到学校要走15分钟，他每天早晨要在8:35到校，他至少应在几时几分从家出发？30．（2015秋•市南区月考）看图填一填．答案与解析1．（2019秋•汉川市期中）()时整，时针、分针、秒针重合在一处．A．9时整B．6时整C．12时整D．3时整【解答】解：12时整，时针、分针、秒针重合在一处；故选：C．2．（2019春•单县期末）用24时记时法，下午5时是()A．5时B．17时C．17小时【解答】解：5时12+时17=时，答：用24时记时法，下午5时是17时；故选：B．3．（2019•福建模拟）当6:00时，时针和分针成()A．直角B．锐角C．平角D．钝角【解答】解：6时整，时针指着6，分针指着12，两针成一直线，组成平角．故选：C．4．（2017春•靖州县期末）某商店的营业时间如下：8:0011:00-．这个商店一天共营业(-，13:0020:30)A．8小时30分钟B．9小时30分钟C．10小时30分钟【解答】解：11时8=小时-时320时30分13-时7=小时30分3小时7+小时30分10=小时30分答：这个商店一天共营业10小时30分钟．故选：C．5．（2017•长沙）时针从第一个数字到第二个数字经过的时间是()A．60秒B．60分C．2小时【解答】解：时针从第一个数字到第二个数字经过的时间是1小时，1小时60=分；故选：B．6．（2017春•上城区校级期末）一个门卫晚上9时上班，第二天早上7时下班，他工作的时间是() A．10小时B．9小时C．8小时【解答】解：129710-+=（小时）；故选：A．二．填空题7．（2018秋•博兴县期末）小红练琴从开始，到结束，一共练了分钟．【解答】解：小红练琴从5时15分开始到5时50分结束5时50分5-时15分35=分答：小红练琴从5:15开始，到5:50结束，一共练了35分钟．故答案为：5:15，5:50，35．8．（2019春•英山县期末）22:009:4513:00晚上10时下午3时20分凌晨4时30分【解答】解：下午3时20分是15:209时45分时9:45凌晨4:30是4:3013:00是下午1时故答案为：22:0015:209:454:3013:00晚上10时下午3时20分上午9时45分凌晨4时30分下午1时9．（2019春•营山县月考）80分=小时．【解答】解：80分43=小时．故答案为：43．10．（2016秋•青岛期中）经过了小时分钟．【解答】解：4时30分3-时1=小时30分答：经过了1小时30分钟．故答案为：1，30．11．（2012秋•上海期末）上海开往某地的列车，上午6时24分开车，当天晚上8时50分到达，这列火车共行驶了小时分．【解答】解：上午6时24分是6时24分；晚上8时50分是20时50分；20时50分6-时24分14=时26分．答：共行驶了14时26分．故答案为：14，26．12．（2010•南通校级模拟）小明每天8时半到学校上课，11时50分放学回家，他上午在校的时间是分．【解答】解：上午在校的时间：11时50分8=时20分，-时30分33时20分200=分；答：他上午在校的时间是200 分．故答案为；200分．三．判断题13．（2019春•秦皇岛期末）深夜12时，用24时计时法既可以表示为今天的24时，也可以表示为明天的0时．√（判断对错）【解答】解：深夜12时，用24时计时法既可以表示为今天的24时，也可以表示为明天的0时此种说法正确．故答案为：√．14．（2019春•新田县期中）分针从数字3走到数字6，经过的时间是15分．√．（判断对错）【解答】解：(63)5-⨯=⨯3515=（分钟）分针从数字3走到数字6，经过的时间是15分；原题说法正确．故答案为：√．15．（2019春•宁远县期中）笑笑一秒钟可以写30个字．⨯（判断对错）【解答】解：笑笑一秒可以写30个字不符合生活实际．所以笑笑一秒钟可以写30个字说法错误．故答案为：⨯．16．90分90=秒．⨯．（判断对错）【解答】解：90分5400=秒，所以90分90>秒原题说法错误．故答案为：⨯．17．午休时间从11:30到1:00，午休时间为2时30分．⨯．（判断对错）【解答】解：下午1时12=时60分12时60分11--时30分1=时30分所以“午休时间从11:30到1:00，午休时间为2时30分”的说法是错误的；故答案为：⨯．18．时针指着6，分针指着12，这时是6:00．√．（判断对错）【解答】解：时针指着6，分针指着12，这时是6:00，说法正确；故答案为：√．四．应用题19．机灵狗从家出发去给距离22千米的森林老人送信，机灵狗平均每小时跑多少千米？【解答】解：出发时刻为上午8时30分，到达时刻为上午10时30分10时30分8-时30分2=小时÷=（千米）22211答：机灵狗平均每小时跑11千米．20．看图回答问题．（1）3月22日下午5时爸爸开车走了这条道路，他违反交通规则了吗？（2）爸爸晚上11时下火车，要坐207路夜班车，有车吗？【解答】解：（1）3月22日下午5时爸爸开车走了这条道路，根据交通规则：下午5:30至7:00禁止小汽车通行．5时在5:30之前答：他没有违反交通规则．（2）爸爸晚上11时下火车，207夜班车首尾时刻为22:50，末班为4:50，晚上11时，即23:00，在 之间22:504:50答：爸爸晚上11时下火车，要坐207路夜班车，有车．五．操作题21．（2017秋•新晃县期末）根据时间，在钟表内画时针和分针．【解答】解：根据时间，在钟表内画时针和分针．22．（2016秋•济南期末）填一填，画一画．【解答】解：填一填，画一画：23．（2017秋•浠水县期中）【解答】解：8时5分7-时35分30=分钟故答案为：30．24．（2016秋•宁城县期中）填一填、画一画（1）我会填（2）我会画：画一条比5厘米少20毫米的线段．【解答】解：我会填：（2）我会画：画一条比5厘米少20毫米的线段：25．（2015秋•成都期末）连一连【解答】解：连一连：六．解答题26．（2017秋•海安县校级期末）写出下列钟表的时间【解答】解：写出下列钟表的时间27．（2017秋•博兴县期末）看钟面填空（1）电影从时分放映，在时分放映结束．放映了时分．（2）李新看完电影在时分回到家里．电影院到李新家要走分钟．【解答】解：（1）电影从9时30分放映，在11时10分放映结束；11时10分9-时30分1=时40分答：放映了1时40分．（2）李新看完电影在11时25分回到家里．11时25分11-时10分15=分答：电影院到李新家要走15分钟．故答案为：9，30，11，10，1，40；11，25，15．28．（2018春•南郊区月考）奶奶今天早上6:30去活动中心锻炼身体，比昨天提前了10分钟．她昨天什么时间去锻炼身体的？【解答】解：6时30分10+分6=时40分；答：她昨天6时40分去锻炼身体的．29．（2017秋•蔡甸区月考）小青到学校要走15分钟，他每天早晨要在8:35到校，他至少应在几时几分从家出发？【解答】解：8时35分15-分8=时20分．答：他至少应在8:20分从家出发．30．（2015秋•市南区月考）看图填一填．【解答】解：。

人教版数学三年级上学期第三单元测试一．选择题1．(2019•衡水模拟)一辆东风汽车的载重约为千克．A．80 B．8000 C．8002．(2018秋•巨野县期中)2袋糖果重1千克,平均每袋糖果重A．50克B．5千克C．500克3．(2019•衡水模拟)一辆汽车的载重量是10吨,合千克．A．1000 B．100 C．100004．(2019春•邳州市校级月考)100张纸大约厚1厘米,张这样的纸大约厚10米．A．1000 B．10000 C．1000005．(2019秋•河南期中)计量重型物品或大宗物件的重量,通常用作单位．A．吨B．千克C．克6．(2018•海安县)质量最接近1吨的是A．10瓶矿泉水B．25名六年级学生C．1000枚1元硬币D．100升水二．填空题7．(2019•南昌)2070米千米；4小时35分小时．8．(2019春•远安县期末)6020克千克；405厘米米．9．(2019•郴州模拟)单位换算38厘米米4吨25千克吨3元5分元6042克千克10．(2018秋•单县期末)5千米200+秒秒+米米3500克500-克千克2分306吨千克2分米15+毫米厘米-厘米厘米36毫米64 11．(2016秋•镇江月考)在下面的括号里填上合适的单位使不等式成立．0.5)0.5(<．<)0.5(12．(2015秋•萧县期中)我会站队(按从小到大的顺序排列)．600分米1千米400厘米30米500毫米．三．判断题13．(2019春•镇康县校级月考)1吨棉花和1000千克铁一样重．．(判断对错) 14．(2018秋•格尔木市校级期末)5千克的海绵比5000克的石头轻得多．(判断对错) 15．(2018秋•单县期末)8千克的木块比8000克的砖块轻．．(判断对错)16．一个西瓜重5克．．(判断对错)17．8千克的木块和8000克的砖块一样重．(判断对错)18．5.5千克的铁块比5.5千克的棉花重．(判断对错)四．应用题19．一根彩带长800厘米,比另一根彩带长2米,另一根彩带长多少厘米?合多少米? 20．小胖前年身高1米35厘米,今年比前年长高了1分米,小胖现在身高多少厘米? 21．一支铅笔原来长1分米,用去1厘米,还剩多少毫米?22．用吨作单位的物品有那些?五．操作题23．(2016秋•海安县月考)估计它们分别有多重,用线连一连．24．根据要表示的千克数,在秤面上画出指针．六．解答题25．(2016春•石台县校级期中)按从大到小的顺序排列．(1)1200千克6吨1400千克8吨(2)1726米11千米3050米2千米450米．26．(2018秋•重庆期中)在〇里填上“”“”或“”3000克〇3千克2吨〇2千克9分〇90秒4米6分〇46分米27．(2015秋•成都期末)2.5米米分米厘米．4.05元元角分8分米2厘米米2角元．28．(2018秋•聊城期中)一头大象重4吨,一头牛重500千克,一头大象比一头牛重多少千克?29．(2016秋•纳雍县月考)杯子里原有1500克水,喝了1千克,还剩多少克?30．(2015春•江岸区期末)桥上有重为2.8吨,0.8吨,0.3吨的三只动物,已知桥限重4吨,长颈鹿1.5吨,长颈鹿现在能上桥吗?请用算式说明理由．答案与解析一．选择题1．(2019•衡水模拟)一辆东风汽车的载重约为千克．A．80 B．8000 C．800【解答】解：一辆东风汽车的载重约为8000千克；故选：．2．(2018秋•巨野县期中)2袋糖果重1千克,平均每袋糖果重A．50克B．5千克C．500克【解答】解：1千克1000=克÷=(克)10002500所以2袋糖果重1千克,平均每袋糖果重500克；故选：．3．(2019•衡水模拟)一辆汽车的载重量是10吨,合千克．A．1000 B．100 C．10000【解答】解：10吨10000=千克所以一辆汽车的载重量是10吨,合10000千克；故选：．4．(2019春•邳州市校级月考)100张纸大约厚1厘米,张这样的纸大约厚10米．A．1000 B．10000 C．100000【解答】解：10米1000=厘米,⨯=(张)1000100100000故选：．5．(2019秋•河南期中)计量重型物品或大宗物件的重量,通常用作单位．A．吨B．千克C．克【解答】解：计量大宗物品,通常不会运用小的重量单位,克或千克,应用吨作单位．因此通常用吨作单位．故选：．6．(2018•海安县)质量最接近1吨的是A．10瓶矿泉水B．25名六年级学生C．1000枚1元硬币D．100升水【解答】解：由分析可知：质量最接近1吨的是25名六年级学生的体重；故选：．二．填空题7．(2019•南昌)2070米千米；4小时35分小时．【解答】解：(1)2070米 2.07=千米；(2)4小时35分7412=小时．故答案为：2.07,7412．8．(2019春•远安县期末)6020克千克；405厘米米．【解答】解：6020克 6.02=千克405厘米 4.05=米故答案为：6.02；4.05．9．(2019•郴州模拟)单位换算38厘米米4吨25千克吨3元5分元6042克千克【解答】解：(1)38厘米0.38=米(2)4吨25千克 4.025=吨(3)3元5分 3.05=元(4)6042克 6.042=千克．故答案为：0.38,4.025,3.05,6.042．10．(2018秋•单县期末)5千米200+米米3500克500-克千克2分30+秒秒6吨千克2分米15-厘米厘米36毫米64+毫米厘米【解答】解：5千米200+米5200=米 3500克500-克3=千克 2分30+秒150=秒 6吨6000=千克2分米15-厘米5=厘米36毫米64+毫米10=厘米故答案为：5200,3,150,6000,5,10．11．(2016秋•镇江月考)在下面的括号里填上合适的单位使不等式成立． 0.5 厘米 )0.5(< )0.5(< ． 【解答】解：0.5 (厘米)0.5<(分米)0.5<(米)． 故答案为：厘米、分米,米．12．(2015秋•萧县期中)我会站队(按从小到大的顺序排列)． 600分米 1千米 400厘米 30米 500毫米 ．【解答】解：500毫米400<厘米30<米600<分米千米； 故答案为：500毫米,400厘米,30米,600分米,1千米． 三．判断题13．(2019春•镇康县校级月考)1吨棉花和1000千克铁一样重． ．(判断对错) 【解答】解：1吨1000=千克 1000千克铁和1吨棉花一样重； 故答案为：．14．(2018秋•格尔木市校级期末)5千克的海绵比5000克的石头轻得多． (判断对错) 【解答】解：5千克5000=克, 或5000克5=千克,因此,5千克海绵与5000克石头的质量相等； 故答案为：．15．(2018秋•单县期末)8千克的木块比8000克的砖块轻． ．(判断对错) 【解答】解：8千克8000=克 块砖块都是8千克或8000克,同样重． 因此,原题的说法是错误的． 故答案为：．16．一个西瓜重5克． ．(判断对错)【解答】解：根据分析,一个西瓜重5千克,故原题说法错误．故答案为：．17．8千克的木块和8000克的砖块一样重．(判断对错)【解答】解：8千克8000=克即8千克的木块与8000克的砖块同样重．所以8千克的木块和8000克的砖块一样重说法正确．故答案为：．18．5.5千克的铁块比5.5千克的棉花重．(判断对错)【解答】解：5.5千克的铁与5.5千克的棉花一样重,故原题说法错误；故答案为：．四．应用题19．一根彩带长800厘米,比另一根彩带长2米,另一根彩带长多少厘米?合多少米? 【解答】解：2米200=厘米-=(厘米)800200600600厘米6=米答：另一根彩带长600厘米,合6米．20．小胖前年身高1米35厘米,今年比前年长高了1分米,小胖现在身高多少厘米? 【解答】解：1分米10=厘米1米35厘米135=厘米+=(厘米)13510145答：小胖现在身高145厘米．21．一支铅笔原来长1分米,用去1厘米,还剩多少毫米?【解答】解：1分米10=厘米-=(厘米)10199厘米90=毫米答：还剩90毫米．22．用吨作单位的物品有那些?【解答】解：由分析可得：用吨作单位的动物有狮子,鲸鱼,大象等(答案不唯一)用吨作单位的交通工具有火车,轮船等(答案不唯一)五．操作题23．(2016秋•海安县月考)估计它们分别有多重,用线连一连．【解答】解：估计它们分别有多重,用线连一连：24．根据要表示的千克数,在秤面上画出指针．【解答】解：如图,六．解答题25．(2016春•石台县校级期中)按从大到小的顺序排列． (1)1200千克 6吨 1400千克 8吨(2)1726米 11千米 3050米 2千米450米． 【解答】解：(1)6吨6000=千克,8吨8000=千克, 因此,8000千克6000>千克1400>千克1200>千克, 即8吨6>吨1400>千克1200>千克．(2)11千米11000=米,2千米450米2450=米, 因此,11000米3050>米2450>米1726>米, 即11千米3050>米2>千米450米1726>米． 26．(2018秋•重庆期中)在〇里填上“”“”或“” 3000克〇3千克 2吨〇2千克 9分〇90秒 4米6分〇46分米【解答】解：(1)3000克3=千克 (2)2吨2>千克 (3)9分90>秒(4)4米6分46=分米． 故答案为：, , ,．27．(2015秋•成都期末)2.5米 2 米 分米 厘米． 4.05元 元 角 分 8分米2厘米 米 2角 元．【解答】解：①2.5米2=米5分米0厘米．②4.05元4=元0角5分③8分米2厘米0.82=米④2角0.2=元．故答案为：2,5,0,4,0,5,0.82,0.2．28．(2018秋•聊城期中)一头大象重4吨,一头牛重500千克,一头大象比一头牛重多少千克?【解答】解：4吨4000=千克-=(千克)40005003500答：一头大象比一头牛重3500千克．29．(2016秋•纳雍县月考)杯子里原有1500克水,喝了1千克,还剩多少克?【解答】解：1千克1000=克-=(克)150********答：还剩500克．30．(2015春•江岸区期末)桥上有重为2.8吨,0.8吨,0.3吨的三只动物,已知桥限重4吨,长颈鹿1.5吨,长颈鹿现在能上桥吗?请用算式说明理由．【解答】解：2.80.80.3 1.5 5.4+++=(吨)5.4吨4>吨,所以长颈鹿不能上桥；答：长颈鹿现在不能上桥．。