人教版数学六年级下册画图解决数学问题

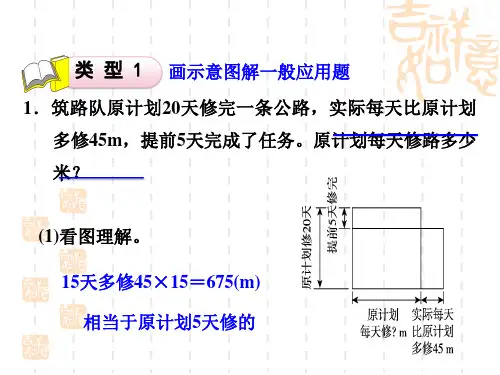
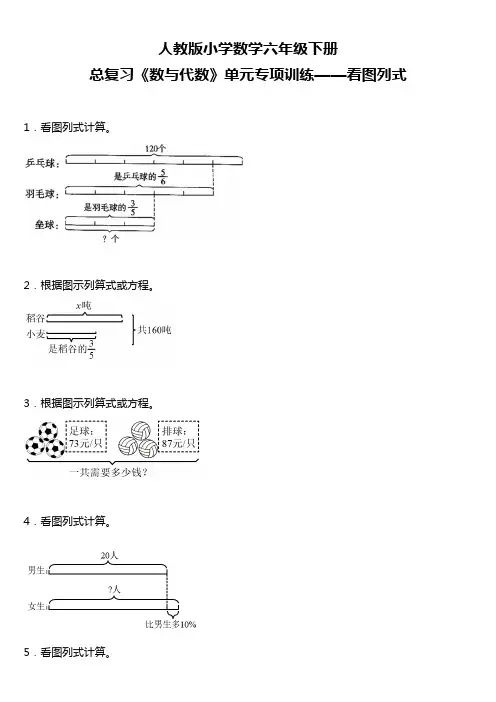
人教版小学数学六年级下册总复习《数与代数》单元专项训练——看图列式1．看图列式计算。

2．根据图示列算式或方程。

3．根据图示列算式或方程。

4．看图列式计算。

5．看图列式计算。

6．看图列式。

（不计算）7．苹果的重量是多少千克？8．看图列式计算。

9．看图列出算式，不用计算。

10．看图列算式或方程解答。

11．看图列式计算。

12．看图列式并解答。

13．看图列式计算。

14．看图列算式。

15．列式计算。

16．根据线段图，列出算式并解答。

17．只列式，不计算。

18．看图列式计算。

19．看图列式计算。

20．只列式，不计算。

21．只列式，不计算。

22．列式计算或用方程计算。

23．列式计算或用方程计算。

24．看图列式计算。

25．用方程：读线段图，列方程计算总支出（元）。

参考答案：1．60个【分析】用乒乓球的个数乘56，可以计算出羽毛球的个数，再用羽毛球的个数乘35，可以计算出垒球的个数。

【详解】120×5365＝100×35＝60（个）2．x＝100【分析】观察线段图可知，稻谷有x吨，小麦的重量是稻谷的35，则小麦有35x吨，根据稻谷的重量＋小麦的重量＝160，据此列方程解答即可。

【详解】x＋35x＝160解：85x＝1608 5x÷85＝160÷85x＝160×58x＝1003．480元【分析】观察图形可知，足球和排球的个数相同，根据单价×数量＝总价，分别求出足球和排球的总价，再相加即可。

【详解】73×3＋87×3＝219＋261＝480（元）4．22人【分析】看图可知，男生人数是单位“1”，女生人数是男生的（1＋10%），男生人数×女生对应百分率＝女生人数，据此列式计算。

【详解】20×（1＋10%） ＝20×1.1 ＝22（人） 女生人数为22人。

5．20棵【分析】看图可知，杨树棵数是单位“1”，柳树棵数是杨树的（1＋25%），柳树棵数÷对应百分率＝杨树棵数，据此列式计算。

小学数学6类“画图”解题1.平面图对于题目中条件比较抽象、不易直接根据所学知识写出答案的问题,可以借助画平面图帮助思考解题.例1 有两个自然数A和B,如果把A增加12,B不变,积就增加72；如果A 不变,B增加12,积就增加120,求原来两数的积.根据题目的条件比较抽象的特点,不妨借用长方形图,把条件转化为因数与积的关系.先画一个长方形,长表示A,宽表示B,这个长方形的面积就是原来两数的积.如图（1）所示.根据条件把A增加12,则长延长12,B不变即宽不变,如图（2）；同样A不变即长不变,B增加12,则宽延长12,如图（3）.从图中不难找出：原长方形的长（A）是120÷12＝10原长方形的宽（B）是72÷12＝6则两数的积为10×6＝60借助长方形图,弄清了题中的条件,找到了解题的关键.例2 一个梯形下底是上底的1.5倍,上底延长4厘米后,这个梯形就变成一个面积为6O平方厘米的平行四边形.求原来梯形面积是多少平方厘米？根据题意画平面图：从图中可以看出：上、下底的差是4厘米,而这4厘米对应的正好是1.5－1＝O.5倍.所以上底是4÷（1.5－1）＝8（厘米）,下底是8×1.5＝12（厘米）,高是60÷12＝5（厘米）,则原梯形的面积是（8＋12）×5÷2＝5O（平方厘米）.2.立体图一些求积题,结合题目的内容画出立体图,这样做,使题目的内容直观、形象,有利于思考解题.例1把一个正方体切成两个长方体,表面积就增加了8平方米.原来正方体的表面积是多少平方米？如果只凭想象,做起来比较困难.按照题意画图,可以帮助我们思考,找出解决问题的方法来.按题意画立体图：从图中不难看出,表面积增加了8平方米,实际上是增加2个正方形的面,每个面的面积是8÷2＝4（平方米）.原正方体是6个面,即表面积为4×6＝24（平方米）.例2 用3个长3厘米、宽2厘米、高1厘米的长方体,拼成一个大长方体.这个大长方体的表面积是多少？按题意画立体图来表示,三个长方体拼成的大长方体有以下三种（1）拼成长方体的长是2×3＝6（厘米）,宽3厘米,高1厘米.表面积为（6×3＋6×1＋3×1）×2＝54（平方厘米）.（2）拼成长方体的长是3×3＝9（厘米）,宽2厘米,高1厘米.表面积为（9×2＋9×1＋2×1）×2＝58（平方厘米）.（3）拼成长方体的长是3厘米,宽是2厘米,高是1×3＝3（厘米）.表面积为（3×2＋3×3＋2×3）×2＝42（平方厘米）.这道题有以上三种答案,通过画图起到审题和理解题意的作用.3.分析图一些应用题,为了能正确审题和分析题目中的数量关系,可以把题目中的条件、问题的相互关系用分析图表示出来.例1新华中学买来8张桌子和几把椅子,共花了817.6元.每张桌子价78.5元,比每把椅子贵62.7元,买来椅子多少把？分析图：（l）买椅子共花多少钱？817.6－78.5×8＝189.6元）（2）每把椅子多少钱？78.5－62.7＝15.8（元）（3）买来椅子多少把？189.6÷15.8＝12（把）综合算式为：（817.6－78.5×8）÷（78.5－62.7）＝189.6÷15.8＝12（把）答：买来椅子12把.4.线段图一些题目条件多,条件之间关系复杂,一时难以解答.可画线段图表示,寻求解题的突破口.例1光明小学六年级毕业生比全校总人数的还多30人.新学期一年级新生人学360人,这样现在比原全校总人数增加了.求原来全校学生有多少人？从图中可以清楚看出,（360－30）人与全校人数的（＋）相对应,求全校人数用除法计算.列式为：（360－30）÷（＋）＝330÷＝900（人）.例2 甲乙两人同时从相距88千米的两地相向而行,8小时后在距中点4千米处相遇.甲比乙速度快,甲、乙每小时各行多少千米？按照题意画线段图：从图中可以清楚看出,甲、乙8小时各行的距离,甲行全程的一半又多出4千米,乙行全程的一半少4千米,这样就可以求出甲、乙的速度了.甲速：（88÷2＋4）÷8＝6（千米）乙速：（88÷2－4）÷8＝5（千米）5.表格图有些问题,通过列表不仅能分清题目的条件和问题,而且便于区分比较,起到从表中不难看出,又搬4次和共搬多少块,这两个数量不相对应,要先求一共搬多少次,才能求出共搬多少块,列式为：15÷3×（3＋4）＝35（块）另一种思路为,先求又搬4次搬的块数,再加上原有的块数,就是共搬的块数.列式为：15÷3×4＋15＝35（块）6.思路图有些问题因为分析的角度不同,因此解题的思路也不同.通过画图能清楚看出解题思路,便于分析比较.例1有一个伍分币、4个贰分币、8个壹分币,要拿出8分钱,一共有多少种拿法？这道题从表面港一点也不难,但是要不重复.不遗漏地把全部拿法一一说出来也不容易,可以用枚举法把各种情况一一列举出来,把思路写出来.从图表中可以清楚着出不同的拿法.此题一共有不重复的7种拿法.从以上各例题中可看出：解题时通过画图来帮助理解题意,起到了化繁为简、化难为易的作用.我们不妨在解题中广泛使用.。

小学六年级数学必会6类“画图”解题法1平面图对于题目中条件比较抽象、不易直接根据所学知识写出答案的问题，可以借助画平面图帮助思考解题。

例1 有两个自然数A和B，如果把A增加12，B不变，积就增加72；如果A不变，B增加12，积就增加120，求原来两数的积。

根据题目的条件比较抽象的特点，不妨借用长方形图，把条件转化为因数与积的关系。

先画一个长方形，长表示A，宽表示B，这个长方形的面积就是原来两数的积。

如图（1）所示。

根据条件把A增加12，则长延长12，B不变即宽不变，如图（2）；同样A不变即长不变，B增加12，则宽延长12，如图（3）。

从图中不难找出：原长方形的长（A）是120÷12＝10原长方形的宽（B）是72÷12＝6则两数的积为10×6＝60借助长方形图，弄清了题中的条件，找到了解题的关键。

例2 一个梯形下底是上底的1.5倍，上底延长4厘米后，这个梯形就变成一个面积为6O平方厘米的平行四边形。

求原来梯形面积是多少平方厘米？根据题意画平面图：从图中可以看出：上、下底的差是4厘米，而这4厘米对应的正好是1.5－1＝0.5倍。

所以上底是4÷（1.5－1）＝8（厘米），下底是8×1.5＝12（厘米），高是60÷12＝5（厘米），则原梯形的面积是（8＋12）×5÷2＝50（平方厘米）。

2立体图一些求积题，结合题目的内容画出立体图，这样做，使题目的内容直观、形象，有利于思考解题。

例1 把一个正方体切成两个长方体，表面积就增加了8平方米。

原来正方体的表面积是多少平方米？如果只凭想象，做起来比较困难。

按照题意画图，可以帮助我们思考，找出解决问题的方法来。

按题意画立体图：从图中不难看出，表面积增加了8平方米，实际上是增加2个正方形的面，每个面的面积是8÷2＝4（平方米）。

原正方体是6个面，即表面积为4×6＝24（平方米）。

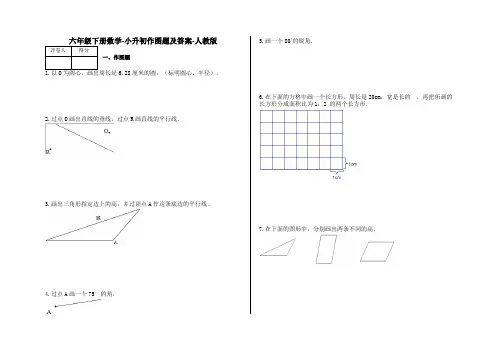
六年级下册数学-小升初作图题及答案-人教版评卷人得分一、作图题1.以O为圆心，画出周长是6.28厘米的圆：（标明圆心、半径）．2.过点O画出直线的垂线，过点R画直线的平行线．3.画出三角形指定边上的高，并过顶点A作这条底边的平行线．4.过点A画一个75°的角．5.画一个80˚的锐角．6.在下面的方格中画一个长方形，周长是20cm，宽是长的，再把所画的长方形分成面积比为1：2 的两个长方形．7.在下面的图形中，分别画出两条不同的高．8.如下图，从A、B两村各挖一条水渠与河道相通，要使水渠最短，应该怎样挖?请在图中画出来。

9.过点P分别作直线a的垂线和直线b 的平行线。

10.在下面的格子图中分别画一个平行四边形、一个三角形和一个梯形，使它们的面积都与图中长方形的面积相等．（每个小方格的面积是1平方厘米．）答案1.解： 6.28÷2÷3.14=3.14÷3.14=1（厘米）画圆如下：【解析】1.根据圆的周长公式“C=2πr”求出圆的半径，再确定圆心0，以O为圆心，以求出的半径画圆即可．画圆时，圆心定位置，半径定大小，关键是求半径．2.解：画图如下：【解析】2.①把三角板的一条直角边与已知直线重合，沿直线移动三角板，使三角板的另一条直角边和O点重合，过O点沿三角板的直角边，向已知直线画直线即可．②把三角板的一条直角边与已知直线重合，用直尺靠紧三角板的另一条直角边，沿直尺移动三角板，使三角板的原来和已知直线重合的直角边和R点重合，过R点沿三角板的直角边画直线即可．本题考查了学生平行线和垂线的作法，培养学生的作图能力．3.解：画图如下：【解析】3.（1）从三角形的一个顶点向它的对边引垂线，从顶点到垂足之间的线段是三角形的高，（2）把三角板的一条直角边与底边重合，用直尺靠紧三角板的另一条直角边，沿直尺移动三角板，使三角板的原来和底边重合的直角边和A点重合，过A点沿三角板的直角边画直线即可．本题主要考查了学生利用三角板和直尺画三角形的高和平行线的作图能力．4.解：作图如下：【解析】4.用量角器的圆点和顶点A重合，0刻度线和射线重合，在量角器75°的刻度上点上点，过A点和刚作的点，画射线即可．本题考查了学生画角的能力，是基础题型．5.解：由分析作图如下：【解析】5.（1）画出一条射线，用量角器的原点和射线的端点重合，0刻度线与射线重合，（2）在量角器上找出80°的点，点上点，（3）以射线的端点过刚画出的点，画出射线即可．本题考查了学生利用量角器作角的掌握情况．6.解：20÷2=10（厘米）设长为a，则宽为 aa+ a=10a=10a=6 6× =4（厘米）；6×4=24（平方厘米）24× =8（平方厘米）24× =16（平方厘米）；画图如下：【解析】6.根据题干，先求出这个长方形的长与宽的值，进而画出符合要求的长方形；再据面积比1：2，进行划分即可．此题主要考查长方形的周长的计算方法，以及长方形的画法．7.解：在下面的图形中，分别画出两条不同的高（图中红色虚线）：【解析】7.经过三角形的顶点（与底相对的点）向对边（底）作垂线，顶点和垂足之间的线段就是三角形的一条高，用三角板的直角可以画出三角形的高；在平行四边形中，从一条边上的任意一点向对边作垂线，这点与垂足间的距离叫做以这条边为底的平行四边形的高，平行四边形有无数条高，习惯上作平行四边形的高时都从一个顶点出发作一边的垂线，用三角板的直角可以画出平行四形的高．8.解：如图所示，只要作出从A、B两村到河道的垂线段，所得到的水渠就最短．【解析】8.画图如下：从A点挖到C点，从B点挖到D点．9.解：如图所示【解析】9.用三角板的一条直角边与已知直线重合，另一条直角边紧靠点P，过P点画已知直线的垂线即可；用三角板的一条直角边与已知直线重合，用直尺紧靠三角板的另一条直角边，沿直尺推动三角板，直到三角板与已知直线平行的直角边与点P重合，过P点画已知直线的平行线即可. 10.解：如图所示：【解析】10.图中长方形的面积是4×3=12平方厘米．根据“平行四边形的面积=底×高”画一个底与长方形的长相等，宽与长方形的高相等的平行四边形即可；根据“三角形的面积=底×高÷2”可画一个底为平行四边底相等，高为平行四边形2倍的三形或底为平行四边形底2倍，高与平行四边形高相同的三角形；根据“梯形的面积=(上底+下底)×高÷2”，画一个上、下底之和与三角形底相等，高与三角形高相同的梯形即可．长方形的面积：4×3=12(平方厘米)，平行四边形的面积：4×3=12(平方厘米)，三角形的面积：8×3÷2=12(平方厘米)，梯形的面积：(5+3)×3÷2=12(平方厘米).。

-小升初作图题及答案-人教版一、作图题10cm 2的平行四边形、梯形、三角形各一个．（每个方格代表1cm 2）2.下面每个小方格边长是1cm ，请你画一个长是4cm ，宽是3cm 的长方形；画一个底是4cm ，高是3cm 的平行四边形；画一个底是8cm ，这条边上的高是3cm 的三角形．3.作图题：①过A 点作直线L 的垂直和平行线；②画一个70°的角．4.过A 点，分别画出已知直线L 的平行线和垂线．5.在如图方格图中画一个面积是16平方厘米的图形．（每个小方格表示面积是1平方厘米．）6.请你在下面的方格纸上分别画一个长方形和一个正方形，它们的周长都是8厘米．7.图中每个小正方形的边长是1厘米，按要求完成下列各题．（i）画一个底是3厘米，高是4厘米的平行四边形．（不能画成长方形）（ii）画一个上底是3厘米，下底是5厘米的直角梯形．8.手脑并用，操作思考。

（i）画出图形A以直线MN为对称轴的另一半。

（ii）将图形B先向右平移7格，再向上平移2格。

（iii）画出图形C按2：1放大后的图形D。

（iv）以点O为圆心，画一个直径是4厘米的半圆。

(一小格为1平方厘米)9.画一个周长为10厘米的长方形。

10.画一个135°的角。

参数答案1.解：根据题干分析可得：【解析】1.可以画一个底为5厘米，高为2厘米的平行四边形，其面积是5×2=10（平方厘米）；画一个上底为4厘米、下底为6厘米，高为2厘米的梯形，其面积是：（4+6）×2÷2=10（平方厘米）；可以画一个底为5厘米，高为4厘米的三角形，其面积是5×4÷2=10（平方厘米）．此题主要是考查平行四边形、三角形、梯形的意义及面积的计算．所画图形的形状只有是平行四边形、三角形、梯形，即面积都是10平方厘米即可．2.解：根据分析作图如下：【解析】2.①可先画一条长4厘米的线段，然后再在线段的两端作垂线，使垂线长3厘米，最后再连接垂线的两端即可得到答案；②先画一条长4厘米的线段，然后再这条线段的垂线，使垂线长3厘米，再通过垂线的一端画原来线段的平行线，最后再连接两条平行线的两端即可得到答案．③先画一条长8厘米的线段，然后再这条线段的垂线，使垂线长3厘米，再把垂线的一端与原来线段的两端分别相连即可得到答案．此题主要考查了长方形、平行四边、三角形的画法．3.解：①作图如下：②作图如下：【解析】3.（1）把三角板的一条直角边与已知直线重合，沿直线移动三角板，使三角板的另一条直角边和A点重合，过A点沿三角板的直角边，向已知直线画直线即可．把三角板的一条直角边与已知直线重合，用直尺靠紧三角板的另一条直角边，沿直尺移动三角板，使三角板的原来和已知直线重合的直角边和A点重合，过A点沿三角板的直角边画直线即可．（2）画出一条射线，用量角器的原点和射线的端点重合，0刻度线与射线重合；在量角器上找出所要画的角的点，点上点；以射线的端点过刚画出的点，画出射线即可．本题考查了学生平行线和垂线的作法，培养学生的作图能力．同时考查了学生利用量角器作角的运用情况．4.解：依据过直线外一点作直线的垂线和平行线的方法，作图如下：．【解析】4.（1）将三角板的一条直角边和已知直线重合，然后平移三角板，让其另一条直角边与A点重合，过A点和三角板的直角顶点作直线，就是L的垂线；（2）将三角板的一条直角边和直尺的上边缘都与直线L重合，然后平移直尺，当直尺的上边缘正好与A重合时，过A沿直尺上边缘画直线，即为平行于L的直线．此题主要考查：过直线外一点作直线的垂线和平行线的方法．5.解：【解析】5.依据正方形的面积公式可得：边长为4厘米的正方形的面积是16平方厘米解答此题的关键是，先依据正方形的面积，确定出正方形的边长，从而画出符合要求的图形．6.解：作图如下：【解析】6.根据题意，长方形的周长=（长+宽）×2，正方形的周长=边长×4，可知周长为8厘米的长方形的宽可以为1厘米，长为3厘米，正方形的边长是2厘米，据此即可画图．解答此题的关键是根据长方形和正方形的周长确定长方形的长与宽以及正方形的边长各是多少，然后再进行作图即可．7.解：如图：【解析】7.根据题意即画出的平行四边形底为3格（3厘米）、高为4格（4厘米）的平行四边形即可，角的大小不必考虑；根据直角梯形的特征，一个角是直角，因此，能画上底是3个格子（3厘米），下底是5个格子（5厘米）的直角梯形即可．8.解：（i）图形A以直线MN为对称轴的另一半如图黑色部分；（ii）将图形B先向右平移7格，再向上平移2格的图形如图B'；（iii）图形C按2：1放大后的图形D如图红色部分；（iv）以点O为圆心，直径是4厘米的半圆如图蓝色部分；9.解：如图：【解析】8.长与宽的和：10÷2=5(厘米)，因此长可以画3厘米，宽可以画2厘米；或者长4厘米、宽1厘米.10.解：如图：【解析】9.先画出一条射线，用量角器的中心点与射线的端点重合，0刻度线与射线重合，在量角器的边缘135°处作出标记，从射线的端点出发过这个标记画出一条射线就组成一个135°的角.。

人教版小学数学六年级下册第四单元专项训练——《作图题》班级：_________ 姓名：__________1．在答题卡上画图,先按4∶1把下面的三角形放大,再把放大后的图形按1∶2缩小。

（画图即可,无需写出计算过程。

）2．（1）画出长方形绕点A顺时针旋转90°后的图形,并在图内标上①（2）以点O为圆心画一个半径是3m的圆。

（3）在空白处画出原长方形按1∶2缩小后的图形并在图内标上②。

3．按要求作图。

（1）根据对称轴画出图形A的轴对称图形B。

（2）将图形B向下平移5格,得到图形C。

（3）在空白处将图形C按2∶1的比放大,得到图形D。

4．（1）画出三角形向右平移5格后的图形；（2）画出三角形绕O点逆时针方向旋转90°后的图形；（3）画出三角形按2∶1放大后的图形。

5．（1）在下面方格中画△ABC,它的三个顶点位置用数对表示分别为：A（2,4）、B （6,4）、C（5,7）。

（2）画出△ABC绕点B顺时针旋转90°后的图形,并标上①。

（3）请在方格中画一个和这个三角形面积相等,但形状不同的图形,并标上②。

（4）画出△ABC按2∶1的比例放大后的图形,并标上③。

6．画出下图三角形按1∶3缩小后的图形B,再画出图形B绕直角顶点顺时针旋转90°后的图形C。

（先用铅笔画好,检查无误后再用签字笔描黑。

）7．已知：三角形A在如图所示的网格中。

（1）将三角形A的各条边按41：放大,得到三角形B,请在网格中画出三角形B；（2）将（1）中画出的三角形B的各条边按12：缩小,得到三角形C,请在网格中画出三角形C。

8．按要求画图形。

（1）按给定的对称轴,画出图A的另一半,使它成为一个轴对称图形。

（2）画出图B先向右平移6格,再向下平移4格后得到的图形B'。

（3）画出图C绕点O顺时针旋转90°后得到的图形C'。

（4）画出图形D放大后的图形D,使新图形与原图形对应线段长的比为2∶1。

2022-2023学年人教版数学六年级下册图形的放大和缩小练习题学校:___________姓名：___________班级：_______________一、选择题1．一个正方形的边长是10厘米，如果按照2∶1放大，放大后的图形的面积是（ ）平方厘米。

A ．200B ．400C ．10002．一个长4.8厘米、宽2.4厘米的长方形按2∶1放大，得到的图形的面积是（ ）cm 2。

A ．2.88B ．11.52C ．23.04D ．46.083．下面说法正确的有（ ）句。

∶把长与宽的比是3∶1的长方形按2∶1放大后，新长方形的长和宽的比是6∶1。

∶等底等高的两个三角形能拼成一个平行四边形。

∶墨水瓶包装盒上的“净含量60mL”指的是墨水瓶的体积。

∶下图中一共有7个平行四边形。

A ．0B ．1C ．2D ．34．把一个图形先按2:1放大，再把放大后的图形按1:3缩小，最后得到的图形的面积是原图形的（ ）。

A ．94B ．49C ．14D ．235．把线段比例尺改写成数值比例尺是（ ）。

A ．1∶60B ．1∶120C ．1∶180D ．1∶20000006．如果1118和12m相等，则m 等于（ ）。

A ．223B ．323C ．173D ．3337．一个长4.4厘米、宽2.2厘米的长方形按1∶2缩小，得到的图形的面积是（ ）cm²。

A ．2.42B ．9.68C ．38.72D ．4.848．若a b c d >>>，(a ，b ，c ，0)d ≠并且四个数能组成比例，那么下面四个比例中正确的是（ ）。

A ．a c b d =∶∶B ．a ad c= C ．b a c d =∶∶ D ．a b d c =∶∶9．下图中，（ ）图形是∶号长方形按2:1放大后的图形；（ ）图形是∶号长方形按1:2缩小后的图形。

A ．A ，CB ．B ，AC ．C ，BD ．D ，B10．一幅地图的比例尺是1∶1000000，下列说法不正确的是（ ）。

画线段图解决问题大化县第二小学兰玉珍设计意图：一直以来，较复杂的分数应用题的数量关系较为抽象，难于理解。

在教学中，想让学生通过将生活中的实际问题利用转化的思想抽象成数学问题，利用画线段图的方法分析数量关系，有助于学生理解分数应用题中各数量之间的对比关系，从而能解决不同的问题，帮助他们愉悦地学好数学，树立学数学的信心。

目标：1.通过复习加深理解和掌握单位“1”和各数量之间的数量关系，并能正确解答。

2.通过系统复习，培养学生学会用线段图表示数量关系，培养学生的分析能力和探究能力。

3.通过复习，培养学生认真仔细学习习惯。

重难点：利用线段图，能准确地表示题中的数量关系并能正确解答。

同学们，我们先来回顾一下分数应用题的解题技巧，（课件出示，全班齐读）。

师：分率师谁的，谁就是单位“1”，单位“1”是已知的用乘法计算，求单位“1”的用除法计算。

那我们给下面的式子连线，生口头回答，师连线，（课件出现），这是分数应用题中最常见的类型，在小学阶段中，稍复杂分数应用题对于一些同学来讲，不知从何入手找到正确的数量关系，而通过画线段图的方法可以帮助同学们快速而有效的找到准确的数量关系，得出正确的式子，从而达到事半功倍的效果，那今天我们就来重点复习，用线段图解应用题。

请大家把课题读一遍（用线段图解决分数应用题）。

出示例题：例1，有一条绳子，第一次剪去全长的 1/3 ，第二次剪去3米，这时正好剩下一半，这条绳子原来是多少米？由已知条件可知分率是（），单位“1”是（全长的），剩下一半就是全长的（），那剪去的也是全长的（），请大家尝试画出线段图。

学生尝试后展示结果。

列式计算。

例2，有一桶汽油，第一次取出40%，第二次取出的比第一次少12千克，桶里还剩下28千克，这桶油原有多少千克？请一生读题后问如何画线段图表示。

（课件演示），生说，师画后生自己列式解答，第二次取出的比第一次少12千克，就是第二次也取出这桶油的40%少12KG。

练习：1、李玉看一本书，第一天看了 1/5 ，第二天比第一天多看7页，这时还有56页没有看，这本书有多少页？一生读题目后请一生上台板演，线段图。

数学小升初试题∶解决问题解答应用题训练真题带答案解析1一、人教六年级下册数学应用题1．如下图，瓶底的面积和锥形杯口的面积相等，将瓶子中的液体倒入锥形杯子中，能倒满几杯？小力：假设瓶底的面积是100平方厘米，高是6厘米。

V圆柱=100×6×2=1200毫升V圆锥=100×6× =200毫升1200÷200=6杯答：可以倒6杯。

笑笑：V圆柱=sh×2=2shV圆锥= ×s×h= shV圆柱：V圆锥=2sh： sh=6：1答：可以倒6杯。

小明：等底等高的圆柱体积是圆锥体积的3倍。

3×2=6杯答：可以倒6杯。

（1）三位同学的方法，你认为正确的在打√。

（2）你最喜欢（）的解答方法，请用你喜欢的解答方法解决下面的问题。

乐乐说：“如果一个圆锥的体积和底面积都相等，那么圆锥的高是圆柱的高的3倍”乐乐的说法对吗？为什么？2．某商品按定价出售，每个获利45元，现在按定价的八五折出售8个，所获利润与按定价每个减价35元出售12个所获利润一样。

这个商品每个的定价是多少元?3．一批零件20人去做需要15天，照这样计算，如果增加5人，几天可以做完？（用比例知识解答）4．某商品的成本为1500元，先按20%的成本利润定价，然后按八八折出售，这件商品出售后的利润是多少元？5．王明正在读一本350页的故事书，读了5天，正好读了这本书的，照这样的速度，还要多少天才能读完这本书？（用比例解）6．一个圆柱形的容器，底面周长是62.8厘米，容器里面水面高0.8分米，现把一个小圆柱体和一个与圆柱等底、高是圆柱一半的圆锥放入容器中，结果圆锥完全浸没在水中，圆柱有在水面之上，容器内的水比放入前上升了3厘米，求圆柱和圆锥的体积？7．某车间为了能高质量准时完成一批齿轮订单，对车间工人提前进行了加工齿轮效率的测试，经过统计测算，平均每个工人加工齿轮效率情况如图。

复习课：画图解决数学问题沙洋县实验小学任兴梅【教学内容】：复习画图解决数学问题【课型】：六年级数学复习课【设计意图】：一直以来，行程应用题、分数应用题中的数量关系都较为抽象、难于理解，在实践教学中，主要让学生通过将这两种类型的应用题利用“数形结合”的思想抽象成数学信息，利用画线段图的方法分析数量关系，在逐层学习的过程中，通过小组讨论交流和适量的练习使大部分学生能够复习归纳各自的画图方法。

复习课中特别要引导学生学会找出线段图中的“隐含信息”，从而能够通过画图直观的理解不同的问题，解决行程问题和分数应用题，帮助学生愉悦的学习数学，树立学好数学的信心。

【教学目标】：1、通过本课复习，使学生能够复习巩固画线段图解决行程问题、分数应用题。

2、通过学习，培养学生学会用线段图的方法表示数量关系，寻找线段图里的隐含信息，渗透“数形结合”的思想。

3、培养学生多角度解决数学问题的能力，提升对数学学习的兴趣。

【复习重点】：使学生掌握行程问题、分数应用题的数量关系，较复杂的题目能准确的画线段图，并做出正确的解答。

【复习难点】：能够根据线段图寻找隐含的数学信息，并能将线段图与数学问题灵活转化。

【复习过程】：一、导通过观看古代、现代图形以及多个学科图形引入复习课。

二、学出示典型线段图，引导学生归纳总结行程问题、分数应用题画图的方法。

1、出示复习提示，分组展开复习讨论三、展与拨小组汇报编题情况，师生共同归纳总结画线段图的方法。

四、练学生独立作业“看题画图”：先画图，再列式计算，最后分组开展竞赛评分。

1、甲乙二人同时从A 地到B 地,甲每分钟走260米,乙每分钟走100米.甲到达B 地后立即返回A 地,在离B 地3200米处相遇.A 、B 两地之间相距多少千米?2、玲玲这几天正在看《窗边的小豆豆》一书，第一天看的页数看图编题 ：1、小组讨论。

对照上面的线段图口述编出完整的数学应用题。

再说一说画线段图要注意些什么？2、独立作业。

-小升初作图题(含答案)人教版一、作图题10cm 2的平行四边形、梯形、三角形各一个．（每个方格代表1cm2）2.分别画出从正面、上面看到的立体图形的形状．3.画出一个平角．4.过直线外一点A画直线M的平行线和垂线．5.以A点为圆心画一个r=2cm的圆，并在圆上画出两条互相垂直的对称轴．6.在如图格子里画一个周长是12厘米的长方形和一个正方形（每格表示1厘米）7.过点A画直线的垂线，过点B画直线的平行线．8.如图，过点A画出直线a、b的垂线，直线a的平行线。

9.如图，过已知直线外一点A，分别作已知直线的平行线和垂线。

10.用16个小正方形拼成一个长方形，怎么拼周长最长，怎么拼周长最短？在下面的方格纸上画一画。

（每个小方格的边长为1厘米）参数答案1.解：根据题干分析可得：【解析】1.可以画一个底为5厘米，高为2厘米的平行四边形，其面积是5×2=10（平方厘米）；画一个上底为4厘米、下底为6厘米，高为2厘米的梯形，其面积是：（4+6）×2÷2=10（平方厘米）；可以画一个底为5厘米，高为4厘米的三角形，其面积是5×4÷2=10（平方厘米）．此题主要是考查平行四边形、三角形、梯形的意义及面积的计算．所画图形的形状只有是平行四边形、三角形、梯形，即面积都是10平方厘米即可．2.解：根据题干分析可得：【解析】2.3.解：根据分析画图如下：【解析】3.平角是180°的角，其两边在同一条直线上，因此只要先画一条直线，再在直线上点上一点作为角的顶点即可．此题考查了画指定度数的角，根据平角的意义画图即可．一定要注意不要画一条直线就认为是一个平角，还需要画出角的顶点．4.解：由分析作图如下：【解析】4.（1）用三角板的一条直角边的已知直线M重合，沿重合的直线平移三角板，使三角板的另一条直角边和A点重合，过A沿直角边向已知直线画直线即可．（2）把三角板的一条直角边与已知直线M重合，用直尺靠紧三角板的另一条直角边，沿直尺移动三角板，使三角板的原来和已知直线重合的直角边和A点重合，过A点沿三角板的直角边画直线即可．本题考查了学生过直线外一点作已知直线的平行线和垂线的画图能力．5.解：以点A为圆心，以2厘米为半径画圆，并画出它的互相垂直的两条对称轴如图所示：【解析】5.（1）圆心确定圆的位置，半径确定圆的大小，由此以点A为圆心，以2厘米为半径画圆；（2）圆的对称轴有无数条，分别是经过圆心的直线，由此经过圆心画出两条互相垂直的直线即可．此题考查了利用圆的两大要素：圆心与半径画圆的方法，以及利用轴对称图形的定义确定圆的对称轴位置的方法的灵活应用．6.解：【解析】6.画周长是12厘米的长方形，那么长与宽的和就是6厘米，6=4+2，所以长方形的长和宽为4和2；画周长是12厘米的正方形，它的边长就是12÷4=3厘米，画出边长为3厘米的正方形即可．本题主要是考查指定周长画长方形以及正方形．指定周长画长方形先要计算出长方形的长、宽再画，只要符合条件即可．但是周长一定时正方形的边长是唯一的．7.解：画图如下：【解析】7.用三角板的一条直角边与已知直线重合，另一条直角边紧靠点A，过A点沿这条直角边画出已知直线的垂线即可；用三角板的一条直角边与已知直线重合，用直尺与另一条直角边重合，沿直尺推动三角板使三角板与直线重合的边与B点重合，过B点画已知直线的平行线即可.8.解：如图所示：【解析】8.用三角板的一条直角边与已知直线重合，另一条直角边与直线外的点重合，沿另一条直角边画出已知直线的垂线即可；用三角板的一条直角边与已知直线重合，用直尺紧靠三角板的另一条直角边，沿直尺推动三角板直到与已知直线重合的边与直线外的点重合，沿原来与已知直线重合的边画出已知直线的平行线即可.9.解：如图：【解析】9.用三角板的一条直角边与已知直线重合，另一条直角边紧靠点A，过A点作已知直线的垂线即可；用三角板的一条直角边与已知直线重合，用直尺紧靠三角板的另一条直角边，沿直尺推动三角板直到三角板与已知直线重合的直角边与点A重合，过A点画出已知直线的平行线即可.10.解：如图：黑色长方形周长最长，红色长方形(正方形)周长最短，【解析】10.拼成的长方形长和宽的差越大，长方形的周长就最长；长与宽的差越小，周长就最短；注意正方形是特殊的长方形.。

画线段图解决问题大化县第二小学兰玉珍设计意图：一直以来，较复杂的分数应用题的数量关系较为抽象，难于理解。

在教学中，想让学生通过将生活中的实际问题利用转化的思想抽象成数学问题，利用画线段图的方法分析数量关系，有助于学生理解分数应用题中各数量之间的对比关系，从而能解决不同的问题，帮助他们愉悦地学好数学，树立学数学的信心。

目标：1.通过复习加深理解和掌握单位“1”和各数量之间的数量关系，并能正确解答。

2.通过系统复习，培养学生学会用线段图表示数量关系，培养学生的分析能力和探究能力。

3.通过复习，培养学生认真仔细学习习惯。

重难点：利用线段图，能准确地表示题中的数量关系并能正确解答。

同学们，我们先来回顾一下分数应用题的解题技巧，（课件出示，全班齐读）。

师：分率师谁的，谁就是单位“1”，单位“1”是已知的用乘法计算，求单位“1”的用除法计算。

那我们给下面的式子连线，生口头回答，师连线，（课件出现），这是分数应用题中最常见的类型，在小学阶段中，稍复杂分数应用题对于一些同学来讲，不知从何入手找到正确的数量关系，而通过画线段图的方法可以帮助同学们快速而有效的找到准确的数量关系，得出正确的式子，从而达到事半功倍的效果，那今天我们就来重点复习，用线段图解应用题。

请大家把课题读一遍（用线段图解决分数应用题）。

出示例题：例1，有一条绳子，第一次剪去全长的 1/3 ，第二次剪去3米，这时正好剩下一半，这条绳子原来是多少米？由已知条件可知分率是（），单位“1”是（全长的），剩下一半就是全长的（），那剪去的也是全长的（），请大家尝试画出线段图。

学生尝试后展示结果。

列式计算。

例2，有一桶汽油，第一次取出40%，第二次取出的比第一次少12千克，桶里还剩下28千克，这桶油原有多少千克？请一生读题后问如何画线段图表示。

（课件演示），生说，师画后生自己列式解答，第二次取出的比第一次少12千克，就是第二次也取出这桶油的40%少12KG。

练习：1、李玉看一本书，第一天看了 1/5 ，第二天比第一天多看7页，这时还有56页没有看，这本书有多少页？一生读题目后请一生上台板演，线段图。

小学人教版六年级数学下册求几何图形阴影部分的面积1.如图，大圆半径为5厘米，小圆半径为3厘米,求阴影部分的面积,2.如图，已知两同心圆（圆心相同，半径不相等的两个圆），大圆半径为3厘米，小圆半径为1厘米，求阴影部分的面积3.如图，大圆半径为6cm，小圆半径为4cm，求阴影部分的面积4.已知如图大圆的半径为4cm，小圆的半径为3cm，求两个圆阴影部分的面积的差5.求图中阴影部分的面积(单位:厘米)6.求阴影部分的面积(单位:厘米)7.求阴影部分的面积(单位:厘米)8.如图,已知小圆半径为2厘米，大圆半径是小圆的3倍，问空白部分甲比乙的面积多多少厘米？9.求阴影部分的面积(单位:厘米)10.求阴影部分的面积(单位:厘米)11.已知直角三角形面积是12平方厘米，求阴影部分的面积12.求阴影部分的面积(单位:厘米)13.如图，在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长14.正方形边长为2厘米，求阴影部分的面积15.图中四个圆的半径都是1厘米，求阴影部分的面积16.如图，正方形边长为8厘米，求阴影部分的面积17.图中的4个圆的圆心是正方形的4个顶点，，它们的公共点是该正方形的中心，如果每个圆的半径都是1厘米，那么阴影部分的面积是多少？18.如图，有8个半径为1厘米的小圆，用他们的圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心。

如果圆周π率取3.1416，那么花瓣图形的的面积是多少平方厘米？19.如图，四个扇形的半径相等，求阴影部分的面积(单位:厘米)20.如图，等腰直角三角形ABC和四分之一圆DEB，AB=5厘米，BE=2厘米，求图中阴影部分的面积21.如图，正方形ABCD的对角线AC=2厘米，扇形ACB是以AC为直径的半圆，扇形DAC是以D为圆心，AD为半径的圆的一部分，求阴影部分的面积22.求阴影部分的面积(单位:厘米)23.图中直角三角形ABC的直角三角形的直角边AB=4厘米，BC=6厘米，扇形BCD所在圆是以B为圆心，半径为BC的圆，∠CBD=500,问阴影部分甲比乙面积小多少？24.如图，三角形ABC是直角三角形，阴影部分甲比阴影部分乙面积大28平方厘米，AB=40厘米,求BC的长度25.如图是一个正方形和半圆所组成的图形，P为半圆周的中点，Q为正方形一边上的中点，求阴影部分的面积26.如图，大正方形的边长为6厘米，小正方形的边长为4厘米。