标准数独(1)讲解

1.数独简介数独起源于18世纪初瑞士数学家欧拉等人研究的拉丁方阵（Latin Square ），拉丁方阵的规则是在n 阶方阵中，每一行和每一列均含有1~n ，且不重复。

与标准数独相比非常类似，唯独少了一个“宫”的规则。

2.数独分类数独按照大小可分为四宫数独、六宫数独、九宫数独等，按照题型可分为标准数独和变形数独，其中变形数独的类型非常多，常见的对角线数独、摩天楼数独、杀手数独等都属于变形数独。

3.数独规则（九宫）在空格内填入1~9，使得每行、每列及每宫内的数字都不重复，解题过程就是按照数独规则要求在每个空格内填入数字，使得每行、每列、每宫内都出现一组1~9的数字。

下图中，图1为一道数独题目（简称初盘），其中初始数字称为已知数，没有数字的格子称为空格，图2为该题目的答案（简称终盘）。

图1图2数独的认识盘面：所有格所组成的整体，4宫格由16格构成，6宫格由36格构成，9宫格由81格构成；格：数独盘面中最小的单位，每格中只有1个数字；行：由一组横向格组成的区域，由大写英文字母表示其顺序，从上至下分别为A至I行；列：由一组纵向格组成的区域，由阿拉伯数字表示其顺序，从左至右分别为1至9列；宫：由粗线划分成的3×3的区域，从左上到右下依次是一至九宫；区：填入一组数字1~9的区域的统称，行、列、宫都是区的一种形式；坐标：每个格子位置的名称，由代表其所在行的字母和所在列的数字组成，在图4九宫格中，黄色格在第9列、D行，所以这格的坐标为9D；图3是标准9宫数独每一宫的区分，图4是标准4宫数独、标准6宫数独和标准9宫数独的形式。

图3图41.宫内排除法：以某个宫为目标，用相同的数字对它进行排除，使得这一宫内只有一格能填入该数字。

第四宫缺少4、5、6、9这4个数，而E 行不能填6，所以6只能填在3F 的位置。

数独的解法第二宫缺少2、3、4、7、8、9这6个数，而C 行和第6列不能填7，所以7只能填在4A 的位置。

数独入门及技巧9宫格全文共四篇示例，供读者参考第一篇示例：数独是一种益智游戏，源自日本，通过填入数字1-9在一个9x9的网格中，使每一行、每一列和每一个3x3的小方格中都包含数字1-9，且数字不重复。

数独看似简单，实际上需要一定的逻辑推理和技巧。

下面我们将介绍一些数独的入门知识和技巧，帮助您更好地解决数独难题。

第一步：了解数独规则第二步：找准切入点在解数独时，需要找准一个切入点，通常从一些已知数字比较多的行、列、小方格入手。

首先找出可确定的数字，填入网格中，然后逐步填入其他数字。

第三步：排除法在填字过程中，遇到疑难问题时，可以运用排除法。

在某个方格中，可能有几个数字都是可能的选择，可以通过推理和逻辑排除那些不可能的数字，从而确定正确的数字。

第四步：观察法观察法是解决数独问题的有效技巧之一。

通过观察每一行、每一列和每个小方格中已经存在的数字，来推断其他方格中应该填入的数字。

定位已知数字和求解未知数字之间的联系，是解决数独难题的关键。

第五步：尝试法在遇到难题时，可以尝试填入一些可能的数字，然后根据填入的数字继续遍历推断解题。

如果发现填入的数字有矛盾或者无解，就需要重新考虑填入的数字，并尝试其他可能的解决方法。

数独是一项耐心和逻辑的游戏，通过不断练习和探索，可以提高解决问题的能力。

希望上述数独入门及技巧可以帮助您更好地解决数独难题，提高数独游戏的乐趣和挑战性。

祝您解题愉快，享受数独的乐趣！第二篇示例：数独，又称“九宫格”，是一种风靡全球的数学逻辑游戏。

它的规则很简单，只需填入1至9的数字，保证每行、每列和每个九宫格内的数字都不重复即可。

虽然规则简单，但数独却是一款极具挑战性的益智游戏，需要玩家在排除多种可能性的灵活运用逻辑推理和专注力，才能完成每一道题目。

入门技巧：1. 专注观察：数独游戏的第一步是观察。

仔细观察整个数独盘面，找出已知数字的位置，并根据它们的位置和限制条件，推断其他数字的可能位置。

2. 逻辑推理：数独的一个核心技巧就是逻辑推理。

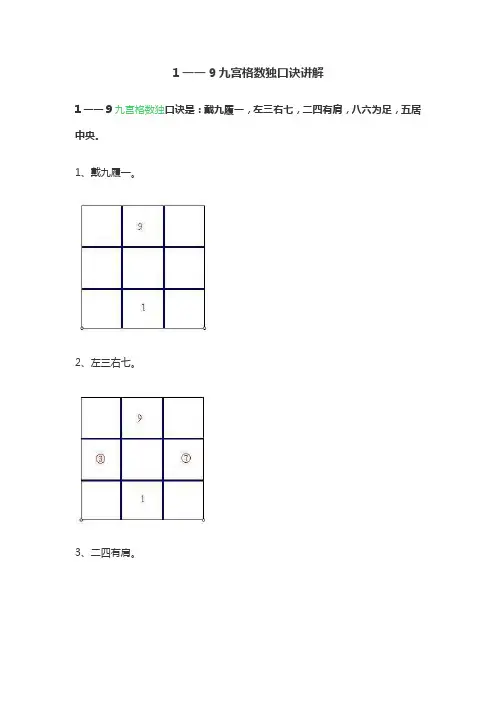
1一一9九宫格数独口诀讲解
1一一9九宫格数独口诀是：戴九履一，左三右七，二四有肩，八六为足，五居中央。

1、戴九履一。

2、左三右七。

3、二四有肩。

4、八六为足。

5、五居中央。

九宫格有两种玩法：
第一种是在在3×3方格盘上，是把1至8八个小木块随意摆放，每一空格其周围的数字可移至空格。

玩者要将小木块按12345678的顺序重新排好，以最少的移动次数拼出结果者为胜。

第二种玩法如九宫格算术游戏玩法，推动木格中8个数字排列，横竖都有3个格，使每行、每列两个对角线上的三数之和都等于15。

在计算的同时，还必须思考怎么把数字方块推动到相对应的位置上，这个游戏不仅仅考验人的数字推理能力，也同时考验了人的思维逻辑能力。

标准数独解析No.001
本版块将精选我们教研组的谢道台老师在
新浪微博发表的每日五题中的题目，由谢道台
和林敏舫两位老师进行关键解题点分析。

今日题目选自2018.09.18高级题，题号
13358。

标准数独规则：将1-9填入空格，使得每行、列、宫内均含1-9不重复。

观察第九宫：
数字4、6、9对第九宫摒除，得到第九宫的4、6、9只能在r8c7、r8c8、r8c9这三格，形成{469}三链数，故这三格除了4、6、9之外不能是其他数字。

继续观察第九宫：
数字3对第九宫摒除，由前面的{469}三链数可得，r8c8不能是3，故第九宫的3只能在r9c8。

之后通过基础解法可以解到这一步。

观察第八宫：
数字3和7同时对第八宫摒除，得到第八宫的3和7只能在r7c6和r8c6，形成{37}数对。

故r7c6和r8c6除了3和7之外不能填其他数字。

观察第六列：
数字5对第六列摒除，由{37}数对可得，r7c6和r8c6不能填5，故第六列的5只能在r6c6。

数独介绍ppt课件CONTENTS •数独基本概念与规则•初级解法与技巧•中级解法与技巧•高级解法与技巧•数独变形与变种介绍•数独挑战与赛事介绍•数独在教育中的应用价值•总结与展望数独基本概念与规则01数独起源与发展起源数独是一种源自18世纪瑞士的数学游戏。

发展在日本得以发扬光大，并在21世纪初传入中国，逐渐在大众中普及。

现状数独已成为全球最受欢迎的智力游戏之一，拥有广泛的爱好者群体。

在一个9x9的盘面上，根据已知数字，推理出所有剩余空格的数字。

每行、每列以及每个3x3的小宫格内，数字1-9均不重复。

每个数独题目有且仅有一个正确解。

填数字每行每列不重复唯一解规则解读题目中给出的数字，是解题的线索和依据。

根据已知数和规则，推理得出的可能填入空格的数字。

9x9盘面被划分为9个3x3的小宫格，每个宫格内数字1-9不重复。

通过排除法确定某个空格内应填入的数字。

宫格已知数候选数摒除法术语解析初级解法与技巧02唯一解法当某一行（列）或宫格中只有一个空格时，填入唯一可填的数字。

隐性唯一解法当某一行（列）或宫格中有两个空格，且这两个空格只能填某两个数字时，若这两个数字在其他行（列）或宫格中只能填在其中一个空格中，则可根据此条件确定这两个空格的数字。

行列排除法运用数独中每行每列数字不重复且必须包含1-9的规则，通过已知数字排除某些数字不可能出现在某些行或列中，进而确定某些空格的数字。

宫内排除法利用宫内数字不重复且必须包含1-9的规则，通过已知数字排除某些数字不可能出现在某个宫中，从而确定某些空格的数字。

区块摒除法当某个数字在某行、某列或某个宫中可能填入的位置构成了一个区块时，利用该区块中已经填入的数字或其他已知条件，可以排除掉区块外某些位置填入该数字的可能性，进而确定某些空格的数字。

宫内区块摒除法当某个数字在某个宫中可能填入的位置构成了一个区块时，利用该区块中已经填入的数字或其他已知条件，可以排除掉该宫内其他位置填入该数字的可能性，从而确定某些空格的数字。

【0626】数独元素、规则及基本解法（多图警告）数独是一种可爱的益智游戏。

它需要你在空格内填入1到9的其中任意一个数字，使得每一行、每一列以及每一个正方形的小九宫格内的数字都不能够有重复数字。

例如下面三个盘面格子（以后均简称盘面）所示，分别是行、列和小九宫格（以后均简称为宫）不重复的情况。

盘面1到盘面3当然，整个盘面的每一行、每一列和每一个宫都得做到像上面三个图所示的那样，不重复。

只要有两个数字相同了，那就一定错了。

数独，顾名思义，数字的出现必须要“独”，也就是不得重复。

但是“独”不仅仅只有这个意思。

它还有一“独”，是任意合格数独盘面都只有唯一的一个答案，这被称为唯一解定理（Unique Law）。

说白了，每一个格子都只有唯一的一种填法。

这样，才能真正体现数独的“独”的特性。

这样才叫“独”之道。

每一个数独盘面最少都得有17个用于推理解题的提示数（Hints/Clues），因为经电脑演算发现，能够保证唯一解的数独盘面至少都得17个提示数，但目前暂未发现其逻辑证明手段。

如果提示数少于17个的话，那么它一定是一个多解题，这样的题就是不合适的。

但是，也并不是随意写上17个提示数，就一定是唯一解的数独题。

在任意一个数独中，每一行我们记为字母A到I，而每一列我们记为数字1到9。

那么在第3行的第6格我们就会简记为“单元格C6”，而其前面的单元格三个字可以被省略。

盘面4盘面5上面有4个数字，那么我们可以将“第5行第5格内是数字1”简记做“E5=1”；同理，其他的3格可以记作“A3=9”、“C7=5”和“H7=6”。

单独只说第3行的话，就可以直接记作“行C”，第6列就记作“列6”。

如果单元格C7在哪个宫，则是按照从左到右、从上到下的顺序依次排序得到的宫的编号，如盘面5所示，A3在宫1，C7在宫3，等等。

还有一种表示方法。

我们提到的行、列、宫的概念，它们被统称为单元（Unit）或者区块（Region）；而每一个格子，则都被叫做单元格；另外，盘面上给出的所有已知数字，我们都称为“提示数”。

一、数独简介数独是一种以数字为表现形式的逻辑推理谜题。

数独起源于18世纪末的瑞士，后在美国发展、并在日本得以发扬光大。

1783年，瑞士数学家欧拉发明了一种拉丁方块的游戏，这就是现代数独的雏形。

1984年，在日本游戏杂志上出现了“数独”游戏，提出了“独立的数字”的概念，意思就是“这个数字只能出现一次”，并将这个游戏命名为“数独”（sudoku ）。

数独一次的命名也就源于日本语，我们直接把日语中“数独”这两个同音字引用过来，也就成为了对其的命名。

每一道合格的数独谜题都有且仅有唯一答案，推理方法也以此为基础，任何无解或多解的题目都是不合格的二、数独规则标准数独的规则一般只有三点：1、数独中每行内的数字为1-9且不重复；2、数独中每列内的数字为1-9且不重复；3、数独中每宫内的数字为1-9且不重复。

三、数独元素标准数独的基本元素包括单元格、行、列、宫、区、区块、已知数、候选数等等。

单元格：简称格，是数独盘面中最小的格子，只可以填入一个数字； 行：数独盘面中横向9个单元格的总称； 列：数独盘面中纵向9个单元格的总称；宫：数独盘面中粗线划分出的9格单元格的总称；区：填入一组1-9数字的区域，行、列、宫、都是区的一种具体表现形式； 区块：某宫中横向或者纵向3个并排单元格的总称； 已知数：数独题目初始给出的数字；候选数：某空单元格中目前还可以填入的数字。

IH G F E D C B A数独直观解法，指的是我们在解数独的时候，不需要标记候选数，直接可以凭借直观判断填出格内得数的方法。

（有时候标记会大大增加解题效率，不能说标记就不属于直观解法）单区唯一解法、简单排除法、单元排除法、区块排除法、数组占位法、多区唯一解法第一节 单区唯一解法一、什么是单区唯一解法单区唯一解法，顾名思义“单区”指的是一行、一列或者一宫，“唯一解”指的是某格内只有唯一一个解。

由于数独规则的要求，数独中每行、每列及每一宫内数字都为1-9,。