高中数学苏教版选修2-3：课下能力提升(十八)独立性检验Word版含解析

2018版高中数学第三章统计案例3.1 独立性检验学案苏教版选修2-3 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018版高中数学第三章统计案例3.1 独立性检验学案苏教版选修2-3）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018版高中数学第三章统计案例3.1 独立性检验学案苏教版选修2-3的全部内容。

3.1 独立性检验学习目标1。

了解2×2列联表的意义。

2。

了解统计量χ2的意义。

3。

通过对典型案例分析，了解独立性检验的基本思想和方法．知识点一2×2列联表思考山东省教育厅大力推行素质教育，增加了高中生的课外活动时间,某校调查了学生的课外活动方式,结果整理成下表：体育文娱合计男生210230440女生60290350合计270520790如何判定“喜欢体育还是文娱与性别是否有联系”?梳理（1）2×2列联表的定义对于两个研究对象Ⅰ和Ⅱ,Ⅰ有两类取值，即类A和类B；Ⅱ也有两类取值，即类1和类2。

我们得到如下列联表所示的抽样数据：Ⅱ类1类2合计Ⅰ类A a b类B c d合计a＋b＋c＋d（2)χ2统计量的求法公式χ2＝错误!.知识点二独立性检验独立性检验的概念用χ2统计量研究两变量是否有关的方法称为独立性检验．知识点三独立性检验的步骤1．独立性检验的步骤要判断“Ⅰ与Ⅱ有关系”,可按下面的步骤进行:（1)提出假设H0：__________________；(2）根据2×2列联表及χ2公式,计算________的值；（3）查对临界值，作出判断．其中临界值如表所示：P（χ2≥x0）0。

课时跟踪训练(十八) 独立性检验1．给出下列实际问题：①一种药物对某种病的治愈率；②两种药物治疗同一种病是否有区别；③吸烟者得肺病的概率；④吸烟是否与性别有关系；⑤网吧与青少年的犯罪是否有关系．其中用独立性检验可以解决的问题有( )A ．①②③B ．②④⑤C ．②③④⑤D ．①②③④⑤2．通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：经计算得χ2＝110×(40×30－20×20)260×50×60×50≈7.8.则正确结论是( )A ．在犯错误的概率不超过0.1% 的前提下，认为“爱好该项运动与性别有关”B ．在犯错误的概率不超过0.1% 的前提下，认为“爱好该项运动与性别无关”C ．有99%以上的把握认为“爱好该项运动与性别有关”D ．有99%以上的把握认为“爱好该项运动与性别无关”3．在吸烟与患肺病这两个分类变量的计算中，下列说法正确的是( )A ．若χ2>6.635，我们有99%的把握认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病B ．从独立性检验可知，有99%的把握认为吸烟与患肺病有关系时，我们说某人吸烟，那么他有99%的可能患有肺病C ．若从χ2统计量中得出有95%的把握认为吸烟与患肺病有关系，是指有5%的可能性使得推断出现错误D ．以上三种说法都不正确4．考察棉花种子经过处理与生病之间的关系，得到下表中的数据：A．种子是否经过处理与是否生病有关B．种子是否经过处理与是否生病无关C．种子是否经过处理决定是否生病D．有90%的把握认为种子经过处理与生病有关5．下面2×2列联表中a，b的值分别为6．某医疗研究所为了检验某种血清预防甲型H1N1流感的作用，把500名使用血清的人与另外500名未用血清的人一月中的甲型H1N1流感记录作比较，提出假设H0：“这种血清不能起到预防甲型H1N1流感的作用”，利用2×2列联表计算得χ2≈3.918.对此，有以下四个判断：①有95%的把握认为“这种血清能起到预防甲型H1N1流感的作用”②若某人未使用该血清，那么他在一月中有95%的可能性得甲型H1N1流感③这种血清预防甲型H1N1流感的有效率为95%④这种血清预防甲型H1N1流感的有效率为5%则正确命题的序号是____________．(把你认为正确的命题序号都填上)7．某校在两个班进行教学方式对比试验，两个月后进行了一次检测，试验班与对照班成绩统计如下表所示(单位：人)：(1)求m，n；(2)根据表中数据能得到什么结论？8．某企业有两个分厂生产某种零件，按规定内径尺寸(单位：mm)的值落在[29.94,30.06)的零件为优质品．从两个分厂生产的零件中各抽出了500件，量其内径尺寸，得结果如下表：甲厂：乙厂：(1)试分别估计两个分厂生产的零件的优质品率；(2)由以上统计数据填下面2×2列联表，并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”？附χ2＝n (n 11n 22－n 12n 21)2n 1＋n 2＋n ＋1n ＋2，答 案1．选B 独立性检验是判断两个分类变量是否有关系的方法，而①③都是概率问题，不能用独立性检验．2．选C 根据独立性检验的思想方法，正确选项为C.3．选C A 、B 是对χ2的误解，99%的把握认为吸烟和患肺病有关，是指通过大量的观察实验得出的一个数值，并不是100个人中必有99个人患肺病，也可能这100个人全健康．4．选B χ2＝407×(32×213－61×101)293×314×133×274≈0.164<3.841，即没有充足的理由认为种子是否经过处理跟生病有关．5．解析：∵a ＋21＝73，∴a ＝52. 又∵a ＋2＝b ，∴b ＝54. 答案：52 546．解析：χ2≈3.918>3.841，故判断有95%的把握认为“血清能起到预防H1N1流感的作用”，只有①正确． 答案：①7．解：(1)m ＝45－15＝30，n ＝50＋50＝100. (2)由表中的数据，得χ2＝100×(35×30－15×20)250×50×55×45≈9.091.因为9.091＞6.635，所以有99%的把握说“教学方式与成绩有关系”．8．解：(1)甲厂抽查的产品中有360件优质品，从而甲厂生产的零件的优质品率估计为360500＝72%； 乙厂抽查的产品中有320件优质品，从而乙厂生产的零件的优质品率估计为320500＝64%.(2)χ2＝1 000×(360×180－320×140)2500×500×680×320≈7.35＞6.635，所以有99%的把握认为“两个分厂生产的零件的质量有差异”．。

课下能力提升(十八)独立性检验一、填空题1．在一项打鼾与患心脏病的调查中，共调查了1 671人，经过计算χ2＝27.63，根据这一数据分析，我们有理由认为打鼾与患心脏病是________的．(有关，无关) 2．若两个研究对象X和Y则X与Y之间有关系的概率约为________．3．在吸烟与患肺病这两个对象的独立性检验的计算中，下列说法正确的是________．(填序号)①若χ2＝6.635，则我们认为有99%的把握认为吸烟与患肺病有关系．那么在100个吸烟的人中必有99人患肺病．②从独立性检验的计算中求有99%的把握认为吸烟与患肺病有关系时，我们认为如果某人吸烟，那么他有99%的可能患肺病．③若从统计量中求出有95%的把握认为吸烟与患肺病有关系，是指有5%的可能性使得推断出现错误．④以上三种说法都不正确．4．调查者询问了72名男女大学生在购买食品时是否观看营养说明得到如下2×2列联表：从表中数据分析大学生的性别与看不看营养说明之间的关系是________．(填“有关”或“无关”)5则由表可知大约有________的把握认为多看电视与人变冷漠有关系．二、解答题6．为研究学生的数学成绩与对学习数学的兴趣是否有关，对某年级学生作调查，得到如下数据：学生的数学成绩好坏与对学习数学的兴趣是否有关？7．考察小麦种子经过灭菌与否跟发生黑穗病的关系，经试验观察，得到数据如下列联表.试按照原试验目的作统计推断．8．为了调查某生产线上质量监督员甲是否在生产现场对产品质量好坏有无影响，现统计数据如下：甲在生产现场时，990件产品中有合格品982件，次品8件；甲不在生产现场时，510件产品中有合格品493件，次品17件．试用独立性检验的方法分析监督员甲是否在生产现场对产品质量好坏有无影响．答案1．解析：由χ2值可判断有关． 答案：有关2．解析：因为χ2＝（5＋15＋40＋10）×（5×10－40×15）2（5＋15）×（40＋10）×（5＋40）×（15＋10）≈18.8，查表知P (χ2≥10.828)≈0.001.答案：99.9%3．解析：由独立性检验的意义可知，③正确． 答案：③4．解析：提出假设H 0：大学生的性别与看不看营养说明无关，由题目中的数据可计算χ2＝72×（28×20－16×8）244×28×36×36≈8.42，因为当H 0成立时，P (χ2≥7.879)≈0.005，这里的χ2≈8.42>7.879，所以我们有99.5%的把握认为大学生的性别与看不看营养说明有关．答案：有关5．解析：由公式得χ2＝168×（68×38－42×20）2110×58×88×80≈11.377>10.828，所以我们有99.9%的把握说，多看电视与人变冷漠有关．答案：99.9%6．解析：提出假设H 0：学生数学成绩的好坏与对学习数学的兴趣无关． 由公式得χ2的值为χ2＝189×（64×73－22×30）286×103×95×94≈38.459.∵当H 0成立时，χ2≥10.828的概率约为0.001， 而这里χ2≈38.459>10.828，∴有99.9%的把握认为学生数学成绩的好坏与对学习数学的兴趣是有关的． 7．解：提出假设H 0：种子是否灭菌与有无黑穗病无关． 由公式得，χ2＝460×（26×200－184×50）2210×250×76×384≈4.804.由于4.804>3.841，即当H 0成立时，χ2>3.841的概率约为0.05，所以我们有95%的把握认为种子是否灭菌与有无黑穗病是有关系的．8．解：2×2提出假设H 0：质量监督员甲是否在生产现场与产品质量的好坏无明显关系． 根据χ2公式得χ2＝1 500（982×17－493×8）2990×510×1 475×25≈13.097.因为H 0成立时，χ2>10.828的概率约为0.001， 而这里χ2≈13.097>10.828，所以有99.9%的把握认为质量监督员甲是否在生产现场与产品质量的好坏有关系．。

独立性检验教学目标知识与技能：通过对典型案例的探究，了解独立性检验的基本思想、方法及初步应用。

过程与方法：经历由实际问题建立数学模型的过程，体会其基本方法.情感、态度与价值观：引导学生形成“自主学习〞与“合作学习〞等良好的学习方式.教学重点教学难点2×2列联表及X2统计量由实际问题建立数学模型的过程，体会其基本方法.教具准备：与教材内容相关的资料。

教学设想：通过对典型案例的探究，了解独立性检验的基本思想、方法及初步应用。

教学过程：学生探究过程：问题情景问题1某医疗机构为了了解患肺癌与吸烟是否有关，进行了一次抽样调查，共调查了9965个成年人，其中吸烟者2148人，不吸烟者7817 人，调查结果是：吸烟的2148 人中49人患肺癌， 2099人不患肺癌；不吸烟的7817人中42人患肺癌， 7775人不患肺癌。

根据这些数据能否断定：患肺癌与吸烟有关？学生活动为了调查吸烟是否对肺癌有影响，某肿瘤研究所随机地调查了9965人，得到如下结果〔单位：人〕吸烟与肺癌列联表患肺癌不患肺癌总计吸烟4920992148不吸烟4277757817总计9198749965在不吸烟者中患肺癌的比重是在吸烟者中患肺癌的比重是问题1：判断的标准是什么？吸烟与不吸烟，患病的可能性的大小是否有差异？说明：吸烟者和不吸烟者患肺癌的可能性存在差异，吸烟者患肺癌的可能性大 问题2：差异大到什么程度才能作出“吸烟与患病有关〞的判断？问题3：能否用数量刻画出“有关〞的程度？建构数学独立性检验：通过数据和图表分析，得到结论是：吸烟与患肺癌有关思考：结论的可靠程度如何？吸烟与肺癌列联表患肺癌不患肺癌总计 吸烟aba+b不吸烟cdc+d总计a+cb+da+b+c+dH 0： 吸烟和患肺癌之间没有关系引入一个随机变量：卡方统计量作为检验在多大程度上可以认为“两个变量有关系〞的标准 。

例题讲解 例1:见引例通过公式计算在H 0成立的情况下， 即在 H 0成立的情况下，χ2大于10.828概率非常小，近似为0.001现在的χ2=56.632的观测值远大于10.828，出现这样的观测值的概率不超过0.001。

独立性检验
．了解独立性检验的概念，会判断独立性检验事件．
．能列出×列联表，会求χ(卡方统计量的值)．
．能够利用临界值，作出正确的判断．(重点)
．应用独立性检验分析实际问题．(难点)
[基础·初探]
教材整理×列联表的意义
阅读教材～“例”以上部分，完成下列问题
一般地，对于两个研究对象Ⅰ和Ⅱ，Ⅰ有两类取值，即类和类(如吸烟与不吸烟)；Ⅱ也有两类取值，即类和类(如患呼吸道疾病和未患呼吸道疾病)．我们得到如下表所示的抽样数据：
形如上表的表格称为×列联表，×列联表经常用来判断和Ⅱ之间是否有关系．
下面是一个×列联表：
【解析】∵＋＝，∴＝.
又＝＋＝＋＝.
【答案】
教材整理独立性检验
阅读教材～“例”以上部分完成下列各题．
．独立性检验
×列联表中的数据是样本数据，它只是总体的代表，具有随机性，结果并不唯一．因此，由某个样本得到的推断有可能正确，也有可能错误．为了使不同样本量的数据有统一的评判标准，统计学中引入下面的量(称为卡方统计量)：
χ＝(*)，
其中＝＋＋＋为样本容量．
用统计量研究这类问题的方法称为独立性检验( )．
．独立性检验的基本步骤
要推断“Ⅰ与Ⅱ有关系”，可按下面的步骤进行：
()提出假设：Ⅰ与Ⅱ没有关系；
()根据×列联表与公式(*)计算χ的值；
()查对临界值(如下表)，作出判断.
．关于分类变量与的随机变量χ的观测值，下列说法正确的是．(填序号) ()的值越大，“和有关系”可信程度越小；
()的值越小，“和有关系”可信程度越小；。

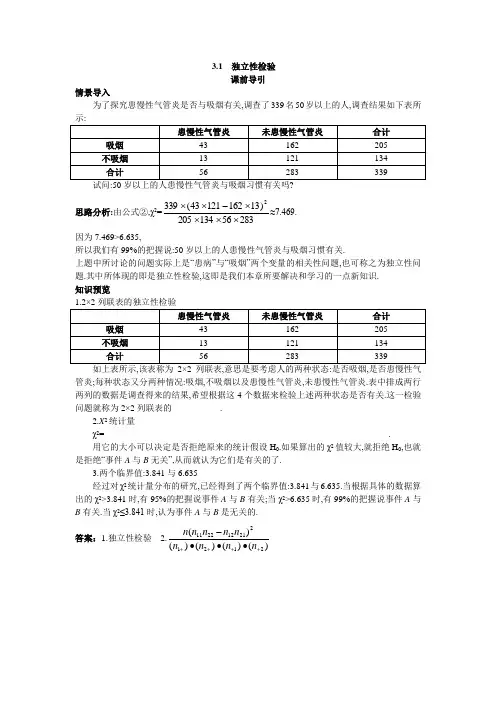
3.1 独立性检验课前导引情景导入为了探究患慢性气管炎是否与吸烟有关,调查了339名50岁以上的人,调查结果如下表所试问:50岁以上的人患慢性气管炎与吸烟习惯有关吗?思路分析:由公式②,χ2=28356134205)1316212143(3392⨯⨯⨯⨯-⨯⨯≈7.469.因为7.469>6.635,所以我们有99%的把握说:50岁以上的人患慢性气管炎与吸烟习惯有关.上题中所讨论的问题实际上是“患病”与“吸烟”两个变量的相关性问题,也可称之为独立性问题.其中所体现的即是独立性检验,这即是我们本章所要解决和学习的一点新知识. 知识预览管炎;每种状态又分两种情况:吸烟,不吸烟以及患慢性气管炎,未患慢性气管炎.表中排成两行两列的数据是调查得来的结果,希望根据这4个数据来检验上述两种状态是否有关.这一检验问题就称为2×2列联表的___________.2.X 2统计量χ2=_________________________________________________________________.用它的大小可以决定是否拒绝原来的统计假设H 0.如果算出的χ2值较大,就拒绝H 0,也就是拒绝“事件A 与B 无关”,从而就认为它们是有关的了.3.两个临界值:3.841与6.635经过对χ2统计量分布的研究,已经得到了两个临界值:3.841与6.635.当根据具体的数据算出的χ2>3.841时,有95%的把握说事件A 与B 有关;当χ2>6.635时,有99%的把握说事件A 与B 有关.当χ2≤3.841时,认为事件A 与B 是无关的.答案：1.独立性检验 2.)()()()()(2121221122211++++∙∙∙-n n n n n n n n n。

2018年高中数学第3章统计案例3.1 独立性检验教学案苏教版选修2-3 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018年高中数学第3章统计案例3.1 独立性检验教学案苏教版选修2-3）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018年高中数学第3章统计案例3.1 独立性检验教学案苏教版选修2-3的全部内容。

3.1 独立性检验1．2×2列联表的定义对于两个研究对象Ⅰ和Ⅱ，Ⅰ有两类取值，即类A和类B；Ⅱ也有两类取值，即类1和类2.这些取值可用下面的2×2列联表表示。

2。

χ2统计量的求法公式χ2＝错误!．3．独立性检验的概念用统计量χ2研究两变量是否有关的方法称为独立性检验．4．独立性检验的步骤要判断“Ⅰ与Ⅱ有关系”，可按下面的步骤进行:（1）提出假设H0：Ⅰ与Ⅱ没有关系；(2)根据2×2列联表及χ2公式，计算χ2的值；（3）查对临界值，作出判断．其中临界值如表所示:P(χ2≥x0）0。

500。

400。

250.150。

100。

050。

0250。

0100。

0050。

001χ00。

4550.7081.3232。

0722.7063.8415。

0246.6357。

87910.828表示在H0成立的情况下,事件“χ2≥x0”发生的概率．5．变量独立性判断的依据（1)如果χ2〉10。

828时,那么有99.9％的把握认为“Ⅰ与Ⅱ有关系”；（2)如果错误!〉6。

635时，那么有99%的把握认为“Ⅰ与Ⅱ有关系”；（3）如果错误!>2.706时，那么有90%的把握认为“Ⅰ与Ⅱ有关系"；（4)如果错误!≤2。