画法几何——点线面应用

大一上学期画法几何知识点在大一上学期的数学课程中，画法几何是一个重要的知识点。

通过学习画法几何，我们可以了解到如何使用几何工具和方法来描述和探索空间形状和结构。

下面将介绍几个画法几何的重要知识点。

1. 点、线和面在几何学中，点是最基本的图形元素，它没有大小和形状，只有位置。

通过将点连接起来，我们可以得到线段和直线。

线段有起点和终点，而直线是没有端点的。

面是由三条或更多的线段围成的区域，可以是平面、曲面或多面体。

2. 图形的绘制在绘制几何图形时，我们通常会用到几何工具，如直尺、圆规和量角器。

直尺用于绘制直线和线段，圆规用于绘制圆和弧线，量角器用于测量和绘制角度。

在画法几何中，我们需要注意使用工具的准确性和规范性，以确保图形的准确性和美观性。

3. 几何图形的分类几何图形可以分为平面图形和立体图形两大类。

平面图形包括点、线、面以及由它们组成的多边形，如三角形、四边形和多边形等。

立体图形则是由平面图形在空间中的运动而形成的，如球体、长方体和圆锥等。

4. 角和三角形在几何学中，角是由两条线段或线段与线交点组成的图形。

角可分为锐角、直角、钝角和平角等不同类型。

三角形是由三条线段所围成的图形，根据三边的关系，可以分为等边三角形、等腰三角形和一般三角形等类型。

5. 圆和圆的性质圆是由一个固定点到平面上所有与该点的距离相等的点组成的图形。

圆的性质包括圆心、半径、直径和弧等概念。

圆的周长是指圆周的长度，而圆的面积则是指圆内所有点到圆心的距离之和。

6. 相似和全等在画法几何中，相似和全等是两个重要的相对概念。

如果两个图形的形状和大小相同，那么它们是全等的；如果两个图形的形状相似但大小不同，那么它们是相似的。

相似和全等的概念在证明和计算几何问题中具有重要的应用。

7. 平行和垂直关系在几何学中，平行和垂直是两种重要的直线关系。

当两条直线永远不相交时，它们是平行的；当两条直线相交时，形成的角度为90度，它们是垂直的。

平行和垂直关系在平面和空间中的几何图形描述和计算中具有重要的作用。

空间几何体——点、线、面一、空间中最基本的元素：点、线、面的画法 点 A ·引申：斜二测画法1、公理1：如果一条直线上两点在一个平面内，那么这条直线在此平面内。

,,A l B ll A B ααα∈∈⎧⇒⊂⎨∈∈⎩ 公理1的作用：判断直线是否在平面内2、公理2：过不在一条直线上的三点，有且只有一个平面。

若A ，B ，C 不共线，则A ，B ，C 确定平面α推论1：过直线的直线外一点有且只有一个平面若A l ∉，则点A 和l 确定平面α推论2：过两条相交直线有且只有一个平面若m nA = ，则,m n 确定平面α推论3：过两条平行直线有且只有一个平面若m n ，则,m n 确定平面α 公理2及其推论的作用：确定平面；判定多边形是否为平面图形的依据。

3、公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

,P P l P l αβαβ∈∈⇒=∈ 且公理3作用：（1）判定两个平面是否相交的依据；（2）证明点共线、线共点等。

4、公理4：也叫平行公理，平行于同一条直线的两条直线平行.,a b c b a c ⇒公理4作用：证明两直线平行。

5、定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补。

,1212a a b b ''∠∠⇒∠∠ 且与方向相同＝,1212180a a b b ''∠∠⇒∠+∠︒ 且与方向相反＝ 作用：该定理也叫等角定理，可以用来证明空间中的两个角相等。

lBAαB AαClαAlm αAmnαP· αL βa b b a b 'a '方向相反则∠1+∠2＝180°方向相同则∠1＝∠22121a 'b '二、点、线、面之间的位置关系1.点与线位置关系：点在线上，点不在线上 引申：点到直线的距离点在线上的投影（垂直）2.点与面位置关系：点在面上，点不在面上 引申：点在面上的投影 点到面的距离3.线线位置关系：平行、相交、异面。

点线面的构成点线面的运用点、线、面是几何学中的基本概念和几何事物的基本元素。

它们有着广泛的运用和重要的作用，无论是在几何学中的研究，还是在实际应用中的设计和建造中。

首先，点是几何学中的基本概念，它是没有长度、宽度和厚度的。

点可以用来表示物体的位置，它在空间中没有实际的形状和大小。

在几何学中，点通常用一个大写字母表示，如"A"、"B"、"C"，并用线来连接它们。

点的运用可以帮助我们确定和描述几何图形中的位置和关系。

其次，线是由一组点按照特定的次序连接起来形成的，线是有长度但没有宽度和厚度的。

线段是线的一种特殊情况，它是由两个端点连接而成的线。

在线上可以选择任意两点连接来得到一条线段，线段的长度可以用来描述两个点之间的距离。

线的运用可以帮助我们确定几何图形的边界和形状，描述物体的运动轨迹等。

线的运用还体现在几何中的直线、射线等概念中。

直线是一条无限延伸的线，它的两个方向都没有限制。

直线也可以由两个点确定，通过这两个点可以找到其他的点。

射线是以一个起点为基准点向一个方向无限延伸的线，射线可以用一个大写字母表示，如"AB"，其中"A"为起点，"B"为在射线上的另一个点。

除了直线和射线，线段的运用也很重要，线段可以用来测量和描述物体的长度、宽度等。

线段在实际应用中有广泛的运用，如建筑设计中的测量和绘制，制造业中的切割和加工等。

最后，面是由无数条连接在一起的线段构成的，面是有长度和宽度但没有厚度的。

通过将线段相连接，我们可以得到一个封闭的图形，这个图形就是面。

在几何学中，面可以用来表示一个平面或者一个图形的表面。

面的运用可以帮助我们确定和描述图形的形状、面积等。

面还可以进一步扩展为平面和曲面的概念。

平面是由无数个点构成的，可以看做是无限延伸的面。

平面是平行于地面的理想水平面，使用平面可以帮助我们描述地图、建筑图纸等。

点线面的关系和投影的特点及其在几何学中的应用几何学是关于点、线和面等几何元素之间相互关系的研究。

而点线面之间的关系以及它们在投影中的特点，是几何学中重要的概念。

本文将探讨点线面之间的关系，并着重介绍投影的特点以及它们在几何学中的应用。

一、点线面之间的关系在几何学中，点线面是最基本的几何元素。

点是几何学的最小单位，没有长度、面积和体积。

线由无数个无限接近的点组成，具有长度但没有宽度和高度。

面由无数个无限接近的线组成，具有长度和宽度但没有厚度。

点、线和面之间存在着紧密的关系。

首先，一条线可以由无数个点组成。

例如，直线AB可以由A点到B点的无数个点组成。

其次，一个面可以由无数个线组成。

例如，平面P可以由无数条线上的点组成。

最后，一个面可以包含无数个点。

例如，平面P可以包含A、B、C等无数个点。

通过点线面的关系，我们可以更好地理解几何学中的各种概念和定理。

例如，在证明平行线之间的性质时，我们可以利用线与线之间的交点关系来推导出结论。

同时，点线面的关系也为解决几何学问题提供了基础。

在解决平面几何问题时，我们可以通过线与线之间的交点来确定点在平面上的位置。

二、投影的特点投影是一个重要的几何工具，它在几何学中具有广泛的应用。

投影是指将一个物体在另一个平面上的投射，使得原物体的形状、大小和位置在投影中得到保持。

在投影过程中，我们常常遇到以下几个特点：1. 平行投影：平行投影是指当物体与平面平行时，其投影在投影面上的大小和形状与原物体完全相同。

例如，一根竖直的杆子在垂直投影面上的投影仍然是一根竖直的线段。

2. 正交投影：正交投影是指当物体与投影面垂直时，其投影在投影面上的大小和形状发生改变，但仍然保持垂直关系。

例如，一个立方体在平面上的投影是一个正方形，虽然大小和形状发生变化，但其边与投影面垂直。

3. 等距投影：等距投影是指当物体与投影面成一定角度时，其投影与原物体形状相似但大小发生变化。

例如，一个立方体在斜投影面上的投影是一个倾斜的正方形，与原立方体相似但稍微变形。

点线面的运用第一篇：点线面的运用点线面的运用教学目的：通过本课使同学们明确学习的意义和点线面的构成方法，培养同学们的创造思维和设计能力。

教学重点：点线面在构成中的意义和重要位置。

教学难点：使同学们通过对抽象形态组合建立新的思维方式。

教具：点线面作品若干~PPT课件学习过程：一、导入新课找一找，这些图片中的点线面分别有哪些？，从生活用品、住房、交通工具等方面进行分析。

点线面组成了各种各样漂亮的花纹，组成多姿多彩的世界。

二、讲授新课在生活中，点线面随处可见，举例说明它存在于生活的那些方面？什么样叫点什么叫线面呢？我们一起去探索空间、位置、方向、形状、大小、色彩作为平面构成，它的构成形态无论如何复杂，都离不开点线面几种基本形态1、点点是相对细小的形象。

所谓细小是相对与周围的环境而言。

分为有序和无序两种组合。

结合生活中的实际考虑一下点给人一种什么样的感觉？2、线线是点的移动轨迹。

线有粗细。

当其宽度与长度差异悬殊是方能成为线。

线分为直线、曲线。

结合生活中的实际考虑一下线存在于何处？给人一种什么样的感觉？3、面面：线的移动轨迹成为面。

面是宽窄比利适当的形。

结合生活中的实际考虑一下面存在于何处？给人一种什么样的感觉？总结点线面；小巧简洁，活泼灵动的是点，千变万化，富于表现力的是线，占据大空间，沉稳而概括的是面4,总结点线面；小巧简洁，活泼灵动的是点，千变万化，富于表现力的是线，占据大空间，沉稳而概括的是面。

点线面，组成了丰富的形象世界，是造型的基本条件。

性能（造型中）或情感：点：点的组合适于表现节奏感和紧缩感。

线：线适于表现动感和速度感。

例：动画、漫画中的人物。

面：面适于表现量感和扩张感。

三、作业在了解了点线面特征后，以点线面中的任何一种形态来设计一幅平面构成的图形四．展示与评价教师展示学生作业并进行评讲，并鼓励学生：多看多想多动脑一定会创作出更好的作品第二篇：点线面第十二课点线面一、教学目标：1.了解点、线、面是造型语言中最基本的要素，知道点、线、面的各种视觉感受。

画法几何知识点画法几何是一门研究在平面上用图形表示空间几何形状和位置关系的学科。

它是工程制图的基础，对于建筑、机械、航空航天等领域的设计和制造有着至关重要的作用。

下面就让我们一起来了解一些画法几何的重要知识点。

一、投影法投影法是画法几何的核心概念之一。

投影法分为中心投影法和平行投影法。

中心投影法是指投影线由一点发出，所得到的投影图大小会随物体与投影中心的距离变化而变化。

这种投影法常用于绘制透视图，能给人一种立体感和真实感，但在工程制图中应用较少。

平行投影法又分为正投影法和斜投影法。

正投影法是指投影线相互平行且垂直于投影面，所得到的正投影图能够准确地反映物体的形状和大小，度量性好，是工程制图中最常用的投影方法。

斜投影法的投影线相互平行但不垂直于投影面，常用于绘制某些具有倾斜结构的物体。

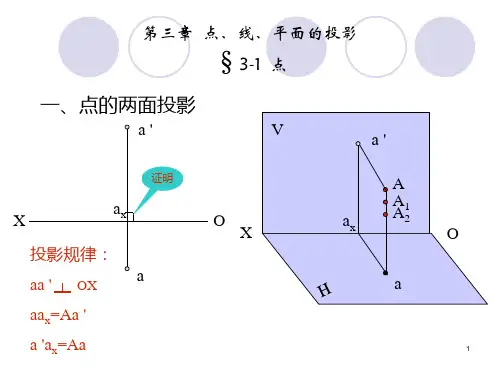
二、点、线、面的投影（一）点的投影点的投影规律是：点的正面投影与水平投影的连线垂直于 X 轴，点的正面投影与侧面投影的连线垂直于 Z 轴，点的水平投影到 X 轴的距离等于侧面投影到 Z 轴的距离。

（二）直线的投影直线在投影面上的投影可分为三种情况：一般位置直线、投影面平行线和投影面垂直线。

一般位置直线与三个投影面都倾斜，其三个投影都倾斜于投影轴，且长度小于实长。

投影面平行线平行于一个投影面，与另外两个投影面倾斜。

其中，平行于 H 面的直线称为水平线，平行于 V 面的直线称为正平线，平行于 W 面的直线称为侧平线。

投影面垂直线垂直于一个投影面，与另外两个投影面平行。

垂直于H 面的直线称为铅垂线，垂直于 V 面的直线称为正垂线，垂直于 W 面的直线称为侧垂线。

（三）平面的投影平面在投影面上的投影可分为一般位置平面、投影面垂直面和投影面平行面。

一般位置平面与三个投影面都倾斜，其三个投影都是类似形。

投影面垂直面垂直于一个投影面，与另外两个投影面倾斜。

其中，垂直于 H 面的平面称为铅垂面，垂直于 V 面的平面称为正垂面，垂直于 W 面的平面称为侧垂面。

点线面的关系及其在几何学中的应用几何学是研究点、线、面等几何对象之间的关系和性质的学科。

在几何学中，点、线、面是最基本的概念，它们之间存在着密切的关系，并且在几何学中扮演着重要的角色。

本文将介绍点线面的关系以及它们在几何学中的应用。

一、点线面的关系1. 点与线的关系点是几何学中最基本的概念，它没有长度、宽度和高度，只有位置。

而线则是由无数个点组成的集合，是一维的几何对象。

点与线之间存在着以下几种关系：（1）点在线上：当一个点与一条线上的点完全重合时，我们可以说这个点在这条线上。

（2）点在线上的垂直投影：一个点在一条线上的垂直投影是指从该点向垂直于线的方向下落，与线交于一点。

这个交点就是点在线上的垂直投影点。

（3）点在线的延长线上：当一个点不在一条线上，但点的连线与线的延长线相交时，我们可以说这个点在线的延长线上。

2. 点与面的关系面是由无数个点和线组成的集合，是二维的几何对象。

点与面之间存在着以下几种关系：（1）点在面上：当一个点与一个面上的点完全重合时，我们可以说这个点在这个面上。

（2）点在面的投影上：一个点在一个面上的投影是指从该点向面垂直方向投影，与面交于一点。

这个交点就是点在面上的投影点。

（3）点在面的上方或下方：当一个点不在面上，但点与面的连线与面平行时，我们可以根据点与面的位置关系，称这个点在面的上方或下方。

3. 线与面的关系线是由无数个点组成的集合，面是由无数个点和线组成的集合，线与面之间存在着以下几种关系：（1）线在面上：当一条线上的所有点都在一个面上时，我们可以说这条线在这个面上。

（2）线与面的交点：当一条线与一个面相交时，这个交点就是线与面的交点。

二、点线面在几何学中的应用1. 平面几何平面几何是几何学中的一个重要分支，与点线面的关系密切相关。

在平面几何中，我们研究平面上的点、直线和封闭曲线等几何对象之间的关系和性质，并应用它们来解决问题。

例如，通过研究点在线上的投影，我们可以得到很多有关垂直关系的定理；通过研究直线与平面的交点，我们可以得到很多有关平行关系的定理。

点线面的应用方式以及点,线,面分别的作
用
点线面的应用方式以及点,线,面分别的作用如下：
1、点动成线：如针式打印机打字时，一个个点形成线。

一辆汽车运动一段距离，他运动的距离就是一段线。

2、线动成面：如在医疗领域用激光刀手术时，激光经过处形成的刀口。

一个木棒绕一个端点旋转画出一个圆，这个圆所形成的就是面。

3、面动成体：如我们在刷牙时，牙膏口是一个圆面，挤牙膏时形成一个圆柱。

扇扇子的时候，扇子在空中划过的空间就是面动成体。

点线面三者关系如下：
1、点最重要的功能在于表明位置和进行聚焦，点与面是比较而形成的，同样一个点，如果布满整个或大面积的平面，它就是面了，如果在一个平面中多次出现，就可以理解为点。

2、点与点之间连接形成线，或者点沿着一定方面规律性的延伸可以成为线，线强调方向和外形。

3、平面上三个以上点的连接可以形成面，同时，平面上线的封闭或者线的展开也可以形成面，面强调形状和面积。

如何在绘画中运用点线面的组合来表现物体的形状和结构？在绘画中，点、线和面是最基本的视觉元素，它们的组合可以帮助我们表现物体的形状和结构。

以下是一些常用的技巧和方法，可以帮助我们在绘画中运用点线面的组合来表现物体的形状和结构：1. 点的运用：- 点可以被用来表示物体的位置或细节。

通过使用不同大小、形状和颜色的点，我们可以创造出不同的视觉效果。

- 点可以被运用来描绘物体的纹理和细节。

通过使用点状的笔触或者点彩的技法，我们可以模拟出物体表面的纹理和细微的变化。

2. 线的运用：- 线可以被用来描绘物体的轮廓和结构。

通过运用不同的线条粗细、弯曲和方向，我们可以准确地勾勒出物体的形状，并表达出物体的体积感。

- 线可以被用来描绘物体的纹理和细节。

通过使用线状的笔触或者交叉的线条，我们可以创造出物体表面的纹理和细节。

3. 面的运用：- 面可以被用来填充物体的形状，并表现物体的表面特征。

通过使用不同颜色的填充，我们可以创造出物体的明暗关系和光影效果，以增强物体的立体感。

- 面可以被用来描绘物体的纹理和细节。

通过使用不同形状和大小的面，我们可以模拟出物体表面的纹理和细微的变化。

4. 组合运用：- 点、线和面可以结合运用，相互补充，共同表现物体的形状和结构。

我们可以通过将点、线和面相互重叠、交叉或叠加，创造出更丰富的视觉效果。

- 我们可以根据物体的特点和表现目标，灵活运用点、线和面的组合。

通过多次尝试和实践，我们可以逐渐掌握如何运用点线面的组合来表现物体的形状和结构。

5. 视角和观察：- 视角和观察对于运用点线面的组合来表现物体的形状和结构至关重要。

我们需要选择合适的视角来观察物体，并注意物体的形状、比例和细节。

- 观察真实的物体或使用参考资料可以帮助我们更准确地捕捉物体的形状和结构。

通过观察和实践，我们可以提高自己的观察和表现能力。

总结来说，通过运用点、线和面的组合，我们可以表现物体的形状和结构。

通过点的运用来表示位置和细节，线的运用来勾勒轮廓和描绘纹理，面的运用来填充形状和表现明暗关系。

谈绘画构图中点、线、面的应用作者：王冬艳来源：《现代职业教育.高职本科》 2018年第3期绘画最基本的构成元素就是点、线、面，为了能够对绘画的构成关系有所明确，灵活地应用点、线、面进行绘画构图，有必要对点、线、面的变化规律进行掌握，这既是美术绘画创作的基本方法，也是绘画构图的基础。

因此，美术教师有必要从构成和特性方面人手对点、线、面进行了解和学习，加强点、线、面的构图训练，使学生的创造性思维方式得到培养，促进学生想象力的提高，从而促进其绘画水平的提升，为其创作出更好的绘画作品提供保障。

一、对点、线、面进行正确认识绘画构图中的点、线、面具有一定的抽象性，这也就增大了学生的理解难度。

美术教师在开展“绘画构图点、线、面”教学时，可以通过多媒体动画的形式将绘画构图中的点、线、面进行直观、形象的展示。

在介绍点的时候可以采用跳动的圆点，线可以是这个圆点所产生的扭动轨迹，面则是线条开始往下所形成的一片区域，除了这种直观的视觉感受教学方式，教师还可以引导学生对生活中的点、线、面进行发现和分析，由此使学生对点、线、面有正确的认识和了解，学生也能够在教师的引导和交流中更好地掌握绘画构图中点线面的应用。

二、绘画构图中点、线、面的应用（一）绘画构图中的“点”“点”是绘画构图中最为基本的元素，通常惰况下，“点”这个元素在绘画构图中所占比例相对较少，但是“点”并不仅是指点状的图形。

“点”一般会在绘画构图中发挥点缀作用，由此使其画面中的活泼元素得到增加，比如，太阳、花、苹果等都可以被称之为绘画构图中的“点”，因此，在绘画构图中应用“点”时需要注意：(1)结合色彩和大小对“点”进行应用。

不同大小和色彩的色块是点在绘画构图中的主要存在形式，除了点的面积会影响绘画构图的成效之外，点的色彩也会影响绘画构图的成效。

换言之，绘画构图的主题势必会被过大面积的点所影响。

例如，在一副山水绘画构图中应用过大面积的人物构图，则会对其作品主体创意造成影响。

小学美劳二年级点线面的运用在小学美术课程中，点线面是基本的元素，也是创作的基础。

在二年级的美术学习中，学生需要通过点线面的运用，培养对艺术的感知能力和创造力。

本文将介绍小学美劳二年级点线面的运用，并提供一些练习题，供老师和学生下载打印，以便更好地进行美术学习和实践。

1. 点的运用点是最简单的图形元素之一，它没有长宽，只有位置的大小。

在绘画中，点可以用来表现事物的形态、位置和构成。

在作品中使用点可以起到突出主题、增强表现力的作用。

在绘画课上，老师可以准备一些点的练习题，让学生通过点的不同分布和形态来表达自己的想法。

2. 线的运用线是由一连串点连接而成的，它能够表现出事物的形状、轮廓和结构。

在绘画中，线可以用来描绘物体的边缘、纹理和运动轨迹等。

在二年级的美术学习中，学生可以通过练习画线来提高手眼协调能力和绘画技巧。

老师可以设计一些线的练习题，如画直线、曲线、波浪线等，并鼓励学生发挥想象力，自由创作。

3. 面的运用面是由一连串线连接而成的，它是二维空间中的平面形状。

在绘画中，面可以用来表现事物的形状、色彩和纹理等。

在二年级的美术学习中，学生可以通过填充颜色或者贴纸来练习运用面。

可以使用一些简单的几何形状，如正方形、三角形、圆形等，让学生进行填充或者贴纸创作。

这样可以培养学生对色彩的感知和运用能力。

除了点线面的基本运用，老师还可以通过一些综合性的练习题来提升学生的美术水平。

比如让学生观察周围的环境，然后绘画出自己的视觉感受；或者让学生模仿一些有趣的图案，自由发挥创作能力。

通过这些综合性的练习，学生可以提高自己的观察力、表达能力和创造力。

在美术学习中，点线面的运用是非常重要的基础，它不仅可以培养学生对艺术的理解和欣赏能力，还可以促进学生的创造思维和审美意识的培养。

通过下载打印练习题，学生可以在课余时间进行更多的练习和实践，提高自己的美术水平。

希望本文对老师和学生在小学美劳二年级点线面的运用方面有所帮助，祝愿大家在美术学习中取得更好的成绩！。