信道编码仿真实践

信道编码实验报告引言：信道编码是一种常用的通信技术，用于增强数据传输的可靠性和效率。

通过在发送端对数据进行编码，并在接收端进行解码，可以有效地纠正或检测在信道传输过程中产生的错误。

本实验旨在研究不同的信道编码方法，并分析它们在不同信道条件下的性能。

一、实验目的：1.了解信道编码的概念和基本原理；2.掌握常用的信道编码方法和相关算法；3.通过实验验证不同信道编码方法的性能；4.分析信道编码在不同信道条件下的适用性。

二、实验原理：1.信道编码概述：信道编码主要分为前向纠错编码（Forward Error Correction, FEC）和自动重传请求（Automatic Repeat reQuest, ARQ）两类。

其中，FEC方法通过在数据流中引入冗余信息，使接收端能够检测和纠正一定数量的错误。

而ARQ方法则是通过接收端向发送端发送请求进行重传，从而实现数据的可靠传输。

2.常用的信道编码方法：在实验中，我们主要研究了以下几种常用的信道编码方法：（1）奇偶校验编码：奇偶校验编码是最简单的一种编码方式，它通过在数据末尾添加一个校验位来实现错误检测。

若校验位与数据位中的奇偶性不一致，则认为出现错误。

（2）海明码编码：海明码是一种通过添加冗余位来实现错误检测和纠正的编码方法。

通过在数据位中插入冗余位，接收端可以检测到并纠正一定数量的错误。

（3）卷积码编码：卷积码是一种递归线性均匀的编码方法，通过引入冗余信息来增强信号的可靠性。

它具有较好的纠错性能，广泛应用于无线通信领域。

三、实验过程：1.实验环境准备：在实验中，我们使用了Matlab软件进行信道编码的仿真实验。

通过编写相应的算法和程序，可以模拟不同的信道编码方法，并分析它们的性能。

2.编写奇偶校验编码程序：首先，我们编写了奇偶校验编码的程序，通过向数据流中添加校验位实现错误检测。

然后，对不同的信道条件进行仿真实验，并记录不同错误率下的传输性能。

3.编写海明码编码程序：接下来，我们编写了海明码编码的程序，通过插入冗余位实现错误检测和纠正。

考虑BSC信道，令错误概率0.02:0.02:0p通过仿真分别确定无编码、码率1/3重复码以及(7,4)汉明码的BER clear allclcK=10000;N=3*K;G=[1 1 0 1 0 0 0; 0 1 1 0 1 0 0; 1 1 1 0 0 1 0; 1 0 1 0 0 0 1;];H=[1 0 0 1 0 1 1; 0 1 0 1 1 1 0; 0 0 1 0 1 1 1;]; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%±àÂëx0=randi([0,1],K,1)';y0=repmat(x0,3,1);y0=reshape(y0,1,numel(y0));for i=1:K/4z0(7*i-6:7*i)=mod(x0(4*i-3:4*i)*G,2);end%%%%%%%%%%%%%%%%%%%%%%%%´«Êäc=rand(1,7*N/4);for ii=1:6p=ii*0.02;x1=zeros(1,K);for i=1:Kif c(i)<px1(i)=-x0(i)+1;elsex1(i)=x0(i);endendy1=zeros(1,N);for i=1:Nif c(i)<py1(i)=-y0(i)+1;elsey1(i)=y0(i);endendz1=zeros(1,7*K/4);for i=1:7*K/4if c(i)<pz1(i)=-z0(i)+1;elsez1(i)=z0(i);endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%ÒëÂëx2=x1;y2=zeros(1,K);for i=1:Kif y1(3*i-2)+y1(3*i-1)+y1(3*i)<2y2(i)=0;elsey2(i)=1;endendz2=zeros(1,7*K/4);mask=[0 0 0 0 0 0 0];for i=1:K/4zz=mod(z1(7*i-6:7*i)*H',2);zzz=zz(1)*4+zz(2)*2+zz(3)*1;switch(zzz)case 4mask=[1 0 0 0 0 0 0];case 2mask=[0 1 0 0 0 0 0];case 1mask=[0 0 1 0 0 0 0];case 6mask=[0 0 0 1 0 0 0];case 3mask=[0 0 0 0 1 0 0];case 7mask=[0 0 0 0 0 1 0];case 5mask=[0 0 0 0 0 0 1];case 0mask=[0 0 0 0 0 0 0];endz2(7*i-6:7*i)=double(bitxor(int8(mask),int8(z1(7*i-6:7*i)))); endfor i=1:K/4z3(4*i-3:4*i)=z2(7*i-3:7*i);endUncoded(ii)=length(find((x0-x2)==0))/K;Repitition(ii)=length(find((x0-y2)==0))/K;Hamming(ii)=length(find((x0-z3)==0))/K;endx=0.02:0.02:0.12;semilogx(x,Repitition,x,Hamming,x,Uncoded);xlabel('BER'); legend('Repitition','Hamming','Uncoded');BSC信道中无编码性能最差(7,4)汉明码性能次之，复杂度最高1/3重复吗性能最优BER越高，三种编码的差距越明显考虑AWGN信道，设定单位信息比特能量Eb =1，信噪比Eb/ 变化范围为0:2:12dB，通过仿真分别确定无编码、码率1/3重复码以及(7,4)汉明码的BER（后两种采用硬译码算法）clear allclcK=10000;N=3*K;G=[1 1 0 1 0 0 0; 0 1 1 0 1 0 0; 1 1 1 0 0 1 0; 1 0 1 0 0 0 1;];H=[1 0 0 1 0 1 1; 0 1 0 1 1 1 0; 0 0 1 0 1 1 1;]; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%±àÂëx0=randi([0,1],K,1)';y0=repmat(x0,3,1);y0=reshape(y0,1,numel(y0));for i=1:K/4z0(7*i-6:7*i)=mod(x0(4*i-3:4*i)*G,2);end%%%%%%%%%%%%%%%%%%%%%%%%´«Êäfor ii=1:7SNR=2*ii-2;Eb=1;SNR=10^(SNR/10);sigma=sqrt(Eb/SNR);AWGN=sigma*randn(1,N); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%a0=Eb*(-2*x0+1) +AWGN(1:K);b0=Eb*(-2*y0+1)/sqrt(3) +AWGN(1:N);c0=Eb*(-2*z0+1)*2/sqrt(7)+AWGN(1:7*K/4); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%a1=(sign(a0)-1)/(-2);b1=(sign(b0)-1)/(-2);c1=(sign(c0)-1)/(-2);a2=a1;b2=zeros(1,K);for i=1:Kif b1(3*i-2)+b1(3*i-1)+b1(3*i)<2b2(i)=0;elseb2(i)=1;endendc2=zeros(1,7*K/4);mask=[0 0 0 0 0 0 0];for i=1:K/4cc=mod(c1(7*i-6:7*i)*H',2);ccc=cc(1)*4+cc(2)*2+cc(3)*1;switch(ccc)case 4mask=[1 0 0 0 0 0 0];case 2mask=[0 1 0 0 0 0 0];case 1mask=[0 0 1 0 0 0 0];case 6mask=[0 0 0 1 0 0 0];case 3mask=[0 0 0 0 1 0 0];case 7mask=[0 0 0 0 0 1 0];case 5mask=[0 0 0 0 0 0 1];case 0mask=[0 0 0 0 0 0 0];endc2(7*i-6:7*i)=double(bitxor(int8(mask),int8(c1(7*i-6:7*i))));endfor i=1:K/4c3(4*i-3:4*i)=c2(7*i-3:7*i);endUncoded(ii)=length(find((x0-a2)==0))/K;Repitition(ii)=length(find((x0-b2)==0))/K;Hamming(ii)=length(find((x0-c3)==0))/K;endx=0:2:12;plot(x,Uncoded,x,Repitition,x,Hamming);xlabel('SNR');ylabel('BER'); legend('Uncoded','Repitition','Hamming');AWGN信道中在SNR<5dB无编码性能最优1/3重复码性能次之汉明码性能最差在SNR<5dB无编码性能最优汉明码性能次之1/3重复码性能最差SNR越低，三种编码的差距越明显。

无线通信基础课程设计报告（信道编码）小组成员：指导老师：完成时间：无线通信系统课程设计报告实验摘要：数字信号在传输中往往由于各种原因，使得在传送的数据流中产生误码，从而使接收端产生图象跳跃、不连续等现象。

信道编码通过对数码流进行相应的处理，使系统具有一定的检错和纠错能力，可极大地避免码流传送中误码的发生。

提高数据传输可靠性，降低误码率是信道编码的任务。

实验名称：信道编码实验目标：本实验的目标是领会信道编码的基本思想。

并通过比较有无信道编码模块的不同系统误码率性能，感受信道编码技术对于提高系统性能的重要意义。

实验原理：打开“Channel_Coding_74.vi”前面板如图1所示，打开程序框图并理解参与信道编码的整个数据流。

程序包含上下两个独立的部分如图2所示，下面部分是生成误码率曲线如图1(b)，其结构和上面部分类似，你只需要关注上面部分程序即可；上面部分代码大致可由做7个模块组成，每一模块完成一项功能。

你负责的是这个实验的“编码和解码”功能。

这些模块为：1、读取图片LabVIEW提供了一个能够读取JPEG格式的图像并输出图像数据的模块。

提供的还原像素图.vi完成图像数据到一维二进制数据的转换（图像数据→十进制二维数组→二进制一维数组），输出信源比特流。

(a)实验操作部分(b)误码率曲线图1 前面板2、信道编码我们的下一个目标是对信源比特流进行信道编码。

信道编码方案很多，线性分组码、卷积码、LDPC码等等；这里我们采用简单的（7，4）线性分组码。

图2 程序框图线性分组码是一类重要的纠错码。

在（n ，k ）线性分组码中，常用到能纠正一位错误的汉明码。

其主要参数如下：码长：21mn =-； 信息位：21mk m =--； 校验位：m n k =-； 最小距离： d = 3； 纠错能力： t = 1；本次实验需要用到的是(7,4)分组码，属系统码，前四位为信息位，后三位为冗余位。

3、BPSK 调制上一步得到的是二进制的信息比特流，需要采用一定的调制方案，将二进制的信息比特映射成适合信道传输的符号。

移动通信中的信道编码和信源编码仿真摘要：人们对追求最佳的通信性能的有效性和靠得住性为目标的信源编码技术和信道编码技术提出愈来愈高的要求。

本设计第一学习了移动通信系统中信道编码和信源编码的大体理论，和通信仿真的概念、一样步骤。

然后在此基础上利用编程和Matlab 中的仿真模块库Simulink进行仿真。

通过模型搭建、编写程序、运行、调试整个进程以后，取得了以下功效。

要紧包括：通过仿真分析发觉A律、μ律紧缩在A大于、μ大于100以后紧缩成效比较理想；关于A律十三折和μ律十五折，都是比较好的非均匀量化方式，但在处置小信号时，μ律十五折能取得更大的量化信噪比；在进行脉冲调制(PCM, Pulse Code Modulation)编码和差分脉冲调制(DPCM,Differential Pulse Code Modulation)编码比较时，咱们看到DPCM编码比PCM编码的量化误差更小；关于RS(Reed-Solomon)编码如RS(60，44)，当信道的误比特率低于1%时，RS编码信号不产生误比特数，而当高于1%，编码信号的误比特率与信道的误比特率成反比；关于循环冗余码(CRC-16,Cyclic redundancy check)编码，咱们发觉CRC检测性能比较理想，如在帧距离为，仿真时刻为1000时，CRC检测器发生错误裁决的比例低于%。

关键词：移动通信；信源编码；信道编码；仿真目录1 绪论.............................................................................................................................. 错误!未定义书签。

通信系统的组成......................................................................................................... 错误!未定义书签。

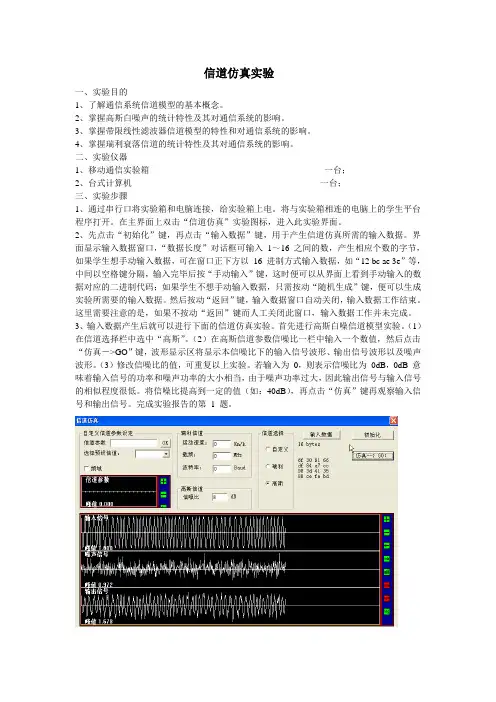
信道仿真实验一、实验目的1、了解通信系统信道模型的基本概念。

2、掌握高斯白噪声的统计特性及其对通信系统的影响。

3、掌握带限线性滤波器信道模型的特性和对通信系统的影响。

4、掌握瑞利衰落信道的统计特性及其对通信系统的影响。

二、实验仪器1、移动通信实验箱一台；2、台式计算机一台；三、实验步骤1、通过串行口将实验箱和电脑连接，给实验箱上电。

将与实验箱相连的电脑上的学生平台程序打开。

在主界面上双击“信道仿真”实验图标，进入此实验界面。

2、先点击“初始化”键，再点击“输入数据”键，用于产生信道仿真所需的输入数据。

界面显示输入数据窗口，“数据长度”对话框可输入1～16 之间的数，产生相应个数的字节，如果学生想手动输入数据，可在窗口正下方以16 进制方式输入数据，如“12 bc ae 3e”等，中间以空格键分隔，输入完毕后按“手动输入”键，这时便可以从界面上看到手动输入的数据对应的二进制代码；如果学生不想手动输入数据，只需按动“随机生成”键，便可以生成实验所需要的输入数据。

然后按动“返回”键，输入数据窗口自动关闭，输入数据工作结束。

这里需要注意的是，如果不按动“返回”键而人工关闭此窗口，输入数据工作并未完成。

3、输入数据产生后就可以进行下面的信道仿真实验。

首先进行高斯白噪信道模型实验。

（1）在信道选择栏中选中“高斯”。

（2）在高斯信道参数信噪比一栏中输入一个数值，然后点击“仿真－>GO”键，波形显示区将显示本信噪比下的输入信号波形、输出信号波形以及噪声波形。

（3）修改信噪比的值，可重复以上实验。

若输入为0，则表示信噪比为0dB，0dB 意味着输入信号的功率和噪声功率的大小相当，由于噪声功率过大，因此输出信号与输入信号的相似程度很低。

将信噪比提高到一定的值（如：40dB），再点击“仿真”键再观察输入信号和输出信号。

完成实验报告的第 1 题。

4、下面进行带限线性滤波器信道模型实验，这个信道模型是对存在码间干扰的信道的建模，反映信道特性的信道参数由学生自定义输入。

电子信息工程毕设设计__基于matlab的信道编码仿真基于matlab的信道编码仿真海南大学毕业论文(设计)题目:基于matlab的信道编码仿真学号:姓名: 年级: 学院:信息科学技术学院系别:电子信息工程专业:电子信息工程指导教师:完成日期:1基于matlab的信道编码仿真摘要通信技术的飞速发展，信道编码已经成功地应用于各种通信系统中。

以及各种传输方式对可靠性要求的不断提高，信道编码技术作为抗干扰技术的一种重要的手段，在数字通信技术领域和数字传输系统中显示出越来越重要的作用。

信道编码的目的是为了改善通信系统的传输质量。

由于实际信道存在噪声和干扰，使发送的码字与信道传输后所接收的码字之间存在差异，称这种差异为差错。

一般情况下，信道噪声、干扰越大，码字产生差错的概率也就越大。

本文利用matlab对二进制对称信道(BSC)，高斯白噪声信道(AWGN)两种信道的仿真，(7,4)Hamming码对信道的仿真，通过误码率的曲线图来了解信道的编码。

并利用matlab的simulink模块仿真，运用simulink里的卷积码viterbi译码器来对二进制对称信道和高斯白噪声信道的仿真，观察误码率的曲线图来了解2个信道的不同。

关键字:matlab，信道，编码，译码，Simulink。

1基于matlab的信道编码仿真AbstractWith the rapid development of communication technology, channelcoding has been successfully applied to various communications systems. And a variety of transmission of the continuous improvement ofreliability requirements, anti-jamming channel coding technology as an important means of technology in the field of digital communications technology and digital transmission systems in a more and more important role.The purpose of channel coding is to improve the transmission quality of communications systems. As the actual existence of the channel noise and interference, the transmitted codewords and channel transmission received after the difference between code words, said this differenceis wrong. Under normal circumstances, channel noise, the greater the interference, the code word generated the greater the probability of error.In this paper, matlab binary symmetric channel (BSC), Gaussian white noise channel (AWGN) two channel simulation, (7,4) Hamming code simulation of the channel, through the bit error rate curve to understand the channel coding. Using matlab to simulink block simulation, using simulink in the viterbi decoder to convolutional codes on the binary symmetric channel and Gaussian white noise channel simulation, observation error rate graphs to understand the two different channelsKeywords: matlab, channel, coding, decoding, Simulink.2基于matlab的信道编码仿真目录1引言 ..................................................................... ...........................................................1 1.1选题的目的和意义 ..................................................................... .................................1 1.2本选题的理论依据、研究内容 ..................................................................... .............1 2.信道编码以及其运行环境MATLAB的介绍 (2)2.1 信道编码的概念及分类 ..................................................................... ........................2 2.2 信道编码定理及信道编码中所包含的各种码类的简介 ...........................................2 2.2.1卷积码 ..................................................................... .................................................2 2.2.2线性分组码 ..................................................................... .........................................3 2.2.3循环码 ..................................................................... .................................................3 2.3 MATLAB语言的简介 ...................................................................................................4 2.4Simulink ............................................................... ........................................................5 3.信道 ..................................................................... ...........................................................5 3.1二进制对称信道(BSC) .................................................................. ..........................5 3.2二进制删除信道(BEC) .................................................................. ..........................6 3.3高斯白噪声信道(AWGN) ................................................................. ............................6 4. Hamming 码...................................................................... .............................................7 4.1汉明码 ..................................................................... ....................................................7 4.2校验方法 ..................................................................... ................................................7 4.3汉明码编码 ..................................................................... ............................................9 4.3.1汉明码对高斯白噪声信道 ..................................................................... ..................9 4.3.2汉明码对二进制对称信道的仿真 ..................................................................... .....11 5.卷积码 ..................................................................... .....................................................15 5.1卷积码定义与原理 ..................................................................... ...............................15 5.2维特比译码原理 ..................................................................... ..................................15 5.3卷积码译码器对高斯白噪声信道的设计与仿真 .....................................................18 5.3.1卷积码译码器的设计与仿真 ..................................................................... (19)3基于matlab的信道编码仿真5.3.2简化维特比译码器的仿真 ..................................................................... ................22 5.3.3卷积码译码器的误码率分析 ..................................................................... ............24 5.4卷积编码器在二进制对称信道(BSC)中的性能 ................................................... 25 6.卷积码译码器对二进制对称信道和高斯白噪声信道仿真比较 .................................30 7.总结 ..................................................................... .........................................................31 致谢.................................................................................................................................32 参考文献 ..................................................................... ....................................................33 附录1: ..................................................................... .....................................................34 附录2: ..................................................................... ..................................................... 37 附录3: ..................................................................... .....................................................40 附录4: ..................................................................... .. (41)4基于matlab的信道编码仿真1引言1.1选题的目的和意义数字信号在传输中往往由于各种原因，使得在传送的数据流中产生误码，从而使接收端产生图象跳跃、不连续、出现马赛克等现象。

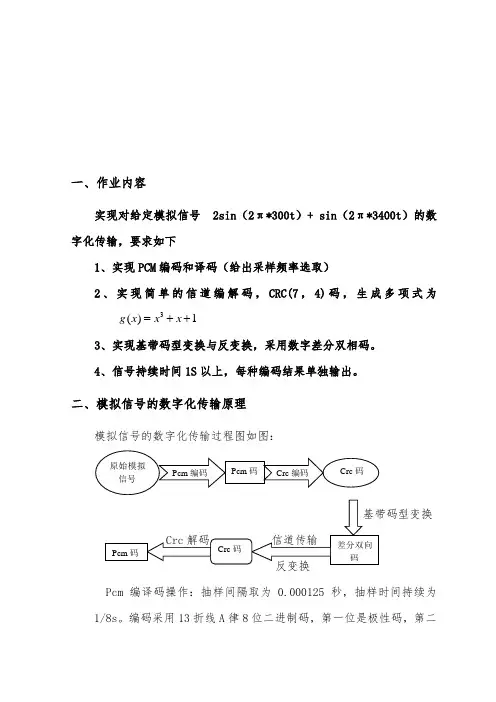
一、作业内容实现对给定模拟信号 2sin （2π*300t ）+ sin （2π*3400t ）的数字化传输，要求如下1、实现PCM 编码和译码（给出采样频率选取）2、实现简单的信道编解码，CRC(7，4)码，生成多项式为3、实现基带码型变换与反变换，采用数字差分双相码。

4、信号持续时间1S 以上，每种编码结果单独输出。

二、模拟信号的数字化传输原理模拟信号的数字化传输过程图如图：Pcm 编译码操作：抽样间隔取为0.000125秒，抽样时间持续为1/8s 。

编码采用13折线A 律8位二进制码，第一位是极性码，第二1)(3++=x x x g到第四位是段落码，五到八位是段内码，段内码采用折叠码。

首先，对模拟信号的量化结果进行归一化后乘以2048得到当前信号量化值。

判断量化值正负，得到第一位极性码。

而后比较量化值与起电平，确定段落码，最后通过量化台阶计算段内码。

其译码过程与其相反。

Crc编译码操作：应题中要求将一个8位pcm信息码分为两个4位码。

生成多项式为g(x)=x3+x+1,计算x r M(x)。

用g(x)除x r M(x)得到余式r(x)。

最后得到的码组为A(x)=x r M(x)+r(x)。

在进行crc译码时看，可取连续两个crc码前四位信息码，将信息码合并即可得传输的pcm码。

差分双向码编解码操作：将crc码当做数据输入，这里假设参考码为01，若crc码第一位信息码为1时相位改变，输出10。

为0时相位不变输出仍为01。

后面信息码变换方式相同，若输入为1，则输出相对前一输出相位改变。

反之，相位不变。

结合作业内容，分析所给定的模拟信号的数字化传输过程，描述该过程中各模块所处的位置（佐以框图）、实现的功能及关键参数的选择。

三、代码设计与实现头文件：shuzi.h#ifndef SHUZI_H#define SHUZI_Hclass shuzi{public:void liangh();void dnm(double x,double y,double z);void pcmbm();void pcmym();void crcbm();void crcjm();void jdmbh();void jdfbh();void jym();private:double T[1000],gycy[1000],cyz[1000];double pcmy[2000];int crcb[1000][14],crcj[1000][8],pcm[1000][8];};#endif功能函数：math.cpp#include<iostream>#include<fstream>#include<cmath>#include<string>#include"shuzi.h"using namespace std;#define pi 3.1415926int i;void shuzi::liangh(){double t=0.000125;int i;for(i=0;i<1000;i++)T[i]=i*t;}void shuzi::pcmbm(){ofstream f("pcmbm.txt");int j,k,flag=1;double a;for(i=0;i<1000;i++){cyz[i]=2*sin(2*pi*300*T[i])+sin(2*pi*3400*T[i]);a=cyz[i]/3;gycy[i]=a*2048;pcm[i][0]=1;else{pcm[i][0]=0;gycy[i]=gycy[i]*(-1);}if(gycy[i]>=0&&gycy[i]<16){pcm[i][1]=0;pcm[i][2]=0;pcm[i][3]=0;dnm(gycy[i],0,1);}else if(gycy[i]>=16&&gycy[i]<32) {pcm[i][1]=0;pcm[i][2]=0;pcm[i][3]=1;dnm(gycy[i],16,1);}else if(gycy[i]>=32&&gycy[i]<64) {pcm[i][1]=0;pcm[i][2]=1;pcm[i][3]=0;dnm(gycy[i],32,2);}else if(gycy[i]>=64&&gycy[i]<128) {pcm[i][1]=0;pcm[i][2]=1;pcm[i][3]=1;dnm(gycy[i],64,4);}else if(gycy[i]>=128&&gycy[i]<256) {pcm[i][1]=1;pcm[i][2]=0;pcm[i][3]=0;dnm(gycy[i],128,8);}else if(gycy[i]>=256&&gycy[i]<512) {pcm[i][1]=1;pcm[i][3]=1;dnm(gycy[i],256,16);}else if(gycy[i]>=512&&gycy[i]<1024){pcm[i][1]=1;pcm[i][2]=1;pcm[i][3]=0;dnm(gycy[i],512,32);}else if(gycy[i]>=1024&&gycy[i]<2048){pcm[i][1]=1;pcm[i][2]=1;pcm[i][3]=1;dnm(gycy[i],1024,64);}}for(j=0;j<1000;j++){for(k=0;k<8;k++)f<<pcm[j][k];flag++;f<<' ';if(flag==18){f<<'\n';flag=1;}}f.close();}void shuzi::dnm(double x,double y,double z){int a;a=(x-y)/z;switch(a){case 0:pcm[i][4]=0;pcm[i][5]=0;pcm[i][6]=0;pcm[i][7]=0;break;case 1:pcm[i][4]=0;pcm[i][5]=0;pcm[i][6]=0;pcm[i][7]=1;break;case 2:pcm[i][4]=0;pcm[i][5]=0;pcm[i][6]=1;pcm[i][7]=0;break;case 3:pcm[i][4]=0;pcm[i][5]=0;pcm[i][6]=1;pcm[i][7]=1;break;case 4:pcm[i][4]=0;pcm[i][5]=1;pcm[i][6]=0;pcm[i][7]=0;break;case 5:pcm[i][4]=0;pcm[i][5]=1;pcm[i][6]=0;pcm[i][7]=1;break;case 6:pcm[i][4]=0;pcm[i][5]=1;pcm[i][6]=1;pcm[i][7]=0;break;case 7:pcm[i][4]=0;pcm[i][5]=1;pcm[i][6]=1;pcm[i][7]=1;break;case 8:pcm[i][4]=1;pcm[i][5]=0;pcm[i][6]=0;pcm[i][7]=0;break;case 9:pcm[i][4]=1;pcm[i][5]=0;pcm[i][6]=0;pcm[i][7]=1;break;case 10:pcm[i][4]=1;pcm[i][5]=0;pcm[i][6]=1;pcm[i][7]=0;break;case 11:pcm[i][4]=1;pcm[i][5]=0;pcm[i][6]=1;pcm[i][7]=1;break;case 12:pcm[i][4]=1;pcm[i][5]=1;pcm[i][6]=0;pcm[i][7]=0;break;case 13:pcm[i][4]=1;pcm[i][5]=1;pcm[i][6]=0;pcm[i][7]=1;break;case 14:pcm[i][4]=1;pcm[i][5]=1;pcm[i][6]=1;pcm[i][7]=0;break;case 15:pcm[i][4]=1;pcm[i][5]=1;pcm[i][6]=1;pcm[i][7]=1;break;default:cout<<"error!";}}void shuzi::pcmym(){ofstream f("pcmym.txt");int j,k,m,o=1;double p,flag,s,n;for(j=0;j<1000;j++){if(pcm[j][0]==0)flag=-1;else flag=1;m=pcm[j][1]*4+pcm[j][2]*2+pcm[j][3];n=pcm[j][4]*8+pcm[j][5]*4+pcm[j][6]*2+pcm[j][7];switch(m){case 0:s=0;p=1;break;case 1:s=16;p=1;break;case 2:s=32;p=2;break;case 3:s=64;p=4;break;case 4:s=128;p=8;break;case 5:s=256;p=16;break;case 6:s=512;p=32;break;case 7:s=1024;p=64;break;default:cout<<"error!";}pcmy[j]=(flag*(s+n*p+0.5*p))/2048*3;}for(j=0;j<1000;j++){f<<pcmy[j]<<' ';o++;if(o==18){f<<'\n';o=1;}}f.close();}void shuzi::crcbm(){ofstream f("crcbm.txt");int p,j,k,m1,m2,n,s1,s2,flag=1;int e[2000][7],l[2000][7];n=11;for(j=0;j<1000;j++){k=0;while(k<8){if(k<4){e[2*j][k]=pcm[j][k];l[2*j][k]=pcm[j][k];}else {e[2*j+1][k-4]=pcm[j][k];l[2*j+1][k-4]=pcm[j][k];}k++;}e[2*j][4]=0;e[2*j][5]=0;e[2*j][6]=0;e[2*j+1][4]=0;e[2*j+1][5]=0;e[2*j+1][6]=0;}for(j=0;j<2000;j++){for(p=0;p<4;p++)if(e[j][p]==1){e[j][p+2]=1-e[j][p+2];e[j][p+3]=1-e[j][p+3];}l[j][4]=e[j][4];l[j][5]=e[j][5];l[j][6]=e[j][6];}for(j=0;j<2000;j++)for(k=0;k<7;k++){if(j%2==0)crcb[j/2][k]=l[j][k];else crcb[j/2][k+7]=l[j][k];}for(j=0;j<1000;j++){for(k=0;k<14;k++)f<<crcb[j][k];flag++;f<<' ';if(flag==18){f<<'\n';flag=1;}}f.close();}void shuzi::crcjm(){ofstream f("crcjm.txt");int j,k,sum1,sum2,sum,flag=1;for(j=0;j<1000;j++){k=7;sum=crcb[j][0]*8+crcb[j][1]*4+crcb[j][2]*2+crcb[j][3];sum=sum*16+crcb[j][7]*8+crcb[j][8]*4+crcb[j][9]*2+crcb[j][10];while(k>=0){crcj[j][k]=sum%2;sum=sum/2;k--;}}for(j=0;j<1000;j++){for(k=0;k<8;k++)f<<crcj[j][k];flag++;f<<' ';if(flag==18){f<<'\n';flag=1;}}f.close();}void shuzi::jdmbh() //参考码是01{ofstream f("cfsxm.txt");int j,k,flag=1;string a,b,c;a="01";b="10";for(j=0;j<1000;j++){f<<' ';for(k=0;k<14;k++){if(k==0)if(crcb[j][k]==0){f<<a;c=a;}else {f<<b;c=b;}else if(crcb[j][k]==0&&c==a){f<<a;c=a;}else if(crcb[j][k]==0&&c==b){f<<b;c=b;}else if(crcb[j][k]==1&&c==a){f<<b;c=b;}else if(crcb[j][k]==1&&c==b){f<<a;c=a;}}flag++;if(flag==7){f<<'\n';flag=1;}}f.close();}void shuzi::jdfbh(){ifstream f("cfsxm.txt");ofstream f1("cffbh.txt");int j,k,b,flag1=0,flag2=0;char a[2];for(k=0;k<14000;k++){flag1++;flag2++;for(j=0;j<2;j++)f>>a[j];if(k%14==0&&a[0]=='1'){f1<<'1';b=1;cout<<1;}else if(k%14==0&&a[0]=='0'){f1<<'0';b=0;}else if(a[0]=='0'&&b==0){f1<<'0';b=0;}else if(a[0]=='1'&&b==1){f1<<'0';b=1;}else if(a[0]=='0'&&b==1){f1<<'1';b=0;}else if(a[0]=='1'&&b==0){f1<<'1';b=1;}if(flag1==14){f1<<' ';flag1=0;}if(flag2==238){f1<<'\n';flag2=0;}}f.close();f1.close();}主函数：main()#include<iostream>#include"shuzi.h"using namespace std;void main(){shuzi s;s.liangh();s.pcmbm();s.pcmym();s.crcbm();s.crcjm();s.jdmbh();s.jdfbh();}四、实验结果Pcm编码结果：10000000 11100011 10110000 11111000 11011100 11111011 11110001 11110011 11111010 11100001 11111001 10111010 11101001 10000000 01011010 00100011 01110110 01010110 01111011 01101111 01110101 01111001 01100100 01111010 01000011 01101111 00000010 11001010 10010100 11110100 11010001 11111011 11101100 11110110 11111000 11101000 11111011 11001010 11110010 10001000 00000000 00001000 01110010 01001010 01111011 01101000 01111000 01110110 01101100 01111011 01010001 01110100 00010100 01001010 10000010 11101111 11000011 11111010 11100100 11111001 11110101 11101111 11111011 11010110 11110110 10100011 11011010 00000000 01101001 00111010 01111001 01100001 01111010 01110011 01110001 01111011 01011100 01111000 00110000 01100011 00000000 11100011 10110000 11111000 11011100 11111011 11110001 11110011 11111010 11100001 11111001 10111010 11101001 10000000 01011010 00100011 01110110 01010110 01111011 01101111 01110101 01111001 01100100 01111010 01000011 01101111 00000010 11001010 10010100 11110100 1101000111111011 11101100 11110110 11111000 11101000 11111011 11001010 11110010Crc编码结果：10001010000000 11101000011101 10110000000000 11111111000101 11010011100010 11111111011000 11111110001011 11111110011101 11111111010011 11101000001011 11111111001110 10110001010011 11101001001110 10001010000000 01011001010011 00101100011101 0111010011000101011000110001 01110101011000 01100011111111 01110100101100 01110101001110 01100010100111 01110101010011 01001110011101 01100011111111 00000000010110 11000101010011 10011100100111 11111110100111 11010010001011 11111111011000 11101001100010 1111111011000111111111000101 11101001000101 11111111011000 11000101010011 11111110010110 10001011000101 00000000000000 00000001000101 01110100010110 01001111010011 01110101011000 01100011000101 01110101000101 01110100110001 01100011100010 01110101011000 0101100000101101110100100111 00010110100111 01001111010011 10001010010110 11101001111111 11000100011101 11111111010011 11101000100111 11111111001110 11111110101100 11101001111111 11111111011000 11010010110001 11111110110001 10100110011101 11010011010011 00000000000000差分双向码:1010101001011010101010101010 1001101001010101011001101001 1010011010101010101010101010 1001100110011001010101101001 1001011010100110010101011010 10011001100110010110010101011001100110011010101001011001 1001100110011010100110010110 1001100110011001011010100110 1001101001010101010110100110 1001100110011001010110011010 1010011010101001011010100110 1001101001010110101001100101 1010101001011010101010101010 0110100110101001011010100110 0101101001101010100110010110 0110011010010101100101010110 0110100110101010011010101001 0110011010010110100110101010 0110010101011001100110011001 0110011010010101101001101010 0110011010010110101001100101 0110010101011010010101100110 0110011010010110100101011001基带码型反变换结果：10001010000000 11101000011101 10110000000000 11111111000101 11010011100010 11111111011000 11111110001011 11111110011101 11111111010011 11101000001011 11111111001110 10110001010011 11101001001110 10001010000000 01011001010011 00101100011101 0111010011000101011000110001 01110101011000 01100011111111 01110100101100 01110101001110 01100010100111 01110101010011 01001110011101 01100011111111 00000000010110 11000101010011 10011100100111 11111110100111 11010010001011 11111111011000 11101001100010 1111111011000111111111000101 11101001000101 11111111011000 11000101010011 11111110010110 10001011000101 00000000000000 00000001000101 01110100010110 01001111010011 01110101011000 01100011000101 01110101000101 01110100110001 01100011100010 01110101011000 0101100000101101110100100111 00010110100111 01001111010011 10001010010110 11101001111111 11000100011101 11111111010011 11101000100111 11111111001110 11111110101100 11101001111111 11111111011000 11010010110001 11111110110001 10100110011101 11010011010011 0000000000000001100011001110 00111011010011 01110101001110 01100010001011 01110101010011 01110100011101 01110100001011 01110101011000 01011001100010 01110101000101 00111010000000 01100010011101 00000000000000 11101000011101 10110000000000 11111111000101 11010011100010Crc解码结果：10000000 11100011 10110000 11111000 11011100 11111011 11110001 11110011 11111010 11100001 11111001 10111010 11101001 10000000 01011010 00100011 0111011001010110 01111011 01101111 01110101 01111001 01100100 01111010 01000011 01101111 00000010 11001010 10010100 11110100 11010001 11111011 11101100 1111011011111000 11101000 11111011 11001010 11110010 10001000 00000000 00001000 01110010 01001010 01111011 01101000 01111000 01110110 01101100 01111011 0101000101110100 00010100 01001010 10000010 11101111 11000011 11111010 11100100 11111001 11110101 11101111 11111011 11010110 11110110 10100011 11011010 0000000001101001 00111010 01111001 01100001 01111010 01110011 01110001 01111011 01011100 01111000 00110000 01100011 00000000 11100011 10110000 11111000 11011100Pcm译码结果：0.000732422 0.914063 0.0966797 2.29688 0.667969 2.57813 1.64063 1.82813 2.48438 0.820313 2.39063 0.155273 1.19531 0.000732422 -0.621094 -0.0571289 -2.10938-0.527344 -2.57813 -1.47656 -2.01563 -2.39063 -0.960938 -2.48438 -0.228516 -1.47656 -0.00366211 0.310547 0.0300293 1.92188 0.410156 2.57813 1.33594 2.109382.29688 1.14844 2.57813 0.310547 1.73438 0.0124512 -0.000732422 -0.0124512 -1.73438 -0.310547 -2.57813 -1.14844 -2.29688 -2.10938 -1.33594 -2.57813 -0.410156-1.92188 -0.0300293 -0.310547 0.00366211 1.47656 0.228516 2.48438 0.960938 2.39063 2.015631.476562.57813 0.527344 2.10938 0.0571289 0.621094 -0.000732422-1.19531 -0.155273 -2.39063 -0.820313 -2.48438 -1.82813 -1.64063 -2.57813 -0.667969 -2.29688-0.0966797 -0.914063 -0.000732422 0.914063 0.0966797 2.29688 0.667969五、收获与体会通过此次试验，在不断查阅相关知识后，我对pcm编译码，crc编解码以及差分双相码的变换与反变换过程更加熟悉，真正理解了他们各自编解码的原理。

实验七信道编码仿真实现一、实验目的理解信道编码的思想，掌握信道编码的编程实现原理及技术。

二、实验原理信道编码的基本思想信道编码的对象：是信源编码器输出的信息序列m。

通常是二元符号1、0组成的序列。

信道编码的基本思想按一定规则给数字序列m增加一些多余的码元，使不具有规律性的信息序列 m 变换为具有某种规律性的数码序列 C；码序列中的信息序列码元与多余码元之间是相关的；信道译码器利用这种预知的编码规则译码。

检验接收到的数字序列 R 是否符合既定的规则，从而发现 R 中是否有错，或者纠正其中的差错；编码采用汉明码汉明码的编码原理汉明码编码Hamming码中文称作汉明码。

汉明码是由汉明于1950年提出的，具有纠正一位错误能力的线性分组码它的突出特点是：编译码电路简单，易于硬件实现；用软件实现编译码算法时，软件效率高；而且性能比较好.汉明码的定义：若一致监督矩阵H 的列是由不全为0且互不相同的所有二进制m(m≥2的正整数)重组成，则由此H矩阵得到的线性分组码称为[2m-1,2m-1-m，3]汉明码。

1.3.2 汉明码的构造特点：1)．绐定一个m，我们由二进制m 重组成线性分组码的监督矩阵H，由二进制m重来标定一个发生错误的位置。

由此可知，二进制m 重共有2 种位组合，去掉一个全为0的位组合，则余下共有2m-1种位组合。

故汉明码的最大码长n=2m-1。

2)．由上面分析，我们可以知道：m 即是汉明码监督位的位数。

故一个汉明码中，信息位的位数k=n—m=2m-1-m3)．汉明码的距离为3，因此可以纠正1位错误，检出2位错误。

汉明码编码的主要算法：汉明码的编码就是如何根据信息位数k，求出纠正一个错误的监督矩阵H，然后根据H求出信息位所对应的码字。

构造汉明码监督矩阵H的方法很多，这里仅介绍一种。

1)根据已知的信息位数k，从汉明不等式中求出校验位数m=n-k；2)在每个码字C：(C1，C2，⋯，C2m -1)中，用c02，c12，c n-12作为监督位，剩下的位作为信息位；3)用二进制数字表示2m-1列，得到2m-1列和m行监督矩阵H；4)用3步的H形成HC T =0，从而得出m个监督方程；5)将已知的信息代入方程组，然后求出满足上述方程组的监督位c (i=0，1，⋯，m一1)。