奥数4

二年级奥数第4讲:积的个位数是多少一个数的个位数，就是指这个数的个位数字。

几个数积的个位数，等于这几个数个位数积的个位数。

如：197 与338 的积的个位数，等于这两个数的个位数7 和8 的积的个位数，即56 的个位数6一个数的个位数，就是指这个数的个位数字。

几个数积的个位数，等于这几个数个位数积的个位数。

如：197与338的积的个位数，等于这两个数的个位数7和8的积的个位数，即56的个位数6。

http://www. /一个数乘几次积的个位数，等于它的个位数的自乘几次后积的个位数。

如：92×92×92×92的积的个位数就等于2×2×2×2的个位数，即16的个位数6.统计积的末尾有多少个0，可以这样考虑：因为2×5=10，积能分解出多少个因数2和5，一一对应后产生了10，这样积的尾数就产生了连续的0，另外要注意积末尾0的个数等于因数2的个数与因数5的个数中较少的那个。

例1、3×3，3×3×3，3×3×3×3，3×3×3×3×3，3×3×3×3×3×3积的个位数分别是多少？解认真计算，仔细观察后，可以发现3的个位数变化规律是四个数一个周期：3，9，7,1.所以3×3，3×3×3，3×3×3×3，3×3×3×3×3，3×3×3×3×3×3积的个位数分别是9,7,1,3,9.随堂练习1：3×3×3 ……×3×3的积的个位数是几？25个3例2、9×9×9……×9×9的积的个位数是几？19个9解9的个位数变化规律是两个数一个周期：9,1. 19÷2=8……1，所以积的个位数是9随堂练习2：4×4×4……×4×4×4×4的积的个位数是几？44个4例3、18×28×38×……×208—17×27×37×……×317，计算结果的个位数是几？解8的个位数变化规律是四个数一个周期：8,4,2,6.20÷4=5，所以18×28×38×……×208的积的个位数是6.7的个位数变化规律是四个数一个周期：7,9,3,1.31÷4=7……3，所以17×27×37×……×317的积的个位数是3.6-3=3. 18×28×38×……×208—17×27×37×……×317的计算结果的个位数是3随堂练习3：12×22×32×……×402—16×26×36×……×462，计算结果的个位数是多少？例4、1×2+2×3+3×4+4×5+5×6+6×7+7×8+8×9，计算结果的个位数是几？解将每个乘法算式积的个位数相加：2+6+2+0+0+2+6+2=20，计算结果的个位数是0.随堂练习4：11×12+12×13+13×14+14×15+15×16+16×17+17×18+18×19，计算结果的个位数是几？例5、有五个连续自然数，它们连乘积的个位数是几？解五个连续自然数中一定包含1个5，也一定有一个2的倍数，所以五个连续自然数的乘积的个位数一定是0.随堂练习5 四个连续自然数的积是3021，求这四个数。

稍复杂的和差. 和倍. 差倍问题例1 把长224cm的铁丝围成一个长方形, 使长比宽多18厘米, 这个长方形的长和宽各是多少？例2甲组的图书是乙组的3倍。

若乙组给不！甲组6本, 则甲组的图书是乙组的5倍, 原来我甲组有图书多少本？例3幼儿园买来苹果的个数是梨的2倍, 大班的同学每7人我一组, 每组领3个梨和4个苹果, 结果梨正好分完, 苹果还剩下16个, 大班共有多少个同学？例4一个书架有三层, 共有图书180本, 我第一层的我不本数是第二层的2倍, 第三层的本数比第一层少20本, 三层你各有书多少本?例5养鸡场新买来100只小鸡, 其中母鸡只数的4倍比我公鸡只数的3倍多120只, 买来母鸡，公鸡各多少只？1甲. 乙两筐苹果共重90千克, 从甲筐取出8千克放入乙筐, 甲筐比乙筐还多4千克, 甲. 乙两筐各不！有苹果多少千克?2 张师傅已经生产的零件个数是学徒工小王的6倍, 如果两人各自再生产20个, 那么张师傅生产的零件个数是小王的4倍. 原来两人各生产零件多少个？3 高年级同学植树你的, 已知杨树的棵数正好是杉树的2倍, 高年级同学每7人一组, 你如果每组分到杉树苗6棵, 杨树苗8棵, 那么, 杉树正好分完, 杨树还剩20棵, 高年级不！植数的有多少人？4 有1800千克的货物, 分装在甲.乙.丙三辆车上, 已知甲车装的千克树正好是乙车的2倍, 乙车比丙车多装200千克, 甲.乙.丙三辆车各装货物多少千克?5 实验小学体育室有排球和篮球30个, 篮球个数的3倍比排球的2倍少我10个, 体育室有排球和篮球各多少个？1一块长方形菜地周长是240米, 长比宽多80米, 这块菜地的面积是多少平方米？2幼儿园买来的苹果的你个数, 是梨的3倍, 吃掉10个不！梨和6个苹果后不！剩下的苹果正好是梨的5倍, 原来买来梨和苹果各多少个?3甲仓库的我存粮是乙仓库的2倍, 甲仓库每天运出粮食40吨, 不！乙仓库每天运你岀30吨, 如干天后, 乙仓库的粮食全部运完，而甲仓库还有80吨, 甲.乙两粮库不！原来各有粮食是多少吨？4某养鸡场养鸡.鸭.鹅共1462只, 不！鸡的只数比鸭的只数的4倍多132只鹅的只数比鸭的2倍少70只, 这个养殖场养的鸡鸭鹅各有不！多少只？5胜利小学五年级共有学生200 t人, 其中男生人数的3倍比女生的2倍多50人, 五年级女生比男生多多少人1三个物体平均重31千克, 甲比乙丙两个物体重量之和轻1千克, 乙比丙的2倍重2千克, 甲乙丙三物各重多少千克？2 A站有公共汽车26辆,B站有公共汽车30辆, 每小时由A站开往B站12辆, B站开往A站8辆, 都是经过1小时到站, 几小时后哼哼B站的公共汽车辆数是A站的3倍?。

华杯赛计数专题：4包含与排除基础知识：1.包含与排除的思想，是为了解决计数分类的过程中，出现重复计数的情况.2.基本的想法：减去重复计算的，多算了几次，就减几次，常用工具文氏图.3.两个对象及三个对象的容斥原理，利用文氏图帮助理解.4.容斥原理中的最值问题，可以利用线段图.引子：从7本不同的数学书和8本不同的语文书中，选出6本书，不能全是同一种的书，那么有多少种不同的选法？用前面学的知识能解决吗？还有别的方法吗？总结：当正面计数比较繁琐、困难时，可以从反面考虑，即从总的数量减去不符合要求的数量.例1.学生要从八门课中选学三门，如果数学课与钢琴课时间冲突，不能同时学，那么共有几种选课的方法？【答案】50（种）【解答】所有的选课方法一共有种，数学课和钢琴课都选学的方法有种，其中代表数学课和钢琴课都选学，其中代表从剩余的课程中再选学1门.所以符合题意的选课方法一共有种.例2.从4台不同型号的TCL电视机和5台不同型号的Haier电视机中任意取出3台,其中至少要有TCL与Haier电视机各1台，不同的取法共有多少种?【答案】70（种）【解答】9台不同的电视，随意选取3台，一共有种方法.其中包括只选取Haier的方法一共种，还包括只选取TCL的方法一共种.所以符合题意的方法一共有84-10-4=70种.例3.7个同学站成一排，要求其中的甲不排头，乙不排尾，有多少种排法?思考：答案是吗？为什么【答案】3720（种）【解答】7个同学随意排列，共有种排法，若甲排在头，则剩下的6个同学全排列，一共有种排法，同理，若乙排在尾，一共有种排法，若同时满足甲在排头、乙在排尾，共有种排法，根据容斥原理，符合题意的排法共有种.例4.板报组有10名同学，每个人至少擅长绘画或写文章中的一种，已知其中7个人擅长绘画，5个人擅长写文章，要从中选出两个人担任组长，要求其中既有擅长绘画的也有擅长写文章的，那么有多少种选组长的方法？如果要从中选出两名同学去参赛，分别参加绘画比赛和作文比赛，那么有多少种参赛方法？【答案】32（种）【解答】因为10名同学中7个人擅长绘画，5个人擅长写文章，所以既擅长绘画又擅长写文章的有5＋7－10=2个人，所以只擅长绘画的有5个人，只擅长写文章的有3个人, 选组长可以分为三类：第一类：先从擅长绘画的人中选1个，再从剩下的人中选1个，共有5×5=25种选法；第二类：从既擅长绘画又擅长写文章的2个人选1个，再从擅长写文章的3个人中选1个，共有2×3=6种选法；第三类：选2个既擅长绘画又擅长写文章的，共有1种选法；综合共有25＋6＋+1=32种.例5.一次考试共有A、B、C三道题，一共有100个人参加了这次考试.其中，答对A 题的有50人，答对B题的有60人，答对C题的有20人.已知答对C题的人在A、B两道题中至少还答对了一道题，且只答对A题的有24人，只答对A题和B题的有10人，还有10个人A、B均未答对.那么有________个人只答对了B题.【答案】36（人）【解答】因为100人中有10人A、B两题均未答对，所以有90人至少答对A，B中的一道.又因为50人答对A题，60人答对B题，所以至少答对A、B两题的有50＋60－90=20人.即答对AB两题或答对ABC三题的人合起来有20个.而只答对AB两题的人有10个，所以ABC三个题全答对的人有20－10=10个.由于有24人只答对A题，所以还有50－24=26人答对A题和至少另外一道题.这26人答对的题目只有3种可能：AB、AC和ABC.由上面的结论知只答对AC两题的应该有26－20=6个人.由于答对C的人在A、B两题中至少答对一道，所以答对C的20个人答对的题目也只有三种可能：AC、BC和ABC.那么只答对BC两题的有20－6－10=4人.现在已知答对AB两题的有10人，答对BC两题的有4人，答对ABC的有10人，而至少答对B一个题目的一共有60人，所以只答对B一个题的有60－10－4－10=36人.例6.某班级要从4名男生、2名女生中选派4人参加某次社区服务，如果要求至少有1名女生，那么不同的选派方案有种.【答案】14（种）【解答】6个人中选4个，共有种选法，选4个男生，共有种选法，所以符合题意的选法共有种.例7.从6双手套中取出4只，则至少取出一双的方法有种.【答案】255（只）【解答】有6双手套，即12只，从12只中任选4只，共有种，若选出的4只均不同双，则分步进行，第一步，从6双中选出4双，共有种；第二步，在选出的4双中分别选出左手或右手，共有，根据乘法原理：若选出的4只均不同双的选法共有种，所以符合题意的选法共有种.例8.在4×4的方格表里写上两个A和两个B（每个方格里至多写一个字母），那么相同字母既不同行也不同列的写法有多少种？【答案】3960（种）【解答】写入两个A既不同行也不同列的写法共有种，同理写入两个B既不同行也不同列的写法共有种，依次写入A、B，共有种写法.若A、B写入同一个方格中，可以分为两类考虑，第一类：A、B有两个格子均重合，共有72种写法；第二类，A、B中有一个格子重合，共有种写法；所以若A、B写入同一个方格中共有种写法，综上符合题意的共有种写法。

第四讲巧填符号三年级奥数知识是从刻苦劳动中得来的，任何成就都是刻苦劳动的结晶。

——宋庆龄知识纵横根据题目给定的条件和要求，填运算符号或括号，使等式成立，这是一种很有趣的游戏，这种游戏需要动脑筋找规律，讲究方法，一旦掌握方法，就有取得成功的把握。

填运算符号问题，通常采用尝试探索法，主要尝试方法有两种：１.如果题目的数字比较简单，可以从等式的结果入手，推想那些算式能得到这个结果，然后拼凑出所求的式子。

２.如果题目中的数字比较多，结果也较大，可以考虑先用几个数字凑出比较接近于等式结果的数，然后再进行调整，使等式成立。

通常情况下，要根据题目的特点，选择方法，有时将以上两种方法组合起来使用，更有助于问题的解决。

例题求解【例１】在下面４个４之间填上＋、－、×、÷或括号，使等式成立４４４４＝８【例２】在下面各题中添上＋、－、×、÷、（），使等式成立。

１２３４５＝１０【例３】拿出都是８的四张牌，添上＋、－、×、÷或（），使等式成立，你能试一试吗？８８８８＝０８８８８＝１８８８８＝２８８８８＝３【例４】在下面算式合适的地方添上＋、－、×，使等式成立。

１２３４５６７８＝１【例５】在下面式子适当的地方添上＋、－号，使等式成立。

９８７６５４３２１＝２１【例６】在下面１２个５之间添上＋、－、×、÷，使下面等式成立。

５５５５５５５５５５５５＝１０００学力训练１.你能在下面数中填上＋、－、×、÷，使结果等于已知数吗？（１）５５５５＝１０（２）９９９９＝１８２.在下面数中填上＋、－、×、÷或（），使等式成立。

（１）３３３３３＝９（２）４４４４４＝８３.在下面几个数中填上＋、－、×、÷或（），使等式成立。

（１）２３５６＝６（２）２３５６＝６４.你能在下面各数中添上运算符号，使等式成立吗？４１２５＝１０５.巧填运算符号，使等式成立。

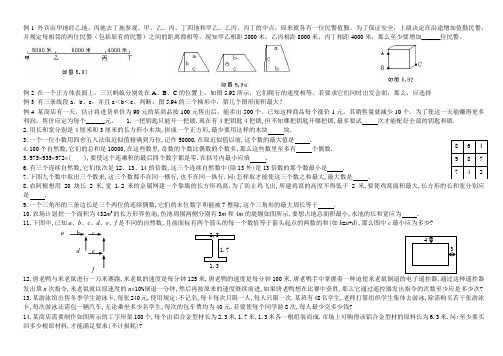
例1 外宾由甲地经乙地、丙地去丁地参观。

甲、乙、丙、丁四地和甲乙、乙丙、丙丁的中点，原来就各有一位民警值勤。

为了保证安全，上级决定在沿途增加值勤民警，并规定每相邻的两位民警（包括原有的民警）之间的距离都相等。

现知甲乙相距5000米，乙丙相距8000米，丙丁相距4000米，那么至少要增加______位民警。

例2 在一个正方体表面上，三只蚂蚁分别处在A 、B 、C 的位置上，如图5.92所示，它们爬行的速度相等。

若要求它们同时出发会面，那么，应选择例3 有三条线段a 、b 、c ，并且a ＜b ＜c 。

判断：图5.94的三个梯形中，第几个图形面积最大？例4 某商店有一天，估计将进货单价为90元的某商品按100元售出后，能卖出500个。

已知这种商品每个涨价1元，其销售量就减少10个。

为了使这一天能赚得更多利润，售价应定为每个______元。

1.一把钥匙只能开一把锁.现在有4把钥匙4把锁,但不知哪把钥匙开哪把锁,最多要试 次才能配好全部的钥匙和锁.2.用长和宽分别是4厘米和3厘米的长方形小木块,拼成一个正方形,最少要用这样的木块 块.3.一个一位小数用四舍五入法取近似值精确到万位,记作50000.在取近似值以前,这个数的最大值是 .4.100个自然数,它们的总和是10000,在这些数里,奇数的个数比偶数的个数多,那么这些数里至多有 个偶数.5.975⨯935⨯972⨯( ),要使这个连乘积的最后四个数字都是零.在括号内最小应填 .6.有三个连续自然数,它们依次是12、13、14的倍数,这三个连续自然数中(除13外)是13倍数的那个数最小是 .7.下图九个数中取出三个数来,这三个数都不在同一横行,也不在同一纵行.问:怎样取才能使这三个数之和最大,最大数是 .8.农阿根想用20块长2米,宽1.2米的金属网建一个靠墙的长方形鸡窝.为了防止鸡飞出,所建鸡窝的高度不得低于2米,要使鸡窝面积最大,长方形的长和宽分别应是 .9.一个三角形的三条边长是三个两位的连续偶数,它们的末位数字和能被7整除,这个三角形的最大周长等于 .10.农场计划挖一个面积为432m 2的长方形养鱼池,鱼池周围两侧分别有3m 和4m 的堤堰如图所示,要想占地总面积最小,水池的长和宽应为 .11.下图中,已知a 、b 、c 、d 、e 、f 是不同的自然数,且前面标有两个箭头的每一个数恰等于箭头起点的两数的和(如b =a +d ),那么图中c 最小应为多少?ab cd ef12.唐老鸭与米老鼠进行一万米赛跑,米老鼠的速度是每分钟125米,唐老鸭的速度是每分钟100米.唐老鸭手中掌握着一种迫使米老鼠倒退的电子遥控器,通过这种遥控器发出第n 次指令,米老鼠就以原速度的n ⨯10%倒退一分钟,然后再按原来的速度继续前进,如果唐老鸭想在比赛中获胜,那么它通过遥控器发出指令的次数至少应是多少次?13.某游泳馆出售冬季学生游泳卡,每张240元,使用规定:不记名,每卡每次只限一人,每人只限一次.某班有48名学生,老师打算组织学生集体去游泳,除需购买若干张游泳卡,每次游泳还需包一辆汽车,无论乘坐多少名学生,每次的包车费均为40元.若要使每个同学游8次,每人最少交多少钱?14.某商店需要制作如图所示的工字形架100个,每个由铝合金型材长为2.3米,1.7米,1.3米各一根组装而成.市场上可购得该铝合金型材的原料长为6.3米.问:至少要买回多少根原材料,才能满足要求(不计损耗)?1.3例1 某工厂每天要生产甲、乙两种产品，按工艺规定，每件甲产品需分别在A、B、C、D四台不同设备上加工2、1、4、0小时；每件乙产品需分别在A、B、C、D四台不同设备上加工2、2、0、4小时。

鸡兔同笼鸡兔同笼的基本问题是：已知鸡、兔总头数和总脚数，求鸡、兔各有多少只? （1）解决鸡兔同笼问题的方法是假设法先假设笼子里装的全是兔，根据鸡兔的总数就可以算出在假设下共有几只脚，把这样得到的脚数与题中给出的脚数相比较，看看差多少，每差2只脚就说明有1只鸡，将所差的脚数除以2，就可以算出共有多少只鸡。

假设兔求出来的是鸡。

（2）解决鸡兔同笼问题的基本关系式是：每次相差数×份数=总的相差数鸡数=(兔脚数×总头数-总脚数)÷(兔脚数-鸡脚数)鸡兔同笼问题的变型已知鸡、兔脚数之差和总头数，求鸡兔各有多少只？已知鸡、兔头数之差和总脚数，求鸡兔各有多少只？已知鸡、兔头数之差和脚数之差，求鸡兔各有多少只？鸡兔的只数互换，求，求鸡兔各有多少只？例1鸡、兔共36只，它们共有脚100只，鸡、兔各是多少只？假设笼子里的全是兔子，则一共有4×36=144（只）脚，比实际多了144-100=44（只）脚。

把鸡的脚当兔子的脚计算时，1只鸡就多算了2只脚，所以鸡有44÷2=22（只）鸡：(4×36-100)÷(4-2)=22(只)兔：36-22=14（只）【举一反三】1、鸡兔同笼，共有头30个，足86只，求鸡兔各有多少只？2、鸡兔同笼，鸡兔共35个头，94条腿，问鸡兔各多少只？3、在一个停车场上，停放的车辆(汽车和三轮摩托车)数恰好是24辆。

其中每辆汽车有四个轮子，每辆摩托车有三个轮子，这些车共有86个轮子。

那么，三轮摩托车有多少辆?例2小学举行一次数学竞赛，共15道题，每做对一题得8分，每做错一题扣4分，小明共得了72分。

他做对了几道题？假设全做对，则一共得8×15=120（分），比实际多了120-72=48分，把错题当对的题计算时，1道错题就多算了8+4=12分，所以错题有48÷12=4（道）错题：（8×15-72）÷（8+4）=4（道）做对：15-4=11（道）【举一反三】1、一次智力测验有10道题，每答对一道得3分，每答错一道扣2分，小红答完了10道题，只得了20分。

四、工程问题（1）年级 班 姓名 得分 一、填空题1.一项工程,甲、乙两队合作20天完成,乙丙两队合作60天完成,丙丁两队合作30完成,甲丁合作 天完成?2.甲乙两队合作一项工程,计划在24天内完成.如果甲队做6天,乙队做4天,只能做完全工程的20%,两队单独做完全工程各需要 天.3.一条公路,甲队独修24天完成,乙队独修30天完成.甲乙两队合修若干天后,乙队停工休息,甲队继续修了6天完成,乙队修了 天.4.某市举办菊展,新建一个喷水池.单开甲管1小时可将喷水池注满,单开乙管40分钟可将水注满,两管同时齐开5210分钟后,共注水314吨.喷水池能装水___吨.5.一项工作,两个师傅和三个徒弟合作需922天完成,如果三个师傅2个徒弟合作需要712天完成,如果一名师傅单独做需 天完成.6.加工一批零件,甲独做需3天完成,乙独做需4天完成,两人同时加工,完成任务时,甲比乙多做24个,这批零件共有 个.7.一项建筑工程,由甲建筑队单独承建要一年半,乙建筑队单独承建要一年零三个月,现在两队合作半年,剩下的由乙队继续完成还要 个月.(假设每月实际工作天数一样)8.甲、乙、丙三人合修一围墙.甲、乙合修6天修好围墙的31,乙、丙合修2天修好余下的41,剩下的三人又合修了5天才完成.共得工资180元,按各人所完成的工作量的多少来合理分配,每人应得 元.9.原计划用24个工人挖一定数量的土方,按计划工作5天后,因为调走6人,于是剩下的工人每天比原定工作量多挖1方土才能如期完成任务,原计划每人每天挖土 方.10.一个水池,底部安有一个常开的排水管,上部安有若干个同样粗细的进水管,当打开4个进水管时,需要5小时才能注满水池,当打开2个进水管时,需要15小时才能注满水池;现在需要在2小时内将水池注满,那么至少要打开 个进水管.二、解答题11.抄一份书稿,甲每天的工作效率等于乙、丙二人每天的工作效率的和;丙每天的工作效率相当于甲、乙二人每天工作效率之和的51;如果三人合抄只需8天就完成了,那么乙一人单独抄需多少天才能完成?12.一项工程,甲独做需10天,乙独做需15天,如果两人合作,甲的工作效率就要降低,只能完成原来的54,乙只能完成原来的109,现在要8天完成这项工程,两人合作天数尽可能少,那么两人要合作多少天?13.一空水池有甲、乙两根进水管和一根排水管.单开甲管需5分钟注满水池,单开乙管需10分钟注满水池,满池水如果单开排水管需6分钟流尽.某次池中没有水,打开甲管若干分钟后,发现排水管未关上,随即关上排水管,同时打开乙管,又过了同样长的时间,水池的1/4注了水.如果继续注满水池,前后一共要花多少时间?14.有一个蓄水池装有9根水管,其中一根为进水管,其余8根为相同的出水管,进水管以均匀的速度不停地向这个蓄水池注水.后来有人想打开出水管,使池内的水全部排光(这时池内已注入一些水).如果把8根出水管全部打开,需3小时把池内的水全部排光;如果仅打开5根出水管,需6小时把池内的水全部排光.问要想在4.5小时内把池内的水全部排光,需同时打开几根出水管?———————————————答 案——————————————————————1. 156********1=÷øöçèæ-+÷(天).2. 乙的工作效率为()()40116244%201=-÷´-, 甲的工作效率为601401241=-. 故甲做60天完成,乙做40天完成.3. 1030124162411=÷øöçèæ+÷÷øöçèæ´-(天).4. 104016015210314=÷øöçèæ+÷÷øöçèæ÷(吨)5. 一个师傅与一个徒弟工作效率之和为:()60112371219221=+÷÷÷÷÷øöççççèæ+, 故师傅的工作效率是101601127121=´-,即一名师傅单独做10天完成.6. 16841311413124=þýüîíìúûùêëé÷øöçèæ+-´÷øöçèæ-÷(个).7. 415161511811=÷úûùêëé´÷øöçèæ+-(月).8. 甲分得的钱为:()3356241311541311311180=+´þýüîíì÷´÷øöçèæ--÷úûùêëé´÷øöçèæ---´(元);丙分得的钱为:()5652631541311311180=+´þýüîíì÷-÷úûùêëé´÷øöçèæ---´(元);乙分得的钱为:180-33-56=91(元).9. 36)624(=÷-(方).10. 进水管一小时进水量为:()()[]15124541521=-÷´-´÷; 排水管一小时排水量为:1515120151=÷÷øöçèæ-´.故只开一进水管、一排水管池中无水,多开进水管数为5.71521=÷,取整为8 个,至少要打开9个进水管.11. 24281511811=úûùêëé÷-÷øöçèæ+÷÷(天).12. 设两人要合作x 天,依题意得:()15078101=+-x x ,故x =5(天).13. 设注满池中41的水需x 分钟,故有23,412615126151==´÷øöçèæ++´÷øöçèæ-x x x .继续注满池中水的43411=-需要251015143=÷øöçèæ+÷(分),共需时间42523=+(分).14. 将每根进水管每小时的进水量看作单位1,则每根出水管每小时的排水量为2)36()3865(=-÷´-´,而池中原有水量为186265=´-´,从而要想在4.5小时内把池中水抽干,需要打开65.4182=÷+(根)出水管.四、工程问题（2）年级 班 姓名 得分一、填空题1.一项工作,甲乙两队合作9天完成,乙丙两队合作12天完成,甲丙两队合作需18天完成,现在三队合作需 天完成.2.某工程先由甲单独做63天,再由乙单独做28天即可完成.如果由甲、乙两人合作,需48天完成.现在甲先单独做42天,然后再由乙来单独完成,那么还需要做 天.3.甲、乙两队合作20天可以完成一项工程.如果两队合作8天后,乙队再独做4天,还剩这项工程的158没有完成.甲、乙两队工作效率之比为: .4.一份稿件,甲单独打字需6小时完成,乙单独打字需10小时完成.现在甲单独打若干小时后,因有事由乙接着打完,共用了7小时,那么甲打字用了 小时.5.有批机器零件,甲单独制作需要218天,比乙单独制作多用了21天,两人合作4天后,剩下210个零件由甲单独去做,自始至终甲共制作了 零件.6.一个水池子,甲、乙两管同时开,5小时灌满,乙、丙两管同时开,4小时灌满,如果乙管先开6小时,还需要甲、丙两管同时开2小时才能注满(这时乙管关闭).那么乙管单独灌满水池需要 小时.7.一个水池,地下水从四壁渗入,每小时渗入该水池的水量是固定的.当这个水池水满时,打开A 管,8小时可将水池排空;打开B 管,10小时可将水池排空;打开C 管,12小时可将水池排空.如果打开A 、B 两管,4小时可将水池排空,那么打开B 、C 两管,将水池排空需要 小时.8.一件工作,如果单独做,甲按规定时间可提前2天完成,乙则要超过规定时间3天才完成.现在,甲乙二人合做2天后,剩下的继续由乙单独做,刚好在规定的日期内完成.若甲乙二人合做,完成这件工作需要 天.9.有一水池,装有甲、乙两个注水管,下面装有丙管放水.池空时,单开甲管5分钟可注满;单开乙管10分钟可注满.水池装满水后,单开丙管15分钟可将水放完.如果在池空时,将甲、乙、丙三管齐开,2分钟后关闭乙管,还要 分钟可以注满水池.10.放满一个水池的水,如果同时开放①、②、③号阀门,7.5小时可以完成;如果同时开放①、③、⑤号阀门,5小时可以完成;如果同时开放①③④号阀门,6小时可以完成;如果同时开放②④⑤号阀门,4小时可以完成.问同时开放这五个阀门, 小时可以放满这个水池.二、解答题11.师徒三人合作承包一项工程,4天能够全部完成.已知师傅单独做所需天数与两个徒弟合作所需天数相等;而师傅与乙徒弟合作所需天数的2倍与甲徒弟单独做完所需的天数相等.那么甲徒弟单独做,完成这项工程需要多少天?乙徒弟单独做,完成这项工程需要多少天?12.甲、乙、丙三人从三月一日开始合作一项工程,甲每天的工作量是乙每天工作量的3倍,乙每天的工作量是丙每天工作量的2倍.三人合作5天完成全工程的31后,甲休3天,乙休2天,丙没有休息,问这项工程是在几月几日完成的?13.一个蓄水池装了一根进水管和三根放水速度一样的出水管.单开一根进水管20分钟可注满空池.单开一根出水管,45分钟可以放完满池水.现有32池的水,如果四管齐开,多少分钟后池水还剩52?14.蓄水池有甲、丙两条进水管,和乙丁两条排水管.要灌满一池水,单开甲管需要3小时,单开丙管需要5小时,要排光一池水,单开乙管需要4小时,单开丁管需要6小时.现在池内有61池水.如果按甲、乙、丙、丁、甲、乙……的顺序,轮流各开一小时,多少时间后水开始溢出水池?———————————————答 案——————————————————————1. 82181121911=úûùêëé÷÷øöçèæ++÷(天).2. 甲乙合做28天,完成任务的1274828=÷, 故甲的工作效率为()84128631271=-÷÷øöçèæ-,乙的工作效率为1121841481=-, 于是乙还需做56112184421=÷÷øöçèæ-(天).3. 乙的工作效率为601482011581=÷÷øöçèæ´--,甲的工作效率为301601201=-,甲乙工作效率之比为1:2601:301=.4. 5.41016171011=÷øöçèæ-÷÷øöçèæ´-(小时).5. 35702102184421218121811210=+´úúúúûùêêêêëé´÷÷÷÷øöççççèæ-+-÷(个).6. 20)46(5141211=þýüîíì-÷úûùêëé÷øöçèæ+´-÷(小时).7. B 管每小时排水量为81421=÷(池)水. 每小时渗水量为4011011081=÷÷øöçèæ-´(池).C 管每小时排水量为1201312124011=÷÷øöçèæ´+(池). 从而B 、C 两管排一池水,需8.440112013811=÷øöçèæ-+÷(小时).8. 甲与乙工作效率之比为3:2,甲独做要101235=÷øöçèæ-÷(天),乙独做需10+5=15(天),甲乙合做要61511011=÷øöçèæ+÷(天).9. 4151512151101511=÷øöçèæ-÷úûùêëé´÷øöçèæ-+-(分钟).10. 434134161515.711=úûùêëé+÷÷øöçèæ-++÷(小时).11. 243412411=÷øöçèæ÷-÷÷(天).12. 甲的工作效率为4522616151=++´,乙的工作效率为13522612151=++´, 丙的工作效率为13512611151=++´. 乙丙三天干了151313511352=´÷øöçèæ+,甲丙二天干了1351421351452=´÷øöçèæ+. 整个工作剩下13567135********=---. 由甲乙丙合干还要9471351135245213567=÷øöçèæ++÷(天), 完成此项工作共需9417947235=+++(天),即3月18日完成.13. 1620134515232=÷øöçèæ-´÷÷øöçèæ-(分).14. 按甲、乙、丙、丁顺序各开一小时水池中进水60761514131=-+-.这样5个周期(即20小时)后,池中有水43560761=´+,再开甲管注满水池需时4331431=÷÷øöçèæ-(小时),故一共要43204320=+(小时)开始溢出.。

小学四年(Nian)级奥数题4一、 新定(Ding)义运算1. 设(She)表示两个不同的(De)数,规定，求(Qiu)。

答(Da)案：180。

解(Jie)析：=3×8+4×7=24+28 =52=3×52+4×6=156+24=1802. 定义(Yi)运算⊖为⊖=5×，求11⊖12。

答案: 637。

解析： 11 12=5×11×12-(11+12)=660-23=6373. b a ,表示两个数,记为:a ※b =2×，求8※(4※16)。

答案：1953。

解析：4※16=2×4×16-×16 =128-4=124 8※124=2×8×124-41×124=1984-31=19534. 设为两个不同的数,规定□，求a □16=10中a 的值。

答案：24。

解析：因为a □16=10，即(a +16)÷4=10a +16=40a =40-16a =24。

5. 规定a ，求21010的值。

答(Da)案：解析：从左到右依(Yi)次计算。

21010 =10 =10 ==731 6. 定义(Yi)新运算x ⊕，求(Qiu)3⊕(2⊕4)的(De)值。

答(Da)案： 解(Jie)析：3⊕(2⊕4)=3⊕=3⊕ ===3167. 有一个(Ge)数学运算符号“⊗”,使下列算式成立:4⊗8=16，10⊗6=26，6⊗10=22，18⊗14=50，求7⊗3=?答案：17。

解析：因为4⊗8=4×2+8=16；10⊗6=10×2+6=26；6⊗10=6×2+10=22；18⊗14=18×2+14=50。

所(Suo)以a ⊗b =a ×2+b7⊗3=7×2+3=14+3=178. “▽”表示一(Yi)种新运算,它表示:，求(Qiu)3▽5的(De)值。

（三年级）备课教员：* * *第四讲错中求解（二）一、教学目标：知识目标在进行计算时，能够利用倒推法，从错误的计算结果中求出正确的结果。

能力目标1. 提高自主分析能力。

2. 锻炼逆向思维能力。

情感目标1.自主探索解决实际问题，并有勇于探索的精神。

2.培养做事认真仔细、严谨的态度。

3. 感悟数学在生活中的应用，以及倒推法的应用。

二、教学重点：1. 在乘法算式中，乘数的扩大（缩小）都直接影响到积的扩大（缩小）。

一个乘数增加几，积就增加另一个乘数的几倍；一个乘数减少几，积就减少另一个乘数的几倍。

2.在除法算式中，被除数扩大（缩小），商也会随着扩大（缩小）；而除数扩大（缩小），商反而缩小（扩大）。

除数和余数都相同时，商增加几，被除数就增加除数的几倍；商减少几，被除数就减少除数的几倍。

三、教学难点：1. 理解应用倒推法。

2. 乘法、除法错中求解时的不同。

四、教学准备：PPT五、教学过程：第一课时（50分钟）一、导入（5分)【设计意图：复习第二讲的旧知识，回顾逆运算的含义，用倒推法从错误的解中得到正确的解，为接下来的新授环节做铺垫。

】师：你们还记得上次我们学的加、减运算时的错中求解吗？生：记得。

师：那大家看一下这两个小题目，看看大家能不能自己做出来。

（PPT出示）1.一个加数个位上的8被看成了3，得到的和是235，正确的和是多少？2.被减数十位上的6被看成了9，得到的差是145，正确的差是多少？生：……师：大家都这么快就做出来了，说明大家对之前的知识掌握的很牢，那加、减法的错中求解主要是用了什么方法？生：逆运算和倒推法。

师：既然学了加、减法的错中求解，你们觉得我们今天会学什么内容呢？生：乘、除法的错中求解。

师：没错，我们今天就来学习一下乘、除法的错中求解，看看逆运算还能不能解决这类问题。

师：你们准备好了吗？生：准备好了！师：那就一起进入我们的课堂吧！【探究新知，引入新课：之前我们学习了加、减法的错中求解，学生对于逆运算有了一定的理解。

巧求周长与面积掌握巧求周长与面积的基本方法；1. 理解并掌握割补、平移等数学思想方法。

【例1】 （2007年“希望杯”第一试）右图中的阴影部分BCGF 是正方形，线段FH 长18厘米，线段AC 长24厘米，则长方形ADHE 的周长是__________厘米。

【分析】 由于图中阴影部分BCGF 是个正方形，其四条边的边长都相等，且等于长方形ADHE 的宽。

FH AC +的和应为长方形ADHE 的长加上正方形BCGF 的边长，所以等于长方形ADHE 的长与宽之和。

所以长方形ADHE 的周长为：(1824)284+⨯=厘米。

【例2】 如右图所示，在一个正方形内画中、小两个正方形，使三个正方形具有公共顶点，这样大正方形被分割成了正方形区域甲，和L 形区域乙和丙。

甲的边长为4厘米，乙的边长是甲的边长的1.5倍，丙的边长是乙的边长的1.5倍，那么丙的周长为多少厘米？EF 长多少厘米？【分析】 乙的周长实际上是正方形AHJE 的周长（我们可将乙与甲重合的两条线段分别向左、向下平移），同样的，丙的周长也就是正方形ABCD 的周长。

由于4 1.56AE =⨯=，6 1.59AD =⨯=，所以丙的周长为9436⨯=厘米，642EF AE AF =-=-=（厘米）。

【例3】 用若干个边长都是2厘米的平行四边形与三角形（如右图）拼接成一个大的平行四边形，已知大平行四边形的周长是244厘米，那么平行四边形和三角形各有多少个？【分析】 大平行四边形上、下两边的长为(24422)2120-⨯÷=厘米，观察上边，每6厘米有两个平行四边形的边，所以共有小平行四边形1206240÷⨯=个，三角形的数量与小平行四边形的数量相等，也是40个。

[拓展] 用若干个边长都是2厘米的平行四边形与三角形（如右图）拼接成一个大的平行四边形，已知大平行四边形的周长是236厘米，那么平行四边形和三角形各有多少个？[分析] 大平行四边形上、下两边的长为(23622)2116-⨯÷=厘米，观察上边，每6厘米有两个平行四边形的边，1166192÷=L ，所以有三角形19238⨯=个，小平行四边形38139+=个。