数据结构课件哈夫曼树讲解

数据结构哈夫曼树和哈夫曼编码权值一、引言在计算机领域，数据结构是非常重要的一部分，而哈夫曼树和哈夫曼编码是数据结构中非常经典的部分之一。

本文将对哈夫曼树和哈夫曼编码的权值进行全面评估，并探讨其深度和广度。

通过逐步分析和讨论，以期让读者更深入地理解哈夫曼树和哈夫曼编码的权值。

二、哈夫曼树和哈夫曼编码的基本概念1. 哈夫曼树哈夫曼树，又称最优二叉树，是一种带权路径长度最短的二叉树。

它的概念来源于一种数据压缩算法，可以有效地减少数据的存储空间和传输时间。

哈夫曼树的构建过程是基于给定的权值序列，通过反复选择两个最小权值的节点构建出来。

在构建过程中，需要不断地重排权值序列，直到构建出一个满足条件的哈夫曼树。

2. 哈夫曼编码哈夫曼编码是一种变长编码方式，它利用了哈夫曼树的特点，对不同的字符赋予不同长度的编码。

通过构建哈夫曼树，可以得到一套满足最优存储空间的编码规则。

在实际应用中，哈夫曼编码经常用于数据压缩和加密传输，能够有效地提高数据的传输效率和安全性。

三、哈夫曼树和哈夫曼编码的权值评估1. 深度评估哈夫曼树和哈夫曼编码的权值深度值得我们深入探究。

从构建哈夫曼树的角度来看，权值决定了节点在树中的位置和层次。

权值越大的节点往往位于树的底层，而权值较小的节点则位于树的高层。

这种特性使得哈夫曼树在数据搜索和遍历过程中能够更快地找到目标节点，提高了数据的处理效率。

而从哈夫曼编码的角度来看，权值的大小直接决定了编码的长度。

权值越大的字符被赋予的编码越短，可以有效地减少数据传输的长度，提高了数据的压缩率。

2. 广度评估另哈夫曼树和哈夫曼编码的权值也需要进行广度评估。

在构建哈夫曼树的过程中，权值的大小直接影响了树的结构和形状。

当权值序列较为分散时，哈夫曼树的结构会更加平衡，节点的深度差异较小。

然而，当权值序列的差异较大时，哈夫曼树的结构也会更不平衡，而且可能出现退化现象。

这会导致数据的处理效率降低，需要进行额外的平衡调整。

重学数据结构之哈夫曼树一、哈夫曼树1.带权扩充二叉树的外部路径长度扩充二叉树的外部路径长度，即根到其叶子节点的路径长度之和。

例如下面这两种带权扩充二叉树：左边的二叉树的外部路径长度为：(2 + 3 + 6 + 9) * 2 = 38。

右边的二叉树的外部路径长度为：9 + 6 * 2 + (2 + 3) * 3 = 36。

2.哈夫曼树哈夫曼树（Huffman Tree）是一种重要的二叉树，在信息领域有重要的理论和实际价值。

设有实数集W = {W0 ，W1 ，···，W m-1 }，T 是一颗扩充二叉树，其m 个外部节点分别以W i (i = 1, 2, n - 1) 为权，而且T 的带权外部路径长度在所有这样的扩充二叉树中达到最小，则称T 为数据集W 的最优二叉树或者哈夫曼树。

二、哈夫曼算法1.基本概念哈夫曼（D.A.Huffman）提出了一个算法，它能从任意的实数集合构造出与之对应的哈夫曼树。

这个构造算法描述如下：算法的输入为实数集合W = {W0 ，W1 ，···，W m-1 }。

在构造中维护一个包含k 个二叉树集合的集合F，开始时k=m 且F = {T0 ，T1 ，···，T m-1 }，其中每个T i 是一颗只包含权为W i 的根节点的二叉树。

该算法的构造过程中会重复执行以下两个步骤，直到集合F 中只剩下一棵树为止：1. 构造一颗二叉树，其左右子树是从集合 F 中选取的两颗权值最小的二叉树，其根节点的权值设置为这两颗子树的根节点的权值之和。

2. 将所选取的两颗二叉树从集合 F 中删除，把新构造的二叉树加入到集合F 中。

注意：给定集合W 上的哈夫曼树并不唯一！2.示例对于实数集合W = {2, 1, 3, 7, 8, 4, 5}，下面的图1到图7 表示了从这个实数集合开始，构造一个哈夫曼树的过程：图1：图2：图3：图4：图5：图6：图7：三、哈夫曼算法的实现1.实现思路要实现哈夫曼算法，需要维护一组二叉树，而且要知道每颗二叉树的根节点的权值，这个可以使用前面定义的二叉树的节点来构造哈夫曼树，只需要在根节点处记录该树的权值。

数据结构与算法--哈夫曼树思想与创建详解1PS:什么是哈夫曼树？ 给定n个权值作为n个叶⼦结点，构造⼀棵⼆叉树，若该树的带权路径长度达到最⼩，称这样的⼆叉树为最优⼆叉树，也称为哈夫曼树(Huffman Tree)。

哈夫曼树是带权路径长度最短的树，权值较⼤的结点离根较近。

计算规则： 假设⼀组权值，⼀个权值是⼀个结点，12 34 2 5 7 ，在这其中找出两个最⼩的权值，然后组成⼀个新的权值，再次找出最⼩的权值结点。

如图：问题： 1：如果程序找出两个最⼩的权值，把两个权值最⼩的相加结果再次添加到数组中呢。

2：完成第⼀步后，⼜怎么让他们成为⼀个⼆叉树呢。

3：这个⼆叉树的结构体怎么定义呢，这组带有权值的结点⼜以什么⽅式存在呢。

思路： 对于这种陆续找出两个最⼩权值的算法可以利⽤排序的⽅式，从⼩到⼤排序，那么最左边的就是最⼩的，这样⼀来最⼩的权值可以挑选出来了，接下来再利⽤特定的结构体（都有左孩⼦和右孩⼦还有存放权值的data域）让每⼀个权值结点存在⼀个数组中。

这样⼦不断的操作数组，从数组中的5个元素到只有1个元素为⽌，此时的这⼀个元素就是⼆叉树的跟。

然后再利⽤遍历⽅式打印这个⼆叉树即可。

代码实现：结构体定义⼀个⼆叉树的结构体，⼀个数组的结构体。

可以看出数组的结构体内部是包含⼀个⼆叉树结点的结构体的。

/*** Created by 刘志通 on 2018/11/22.* @describe 哈夫曼树的简介* 编程思想：* 1：⽅式简介：* 利⽤数组（⼆叉树结构体类型），来存放初始权值（⾸次认为权值就是⼀个树跟，左右孩⼦分别是NULL）,在数组初始化的之后排序，然后拿出index=0，1，更新 * 权值根,* 2：所⽤知识：* 数组，链表存储，⼆叉树结构体。

*/#include "stdlib.h"#include "stdio.h"/*** @describe ⼆叉树结构体* 结构形式：Lchild data Rchild* */typedef struct twoTree {int data;struct twoTree *Lchild, *Rchild;} twoTree, *twoTreeL;typedef struct {twoTreeL data[100];int length;} arrayMy;初始化数组arrayMy InitList(arrayMy &L) {// 初始化表，⼀个空表。

数据结构——哈夫曼（Huffman）树+哈夫曼编码前天acm实验课，⽼师教了⼏种排序，抓的⼀套题上有⼀个哈夫曼树的题，正好之前离散数学也讲过哈夫曼树，这⾥我就结合课本，整理⼀篇关于哈夫曼树的博客。

哈夫曼树的介绍Huffman Tree，中⽂名是哈夫曼树或霍夫曼树，它是最优⼆叉树。

定义：给定n个权值作为n个叶⼦结点，构造⼀棵⼆叉树，若树的带权路径长度达到最⼩，则这棵树被称为哈夫曼树。

这个定义⾥⾯涉及到了⼏个陌⽣的概念，下⾯就是⼀颗哈夫曼树，我们来看图解答。

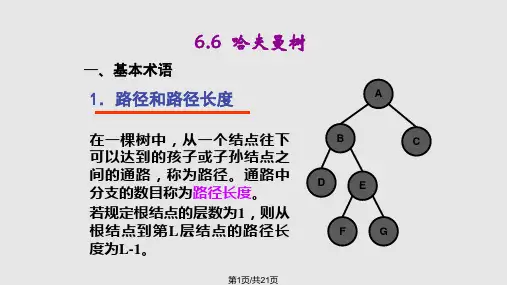
(01) 路径和路径长度定义：在⼀棵树中，从⼀个结点往下可以达到的孩⼦或孙⼦结点之间的通路，称为路径。

通路中分⽀的数⽬称为路径长度。

若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。

例⼦：100和80的路径长度是1，50和30的路径长度是2，20和10的路径长度是3。

(02) 结点的权及带权路径长度定义：若将树中结点赋给⼀个有着某种含义的数值，则这个数值称为该结点的权。

结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。

例⼦：节点20的路径长度是3，它的带权路径长度= 路径长度 * 权 = 3 * 20 = 60。

(03) 树的带权路径长度定义：树的带权路径长度规定为所有叶⼦结点的带权路径长度之和，记为WPL。

例⼦：⽰例中，树的WPL= 1*100 + 2*50 +3*20 + 3*10 = 100 + 100 + 60 + 30 = 290。

⽐较下⾯两棵树上⾯的两棵树都是以{10, 20, 50, 100}为叶⼦节点的树。

左边的树WPL=2*10 + 2*20 + 2*50 + 2*100 = 360 右边的树WPL=350左边的树WPL > 右边的树的WPL。

你也可以计算除上⾯两种⽰例之外的情况，但实际上右边的树就是{10,20,50,100}对应的哈夫曼树。

⾄此，应该堆哈夫曼树的概念有了⼀定的了解了，下⾯看看如何去构造⼀棵哈夫曼树。

数据结构与算法：哈夫曼树哈夫曼树给定N个权值作为N个叶⼦结点，构造⼀棵⼆叉树，若该树的带权路径长度达到最⼩，称这样的⼆叉树为最优⼆叉树，也称为哈夫曼树(Huffman Tree)。

哈夫曼树是带权路径长度最短的树，权值较⼤的结点离根较近。

重要概念路径：从⼀个节点到它往下可以达到的节点所经shu过的所有节点，称为两个节点之间的路径路径长度：即两个节点的层级差，如A节点在第⼀层，B节点在第四层，那它们之间的路径长度为4-1=3权重值：为树中的每个节点设置⼀个有某种含义的数值，称为权重值(Weight)，权重值在不同算法中可以起到不同的作⽤节点的带权路径长度：从根节点到该节点的路径长度与该节点权重值的乘积树的带权路径长度：所有叶⼦节点的带权路径长度之和，也简称为WPL哈夫曼树判断判断⼀棵树是不是哈夫曼树只要判断该树的结构是否构成最短带权路径。

在下图中3棵同样叶⼦节点的树中带权路径最短的是右侧的树，所以右侧的树就是哈夫曼树。

代码实现案例：将数组{13,7,8,3,29,6,1}转换成⼀棵哈夫曼树思路分析：从哈夫曼树的概念中可以看出，要组成哈夫曼树，权值越⼤的节点必须越靠近根节点，所以在组成哈夫曼树时，应该由最⼩权值的节点开始。

步骤：(1) 将数组转换成节点，并将这些节点由⼩到⼤进⾏排序存放在集合中(2) 从节点集合中取出权值最⼩的两个节点，以这两个节点为⼦节点创建⼀棵⼆叉树，它们的⽗节点权值就是它们的权值之和(3) 从节点集合中删除取出的两个节点，并将它们组成的⽗节点添加进节点集合中，跳到步骤(2)直到节点集合中只剩⼀个节点public class HuffmanTreeDemo {public static void main(String[] args) {int array[] = {13,7,8,3,29,6,1};HuffmanTree huffmanTree = new HuffmanTree();Node root = huffmanTree.create(array);huffmanTree.preOrder(root);}}//哈夫曼树class HuffmanTree{public void preOrder(Node root){if (root == null){System.out.println("哈夫曼树为空，⽆法遍历");return;}root.preOrder();}/*** 创建哈夫曼树* @param array 各节点的权值⼤⼩* @return*/public Node create(int array[]){//先将传⼊的各权值转成节点并添加到集合中List<Node> nodes = new ArrayList<>();for (int value : array){nodes.add(new Node(value));}/*当集合中的数组只有⼀个节点时,即集合内所有节点已经组合完成，剩下的唯⼀⼀个节点即是哈夫曼树的根节点*/while (nodes.size() > 1){//将节点集合从⼩到⼤进⾏排序//注意：如果在节点类没有实现Comparable接⼝，则⽆法使⽤Collections.sort(nodes);//在集合内取出权值最⼩的两个节点Node leftNode = nodes.get(0);Node rightNode = nodes.get(1);//以这两个节点创建⼀个新的⼆叉树，它们的⽗节点的权值即是它们的权值之和Node parent = new Node(leftNode.weight + rightNode.weight);parent.left = leftNode;parent.right = rightNode;//再从集合中删除已经组合成⼆叉树的俩个节点，并把它们俩个的⽗节点加⼊到集合中nodes.remove(leftNode);nodes.remove(rightNode);nodes.add(parent);}//返回哈夫曼树的根节点return nodes.get(0);}}//因为要在节点的集合内，以节点的权值value，从⼩到⼤进⾏排序，所以要实现Comparable<>接⼝class Node implements Comparable<Node>{int weight;//节点的权值Node left;Node right;public Node(int weight) {this.weight = weight;}public void preOrder(){System.out.println(this);if (this.left != null){this.left.preOrder();}if (this.right != null){this.right.preOrder();}}@Overridepublic String toString() {return "Node{" +"weight=" + weight +'}';}@Overridepublic int compareTo(Node o) {return this.weight - o.weight;}}哈夫曼编码定长编码固定长度编码⼀种⼆进制信息的信道编码。