CGMO2015-2015第14届中国数学女子奥林匹克试题及答案

2023中国女子数学奥林匹克竞赛试题及评注哎呀，说起今年子那个2023中国女子数学奥林匹克竞赛的题啊，简直是“烧脑”级别的高端操作！我们这些吃瓜群众，虽
然看不懂那些个复杂公式和几何图形，但听那些娃儿们说起来，那叫一个精彩纷呈。

第一题，就像是走迷宫一样，绕来绕去，非得你脑筋转得飞快，还得有股子钻牛角尖的劲儿，才能找到那扇通往答案的秘密门。

听说好多女娃子都被它卡壳了，但最后解出来的，那成就感，简直比吃了火锅还巴适！
第二题呢，更绝了，跟耍杂技似的，要你在一堆数字里玩平衡，既要快又要准，稍微一晃神，就全盘皆输。

这题考的不光是数学能力，还有心理素质，就跟咱们四川人打麻将一样，心态要好，手气更要稳。

后头那些题，更是一个比一个难啃，但咱们的女娃子们，那是真不含糊，一个个都跟小诸葛似的，思路清晰，解题如行云流水。

看得人那叫一个佩服，心想这数学界，以后怕是要多出些女中豪杰了！
评注嘛，就是一句话：这次竞赛，不仅展现了女娃子们在数学领域的天赋和实力，更证明了咱们四川的妹儿，不管干啥子，都能整得巴巴适适，绝不输人！。

姓名年级学校准考证号赛区考场联系电话-------------------装----------------------订----------------------线---------------------第14届世界奥林匹克数学竞赛（中国区）选拔赛全国总决赛------------------------------------------------------------------------------------------------------------------------五年级初赛试卷（本试卷满分120分，考试时间75分钟）一、初试牛刀（单选题Ⅰ，每题5分，共50分）1.在一架天平的两边分别放上以下重量的物体，唯一平衡的一组是（）。

A.左边312×2598克，右边820576克B.左边137×4725克，右边647335克C.左边110×3457克，右边380270克D.左边261×1231克，右边300291克2.将下面四个矩形沿着虚线剪开后，所得的两个部分既能拼成平行四边形，又能拼成三角形和梯形的是（）。

A. B. C. D.3.将图①所示四张扑克牌洗均匀后，如图②所示背面朝上放置在桌面上。

规定游戏规则如下：若同时随机抽取两张扑克牌，抽到两张牌的牌面数字之和是偶数则为胜，是奇数则为负。

则下面四个说法中正确的是（）。

A.胜的可能性比较大B.负的可能性比较大C.胜负的可能性一样大D.不可能胜，一定会负4.俄国著名数学家罗蒙诺索夫向邻居借《数学原理》一书，邻居对他说：“你帮我劈10天柴，我就把书送给你，另给你20个卢布。

”结果他只劈了7天柴。

邻居把书送给他后，另外付了5个卢布。

《数学原理》这本书的价值是（）卢布。

A.9B.20C.30D.805.我们在书写日期时习惯用六位数表示，例如850630表示的是1985年6月30日，用这种方法表示2009年某月某日的日期，其中六个数字都不相同的日期有（）天。

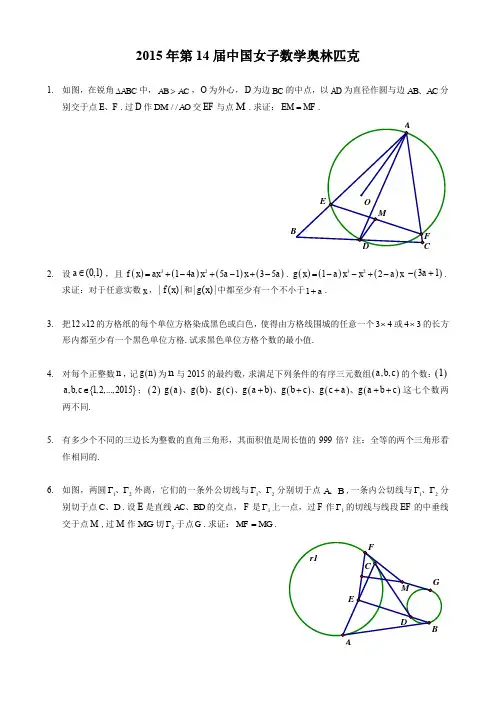
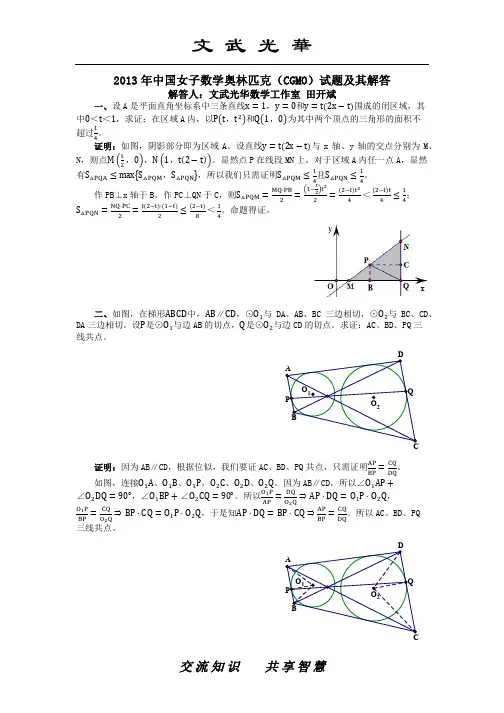
2015中国女子数学奥林匹克第一天2015年8月12日 上午8:00 ~ 12:00广东深圳 深圳市高级中学1．如图，在锐角△ABC 中，AB > AC ，O 为外心，D 为边BC 的中点．以AD 为直径作圆与边AB 、AC 分别交于点E 、F ．过D 作DM ∥AO 交EF 于点M ．求证：EM = MF ．（郑焕供题）2．设(0,1)a ∈，且3232()(14)(51)(35),()(1)(2)(31).f x ax a x a x ag x a x x a x a =+-+-+-=--+--+求证：对于任意实数x ，()f x 和()g x 中都至少有一个不小于1a +．（李胜宏供题）3．把12×12的方格纸的每个单位方格染成黑色或白色，使得由方格线围成的任意一个3×4或4×3的长方形内都至少有一个黑色单位方格．试求黑色单位方格个数的最小值．（梁应德供题）4．对每个正整数n ，记()g n 为n 与2015的最大公约数，求满足下列条件的有序三元数组(,,)a b c 的个数：1) ,,{1,2,,2015}a b c ∈；2) (),(),(),(),(),(),()g a g b g c g a b g b c g c a g a b c +++++这七个数两两不同．（王彬供题）中国女子数学奥林匹克第二天2015年8月13日 上午8:00 ~ 12:00广东深圳 深圳市高级中学OMFEDCBA5．有多少个不同的三边长为整数的直角三角形，其面积值是周长值的999倍？（全等的两个三角形看作相同的）（林常供题）6．如图，两圆12,ΓΓ外离，它们的一条外公切线与12,ΓΓ分别切于点,A B ，一条内公切线与12,ΓΓ分别切于点,C D ．设E 是直线,AC BD 的交点，F 是1Γ上一点，过F 作1Γ的切线与线段EF 的中垂线交于点M ，过M 作MG 切2Γ于点G ．求证：MF MG =．（付云皓供题）7．设12,,,(0,1)n x x x ∈，2n ≥．求证：1212121111n nnx x x n x x x x x x ----+++<．（王新茂供题）8．给定整数2n ≥．黑板上写着n 个集合，然后进行如下操作：选取黑板上两个互相不包含的集合,A B ，擦掉它们，然后写上A B 和A B ．这称为一次操作．如此操作下去，直到任意两个集合中都有一个包含另一个为止．对所有的初始状态和操作方式，求操作次数的最大可能值．（朱华伟供题）试题解答1．如图，在锐角△ABC 中，AB > AC ，O 为外心，D 为边BC 的中点．以AD 为直径作圆与边AB 、AC 分别交于点E 、F ． 过D 作DM ∥AO 交EF 于点M ． 求证：EM = MF ．Γ2Γ1MG F EDCBAO MFCD BEAN 图1证明 如图，连接DE 、DF ，过O 作ON ⊥AB 交AB 于点N ． 由题意可知，DE ⊥AB ，DF ⊥AC ． 因此，ON ∥DE ． 又因为DM ∥AO ，所以∠EDM =∠AON ．因为O 为△ABC 外心，所以∠AON = ∠ACB ． 从而∠EDM =∠ACB ． 同理可得，∠FDM = ∠ABC ． 在△EDF 中，有sin sin sin sin 1sin sin sin sin EM DE EDM DE ACB DB ABC ACBMF DF FDM DF ABC DC ACB ABC⋅∠⋅∠⋅∠⋅∠====⋅∠⋅∠⋅∠⋅∠， 即EM = MF ．2．设(0,1)a ∈，且3232()(14)(51)(35),()(1)(2)(31).f x ax a x a x ag x a x x a x a =+-+-+-=--+--+求证：对于任意实数x ，()f x 和()g x 中都至少有一个不小于1a +．证明 由于(0,1)a ∈，a 与1a -皆为正数，因此对任意实数x ，{}{}{}max (),()(1)max (),()max (),()(1)()()(1)()()f xg x a f x g x a f x g x a f x a g x a f x a g x =-⋅+⋅≥-+≥-⋅-⋅而222 (1)()()[(1)(14)][(1)(51)(2)][(1)(35)(31)](21)(2)1a f x a g x a a a x a a a a x a a a a a x x a-⋅-⋅=--++----+--++=-⋅-+++又22172()024x x x -+=-+>，故{}max (),()1f x g x a ≥+．问题得证．3．把12×12的方格纸的每个单位方格染成黑色或白色，使得由方格线围成的任何3×4和4×3长方形内都至少有一个黑格．试求黑格个数的最小值．解 所求黑格个数的最小值12n =．先证明12n ≥．由于12×12单位方格纸可划分为12121234⨯=⨯个（除边界外）互不相交的3×4方格长方形．由题设可知这些长方形各至少有一个黑色方格，故至少要涂12个黑色方格．要证明12n =，只需构作一个可行的例子，见下图．4．对每个正整数n ，记()g n 为n 与2015的最大公约数，求满足下列条件的有序三元数组(,,)a b c 的个数：1) ,,{1,2,,2015}a b c ∈；2) (),(),(),(),(),(),()g a g b g c g a b g b c g c a g a b c +++++这七个数两两不同．解 分解质因数123201551331p p p =⨯⨯=⨯⨯．()g n 是2015的约数，只有8种情况．我们把满足()1g n =的n 叫做零型数，把满足()g n 取1p 或2p 或3p 的n 叫做一型数，把满足()g n 取12p p 或13p p 或23p p 的n 叫做二型数．我们使用下面两个简单的事实：对任意整数x ，()()(2015)(2015)g x g x g x g x =-=+=-，因此本题可以看做在模2015意义下讨论，即模2015同余的两个数看成相同．对素数p ，若|p x ,|p y 两者都成立则|p x y ±，若恰有一个成立则|p x y ±/．把满足条件三元组(,,)a b c 对应为七元组(,,,,,,)A a b c a b a c b c a b c =+++++，我们考虑A 的七个位置上的数的g 值的分布．首先这七个g 值不能有2015，否则，若某个位置上的数x 是2015的倍数，则A 中存在另外两个位置上的数,y z 满足x y z =+或x y z =-，这样就有()()g y g z =，矛盾．所以七个g 值必须是1,1p ,2p ,3p ,12p p ,13p p ,23p p 各一个．这样A 的七个位置必须是3个二型数、3个一型数、一个零型数．我们关心三个二型数在哪三个位置上．设123,,p p p 是5,13,31的任意排列，若,,x y z 满足12()g x p p =，13()g y p p =，23()g z p p =，则有111|,||p x p y p x y ⇒±±，222|,||p x p y p x y ⇒±±//，333|,||p x p y p x y ⇒±±//，可得1()g x y p ±±=，同理有2()g x z p ±±=，3()g y z p ±±=，()1g x y z ±±±=．因此当确定A 中的三个二型数,,x y z 的位置后，如果其它四个位置可以分别表示为,,x y z 的3个两两线性组合与,,x y z 三个数的线性组合(要求线性组合系数是1±)，我们就可断定A 中的七个位置的g 值互不相同，我们把这种可以线性组合成功表示的三个二型数的一组位置叫做合理位置．在一组合理位置上，当我们确定,,x y z 的取值(模2015意义下)后，七元组A 也被唯一决定了．在模2015意义下，满足12()g n p p =的n 恰好有31p -个，满足13()g n p p =的n 恰好有21p -个，满足23()g n p p =的n 恰好有11p -个，此外,,x y z 的顺序或者说123,,p p p 的顺序可以调换，因此每组合理位置下，,,x y z 的取值有3213!(1)(1)(1)614408640p p p ⨯---=⨯=种可能，也就恰好对应8640个满足条件的三元组．我们关心哪组位置可能是合理的．对素数5,13,31p =，七元组A 中恰好有3个位置是p 的倍数，若,,a b a c b c +++这三个位置至少有两个p 的倍数，不妨设|,|p a b p a c ++，则在此前提下||||p a p b p c p a b c ⇔⇔⇔++并且||()()()p b c p a b a c b c p a p a +⇒+++-+⇒⇒，这时A 中不能恰有3个位置是p 的倍数．所以()g a b +,()g a c +,()g b c +的素因子个数总共不超过3，,,a b a c b c +++这三个位置上至多有一个二型数，也就是,,,a b c a b c ++这四个位置上有2或3个二型数．若,,,a b c a b c ++中有三个二型数，二型数的位置有4种可能情况：若,,x a y b z c ===是三个二型数，则a b x y +=+,a c x z +=+,b c y z +=+是三个一型数，a b c x y z ++=++是零型数，位置合理．若,,x a y b z a b c ===++是二型数，则,,a b x y b c z x a c z y +=++=-+=-，c x y z =--+，位置合理．同理其他两种位置也是合理的．若,,,a b c a b c ++中恰有两个二型数，我们分两类考虑：第一类考虑两个二型数都在,,a b c 中，不妨设a 和b 是二型数，则a b +不可能是二型数，a c +,b c +之一是二型数，不妨设a c +是二型数．这时,,x a y b z a c ===+是三个二型数，,,a b x y c x z a b c y z +=+=-+++=+，b c x y z +=-++，位置合理．这一类由对称性共有6种情况是合理位置．第二类考虑a b c ++是二型数且,,a b c 之一是二型数，不妨设a 和a b c ++是二型数，则b c +不可能是二型数，a b +,a c +之一是二型数，不妨设a b +是二型数．这时,,x a y a b c z a b ==++=+是二型数，则,,b c x y b x z c y z +=-+=-+=-，a c x y z +=+-，位置合理．这一类由对称性共有6种情况是合理位置．综上，三个二型数的合理位置共有16种，(其他不合理位置都不可能使三元组满足条件)．所以满足条件的三元组共有168640138240⨯=．5．有多少个不同的三边长为整数的直角三角形，其面积值是周长值的999倍？（全等的两个三角形看作相同的）解法一 设内切圆半径为r ，1()()2S r a b c m a b c =++=++．故22a b cr m +-==，4c a b m =+-．代入222a b c +=得24480ab ma mb m --+=，2(4)(4)8a m b m m --=．不同的无序解(,)a b 给出不同的三角形，故所求三角形个数为21(8)2d m ．本题999m =，236282337m =⋅⋅，1(31)(61)(21)422+++=．解法二 由勾股数公式，22222, (), ()a k uv b k u v c k u v =⋅=-=+，其中k （三边长的最大公因数）为任意正整数，u 与v 互素，u v >且u 与v 一奇一偶．22231999()()9992()2()19982337ab a b c k uv u v u u v kv u v =⋅++⇔-=⋅+⇔-==⋅⋅ u v -为奇数，因数2只能分给k 或v ，有两种方式．v 与u v -互素，奇素因子p α分给,,k v u v -只能是(,0,0)α或(,,0)i i α-，(,0,)i i α-（1i α≤≤），有21α+种方式．故由乘法原理，素因子的分配共有2(231)(211)42⋅⋅+⋅+=种方式，每种分配方式给出唯一的三角形．因此共有42个所求三角形．评注 一般地，若倍数为112nn m p p ββα=⋅（1,,n p p 为不同的奇素数），则所求三角形个数为1(2)(21)(21)n αββ+⋅++．6. 如图，两圆12,ΓΓ外离，它们的一条外公切线与12,ΓΓ分别切于点,A B ，一条内公切线与12,ΓΓ分别切于点,C D . 设E 是直线,AC BD 的交点，F 是1Γ上一点，过F 作1Γ的切线与线段EF 的中垂线交于点M ，过M 作MG 切2Γ于点G . 求证：MF MG =.证法一 设12,ΓΓ的圆心分别为12,O O ，直线,AB CD 交于点H ，连12,HO HO . 设,J K 分别是线段,AB CD 的中点，连,JE KE .由于,HA HC 是1Γ的切线，故1HO 平分AHC ∠，且1AC HO ⊥. 同理，2HO 平分BHD ∠，且2BD HO ⊥. 由于12,HO HO 分别是AHC ∠的内角平分线和外角平分线，故它们互相垂直，结合1AC HO ⊥及2BD HO ⊥知AC BD ⊥.由于直角三角形斜边中线等于斜边一半，故,JE JA JB KE KC KD ====. 考虑12,ΓΓ及以E 为圆心，0为半径的圆，由JE JA JB ==知J 到这三个圆的幂相等，由KE KC KD ==知K 到这三个圆的幂也相等. 显然,J K 是两个不同的点，因此这三个圆必然有一条公共的根轴. 由于M 在EF 的中垂线上，所以MF ME =，结合MF 是1Γ的切线知M 在这三个圆的公共根轴上，又MG 是2Γ的切线，故MF MG =，证毕.证法二 同证法一可得AC BD ⊥. 设12,ΓΓ的半径分别为12,r r ，则由勾股定理可知222222111JO JE r JA JE r -=+-=，同理有22211KO KE r -=，22211MO ME r -=. 因此22222111J O J E K OK E M O M E -=-=-，由平方差原理知1JK O P ⊥，1KM O P ⊥. 由于过平面上一点有且仅有一条直线与已知直线垂直，所以,,J K M 三点共线.由于22222222J O J E r J B J E r -=+-=，同理2222KO KE r -=，由此可得22222JO JE KO KE -=-，由平方差原理知2JK O E ⊥，故2J M O E ⊥，因此2222222M O M E J O J E r -=-=，结合22222MO MG r =+得MG ME =，故MG MF =，证毕. 评注 事实上，点E 在直线12O O 上，两个证法均证明了这一点，但这个结论在本题中作用不大.7．设12,,,(0,1)n x x x ∈，2n ≥．求证：Γ2 Γ1 M G F E DC BAKHJ O 2O 1Γ2 Γ1M G FED CBA1212121111n nnx x x n x x x x x x ----+++<．证法一：对n 应用数学归纳法．当2n =时，由Cauchy 不等式可得221221121122121212121111111x x x x x x x x x x x x x x x x x x ---+--+-++=≤< 当3n ≥时，由归纳假设和Cauchy 不等式，得12121212212112112121211112212()11n n n n nn n n n n nn n nx x x x n x x x x x x x n x x x x x n x x x x x n x x x x x x x x x --------+++<+-⋅+--+-+-=≤<证法二：设1111212()n n A x x x x x x ---=+++，12n B x x x =．两边同乘以B ，只需证明1223411211111n n n n x x x x x x x x x x x x n --+-++-<-．由Cauchy 不等式，左边2341121n n n x x x x x x x x x -≤+++⋅122341121(1)(1)(1)()n n n n x x x x x x x x x x x x A A nB --+-++-=-．故只需证明()1A A nB n -<-．我们先证明1(1)A n B <+-．事实上，12312341234512211(1)(1)(1)(1)(1) (1)(1)(1)(1)0n n n n n n n B A x x x x x x x x x x x x x x x x x x x x --+--=--+--+--++-->（这也可以用调整法或一次函数极值来证明）．故()()()2222()1(1)1(1)1(1)(1)2(2)(1)(2)1(1)12(1)4(1)(2)11(2)14(1)A A nB n B n B nB n B B n n n B n B n B n n n n n n -<+-+--=+--⎛⎫⎛⎫--=--+-+=---++⎪ ⎪--⎝⎭⎝⎭-≤+≤+-=-- 证毕．8．给定整数2n ≥．黑板上写着n 个集合，然后进行如下操作：选取黑板上两个互相不包含的集合,A B ，擦掉它们，然后写上A B 和A B ．这称为一次操作．如此操作下去，直到任意两个集合中都有一个包含另一个为止．对所有的初始状态和操作方式，求操作次数的最大可能值．解 首先我们证明操作次数不可能超过2(1)2n n n C -=．当黑板上写着n 个集合时，考虑成包含关系的集合对的数量，我们证明，每次操作后，这个数量至少增加1．假设我们将,A B 变成A B 和A B ．首先,A B 不是包含关系，而A B 和A B 是包含关系，故这里至少增加了一对成包含关系的集合对．对于另一集合C ，若C 与,A B 之一成包含关系，由对称性不妨设A C ⊆，则A B C ⊆，即C 至少与A B 和A B 之一成包含关系；若C 与,A B 均成包含关系，则由,A B 不成包含关系知或者,A C B C ⊆⊆，或者,A C B C ⊇⊇，若为前者，则,A B C A B C ⊆⊆，若为后者，则,A B C A B C ⊇⊇．因此，在操作之后，其余成包含关系的集合对的数量不会减少，因此每次操作后，这个数量至少增加1．由于此数量最少为0，最多为2(1)2n n n C -=，故操作至多进行(1)2n n -次．另一方面，我们给出操作次数达到(1)2n n -的例子．定义集合{,1,...,2}i A i i i n =++-，1,2,...,i n =，我们证明由12,,...,n A A A 出发，可以进行(1)2n n -次操作．使用数学归纳法，当2n =时，12{1},{2}A A ==，可进行2(21)12⨯-=次操作． 若结论对n 成立，考虑1n +的情况．先将1{1,2,...,}A n =与2{2,3,...,1}A n =+进行一次操作，得到的交集{2,3,...,}n 留下，并集继续与3{3,4,...,2}A n =+进行操作，得到的交集{3,4,...,1}n +留下，并集继续与4A 进行操作，依此类推．进行完n 次操作后，得到原来所有集合的并集{1,2,...,2}n 及另外n 个集合{2,3,...,}n ，{3,4,...,1}n +，……，{1,2,...,21}n n n ++-．下面仅考虑后n 个集合之间的操作．由于将所有元素都减1并不改变集合间的关系，故可考虑集合{1,2,...,n -，{2,3,...,}n ，……，{,1,...,2n n n +-．而由归纳假设，这些集合之间可以操作2(1)2n n n C -=次，故原来的1n +个集合可以操作21(1)(1)22n n n n n n C +-++==次，即此结论对1n +也成立． 综上所述，操作次数的最大可能值为2(1)2n n n C -=．。

2015年全国高中数学联赛（B 卷）（一试）一、填空题（每个小题8分，满分64分 1：已知函数⎩⎨⎧+∞∈∈-=),3(log ]3,0[)(2x a x xa x f x，其中a 为常数，如果)4()2(f f <，则a 的取值范围是2：已知3)(x x f y +=为偶函数，且15)10(=f ，则)10(-f 的值为3：某房间的室温T （单位：摄氏度）与时间t （单位：小时）的函数关系为：),0(,cos sin +∞∈+=t t b t a T ，其中b a ,为正实数，如果该房间的最大温差为10摄氏度，则b a +的最大值是4：设正四棱柱1111D C B A ABCD -的底面ABCD 是单位正方形，如果二面角11C BD A --的大小为3π，则=1AA 5：已知数列{}n a 为等差数列，首项与公差均为正数，且952,,a a a 依次成等比数列，则使得121100a a a a k >+⋅⋅⋅++的最小正整数k 的值是6：设k 为实数，在平面直角坐标系中有两个点集{})(2),(22y x y x y x A +=+=和{}03),(≥++-=k y kx y x B ，若B A 是单元集，则k 的值为7：设P 为椭圆13422=+x y 上的动点，点)1,0(),1,1(-B A ，则PB PA +的最大值为 8：正2015边形201521A A A ⋅⋅⋅内接于单位圆O ，任取它的两个不同顶点j i A A ,， 则1≥+j i OA OA 的概率为 二、解答题9：（本题满分16分）数列{}n a 满足,31=a 对任意正整数n m ,，均有mn a a a n m n m 2++=+ （1）求{}n a 的通项公式； （2）如果存在实数c 使得c a ki i<∑=11对所有正整数k 都成立，求c 的取值范围10：（本题满分20分）设4321,,,a a a a 为四个有理数，使得：{}⎭⎬⎫⎩⎨⎧----=≤<≤3,1,81,23,2,2441j i aa ji，求4321a a a a +++的值11：（本题满分20分）已知椭圆)0(12222>>=+b a by a x 的右焦点为)0,(c F ，存在经过点F的一条直线l 交椭圆于B A ,两点，使得OB OA ⊥，求该椭圆的离心率的取值范围（加试）1：（本题满分40分）证明：对任意三个不全相等的非负实数c b a ,,都有：21)()()()()()(222222≥-+-+--+-+-a c c b b a ab c ac b bc a ，并确定等号成立的充要条件 2：（本题满分40分）如图，在等腰ABC ∆中，AC AB =，设I 为其内心，设D 为ABC ∆内的一个点，满足D C B I ,,,四点共圆，过点C 作BD 的平行线，与AD 的延长线交于E 求证：CE BD CD ⋅=23：（本题满分50分）证明：存在无穷多个正整数组)2015,,)(,,(>c b a c b a 满足：1,1,1++-ab c ac b bc a4：（本题满分50分）给定正整数)2(,n m n m ≤≤，设m a a a ,,,21⋅⋅⋅是n ,,2,1⋅⋅⋅中任取m 个互不相同的数构成的一个排列，如果存在{}m k ,,2,1⋅⋅⋅∈使得k a k +为奇数，或者存在整数 )1(,m l k l k ≤<≤，使得l k a a >，则称m a a a ,,,21⋅⋅⋅是一个“好排列”，试确定所有好排列的个数。

2015中国女子数学奥林匹克第一天2015年8月12日 上午8:00 ~ 12:00广东深圳 深圳市高级中学1．如图，在锐角△ABC 中，AB > AC ，O 为外心，D 为边BC 的中点．以AD 为直径作圆与边AB 、AC 分别交于点E 、F ．过D 作DM ∥AO 交EF 于点M ．求证：EM = MF ．（郑焕供题）2．设(0,1)a ∈，且3232()(14)(51)(35),()(1)(2)(31).f x ax a x a x ag x a x x a x a =+-+-+-=--+--+求证：对于任意实数x ，()f x 和()g x 中都至少有一个不小于1a +．（李胜宏供题）3．把12×12的方格纸的每个单位方格染成黑色或白色，使得由方格线围成的任意一个3×4或4×3的长方形内都至少有一个黑色单位方格．试求黑色单位方格个数的最小值．（梁应德供题）4．对每个正整数n ，记()g n 为n 与2015的最大公约数，求满足下列条件的有序三元数组(,,)a b c 的个数：1) ,,{1,2,,2015}a b c ∈；2) (),(),(),(),(),(),()g a g b g c g a b g b c g c a g a b c +++++这七个数两两不同．（王彬供题）中国女子数学奥林匹克第二天2015年8月13日 上午8:00 ~ 12:00广东深圳 深圳市高级中学5．有多少个不同的三边长为整数的直角三角形，其面积值是周长值的999倍？（全等OMFED CB A的两个三角形看作相同的）（林常供题）6．如图，两圆12,ΓΓ外离，它们的一条外公切线与12,ΓΓ分别切于点,A B ，一条内公切线与12,ΓΓ分别切于点,C D ．设E 是直线,AC BD 的交点，F 是1Γ上一点，过F 作1Γ的切线与线段EF 的中垂线交于点M ，过M 作MG 切2Γ于点G ．求证：MF MG =．（付云皓供题）7．设12,,,(0,1)n x x x ∈，2n ≥．求证：121211n n nx n x x --+<．（王新茂供题）8．给定整数2n ≥．黑板上写着n 个集合，然后进行如下操作：选取黑板上两个互相不包含的集合,A B ，擦掉它们，然后写上A B 和A B ．这称为一次操作．如此操作下去，直到任意两个集合中都有一个包含另一个为止．对所有的初始状态和操作方式，求操作次数的最大可能值．（朱华伟供题）试题解答1．如图，在锐角△ABC 中，AB > AC ，O 为外心，D 为边BC 的中点．以AD 为直径作圆与边AB 、AC 分别交于点E 、F ． 过D 作DM ∥AO 交EF 于点M ． 求证：EM = MF ．证明 如图，连接DE 、DF ，过O 作ON ⊥AB 交AB 于点N ． 由题意可知，DE ⊥AB ，DF ⊥AC ． 因此，ON ∥DE ． 又因为DM ∥AO ，所以∠EDM =∠AON ．因为O 为△ABC 外心，所以∠AON = ∠ACB ． 从而∠EDM =∠ACB ．Γ2Γ1MG FEDCBA图1同理可得，∠FDM = ∠ABC ． 在△EDF 中，有sin sin sin sin 1sin sin sin sin EM DE EDM DE ACB DB ABC ACBMF DF FDM DF ABC DC ACB ABC ⋅∠⋅∠⋅∠⋅∠====⋅∠⋅∠⋅∠⋅∠， 即EM = MF ．2．设(0,1)a ∈，且3232()(14)(51)(35),()(1)(2)(31).f x ax a x a x ag x a x x a x a =+-+-+-=--+--+求证：对于任意实数x ，()f x 和()g x 中都至少有一个不小于1a +．证明 由于(0,1)a ∈，a 与1a -皆为正数，因此对任意实数x ，{}{}{}max (),()(1)max (),()max (),()(1)()()(1)()()f xg x a f x g x a f x g x a f x a g x a f x a g x =-⋅+⋅≥-+≥-⋅-⋅而222 (1)()()[(1)(14)][(1)(51)(2)][(1)(35)(31)](21)(2)1a f x a g x a a a x a a a a x a a a a a x x a-⋅-⋅=--++----+--++=-⋅-+++又22172()024x x x -+=-+>，故{}max (),()1f x g x a ≥+．问题得证．3．把12×12的方格纸的每个单位方格染成黑色或白色，使得由方格线围成的任何3×4和4×3长方形内都至少有一个黑格．试求黑格个数的最小值．解 所求黑格个数的最小值12n =．先证明12n ≥．由于12×12单位方格纸可划分为12121234⨯=⨯个（除边界外）互不相交的3×4方格长方形．由题设可知这些长方形各至少有一个黑色方格，故至少要涂12个黑色方格．要证明12n =，只需构作一个可行的例子，见下图．4．对每个正整数n ，记()g n 为n 与2015的最大公约数，求满足下列条件的有序三元数组(,,)a b c 的个数：1) ,,{1,2,,2015}a b c ∈；2) (),(),(),(),(),(),()g a g b g c g a b g b c g c a g a b c +++++这七个数两两不同．解 分解质因数123201551331p p p =⨯⨯=⨯⨯．()g n 是2015的约数，只有8种情况．我们把满足()1g n =的n 叫做零型数，把满足()g n 取1p 或2p 或3p 的n 叫做一型数，把满足()g n 取12p p 或13p p 或23p p 的n 叫做二型数．我们使用下面两个简单的事实：对任意整数x ，()()(2015)(2015)g x g x g x g x =-=+=-，因此本题可以看做在模2015意义下讨论，即模2015同余的两个数看成相同．对素数p ，若|p x ,|p y 两者都成立则|p x y ±，若恰有一个成立则|p x y ±/．把满足条件三元组(,,)a b c 对应为七元组(,,,,,,)A a b c a b a c b c a b c =+++++，我们考虑A 的七个位置上的数的g 值的分布．首先这七个g 值不能有2015，否则，若某个位置上的数x 是2015的倍数，则A 中存在另外两个位置上的数,y z 满足x y z =+或x y z =-，这样就有()()g y g z =，矛盾．所以七个g 值必须是1,1p ,2p ,3p ,12p p ,13p p ,23p p 各一个．这样A 的七个位置必须是3个二型数、3个一型数、一个零型数．我们关心三个二型数在哪三个位置上．设123,,p p p 是5,13,31的任意排列，若,,x y z 满足12()g x p p =，13()g y p p =，23()g z p p =，则有111|,||p x p y p x y ⇒±±，222|,||p x p y p x y ⇒±±//，333|,||p x p y p x y ⇒±±//，可得1()g x y p ±±=，同理有2()g x z p ±±=，3()g y z p ±±=，()1g x y z ±±±=．因此当确定A 中的三个二型数,,x y z 的位置后，如果其它四个位置可以分别表示为,,x y z 的3个两两线性组合与,,x y z 三个数的线性组合(要求线性组合系数是1±)，我们就可断定A 中的七个位置的g 值互不相同，我们把这种可以线性组合成功表示的三个二型数的一组位置叫做合理位置．在一组合理位置上，当我们确定,,x y z 的取值(模2015意义下)后，七元组A 也被唯一决定了．在模2015意义下，满足12()g n p p =的n 恰好有31p -个，满足13()g n p p =的n 恰好有21p -个，满足23()g n p p =的n 恰好有11p -个，此外,,x y z 的顺序或者说123,,p p p 的顺序可以调换，因此每组合理位置下，,,x y z 的取值有3213!(1)(1)(1)614408640p p p ⨯---=⨯=种可能，也就恰好对应8640个满足条件的三元组．我们关心哪组位置可能是合理的．对素数5,13,31p =，七元组A 中恰好有3个位置是p 的倍数，若,,a b a c b c +++这三个位置至少有两个p 的倍数，不妨设|,|p a b p a c ++，则在此前提下||||p a p b p c p a b c⇔⇔⇔++并且||()()()|2|p b c p a b a c b c p a p a +⇒+++-+⇒⇒，这时A 中不能恰有3个位置是p 的倍数．所以()g a b +,()g a c +,()g b c +的素因子个数总共不超过3，,,a b a c b c +++这三个位置上至多有一个二型数，也就是,,,a b c a b c ++这四个位置上有2或3个二型数．若,,,a b c a b c ++中有三个二型数，二型数的位置有4种可能情况：若,,x a y b z c ===是三个二型数，则a b x y +=+,a c x z +=+,b c y z +=+是三个一型数，a b c x y z ++=++是零型数，位置合理．若,,x a y b z a b c ===++是二型数，则,,a b x y b c z x a c z y +=++=-+=-，c x y z =--+，位置合理．同理其他两种位置也是合理的．若,,,a b c a b c ++中恰有两个二型数，我们分两类考虑：第一类考虑两个二型数都在,,a b c 中，不妨设a 和b 是二型数，则a b +不可能是二型数，a c +,b c +之一是二型数，不妨设a c +是二型数．这时,,x a y b z a c ===+是三个二型数，,,a b x y c x z a b c y z +=+=-+++=+，b c x y z +=-++，位置合理．这一类由对称性共有6种情况是合理位置．第二类考虑a b c ++是二型数且,,a b c 之一是二型数，不妨设a 和a b c ++是二型数，则b c +不可能是二型数，a b +,a c +之一是二型数，不妨设a b +是二型数．这时,,x a y a b c z a b ==++=+是二型数，则,,b c x y b x z c y z +=-+=-+=-，a c x y z +=+-，位置合理．这一类由对称性共有6种情况是合理位置．综上，三个二型数的合理位置共有16种，(其他不合理位置都不可能使三元组满足条件)．所以满足条件的三元组共有168640138240⨯=．5．有多少个不同的三边长为整数的直角三角形，其面积值是周长值的999倍？（全等的两个三角形看作相同的）解法一 设内切圆半径为r ，1()()2S r a b c m a b c =++=++．故22a b c r m +-==，4c a b m =+-．代入222a b c +=得24480ab ma mb m --+=，2(4)(4)8a m b m m --=．不同的无序解(,)a b 给出不同的三角形，故所求三角形个数为21(8)2d m ．本题999m =，236282337m =⋅⋅，1(31)(61)(21)422+++=．解法二 由勾股数公式，22222, (), ()a k uv b k u v c k u v =⋅=-=+，其中k （三边长的最大公因数）为任意正整数，u 与v 互素，u v >且u 与v 一奇一偶．22231999()()9992()2()19982337ab a b c k uv u v u u v kv u v =⋅++⇔-=⋅+⇔-==⋅⋅ u v -为奇数，因数2只能分给k 或v ，有两种方式．v 与u v -互素，奇素因子p α分给,,k v u v -只能是(,0,0)α或(,,0)i i α-，(,0,)i i α-（1i α≤≤），有21α+种方式．故由乘法原理，素因子的分配共有2(231)(211)42⋅⋅+⋅+=种方式，每种分配方式给出唯一的三角形．因此共有42个所求三角形．评注 一般地，若倍数为112nn m p p ββα=⋅（1,,n p p 为不同的奇素数），则所求三角形个数为1(2)(21)(21)n αββ+⋅++．6. 如图，两圆12,ΓΓ外离，它们的一条外公切线与12,ΓΓ分别切于点,A B ，一条内公切线与12,ΓΓ分别切于点,C D . 设E 是直线,AC BD 的交点，F 是1Γ上一点，过F 作1Γ的切线与线段EF 的中垂线交于点M ，过M 作MG 切2Γ于点G . 求证：MF MG =.证法一 设12,ΓΓ的圆心分别为12,O O ，直线,AB CD 交于点H ，连12,HO HO . 设,J K 分别是线段,AB CD 的中点，连,JE KE .由于,HA HC 是1Γ的切线，故1HO 平分AHC ∠，且1AC HO ⊥. 同理，2HO 平分BHD ∠，Γ2 Γ1 M G F E D C BA且2BD HO ⊥. 由于12,HO HO 分别是AHC ∠的内角平分线和外角平分线，故它们互相垂直，结合1AC HO ⊥及2BD HO ⊥知AC BD ⊥.由于直角三角形斜边中线等于斜边一半，故,JE JA JB KE KC KD ====. 考虑12,ΓΓ及以E 为圆心，0为半径的圆，由JE JA JB ==知J 到这三个圆的幂相等，由KE KC KD ==知K 到这三个圆的幂也相等. 显然,J K 是两个不同的点，因此这三个圆必然有一条公共的根轴. 由于M 在EF 的中垂线上，所以MF ME =，结合MF 是1Γ的切线知M 在这三个圆的公共根轴上，又MG 是2Γ的切线，故MF MG =，证毕.证法二 同证法一可得AC BD ⊥. 设12,ΓΓ的半径分别为12,r r ，则由勾股定理可知222222111JO JE r JA JE r -=+-=，同理有22211KO KE r -=，22211MO ME r -=. 因此222222111JO JE KO KE MO ME -=-=-，由平方差原理知1JK O P ⊥，1KM O P ⊥. 由于过平面上一点有且仅有一条直线与已知直线垂直，所以,,J K M 三点共线.由于222222222JO JE r JB JE r -=+-=，同理22222KO KE r -=，由此可得222222JO JE KO KE -=-，由平方差原理知2JK O E ⊥，故2JM O E ⊥，因此22222222MO ME JO JE r -=-=，结合22222MO MG r =+得MG ME =，故MG MF =，证毕.评注 事实上，点E 在直线12O O 上，两个证法均证明了这一点，但这个结论在本题中作用不大.7．设12,,,(0,1)n x x x ∈，2n ≥．求证：121211n nx n x x x x --+++<．证法一：对n 应用数学归纳法．当2n =时，由Cauchy 不等式可得121212121x x=≤<当3n ≥时，由归纳假设和Cauchy 不等式，得121212212112112121211212()11n n nn nn n nnnnx n x x x x x n x x x x xn x x x x x x x -----+<+--+-+-=≤<证法二：设1111212()n n A x x x x x x ---=+++，12n B x x x =．两边同乘以B ，只需证明22341121111n n n n x x x x x x x x x x n -+-++-<-．由Cauchy 不等式，左边2341121n n n x x x x x x x x -+++⋅22341121(1)(1)(n n n n x x x x x x x x x x A A nB -+-++-=-．故只需证明()1A A nB n -<-．我们先证明1(1)A n B <+-．事实上，12312341234512211(1)(1)(1)(1)(1) (1)(1)(1)(1)0n n n n n n n B A x x x x x x x x x x x x x x x x x x x x --+--=--+--+--++-->（这也可以用调整法或一次函数极值来证明）．故()()()2222()1(1)1(1)1(1)(1)2(2)(1)(2)1(1)12(1)4(1)(2)11(2)14(1)A A nB n B n B nB n B B n n n B n B n B n n n n n n -<+-+--=+--⎛⎫⎛⎫--=--+-+=---++⎪ ⎪--⎝⎭⎝⎭-≤+≤+-=-- 证毕．8．给定整数2n ≥．黑板上写着n 个集合，然后进行如下操作：选取黑板上两个互相不包含的集合,A B ，擦掉它们，然后写上A B 和A B ．这称为一次操作．如此操作下去，直到任意两个集合中都有一个包含另一个为止．对所有的初始状态和操作方式，求操作次数的最大可能值．解 首先我们证明操作次数不可能超过2(1)2n n n C -=． 当黑板上写着n 个集合时，考虑成包含关系的集合对的数量，我们证明，每次操作后，这个数量至少增加1．假设我们将,A B 变成A B 和A B ．首先,A B 不是包含关系，而A B 和A B 是包含关系，故这里至少增加了一对成包含关系的集合对．对于另一集合C ，若C 与,A B 之一成包含关系，由对称性不妨设A C ⊆，则A B C ⊆，即C 至少与A B 和A B 之一成包含关系；若C 与,A B 均成包含关系，则由,A B 不成包含关系知或者,A C B C ⊆⊆，或者,A C B C ⊇⊇，若为前者，则,A B C A B C ⊆⊆，若为后者，则,A B C A B C ⊇⊇．因此，在操作之后，其余成包含关系的集合对的数量不会减少，因此每次操作后，这个数量至少增加1．由于此数量最少为0，最多为2(1)2n n n C -=，故操作至多进行(1)2n n -次． 另一方面，我们给出操作次数达到(1)2n n -的例子．定义集合{,1,...,2}i A i i i n =++-，1,2,...,i n =，我们证明由12,,...,n A A A 出发，可以进行(1)2n n -次操作． 使用数学归纳法，当2n =时，12{1},{2}A A ==，可进行2(21)12⨯-=次操作．若结论对n 成立，考虑1n +的情况．先将1{1,2,...,}A n =与2{2,3,...,1}A n =+进行一次操作，得到的交集{2,3,...,}n 留下，并集继续与3{3,4,...,2}A n =+进行操作，得到的交集{3,4,...,1}n +留下，并集继续与4A 进行操作，依此类推．进行完n 次操作后，得到原来所有集合的并集{1,2,...,2}n 及另外n 个集合{2,3,...,}n ，{3,4,...,1}n +，……，{1,2,...,21}n n n ++-．下面仅考虑后n 个集合之间的操作．由于将所有元素都减1并不改变集合间的关系，故可考虑集合{1,2,...,1}n -，{2,3,...,}n ，……，{,1,...,22}n n n +-．而由归纳假设，这些集合之间可以操作2(1)2n n n C -=次，故原来的1n +个集合可以操作21(1)(1)22n n n n n n C +-++==次，即此结论对1n +也成立． 综上所述，操作次数的最大可能值为2(1)2n n n C -=．。

2015 年全国高中数学联合竞赛参考答案及评分标准一试一、填空题：本大题共8小题，每小题8分，满分64分．1．设b a ,为不相等的实数，若二次函数b ax x x f ++=2)(满足)()(b f a f =，则=)2(f 答案：4.解：由己知条件及二次函数图像的轴对称性，可得22a b a+=-，即20a b +=，所以(2)424f a b =++=．2．若实数α满足ααtan cos =，则αα4cos sin 1+的值为 ． 答案：2. 解：由条件知，ααsin cos 2=，反复利用此结论，并注意到1sin cos 22=+αα，得)cos 1)(sin 1(sin sin sin cos cos sin 122224αααααααα-+=++=+ 2cos sin 22=-+=αα．3．已知复数数列{}n z 满足),2,1(1,111⋅⋅⋅=++==+n ni z z z n n ，其中i 为虚数单位，n z 表示n z 的共轭复数，则=2015z ．答案：2015 + 1007i ．解：由己知得，对一切正整数n ，有211(1)11(1)2n n n n z z n i z ni n i z i ++=+++=+++++=++, 于是201511007(2)20151007z z i i =+⨯+=+．4．在矩形ABCD 中，1,2==AD AB ，边DC 上（包含点D 、C ）的动点P 与CB 延长线上（包含点B ）的动点Q =，则PQ PA ⋅的最小值为 ． 答案34． 解：不妨设 A ( 0 , 0 ) , B ( 2 , 0 ) , D ( 0 , l ) ．设 P 的坐标为（t , l) （其中02t ≤≤），则由||||DP BQ =得Q 的坐标为（2，-t )，故(,1),(2,1)PA t PQ t t =--=---,因此，22133()(2)(1)(1)1()244PA PQ t t t t t t ⋅=-⋅-+-⋅--=-+=-+≥．当12t =时，min 3()4PA PQ ⋅=．5．在正方体中随机取三条棱，它们两两异面的概率为 ． 答案：255．解：设正方体为ABCD-EFGH ，它共有12条棱，从中任意取出3条棱的方法共有312C =220种．下面考虑使3条棱两两异面的取法数．由于正方体的棱共确定3个互不平行的方向（即 AB 、AD 、AE 的方向），具有相同方向的4条棱两两共面，因此取出的3条棱必属于3个不同的方向．可先取定AB 方向的棱，这有4种取法．不妨设取的棱就是AB ，则AD 方向只能取棱EH 或棱FG ，共2种可能．当AD 方向取棱是EH 或FG 时，AE 方向取棱分别只能是CG 或DH ．由上可知，3条棱两两异面的取法数为4×2=8，故所求概率为8222055=．6．在平面直角坐标系xOy 中，点集{}0)63)(63(),(≤-+-+y x y x y x 所对应的平面区域的面积为 ． 答案：24．解：设1{(,)||||3|60}K x y x y =+-≤． 先考虑1K 在第一象限中的部分，此时有36x y +≤,故这些点对应于图中的△OCD 及其内部．由对称性知，1K 对应的区域是图中以原点O为中心的菱形ABCD 及其内部．同理，设2{(,)||3|||60}K x y x y =+-≤，则2K 对应的区域是图中以O 为中心的菱形EFGH 及其内部．由点集K 的定义知，K 所对应的平面区域是被1K 、2K 中恰好一个所覆盖的部分，因此本题所要求的即为图中阴影区域的面积S ．由于直线CD 的方程为36x y +=，直线GH 的方程为36x y +=，故它们的交点P 的坐标为33(,)22．由对称性知，138842422CPG S S ∆==⨯⨯⨯=．7．设ω为正实数，若存在实数)2(,ππ≤<≤b a b a ，使得2sin sin =+b a ωω，则ω的取值范围为 ． 答案：9513[,)[,)424w ∈+∞．解：2sin sin =+b a ωω知，1sin sin ==b a ωω，而]2,[,ππωωw w b a si ∈，故题目条件等价于：存在整数,()k l k l <，使得 ππππππw l k w 22222≤+≤+≤． ① 当4w ≥时，区间]2,[ππw w 的长度不小于π4，故必存在,k l 满足①式． 当04w <<时，注意到)8,0(]2,[πππ⊆w w ，故仅需考虑如下几种情况：(i) ππππw w 2252≤<≤，此时21≤w 且45>w 无解；(ii) ππππw w 22925≤<≤，此时2549≤≤w ;(iii) ππππw w 221329≤<≤，此时29413≤≤w ,得4413<≤w ．综合(i)、(ii)、(iii)，并注意到4≥w 亦满足条件，可知9513[,)[,)424w ∈+∞．8．对四位数abcd (9d ,0,91≤≤≤≤c b a ，)，若,,,d c c b b a ><>则称abcd 为P 类数；若d c c b b a <><,,，则称abcd 为Q 类数，用N(P)和N(Q)分别表示P 类数与Q 类数的个数，则N(P)-N(Q)的值为 ．答案：285．解：分别记P 类数、Q 类数的全体为A 、B ，再将个位数为零的P 类数全体记为0A ，个位数不等于零的尸类数全体记为1A ．对任一四位数1A abcd ∈，将其对应到四位数dcba ，注意到1,,≥><>d c c b b a ，故B dcba ∈．反之，每个B dcba ∈唯一对应于从中的元素abcd ．这建立了1A 与B 之间的一一对应，因此有011()()||||||||||||N P N Q A B A A B A -=-=+-=．下面计算0||A 对任一四位数00A abc ∈, b 可取0, 1，…，9，对其中每个b ，由9≤<a b 及9≤<c b 知，a 和c 分别有b -9种取法，从而992200191019||(9)2856b k A b k ==⨯⨯=-===∑∑． 因此，()()285N P N Q -=．二、解答题：本大题共3小题，满分56分，解答应写出文字说明、证明过程或演算步骤。

中国女子数学奥林匹克竞赛获奖名单中国女子数学奥林匹克竞赛是中国数学学会举办的一项重要赛事，旨在选拔和培养我国优秀的女生数学人才。

自1987年首次举办以来，已经有许多杰出的女生在这个赛场上展现了自己的才华和智慧。

本文将为您呈现中国女子数学奥林匹克竞赛的获奖名单。

第一届中国女子数学奥林匹克竞赛于1987年在北京举行。

在这届比赛中，共有来自各省市的237名优秀女生参加了角逐。

最终，经过激烈的竞争，有数名选手脱颖而出，收获了一等奖，并成为了第一届比赛的获奖者。

随着时间的推移，中国女子数学奥林匹克竞赛逐渐吸引了更多女生的参与。

每年，来自全国各地的女生都会积极备战这个赛事。

在接下来的几届比赛中，越来越多的女生展现出非凡的数学才华，并获得了丰厚的奖励。

记忆最深刻的莫过于2010年的中国女子数学奥林匹克竞赛。

该次比赛吸引了全国范围内的顶尖女生参与，在激烈的角逐中，一位名叫李婷婷的选手表现出色，以出色的答题能力和深厚的数学素养获得了一等奖，并成为这一届比赛的明星选手。

中国女子数学奥林匹克竞赛一直以来都受到了社会各界的高度关注和重视。

这也得益于这个赛事对于提高女生数学水平和培养数学人才的重要作用。

更为令人振奋的是，中国女子数学奥林匹克竞赛的获奖选手也在国际舞台上崭露头角，为中国的数学事业赢得了荣誉。

作为中国数学事业的重要组成部分，中国女子数学奥林匹克竞赛的获奖名单就如同一本鲜活的年鉴，记录了中国女生们在数学领域的卓越表现。

让我们一同期待，未来还会有更多优秀的中国女生在数学的舞台上绽放光彩。

总结：中国女子数学奥林匹克竞赛自1987年首次举办以来，已经有许多杰出的女生在这个赛场上展现了自己的才华和智慧。

每年来自全国各省市的女生积极备战并参加比赛。

通过这个赛事，不仅提高了女生的数学水平，也为国家培养了一大批数学人才。

中国女子数学奥林匹克竞赛的获奖选手还在国际舞台上取得了优异的成绩，为中国争得了光荣。

期待未来会有更多优秀的中国女生在数学领域继续发光发热。

P 1 B ． C ．P 3 D ．P 4
第2题图 第3题图 第4题图
．如图，圆上有A 、B 、C 三点，直线l 与圆相切于点CD 平分∠ACB ，且与=80°，=60°ADC 的度数为（ ⌒
BC 80° B ．D ．95°
．如图，△OAB 与△OCD 为位似中心的位似图形，相似比为1：4，∠AD ＜tan α＜334
3
3，与直
第13题图 第14题图 第16题图
．如图，将半径为5的半圆的直径平行于桌面上的直线b ，然后把半圆沿直线b 进行无滑动滚动，直到半圆的直径与直线b 重合为止，则圆心O 运动路径的长度为 ．．正数m ，n 满足m +的值为　
42016
8
23
≈1.414，≈1.732）
备用图
、AB 、AD 三次反弹后整理得：x 2－2x +2=0，5，过D 作DE ⊥x 轴，∴无论k 取何
-=-=.1,
1y x 的图象的示意图如图，
轴的交点为B （+-n n =90°，=AD － 圆的周长，则圆心O 运动路径的长度为：
n
）－3=0，。