电路的暂态分析习题解答

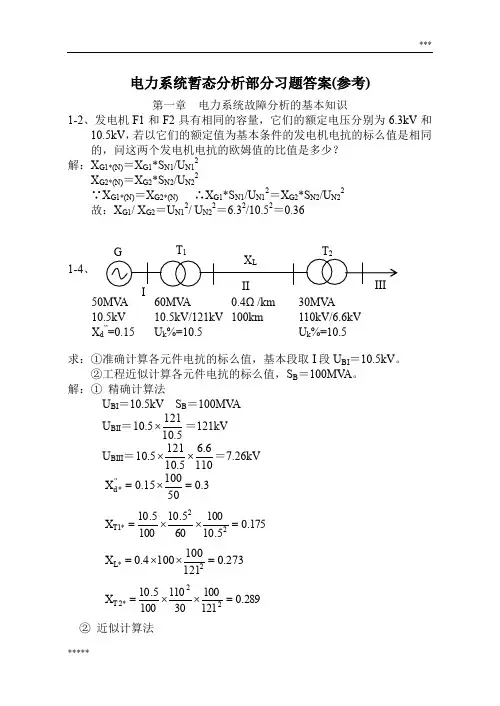
电力系统暂态分析部分习题答案(参考)第一章 电力系统故障分析的基本知识1-2、发电机F1和F2具有相同的容量，它们的额定电压分别为6.3kV 和10.5kV ，若以它们的额定值为基本条件的发电机电抗的标么值是相同的，问这两个发电机电抗的欧姆值的比值是多少？ 解：X G1*(N)＝X G1*S N1/U N12 X G2*(N)＝X G2*S N2/U N22∵X G1*(N)＝X G2*(N) ∴X G1*S N1/U N12＝X G2*S N2/U N22 故：X G1/ X G2＝U N12/ U N22＝6.32/10.52＝0.361-4、求：①准确计算各元件电抗的标么值，基本段取I 段U BI ＝10.5kV 。

②工程近似计算各元件电抗的标么值，S B ＝100MV A 。

解：① 精确计算法U BI ＝10.5kV S B ＝100MV AU BII ＝5.101215.10⨯＝121kVU BIII ＝1106.65.101215.10⨯⨯＝7.26kV 3.05010015.0''*=⨯=d X 175.05.10100605.101005.1022*1=⨯⨯=T X 273.01211001004.02*=⨯⨯=L X 289.0121100301101005.1022*2=⨯⨯=T X ② 近似计算法50MV A 10.5kV X d ’’=0.15 60MV A 10.5kV/121kV U k %=10.5 0.4Ω/km 100km 30MV A 110kV/6.6kV U k %=10.5U B ＝U av S B ＝100MV A3.05010015.0''*=⨯=d X 175.0601001005.10*1=⨯=T X302.01151001004.02*=⨯⨯=L X 35.0301001005.10*2=⨯=T X1-5、某一线路上安装一台Xk%＝5的电抗器，其额定电流为150A ，额定电压为6kV ，若另一台额定电流为300A 、额定电压为10kV 的电抗器来代替它，并要求保持线路的电抗欧姆值不变，问这台电抗器的电抗百分数值应是多少？ 解：∵2221113100%3100%N N R N N R R I UX I U X X ⨯=⨯=∴61503001065%%122112=⨯⨯=⨯⨯=N N N N R R I I U U X X1-12、(1) 若短路前空载，计算短路电流的周期分量及短路电流最大有效值； (2) 若A 相非周期分量电流的初值为零及最大时，计算相应的B 、C 相非周期分量电流的初始值；(3) 若短路前变压器满负荷运行，功率因数为0.9（低压侧），计算最大非周期分量电流的初始值，并与空载时短路比较。

暂态分析复习题一、单项选择题：1、 储能元件的初始储能在电路中产生的响应(零输入响应)( )。

(a)仅有稳态分量(b)仅有暂态分量 (c)既有稳态分量，又有暂态分量2、 图示电路在换路前处于稳定状态，在t = 0 瞬间将开关S 闭合，则 i ( 0+ )为 ( )。

(a) 0 A (b) 0.6 A(c) 0.3 AF3、R ，C 电路外部激励为零，而由初始储能引起的响应称为( ) 响 应。

(a) 稳 态(b) 零 输 入(c) 零 状 态4、 R ，C 电 路 初 始 储 能 为 零，而 由 初 始 时 刻 施 加 于 电 路 的 外 部 激 励引 起 的 响 应 称 为( ) 响 应。

(a) 暂 态(b) 零 输 入 (c) 零 状 态二、非客观题：图 示 电 路 原 已 稳 定，t = 0 时 将 开 关 S 闭 合, 已 知 : R 1 = 60 Ω，R 2 = 120Ω，R 3 = 40 Ω， L = 4 H ，U S V 124=，U S V 220=。

求 开 关 S 闭 合 后 的 线 圈 电流 i t L ()。

S 2三、非客观题：图 示 电 路 原 已 稳 定，t = 0 时 将 开 关 S 闭 合。

已 知：R 1 = 6 Ω，R 2 = 3 Ω，C = 1 F ，U S = 9 V 。

求 S 闭 合 后 的 i t () 和 u t ()。

u+四、非客观题：图 示 电 路 原 已 稳 定，t = 0 时 将 开 关 S 闭 合。

已 知：R 1 = R 2 = 2 k Ω，L =200 mH ，U S = 12 V 。

求 S 闭 合 后 的 电 流 i t L ()，并 画 出 其 变 化 曲 线。

L五、非客观题：图 示 电 路 原 已 稳 定，已 知：R = 1 k Ω，C = 20 μF ，U S = 50 V ，t = 0 时 将 开 关S 闭 合。

(1) 若 u C ()00-= ，求 C 充 电 到 u U C =S /2 所 需 时 间 t 1 ；(2) 若 u C = (0－) = U S / 2 ， 求 C 充 电 t 1 秒 后 的 u C 值 。

电路暂态过程试题及答案一、选择题（每题5分，共20分）1. 在电路暂态过程中，电感元件的初始电流为零，其电压初始值是多少？A. 0B. ∞C. 0VD. ∞V答案：D2. 电容器在电路暂态过程中，初始电压为零，其初始电流是多少？A. 0B. ∞C. 0AD. ∞A答案：B3. 电路暂态过程的时间常数τ是由什么决定的？A. 电阻B. 电感C. 电容D. 电阻和电感的比值答案：D4. 在RC电路中，时间常数τ等于什么？A. R/CB. C/RC. R*CD. R+C答案：C二、填空题（每题5分，共20分）1. 在RL电路中，时间常数τ等于__________。

答案：L/R2. 当电路中的电感元件突然断开时，电感两端的电压会__________。

答案：瞬间增大3. 在RC电路中，电容两端的电压在时间常数τ后将达到稳态值的__________。

答案：63.2%4. 在RL电路中，电感两端的电压在时间常数τ后将达到稳态值的__________。

答案：63.2%三、简答题（每题10分，共40分）1. 简述电路暂态过程的特点。

答案：电路暂态过程是指电路在受到外部激励或参数变化后，电路状态从初始状态向稳态过渡的过程。

在这个过程中，电路中的电感、电容等元件会表现出与稳态不同的特性，如电感的电压初始值无穷大，电容的初始电流无穷大。

2. 什么是电路的时间常数τ，它在电路分析中有什么作用？答案：时间常数τ是电路暂态过程中的一个重要参数，它表征了电路达到稳态的快慢。

对于RC电路，τ=R*C；对于RL电路，τ=L/R。

时间常数τ越大，电路达到稳态所需的时间越长。

3. 在电路暂态过程中，电感元件的电压和电流是如何变化的？答案：在电路暂态过程中，电感元件的电压会随着电流的变化而变化，根据电感的伏秒特性，电流变化率越大，电感两端的电压变化也越大。

而电感元件的电流变化则受到电压变化的影响，电压变化越快，电流变化也越快。

4. 在电路暂态过程中，电容元件的电压和电流是如何变化的？答案：在电路暂态过程中，电容元件的电压会随着电荷的积累而逐渐增加，而电流则会随着电压的增加而逐渐减小。

电路的暂态分析习题解答公司内部档案编码：[OPPTR-OPPT28-OPPTL98-第五章 电路的暂态分析题图所示各电路在换路前都处于稳态，求换路后电流i 的初始值和稳态值。

解：（a ）A i i L L 326)0()0(===-+，换路后瞬间 A i i L 5.1)0(21)0(==++稳态时，电感电压为0， A i 326==（b ）V u u C C 6)0()0(==-+， 换路后瞬间 02)0(6)0(=-=++C u i 稳态时，电容电流为0， A i 5.1226=+=（c ）A i i L L 6)0()0(11==-+，0)0()0(22==-+L L i i 换路后瞬间 A i i i L L 606)0()0()0(21=-=-=+++ 稳态时电感相当于短路，故 0=i(a)(b)(d)(c)CC2Ω2+6V -题5.1图i（d ）2(0)(0)6322C C u u V +-==⨯=+ 换路后瞬间 6(0)63(0)0.75224C u i A ++--===+ 稳态时电容相当于开路，故 A i 12226=++=题图所示电路中，S 闭合前电路处于稳态，求u L 、i C 和i R 的初始值。

解：换路后瞬间 (0)6L i A +=，(0)3618C u V +=⨯=(0)6(0)0R L i i ++=-=(0)18(0)(0)6033C C L u i i +++=-=-=(0)(0)(0)0L C R u u Ri ++++==，(0)(0)18L C u u V ++=-=-求题图所示电路换路后u L 和i C 的初始值。

设换路前电路已处于稳态。

解：换路后，(0)(0)4L L i i mA +-==，所以换路后4mA 电流全部流过R 2，即(0)4C i mA +=由于(0)(0)8C C u u V +-==，故2(0)(1)(0)(0)20812L L c u R R i u V +++=-++=-+=-Ω+u L -题5.2图题5.3图C题图所示电路中，换路前电路已处于稳态，求换路后的i 、i L 和 u L 。

第一章1-2-1 对例1-2，取kV 1102=B U ，MVA S B 30=,用准确和近似计算法计算参数标幺值。

解：①准确计算法：选取第二段为基本段，取kV 1102=B U ，MVA S B 30=，则其余两段的电压基准值分别为：9.5kV kV 1101215.10211=⨯==B B U k U kV6.66.6110110223===k U U B B 电流基准值：kA U S I B B B 8.15.9330311=⨯==kA U S I B B B 16.0110330322=⨯==3 2.62B I kA ===各元件的电抗标幺值分别为：发电机：32.05.930305.1026.0221=⨯⨯=*x变压器1T ：121.05.3130110121105.02222=⨯⨯=*x输电线路：079.011030804.023=⨯⨯=*x 变压器2T ：21.01103015110105.02224=⨯⨯=*x电抗器： 4.03.062.26.6605.05=⨯⨯=*x 电缆线路：14.06.6305.208.026=⨯⨯=*x 电源电动势标幺值： 16.15.911==*E ②近似算法：取MVA S B 30=，各段电压电流基准值分别为：kV U B 5.101=，kA I B 65.15.103301=⨯=kV UB 1152=，20.15B I kA ==kV UB 3.63=，3 2.75B I kA ==各元件电抗标幺值：发电机：26.05.1030305.1026.0221=⨯⨯=*x变压器1T ： 2300.1050.131.5x *=⨯= 输电线路： 073.011530804.023=⨯⨯=*x 变压器2T ： 4300.1050.2115x *=⨯= 电抗器： 44.03.075.23.6605.05=⨯⨯=*x 电缆线路：151.03.6305.208.026=⨯⨯=*x 电源电动势标幺值： 05.15.1011==*E 习题2 解：（1）准确计算：3(110)115B B U U kV ==322220115209.1121B B U U kV k ==⨯= 312122010.51159.1121242B B U U kV k k ==⨯⨯= 各段的电流基准值为：114.0B I kA ===20.6B I kA ===3 1.1B I kA ===各元件的电抗标幺值分别为：发电机：21210.52200.300.292400.89.1x *=⨯⨯=变压器1T ：222210.52200.140.143009.1x *=⨯⨯=输电线路：322200.422300.49209.1x *=⨯⨯= 变压器2T ：24222202200.140.12280209.1x *=⨯⨯= (2) 近似算法：kV UB 5.101=，112.10B I kA ==2231B U kV =，20.55B I kA ==3121B U kV =，3 1.05B I kA ==各元件电抗标幺值：发电机：12200.300.22240/0.8x *=⨯=变压器1T ： 22200.140.10300x *=⨯= 输电线路：322200.422300.40231x *=⨯⨯=变压器2T ： 42200.140.11280x *=⨯= 习题3 要点：以下摘自《国家电网公司电力系统安全稳定计算规定》：暂态稳定是指电力系统受到大扰动后，各同步电机保持同步运行并过渡到新的或恢复到原来稳态运行方式的能力，通常指保持第一、第二摇摆不失步的功角稳定，是电力系统功角稳定的一种形式。

一、单选题1、工程上认为R＝25Ω、L=50mH的串联电路中发生暂态过程时将持续（）。

A.0～2msB.37.5～62.5msC.6～10msD.30～50ms正确答案：C2、在换路瞬间，下列说法中正确的是（）。

A.电感电流不能跃变B.电容电流不能跃变C.电感电压必然跃变D.电容电流必然跃变正确答案：A3、电容元件是（）元件。

A.线性元件B.耗能元件C.储能元件D.以上答案都不对正确答案：C4、关于RL电路的时间常数，下面说法正确的是（）A.与R成反比，与L成正比B.与R、L成正比C.与R成正比，与L成反比D.与R、L成反比正确答案：A5、动态电路工作的全过程是（）。

A.换路—前稳态—过渡过程—后稳态B.换路—前稳态—后稳态—过渡过程C.前稳态—过渡过程—换路—后稳态D.前稳态—换路—过渡过程—后稳态正确答案：D二、判断题1、换路定理指出：电感两端的电压是不能发生跃变的，只能连续变化。

（）正确答案：×2、RC串联电路如果在C两端再并联一个电阻，则时间常数会变大。

（）正确答案：×3、三要素法只能计算全响应，不能计算零输入响应和零状态响应。

（）正确答案：×4、求解时间常数时，一定要使动态电路处于换路之前的状态。

（）正确答案：×5、动态电路在换路时一定产生过渡过程。

（）正确答案：√6、时间常数越小，电路的变化速度越慢。

（）正确答案：×。

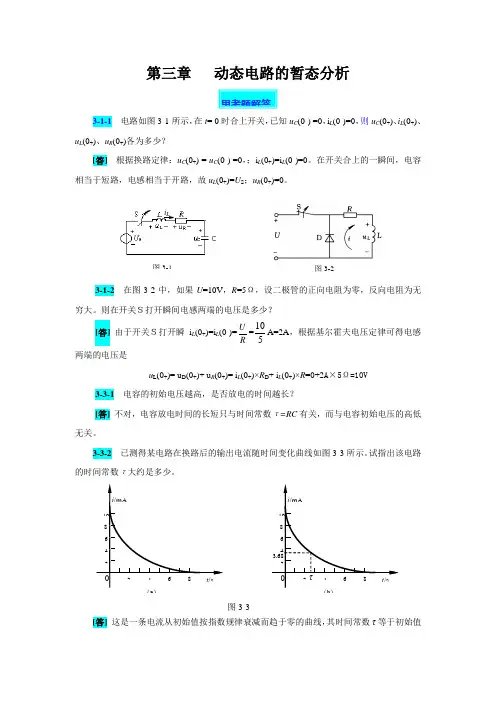
第三章 动态电路的暂态分析 3-1-1 电路如图3-1所示，在t = 0时合上开关，已知u C (0-) =0，i L (0-)=0，则u C (0+)、i L (0+)、u L (0+)、u R (0+)各为多少？[答] 根据换路定律：u C (0+) = u C (0-) =0，；i L (0+)=i L (0-)=0。

在开关合上的一瞬间，电容相当于短路，电感相当于开路，故u L (0+)=U S ；u R (0+)=0。

3-1-2 在图3-2中，如果U =10V ，R =5Ω，设二极管的正向电阻为零，反向电阻为无穷大。

则在开关Ｓ打开瞬间电感两端的电压是多少？[答] 由于开关Ｓ打开瞬i L (0+)=i L (0-)=R U =510A=2A ，根据基尔霍夫电压定律可得电感两端的电压是u L (0+)= u D (0+)+ u R (0+)= i L (0+)×R D + i L (0+)×R =0+2A ×5Ω=10V3-3-1 电容的初始电压越高，是否放电的时间越长？[答] 不对，电容放电时间的长短只与时间常数τ=RC 有关，而与电容初始电压的高低无关。

3-3-2 已测得某电路在换路后的输出电流随时间变化曲线如图3-3所示。

试指出该电路的时间常数τ大约是多少。

[答] 这是一条电流从初始值按指数规律衰减而趋于零的曲线，其时间常数τ等于初始值思考题解答 图3-3 0 2 4 6 8 2 46810i /mAt /s (a) 02 4 6 8 24 6 8 10 i /mA t /s τ 3.68(b) ii iii L 图3-1 图3-2下降了总变化量的63.2%所需的时间。

电流初始值为10mA，故下降到3.68 mA所需的时间即为时间常数τ。

据此作图如图3-3（b）所示，可知τ大约为2.7s左右。

3-3-3 在图3-4中，开关长期合在A上，如在ｔ＝0时把它合到B上。

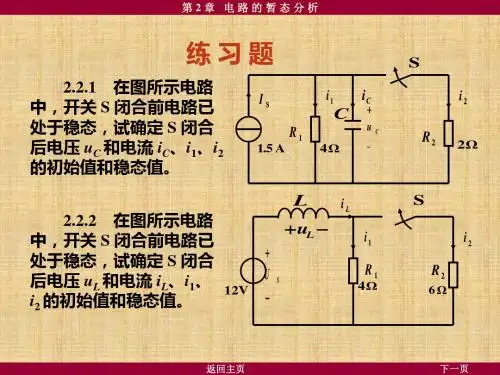
《电工技术基础》复习题电路的暂态分析一、填空题1、图示电路在换路前处于 稳 定 状 态，在 t = 0 瞬 间 将 开 关 S 闭 合，则 i ( 0+ )为 。

F2、R ，C 电 路 外 部 激 励 为 零， 而 由 初 始 储 能 引 起 的 响 应 称 为 响 应。

3、R ，C 电 路 初 始 储 能 为 零，而 由 初 始 时 刻 施 加 于 电 路 的 外 部 激 励 引 起 的响 应 称 为 响 应。

4、在开关S 闭合瞬间，图示电路中的 i R ，i L ，i C 和 i 这 四个量中，发 生 跃 变 的 量 是 。

5、在 图 示 电 路 中，开 关 S 在 位 置“1” 的 时 间 常 数 为 τ1，在 位 置“2” 的 时 间 常数 为 τ2 ， τ1 和 τ2 的 关 系 是 。

6、图 示 电 路 在 开 关 S 闭 合 后 的 时 间 常 数 τ 值 为 。

7、图 示 电 路 中，开 关 S 在 t = 0 瞬 间 闭 合，若 u C ()00-=V ，则 i 1 ( 0+) 为 。

C8、在 图 示 电 路 中，开 关 S 在 t = 0 瞬 间 闭 合，若 u C ()00-=V ， 则 u L ()0+= 。

S10 V 1 Ω10 μFu C 1 H 1 ΩU Su Lk k －+－++－9、R ，L 串 联 电 路 与 电 压 为 8 V 的 恒 压 源 接 通，如 图 1 所 示。

在 t = 0 瞬 间 将 开 关S 闭 合，当 电 阻 分 别 为 10 Ω，50 Ω，20 Ω，30 Ω 时 所 得 到 的 4 条 u t L () 曲 线 如 图 2。

其 中 10 Ω 电 阻 所 对 应 的 u t L () 曲 线 是 。

10、图 示 电 路 i 1 (t ) 的 时 间 常 数 为 。

U S 6 Ω3 Ω12 Vi 10.8 H1L－+二、选择题1、 储 能 元 件 的 初 始 储 能 在 电 路 中 产 生 的 响 应 ( 零 输 入 响 应 )( )。

第5章 思考与练习一、填空1． 电路在换路时，电路中的 不能突变。

2． 电路在换路时，电感上的电流不能突变，电容上的 不能突变。

3． 电路形成过渡过程的充分必要条件： 。

4． 暂态的分析方法分为 和 。

5． RC 电路充电过程的快慢是由时间常数来决定的，其大小为 。

6． 一阶电路的三要素是 、 和 。

7． 换路定则是 。

二、选择题1．电容在充电过程中，其 是不能突变的。

A ．电流B ．电路C ．端电压2．RC 电路充电过程的快慢是由时间常数来决定的，τ越大，充电越 ，过渡过程需要的时间就越 。

A ．慢，长B ．慢，短C ．快，长3．电路从一个稳定状态过渡到另一个稳定状态所经历的过程称 。

A ．稳定过程B ．过渡过程C ．暂态过程4．电路在换路时，电路中的能量不能突变，对于电容元件，其储有电能为 。

A ．221C Cu B ．241C Cu C ．C Cu 21 5．电路在换路时，电路中的能量不能突变，对于电感元件，其储有电能为 。

A ．221L Li B ．241L Li C ．L Li 21 三、思考与计算1．在图5.01中，V 100=E ，Ω=11R ，Ω=992R ，µ10=C F ，试求：S 闭合瞬间（+=0t ），各支路电流及各元件两端电压的数值；（2）S 闭合后到达稳定状态时各支路电流及各元件两端电压的数值。

图5.01 习题5.01图 图5.02 习题5.02图 2. 如图6.02所示，开关闭合时电容充电，再断开时电容放电，分别求充电及放电时电路的时间常数。

选 择 题1. 电路如图5-47所示，换路前电路处于稳态，在0=t 时开关S 闭合，则电路的初始值电流)0(+i 为（ ）。

（a ）0.25A （b ） 0.5A （c ）0.75A （d ） 0 A分析：根据换路定则，换路瞬间电容两端的电压不变为10)0()0(==−+C C u u V ，而换路后的瞬间电路的初始值电流)0(+i 与电容两端的电压满足欧姆定律，A 5.020)0()0(==++C U i 。

答案：（b ）2. 电路如图5-48所示，换路前电路处于稳态，在0=t 时开关S 闭合，则电路的初始值电流)0(+C i 为（ ）。

（a ）0.25A （b ） 0.5A （c ）0.75A （d ） 0A分析：根据换路定则，换路后的瞬间电容两端的电压保持不变，为0)0()0(==−+C C u u V ，电阻电流为0A ，电路的初始值电流A 5.0A 2010)0(C ==+i 。

答案：（b ）3. 电路如图5-49所示，换路前电路处于稳态，在0=t 时开关S 闭合，则电路的初始值电流)0(+i 为（ ）。

图5-47 选择题1图Fμ10图5-48 选择题2图FμC 1020（a ） 0A （b ） 0.25A （c ）0.5A （d ） 0.75A分析：根据换路定则，换路后的瞬间流过电感的电流保持不变，A 5.0A 2010)0()0(L L ===−+i i ，+=0t 时刻的等效电路如下图所示由+=0t A 0)0(=+。

答案：（a ）4. 电路如图5-500=时开关S 闭合，则电路的初始值电压)0(L +u 为（ ）。

（a ） 0V （d ） 7.5V分析：根据换路定则，换路后的瞬间流过电感的电流保持不变，A 0)0()0(L L ==−+i i ，所以在+=0t 时刻，电感相当于开路，由+=0t 时刻的等效电路可知，V 5)0(L =+u 。

答案：（b ）5-5. 电路如图5-51所示，换路前电路处于稳态，在0=t 时开关S 闭合，该电路将产生过渡过程的原因是（ ）。

电力系统暂态分析试卷（1）一、（25分）简答1．什么是电力系统短路故障？故障的类型有哪些？2．列出电力系统的各电压等级对应的平均额定电压？3．同步发电机三相短路时为什么要进行派克变换？4．分裂电抗的作用是什么？5．简述运算曲线法计算三相短路电流的步骤。

二、(15分)下图为一无穷大功率电源供电系统，设在K点发生三相短路，如果设计要求通过电源的冲击电流不得超过30 KA,问并行敷设的电缆线路最多容许几条？(K M=1.8)若选S B=100 MVA，U B=U av，试计算：(1) 电源G及系统S对f 点的转移电抗x Gf、x Sf。

(2) 如果根据运算曲线查得t = 0.2 秒时电源G的短路电流标么值为=2.6，则t = 0.2 秒时短路点总电流的有名值是多少？IG02.''四、（10分）系统接线如图所示, 当f 点发生不对称接地短路故障时, 试作出相应的各序等值网络。

(略去各元件电阻和所有对地导纳及变压器励磁导纳)五、（10分）如图所示系统，电抗为归算到统一基准值下的标么值（S B =100MVA ，U B =平均额定电压），用正序等效定则计算以下各种情况短路时，短路点的A 相正序电流有名值，（1）三相短路；（2）A 相接地短路；六、（10分）如图所示系统，求发电机电势E q 和静态稳定储备系数K p ？（注：图中参数为归算到统一基准值下的标么值S B =100MVA ，U B =平均额定电压）七、（15分）有一简单系统，已知发电机参数2.0='dx ，E΄ =1.2，原动机功率P T =1.5，线路参数如图所示，无穷大电源电压000.1∠=c U ，如果开关K 突然合上，电容电抗Xc=0.3试判断该系统能否保持暂态稳定?电力系统暂态分析试卷(2)一、简答（25分）1. 什么是短路？简述短路的现象和危害？2. 什么是短路冲击电流？出现冲击电流的条件是什么？3. 为什么同步发电机定、转子绕组的电感系数矩阵中会有零元素？4. 变压器中性点接小电阻的作用是什么？简要分析理由。

第三章 电路的暂态分析含有电感或电容储能元件的电路，在换路时会出现暂态过程。

本章研究了暂态过程中电压与电流的变化规律。

主要内容：1．暂态过程的基本概念。

2．换路定则：在换路瞬间，电容电流和电感电压为有限值的情况下，电容电压 和电感电流在换路前后的瞬间保持不变。

3．RC 电路的零输入响应、零状态响应和全响应。

4．RL 电路的零输入响应、零状态响应和全响应。

5．一阶线性电路暂态分析的三要素法：一阶线性电路在直流激励下的全响应零、 输入响应和零状态响应都可以用三要素法τte f f f t f -+∞-+∞=)]()0([)()(来求出。

6．暂态过程的应用：对于RC 串联电路，当输入矩形脉冲，若适当的选择参数 和输出，可构成微分电路或积分电路。

[练习与思考]解答3-1-1什么是稳态？什么是暂态？解：当电路的结构、元件参数及激励一定时，电路的工作状态也就一定，且电流和电压为某一稳定的值，此时电路所处的工作状态就称为稳定状态，简称为稳态。

在含有储能元件的电路中，当电路的发生换路时，由于储能元件储的能量的变化，电路将从原来的稳定状态经历一定时间变换到新的稳定状态，这一变换过程称为过渡过程，电路的过渡过程通常是很短的，所以又称暂态过程。

3-1-2什么是暂态过程？产生暂态过程的原因是什么？解：含有储能元件的电路从一个稳态转变到另一个稳态的所需的中间过程称为电路的暂态过程（过渡过程）。

暂态过程产生的内因是电路中含有储能元件，外因是电路发生换路。

3-2-1 初始值和稳态值分别是暂态过程的什么时刻的值？解：初始值是暂态过程的+=0t 时刻的值，稳态值是暂态过程的∞=t 时刻的值。

3-2-2 如何求暂态过程的初始值？解：求暂态过程初始值的步骤为:⑴首先画出换路前-=0t 的等效电路，求出-=0t 时刻电容电压)0(-C u 和电感电流)0(-L i 的值。

对直流电路，如果换路前电路处于稳态，则电容相当于开路，电感相当于短路。

第三章 电路的暂态分析3.2.1 图3.01所示各电路在换路前都处于稳态，试求换路后其中电流i 的初始值(0)i +和稳态值()i ∞。

(b)(a)(c)(d)图3.01解： （a ）A 5.1265.0)0(5.0)0(21)0(=×===−++L L i i i A 326)(==∞i（b ）02662)0(62)0(6)0(=−=−−=−=++c c u u iA 5.1226)(=+=∞i （c ）A 6)0()0(==−+i i A 0)(=∞i（d ）A 75.04364)0(622)0(6)0(=−=−=+−=−++c c u u iA 12226)(=++=∞i3.4.1 在图3.07(a)的电路中，u 为一阶跃电压，如图3.07(b)所示，试求3i 和c u 。

设V 1)0(c =−u 。

(a)图3.07(b)解：s 102)(331312−×=++=C R R R R R τV 22224)(C =+×=∞u V 1)0()0(C C ==−+u u V 2)(500C t e t u −−=mA 75.0)(1)(4)0(31131312322323213=+++++++=+R R R R R R R R R R R R R R R R i mA 144)(3==∞imA 25.01)(5003t e t i −−=3.4.2 电路如图3.08所示，求0t ≥时(1)电容电压C u ，(2)B 点电位B v 和(3)A 点电位A v 的变化规律。

换路前电路处于稳态。

Sk 10图3.08解：(1)求0≥t 时的电容电压C uV 15255)6(0)0()0(C =×+−−==−+C u uV 5.1525510)6(6)(C =×++−−=∞u[]s 1044.010100105//)2510(6123−−×=×××+=τ故V 5.05.1)5.11(5.1)(66103.21044.0C t t e et u ×−×−−=−+=−t =0_时k 10t =0+时+6V Ωk 10（2）求0≥t 时的B 点电位B v注意，+=0t 时，由于电容中存在电流，0CC ≠=dtdu Ci 因此，10K 和5K 电阻中的电流不等。

单项选择题1、短路电流最大有效值出现在（1）。

A 、短路发生后约半个周期时;2、利用对称分量法分析计算电力系统不对称故障时,应选（2)相作为分析计算的基本相.B 、特殊相3、关于不对称短路时短路电流中的各种电流分量,下述说法中正确的是（3）.C 、短路电流中除非周期分量将逐渐衰减到零外，其它电流分量都将从短路瞬间的起始值衰减到其稳态值。

4、不管电力系统发生什么类型的不对称短路，短路电流中一定存在（2）。

B 、正序分量和负序分量；5、在简单电力系统中，如某点的三序阻抗021∑∑∑==Z Z Z ，则在该地点发生不同类型短路故障时，按对发电机并列运行暂态稳定性影响从大到小排序，应为(2）.B 、三相短路、两相短路接地、两相短路、单相接地短路;6、发电机－变压器单元接线，变压器高压侧母线上短路时,短路电流冲击系数应取(2).B 、1.8；7、电力系统在事故后运行方式下,对并列运行静态稳定储备系数(%)P K 的要求是(3）.C 、(%)P K ≧10。

8、下述各组中，完全能够提高电力系统并列运行暂态稳定性的一组是（2)。

B 、变压器中性点经小电阻接地、线路装设重合闸装置、快速切除线路故障；9、对于三相三柱式变压器，其正序参数、负序参数和零序参数的关系是（2）.B 、正序参数与负序参数相同，与零序参数不同；10、分析计算电力系统并列运行静态稳定性的小干扰法和分析计算电力系统并列运行暂态稳定性的分段计算法，就其实质 而言都是为了求（1）。

A 、t -δ曲线1、计算12MW 以上机组机端短路冲击电流时,短路电流冲击系数应取（2）. B 、1。

9；2、发电机三相电压为：)sin(αω+=t U u m a 、)120sin(0-+=αωt U u m b ，)120sin(0++=αωt U u m c ，如将短路发生时刻作为时间的起点（0=t ),当短路前空载、短路回路阻抗角为800(感性）时，B 相短路电流中非周期分量取得最大值的条件是（2） B 、0110=α；3、具有阻尼绕组的凸极式同步发电机，机端发生三相短路时，电磁暂态过程中定子绕组中存在（1）。