四年级数学三角形练习题及答案.doc

人教版四年级数学下册第五单元《三角形》测试题（含答案）一、单选题1.三角形内角的度数相等，三角形内角是（）度。

A. 30B. 60C. 90D. 1502.张叔叔不小心把一块三角形的玻璃摔成了三块，他想到玻璃店买一块一样大的玻璃，他应带第（）块去。

A. 1B. 2C. 3D. 以上任意一块都行3.一个三角形如果有两条边一样长，下面描述不正确的是（）A. 一定有两个角相等B. 一定是等腰三角形C. 一定是锐角三角形D. 有可能是等边三角形4.若一个三角形的三条边长的比是1：1：1，则这是一个（）A. 钝角三角形B. 直角三角形C. 锐角三角形二、判断题5.三角形越大，它的内角和就越大。

（）6.任意一个三角形，至少有两个角是锐角。

（）7.等边三角形一定是等腰三角形。

（）8.如果一个三角形每两个内角之差都等于0，这个三角形一定是等边三角形。

（）三、填空题9.三角形的三个角∠A、∠B、∠C之和为180°，∠C=________°10.一个等腰三角形的顶角是72°，它的一个底角是________°．11.一根绳子长48厘米．（1）如果用这根绳子围成一个底为12厘米的等腰三角形，这个三角形的腰是________厘米?（2）如果用这根绳子围成一个等边三角形，这个三角形的边长是________厘米?四、解答题12.求下面角的度数．=________13.一个等腰三角形的周长是30厘米，如果三角形的腰长是8厘米，那么这个三角形的底边长是多少厘米？五、应用题14.等腰三角形有一个角是70°，它的另外两个角是多少度？参考答案一、单选题1.【答案】C【解析】【解答】解：180°÷（1+2+3）=180°÷6=30°，所以最大的内角是：3×30°=90°。

故答案为：C。

【分析】三角形的内角和是180°，先计算出每份的度数，再求出最大的内角的度数即可。

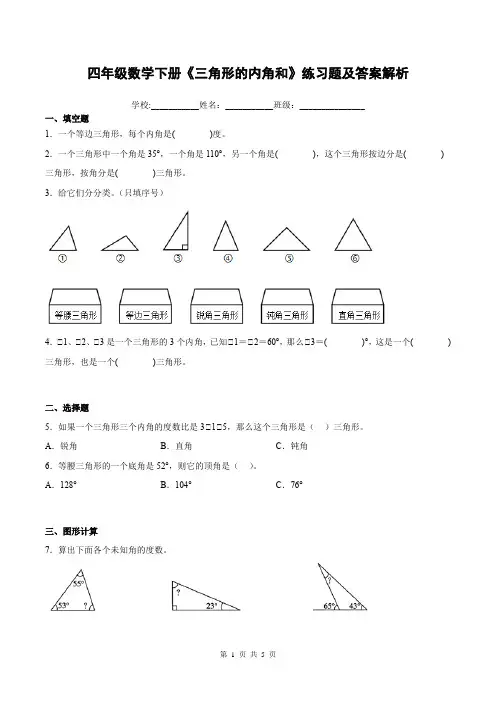
四年级数学下册《三角形的内角和》练习题及答案解析学校:___________姓名：___________班级：_______________一、填空题1．一个等边三角形，每个内角是( )度。

2．一个三角形中一个角是35°，一个角是110°，另一个角是( )，这个三角形按边分是( )三角形，按角分是( )三角形。

3．给它们分分类。

（只填序号）4．∠1、∠2、∠3是一个三角形的3个内角，已知∠1＝∠2＝60°，那么∠3＝( )°，这是一个( )三角形，也是一个( )三角形。

二、选择题5．如果一个三角形三个内角的度数比是3∠1∠5，那么这个三角形是（）三角形。

A．锐角B．直角C．钝角6．等腰三角形的一个底角是52°，则它的顶角是（）。

A．128°B．104°C．76°三、图形计算7．算出下面各个未知角的度数。

四、解答题8．用一根铁丝能围成一个长是10厘米，宽8厘米的长方形，如果用这根铁丝围成一个底边是16厘米的等腰三角形（铁丝无剩余），腰长是多少厘米？9．求出下面三角形各个角的度数。

参考答案与解析：1．60【分析】等边三角形的三个内角都相等，三角形的内角和为180°，因此用180°除以3即可，依此计算并填空。

【详解】180°÷3＝60°【点睛】此题考查的是等边三角形的特点，以及三角形的内角和，应熟练掌握。

2．35°等腰钝角【分析】利用三角形内角和定理，用180°减去已知的两个角的度数，就是第三个角的度数；然后根据三角形按边、按角分类的特点，写出三角形的分类即可。

【详解】180°﹣35°﹣110°＝35°，因为三角形中有两个角相等，所以有两条边也相等，所以这个三角形是等腰三角形；因为一个角是110°，是钝角，所以这个三角形是钝角三角形。

人教版小学数学四年级下册三角形的内角和练习卷（带解析）1．一个三角形中，有1个角是44°，另外两个角可能是（）A．96°，50° B．80°，56° C．90°，36°2．用10倍的放大镜看一个三角形，这个三角形三内角和是（）。

A．108° B．180° C．1800° D．1080°3．三角形中最大的一个角一定（）A．不小于60° B．大于90° C．小于90° D．大于60°而小于90°4．两个不相等的三角形，它们的内角和（）。

A．相等 B．面积大的三角形内角和大C．面积小的三角形内角和小 D．不能比较5．一个三角形最小的内角是50度，这是一个（）A.锐角三角形B.直角三角形C.钝角三角形D.以上都不对6．一个三角形中，有两个角都是锐角，另一个角（）A．一定是钝角 B．一定是锐角C．可能是钝角、锐角或直角7．下面能组成一个三角形的三个角是（）A．∠1= 80度，∠2= 70度，∠3 =15度B．∠1= 50度，∠2= 85度，∠3 =63度C．∠1= 60度，∠2= 60度，∠3 =70度D．∠1= 74度，∠2= 16度，∠3 =90度8．把一个等边三角形从顶点起用一条直线分成两个同样大小的三角形，其中一个三角形的内角和是（）A．30 B．60° C．90° D．180°9．一个三角形中，如图所示，∠1=70度，∠3=35度，∠2=（）A．45度 B．180度 C．75度 D．90度10．在一个等腰直角三角形中，它的一个底角是（）A．30° B．45° C．60°11．下列图形中，内角和不是180度的图形是（）A．等腰三角形 B．平行四边形 C．锐角三角形12．一个等腰三角形的顶角是60度，它的底角和是（）A．70° B．120° C．140°13．下面每组三个角，不可能在同一个三角形内的是（）A.15度、87度、78度B.120度、55度、5度C.80度、50度、50度D.90度、16度、104度14．一个直角三角形中的一个锐角是另一个锐角的2倍，则这个三角形中最小锐角是（）A．450° B．30° C．25°15．一个等腰三角形的底角为a度，顶角可表示为（）度。

四年级下册小学数学第五单元三角形测试（含答案解析）一、选择题1．下面哪一组中的三根小棒不能围成一个三角形（）A. 10cm、8cm、3cmB. 10cm、8cm、7cmC. 10cm、3cm、7cm2．等腰三角形中，有一个内角是50°，另外两个内角（）．A. 一定是50°和80°B. 一定都是65°C. 可能是50°和80°，也可能都是65°3．已知三角形的两条边长分别为1.6厘米和1.2厘米，第三条边可能长（）。

A. 0.4厘米B. 2.8厘米C. 2厘米4．在一个三角形中，其中两角之和是130°，另一个角是（）。

A. 30°B. 40°C. 50°5．如果三角形的两条边的长分别是6厘米和9厘米，那么第三条边的长度范围应是（）。

A. 大于3厘米B. 小于15厘米C. 大于3厘米小于15厘米D. 小于3厘米大于15厘米6．下面几幅图中，不能直接判断被遮三角形种类的是（）图。

A. B. C.7．下面三组木棒中（）不能拼成三角形。

（单位：厘米）A.B.C.8．如果一个三角形的两条边分别是30厘米、40厘米，第三条边的长度要在下面的三个量中选出，只能选（）A. 50厘米B. 70厘C. 80厘米9．下面三组小棒不能围成三角形的是（）A. 6cm、6cm、12cmB. 4cm、6cm、7cmC. 3cm、3cm、3cm10．三角板上最大的角是（）。

A. 锐角B. 直角C. 钝角D. 平角11．下面第（）组的三条线段不能围成三角形。

（单位：cm）A. B. C.12．下面各说法正确的是（）。

A. 直角三角形只有1条高。

B. 把1.230末尾的0去掉后，所得的数缩小到原来的。

C. 按照“四舍五入”法，近似数为5.21的最大的一位小数是5.209。

D. 所有的等边三角形都是锐角三角形。

二、填空题13．三角形ABC中，∠A=35°，∠B=52°，∠C=________，这是一个________三角形．14．用两个相同的直角三角形拼成的一个大长方形，这个大长方形的内角和是________。

三⻆角形分类练习题班级：＿＿＿＿姓名：＿＿＿＿＿⼀一、填空题。

1.三⻆角形具有（）性。

2.任何三⻆角形都有（）条⾼高。

3.如果⼀一个三⻆角形中的两条边的⻓长分别是6厘⽶米和10厘⽶米，那么这个三⻆角形中的第三条边的⻓长⼀一定⼤大于（）厘⽶米并且⼩小于（）厘⽶米。

4.⼀一个三⻆角形的两条边⻓长分别是4分⽶米和5分⽶米，那么第三条边的⻓长可能是（）分⽶米。

5.如果三⻆角形的两边分别是3厘⽶米和6厘⽶米，那么第三条边可能是（）厘⽶米，第三条边⻓长是整数的共有（）种情况。

6.⼀一个等腰三⻆角形，它的⼀一条边为3厘⽶米，另⼀一条边为6厘⽶米，这个三⻆角形的周⻓长是（）厘⽶米。

7.有（）个⻆角是锐⻆角的三⻆角形是锐⻆角三⻆角形。

有（）个⻆角是直⻆角的三⻆角形是直⻆角三⻆角形。

有（）个⻆角是钝⻆角的三⻆角形是钝⻆角三⻆角形。

8.三⻆角形按照⻆角分类可分为（）、（）和（）。

9.在⼀一个三⻆角形中，最⼤大的⼀一个⻆角是72度，这个三⻆角形是（）三⻆角形。

10.⼀一个钝⻆角三⻆角形有（）个锐⻆角，（）个钝⻆角。

11.两条边相等的三⻆角形叫做（）三⻆角形，它的两个底⻆角（）。

12.三条边都相等的三⻆角形叫做（）三⻆角形，它的每⼀一个⻆角都是（）度。

13.⼀一个等边三⻆角形的边⻓长是6厘⽶米，那么它的周⻓长是（）厘⽶米。

14.把⼀一个正⽅方形沿着⼀一条对⻆角线剪开可以得到（）个三⻆角形。

这些三⻆角形都是（）三⻆角形。

15.如果三⻆角形的三个⻆角都是60°，这个三⻆角形是（）三⻆角形。

16.任何⼀一个三⻆角形的内⻆角和都是（）度。

17.把⼀一个⼤大三⻆角形剪成两个⼩小三⻆角形，每个⼩小三⻆角形的内⻆角和是（）度。

18.⼀一个三⻆角形最多有（）个钝⻆角，最多有（）个直⻆角，最多有（）个锐⻆角。

19.⼀一个三⻆角形最少有（）个钝⻆角，最少有（）个直⻆角，⾄至少有（）个锐⻆角。

20.在⼀一个直⻆角三⻆角形中，⼀一个锐⻆角是35°，则另⼀一个锐⻆角是（）°。

人教版数学四年级下册【期末复习】《三角形解决问题》专项练习卷（附答案）1、一个等腰三角形两条边的长度分别是3 cm和8 cm，它的第三条边长多少厘米？2、将一根40 cm长的木条截成整厘米长的木条3段，做一个三角形，怎样截能使3段木条围成三角形？(请你举出三个例子)3、已知一个三角形(每条边长都是整厘米数)的周长是20 cm，它的最长边的长度最大是几厘米？4、在一个等腰三角形中，一个内角的度数是另一个内角的4倍，这个等腰三角形的顶角可能是多少度？5、用一根铁丝围成了一个长是20 cm，宽是10 cm的长方形，如果改围成一个腰长是22 cm的等腰三角形，这个等腰三角形的底是多少厘米？6、已知正三角形三条边的长度之和为33 cm,求此正三角形每条边的长度。

7、丹丹为妈妈制作了一张精美的贺卡,这张贺卡是一个等腰三角形。

已知它的顶角是100°,请问它的底角是多少度?8、一个直角三角形的一个锐角是另一个锐角的2倍,这两个锐角各是多少度?9、三角形ABC的周长是84 cm,∠B=∠C,BC=24 cm,求AB的长。

10、从小明家到学校走哪条路最近?为什么?11、如果三角形的两边长分别是9 cm和7 cm,那么第三边长可能是多少厘米?(取整厘米数)12、一个等腰三角形的一条边长8 cm,另一条边长6 cm,围成这个等腰三角形至少需要多长的绳子?13、一个等腰三角形的底边长9厘米,腰比底边少2厘米,这个三角形的周长是多少厘米?14、在一个直角三角形中,其中一个锐角的度数是另一个锐角的2倍。

这两个锐角各是多少度?15、已知∠1=95°,∠4=137°,∠2、∠3的度数各是多少?16、一个等腰三角形的一条边长15厘米,另一条边长20厘米,那么这个三角形的周长至少是多少厘米?17、在一个直角三角形中,一个锐角是另一个锐角的4倍,这个直角三角形的两个锐角分别是多少度?18、如右图所示,小熊每天早上从家里出发,先用9分钟到200米外的小鹿家,然后和小鹿一起用18分钟走400米到学校上学。

小学四年级下册三角形练习题一．填空：1、一个等边三角形的周长是48厘米，那么它的每条边长是（）厘米，每个角是（）°2、我们的红领巾按边分是（）三角形，其中一个底角是30°，它的顶角是（）°3、三角形的一个内角为45°，另一个内角是它的2倍，第三个内角是( )度，这个三角形叫( )三角形。

4、用两个完全一样的三角形可以拼成一个（）形；用两个完全一样的直角三角形可以拼成（）形，（）形和（）形。

5、用（）个完全一样的等边三角形可以拼成一个等腰梯形；用（）个完全一样的等边三角形可以拼成一个大的等边三角形。

6、（）是0.07的计数单位，7个（）0.007，27个0.1（），（）个0.01是10。

7. 自行车的支架常常做成三角形，是利用了三角形（）的特性。

8、一个三角形中最大的一个内角是105°，那么这个三角形是（）。

9、在三角形中，如果两个内角的度数之和等于第三个内角，那么这个三角形是（）。

A、直角三角形B、锐角三角形C、钝角三角形10、三角形越大，内角和( )A．越大 B．不变 C．越小11、等腰三角形中，有一个内角是40°，另外两个内角是( )。

A、一定是40°和100°。

B一定都是70°。

C、可能是40°和100°也可能都是70°。

12、一个三角形最少有( )个锐角。

A、3个B、2个C、1个13、用两个完全一样的直角三角形可以拼成（）A、长方形B、正方形C、长方形或正方形二．解决问题1、在一个等腰三角形中，顶角是720，求底角的度数。

2、有一个等腰三角形的地，周长是108米，底边是320分米，它的腰长多少米?3、一个直角三角形中，已知其中一个锐角是55。

，求另一个锐角是多少度？4、已知一个等腰三角形的一个顶角是70。

，它的每一个底角是多少度？5、已知一个等腰三角形的一个底角是35。

四年级下册数学单元测试-5.三角形一、单选题1.在笔直的公路上有三条小路通往小明家，它们的长度分别是225米、309米、212米，其中有一条小路与公路是垂直的，那么这条小路的长度是（）米．A. 225米B. 309米C. 212米2.一个等腰三角形的顶角和一个底角和是135度，这个三角形的顶角度数是内角和的（）A. B. C.3.一个三角形任意一条边上的高所在的直线，都是这个三角形的对称轴．这个三角形是（）A. 等腰三角B. 等腰直角三角形C. 等边三角形二、判断题4.每个三角形里一定有2个锐角。

（）5.火眼金睛判对错．三角形任意两个内角的和都大于第三个内角．6.小强画了一个三个角分别是50°、70°、50°的等腰三角形．7.三条长度相等的线段一定能围成一个三角形。

三、填空题8.在三角形中，∠1=30°，∠2=70°，∠3=________，它是________三角形。

9.已知∠1和∠2是直角三角形中的两个锐角。

（1）∠1=35°，∠2=________（2）∠1=28°，∠2=________（3）∠1=47°，∠2=________10.在一个三角形的3个角中，一个是35°，一个是110°，这个三角形既是________三角形，又是________三角形。

11.从直线外一点到这条直线所画的垂直线段的长，叫做这点到直线的________四、解答题12.一块三角尺的内角和是180°。

用两块完全一样的三角尺拼成一个三角形，拼成的三角形内角和是多少度？13.如图AB=AC，求∠1、∠C的度数？五、综合题14.（1）在一个三角形中，1=42°，2=50°，则3=________°。

（2）等腰三角形中的一个底角是30°，则它的顶角是________°。

2021人教版四年级数学下册《三角形》试题第一课时一、填空。

1. 由三条（）围成的图形叫做三角形，一个三角形有（）个角。

2. 三角形按角分，可以分为（）、（）和（）。

按边分，可以分为（）、（）和（）。

3. 任意一个三角形中最多有（）个锐角，最少有（）个锐角。

4. 一个三角形有（）个顶点，最多可以画（）条高。

5. （1）锐角三角形：（）（2）直角三角形：（）（3）钝角三角形：（）6. （1）等腰三角形：（）（2）等边三角形：（）（3）不等边三角形：（）7. 这个架子太危险，怎样加固呢？这是利用了三角形的（）特性。

8. 一个等边三角形的周长是48厘米，那么它的每条边长是（）厘米，每个角是（）。

二、判断。

(对的打“√”，错的打“×”)1. 有三个角的图形叫做三角形。

( )2. 三角形的高就是一条垂线。

( )3. 钝角三角形里可以有2个钝角。

( )4. 把直角三角形的一条直角边作三角形的高，则另一条直角边就是这个三角形的底。

( )5. 等边三角形一定是锐角三角形。

( )6. 两个面积相等的三角形，可以拼成一个平行四边形。

( )7. 从三角形一个顶点向对边只能画一条高。

( )8. 角的两边越长，这个角就越大。

( )9. 任何一个三角形至少有两个锐角。

( )10. 一个三角形中可以画无数条高。

( )三、选一选。

你能把1—8号三角形分类放在下面的盘中吗？四、动手操作。

1. 找出下面每个三角形的底和对应的高。

2. 画出下面每个三角形指定底边上的高。

3. 分别画一个等腰钝角三角形，一个直角三角形和一个锐角三角形。

五、解决问题。

1. 一个等腰三角形周长1米，腰长是0.4米，这个三角形底边长多少米?2. 有一个等腰三角形的地，周长是108米，底边是320分米，它的腰长多少米?3. 一根铁丝可以围成一个边长为3厘米的正方形，如果改围一个等边三角形，那么等边三角形的边长是多少厘米？第二课时一、填空题。

四年级下册数学单元测试-4.三角形一、单选题1.一个三角形的三个内角中，如果∠1=∠2+∠3，那么它一定是( )三角形。

A. 锐角B. 直角C. 钝角D. 无法确定2.在钝角三角形中，两个锐角的和（）90°A. 大于B. 等于C. 小于3.下面三角形中未知角的度数是（）A. 40°B. 50°C. 60°D. 7 0°二、判断题4.有一个锐角的三角形就是锐角三角形。

（）5.在同一个三角形中，至少有两个角是钝角。

6.一个三角形有一个锐角，那么，这个三角形就一定是锐角三角形。

7.三角形中最多有一个直角。

三、填空题8.红领巾是一个________三角形，还是一个________三角形。

A.锐角B.直角C.钝角D.等腰9.三角形最多有________个锐角，最多有________个直角，最多有________个钝角。

10.一个等腰三角形的一个底角是40°，它的顶角是________度。

11.用四个完全一样的等边三角形拼成一个大三角形，这个大三角形的内角和是________。

四、解答题12.一个三角形的一个内角是60°，这个三角形一定是锐角三角形吗?为什么?13.下面3个三角形被盖住了一个或两个角，你能知道各是什么三角形吗？五、综合题14.求出下面已知角的度数。

（1）（2）六、应用题15.等腰三角形有一个角是70°，它的另外两个角是多少度？参考答案一、单选题1.【答案】B【解析】【解答】因为∠1=∠2+∠3，所以∠1=180°÷2=90°，所以这个三角形是直角三角形．故答案为：B．【分析】本题考点：三角形的分类．此题考查了三角形的内角和定理以及三角形的分类，三角形按角分类有锐角三角形、直角三角形、钝角三角形．根据三角形的内角和为180°结合已知，可求∠1=90°，即可判断三角形的形状．2.【答案】C【解析】【解答】三角形的内角和是180°，一个角大于90°，所以剩下的两个角的和一定小于90°。

三角形内角和典题探究一个1、三角形的两个内角和是850，你知道这是一个什么三角形吗？2、在一个三角形中，已知∠1是∠2的2倍，∠2是∠3的31。

这个三角形各个角是多少度？这是一个什么三角形？3、同学们知道三角形的内角和是1800，你能运用这个知识分别求出四边形、五边形、六边形的内角和吗？4、如图，两个三角形都是等腰三角形，∠3是多少度？演练方阵A 档（巩固专练）1．由三条( )围成的图形叫三角形。

2．三角形按角可分为( )三角形、( )三角形、( )三角形。

3．三角形的内角和是( )。

4．等腰直角三角形中三个内角分别是( )，( )和( )。

5、判 断，(对的画“√”，错的画“X ”)(1)．一个三角形有一个锐角，那么，这个三角形就一定是锐角三角形。

( )(2)．直角三角形中只能有一个角是直角。

( )(3)．等边三角形一定是锐角三角形。

( )(4)．三角形共有一条高。

( )(5)．一个三角形中，最大的角是锐角，那么，这个三角形一定是锐角三角形。

( )(6)．两个底角都是280的三角形，一定是钝角三角形。

( )6、选 择。

(1)．一个等腰三角形，其中一个底角是750，顶角是( )A ．750B ．450C ．300D ．600(2)．任意一个三角形都有( )高。

A ．一条B ．两条C 三条D ．无数条(3)．( )个角是锐角的三角形，叫锐角三角形。

A．三 B．二 C．—(4)．三角形越大，内角和( )A．越大 B．不变 C．越小7、求下面三角形中／3的度数，并指出是什么三角形。

1．∠1＝300，∠2＝1080，∠3＝ ( )，它是( )三角形。

2．∠1＝900，∠2＝450，∠3＝( )，它是( )三角形。

3．∠1＝700，∠2＝700，∠3＝( )。

它是( )三角形。

4．∠1＝900，∠2＝300，∠3＝( )，它是( )三角形。

8、一个三角形的两个内角和是1100，你知道这是一个什么三角形吗？9、在△ABC中，已知∠A是∠B的3倍，且∠A比∠B大600，这个三角形各个角是多少度？你知道这是一个什么三角形？10、一个等腰三角形的顶角是一个底角的2倍，这个三角形各个角是多少度？B档（提升精练）1、任意三角形的内角和是度；一个直角三角形的两个锐角的和是度。

第5单元三角形一、认真审题，填一填。

(每小题3分，共24分)1.【新情境】为了避免梦梦长时间低头看书，妈妈给她买了阅读支架，让她抬头阅读，保护颈椎。

如图，书本放在阅读支架上不晃动是应用了()。

2.如右图，一张三角形纸片被撕去了一个角，这个角是()°，原来这个三角形是一个()三角形，也是一个()三角形。

3.如下图，典典从家去爷爷家走第②条路最近。

第②条路比第①条路近，是因为两点间所有连线中()最短；第②条路比第③条路近，是因为三角形任意两边之和()第三边。

4.我国的空间引力波探测计划系统“天琴”，需要三颗卫星以极高的精度组成周长为51万千米的等边三角形。

组成的这个等边三角形的边长是()万千米，它的每个内角是()°。

5.如图，把一个等边三角形沿一条边上的高剪成两个直角三角形，每个直角三角形的内角和是()°，直角三角形中最小的一个内角是()°。

6.【新角度】天天准备用图钉固定硬纸条做一个三角形。

他最少应该准备()根硬纸条，准备()个图钉。

如果有2根硬纸条分别长3 cm和5 cm，那么另一根硬纸条最长为()cm(取整数)。

7.若一个等腰三角形的顶角是40°，则它的底角是()°。

若一个等腰三角形的底角是40°，则它的顶角是()°。

8.【说理题】已知一个等腰三角形的两条边分别长4厘米、8厘米，那么它的第三条边是()厘米，你的理由是()。

二、仔细推敲，选一选。

(将正确答案的序号填在括号里)(每小题2分，共12分)1.下面图形中，三角形底边上的高的画法不正确的是()。

A. B. C. D.2.龙龙有4根小棒，2根3厘米长，1根4厘米长，1根5厘米长，用其中的3根围成三角形，可以围出()种不同的三角形。

A.2B.3C.43.下列说法中不正确的是()。

A.等边三角形是锐角三角形B.直角三角形不可能是等腰三角形C.最大角是直角的三角形一定是直角三角形4.【新角度】张爷爷想用一根长13分米的竹片制作一个三角形的风筝框架，如果第一次从4分米处锯断，第二次锯的位置可以是()。

人教版数学四年级下册第5单元《三角形》精选练习题（含详细解析）姓名：__________ 班级：__________考号：__________一、单选题（共9题；共18分）1.下面三种物品，利用了三角形稳定性的是（）A. 三角形花坛B. 红领巾C. 自行车的三角形车架2.一个三角形的两个内角和是90°，这个三角形是( )三角形。

A. 锐角B. 直角C. 钝角3.有4厘米、6厘米长的两根小棒，从下面各种长度的小棒中再挑一根，首尾相连，不能围成三角形的是（）。

A. 2厘米B. 4厘米C. 6厘米D. 8厘米4.三角形的两条边分别是3厘米和7厘米，第三条边的长度不可能是（）。

A. 5B. 7C. 9D. 115.三角形的两边之和为6，另一条边不能为（）。

A. 3B. 4C. 66.有一个三角形的三个角中，有一个角是平角的四分之一，还有一个角是周角的六分之一，这个三角形是（）A. 锐角三角形B. 等腰三角形C. 直角三角形D. 钝角三角形7.一个等腰三角形，其中一个角是60°，这个等腰三角形一定是（）。

A. 直角三角形B. 等边三角形C. 无法判断8.若三角中有一个角是90°，那么另外两个角中，任意一个角的度数一定（）A. 大于60°B. 大于90°C. 小于60°D. 不等于90°9.有一个直角三角形，两个锐角分别是（）A. 48°和52。

B. 38°和42°C. 48°和42°D. 60°和35°二、判断题（共6题；共18分）10.一个三角形三边的长度分别是4dm、12dm、7dm，这个三角形的周长是23dm。

（）11.在等腰三角形中，有一个内角是80°，另外两个内角和一定是100°。

（）12.两边相等的三角形一定是等腰三角形。

（）13.一个三角形里最少有2个锐角。

人教版小学数学四年级下册第5单元三角形单元练习一、单选题1．一个三角形其中的两条边的长度分别是4cm、6cm,那么第三条边的长度可能是（）。

A．2cm B．5cm C．11cm2．一个等腰三角形相邻的两边分别长15分米和7分米,这个等腰三角形的周长是（）A．37分米B．29分米C．29分米或37分米3．三角形中是轴对称图形的是（）。

A．所有三角形B．等腰三角形C．等边三角形和等腰三角形4．如图,有()个三角形。

A．7B．8C．9D．105．在学习三角形特征时,四名同学分别选取了三根小棒。

不可以围成三角形的是（）。

A．B．C．D．6．在一个三角形中,三个内角度数的比是1：3：5,这个三角形是（）。

A．锐角三角形B．直角三角形C．钝角三角形D．不能确定7．下面的（）线段,能围成一个三角形。

A．5cm、7cm和2cm B．4cm、6cm和8cm C．1cm、1cm和3cm 8．一个三角形三个角的度数的比是1：3：5,这个三角形是（）A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形9．下面各组线段中,能围成三角形的是（）A．4cm 7cm 3cm B．5cm 5cm 1cm C．3cm 6cm 10cm10．房屋的屋架运用了三角形的（）。

A．有三条边的特性B．易变形的特性C．稳定不变形的特性二、判断题11．一个钝角三角形里有两个钝角。

12．一个等腰三角形,顶角是75 o,底角肯定是52.5o.13．任意一个三角形至少有两个锐角。

（）14．用长度分别是10厘米、4厘米和3厘米的一根小棒,头尾相连,一定能摆出一个三角形。

（）15．判断对错.直角三角形的内角和大于锐角三角形的内角和．三、填空题16．一个等腰直角三角形的一条直角边长26厘米,这个三角形的面积是平方厘米．17．一个等腰三角形的底长是5cm,它的腰长是8cm,这个三角形的周长是cm．18．求角的度数．∠5=°19．李老师用一根27厘米长的铁丝正好围成了一个三角形,并且三条边长的厘米数是三个不同的质数,这个三角形的最长边与最短边相差厘米．20．三角形的内角和是°,一个等腰三角形,它的一个底角是26°,它的顶角是。

三角形三边之间的关系和三角形的内角和考点题库一、我会填。

1．三角形的内角和是( )。

2．在一个直角三角形中，一个锐角是30°，另一个锐角是( )。

3．在一个三角形中，∠1＝50°，∠2＝26°，∠3＝( )。

这是一个( )三角形。

4．一个三角形的三个内角的度数都是60°，这个三角形是( )三角形。

5．三角形任意两边的和( )第三条边。

6．一个三角形中，至少有( )个锐角，最多有( )个钝角。

7．两个( )三角形能拼成一个正方形。

二、我会判。

(正确的画“√”，错误的画“×”。

)1．三角形越大，它的内角和就越大。

( )2．等边三角形可能是直角三角形。

( )3．一个三角形最少有两个锐角。

( )4．一个三角形的三个内角的度数：96度、54度、31度。

( )5．把一个大三角形分成两个小三角形，每个小三角形的内角和都是180°。

() 6．锐角三角形的两个锐角和一定大于90°。

( )三、求出图中各角的度数。

已知∠1＝60°，∠2＝50°，∠3＝( )度∠4＝( )度四、我会解答。

1．一个三角形的一个内角是32°，另一个内角是105°，第三个内角是多少度？这个三角形是什么三角形？2．等腰三角形的一个顶角是70°，一个底角是多少度？3．一个直角三角形的两个内角相等，这个直角三角形的三个内角分别是多少度？五、先画一画，再算一算，你能发现什么规律？图形…名称三角形四边形五边形六边形…边数34…内角和180°×1( )×2…我发现n(n≥3)边形的内角和是：____________________________。

六、小熊盖房子，他准备了2根3米长的木料做房顶，还要选一根木料做横梁，请帮他想一想，该选几米长的木料最合适呢?参考答案：一、1．180°2．60°3．104°钝角4．等边(或正)5．大于6．217．完全相同的等腰直角二、1．×2．×3．√4．×5．√6．√三、70130四、1．43°钝角2．55°3．90°45°45°五、180°5180°×36180°×4180°×（n－2)六、根据三角形的任意两边之和大于第三边，可断定横梁的长度在6米之内，选横梁时要尽量选长一些，因此，选5米左右长的横梁比较合适。

四年级数学三角形试题答案及解析1.有两个角是锐角的三角形叫锐角三角形．．（判断对错）【答案】×【解析】根据锐角三角形的含义：三个角都是锐角的三角形是锐角三角形；据此判断即可．解：根据锐角三角形的含义可知：有两个角是锐角的三角形叫锐角三角形，说法错误；故答案为：×．【点评】此题考查了锐角三角形的含义，注意基础知识的积累和理解．2.一个三角形中，有一个角75°，另外两个角的度数可能是（）A．95°，20° B．35°，60° C．55°，50°【答案】C【解析】三角形内角和为180°，三角形有一个角是75°，另外两个角的度数和是180度减去75度得105度，再逐项判断两个度数的和是不是75度即可解答．解：180°﹣75°=105°A.95°+20°=115°，不是105°，错误．B.35°+60°=95°，不是105°，错误．C.55°+50°=105°，是105°，所以选择C．故选：C．【点评】本题考查了三角形内角和定理，属于基础题，关键是掌握三角形内角和为180度．3.请在下面的方格图中画出一个钝角三角形，并画出最长边上的高．【答案】见解析【解析】有一个角是钝角的三角形是钝角三角形，三角形最长边上的高是从三角形的最大的角的顶点向对边引垂线，从这点到对边垂足之间的线段就是三角形要求的高．解：根据分析作图如下：【点评】此题考查了利用方格图画钝角三角形的方法，也考查了三角形的高的画法．4.如果在一个三角形中，有两个内角的度数之和等于90°，那么这个三角形一定是三角形．在这个三角形中，角所对的边的长度比其余两个边都长．【答案】直角，90°．【解析】解：180°﹣90°=90°，因此，这个三角形是直角三角形；所以在这个三角形中，90°角所对的边的长度比其余两个边都长．故答案为：直角，90°．5.在一个等腰三角形中，一个顶角是1000，那么两个底角分别是度和度．【答案】40、40．【解析】解；（180﹣100）÷2=80÷2=40（度）答：它的两个底角都是40°．故答案为：40、40．6.直角三角形只有斜边上的一条高．．（判断对错）【答案】×【解析】解：根据三角形的高的含义可知：直角三角形有三条高，两条直角边分别是它的两条高，过直角顶点向斜边也可做一条高，共三条高，所以直角三角形只有斜边上的一条高的说法是错误的．故答案为：×．7.用7厘米，13厘米和第三根小棒首尾相连组成三角形，第三根小棒最短厘米，最长厘米．【答案】7，19．【解析】根据三角形的特征：任意两边之和大于第三边，任意两边之差小于第三边；由此解答即可．解：13﹣7＜第三边＜13+7，所以：6＜第三边＜20，即第三边的取值在6～20厘米（不包括6厘米和20厘米），因为三根小棒都是整厘米数，所以第三根小棒最长为：20﹣1=19（厘米），最短为：6+1=7（厘米）；故答案为：7，19．【点评】此题关键是根据三角形的特性进行分析、解答．8.把一根13厘米长的小棒截成三段，围成一个等腰三角形，下面（）是正确的．A．3厘米，4厘米，6厘米B．7厘米，3厘米，3厘米C．4厘米，5厘米，4厘米D．2厘米，2厘米，9厘米【答案】C【解析】依据等腰三角形的两条腰相等，以及三角形的两边之和大于第三边，即可进行正确选择．解：选项A，因为三条边的长度都不相等，不符合题意；选项B，因为3+3＜7，不符合题意；选项C，4+4＞5，符合题意，所以可选；选项D，2+2＜9，不符合题意；故选：C．【点评】此题主要考查三角形的特性以及等腰三角形的特点．9.根据要求在下列图形中分别画一条线段．（1）分成两个钝角三角形．（2）分成一个平行四边形和一个三角形．【答案】见解析【解析】（1）连接平行四边形相对的锐角的两个顶点，即可把这个平行四边形分成两个钝角三角形；（2）过梯形的上底的一个顶点，画出一条腰的平行线，则即可把梯形分成一个平行四边形和三角形．解：根据题干分析画图如下：【点评】解答此题的关键是根据平行四边形、钝角三角形、以及已知图形的特征进行解答．10.按角的大小，三角形可以分为三角形、三角形、三角形．【答案】锐角；直角；钝角．【解析】根据三角形按角分类的方法即可解决．解：三个角都是锐角的三角形叫锐角三角形，有一个角是直角的三角形叫直角三角形，有一个角是钝角的三角形叫钝角三角形，答：按照三角形中角的不同可以把三角形分为锐角三角形、直角三角形和钝角三角形．故答案为：锐角；直角；钝角．【点评】此题考查了三角形按角分类的方法．11.三角形具有性，平行四边形具有性．【答案】稳定，易变．【解析】根据三角形的特性：稳定性；平行四边形的特性：具有易变形；进行解答即可．解：三角形具有稳定性，平行四边形具有易变形；故答案为：稳定，易变．【点评】此题考查了三角形的特性和平行四边形的特性．12.一个三角形的两条边分别是40厘米、50厘米，第三条边的长度只能选（）A．80厘米 B．90厘米 C．110厘米【答案】A【解析】根据三角形的特性：两边之和大于第三边，三角形的两边的差一定小于第三边；进行解答即可．解：50﹣40＜第三边＜40+50，所以10＜第三边＜90，即第三边在10厘米～90厘米之间（不包括10厘米和90厘米），所以第三边应为80厘米；故选：A．【点评】解答此题的关键是根据三角形的特性进行分析、解答即可．13.下面分别是三角形的三条边长度，不能围成三角形的是（）A．3cm、4cm、9cm B．2cm、3cm、4cm C．5cm、6cm、7cm【答案】A【解析】根据三角形的特性：两边之和大于第三边，三角形的两边的差一定小于第三边；进行解答即可．解：A、因为3+4＜9，所以三边不能围成三角形；B、因为2+3=5＞4，所以三边能围成三角形；C、因为5+6=11＞7，所以三边能围成三角形；故选：A．【点评】解答此题的关键是根据三角形的特性进行分析、解答即可．14.用三根分别长7厘米、7厘米、14厘米的小棒能围成一个三角形．．（判断对错）【答案】×【解析】根据三角形的特性：两边之和大于第三边，三角形的两边的差一定小于第三边；进行解答即可．解：7+7=14，所以三根分别长7厘米、7厘米、14厘米的小棒，不能围成一个三角形；故答案为：×．【点评】解答此题的关键是根据三角形的三边关系进行分析、解答．15.一个三角形中的两个角分别是35°、72°，第三个角是，这是一个三角形．【答案】73°，锐角．【解析】因为三角形的内角度数和是180°，已知两个内角，先用减法求出第三个内角的度数，进而根据三角形的分类判定出这个三角形的类型；由此得解．解：180°﹣35°﹣72°，=145°﹣72°，=73°，因为有三个角都是锐角的三角形是锐角三角形，所以该三角形是锐角三角形；故答案为：73°，锐角．【点评】此题主要考查三角形的内角和是180度及判定三角形类别的方法．16.下面每组线段能围成三角形的是（）A．3厘米，4厘米，6厘米B．7厘米，2厘米，3厘米C．4厘米，5厘米，1厘米D．2厘米，2厘米，9厘米【答案】A【解析】根据三角形任意两边的和大于第三边，用较短的两边的和与最长边比较，比最长边大，就能构成三角形，否则就不能构成三角形．解：A，3+4=7；7＞6，所以能构成三角形；B，2+3=5；5＜7，所以不能构成三角形；C，4+1=5；5=5，所以不能构成三角形；D，2+2=4；4＜9，所以不能构成三角形．故选：A．【点评】本题考查了三角形三边的关系：任意两边的和大于第三边，任意两边的差小于第三边．17.画出下面三角形底边上的高．【答案】【解析】经过三角形的顶点（与底相对的点）向对边（底）作垂线，顶点和垂足之间的线段就是三角形的一条高，用三角板的直角可以画出三角形的高；直角三角形一条直角边就是另一直角边上的高．解：画出下面指定底边的高：【点评】本题是考查作三角形的高．注意作高用虚线，并标出垂足．18.等边三角形的三条边相等，三个内角也相等，而且都是60°．．（判断对错）【答案】√【解析】三条边都相等的三角形叫做等边三角形，其三个内角都相等，根据三角形的内角和是180度，即可进行判断．解：因为等边三角形的三个内角都相等，所以每个内角的度数是：180°÷3=60°，所以，等边三角形的三条边相等，三个内角也相等，而且都是60°，说法正确；故答案为：√．【点评】解答此题的主要依据是：等边三角形的三个内角都相等以及三角形的内角和定理．19.小猴要给一块地围上篱笆，你认为（）的围法更牢固些．A． B． C．【答案】B【解析】紧扣三角形具有稳定性的性质，即可选择正确答案．解：A和C中，围成的图形为四边形，而四边形有容易变形的特点，B中，围成的图形为三角形，三角形具有稳定性，所以B的围法更牢固些．故选：B．【点评】此题考查了三角形的稳定性．20.用三根分别长4厘米，3厘米和8厘米的小棒能拼成一个三角形．（判断对错）【答案】错误【解析】根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，进行分析．解：4+3=77＜8，所以不能够组成三角形．所以这句话是错误的．故答案为：错误．【点评】此题考查了三角形的特性中的三角形的三边关系．判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数．21.三角形的两个内角之和是85°，这个三角形是．【答案】钝角三角形．【解析】因为三角形的内角和是180度，已知两个内角的和是85度，用“180°﹣85°”求出第三个内角的度数，进而根据三角形的分类进行解答．解：第三个内角：180°﹣85°=95°，因为有一个角是钝角的三角形，是钝角三角形；故答案为：钝角三角形．【点评】解答此题用到的知识点：三角形的内角和公式；（2）三角形的分类．22.一个锐角三角形放在放大镜下看就变成了钝角三角形．（判断对错）．【答案】×【解析】角的大小与两边的长短无关，只与角两边张开的大小有关，所以用一个放大镜看一个锐角三角形，这个锐角三角形各角的度数不变，仍然是锐角三角形．解：用一个放大镜看一个锐角三角形，这个锐角三角形各角的度数不变，仍然是锐角三角形．所以原题说法错误．故答案为：×．【点评】此题主要考查角的意义，应理解放大镜放大的只是角两边的长短．23.任何一个三角形至少有（）个锐角．A．1 B．2 C．3【答案】B【解析】紧扣三角形的内角和是180°即可解决问题．解：假设三角形中锐角的个数少于2个，那么三角形中就会出现两个或两个以上的角是钝角或直角，两个钝角或两个直角的和加上第三个角的度数一定大于180°，这就违背了三角形内角和是180°的性质，所以一个三角形至少有2个锐角，最多有1个钝角．故选：B．【点评】此题考查了三角形内角和在三角形分类中的应用．24.一个三角形中，∠1=40°，∠2=50°，那么∠3= ，它是一个三角形．【答案】90°，直角．【解析】根据三角形的内角和是180°，用180°分别减去∠1和∠2的度数，即可求出∠3的度数，继而根据三角形的分类判断即可．解：180°﹣40°﹣50°=140°﹣50°=90°所以这个三角形是直角三角形．故答案为：90°，直角．【点评】本题主要考查的是三角形内角和定理和三角形的分类方法，即三个角都是锐角，这个三角形是锐角三角形；有一个角是钝角的三角形是钝角三角形；有一个角是直角的三角形是直角三角形．25.如果一个三角形有两个内角之和等于90度，那么这个三角形是三角形．【答案】直角【解析】根据三角形的内角和是180°，和两个内角之和等于90°，由此判定这个三角形是直角三角形．解：三角形的内角和是180°，如果有两个内角之和等于90°，那么另一个内角是180°﹣90°=90°，因此，这个三角形是直角三角形；故答案为：直角【点评】本题是考查三角形的分类、三角形的内角和．26.三条边分别是4厘米、4厘米、8厘米的三角形是一个等腰三角形．．（判断对错）【答案】×【解析】因为4厘米+4厘米=8厘米，不符合两边之和大于第三边，则不能构成一个三角形，更谈不上是否是等腰三角形了．解：因为4厘米+4厘米=8厘米，不符合两边之和大于第三边，所以这三条线段组不成一个三角形；故答案为：×．【点评】判断三条线段能否组成等腰三角形，不能只看数值，关键是看是否满足两边之和大于第三边．27.一个三角形最少有2个锐角．．【答案】√【解析】根据三角形的内角和等于180°，三个角中最多有一个直角或钝角，所以最少有两个锐角，据此解答即可．解：因为三角形的内角和等于180°，所以三角形最多有一个直角或钝角，最少有两个为锐角；故答案为：√【点评】本题考查了三角形的内角和等于180°，根据直角、钝角、锐角的特点解答即可．28.一个等腰三角形的底角是93°（判断对错）【答案】×【解析】依据三角形的内角和是180度，以及等腰三角形两个底角的度数相等的特点，即可进行判断．解：因为一个等腰三角形的底角是93°，则两个底角的度数和为：93°×2=186°，这样不符合三角形的内角和定理；故答案为：×．【点评】此题主要考查等腰三角形的性质及三角形内角和定理的综合运用．29.有一个内角是60°的等腰三角形一定是等边三角形．（判断对错）【答案】√【解析】由等腰三角形的特点可知：等腰三角形的两个底角相等，再据三角形的内角和是180度，即可求得三角形的另外两个角的度数，从而判定这个等腰三角形是否是等边三角形．解：假设已知度数的角是底角，则另一个底角也是60°，于是求得顶角为180°﹣60°×2=60°，所以这个三角形是等边三角形；假设这个角是顶角，则每个底角的度数为（180°﹣60°）÷2=60°，所以这个三角形是等边三角形．故答案为：√．【点评】解答此题的主要依据是：等腰三角形和等边三角形的特点以及三角形的内角和定理．30.画出下面三角形的高【答案】【解析】经过三角形的顶点（与底相对的点）向对边（底）作垂线，顶点和垂足之间的线段就是三角形的一条高，用三角板的直角可以画出三角形的高．解：画出下面三角形的高：【点评】本题是考查作三角形的高．注意作高用虚线，并标出垂足．。

小学数学-有答案-人教版数学四年级下册5.3 三角形的内角和练习卷一、选择题1. 直角三角形的内角和()锐角三角形的内角和．A.等于B.小于C.大于2. 把一个三角形沿高剪开分成两个小三角形，每个小三角形的内角和是()．A.360∘B.180∘C.90∘3. 一个等腰三角形，顶角的度数是底角的2倍，底角是（）。

A.20∘B.45∘C.60∘D.90∘4. 一个等腰三角形的一个底角是35度，它的顶角是（）A.1450度B.110度C.20度5. ∠1和∠2是一个直角三角形中的两个锐角，已知∠1=52∘，∠2=()A.38∘B.28∘C.不能求出6. 等腰三角形的一个底角是30∘，它的顶角是()。

A.30∘B.60∘C.120∘7. 三角形的内角和是（）A.180度B.270度C.360度二、判断题把一个大三角形分成两个小三角形，每个小三角形的内角和都是90∘(________)将一个等腰三角形沿高对折，每个三角形的内角和都是90∘．(________)直角三角形的内角和大于锐角三角形的内角和．(________)在三角形中，最大的一个内角一定不能小于60∘．(________)一个三角形中最多有两个直角，这种说法是正确的．(________)三、填空题三角形的三个角∠A、∠B、∠C之和为180∘，∠C=________∘用5倍的放大镜看一个三角形，看到的这个三角形的内角和是________度．一个等腰三角形的一个底角是50∘,它的顶角是(________)．直角三角形中，一个锐角是43∘，另一个锐角是________。

直角三角形中的一个角是30∘，另一个角是________。

一个三角形中至少有________个角是锐角．把一个大三角形剪成两个小三角形。

每个三角形的内角和是(________)。

四、解答题求下面三角形中未知角的度数．已知：∠1=80∘，∠2=68∘．求：∠3=?∠4=?如图AB=AC，求∠1、∠C的度数？在直角三角形中，∠1和∠2分别是直角三角形的两个锐角．其中∠1=43∘，求∠2．下面的三个角是否能组成三角形（1）90∘，50∘，40∘（2）50∘，50∘，50∘（3）120∘，30∘，30∘（4）100∘，32∘，19∘（5）60∘，60∘，60∘妈妈给淘气买了一个等腰三角形的风筝．它的顶角是40∘，它的一个底角是多少？参考答案与试题解析小学数学-有答案-人教版数学四年级下册5.3 三角形的内角和练习卷一、选择题1.【答案】A【考点】三角形的内角和【解析】此题暂无解析【解答】任意一个三角形的内角和都是180∘，直角三角形的内角和等于锐角三角形的内角和．故答案为A．2.【答案】B【考点】三角形的内角和【解析】此题暂无解析【解答】略3.【答案】B【考点】三角形的内角和【解析】等腰三角形的两个底角相等，可以用列方程的方法解答，设一个底角是x度，则顶角就是2x度，根据三角形内角和是180度列出方程解答即可．【解答】解：设底角的度数为x，则顶角的度数为2x．x+x+2x=1804x=180x=45故答案为B．4.【答案】B【考点】三角形的特性【解析】180∘−35∘−35∘=145∘−35∘=110∘答：顶角为10∘故选B．解决本题的关键是根据等腰三角形的底角相等，求出另一底角，再根据三角形的内角和是180∘计算出顶角．【解答】此题暂无解答5.【答案】A【考点】三角形的内角和三角形的分类【解析】此题暂无解析【解答】22=90∘−52∘=38∘故答案为：A6.【答案】C【考点】三角形的内角和【解析】等腰三角形的两个底角是相等，用180度减去两个底角的度数就是顶角的度数．【解答】180∘−30∘−30∘=150∘−30∘=120∘故选C7.【答案】A【考点】三角形的特性【解析】根据三角和定理可得：三角形的内角和是180度：．故选A．【解答】此题暂无解答二、判断题【答案】错误三角形的内角和【解析】此题暂无解析【解答】略【答案】错误【考点】三角形的内角和【解析】此题暂无解析【解答】任意三角形的内角和都是180∘，这与三角形的形状、大小无关．将一个等腰三角形沿高对折，每个三角形的内角和都是180∘，原题说法错误故答案为错误【答案】错误【考点】三角形的内角和【解析】此题暂无解析【解答】直角三角形的内角和大于锐角三角形的内角相同．故答案为：错误．【答案】√【考点】三角形的特性【解析】如果一个三角形中，最大的一个内角小于60∘，那么这个三角形的内角和就小于180∘________，这样的三角形不存在．【解答】此题暂无解答【答案】错误【考点】三角形的内角和【解析】此题暂无解析【解答】三角形内角和是180∘，如果一个三角形中有两个直角，那么三个内角和就会大于180∘，这与三角形的内角和是180∘相矛盾．一个三角形中最多有一个直角，原题说法错误．【答案】30【考点】三角形的特性【解析】180∘−(125∘+25∘)=180∘−150∘=30∘故答案为30三角形的内角和是180∘，用三角形的内角和减去两个已知角的度数和即可求出ΔC的度数．【解答】此题暂无解答【答案】180【考点】三角形的内角和【解析】此题暂无解析【解答】用5倍的放大镜看一个三角形，看到的这个三角形的内角和是180度．故答案为180．三角形的内角和是180度，三角形的内角和是永远不变的．【答案】80【考点】三角形的特性【解析】因为其一个底角为50∘，所以另一个底角是50∘顶角=180∘−50∘×2=80∘由已知一个底角为50∘，根据等腰三角形的性质可求另一个底角的度数，根据三角形的内角和求得其顶角的度数．答：它的顶角是80度．【解答】此题暂无解答【答案】47∘【考点】三角形的内角和【解析】此题暂无解析【解答】直角三角形中，两个锐角的和是90∘90∘−其中一个锐角度数=另一个锐角度数90∘−43∘=47∘故答案为：47∘【答案】60∘【考点】三角形的内角和【解析】三角形内角和是180∘，直角三角形中有一个角是90∘，另外两个锐角的度数和是90∘，由此用90∘减去一个锐角的度数即可求出另一个锐角的度数．【解答】90∘−30∘=60∘故答案为：60∘【答案】2【考点】三角形的内角和【解析】此题主要考查三角形的内角和定理，利用假设法即可求解．【解答】假设任意一个三角形至少有1个锐角，则另外两个内角的度数和就会等于或大于180度，三角形的内角和就大于180度，这与三角形的内角和是180度是相违背的，故假设不成立，从而可以判断出任意一个三角形至少有2个内角．故答案为2．【答案】180∘【考点】三角形的内角和【解析】只要是三角形，那么它的三个内角的和就是180度，据此解答即可．【解答】把一个大三角形剪成两个小三角形．每个三角形的内角和是180∘四、解答题【答案】∠3=32∘∠4=145∘【考点】三角形的内角和【解析】因为三角形内角和是180∘，所以∠3=180∘−∠1−2；又因为∠3+∠4=180∘，所以∠A=180∘−3【解答】∠3=180∘−∠1−∠2=180∘−80∘−60∘−62∘=32∠4=180∘−∠3=180∘−32∘=148∘故答案为∠3=32∘,∠4=14∘【答案】∠是70∘∠C是55∘【考点】线段与角的综合三角形的内角和【解析】因为AB=AC，所以三角形ABC是等腰三角形，所以∵ B=CC，然后用180∘−110∘即可求出∠1的度数，然后根据等腰三角形的性质以及三角形内角和是180度即可求出2C的度数．【解答】解：∠1=180∘−140∘=70∘∠C=(180∘−70∘)÷2=110∘=2=55∘答：∠1是70∘，△C是55∘【答案】47∘【考点】三角形的内角和【解析】任何一个三角形的内角和是180∘，直角三角形中，有一个直角，已知一个锐角的度数，求另一个锐角的度数，用三角形的内角和-直角-已知锐角的度数=要求的角的度数，据此解答．【解答】直角三角形，所以直角是90∘180∘−90∘−43∘=47∘∠2=47∘【答案】（1）能（2）不能（3）能（4）不能（5）能【考点】三角形的内角和【解析】此题暂无解析【解答】（1）90∘+50∘+40∘=180∘，能（2）50∘+50∘+50∘=150∘，不能（3）120∘+30∘+30∘=180∘，能（4）100∘+32∘+19∘=15∘，不能（5）60∘+60∘+60∘=180∘，能【答案】70∘【考点】三角形的内角和等腰三角形与等边三角形三角形的分类【解析】此题暂无解析【解答】已知这个风筝是等腰三角形的，等腰三角形的特点即是两条腰相等，并且所对应的两个底角也相等，三个内角和度数是180度，顶角是40度，180度减40度得140度，两个底角和是140度，一个即为70度，因为等腰三角形的两个相等的底角．。