《三角形与全等三角形》综合测试题一(最新整理)

三角形全等测试题及答案一、选择题1. 两个三角形全等的条件是（）A. 有两条边和它们的夹角对应相等B. 三条边对应相等C. 有两条边和其中一条边的对角对应相等D. 有两条边和其中一条边的邻角对应相等答案：B2. 如果两个三角形的对应角相等，那么这两个三角形（）A. 一定全等B. 可能相似C. 一定相似D. 无法确定答案：B二、填空题3. 已知三角形ABC与三角形DEF全等，且∠A=∠D，AB=DE，那么AC=______。

答案：EF4. 如果两个三角形的两边和夹角对应相等，那么这两个三角形是______。

答案：全等三、判断题5. 如果两个三角形的对应边成比例，那么这两个三角形一定全等。

（）答案：错误6. 如果两个三角形的两边和夹角对应相等，那么这两个三角形一定相似。

（）答案：正确四、解答题7. 如图所示，已知三角形ABC与三角形DEF全等，且AB=5cm，BC=7cm，∠A=∠D=90°，求DE的长度。

答案：DE=7cm8. 已知三角形ABC与三角形DEF相似，且AB=3cm，BC=4cm，DE=6cm，求AC的长度。

答案：AC=8cm五、证明题9. 已知三角形ABC与三角形DEF全等，且∠A=∠D，AB=DE，证明：AC=EF。

证明：由于三角形ABC与三角形DEF全等，根据全等三角形的性质，对应边相等，所以AC=EF。

10. 已知∠A=∠D，AB=DE，AC=DF，求证：三角形ABC≌三角形DEF。

证明：根据SAS（边角边）判定方法，已知∠A=∠D，AB=DE，AC=DF，所以三角形ABC≌三角形DEF。

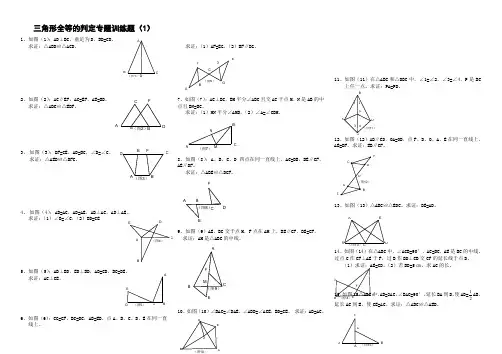
三角形全等的判定专题训练题（1）1、如图（1）：AD ⊥BC ，垂足为D ，BD=CD 。

求证：△ABD ≌△ACD 。

2、如图（2）：AC ∥EF ，AC=EF ，AE=BD 。

求证：△ABC ≌△EDF 。

3、 如图（3）：DF=CE ，AD=BC ，∠D=∠C 。

求证：△AED ≌△BFC 。

4、 如图（4）：AB=AC ，AD=AE ，AB ⊥AC ，AD ⊥AE 。

求证：（1）∠B=∠C ，（2）BD=CE5、如图（5）：AB ⊥BD ，ED ⊥BD ，AB=CD ，BC=DE 。

求证：AC ⊥CE 。

6、如图（6）：CG=CF ，BC=DC ，AB=ED ，点A 、B 、C 、D 、E 在同一直线上。

求证：（1）AF=EG ，（2）BF ∥DG 。

7、如图（7）：AC ⊥BC ，BM 平分∠ABC 且交AC 于点M 、N 是AB 的中点且BN=BC 。

求证：（1）MN 平分∠AMB ，（2）∠A=∠CBM 。

8、如图（8）：A 、B 、C 、D 四点在同一直线上，AC=DB ，BE ∥CF ，AE ∥DF 。

求证：△ABE ≌△DCF 。

9、如图（9）AE 、BC 交于点M ，F 点在AM 上，BE ∥CF ，BE=CF 。

求证：AM 是△ABC 的中线。

10、如图（10）∠BAC=∠DAE ，∠ABD=∠ACE ，BD=CE 。

求证：AB=AC 。

11、如图（11）在△ABC 和△DBC 中，∠1=∠2，∠3=∠4，P 是BC上任一点。

求证：PA=PD 。

12、如图（12）AB ∥CD ，OA=OD ，点F 、D 、O 、A 、E 在同一直线上，AE=DF 。

求证：EB ∥CF 。

13、如图（13）△ABC ≌△EDC 。

求证：BE=AD 。

14、如图（14）在△ABC 中，∠ACB=90°，AC=BC ，AE 是BC 的中线，过点C 作CF ⊥AE 于F ，过B 作BD ⊥CB 交CF 的延长线于点D 。

人教版八年级上册《全等三角形》综合测试卷满分：100分姓名：___________班级：___________考号：___________成绩：___________一．选择题（共10小题，满分30分，每小题3分）1．下列各组图形中不是全等形的是（）A．B．C．D．2．如图，一块三角形玻璃裂成①、②、③三块，现需要划一块同样大小的三角形玻璃，为了方便只需带上一块，号码和依据是（）A．①SAS B．②ASA C．③AAS D．③ASA 3．如图，△ABC≌△ADE，若∠E＝70°，∠D＝30°，∠CAD＝35°，则∠BAD＝（）A．40°B．45°C．50°D．55°4．如图是由4个相同的小正方形组成的网格图，其中∠1+∠2等于（）A．150°B．180°C．210°D．225°5．如图，若△ABC≌△DEF，BC＝7，CF＝5，则CE的长为（）A．1 B．2 C．2.5 D．36．如图，点B，E，C，F在同一条直线上，已知AB＝DE，AC＝DF，添加下列条件还不能判定△ABC≌△DEF的是（）A．∠ABC＝∠DEF B．∠A＝∠D C．BE＝CFD．BC＝EF7．如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线AP交边BC 于点D，若CD＝5，AB＝12，则△ABD的面积是（）A．15 B．30 C．45 D．608．如图，在△ABC中，∠C＝90°∠ABC的平分线BD交AC于点D，若BD＝10厘米，BC＝8厘米，DC＝6厘米，则点D到直线AB 的距离是（）A．6cm B．8cm C．10cm D．14cm 9．在平面直角坐标系xOy中，点A（﹣3，0），B（2，0），C（﹣1，2），E（4，2），如果△ABC与△EFB全等，那么点F的坐标可以是（）A．（6，0）B．（4，0）C．（4，﹣2）D．（4，﹣3）10．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC 交ED的延长线于点F，若BC恰好平分∠ABF，AE＝2BF．给出下列四个结论：①DE＝DF；②DB＝DC；③AD⊥BC；④AC＝3BF，其中正确的结论共有（）A．①②③④B．①②④C．①②③D．②③④二．填空题（共6小题，满分24分，每小题4分）11．如图，在△ABC中，∠C＝90°，AC＝8，DC＝AD，BD平分∠ABC，则点D到AB的距离等于．12．如图，小敏做了一个角平分仪ABCD，其中AB＝AD，BC＝DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ 的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC ≌△ADC，这样就有∠QAE＝∠PAE．则说明这两个三角形全等的依据是．13．如图，△ADE≌△BCF，AD＝8cm，CD＝6cm，则BD的长为cm．14．如图，AC⊥BC，AD⊥BD，垂足分别是C，D，（若要用“HL”得到Rt△ABC≌Rt△BAD，则应添加的条件是．（写一种即可）15．在正方形网格中，∠AOB的位置如图所示，点P，Q，M，N是四个格点，则这四个格点中到∠AOB两边距离相等的点是点．16．如图所示，AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝22°，∠2＝34°，则∠3＝．三．解答题（共7小题，满分46分）17．（5分）已知：如图，点A、E、F、C在同一条直线上，AD∥CB，∠1＝∠2，AE＝CF．求证：△ADF≌△CBE．18．（5分）如图所示，在△ABC中，AB＝CB，∠ABC＝90°，F为AB延长线上一点，点E在BC上，且AE＝CF．求证：Rt△ABE≌Rt△CBF．19．（6分）问题：已知线段AB、CD相交于点O，AB＝CD．连接AD、BC，请添加一个条件，使得△AOD≌△COB小明的做法及思路小明添加了条件：∠DAB＝∠BCD．他的思路是分两种情况画图①、图②，在两幅图中，都作直线DA、BC，两直线交于点E由∠DAB＝∠BCD，可得∠EAB＝∠ECD∵AB＝CD，∠E＝∠E∴△EAB≌△ECD，∴EB＝ED，EA＝EC图①中ED﹣EA＝EB﹣EC，即AD＝CB图②中EA﹣ED＝EC﹣EB，即AD＝CB又∵∠DAB＝∠BCD，∠AOD＝∠COB∴△AOD≌△COB（1）数学老师说：小明的做法不正确，请你给出解释；（2）请你重新添加一个满足问题要求的条件，并说明理由．20．（7分）如图，已知点E，D，A，B在一条直线上，BC∥EF，∠C＝∠F，AD＝1，AE＝2.5，AB＝1.5．（1）试说明：△ABC≌△DEF．（2）判断DF与AC的位置关系，并说明理由．21．（7分）已知：在△ABC中，∠ABC＝60°，∠ACB＝40°，BD平分∠ABC，CD平分∠ACB，（1）如图1，求∠BDC的度数；（2）如图2，连接AD，作DE⊥AB，DE＝2，AC＝4，求△ADC 的面积．22．（7分）如图①，在Rt△ABC中，∠C＝90°，BC＝9cm，AC＝12cm，AB＝15cm，现有一动点P，从点A出发，沿着三角形的边AC→CB→BA运动，回到点A停止，速度为3cm/s，设运动时间为ts．（1）如图（1），当t＝时，△APC的面积等于△ABC面积的一半；（2）如图（2），在△DEF中，∠E＝90°，DE＝4cm，DF＝5cm，∠D＝∠A．在△ABC的边上，若另外有一个动点Q，与点P同时从点A出发，沿着边AB→BC→CA运动，回到点A停止．在两点运动过程中的某一时刻，恰好△APQ≌△DEF，求点Q的运动速度．23．（9分）如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC，AF ⊥CB，垂足为F．（1）求证：△ABC≌△ADE；（2）求∠FAE的度数；（3）求证：CD＝2BF+DE．参考答案一．选择题（共10小题，满分30分，每小题3分）1．解：观察发现，A、C、D选项的两个图形都可以完全重合，∴是全等图形，B选项中圆与椭圆不可能完全重合，∴不是全等形．故选：B．2．解：只需带上碎片③即可．理由：碎片③中，可以测量出三角形的两角以及夹边的大小，三角形的形状即可确定．故选：D．3．解：∵∠B＝70°，∠C＝30°，∴∠BAC＝180°﹣∠B﹣∠C＝180°﹣70°﹣30°＝80°，∵△ABC≌△ADE，∴∠EAD＝∠BAC＝80°，∴∠EAC＝∠EAD﹣∠DAC＝80°﹣35°＝45°，故选：B．4．解：由题意得：AB＝ED，BC＝DC，∠D＝∠B＝90°，∴△ABC≌△EDC（SAS），∴∠BAC＝∠1，∠1+∠2＝180°．故选：B．5．解：∵BC＝7，CF＝5，∴BF＝7﹣5＝2，∵△ABC≌△DEF，∴EF＝CB，∴EF﹣CF＝CB﹣CF，∴EC＝BF＝2，故选：B．6．解：已知AB＝DE，AC＝DF，添加的一个条件是∠ABC＝∠DEF，根据条件不可以证明△ABC≌△DEF，故选项A符合题意；已知AB＝DE，AC＝DF，添加的一个条件是∠A＝∠D，根据SAS 可以证明△ABC≌△DEF，故选项B不符合题意；已知AB＝DE，AC＝DF，添加的一个条件是EB＝CF，可得得到BC＝EF，根据SSS可以证明△ABC≌△DEF，故选项C不符合题意；已知AB＝DE，AC＝DF，添加的一个条件是BC＝EF，根据SSS 可以证明△ABC≌△DEF，故选项D不符合题意；故选：A．7．解：作DE⊥AB于E，由基本尺规作图可知，AD是△ABC的角平分线，∵∠C＝90°，∴DC⊥AC，∵DE⊥AB，DC⊥AC，∴DE＝DC＝5，∴△ABD的面积＝×AB×DE＝×12×5＝30，故选：B．8．解：过D作DE⊥AB，交AB于点E，∵BD平分∠ABC，DC⊥CB，DE⊥BA，∴DE＝DC＝6厘米，则点D到直线AB的距离是6厘米，故选：A．9．解：如图所示：△ABC与△EFB全等，点F的坐标可以是：（4，﹣3）．故选：D．10．解：∵BC恰好平分∠ABF，∴∠FBC＝∠ABC∵BF∥AC，∴∠FBC＝∠ACB，∴∠ACB＝∠ABC＝∠CBF，在△ABC中，AD是△ABC的角平分线，∠ACB＝∠ABC，∴△ABC为等腰三角形，∴CD＝BD，（故②正确），CA＝AB，AD⊥BC（故③正确），∵∠ACB＝∠CBF，CD＝BD，∴Rt△CDE≌Rt△BDF（AAS），∴DE＝DF，（故①正确），BF＝CE，CA＝AB＝AE+CE＝2BF+BF ＝3BF，（故④正确），故选：A．二．填空题（共6小题，满分24分，每小题4分）11．解：如图，过点D作DH⊥AB，垂足为H，∵AC＝8，DC＝AD，∴DC＝2，∵BD平分∠ABC，∠C＝90°，DH⊥AB，∴CD＝DH＝2，∴点D到AB的距离等于2，故答案为2．12．解：在△ADC和△ABC中，，∴△ADC≌△ABC（SSS）．∴∠DAC＝∠BAC，即∠QAE＝∠PAE．故答案为：SSS．13．解：∵△ADE≌△BCF，∴AD＝BC＝8cm，∵BD＝BC﹣CD，CD＝6cm，∴BD＝8﹣6＝2（cm）．故答案为：2．14．解：若添加AC＝BD，在Rt△ABC和Rt△BAD中，，∴Rt△ABC≌Rt△BAD（HL）；若添加BC＝AD，在Rt△ABC和Rt△BAD中，，∴Rt△ABC≌Rt△BAD（HL）．故答案为：AC＝BD或BC＝AD．15．解：由图形可知，点M在∠AOB的角平分线上，∴点M到∠AOB两边距离相等，故答案为：M．16．解：∵∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，在△BAD和△CAE中，，∴△BAD≌△CAE（SAS），∴∠ABD＝∠2＝34°，∵∠3＝∠1+∠ABD，∠1＝22°，∴∠3＝56°，故答案为：56°．三．解答题（共7小题，满分46分）17．证明：∵AD∥CB，∴∠A＝∠C，∵AE＝CF，∴AE+EF＝CF+EF，即AF＝CE，在△ADF和△CBE中，∴△ADF≌△CBE（ASA）．18．证明：在Rt△ABE和Rt△CBF中，∵，∴Rt△ABE≌Rt△CBF（HL）．19．解：（1）可画出下面的反例：图中，AB＝CD，DA∥BC，小明的证明方法就错误了，理由直线AD与BC没有交点．（2）答案不唯一，如OA＝OC．理由如下：∵AB＝CD，OA＝OC，∴AB﹣OA＝CD﹣OC，即OB＝OD．在△AOD和△COB中，∴△AOD≌△COB（SAS）．20．（1）证明：∵BC∥EF，∴∠B＝∠E，∵AD＝1，AE＝2.5，∴DE＝AE﹣AD＝2.5﹣1＝1.5，∵AB＝1.5，∴AB＝DE，∵∠C＝∠F，∴△ABC≌△DEF（AAS）；（2）DF∥AC．∵△ABC≌△DEF，∴∠BAC＝∠EDF，∵∠BAC+∠DAC＝∠EDF+∠ADF＝180°，∴∠DAC＝∠ADF，∴DF∥AC．21．解：（1）∵BD平分∠ABC，∴∠DBC＝∠ABC＝×60°＝30°，∵CD平分∠ACB，∴∠DCB＝∠ACB＝×40°＝20°，∴∠BDC＝180°﹣∠DBC﹣∠DCB＝180°﹣30°﹣20°＝130°；（2）作DF⊥AC于F，DH⊥BC于H，如图2，∵BD平分∠ABC，DE⊥AB，DH⊥BC，∴DH＝DE＝2，∵CD平分∠ACB，DF⊥AC，DH⊥BC，∴DF＝DH＝2，∴△ADC的面积＝DF•AC＝×2×4＝4．22．解：（1）①当点P在BC上时，如图①﹣1，若△APC的面积等于△ABC面积的一半；则CP＝BC＝cm，此时，点P移动的距离为AC+CP＝12+＝，移动的时间为：÷3＝秒，②当点P在BA上时，如图①﹣2若△APC的面积等于△ABC面积的一半；则PD＝BC，即点P为BA中点，此时，点P移动的距离为AC+CB+BP＝12+9+＝cm，移动的时间为：÷3＝秒，故答案为：或；（2）△APQ≌△DEF，即，对应顶点为A与D，P与E，Q与F；①当点P在AC上，如图②﹣1所示：此时，AP＝4，AQ＝5，∴点Q移动的速度为5÷（4÷3）＝cm/s，②当点P在AB上，如图②﹣2所示：此时，AP＝4，AQ＝5，即，点P移动的距离为9+12+15﹣4＝32cm，点Q移动的距离为9+12+15﹣5＝31cm，∴点Q移动的速度为31÷（32÷3）＝cm/s，综上所述，两点运动过程中的某一时刻，恰好△APQ≌△DEF，点Q 的运动速为cm/s或cm/s．23．证明：（1）∵∠BAD＝∠CAE＝90°，∴∠BAC+∠CAD＝90°，∠CAD+∠DAE＝90°，∴∠BAC＝∠DAE，在△BAC和△DAE中，，∴△BAC≌△DAE（SAS）；（2）∵∠CAE＝90°，AC＝AE，∴∠E＝45°，由（1）知△BAC≌△DAE，∴∠BCA＝∠E＝45°，∵AF⊥BC，∴∠CFA＝90°，∴∠CAF＝45°，∴∠FAE＝∠FAC+∠CAE＝45°+90°＝135°；（3）延长BF到G，使得FG＝FB，∵AF⊥BG，∴∠AFG＝∠AFB＝90°，在△AFB和△AFG中，，∴△AFB≌△AFG（SAS），∴AB＝AG，∠ABF＝∠G，∵△BAC≌△DAE，∴AB＝AD，∠CBA＝∠EDA，CB＝ED，∴AG＝AD，∠ABF＝∠CDA，∴∠G＝∠CDA，∵∠GCA＝∠DCA＝45°，在△CGA和△CDA中，，∴△CGA≌△CDA（AAS），∴CG＝CD，∵CG＝CB+BF+FG＝CB+2BF＝DE+2BF，∴CD＝2BF+DE．。

全等三角形测试题及答案一、选择题1. 下列选项中，哪两个三角形是全等的？A. ∠A=∠B，AB=BCB. ∠A=∠B，AC=BDC. ∠A=∠C，AB=ACD. ∠A=∠B，AB=BC，AC=BD2. 如果两个三角形的对应边成比例，且夹角相等，这两个三角形是：A. 相似但不全等B. 必然全等C. 不一定全等D. 无法判断二、填空题3. 根据全等三角形的性质，如果两个三角形的对应角相等，且对应边成比例，那么这两个三角形是_________。

4. SAS全等条件指的是_________。

三、判断题5. 如果两个三角形的三边对应相等，那么这两个三角形一定全等。

（）6. 根据HL全等条件，直角三角形中，如果斜边和一条直角边对应相等，那么这两个直角三角形全等。

（）四、解答题7. 已知三角形ABC和三角形DEF，其中∠A=∠D=90°，AB=DE，AC=DF，求证：三角形ABC全等于三角形DEF。

8. 如图所示，三角形ABC和三角形DEF在平面直角坐标系中，点A(2,3)，B(4,5)，C(1,1)，点D(-1,-2)，E(1,-1)，F(-2,-4)。

若AB=DE，AC=DF，∠BAC=∠EDF，请证明三角形ABC全等于三角形DEF。

五、综合题9. 在三角形ABC中，点D在BC上，若AD平分∠BAC，且BD=DC，求证：AB=AC。

10. 已知三角形ABC和三角形DEF，其中AB=DE，∠B=∠D，∠C=∠E，求证：三角形ABC全等于三角形DEF。

答案：一、选择题1. 答案：D2. 答案：A二、填空题3. 答案：相似4. 答案：边角边三、判断题5. 答案：正确6. 答案：正确四、解答题7. 解：由于∠A=∠D=90°，AB=DE，AC=DF，根据直角三角形的HL全等条件，我们可以得出三角形ABC全等于三角形DEF。

8. 解：由于AB=DE，AC=DF，∠BAC=∠EDF，根据SAS全等条件，我们可以得出三角形ABC全等于三角形DEF。

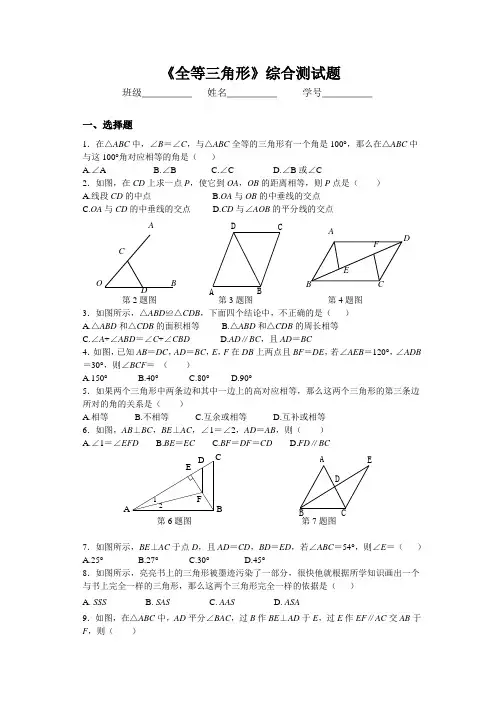
《全等三角形》综合测试题班级_________ 姓名_________ 学号_________一、选择题1．在△ABC 中，∠B ＝∠C ，与△ABC 全等的三角形有一个角是100°，那么在△ABC 中与这100°角对应相等的角是（ ）A.∠AB.∠BC.∠CD.∠B 或∠C2．如图，在CD 上求一点P ，使它到OA ，OB 的距离相等，则P 点是（ ） A.线段CD 的中点 B.OA 与OB 的中垂线的交点 C.OA 与CD 的中垂线的交点 D.CD 与∠AOB 的平分线的交点第2题图 第3题图 第4题图 3．如图所示，△ABD ≌△CDB ，下面四个结论中，不正确的是（ ） A.△ABD 和△CDB 的面积相等 B.△ABD 和△CDB 的周长相等 C.∠A +∠ABD ＝∠C +∠CBD D.AD ∥BC ，且AD ＝BC 4．如图，已知AB ＝DC ，AD ＝BC ，E ，F 在DB 上两点且BF ＝DE ，若∠AEB ＝120°，∠ADB ＝30°，则∠BCF ＝ （ ）5A.6A.78A. SSS B. SAS C. AAS D. ASA9．如图，在△ABC 中，AD 平分∠BAC ，过B 作BE ⊥AD 于E ，过E 作EF ∥AC 交AB 于F ，则（ ）A D AC B OD CB AABC E FA BC D FE O A. AF ＝2BF B.AF ＝BF C.AF ＞BF D.AF ＜BF第8题图 第9题图 第10题图 10．将一张长方形纸片按如图所示的方式折叠，BC BD ，为折痕，则CBD ∠的度数为（ ） A ．60° B ．75° C ．90° D ．95°二、填空题11． 如图，BAC ABD ∠=∠，请你添加一个条件： ，使OC OD =（只添一个即可）．第12题 第13题12．如图，在△ABC 中，AB ＝AC ，BE 、CF 是中线，则由 可得△AFC ≌△AEB .13．如图，AB ＝CD ，AD ＝BC ，O 为BD 中点，过O 点作直线与DA 、BC 延长线交于E 、F ，若∠ADB ＝60°，EO ＝10，则∠DBC ＝ ，FO ＝ .14．已知Rt △ABC 中，∠C ＝90°，AD 平分∠BAC 交BC 于D ，若BC ＝32，且BD ∶CD ＝9∶7，则D 到AB 边的距离为＿＿＿.15．△ABC ≌△DEF ，且△ABC 的周长为12，若AB =3，EF =4，则AC = ．16．如果两个三角形的两条边和其中一条边上的高对应相等，那么这两个三角形的第三边所对的角的关系是__________.17．如图，AB ∥CD ，AD ∥BC ，OE ＝OF ，图中全等三角形共有______对.18．在数学活动课上，小明提出这样一个问题：∠B ＝∠C ＝90°，E 是BC 的中点，DE 平分∠ADC ，∠CED ＝35°，如图，则∠EAB 是多少度？大家一起热烈地讨论交流，小英第一个得出正确答案，是______.第17题 第18题DO CBA 第11题FED C BAAECBA ′ E ′DB19．如图，AD ，A ′D ′分别是锐角三角形ABC 和锐角三角形A ′B ′C ′中BC ，B ′C ′边上的高，且AB ＝A ′B ′，AD ＝A ′D ′．若使△ABC ≌△A ′B ′C ′，请你补充条件________.（填写一个你认为适当的条件即可）20. 如图，AB ∥CD ，AD ∥BC ，OE=OF ，图中全等三角形共有______对。

第1章全等三角形综合检测(满分100分,限时60分钟)一、选择题(每小题3分,共36分)1.下列各组图形中,不是全等形的是( )A B C D2.(2021四川攀枝花中考)如图,一名工作人员不慎将一块三角形模具打碎成三块,他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具,他带去最省事.( )A.①B.②C.③D.①③3.(2019辽宁丹东中考)如图,点C在∠AOB的边OA上,用尺规作出了CP∥OB,作图痕迹中,是( )A.以点C为圆心,OD的长为半径的弧B.以点C为圆心,DM的长为半径的弧C.以点E为圆心,DM的长为半径的弧D.以点E为圆心,OD的长为半径的弧4.(2021山东莘县期中)如图是两个全等三角形,图中字母表示三角形的边长,则∠α的度数为( )A.50°B.58°C.60°D.72°5.(2022山东昌乐期中)如图,测河两岸A,B两点的距离时,先在AB的垂线BF上取C,D两点,使CD=BC,再过点D作出BF的垂线DE,当点A,C, E在同一直线上时,可证明△EDC≌△ABC,从而得到ED=AB,测得ED的长就是A,B两点的距离.判定△EDC≌△ABC的依据是( )A.ASAB.SSSC.AASD.SAS6.(2021山东巨野期中)如图所示,△ABD≌△CDB,下面四个选项中,不一定成立的是( )A.△ABD和△CDB的面积相等B.△ABD和△CDB的周长相等C.AD+AB=CD+BDD.AD∥BC7.(2021山东阳谷期中)一个三角形由六个元素组成,即三条边和三个角,那么关于判定三角形全等的说法,正确的是( )A.六对元素必须相等,才可以判定三角形全等B.任意三对元素相等,即可判定三角形全等C.至少三对元素相等,且必有一组边相等,才可以判定三角形全等D.两个直角三角形全等,只需任意两对元素相等即可8.(2021山东寿光期中)根据下列已知条件,不能画出唯一的△ABC的是( )A.AB=5,BC=3,AC=6B.AB=10,BC=20,∠B=80°C.∠A=50°,∠B=60°,AB=4D.∠A=50°,∠B=60°,∠C=70°9.(2021陕西陇县期末)如图,AB⊥CD,且AB=CD,CE⊥AD于E,BF⊥AD于F.若CE=6,BF=3,EF=2,则AD的长为( )A.7B.6C.5D.410.(2022贵州黔西南州期末)如图,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥OB于点C,BD、AC都经过点E,则图中全等的三角形共有( )A.3对B.4对C.5对D.6对11.(2022山东单县期中)如图,已知线段AC、BD相交于点O,从下列条件:①点O是线段AC的中点;②点O是线段BD的中点;③AB=DC;④AB ∥DC中选两个仍不能说明△ABO≌△CDO的是( )A.①②B.①③C.③④D.①④12.(2022山东潍坊潍城期末)如图,已知锐角∠AOB,根据以下要求作图:(1)在射线OA上取点C和点E,以点O为圆心,OC,OE的长为半径画弧,分别交射线OB于点D,F;(2)连接CF,DE交于点P.则各项结论错误的是( )A.CE=DFB.点P在∠AOB的平分线上C.PE=PFD.若∠AOB=60°,则∠CPD=120°二、填空题(每小题3分,共15分)13.(2021山东阳谷期中)当三角形的三条边的长度确定后,它的形状和大小就被确定了,三角形的这种特性称为三角形的.14.(2020湖南怀化中考)如图,在△ABC和△ADC中,AB=AD,BC=DC, ∠B=130°,则∠D= °.15.已知∠α>∠β,作∠AOB=∠α,再以∠AOB的边OB为一边作∠BOC=∠β,则∠AOC= .(用∠α,∠β表示)16.(2022山东肥城期末)如图,在正方形网格中,∠1+∠2+∠3= .17.(2022独家原创)如图,在△ABC中,∠ACB=90°,AC=BC,∠BAC的平分线AD交BC于点D,过点B作BE⊥AD交AD的延长线于E,AC、BE的延长线相交于点F.若AD=6,则BE的长为.三、解答题(共49分)18.(2021湖南衡阳中考)(6分)如图,点A、B、D、E在同一条直线上, AB=DE,AC∥DF,BC∥EF.求证:△ABC≌△DEF.19.(2022山东临清期中)(8分)如图,D是△ABC的边AC上一点,点E 在AC的延长线上,EC=AD,过点E作EF∥AB,且使EF=AB,连接DF.DF与BC相等吗?为什么?20.(2021河北正定期中)(8分)如图,已知:线段a,c,∠α.求作:△ABC,使BC=a,AB=c,∠ABC=∠α.(用尺规作图,保留作图痕迹,不写作法)请你根据所学的知识,说明尺规作图作出∠ABC=∠α,用到的是三角形全等判定方法中的,作出的△ABC是唯一的,依据是三角形全等判定方法中的.21.(2021山东阳谷期中)(8分)如图,△ABC≌△DEF,AM、DN分别是△ABC、△DEF的对应边上的高.求证:AM=DN.22.(2022山东聊城东昌府期中)(8分)已知△ABC中,AB=AC,∠BAC=90°,分别过B、C向过点A的直线作垂线,垂足分别为点E、F.(1)如图1,当过A的直线与斜边BC不相交时,求证:①△ABE≌△CAF;②EF=BE+CF;(2)如图2,当过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,试求EF的长.图1 图223.(2022山东高密期中)(11分)如图1所示,BD、CE是△ABC的高,点P在BD的延长线上,AC=BP,点Q在CE上,QC=AB.(1)判断:∠1 ∠2(用“>”“<”或“=”填空);(2)探究:AP与AQ之间的关系;(3)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,试探究AP与AQ之间的关系,请画出图形并直接写出结论.图1 备用图答案全解全析一、选择题1.D直接利用全等形的定义即可得出答案.D选项中的两个图形大小不相等,故不全等.故选D.2.C由图形可知,③有完整的两角与夹边,根据“角边角”可以作出与原三角形全等的三角形,所以最省事的做法是带③去.3.C根据“作一个角等于已知角”的步骤可得答案.4.A如图,根据三角形的内角和定理可得∠β=180°-58°-72°=50°.因为两个三角形全等,所以∠α=∠β=50°,故选A.5.A根据题意得AB⊥BC,DE⊥CD,∴∠ABC=∠EDC=90°,∵BC=CD,∠ACB=∠ECD,∴根据“ASA”可判定△EDC≌△ABC.6.C∵△ABD≌△CDB,∴△ABD和△CDB的面积相等,周长相等,AB=CD,AD=BC,∠ADB= ∠CBD,∴AD+AB=CD+BC,AD∥BC,选项C不一定成立.7.C根据全等三角形的判定方法“SAS”“ASA”“AAS”“SSS”可知,至少三对元素相等,且必有一组边相等,才能判定三角形全等.8.D选项A,已知三边,且满足任意两边之和大于第三边,所以能作出三角形,且能画出唯一的△ABC;选项B,已知两边及其夹角,满足SAS,所以能画出唯一的△ABC;选项C,AB是∠A,∠B的夹边,满足ASA,所以能画出唯一的△ABC;选项D,三个角分别相等的三角形有无数个,所以不能画出唯一的△ABC.故选D.9.A∵AB⊥CD,CE⊥AD,BF⊥AD,∴∠A+∠D=90°,∠C+∠D=90°,∠CED=∠AFB=90°,∴∠A=∠C.在△ABF和△CDE中,∴△ABF≌△CDE(AAS),∴AF=CE=6,BF=DE=3,∴AD=AF-EF+DE=6-2+3=7.故选A.10.B△OED≌△OEC(AAS),△AED≌△BEC(ASA),△OAE≌△OBE(SAS),△OAC≌△OBD(SAS).11.B选项A,∵点O是线段AC的中点,点O是线段BD的中点, ∴OA=OC,OB=OD,∵∠AOB=∠COD,∴△ABO≌△CDO(SAS);选项B,∵点O是线段AC的中点,AB=DC,∴OA=OC,已知∠AOB=∠COD,由SSA不能判定△ABO≌△CDO;选项C,∵AB∥DC,∴∠B=∠D,∠A=∠C,∵AB=DC,∴△ABO≌△CDO(ASA);选项D,∵点O是线段AC的中点,∴OA=OC,∵AB∥DC,∴∠B=∠D,∠A=∠C,∴△ABO≌△CDO(AAS).12.D由作图,得OE=OF,OC=OD,所以OE-OC=OF-OD,即CE=DF,选项A正确;在△EOD与△FOC中,所以△EOD≌△FOC(SAS),所以∠OED=∠OFC,ED=FC,在△ECP与△FDP中,所以△ECP≌△FDP(AAS),所以PE=PF,所以ED-PE=FC-PF,即PD=PC,连接OP,在△OCP与△ODP,所以△OCP≌△ODP(SSS),所以∠COP=∠DOP,所以点P在∠AOB的平分线上,选项B、C正确;若∠AOB=60°,没有条件判定OC⊥CF,OD⊥DE,所以无法判定∠CPD=120°,选项D错误.二、填空题13.稳定性解析因为三角形具有稳定性,所以三角形的三条边的长度确定后,它的形状和大小就被确定了.14. 130解析在△ADC和△ABC中,所以△ADC≌△ABC(SSS),所以∠D=∠B=130°.15.∠α+∠β或∠α-∠β解析当OC在∠AOB内部时,∠AOC=∠α-∠β;当OC在∠AOB外部时,∠AOC=∠α+∠β.所以∠AOC=∠α+∠β或∠α-∠β.16.135°解析如图,在△ABC和△ADE中,∴△ABC≌△ADE(SAS),∴∠4=∠3,∵∠1+∠4=90°,∴∠3+∠1=90°,∵∠2=45°,∴∠1+∠2+∠3=135°.17.3解析∵BE⊥AD,∴∠AEB=90°,∵∠ACB=90°,∴∠AEB=∠ACB,∵∠ADC=∠BDE,∴∠CAD=∠CBF,在△ACD和△BCF中,∴△ACD≌△BCF(ASA),∴BF=AD.∵AD平分∠BAF,∴∠BAE=∠FAE,在△BAE和△FAE中,∴△BAE≌△FAE(ASA),∴BE=EF,∴BE=BF=AD=3.三、解答题18.证明∵AC∥DF,∴∠CAB=∠FDE.∵BC∥EF,∴∠CBA=∠FED.在△ABC和△DEF中,∴△ABC≌△DEF(ASA).19.解析DF=BC,理由如下:∵EF∥AB,∴∠E=∠A,∵EC=AD,∴EC+CD=AD+CD,即ED=AC.在△EFD和△ABC中,∴△EFD≌△ABC(SAS),∴DF=BC.20.解析如图,△ABC即为所求.尺规作图作出∠ABC=∠α,用到的是三角形全等判定方法中的“SSS”,作出的△ABC是唯一的,依据是三角形全等判定方法中的“SAS”.21.证明方法一:因为△ABC≌△DEF,所以AB=DE,∠B=∠E,因为AM、DN分别是△ABC、△DEF的对应边上的高,所以AM⊥BC,DN⊥EF,所以∠AMB=∠DNE=90°.在△ABM和△DEN中,所以△ABM≌△DEN(AAS),所以AM=DN.方法二:因为△ABC≌△DEF,所以BC=EF,S△ABC=S△DEF,所以BC·AM=EF·DN,所以AM=DN.22.解析(1)证明:①∵BE⊥EF,CF⊥EF,∴∠AEB=∠CFA=90°,∴∠EAB+∠EBA=90°.∵∠BAC=90°,∴∠EAB+∠FAC=90°,∴∠EBA=∠FAC.在△ABE和△CAF中,∴△ABE≌△CAF(AAS).②∵△ABE≌△CAF,∴EA=FC,EB=FA,∴EF=AF+AE=BE+CF.(2)同(1)可证△ABE≌△CAF(AAS),∴AE=CF=3,BE=AF=10,∴EF=AF-AE=10-3=7.23.解析(1)=.提示:设CE、BD交于点F,∵BD、CE是△ABC的高,∴∠BEF=∠CDF=90°,∵∠BFE=∠CFD,∠1=90°-∠CFD,∠2=90°-∠BFE, ∴∠1=∠2.(2)结论:AP=AQ,AP⊥AQ.证明:在△QAC和△APB中,∴△QAC≌△APB(SAS),∴AQ=AP,∠QAC=∠P,∵∠DAP+∠P=90°,∴∠DAP+∠QAC=90°,即∠QAP=90°,∴AQ⊥AP.(3)AP=AQ,AP⊥AQ,图形如图所示.提示:∵BD、CE是△ABC的高,∴BD⊥AC,CE⊥AB,∴∠1+∠CAE=90°,∠2+∠DAB=90°, ∵∠CAE=∠DAB,∴∠1=∠2.在△QAC和△APB中,∴△QAC≌△APB(SAS),∴AQ=AP,∠QAC=∠P,∵∠PDA=90°,∴∠P+∠PAD=90°,∴∠QAC+∠PAD=90°,∴∠QAP=90°,∴AQ⊥AP.故AP=AQ,AP⊥AQ.。

全等三角形考试题及答案一、选择题1. 两个三角形全等的条件是：A. 两个角相等B. 三条边相等C. 两边夹一角相等D. 两角夹一边相等答案：D2. 已知△ABC≌△DEF，其中AB=DE，AC=DF，∠A=∠D，那么BC与EF 的关系是：A. BC=EFB. BC>EFC. BC<EFD. 不能确定答案：A二、填空题1. 如果两个三角形的对应边成比例，且对应角相等，则这两个三角形______。

答案：相似2. 在△ABC中，∠A=∠B=50°，则∠C=______。

答案：80°三、解答题1. 已知△ABC≌△DEF，且AB=5cm，BC=7cm，求DE的长度。

答案：DE=5cm2. 已知△ABC≌△DEF，且∠A=∠D=60°，∠B=∠E=50°，求∠C和∠F 的度数。

答案：∠C=∠F=70°四、证明题1. 已知△ABC≌△DEF，且∠A=∠D=90°，AB=DE，AC=DF，证明：BC=EF。

答案：根据直角三角形全等的判定定理HL，因为∠A=∠D，AB=DE，AC=DF，所以△ABC≌△DEF，因此BC=EF。

2. 已知△ABC≌△DEF，且∠A=∠D，∠B=∠E，证明：∠C=∠F。

答案：根据全等三角形对应角相等的性质，因为△ABC≌△DEF，所以∠C=∠F。

五、应用题1. 一块三角形的木板ABC需要与另一块三角形的木板DEF进行拼接，已知AB=DE，BC=EF，∠A=∠D，∠B=∠E，判断两块木板是否可以拼接。

答案：可以拼接，因为根据SAS判定定理，△ABC≌△DEF。

2. 已知一个等腰三角形ABC，其中AB=AC，∠A=50°，求∠B和∠C的度数。

答案：因为AB=AC，所以∠B=∠C，又因为三角形内角和为180°，所以∠B=∠C=(180°-50°)/2=65°。

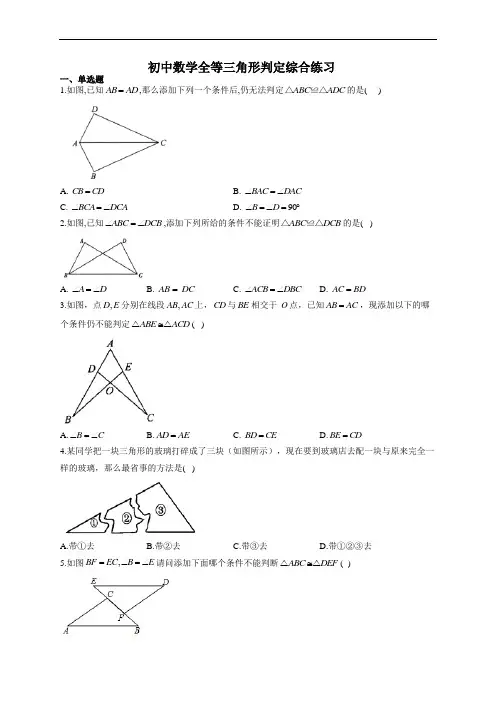
初中数学全等三角形判定综合练习一、单选题1.如图,已知AB AD =,那么添加下列一个条件后,仍无法判定ABC ADC △≌△的是( )A. CB CD =B. BAC DAC ∠=∠C. BCA DCA ∠=∠D. 90B D ∠=∠=︒2.如图,已知ABC DCB ∠=∠,添加下列所给的条件不能证明ABC DCB △≌△的是( )A. A D ∠=∠B. AB DC =C. ACB DBC ∠=∠D. AC BD =3.如图，点,D E 分别在线段,AB AC 上，CD 与BE 相交于O 点，已知AB AC =，现添加以下的哪个条件仍不能判定ABE ACD ≅△△( )A.B C ∠=∠B.AD AE =C. BD CE =D.BE CD =4.某同学把一块三角形的玻璃打碎成了三块（如图所示），现在要到玻璃店去配一块与原来完全一样的玻璃，那么最省事的方法是( )A.带①去B.带②去C.带③去D.带①②③去5.如图,BF EC B E =∠=∠请问添加下面哪个条件不能判断ABC DEF ≅△△( )A.A D ∠=∠B.AB ED =C.//DF ACD.AC DF =6.如图，点B E C F 、、、在同一条直线上，//AB DE ，AB DE =，要用SAS 证明ABC DEF ≅△△，可以添加的条件是( )A ．A D ∠=∠B ．//AC DF C ．BE CF =D ．AC DF =7.下列各图中a b c ,,为三角形的边长，则甲、乙、丙三个三角形和左侧ABC △全等的是( )A.甲和乙B.乙和丙C.甲和丙D.只有丙8.如图，点D E ,分别在线段AB AC ,上，CD 与BE 相交于O 点，已知AB AC =，现添加以下的哪个条件仍不能判定ABE ACD ≅△△？( )A.B C ∠=∠B.AD AE =C. BD CE =D.BE CD =9.如图所示的是用直尺和圆规作一个角等于已知角 的示意图，则说明'''A O B AOB ∠=∠的依据 是（ ）A.S.A.SB.S.S.S.C.A.A.S.D.A.S.A.10.如图，AOB ∠是一个任意角，在边OA OB ,上分别取OM ON =，移动角尺，使角尺两边相同的刻度分别与M N ,重合，过角尺顶点C 的射线OC 便是AOB ∠的平分线这种方法所用的三角形全等的判定方法是( )A.S.A.S.B.S.S.S.C.A.S.A.D.A.A.S.11.如图，AB AD =，BC CD =，点E 在AC 上，则全等三角形共有( )A.1对B.2对C.3对D.4对12.如图，在ABC △和DEF △中，,B E C F ,,在同一直线上，AB DE =，AC DF =，要使ABC DEF ≅△△，还需要添加的一个条件是( )A.EC CF =B.BE CF =C.B DEF ∠=∠D.//AC DF13.如图，ABC △中，AB AC =，EB EC =，则由“S.S.S.”可以判定( )A.ABD ACD ≅△△B.ABE ACE ≅△△C.BDE CDE ≅△△D.以上答案都不对14.如图，点E 在ABC △的外部，点D 在边BC 上，DE 交AC 于点F .若12∠=∠，E C ∠=∠，AE AC =，则( )A.ABC AFE ≅△△B.AFE ADC ≅△△C.AFE DFC ≅△△D.ABC ADE ≅△△15.下列条件能判 断两个三角形全等的是（ ）A.有两边对应相等B.有两角对应相等C.有一边一角对应相等D.能够完全重合16.如图，全等的两个三角形是( )A.③④B.②③C.①②D.①④17.如图,点,,,B E C F 在同一条直线上,//,AB DE AB DE = ,要用“边角边”证明ABC DEF ≅△△,可以添加的条件是( ).A.A D ∠=∠B.//AC DFC.BE CF =D.AC DF =18.如图，点P 是AB 上任一点，ABC ABD ∠=∠,从下列各条件中补充一个条件，不一定能推出APC APD ≅△△.的是( )A.BC BD =B.ACB ADB ∠=∠C.AC AD =D. CAB DAB ∠=∠二、证明题19.如图：点C D 、在AB 上，且//AC BD AE FB AE BF ==，，．求证：//DE CF ．20.如图，已知CA CB =，AD BD =，M N ,分别是CB CA ,的中点，求证：DN DM =.21.如图，已知AB AE =，12∠=∠，B E ∠=∠.求证：BC ED =.22.如图，90A D ∠=∠=︒，AC DB =，AC DB ,相交于点O .求证:OB OC =.23.如图（1）在ABC △中，90ACB AC BC ∠=︒=，,直线MN 经过点C ,且AD MN ⊥于点D ,BE MN ⊥于点E 。

专题15三角形及全等三角形（30题）一、单选题1．（2023·吉林长春·统考中考真题）如图，工人师傅设计了一种测零件内径AB 的卡钳，卡钳交叉点O 为AA '、BB '的中点，只要量出A B ''的长度，就可以道该零件内径AB 的长度．依据的数学基本事实是（）A ．两边及其夹角分别相等的两个三角形全等B ．两角及其夹边分别相等的两个三角形全等C ．两余直线被一组平行线所截，所的对应线段成比例D ．两点之间线段最短【答案】A【分析】根据题意易证()SAS AOB A OB '' ≌，根据证明方法即可求解．【详解】解：O 为AA '、BB '的中点，OA OA ∴'=，OB OB '=，AOB A OB ''∠=∠ （对顶角相等），∴在AOB 与A OB ''△中，OA OA AOB A OB OB OB =⎧⎪∠=∠⎨⎪=''⎩'，()SAS AOB A OB ''∴△≌△，AB A B ''∴=，故选：A ．【点睛】本题考查了全等三角形的证明，正确使用全等三角形的证明方法是解题的关键．2．（2023·四川宜宾·统考中考真题）如图，AB CD ∥，且40A ∠=︒，24D ∠=︒，则E ∠等于（）【答案】D 【分析】可求40ACD ∠=︒，再由ACD D E ∠=∠+∠，即可求解．【详解】解：AB CD ∥ ，40ACD A ∴∠=∠=︒，ACD D E ∠=∠+∠ ，2440E ∴︒+∠=︒，16E ∴∠=︒．故选：D ．【点睛】本题考查了平行线的性质，三角形外角性质，掌握三角形外角的性质是解题的关键．3．（2023·云南·统考中考真题）如图，A B 、两点被池塘隔开，、、A B C 三点不共线．设AC BC 、的中点分别为M N 、．若3MN =米，则AB =（）A ．4米B ．6米C ．8米D ．10米【答案】B 【分析】根据三角形中位线定理计算即可．【详解】解∶∵AC BC 、的中点分别为M N 、，∴MN 是ABC 的中位线，∴26(AB MN ==米)，故选：B ．【点睛】本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．4．（2023·四川眉山·统考中考真题）如图，ABC 中，,40=∠=︒AB AC A ，则ACD ∠的度数为（）【答案】C 【分析】根据等腰三角形的等边对等角和三角形的内角和定理，即可解答．【详解】解：,40AB AC A =∠=︒ ，180702A B ACD ︒-∠∴∠=∠==︒，110ACD A B ∴∠=∠+∠=︒，故选：C ．【点睛】本题考查了等腰三角形的等边对等角性质，三角形内角和定理，熟知上述概念是解题的关键．5．（2023·湖南·统考中考真题）下列长度的各组线段能组成一个三角形的是（）A ．1cm,2cm,3cmB ．3cm,8cm,5cmC ．4cm,5cm,10cmD ．4cm,5cm,6cm 【答案】D【分析】根据两边之和大于第三边，两边之差小于第三边判断即可．【详解】A.1cm+2cm=3cm ，不符合题意；B.3cm+5cm=8cm ，不符合题意；C.4cm+5cm=9cm 10cm <，不符合题意；D.4cm+5cm=9cm 6cm >，符合题意，故选：D ．【点睛】本题考查了是否构成三角形，熟练掌握三角形两边之和大于第三边是解题的关键．6．（2023·山西·统考中考真题）如图，一束平行于主光轴的光线经凸透镜折射后，其折射光线与一束经过光心O 的光线相交于点P ，点F 为焦点．若1155,230∠=︒∠=︒，则3∠的度数为（）A ．45︒B ．50︒C ．55︒D ．60︒【答案】C故选：C ．【点睛】本题考查了平行线的性质，三角形外角的性质等知识，掌握这两个知识点是关键．7．（2023·福建·统考中考真题）阅读以下作图步骤：①在OA 和OB 上分别截取,OC OD ，使,C D 1CD 的长为半径作弧，两弧在A ．12∠=∠且CM DM=C ．12∠=∠且OD DM=【答案】A 【分析】由作图过程可得：OD 角形的性质可得12∠=∠即可解答．【详解】解：由作图过程可得：,OD OC CM DM ==，∵DM DM =，∴()SSS COM DOM ≌．∴12∠=∠．∴A 选项符合题意；不能确定OC CM =,则13∠=∠不一定成立，故B 选项不符合题意；不能确定OD DM =,故C 选项不符合题意，OD CM ∥不一定成立，则23∠∠=不一定成立，故D 选项不符合题意．故选A ．【点睛】本题主要考查了角平分线的尺规作图、全等三角形的判定与性质等知识点，理解尺规作图过程是解答本题的关键．8．（2023·浙江台州·统考中考真题）如图，锐角三角形ABC 中，AB AC =，点D ，E 分别在边AB ，AC 上，连接BE ，CD ．下列命题中，假命题．．．是（）．A ．若CD BE =，则DCB EBC∠=∠B ．若DCB EBC ∠=∠，则CD BE =C ．若BD CE =，则DCB EBC∠=∠D ．若DCB EBC ∠=∠，则BD CE=【答案】A 【分析】由AB AC =，可得A ABC CB =∠∠，再由CD BE BC CB ==，，由SSA 无法证明BCD 与CBE 全等，从而无法得到DCB EBC ∠=∠；证明ABE ACD @V V 可得CD BE =；证明ABE ACD @V V ，可得ACD ABE ∠=∠，即可证明；证明()DBC ECB ASA ≅ ，即可得出结论．【详解】解：∵AB AC =，∴A ABC CB =∠∠，∵若CD BE =，又BC CB =，∴BCD 与CBE 满足“SSA ”的关系，无法证明全等，因此无法得出DCB EBC ∠=∠，故A 是假命题，∵若DCB EBC ∠=∠，∴ACD ABE ∠=∠，在ABE 和ACD 中，ACD ABE AB AC A A ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()ABE ACD ASA ≅ ，∴CD BE =，故B 是真命题；若BD CE =，则AD AE =，在ABE 和ACD 中，AB AC A A AE AD =⎧⎪∠=∠⎨⎪=⎩，∴()ABE ACD SAS ≅ ，∴ACD ABE ∠=∠，∵A ABC CB =∠∠，∴DCB EBC ∠=∠，故C 是真命题；若DCB EBC ∠=∠，则在DBC △和ECB 中，ABC ACB BC BC DCB EBC ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()DBC ECB ASA ≅ ，∴BD CE =，故D 是真命题；故选：A ．【点睛】本题考查等腰三角形的判定和性质，全等三角形的判定和性质，命题的真假判断，正确的命题叫真命题，错误的命题叫假命题，判断命题的真假关键是掌握相关性质定理．9．（2023·河北·统考中考真题）在ABC 和A B C ''' 中，3064B B AB A B AC A C '''''∠=∠=︒====，，．已知C n ∠=︒，则C '∠=（）A ．30︒B ．n ︒C ．n ︒或180n ︒-︒D ．30︒或150︒【答案】C 【分析】过A 作AD BC ⊥于点D ，过A '作A D B C ''''⊥于点D ¢，求得3AD A D ''==，分两种情况讨论，利用全等三角形的判定和性质即可求解．【详解】解：过A 作AD BC ⊥于点D ，过A '作A D B C ''''⊥于点D ¢，∵306B B AB A B '''∠=∠=︒==，，∴3AD A D ''==，当B C 、在点D 的两侧，B C ''、在点D ¢的两侧时，如图，∵3AD A D ''==，4AC A C ''==，∴()Rt Rt HL ACD A C D '''≌△△，∴C C n '∠=∠=︒；当B C 、在点D 的两侧，B C ''、在点D ¢的同侧时，如图，∵3AD A D ''==，4AC A C ''==，∴()Rt Rt HL ACD A C D '''≌△△，∴'''A C D C n ∠=∠=︒，即'''180'''180A C B A C D n ∠=︒-∠=︒-︒；综上，C '∠的值为n ︒或180n ︒-︒．故选：C ．【点睛】本题考查了含30度角的直角三角形的性质，全等三角形的判定和性质，分类讨论是解题的关键．二、填空题10．（2023·江苏连云港·统考中考真题）一个三角形的两边长分别是3和5，则第三边长可以是__________．（只填一个即可）【答案】8【分析】利用三角形中位线定理即可求解．【详解】解：∵点C D ，分别是OA ∴12CD AB =，∴()28cm AB CD ==，故答案为：8．【点睛】本题考查了三角形中位线定理的应用，掌握12．（2023·新疆·统考中考真题）如图，【答案】52【分析】根据等边对等角得出,B C B BAD ∠∠∠∠==，再有三角形内角和定理及等量代换求解即可．【详解】解：∵AB AC =，AD BD =，∴,B C B BAD ∠∠∠∠==，∴B C BAD ∠∠∠==，∵180B C BAC ∠∠∠++=︒，∴180B C BAD CAD ∠∠∠∠+++=︒，即324180C ∠+︒=︒，解得：52C ∠=︒，故答案为：52．【点睛】题目主要考查等边对等角及三角形内角和定理，结合图形，找出各角之间的关系是解题关键．13．（2023·安徽·统考中考真题）清初数学家梅文鼎在著作《平三角举要》中，对南宋数学家秦九韶提出的计算三角形面积的“三斜求积术”给出了一个完整的证明，证明过程中创造性地设计直角三角形，得出了一个结论：如图，AD 是锐角ABC 的高，则2212AB AC BD BC BC ⎛⎫-=+ ⎪⎝⎭．当7,6AB BC ==，5AC =时，CD =____．【答案】1【分析】根据公式求得BD ，根据CD BC BD =-，即可求解．【详解】解：∵7,6AB BC ==，5AC =，∴2212AB AC BD BC BC ⎛⎫-=+ ⎪⎝⎭149256526-⎛⎫=+= ⎪⎝⎭∴651CD BC BD =-=-=,故答案为：1．【点睛】本题考查了三角形的高的定义，正确的使用公式是解题的关键．14．（2023·浙江·统考中考真题）如图，在ABC 中，AC 的垂直平分线交BC 于点D ，交AC 于点E ，B ADB ∠=∠．若4AB =，则DC 的长是__________．【答案】4【分析】由B ADB ∠=∠可得4AD AB ==，由DE 是AC 的垂直平分线可得AD DC =，从而可得4DC AB ==．【详解】解：∵B ADB ∠=∠，∴4AD AB ==，∵DE 是AC 的垂直平分线，∴AD DC =，∴4DC AB ==．故答案为：4．【点睛】本题主要考查了线段垂直平分线的性质以及等角对等边等知识，熟练掌握相关知识是解答本题的关键．15．（2023·湖北随州·统考中考真题）如图，在Rt ABC △中，9086C AC BC ∠=︒==，，，D 为AC 上一点，若BD 是ABC ∠的角平分线，则AD =___________．【答案】3【分析】首先证明CD DP =，6BC BP ==，设CD PD x ==，在Rt ADP 中，利用勾股定理构建方程即可解决问题．【详解】解：如图，过点D 作AB 的垂线，垂足为P ，在Rt ABC △中，∵86AC BC ==，，∴22228610AB AC BC =+=+=，∵BD 是ABC ∠的角平分线，∴CBD PBD ∠=∠，∵90C BPD BD BD ∠=∠=︒=，，∴()AAS BDC BDP ≌，∴6BC BP ==，CD PD =，设CD PD x ==，在Rt ADP 中，∵4PA AB BP =-=，8AD x =-，∴2224(8)x x +=-，∴3x =，∴3AD =．故答案为：3．【点睛】本题考查了角平分线的性质，全等三角形的判定和性质，勾股定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．16．（2023·湖北十堰·统考中考真题）一副三角板按如图所示放置，点A 在DE 上，点F 在BC 上，若35EAB ∠=︒，则DFC ∠=___________________︒．【答案】100︒【分析】根据直角三角板的性质，得到45DFE ∠=︒，90E B ∠=∠=︒，结合12∠=∠得到35EAB BFE ∠=∠=︒，利用平角的定义计算即可．【详解】解：如图，根据直角三角板的性质，得到45DFE ∠=︒，90E B ∠=∠=︒，∵12∠=∠，∴35EAB BFE ∠=∠=︒，1803545100DFC ∠=︒-︒-︒=︒．故答案为：100︒．【点睛】本题考查了三角板的性质，直角三角形的性质，平角的定义，熟练掌握三角板的性质，直角三角形的性质是解题的关键．17．（2023·浙江杭州·统考中考真题）如图，点,D E 分别在ABC 的边,AB AC 上，且DE BC ∥，点F 在线段BC 的延长线上．若28ADE ∠=︒，118ACF ︒∠=，则A ∠=_________．【答案】90︒【分析】首先根据平行线的性质得到28B ADE ∠=∠=︒，然后根据三角形外角的性质求解即可．【详解】∵DE BC ∥，28ADE ∠=︒，∴28B ADE ∠=∠=︒，∵118ACF ︒∠=，∴1182890A ACF B ∠=∠-∠=︒-︒=︒．故答案为：90︒．【点睛】此题考查了平行线的性质和三角形外角的性质，解题的关键是熟练掌握以上知识点．18．（2023·湖北荆州·统考中考真题）如图，CD 为Rt ABC △斜边AB 上的中线，E 为AC 的中点．若8AC =，5CD =，则DE =___________．【答案】3【分析】首先根据直角三角形斜边中线的性质得出AB ，然后利用勾股定理即可得出BC ，最后利用三角形中位线定理即可求解．【详解】解：∵在Rt ABC △中，CD 为Rt ABC △斜边AB 上的中线，5CD =，∴210AB CD ==，∴22221086BC AB AC =-=-=，∵E 为AC 的中点，∴132DE BC ==故答案为：3．【点睛】本题主要考查直角三角形的性质，三角形中位线定理，掌握直角三角形中斜边上的中线等于斜边的一半是解题的关键．19．（2023·湖南·统考中考真题）如图，在Rt ABC △中，90C ∠=︒，按以下步骤作图：①以点A 为圆心，以小于AC 长为半径作弧，分别交,AC AB 于点M ，N ；②分别以M ，N 为圆心，以大于12MN 的长为半径作弧，在BAC ∠内两弧交于点O ；③作射线AO ，交BC 于点D ．若点D 到AB 的距离为1，则CD 的长为__________．【答案】1【分析】根据作图可得AD 为CAB ∠的角平分线，根据角平分线的性质即可求解．【详解】解：如图所示，过点D 作DE AB ⊥于点E ，依题意1DE =，根据作图可知AD 为CAB ∠的角平分线，∵,DC AC DE AB⊥⊥∴1CD DE ==，故答案为：1．【答案】4975【分析】AM BD ⊥于点M ，AN DE ⊥根据3tan 4AM B BM ==得出16BM a =，继而求得3tan tan 4GP C B CP ===，求得3GP a =2216EN AE AN a =-=，故EG EN =【详解】由折叠的性质可知，DA 是到DM DN =，设DM DN x ==，则DG ()()()2221239a x a x a -+=+，化简得17217527AGEADG EG AN EG a DG DG AN S a S ⋅====⋅三角形三角形作AM BD ⊥于点M ，AN DE ⊥于点N ，则AM AN =，过点G 作GP BC ⊥于点P ，∵AM BD ⊥于点M ，∴3tan 4AM B BM ==，设12AM a =，则16BM a =，2220AB AM BM a =+=，又∵AB AC =，AM BD ⊥，∴12CM AM a ==，20AB AC a ==，B C ∠=∠，∵:3:1AG CG =，即14CG AC =，∴5CG a =，15AG a =，在Rt PCG △中，5CG a =，3tan tan 4GP C B CP ===，设3GP m =，则224,5CP m CG GP CP m==+=∴m a=∴3,4GP a CP a ==，∵15AG a =，12AM AN a ==，AN DE ⊥，∴229GN AG AN a =-=，∵20AB AE a ==，12AN a =，AN DE⊥∴2216EN AE AN a =-=，∴7EG EN GN a =-=，∵AD AD =，AM AN =，AM BD ⊥，AN DE ⊥，∴()HL ADM ADN △≌△，∴DM DN =，设DM DN x ==，则9DG DN GN x a =+=+，16412DP CM CP DM a a x a x =--=--=-，在Rt PDG △中，222DP GP DG +=，即()()()2221239a x a x a -+=+，三、解答题21．（2023·江苏苏州·统考中考真题）如图，在ABC 中，,AB AC AD =为ABC 的角平分线．以点A 圆心，AD 长为半径画弧，与,AB AC 分别交于点,E F ，连接,DE DF ．(1)求证：ADE ADF V V ≌；(2)若80BAC ∠=︒，求BDE ∠的度数．【答案】(1)见解析(2)20BDE ∠=︒【分析】（1）根据角平分线的定义得出BAD CAD ∠=∠，由作图可得AE AF =，即可证明ADE ADF V V ≌；（2）根据角平分线的定义得出40EAD ∠=︒，由作图得出AE AD =，则根据三角形内角和定理以及等腰三角形的性质得出70ADE ∠=︒，AD BC ⊥，进而即可求解．【详解】（1）证明：∵AD 为ABC 的角平分线，∴BAD CAD ∠=∠，由作图可得AE AF =，在ADE V 和ADF △中，BAD CAD AD AD ⎪∠=∠⎨⎪=⎩，∴ADE ADF V V ≌()SAS ；（2）∵80BAC ∠=︒，AD 为ABC 的角平分线，∴40EAD ∠=︒由作图可得AE AD =，∴70ADE ∠=︒，∵AB AC =，AD 为ABC 的角平分线，∴AD BC ⊥，∴20BDE ∠=︒【点睛】本题考查了全等三角形的性质与判定，等腰三角形的性质与判定，角平分线的定义，熟练掌握等腰三角形的性质与判定是解题的关键．22．（2023·江西·统考中考真题）（1）计算：038tan 453+︒-（2）如图，AB AD =，AC 平分BAD ∠．求证：ABC ADC △△≌．【答案】（1）2（2）见解析【分析】（1）先计算立方根，特殊角三角函数值和零指数幂，再计算加减法即可；（2）先由角平分线的定义得到BAC DAC ∠=∠，再利用SAS 证明ABC ADC △△≌即可．【详解】解：（1）原式211=+-2=；（2）∵AC 平分BAD ∠，∴BAC DAC ∠=∠，在ABC 和ADC △中，BAC DAC AC AC ⎪∠=∠⎨⎪=⎩，∴()SAS ABC ADC △△≌．【点睛】本题主要考查了实数的运算，零指数幂，特殊角三角函数值，全等三角形的判定，角平分线的定义等等，灵活运用所学知识是解题的关键．23．（2023·云南·统考中考真题）如图，C 是BD 的中点，,AB ED AC EC ==．求证：ABC EDC △≌△．【答案】见解析【分析】根据C 是BD 的中点，得到BC CD =，再利用SSS 证明两个三角形全等．【详解】证明： C 是BD 的中点，BC CD ∴=，在ABC 和EDC △中，BC CD AB ED AC EC =⎧⎪=⎨⎪=⎩，()ABC EDC SSS ∴ ≌【点睛】本题考查了线段中点，三角形全等的判定，其中对三角形判定条件的确定是解决本题的关键．24．（2023·四川宜宾·统考中考真题）已知：如图，AB DE ∥，AB DE =，AF DC =．求证：B E ∠=∠．【答案】见解析【分析】根据平行线的性质得出A D ∠=∠，然后证明AC DF =，证明()SAS ABC DEF ≌△△，根据全等三角形的性质即可得证．【详解】证明：∵AB DE ∥，∴A D ∠=∠，∵AF DC =，∴AF CF DC CF+=+即AC DF=在ABC 与DEF 中AC DF A D AB DE =⎧⎪∠=∠⎨⎪=⎩，∴()SAS ABC DEF ≌△△，∴B E ∠=∠．【点睛】本题考查了全等三角形的性质与判定，熟练掌握全等三角形的性质与判定是解题的关键．25．（2023·福建·统考中考真题）如图，,,OA OC OB OD AOD COB ==∠=∠．求证：AB CD =．【答案】见解析【分析】根据已知条件得出AOB COD ∠=∠，进而证明△≌△AOB COD ，根据全等三角形的性质即可得证．【详解】证明：AOD COB ∠=∠ ，,AOD BOD COB BOD ∴∠-∠=∠-∠即AOB COD ∠=∠．在AOB 和COD △中，,,,OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩AOB COD∴ ≌AB CD ∴=．【点睛】本小题考查等式的基本性质、全等三角形的判定与性质等基础知识，考查几何直观、推理能力等，掌握全等三角形的性质与判定是解题的关键．26．（2023·全国·统考中考真题）如图，点C 在线段BD 上，在ABC 和DEC 中，A D AB DE B E ∠=∠=∠=∠，，．求证：AC DC =．【答案】证明见解析【分析】直接利用ASA 证明ABC DEC ≌△△，再根据全等三角形的性质即可证明．【详解】解：在ABC 和DEC 中，A D AB DE B E ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ASA ABC DEC ≌ ∴AC DC =．【点睛】本题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定方法是解题的关键．27．（2023·四川乐山·统考中考真题）如图，AB 、CD 相交于点O ，AO=BO ，AC ∥DB ．求证：AC=BD ．【答案】见解析【分析】要证明AC=BD ，只要证明△AOC ≌△BOD ，根据AC//DB 可得∠A=∠B ，∠C=∠D ，又知AO=BO ，则可得到△AOC ≌△BOD ，从而求得结论．【详解】（方法一）∵AC//DB ，∴∠A=∠B ，∠C=∠D ．在△AOC 与△BOD 中∵∠A=∠B ，∠C=∠D ，AO=BO ，∴△AOC ≌△BOD ．∴AC=BD ．（方法二）∵AC//DB ，∴∠A=∠B ．在△AOC 与△BOD 中，∵A B AO BO AOC BOD ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AOC ≌△BOD ．∴AC=BD ．28．（2023·山东临沂·统考中考真题）如图，90,,,A AB AC BD AB BC AB BD ∠=︒=⊥=+．(1)写出AB 与BD 的数量关系(2)延长BC 到E ，使CE BC =，延长DC 到F ，使CF DC =，连接EF ．求证：EF AB ⊥．(3)在（2）的条件下，作ACE ∠的平分线，交AF 于点H ，求证：AH FH =．【答案】(1)()21AB BD -=(2)见解析(3)见解析【分析】（1）勾股定理求得2BC AB =，结合已知条件即可求解；（2）根据题意画出图形，证明CBD CEF ≌，得出=45E DBC ∠=∠︒，则EF BD ∥，即可得证；（3）延长,BA EF 交于点M ，延长CH 交ME 于点G ，根据角平分线以及平行线的性质证明EG EC =，进而证明()AAS AHC FHG ≌，即可得证．【详解】（1）解：∵90,A AB AC∠=︒=∴2BC AB =，∵BC AB BD=+∴2AB AB BD =+∴90,A AB AC∠=︒=∴=45ABC ∠︒，∵BD AB ⊥，∴45DBC ∠=︒∵CE BC =，12∠=∠,CF DC=∴CBD CEF≌∴=45E DBC ∠=∠︒∴EF BD∥∴AB EF⊥（3）证明：如图所示，延长,BA EF 交于点∵EF AB ⊥，AC AB ⊥，∴ME AC ∥，∴CGE ACG∠=∠∵CH 是ACE ∠的角平分线，∴ACG ECG ∠=∠，∴CGE ECG∠=∠∴EG EC=∵CBD CEF ≌，∴EF BD =，CE CB =，∴EG CB =，又∵BC AB BD =+，∴EG AB BD AC EF =+=+，即FG EF AC EF +=+，∴AC EG =，又AC FG ∥，则HAG HFG ∠=∠，在,AHC FHG 中，HAG HFG AHG FHG AC FG ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()AAS AHC FHG ≌，∴AH HF=【点睛】本题考查了全等三角形的与判定，等腰三角形的性质与判定，勾股定理，平行线的性质与判定，熟练掌握全等三角形的性质与判定是解题的关键．29．（2023·山东聊城·统考中考真题）如图，在四边形ABCD 中，点E 是边BC 上一点，且BE CD =，B AED C ∠=∠=∠．【点睛】本题考查了三角形内角和定理，全等三角形的判定和性质，等腰三角形的性质，含30︒直角三角形的性质以及勾股定理等知识，正确寻找证明三角形全等的条件是解题的关键．30．（2023·甘肃兰州·统考中考真题）综合与实践问题探究：（1）如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9：“平分一个已知角．”即：作一个已知角的平分线，如图2是欧几里得在《几何原本》中给出的角平分线作图法：在OA 和OB 上分别取点C 和D ，使得OC OD =，连接CD ，以CD 为边作等边三角形CDE ，则OE 就是AOB ∠的平分线．请写出OE 平分AOB ∠的依据：____________；类比迁移：（2）小明根据以上信息研究发现：CDE 不一定必须是等边三角形，只需CE DE =即可．他查阅资料：我国古代已经用角尺平分任意角．做法如下：如图3，在AOB ∠的边OA ，OB 上分别取OM ON =，移动角尺，使角尺两边相同刻度分别与点M ，N 重合，则过角尺顶点C 的射线OC 是AOB ∠的平分线，请说明此做法的理由；拓展实践：（3）小明将研究应用于实践．如图4，校园的两条小路AB 和AC ，汇聚形成了一个岔路口A ，现在学校要在两条小路之间安装一盏路灯E ，使得路灯照亮两条小路（两条小路一样亮），并且路灯E 到岔路口A 的距离和休息椅D 到岔路口A 的距离相等．试问路灯应该安装在哪个位置？请用不带刻度的直尺和圆规．．．．．．．．．．在对应的示意图5中作出路灯E 的位置．（保留作图痕迹，不写作法）【答案】（1）SSS ；（2）证明见解析；（3）作图见解析；【分析】（1）先证明()SSS OCE ODE ≌，可得AOE BOE ∠=∠，从而可得答案；（2）先证明()SSS OCM OCN ≌，可得AOC BOC ∠=∠，可得OC 是AOB ∠的角平分线；（3）先作BAC ∠的角平分线，再在角平分线上截取AE AD =即可．【详解】解：（1）∵OC OD =，CE DE =，DE DE =，∴()SSS OCE ODE ≌，∴AOE BOE ∠=∠，∴OE 是AOB ∠的角平分线；故答案为：SSS（2）∵OM ON =，CM CN =，OC OC =，∴()SSS OCM OCN ≌，∴AOC BOC ∠=∠，∴OC 是AOB ∠的角平分线；（3）如图，点E 即为所求作的点；．【点睛】本题考查的是全等三角形的判定与性质，角平分线的定义与角平分线的性质，作已知角的角平分线，理解题意，熟练的作角的平分线是解本题的关键．。

全等三角形姓名一．填空题(每题3分,共30分)1．如图,△ABC≌△DBC,且∠A和∠D,∠ABC和∠DBC是对应角,其对应边:_______.2．如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边_________．3. 已知:如图,△ABC≌△FED,且BC=DE.则∠A=__________,A D=_______．4. 如图,△ABD≌△ACE,则AB的对应边是_________,∠BAD的对应角是______．5. 已知:如图,△ABE≌△ACD,∠B=∠C,则∠AEB=_______,AE=________．6．已知：如图 , AC⊥BC于C , DE⊥AC于E , AD⊥AB于A , BC=AE．若AB=5 , 则AD=___________．7．已知：△ABC≌△A’B’C’，△A’B’C’的周长为12cm，则△ABC的周长为 .8．如图, 已知：∠1=∠2 , ∠3=∠4 , 要证BD=CD , 需先证△AEB≌△A EC , 根据是_________再证△BDE≌△______ , 根据是__________．4321EDBA9．如图，∠1=∠2，由AAS判定△ABD≌△ACD，则需添加的条件是____________.10．如图，在平面上将△ABC绕B点旋转到△A’BC’的位置时，AA’∥BC，∠ABC=70°，则∠CBC’为________度.AB CD12AA'B CC'二．选择题(每题3分,共30分)11、下列条件中，不能判定三角形全等的是（）A.三条边对应相等B.两边和一角对应相等C.两角的其中一角的对边对应相等D.两角和它们的夹边对应相等12. 如果两个三角形全等,则不正确的是（）A.它们的最小角相等B.它们的对应外角相等C.它们是直角三角形D.它们的最长边相等13. 如图,已知:△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是（）A.AB=ACB.∠BAE=∠CAD C.BE=DC D.AD=DE14. 图中全等的三角形是（）A.Ⅰ和ⅡB.Ⅱ和ⅣC.Ⅱ和ⅢD.Ⅰ和Ⅲ15. 下列说法中不正确的是（）A.全等三角形的对应高相等B.全等三角形的面积相等C.全等三角形的周长相等D.周长相等的两个三角形全等16. AD=AE , AB=AC , BE、CD交于F , 则图中相等的角共有（除去∠DFE=∠BFC）（）A.5对B.4对C.3对D.2对CDEABO17．如图,OA=OB,OC=OD, ∠O=60°, ∠C=25°则∠BED的度数是 ( )A.70°B. 85°C. 65°D. 以上都不对18. 已知:如图,△ABC≌△DEF,AC∥DF,BC∥EF.则不正确的等式是（）A.AC=DFB.AD=BEC.DF=EFD.BC=EF19．如图 , ∠A=∠D , OA=OD , ∠DOC=50°, 求∠DBC的度数为（）A.50°B.30°C.45°D.25°20. 如图 , ∠ABC=∠DCB=70°, ∠ABD=40°, AB=DC , 则∠BAC= （）A.70°B.80°C.100°D.90°三．解答题(每题8分，共40分)21. 已知:如图 , 四边形ABCD中 , AB∥CD , AD∥BC．求证：△ABD≌△CDB.22. 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长到D,使CD=CA.连结BC并延长到E,使EC=CB,连结DE,量出DE的长,就是A、B的距离.写出你的证明．23. 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:AC∥DF．24. 如图,已知: AD是BC上的中线 ,且DF=DE．求证:BE∥CF．25.如图, 已知：AB⊥BC于B , EF⊥AC于G , DF⊥BC于D , BC=DF．求证：AC=EF．FGE D CB A答案1.BC 和BC,CD 和CA,BD 和AB2.AB 和AC,AD 和AE,BD 和CE3. ∠F,CF4.AC, ∠CAE5. ∠ADC,AD6.57.128.ASA DEC SAS9. ∠B=∠C10.40℃ 11.B 12.C 13.D 14.D 15.D 16.B 17. A 18.C 19.D 20.B 21.由ASA 可证 22. 因为AC=CD EC=BC ∠ACB=∠ECD 所以 △ABC ≌△CED AB=ED 23.证△ABC ≌△FED 得∠ACB=∠F 所以AC ∥DF 24.证△BED ≌△CFD 得∠E=∠CFD 所以CF ∥BE 25.由AAS 证△ABC ≌△CED AC=EF.全等三角形 B 卷（考试时间为90分钟，满分100分）一.填空题：(每题3分,共30分)1.如图1，AD ⊥BC ，D 为BC 的中点，则△ABD ≌_________.4. 如图4，△ABC ≌△AED ，若AE AB =，︒=∠271，则=∠2 .图1图25.如图5，已知AB ∥CD ，AD ∥BC ，E.F 是BD 上两点，且BF ＝DE ，则图中共有 对全等三角形.6.如图6，四边形ABCD 的对角线相交于O 点，且有AB ∥DC ，AD ∥BC ，则图中有＿＿＿对全等三角形.7.“全等三角形对应角相等”的条件是 .8.如图8，AE ＝AF ，AB ＝AC ，∠A ＝60°，∠B ＝24°，则∠BOC ＝__________.9.若△ABC ≌△A ′B ′C ′，AD 和A ′D′分别是对应边BC 和B ′C ′的高，则△ABD ≌△A ′B ′D ′，理由是_______________.10.在Rt △ABC 中，∠C ＝90°，∠A.∠B 的平分线相交于O ，则∠AOB ＝_________. 二.选择题：(每题3分,共24分)11.如图9，△ABC ≌△BAD ，A 和B.C 和D 分别是对应顶点，若AB ＝6cm ，AC ＝4cm ，BC ＝5cm ，则AD 的长为 （ ）A.4cmB.5cmC.6cmD.以上都不对 12.下列说法正确的是 （ ） A.周长相等的两个三角形全等B.有两边和其中一边的对角对应相等的两个三角形全等C.面积相等的两个三角形全等D.有两角和其中一角的对边对应相等的两个三角形全等13.在△ABC 中，∠B ＝∠C ，与△ABC 全等的三角形有一个角是100°，那么在△ABC 中与这100°角对应相等的角是 （ ）图5 图6A EB O FC 图8 A CD 图9A.∠AB.∠BC.∠CD.∠B 或∠C 14.下列条件中，能判定△ABC ≌△DEF 的是（ ） A.AB ＝DE ，BC ＝ED ，∠A ＝∠D B.∠A ＝∠D ，∠C ＝∠F ，AC ＝EF C.∠B ＝∠E ，∠A ＝∠D ，AC ＝EF D.∠B ＝∠E ，∠A ＝∠D ，AB ＝DE15.AD 是△ABC 中BC 边上的中线，若AB ＝4，AC ＝6，则AD 的取值范围是（ ） A.AD ＞1 B.AD ＜5 C.1＜AD ＜5 D.2＜AD ＜10 16.下列命题正确的是 （ ） A.两条直角边对应相等的两个直角三角形全等； B.一条边和一个锐角对应相等的两个直角三角形全等C.有两边和其中一边的对角（此角为钝角）对应相等的两个三角形全等D.有两条边对应相等的两个直角三角形全等17.如图10.△ABC 中，AB ＝AC ，BD ⊥AC 于D ，CE ⊥AB 于E ，BD 和CE 交于点O ，AO 的延长线交BC 于F ，则图中全等直角三角形的对数为（ ）A.3对B.4对C.5对D.6对18.如图11，在CD 上求一点P ，使它到OA ，OB 的距离相等，则P 点是 （ ） A. 线段CD 的中点 B. OA 与OB 的中垂线的交点图10图 11B DOCAC. OA与CD的中垂线的交点D. CD与∠AOB的平分线的交点三．解答题(共46分)19. (8分)如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.20. (7分)如图, ∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线,为什么?21. (7分)如图，已知AB＝DC，AC＝DB，BE＝CE,求证：AE＝DE.AB E CD22. (8分)如图，已知AC ⊥AB ，DB ⊥AB ，AC ＝BE ，AE ＝BD ，试猜想线段CE 与DE 的大小与位置关系，并证明你的结论.23. (8分)已知如图，E.F 在BD 上，且AB ＝CD ，BF ＝DE ，AE ＝CF,求证：AC 与BD 互相平分.ABEO FDCACDB24. (8分)如图，∠ABC＝90°，AB＝BC，D为AC上一点，分别过A.C作BD的垂线，垂足分别为E.F,求证：EF＝CF－AE.答案1.△ADC2. ∠B=∠C或AF=DC3.704.27°5.36.37.两个三角形全等8.72°9.HL 10.135°11.B 12.D 13.A 14.D 15.C 16.A 17.D 18.D 19. 对应边:AB AC,AN,AM,BN,CM 对应角:∠BAN=∠CAM, ∠ANB=∠AMC 20. △AMC≌△CON 21.先证△ABC≌△DBC得∠ABC=∠DCB,再证△ABE≌△CED 22.垂直 23. 先证△ABE≌△DFC得∠B=∠D,再证△ABO≌△COD 24.证△ABF≌△BCF图 5人教课标版八年级（上）数学检测试卷全等三角形 C 卷（考试时间为90分钟，满分100分）一.填空题：(每题3分,共30分)1.如图1，若△ABC ≌△ADE ，∠EAC=35°，则∠BAD=_________度.2.如图2，沿AM 折叠，使D 点落在BC 上的N 点处，如果AD=7cm ，DM=5cm ，∠DAM=300，则AN= cm ，NM= cm ，∠NAM= .3.如图3，△ABC ≌△AED ，∠C=85°，∠B=30°，则∠EAD= .4.已知：如图4，∠ABC ＝∠DEF ，AB ＝DE ，要说明△ABC ≌△DEF ， （1）若以“SAS ”为依据，还须添加的一个条件为________________. （2）若以“ASA ”为依据，还须添加的一个条件为________________. （3）若以“AAS ”为依据，还须添加的一个条件为________________.5.如图5，在△ABC 中，∠C ＝90°，AD 平分∠BAC ，DE ⊥AB 于E ，则△______≌△_______..ABCDE图1ABCDMN 图2A9. 如图9,AB=CD ，AD=BC ，O 为BD 中点，过O 点作直线与DA 、BC 延长线交于E 、F ，若︒=∠60ADB ，EO=10，则∠DBC= ，FO= .10. 如图10，△DEF ≌△ABC ，且AC ＞BC ＞AB 则在△DEF 中，______＜ ______＜ _____.图 10二.选择题(每题3分,共30分)11. 在ABC ∆和C B A '''∆中，下列各组条件中，不能保证：C B A ABC '''∆≅∆的是（ ） ① B A AB ''= ② C B BC ''= ③ C A AC ''= ④ A A '∠=∠⑤ B B '∠=∠ ⑥ C C '∠=∠A. 具备①②③B. 具备①②④C. 具备③④⑤D. 具备②③⑥12. 两个三角形只有以下元素对应相等，不能判定两个三角形全等的是（ ） A. 两角和一边 B. 两边及夹角 C. 三个角 D. 三条边ABCDEFA. 一定全等B. 一定不全等C. 不一定全等D. 面积相等14. 如果两个三角形中两条边和其中一边上的高对应相等，那么这两个三角形的第三条边所对的角的15A. 150°B.40°C.80°D. 90°A . 三边对应平行的两个三角形是全等三角形B . 有一边相等，其余两边对应平行的两个三角形是全等三角形C . 有一边重合，其余两边对应平行的两个三角形是全等三角形D. 有三个角对应相等的两个三角形是全等三角形18.下列说法错误的是（）A. 全等三角形对应边上的中线相等B. 面积相等的两个三角形是全等三角形C. 全等三角形对应边上的高相等D. 全等三角形对应角平分线相等19.已知：如图，O为AB中点，BD⊥CD，AC⊥CD，OE⊥CD，则下列结论不一定成立的是（）A. CE=EDB. OC=ODC. ∠ACO=∠ODBD. OE=21CDA BCED A BCDEF12A DB CEF20.如图,已知在△ABC 中,AB =AC ,D 为BC 上一点,BF =CD ,CE =BD ,那么∠EDF 等于( ) A..90°－∠A B. 90°－21∠A C. 180°－∠A D. 45°－21∠A 三．解答题(共40分)21．(8分)如图，△ABC ≌△ADE ，∠E 和∠C 是对应角，AB 与AD 是对应边，写出另外两组对应边和对应角；22．(8分)如图，A 、E 、F 、C 在一条直线上，△AED ≌△CFB ，你能得出哪些结论？23．(7分)如图，已知∠1=∠2，∠3=∠4，AB 与CD 相等吗？请你说明理由..3421DCBAFEDCBA24．(8分)如图，AB ∥CD ，AD ∥BC ，那么AD=BC ，AB=BC ，你能说明其中的道理吗？25．(9分)如图，已知：E 是∠AOB 的平分线上一点，EC ⊥OB ，ED ⊥OA ，C ，D 是垂足，连接CD ，求证:（1）∠ECD=∠EDC ；（2）OD=OC ；（3）OE 是CD 的中垂线.CE DB AO答案1.35°2.7,5,30°3.504.BC=EF, ∠ACB=∠F, ∠A=∠D5.ACD,AED6.28°7.58.SAS9.60°,10 10.ED,EF,DF11.B 12.C 13.C 14.A 15.D 16.D 17.C 18.B 19.D 20.B 21.AE 和AC,ED 和BC, ∠B 和∠D, ∠BAC 和∠DAE 22.AD=BC,AE=CF,DE=BF,AD ∥BC, △ACD ≌△ACB,AB ∥CD 等 23.相等, △AOB ≌△DOC 24.连AC,证△ADC ≌△ABC25.(1)证DE=EC (2) 设BE 与CD 交于F,通过全等证DF=CF.B。

全等三角形综合测试题（100分）1、已知等腰三角形的一个内角为50°，则这个等腰三角形的顶角为（）【单选题】（3分）A.50°B.80°C.50°或80°D.40°或65°正确答案: C2、已知一个三角形的两边长分别是2厘米和9厘米，且第三边为奇数，则第三边长为（）【单选题】（3分）A.5cmB.7cmC.9cmD.11cm正确答案: C3、下列可使两个直角三角形全等的条件是（）【单选题】（3分）A.A、一条边对应相等B.B、两条直角边对应相等C.C、一个锐角对应相等D.D、两个锐角对应相等正确答案: B4、如图，D是BC的中点，E.F分别是AD和AD延长线上的点且DE=DF，连结BF，CE.下列说法:①CE=BF;②ΔABD和ΔACD面积相等;③BF//CE;△BDF≌ΔCDE其中正确的有（）【单选题】（3分）A.1个B.2个C.3个D.4个正确答案: D5、用两个全等的直角三角形，拼下列图形:①平行四边形;②矩形;③菱形;④正方形;⑤等腰三角形;⑥等边三角形，其中不一定能拼成的图形是（）【单选题】（3分）A.①②③B.②③C.③④⑤D.③④⑥正确答案: D6、如图，平行四边形ABCD中，AC、BD相交于点0过点O，过点O作直线分别交于AD、BC于点E、F.那么图中全等的三角形共有（）【单选题】（3分）A.2对B.4对C.6对D.8对正确答案: C7、根据下列条件，能判定△ABC≌△A’B’C’的是（）【单选题】（3分）A.)AB=A’B’，BC=B’C‘，∠A=∠A’B.∠A=∠A’，∠B=∠B‘，AC=BCC.∠A=∠A’，∠B=∠B‘,∠C=∠C’D.AB=A‘B’，BC=B’C’，ABC的周长等于△A’B’C’的周长正确答案: D8、【单选题】（3分）A.HLB.SSSC.SASD.ASA正确答案: B9、【填空题】（4分）________________________答案解析: AC=AD(答案不唯一）10、【填空题】（4分）________________________正确答案: CE=DF（回答与答案完全相同才得分）11、如图，在△ABC中，∠C=90°，AB的垂直平分线交AC于D，垂足为E，若CA=30°，DE=2，∠DBC的度数为____CD的长为____【填空题】（4分）________________________正确答案: 30° 2（回答包含答案即可得分）12、如图，ΔABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点F，若BF=AC.则∠ABC的度数是____【填空题】（4分）________________________正确答案: 45°（回答与答案完全相同才得分）13、【填空题】（8分）________________________正确答案: 证明:(1)∵BF=DE，∴BF+FE=DE+FE,即BE=DF …… 1 分又∵AB=CD，∠B=∠D，∴△ABE≌△CDF(SAS) ……3 分∴AE=CF ……4 分 (2) 先证明△AFE≌△CEF ……6分得∠AFE=∠CEF ……7分∴AF//CE……8 分 (方法不唯一，其他证明方法酌情给分)（回答包含答案即可得分）答案解析: 证明:(1)∵BF=DE，∴BF+FE=DE+FE,即BE=DF …… 1 分又∵AB=CD，∠B=∠D，∴△ABE≌△CDF(SAS) ……3 分∴AE=CF……4 分(2) 先证明△AFE≌△CEF ……6分得∠AFE=∠CEF ……7分∴AF//CE……8 分(方法不唯一，其他证明方法酌情给分)14、【填空题】（6分）________________________正确答案: 证明：(1)·∵∠BHD=∠AHE，∠BDH=∠AEH=90°∴∠DBH+∠BHD=∠HAE+∠AHE=90° ......2分.∴∠DBH=∠HAE......3分∵∠HAE=∠DAC ，∴∠DBH=∠DAC;......4分(2)∵AD⊥BC ∴∠ADB=∠ADC.....5分在△BDH与△ADC中，{∠ADB=∠ADC AD=BD ∠DBH=∠DAC} ∴.△BDH≌△ADC.......6分（回答包含答案即可得分）答案解析: 证明：(1).∵∠BHD=∠AHE，∠BDH=∠AEH=90°∴∠DBH+∠BHD=∠HAE+∠AHE=90° (2)分.∴∠DBH=∠HAE......3分∵∠HAE=∠DAC，∴∠DBH=∠DAC;......4分(2)∵AD⊥BC∴∠ADB=∠ADC.....5分在△BDH与△ADC中，{∠ADB=∠ADCAD=BD∠DBH=∠DAC}∴.△BDH≌△ADC.......6分15、【填空题】（6分）________________________正确答案: 证明:(1)∵BE、CF分别是AC、 AB两边上的高，∴∠AFC=∠AEB=90°(垂直定义)， (1)分∴∠ACG=∠DBA(同角的余角相等 )，......2分又∵BD=CA，AB=GC，∴△ABD≌△GCA; (4)分(2)连接DG，则△ADG是等腰三角形. 证明如下: .∵△ABD≌AGCA .∴AG=AD，......5分∴△ADG 是等腰三角形.......6分（回答包含答案即可得分）答案解析: 证明:(1)∵BE、CF分别是AC、 AB两边上的高，∴∠AFC=∠AEB=90°(垂直定义)， (1)分∴∠ACG=∠DBA(同角的余角相等)，......2分又∵BD=CA，AB=GC，∴△ABD≌△GCA;......4分(2)连接DG，则△ADG是等腰三角形.证明如下:.∵△ABD≌AGCA.∴AG=AD，......5分∴△ADG是等腰三角形.......6分16、【填空题】（7分）________________________正确答案: DF//BC.......2分证明:∵BE⊥AC，.∴∠BEC=90，......3分∴∠C+∠CBE=90° (4)分∵∠AB C=90°，.∴∠ABF+∠CBE=90°，∴∠C=∠ABF (5)分.∵DF//BC，.∴∠C=∠ADF，.∴∠ABF=∠ADF，......6分在△AFD和△AFB中∠1=∠2 ∠ABF=∠ADF AF=AF .∴△AF D≌AAFB(AAS)......7分（回答包含答案即可得分）答案解析: DF//BC.......2分证明:∵BE⊥AC，.∴∠BEC=90，......3分∴∠C+∠CBE=90° (4)分∵∠AB C=90°，.∴∠ABF+∠CBE=90°，∴∠C=∠ABF (5)分.∵DF//BC，.∴∠C=∠ADF，.∴∠ABF=∠ADF，......6分在△AFD和△AFB中∠1=∠2 ∠ABF=∠ADF AF=AF.∴△AF D≌AAFB(AAS)......7分17、【填空题】（7分）________________________正确答案: ①DF//BC.......1分证明:∵BE⊥AC，.∴∠BEC=90，∴∠C+∠CBE=90°，......3分∵∠AB C=90°，.∴∠ABF+∠CBE=90°，∴∠C=∠ABF， (5)分.∵DF//BC，.∴∠C=∠ADF，.∴∠ABF=∠ADF......6分在△AFD和△AFB中{∠1=∠2 ∠ABF=∠ADF AF=AF} .∴△AF D≌△AFB(AAS)......7分（回答包含答案即可得分）答案解析: ①DF//BC.......1分证明:∵BE⊥AC，.∴∠BEC=90，∴∠C+∠CBE=90°，......3分∵∠AB C=90°，.∴∠ABF+∠CBE=90°，∴∠C=∠ABF， (5)分.∵DF//BC，.∴∠C=∠ADF，.∴∠ABF=∠ADF......6分在△AFD和△AFB中{∠1=∠2 ∠ABF=∠ADF AF=AF}.∴△AF D≌△AFB(AAS)......7分18、【填空题】（7分）________________________正确答案: 证明：当动点P运动到AC边上中点位置时，AAPE≌AEDB......1分∵DE//CA，∴△BED∽△BAC，......2分∴BE/AB=DB/CB ∴D是BC的中点......3分∵E是AB中点，.∴BD/CB=1/2 ∴BE/AB=1/2 ∴E是AB中点∴DE=1/2AC，BE=AE,......5分∵DE// AC，∴∠A=∠BED，要使△APE≌△EDB，还缺少一个条件DE=AP，又有DE=1/2AC，∴P 必须是AC 中点......7分（回答包含答案即可得分）答案解析: 证明：当动点P运动到AC边上中点位置时，AAPE≌AEDB......1分∵DE//CA，∴△BED∽△BAC，......2分∴BE/AB=DB/CB∴D是BC的中点......3分∵E是AB中点，.∴BD/CB=1/2∴BE/AB=1/2∴E是AB中点∴DE=1/2AC，BE=AE,......5分∵DE// AC，∴∠A=∠BED，要使△APE≌△EDB，还缺少一个条件DE=AP，又有DE=1/2AC，∴P 必须是AC 中点......7分19、【填空题】（7分）________________________正确答案: 解:连接CD，∵∠ACB=90°，D是AB边的中点∴CD=AD，∠DAC=∠DCF ......2分∵DE 与CF 平行且相等.∴∠EDA=∠DAC......4分.∴∠EDA=∠DCF......5分在AAED和ACFD中 {CD=AD，∠EDA=∠DCF，DE=CF} ∴△AED≌△CFD ∴AE=DF......7分（回答包含答案即可得分）答案解析: 解:连接CD，∵∠ACB=90°，D是AB边的中点∴CD=AD，∠DAC=∠DCF ......2分∵DE与CF 平行且相等.∴∠EDA=∠DAC......4分.∴∠EDA=∠DCF......5分在AAED和ACFD中{CD=AD，∠EDA=∠DCF，DE=CF}∴△AED≌△CFD∴AE=DF......7分20、如图，山脚下有A、B两点，要测出A、B两点的距离，请说说你的解决方案。