原子物理光的粒子性与电子的波动性.ppt
- 格式:ppt
- 大小:2.04 MB
- 文档页数:25

专题二光的波动性和粒子性考情动态分析该专题内容,以对光的本性的认识过程为线索,介绍了近代物理光学的一些初步理论,以及建立这些理论的实验基础和一些重要的物理现象.由于该部分知识和大学物理内容有千丝万缕的联系,且涉及较多物理学的研究方法,因此该部分知识是高考必考内容之一.难度适中.常见的题型是选择题,其中命题率最高的是光的干涉和光电效应,其次是波长、波速和频率.有时与几何光学中的折射现象、原子物理中的玻尔理论相结合,考查学生的分析综合能力.此外对光的偏振降低了要求,不必在知识的深度上去挖掘.考点核心整合1.光的波动性光的干涉、衍射现象说明光具有波动性,光的偏振现象说明光波为横波,光的电磁说则揭示了光波的本质——光是电磁波.(1)光的干涉①光的干涉及条件由频率相同(相差恒定)的两光源——相干光源发出的光在空间相遇,才会发生干涉,形成稳定的干涉图样.由于发光过程的量子特性,任何两个独立的光源发出的光都不可能发生干涉现象.只有采用特殊的“分光”方法——将一束光分为两束,才能获得相干光.如双缝干涉中通过双缝将一束光分为两束,薄膜干涉中通过薄膜两个表面的反射将一束光分为两束而形成相干光.②双缝干涉在双缝干涉中,若用单色光,则在屏上形成等间距的、明暗相间的干涉条纹,条纹间距L Δx和光波的波长λ成正比,和屏到双缝的距离L成正比,和双缝间距d成反比,即Δx=d λ.若用白光做双缝干涉实验,除中央亮条纹为白色外,两侧为彩色条纹,它是不同波长的光干涉条纹的间距不同而形成的.③薄膜干涉在薄膜干涉中,薄膜的两个表面反射光的路程差(严格地说应为光程差)与膜的厚度有关,故同一级明条纹(或暗条纹)应出现在膜的厚度相同的地方.利用这一特点可以检测平面的平整度.另外适当调整薄膜厚度.可使反射光干涉相消,增强透射光,即得增透膜.(2)光的衍射①条件光在传播过程中遇到障碍物时,偏离原来的直线传播路径,绕到障碍物后面继续传播的现象叫光的衍射.在任何情况下,光的衍射现象都是存在的,但发生明显的衍射现象的条件应是障碍物或孔的尺寸与光波的波长相差不多.②特点在单缝衍射现象中,若入射光为单色光,则中央为亮且宽的条纹,两侧为亮度逐渐衰减的明暗相间条纹;若入射光为白光,则除中央出现亮且宽的白色条纹外,两侧出现亮度逐渐衰减的彩色条纹.(3)光的偏振在与光波传播方向垂直的平面内,光振动沿各个方向均匀分布的光称为自然光,光振动沿着特定方向的光即为偏振光.自然光通过偏振片(起偏器)之后就成为偏振光.光以特定的入射角射到两种介质界面上时,反射光和折射光也都是偏振光.偏振现象是横波特有的现象,所以光的偏振现象表明光波为横波.(4)光的电磁本性麦克斯韦的电磁理论预见了电磁波的存在,赫兹用实验证明了电磁波理论的正确性.由于光波和电磁波都为横波、传播都不需要介质、在真空中传播速度相同(皆以光速c=3×108 m/s的速度传播),人们很自然地认为光波为电磁波.电磁波的频率范围很广,光波只是电磁波的一个小小的分支,不同电磁波的产生机理不同,且有不同的作用效果.将电磁波按一定的顺序排列即形成电磁波谱.其中的光谱,按成因可分为发射光谱和吸收光谱,发射光谱又分为连续光谱和明线光谱.可用于光谱分析的是原子特征谱线——明线光谱和吸收光谱.2.光的粒子性(1)光电效应及其规律金属在光照射下发射电子的现象叫光电效应现象,其实验规律如下:①任何金属都存在极限频率,只有用高于极限频率的光照射金属,才会发生光电效应现象.②在入射光的频率大于金属极限频率的情况下,从光照射到逸出光电子,几乎是瞬时的,时间不超过10-9s.③光电子的最大初动能随入射光频率的增大而增大,与光强无关.④单位时间内逸出的光电子数与入射光的强度成正比.(2)光子说因光电效应的规律无法用光的波动理论解释,为解释光电效应规律,爱因斯坦提出了光量子说:光是一份一份的,每一份叫一个光量子,每个光量子的能量为E=hv.并给出光电效应方程:E k m=hv-W.3.光的波粒二象性光在某些现象中显示波动性,在另外的现象中又显示粒子性,为说明光的全部性能,只能说光具有波粒二象性.大量光子的行为往往显示波动性,少数光子的行为往往显示粒子性;频率越低的光子波动性越强,频率越高的光子粒子性越强.链接·提示我们现在所说的光具有波粒二象性,与17世纪惠更斯的光的波动说和牛顿的光的微粒说有本质的区别:惠更斯的光的波动说和牛顿的光的微粒说是截然对立的、互不相容的两种学说,而我们现在所说的光的波粒二象性是既对立又统一的,如表征光的粒子性的光子说中,光的能量E=hv中v为光的频率,就是描述光的波动性的物理量;同样光的波动性实质是大量光子运动所表现出来的几率波.考题名师诠释【例1】如图4-2-1,当电键S断开时,用光子能量为2.5 eV的一束光照射阴极P,发现电流表读数不为零.合上电键,调节滑线变阻器,发现当电压表读数小于0.60 V时,电流表读数仍不为零.当电压表读数大于或等于0.60 V时,电流表读数为零.由此可知阴极材料的逸出功为()图4-2-1A.1.9 eVB.0.6 eVC.2.5 eVD.3.1 eV解析:S断开时电流表示数不为零,说明光电管在光照射下已经发生了光电效应现象.合上开关S后,光电管的两极间加上了一定的电压,两极间形成一定强弱的电场,但该电场是阻碍光电子向光电管的阴极运动的.当电压不够高、电场不够强的情况下,具有初动能的光电子仍可到达阳极而在电路中形成光电流,但当电压增大到一定数值后,若具有最大初动能的光电子不能到达阳极时,则电路中即不能形成光电流.由题设解得,具有最大初动能的光电子恰好克服0.60 V的电压做功后能到达阳极,即光电子的最大初动能E km=0.60 eV.由爱因斯坦光电效应方程E km=hv-W得:W=hv-E k m=(2.5-0.60) eV=1.9 eV.即选项A正确.答案:A点评:本题考查的就是对光电效应规律的理解,具有一定的难度,因为题目中给光电管加的已不是课本上常见的正向电压,而是反向电压.只有看懂电路图并真正理解了光电效应的规律,才有可能给出正确的解答.所以对各物理规律,一定要在理解上下工夫,真正弄懂弄通. 链接·思考若让你设计一个实验,测定某光电效应现象中逸出的光电子的最大初动能,应如何进行? 答案:实际上,该例题就提供了一个测定光电子最大初动能的方法:给光电管两极加一反向电压——光电管阳极接低电势、阴极接高电势,逐渐增大反向电压的大小,并观察串联于电路中的微安表,当电压增大至某一值时,电路中光电流恰为零,该反向电压即称为截止电压.由动能定理知,E km=eU止.可见,只要测出了截止电压v止,即可求出光电子的最大初动能E km.【例2】(经典回放)劈尖干涉是一种薄膜干涉,其装置如图4-2-2(1)所示.将一块平板玻璃放置在另一平板玻璃之上,在一端夹入两张纸片,从而在两玻璃表面之间形成一个劈形空气薄膜.当光垂直入射后,从上往下看到干涉条纹如图(2)所示.干涉条纹有如下特点: ①任意一条明条纹或暗条纹所在位置下面的薄膜厚度相等;②任意相邻明条纹或暗条纹所对应的薄膜厚度差恒定.现若在图(1)装置中抽去一张纸片,则当光垂直入射到新的劈形空气薄膜后,从上往下看到的干涉条纹()A.变疏B.变密C.不变D.消失图4-2-2解析:由薄膜干涉的原理和特点可知:干涉条纹是由膜的上、下表面反射的光叠加干涉而形成的,某一明条纹或暗条纹的位置就由上、下表面反射光的路程差决定,且相邻明条纹或暗条纹对应的该路程差是恒定的,而该路程差又决定于条纹下对应膜的厚度差,即相邻明条纹或暗条纹下面对应的膜的厚度差也是恒定的.当抽去一纸片后,劈形空气膜的劈尖角——上、下表面所夹的角变小,相同的厚度差对应的水平间距离变大,所以相邻的明条纹或暗条纹间距变大,即条纹变疏.选项A正确.答案:A点评:此题的难度实际已超出课本要求的难度,但在题干中对劈形薄膜的干涉特点作了必要的补充说明,属“信息给予”类题型.对此类题的解答,关键在于对题给信息的全面正确理解.此种题型可以考查考生的阅读能力、提取有用信息的能力、理解能力等多种能力,可能代表一种命题倾向,平时做些此类练习,还是有一定好处的.链接·拓展我们观察漂浮在水面上的油膜时,也会观察到彩色的干涉条纹,但水面上的油膜厚度基本上是等厚的,干涉条纹又是如何形成的呢?答案:水面上油膜产生的干涉现象是与劈尖干涉不同的另一种干涉现象,发生干涉的两列光仍是油膜上、下表面的反射光.尽管各处膜的厚度相同,但对同一处膜的上、下表面反射的两列光的路程差除了与膜的厚度有关外,还与观察的角度有关,即在不同角度观察,会产生不同的路程差而出现或明或暗的干涉条纹.仔细观察油膜干涉现象,你会发现:当你改换观察角度时,油膜上彩色条纹的位置(分布情况)也发生相应的变化.为把这两种干涉现象加以区别,通常把劈尖干涉称为等厚干涉,而把后一种干涉称为等倾干涉.【例3】假设一个沿着一定方向运动的光子和一个静止的自由电子相互碰撞后,电子向某一方向运动.光子将偏离原运动方向,这种现象称为光子的散射,散射后的光子跟原来相比()A.光子将从电子处获得能量,因而频率增大B.散射后的光子运动方向将与电子运动方向在同一直线上,但方向相反C.由于电子受到碰撞,散射光子的频率低于入射光子的频率D.散射光子虽改变原来的运动方向,但频率不变解析:由能的转化和守恒定律知,光子与电子碰撞后能量将减少,由光子能量E=hv知,碰后光子频率低于碰前光子频率,即选项C正确.答案:C点评:动量守恒定律和能的转化和守恒定律是自然界中普遍适用的两大主要定律,因此,在讨论任何问题时(无论是宏观问题还是微观问题),一定要注意这两个定律的应用.。


电子的波动性和粒子性的相互关系电子是元素构成原子的基本粒子,具有波动性和粒子性。
在物理学中,波动性和粒子性都是指电子作为震荡能量传递的媒介或作为单个能带电粒子的运动特性。
电子的波动性和粒子性不是互相独立的,而是在一定条件下相互影响、相互制约的。
电子波动性的表现在1801年的双缝干涉实验中,托马斯·杨的同事、英国物理学家弗朗西斯科·马里亚·格拉马齐尼(Francesco Maria Grimaldi)已经发现光的波动特性。
波动理论指出,当波通过两个孔的间距达到相应的大小时,波前形成干涉条纹。
此后,人们发现,不仅光,连事实上所有物质都具有波动特性。
物质波最早是由德国物理学家路德维希·德布罗意(Louis de Broglie)提出的,他认为,物质粒子具有波动性,如同光具有波动性一样。
对于电子,最早能够观察到其波动性的实验证据是电子衍射现象。
电子衍射是一种现象,利用这种现象可以证明,电子是具有波动性的。
电子衍射实验使用的方法和双缝干涉实验非常相似。
一束电子被发射,通过一组细孔或物体,被分成几个波束,这些波束相互干涉,调制获得干涉图样。
这些实验早在20年代末期就已经完成,并被广泛验证。
此后,人们通过这些实验证明了物质粒子能够表现出一种波动行为,如同光波可以在同一时间通过双个开口。
另一个证实电子波动性的实验是维斯曼伯格实验。
维斯曼伯格实验是早期在电子微观研究方面具有里程碑意义的实验之一。
它揭示出粒子和波函数的内在联系。
实验中使用具有许多光学元件的电子光栅,利用这些光片可以将电子光栅拆分成许多单独的瞬时波,从而可以正确描述波函数。
结果发现,如果将光撞击电子光栅,它们的瞬时间重合,增强振幅的波函数将解释光子的物理特性。
这些实验证明了粒子的波函数描述了它们的物理行为,而电子本质上是一种波动行为。
电子粒子性的表现在相对论物理学领域,小贝克耳(Werner Heisenberg)和薛定谔(Erwin Schrödinger)提出了薛定谔方程,为粒子在相对论条件下的运动提供了正确的方程式。




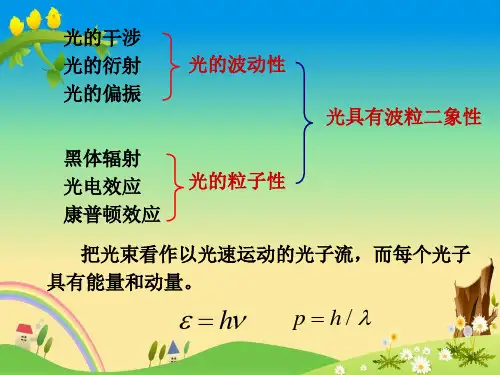
光子同时存在粒子性和波动性特征光子是光的基本单位,也是光的组成部分。
在物理学中,光子不仅展现出粒子性的特征,如其能量量子化和动量量子化,同时还表现出波动性的特征,具有干涉和衍射等现象。
这一独特的性质称为光子的波粒二象性,是量子物理学的重要研究课题之一。
首先,光子的粒子性表现在其能量和动量的量子化上。
根据普朗克的能量量子化假设,光子的能量E与其频率ν成正比。
公式E = hν中,h称为普朗克常数,是一个固定值。
这意味着光子的能量是以离散的方式存在的,无法连续取值。
类似地,根据德布罗意的动量量子化假设,光子的动量p与其波长λ成反比。
公式p = h/λ展示了光子的动量与其波长的关系。
这些理论表明,光子的能量和动量都是以离散的方式存在,类似于微小的能量和动量粒子。
然而,光子同时也具有波动性。
光的干涉和衍射现象无法用粒子模型解释,需要引入波动模型。
光子在运动过程中会形成波动,它的波长决定了波的特性。
光的干涉现象是指光波遇到一对相干光程后会产生明暗交替的干涉条纹,这可以解释为光子的波动性和多光子叠加的结果。
而衍射现象是指当光通过一个狭缝或遇到一个小孔时会发生弯曲和扩散,使光的分布出现特定的图案,这也是光子的波动性所导致的。
更为直观的证据是量子双缝实验。
在该实验中,光源发出的光通过一个屏幕上的两个小缝后,形成干涉条纹。
如果只考虑光子的粒子特性,我们期望在屏幕上看到两个亮斑,但实际上,我们看到了具有明暗相间条纹的干涉图案。
这说明光子不仅具有粒子性,还具有波动性,与传统的直观认知有所不同。
光子同时存在粒子性和波动性的特征,是由于量子力学的本质决定的。
量子力学是研究微观领域的物理学理论,描述了微观粒子行为的规律。
根据量子力学的理论,光子的行为既可以用波动方程来描述(薛定谔方程),也可以用粒子数守恒的方程来描述(波粒二像关系)。
这一理论揭示了光子同时具有波动性和粒子性的本质,深化了我们对光的认识。
光子的波粒二象性在科学和技术中都有广泛的应用。