逻辑代数的基本定理_基本规则_逻辑函数简化(18)

逻辑代数的基本定律逻辑代数的基本定律是指逻辑代数中的基础规则和定理，这些定理是逻辑代数中最基本的概念和方法。

逻辑代数是用数学方法来处理逻辑问题的一种方法，它将逻辑问题转化为数学问题，从而可以用数学方法来解决。

逻辑代数的基本定律主要包括以下几个方面：1. 同一律同一律是指一个逻辑表达式和它自身相与（或相或）的结果不变。

即A ∧ T = A，A ∨ F = A。

这个定律的意思是，当逻辑表达式与真值或假值相与（或相或）时，结果不变。

例如，如果有一个逻辑表达式A ∧ T，它与真值T 相与的结果仍然是A。

同样地，如果有一个逻辑表达式A ∨ F，它与假值 F 相或的结果仍然是 A。

2. 恒等律恒等律是指一个逻辑表达式与一个恒等式相与（或相或）的结果相等。

即A ∧ A = A，A ∨ A = A。

这个定律的意思是，当逻辑表达式与一个恒等式相与（或相或）时，结果相等。

例如，如果有一个逻辑表达式A ∧ A，它与恒等式 A 相与的结果仍然是A。

同样地，如果有一个逻辑表达式A ∨ A，它与恒等式 A 相或的结果仍然是 A。

3. 交换律交换律是指一个逻辑表达式中的两个变量相与（或相或）的顺序可以交换。

即A ∧ B = B ∧ A，A ∨ B = B ∨ A。

这个定律的意思是，当逻辑表达式中的两个变量相与（或相或）时，它们的顺序可以交换。

例如，如果有一个逻辑表达式A ∧ B，它与表达式B ∧ A 相与的结果是相等的。

同样地，如果有一个逻辑表达式A ∨ B，它与表达式B ∨ A 相或的结果是相等的。

4. 结合律结合律是指一个逻辑表达式中的多个变量相与（或相或）时，可以任意加括号，而结果不变。

即A ∧ (B ∧ C) = (A ∧ B) ∧ C，A ∨ (B ∨ C) = (A ∨ B) ∨ C。

这个定律的意思是，当逻辑表达式中有多个变量相与（或相或）时，可以任意加括号，而结果不变。

例如，如果有一个逻辑表达式A ∧ (B ∧ C)，它与表达式(A ∧ B) ∧ C 相与的结果是相等的。

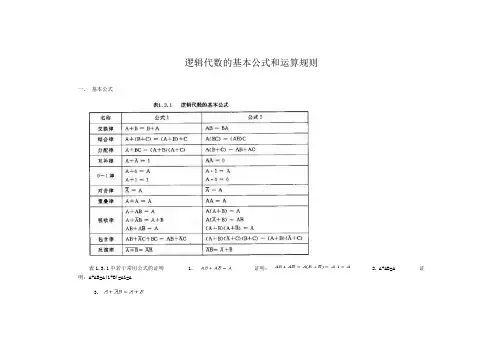
逻辑代数的基本公式和运算规则
一、基本公式
表1.3.1中若干常用公式的证明1．证明： 2. A+AB=A 证明：A+AB=A(1+B)=A1=A
3.
证明：
4.
证明：
推论：
二、运算规则
1．代入定理任何一个含有某变量的等式，如果等式中所有出现此变量的位置均代之以一个逻辑函数式，则此等式依然成立，这称为代入规则。

利用代入规则，反演律能推广到n个变量，即:
2．反演定理对于任意一个逻辑函数式F，若把式中的运算符“.”换成“+”, “+” 换成“.”，常量“0”换成“1”，“1”换成“0”，原变量换成反变量，反变量换成原变量，则得到的结果为。

这个规则叫反演定理运用反演定理时注意两点：① 必须保持原函数的运算次序。

② 不属于单个变量上的非号保留，而非号下面的函数式按反演规则变换。

例如：
其反函数：
3．对偶定理对于任意一个逻辑函数F，若把式中的运算符“.”换成“+”，“+”换成“.”，常量“0”换成“1”，“1”换成“0”，则得到F的对偶式F′。

例如：
其对偶式：
对偶定理：如果两个函数式相等，则它们对应的对偶式也相等。

逻辑代数的运算法则逻辑代数又称布尔代数。

逻辑代数与普通代数有着不同概念，逻辑代数表示的不是数的大小之间的关系，而是逻辑的关系，它仅有0、1两种状态。

逻辑代数有哪些基本公式和常用公式呢？1.变量与常量的关系与运算公式 一、基本公式A·1=AA·0=0或运算公式A+0=A A+1=101律2.与普通代数相似的定律与运算公式A·B=B·A 或运算公式A+B=B+A交换律A·(B·C)=(A·B)·C A+(B+C)=(A+B)+C 结合律A·(B+C)=A·B+A·C A+(B·C)=(A+B)(A+C)分配律3.逻辑代数特有的定律与运算公式或运算公式互补律重叠律（同一律） 反演律（摩根定律）0=⋅A A 1=+A A BA B A +=⋅BA B A ⋅=+ 非非律（还原律）AA =A A A =⋅A A A =+真值表证明摩根定律0001101111111100结论：BA B A +=⋅ 以上定律的证明，最直接的办法就是通过真值表证明。

若等式两边逻辑函数的真值表相同，则等式成立。

【证明】公式1AB A AB =+B A AB +）（B B A += 互补律1⋅=A 01律A= 合并互为反变量的因子【证明】公式2AAB A =+AB A +）（B A +=1 01律A= 吸收多余项【证明】公式3BA B A A +=+B A A +BA AB A ++=B A A A ）（++= 互补律BA += 消去含有另一项的反变量的因子【证明】CA AB BC C A AB +=++BC A A C A AB ）（+++=BC C A AB ++ 分配律BC A ABC C A AB +++= 吸收多余项公式2互补律CA AB += 公式2逻辑代数的运算法则一、基本公式二、常用公式A·1=AA·0=0A+0=A A+1=1 1.变量与常量的关系01律2.与普通代数相似的定律交换律A·B=B·A A+B=B+A结合律 分配律3.逻辑代数特有的定律互补律A·A=A A+A=A 重叠律（同一律）反演律（摩根定律）0=⋅A A 1=+A A BA B A +=⋅BA B A ⋅=+非非律（还原律）AA =AB A AB =+.1AAB A =+.2BA B A A +=+.3CA AB BC C A AB +=++.4A·(B·C )=(A·B )·C A+(B+C )=(A+B )+C A·(B+C )=A·B+A·CA +(B·C )=(A+B )(A+C )谢谢！。

逻辑代数基本定律规则及常⽤公式在四则运算中，我们知道有交换律、结合律以及分配律等。

那么在逻辑运算中，也有它⾃⼰的基本定律，下⾯将介绍逻辑代数运算中的基本定理。

逻辑代数基本定理1.0、1定律0、1定律描述的是单个变量A和0、1之间的运算规则。

其中有以下四条定律：（1）A·0=0，即A和0相与始终为0；（2）A·1=A，即A与1相与结果为A；（3）A+0=A，即A和0相或结果为A；（4）A+1=1，即A和1相或始终为1。

2.重叠律重叠率描述逻辑变量A和其⾃⾝的运算。

（1）A·A=A，即A和⾃⼰相与等于它本⾝；（2）A+A=A，即A和⾃⼰相或亦等于它本⾝。

3.互补律互补律描述A和⾃⾝的反变量¬A之间的关系。

（1）A·¬A=0，即A和⾃⾝反变量相与始终为0；（2）A+¬A=1，即A和⾃⾝反变量相或始终为1。

证明：由于A和¬A之间⾄少有⼀个为0，即⼆者不可能全为1，所以相与得0；同时，A和¬A之间⾄少有⼀个为1，满⾜或运算的“有1出1”，所以相或得0。

4.还原律A的反变量再取反，等于本⾝，即¬(¬A)=A。

5.交换律在此定律及之后的定律中，都将会涉及到两个及以上的逻辑变量。

交换律即两个逻辑变量运算时交换位置，结果不变。

（1）A·B=B·A，即A 与B等于B与A；（2）A+B=B+A，即A或B等于B或A。

6.结合律结合律指三个及以上变量相与或相或时，可以使任意两个变量先进⾏运算，再去和别的变量进⾏运算。

（1）(A·B)·C=A·(B·C)，即A与B后再与C，等于B与C后再与A。

（2）(A+B)+C=A+(B+C)，即A或B后再或C，等于B或C后再或A。

7.分配律逻辑代数的分配律和四则运算的分配律很类似，但是有⼀些不同。

（1）A·(B+C)=A·B+A·C，即A和B或C相与，等于A和B、C分别相与，然后进⾏或运算；（2）(A+B)·(A+C)=A+B·C，这⼀条定律显得有⼀些特殊，它的结果并不像四则运算中展开后有四项的形式，实际上，我们可以这样的得到：(A+B)·(A+C)=A·A+A·C+A·B+B·C=A+AC+AB+BC=A(1+B+C)+BC=A·1+BC=A+BC。

逻辑代数的基本知识 1. 逻辑代数的基本定律根据逻辑变量和逻辑运算的基本定义，可得出逻辑代数的基本定律。

①交换律： A+B = B+A ， A • B = B • A；②结合律： A+(B+C) = (A+B)+ C ， A • (B • C) = (A • B) • C；③分配律: A •(B+C) = A • B+A • C ， A+B • C=(A+B) • (A+C)；④互非定律: A+A = l ，A • A = 0 ；1=+A A ，0=•A A ； ⑤重叠定律（同一定律）：A • A=A， A+A=A ；⑥反演定律(摩根定律）：A • B=A+B 9 A+B=A • B B A B A •=+，B A B A +=•；⑦还原定律: A A = 2. 逻辑代数的基本运算规则 （1）代入规则在逻辑函数表达式中凡是出现某变量的地方都用另一个逻辑函数代替，则等式仍然成立，这个规则称为代入规则。

例如，已知A+AB=A ，将等式中所有出现A 的地方都以函数(C+D)代替则等式仍然成立，即（C+D) + (C+D)B = C+D 。

（2）反演规则对于任意的Y 逻辑式，若将其中所有的“ • ”换成“ + ”换成“ • ”，0换成1，1换成0，原变量换成反变量，反变量换成原变量，则得到原函数Y 的反函数，运用它可以简便地求出一个函数的反函数。

运用反演规则时应注意两点： ① 要注意运算符号的优先顺序，不应改变原式的运算顺序。

例：CD B A Y +=应写为))((D C B A Y ++= 证： ))((D C B A CD B A CD B A Y ++=•=+=② 不属于单变量上的非号应保留不变。

例：)(E D C C B A Y•+•= 则[])()(E D C C B A Y ++•++=D C B A Y +•= 则 D C B A Y •++=（3）对偶规则对于任何一个逻辑函数，如果将其表达式Y 中所有的算符“ • ”换成“ + ”换成“ •”，常量 “0”换成换成“0”，而变量保持不变，则得出的逻辑函数式就是Y 的对偶式，记为Y’。

逻辑代数的基本定律及规则文章来源：互联网作者：佚名发布时间：2012年05月26日浏览次数： 1 次评论：[已关闭] 功能：打印本文一、逻辑代数相等：假定Ｆ、Ｇ都具有ｎ个相同变量的逻辑函数，对于这ｎ个变量中的任意一组输入，如Ｆ和Ｇ都有相同的输出值，则称这两个函数相等。

在实际中，可以通过列真值表来判断。

二、逻辑代数的基本定律：在逻辑代数中，三个基本运算符的运算优先级别依次为：非、与、或。

由此推出10个基本定律如下：1.交换律Ａ＋Ｂ＝Ｂ＋Ａ；Ａ·Ｂ＝Ｂ·Ａ2.结合律Ａ＋（Ｂ＋Ｃ）＝（Ａ＋Ｂ）＋Ｃ；Ａ·（ＢＣ）＝（ＡＢ）·Ｃ3.分配律Ａ·（Ｂ＋Ｃ）＝ＡＢ＋ＡＣ；Ａ＋ＢＣ＝（Ａ＋Ｂ）·（Ａ＋Ｃ）4.0－1律Ａ＋0＝Ａ；Ａ·1＝ＡＡ＋1＝1 ；Ａ·0＝05.互补律Ａ＋＝1 ；Ａ·＝06.重叠律Ａ·Ａ＝Ａ；Ａ＋Ａ＝Ａ7.对合律＝Ａ8.吸收律Ａ＋ＡＢ＝Ａ；Ａ·（Ａ＋Ｂ）＝ＡＡ＋Ｂ＝Ａ＋Ｂ；Ａ·（＋Ｂ）＝ＡＢＡＢ＋Ｂ＝Ｂ；（Ａ＋Ｂ）·（＋Ｂ）＝Ｂ9.反演律＝·；＝＋10.多余项律ＡＢ＋Ｃ＋ＢＣ＝ＡＢ＋Ｃ；(Ａ＋Ｂ）·（＋Ｃ）·（Ｂ＋Ｃ）＝（Ａ＋Ｂ）·（＋Ｃ）上述的定律都可用真值表加以证明，它们都可以用在后面的代数化简中。

三、逻辑代数的基本规则：逻辑代数中有三个基本规则：代入规则、反演规则和对偶规则。

1.代入规则：在任何逻辑代数等式中，如果等式两边所有出现某一变量（如Ａ）的位置都代以一个逻辑函数（如Ｆ），则等式仍成立。

利用代入规则可以扩大定理的应用范围。

例：＝＋，若用Ｆ＝ＡＣ代替Ａ，可得＝＋＋2.反演规则：已知函数Ｆ，欲求其反函数时，只要将Ｆ式中所有的“·”换成“＋”，“＋”换成“·”；“0”换成“1”，“1”换成“0”时，原变量变成反变量，反变量变成原变量，便得到。