当前位置：文档之家 › 第六章 树和二叉树(2)

第六章 树和二叉树(2)

  • 格式：ppt
  • 大小：199.50 KB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

数据结构-6 树和二叉树

数据结构-6 树和二叉树

第六章树和二叉树一．选择题1. 以下说法错误的是。

A.树形结构的特点是一个结点可以有多个直接前趋B.线性结构中的一个结点至多只有一个直接后继C.树形结构可以表达(组织)更复杂的数据D.树(及一切树形结构)是一种"分支层次"结构2. 如图6-2所示的4 棵二叉树中，不是完全二叉树。

图6-2 4 棵二叉树3. 在线索化二叉树中，t 所指结点没有左子树的充要条件是。

A. t->left == NULLB. t->ltag==1C. t->ltag==1 且t->left==NULL D .以上都不对4. 以下说法错误的是。

A.二叉树可以是空集B.二叉树的任一结点最多有两棵子树C.二叉树不是一种树D.二叉树中任一结点的两棵子树有次序之分5. 以下说法错误的是。

A.完全二叉树上结点之间的父子关系可由它们编号之间的关系来表达B.在三叉链表上，二叉树的求双亲运算很容易实现C.在二叉链表上，求根，求左、右孩子等很容易实现D.在二叉链表上，求双亲运算的时间性能很好6. 如图6-3所示的4 棵二叉树，是平衡二叉树。

图6-3 4 棵二叉树7. 如图6-4所示二叉树的中序遍历序列是。

A. abcdgefB. dfebagcC. dbaefcgD. defbagc图6-4 1 棵二叉树8. 已知某二叉树的后序遍历序列是dabec，中序遍历序列是debac，它的前序遍历序列是。

A. acbedB. decabC. deabcD. cedba9. 如果T2 是由有序树T 转换而来的二叉树，那么T 中结点的前序就是T2 中结点的。

A. 前序B.中序C. 后序D. 层次序10. 某二叉树的前序遍历结点访问顺序是abdgcefh，中序遍历的结点访问顺序是dgbaechf，则其后序遍历的结点访问顺序是。

A. bdgcefhaB. gdbecfhaC. bdgaechfD. gdbehfca11. 将含有83个结点的完全二叉树从根结点开始编号，根为1号，后面按从上到下、从左到右的顺序对结点编号，那么编号为41的双亲结点编号为。

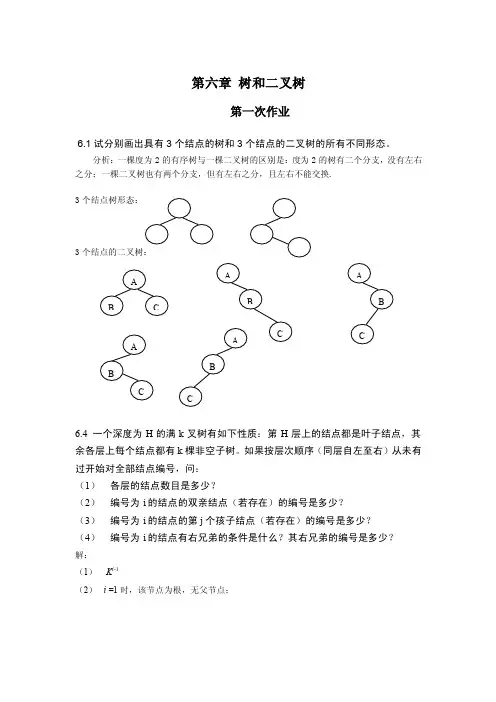
一棵度为2的有序属于一棵二叉树有何区别？

一棵度为2的有序属于一棵二叉树有何区别？

第六章 树和二叉树第一次作业6.1试分别画出具有3个结点的树和3个结点的二叉树的所有不同形态。

分析：一棵度为2的有序树与一棵二叉树的区别是：度为2的树有二个分支，没有左右之分；一棵二叉树也有两个分支，但有左右之分，且左右不能交换.33个结点的二叉树：6.4一个深度为H 的满k 叉树有如下性质：第H 层上的结点都是叶子结点，其余各层上每个结点都有k 棵非空子树。

如果按层次顺序（同层自左至右）从未有过开始对全部结点编号，问：（1） 各层的结点数目是多少？（2） 编号为i 的结点的双亲结点（若存在）的编号是多少？（3）编号为i 的结点的第j 个孩子结点（若存在）的编号是多少？（4） 编号为i 的结点有右兄弟的条件是什么？其右兄弟的编号是多少？ 解：（1） K i -1（2） i =1时，该节点为根，无父节点；否则其父节点编号为(2)i k k +-⎢⎥⎢⎥⎣⎦（k ≥2） 分析：编号为p 的孩子结点的范围[（p -1）*k +2, p *k +1] 得出(i -1)/k ≤p ≤(i -2)/k +1（3） K *i +j +1-k（4）(i -1)MOD K <>0,该结点有右兄弟,其右兄弟的编号是i +16.5 已知一棵度为k 的树中有1n 个度为1的结点，2n 个度为2的结点，…，k n 个度为k 的结点，问该树中有多少个叶子结点?解: ∑=-+=k 1i i 0n )1i (1n分析：结点总数：n=n 0+n 1+n 2+……+n k ，n=1+n 1+2n 2+……+kn k所以得n 0 = n 2 + 2n 3 + …… + (k -1)n k + 1 6.6 已知在一棵含有n 个结点的树中，只有度为k 的分支结点和度为0的叶子结点，试求该树的叶子结点数目解：度：一个结点含有的子树的个数称为该节点的度；设有n k 个度为k 的分支结点，n 0个度为0的分支结点各点度数总和为：n=k*n k +1,最后计算得到叶节点个数为n-(n-1)/k 。

第6章_数据结构习题题目及答案_树和二叉树_参考答案

第6章_数据结构习题题目及答案_树和二叉树_参考答案

一、基础知识题6.1设树T的度为4，其中度为1，2，3和4的结点个数分别为4，2，1，1，求树T中的叶子数。

【解答】设度为m的树中度为0,1,2,…,m的结点数分别为n0, n1, n2,…, nm，结点总数为n，分枝数为B，则下面二式成立n= n0+n1+n2+…+nm (1)n=B+1= n1+2n2 +…+mnm+1 (2)由(1)和(2)得叶子结点数n0=1+即： n0=1+(1-1)*4+(2-1)*2+(3-1)*1+(4-1)*1=86.2一棵完全二叉树上有1001个结点，求叶子结点的个数。

【解答】因为在任意二叉树中度为2 的结点数n2和叶子结点数n0有如下关系：n2=n0-1,所以设二叉树的结点数为n, 度为1的结点数为n1，则n= n0+ n1+ n2n=2n0+n1-11002=2n0+n1由于在完全二叉树中，度为1的结点数n1至多为1，叶子数n0是整数。

本题中度为1的结点数n1只能是0，故叶子结点的个数n0为501.注：解本题时要使用以上公式，不要先判断完全二叉树高10，前9层是满二叉树，第10层都是叶子，……。

虽然解法也对，但步骤多且复杂，极易出错。

6.3 一棵124个叶结点的完全二叉树，最多有多少个结点。

【解答】由公式n=2n0+n1-1,当n1为1时，结点数达到最多248个。

6.4．一棵完全二叉树有500个结点，请问该完全二叉树有多少个叶子结点？有多少个度为1的结点？有多少个度为2的结点？如果完全二叉树有501个结点，结果如何？请写出推导过程。

【解答】由公式n=2n0+n1-1，带入具体数得，500=2n0+n1-1，叶子数是整数，度为1的结点数只能为1，故叶子数为250，度为2的结点数是249。

若完全二叉树有501个结点，则叶子数251，度为2的结点数是250，度为1的结点数为0。

6.5 某二叉树有20个叶子结点，有30个结点仅有一个孩子，则该二叉树的总结点数是多少。

第6章树和二叉树

第6章树和二叉树

2.孩子表示法 孩子表示法 在结点中设置指向每个孩子的指针域， 在结点中设置指向每个孩子的指针域，利用指针 指向该结点的所有孩子结点。 指向该结点的所有孩子结点。 大多采用按树的度设置结点的指针域的个数。 大多采用按树的度设置结点的指针域的个数。
9
6.1.4 树的存储结构
3.孩子兄弟表示法 孩子兄弟表示法 在结点中设置两个指针域， 在结点中设置两个指针域，一个指针域指向该结 点的第一个孩子，另一个指针域指向其右兄弟。 点的第一个孩子，另一个指针域指向其右兄弟。
2
6.1.1树的定义 树的定义
结点的度：结点所拥有子树的个数称为结点的度。 结点的度：结点所拥有子树的个数称为结点的度。 子树 称为结点的度 树的度：树中所有结点的度的最大值称为树的度。 最大值称为树的度 树的度：树中所有结点的度的最大值称为树的度。 叶结点：度为零的结点称为叶结点。也称终端结点 终端结点或 叶结点：度为零的结点称为叶结点。也称终端结点或叶 子 分支结点：度不为零的结点称为分支结点。也称非终端 分支结点：度不为零的结点称为分支结点。也称非终端 结点。除根结点以外，分支结点也称为内部结点。 结点。除根结点以外，分支结点也称为内部结点。 孩子结点和双亲结点： 孩子结点和双亲结点：树中一个结点的子树的根结点称 为孩子结点。该结点就称为孩子结点的双亲结点。 为孩子结点。该结点就称为孩子结点的双亲结点。 兄弟结点：具有同一双亲的孩子结点互为兄弟结点。 兄弟结点：具有同一双亲的孩子结点互为兄弟结点。 结点的祖先：从根到该结点所经分支上的所有结点， 结点的祖先：从根到该结点所经分支上的所有结点，称 为结点的祖先。 为结点的祖先。
17
6.2.2 二叉树的性质
性质4 具有n（ 性质 具有 （n>0）个结点的完全二叉树的深度 ）个结点的完全二叉树的深度h= log 2 n + 1 证明： 证明： 根据完全二叉树的定义可知深度为h-1层及以上的结点构成 根据完全二叉树的定义可知深度为 层及以上的结点构成 满二叉树，因此由性质2得深度为 得深度为h的完全二叉树满足 满二叉树，因此由性质 得深度为 的完全二叉树满足 n>2h-1-1和n≤2h-1 和 整理后得到 2h-1≤n<2h 不等式两边取对数， 不等式两边取对数，得 h-1≤log2n<h 由于h为正整数 为正整数， 由于 为正整数，因此 h= log 2 n + 1
第6章树和二叉树(2)培训讲学

第6章树和二叉树(2)培训讲学

第6章树和二叉树(2)第六章树和二叉树一、选择题1．算术表达式a+b*（c+d/e）转为后缀表达式后为（）A．ab+cde/* B．abcde/+*+ C．abcde/*++ D．abcde*/++2. 设森林F对应的二叉树为B，它有m个结点，B的根为p,p的右子树结点个数为n,森林F中第一棵树的结点个数是（）A．m-n B．m-n-1 C．n+1 D．条件不足，无法确定3．若度为m的哈夫曼树中，其叶结点个数为n，则非叶结点的个数为（）。

A．n-1 B．⎣n/m⎦-1 C．⎡(n-1)/(m-1)⎤ D．⎡n/(m-1)⎤-1E．⎡(n+1)/(m+1)⎤-14．深度为h的满m叉树的第k层有（）个结点。

(1=<k=<h)A．m k-1 B．m k-1 C．m h-1 D．m h-15. 若X是二叉中序线索树中一个有左孩子的结点，且X不为根，则x的前驱为( )A.X的双亲B.X的右子树中最左的结点C.X的左子树中最右结点D.X的左子树中最右叶结点6. 引入二叉线索树的目的是（）A．加快查找结点的前驱或后继的速度 B．为了能在二叉树中方便的进行插入与删除C．为了能方便的找到双亲 D．使二叉树的遍历结果唯一7．由3 个结点可以构造出多少种不同的二叉树？（）A．2 B．3 C．4 D．58．下述编码中哪一个不是前缀码（）。

A．（00，01，10，11） B．（0，1，00，11） C．（0，10，110，111）D．（1，01，000，001）二、判断题1. 给定一棵树，可以找到唯一的一棵二叉树与之对应。

2．将一棵树转成二叉树，根结点没有左子树；3. 在中序线索二叉树中，每一非空的线索均指向其祖先结点。

4. 一棵哈夫曼树的带权路径长度等于其中所有分支结点的权值之和。

5．当一棵具有n个叶子结点的二叉树的WPL值为最小时，称其树为Huffman树，且其二叉树的形状必是唯一的。

三、填空题1．一棵树T中，包括一个度为1的结点，两个度为2的结点，三个度为3的结点，四个度为4的结点和若干叶子结点，则T的叶结点数为___ ___。

数据结构考试题库含答案

数据结构考试题库含答案

数据构造习题集含答案目录目录1选择题2第一章绪论2第二章线性表4第三章栈和队列6第四章串7第五章数组和广义表8第六章树和二叉树8第七章图11第八章查找13第九章排序14简答题19第一章绪论19第二章线性表22第三章栈和队列24第四章串26第五章数组和广义表27第六章树和二叉树28第七章图31第八章查找31第九章排序32编程题34第一章绪论34第二章线性表34第三章栈和队列45第四章串45第五章数组和广义表45第六章树和二叉树45第七章图45第八章查找45第九章排序50选择题第一章绪论1.数据构造这门学科是针对什么问题而产生的？〔A 〕A、针对非数值计算的程序设计问题B、针对数值计算的程序设计问题C、数值计算与非数值计算的问题都针对D、两者都不针对2.数据构造这门学科的研究容下面选项最准确的是〔D 〕A、研究数据对象和数据之间的关系B、研究数据对象C、研究数据对象和数据的操作D、研究数据对象、数据之间的关系和操作3.*班级的学生成绩表中查得三同学的各科成绩记录，其中数据构造考了90分，则下面关于数据对象、数据元素、数据项描述正确的选项是〔C 〕A、*班级的学生成绩表是数据元素，90分是数据项B、*班级的学生成绩表是数据对象，90分是数据元素C、*班级的学生成绩表是数据对象，90分是数据项D、*班级的学生成绩表是数据元素，90分是数据元素4.*数据构造是指〔A 〕。

A、数据元素的组织形式B、数据类型C、数据存储构造D、数据定义5.数据在计算机存储器表示时，物理地址与逻辑地址不一样，称之为〔C 〕。

A、存储构造B、逻辑构造C、链式存储构造D、顺序存储构造6.算法分析的目的是〔C 〕A、找出数据的合理性B、研究算法中的输入和输出关系C、分析算法效率以求改良D、分析算法的易懂性和文档型性7.算法分析的主要方法〔A 〕。

A、空间复杂度和时间复杂度B、正确性和简明性C、可读性和文档性D、数据复杂性和程序复杂性8.计算机部处理的根本单元是〔B 〕A、数据B、数据元素C、数据项D、数据库9.数据在计算机有链式和顺序两种存储方式，在存储空间使用的灵活性上，链式存储比顺序存储要〔B 〕。

第六章-树和二叉树

第六章-树和二叉树


之
树 和 二 叉 树 13
1 2 3 A B C
4 5 6 7 0 D E F
8 0
9 10 0 G
¾ 二叉树顺序存储的算法描述
数 据 结 构
¾ 初始化二叉树
之
树 和 二 叉 树 14
#define Max_Size 100 typedef int TElemType; typedef TElemType SqBT[Max_Size+1]; void InitBT(SqBT bt){//设置空树 int i; for(i=1;i<=Max_Size;i++) bt[i]=0; }
数 据 结 构
之
树 和 二 叉 树 19
¾ 后序遍历顺序二叉树算法 void PostBT(SqBT bt,int i){ if(i>Max_Size||!bt[i]) return; PostBT(bt,2*i); PostBT(bt,2*i+1); printf("%3d ",bt[i]); }
数 据 结 构
之
树 和 二 叉 树 4
5. 孩子结点、双亲结点、兄弟结点、堂兄弟 结点、祖先结点、子孙结点…… 6. 结点的层次从根开始，根为第一层，根的 孩子为第二层；若某结点在第L层，则其 子树的根就在第L+1层。 7. 树的深度或高度：树中结点的最大层次。 8. 有序树：如果将树中结点的各子树看成是 从左至右有次序的；反之，则是无序树。 9. 森林：是m棵互不相交的树的集合。
数 据 结 构
之
树 和 二 叉 树 25
¾ 打印一维数组 void printSq(SqBT bt){ int i; printf("\nSeqArray:"); for(i=1;i<=Max_Size;i++) printf("%3d ",bt[i]); }
第6章树和二叉树2

第6章树和二叉树2

遍历结果：A B C D E F
深度遍历策略

二叉树由根、左子树、右子树三部分组成
二叉树的遍历可以分解为： 访问根（D） 遍历左子树（L） 遍历右子树（R） 有六种遍历方法： D L R，L D R，L R D， D R L，R D L，R L D
A B C
D G
E
F
约定先左后右,有三种遍历方法: 分别称为先序遍历、中序遍历、后序遍历
6.2.3 二叉树的存储结构
二、二叉树的链式存储表示 1、二叉链表（P126） typedef struct BiTNode { lchild data rchild TElemType data; struct BiTNode *lchild, *rchild; // 左右孩子指针 } BiTNode, *BiTree; A B D
B D G E
C F
后序遍历（LRD）
后序遍历动态演示
A B D G
D, G, E, B, F, C, A
C
E F
2007-1 试题

对下图所示的二叉树进行后序遍历（左子树、 右子树、根结点）的结果是 （42） 。
5 2 4 6 3 1
（42）A. 5 2 3 4 6 1 C. 2 6 4 1 3 5
if (!StackEmpty(s)) { p=pop(s); visite(p->data); //访问根结点 p=p->rchild; //通过下一次循环实现右子树遍历 }//endif }//endwhile }//InOrderUnrec
6.3.1 遍历二叉树
后序遍历的非递归算法描述
后序遍历时，每遇到一个结点，先把它推入栈中，让PopTim=0。在遍历其 左子树前，改结点的PopTim=1，将其左孩子推入栈中。在遍历完左子树后，还 不能访问该结点，必须继续遍历右子树，此时改结点的PopTim=2，并把其右孩 子推入栈中。在遍历完右子树后，结点才退栈访问。
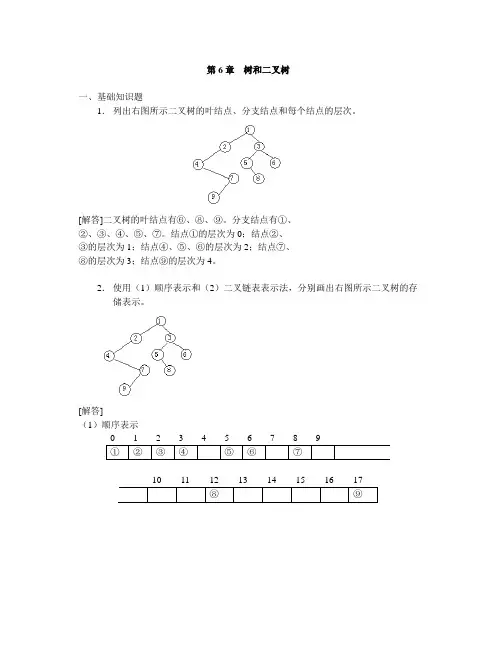
第6-10章 树和二叉树--答案

第6-10章 树和二叉树--答案

第6章树和二叉树一、基础知识题1．列出右图所示二叉树的叶结点、分支结点和每个结点的层次。

[解答]二叉树的叶结点有⑥、⑧、⑨。

分支结点有①、②、③、④、⑤、⑦。

结点①的层次为0；结点②、③的层次为1；结点④、⑤、⑥的层次为2；结点⑦、⑧的层次为3；结点⑨的层次为4。

2．使用（1）顺序表示和（2）二叉链表表示法，分别画出右图所示二叉树的存储表示。

[解答]（1）顺序表示（2）二叉链表表示3．在结点个数为n（n>1）的各棵树中，高度最小的树的高度是多少？它有多少个叶结点？多少个分支结点？高度最大的树的高度是多少？它有多少个叶结点？多少个分支结点？[解答]结点个数为n时，高度最小的树的高度为1，有2层；它有n-1个叶结点，1个分支结点；高度最大的树的高度为n-1，有n层；它有1个叶结点，n-1个分支结点。

4．试分别画出具有3个结点的树和3个结点的二叉树的所有不同形态。

[解答]具有3个结点的树具有3个结点的二叉树5．如果一棵树有n1个度为1的结点，有n2个度为2的结点，…，n m个度为m的结点，试问有多少个度为0的结点？试推导之。

[解答]总结点数n=n0+n1+n2+…+n m总分支数e=n-1= n0+n1+n2+…+n m-1=m×n m+(m-1)×n m-1+…+2×n2+n1则有 n 0=∑=+-mi i n i 21))1((6．试分别找出满足以下条件的所有二叉树：（1） 二叉树的前序序列与中序序列相同； （2） 二叉树的中序序列与后序序列相同； （3） 二叉树的前序序列与后序序列相同。

[解答]（1） 二叉树的前序序列与中序序列相同：空树或缺左子树的单支树；（2） 二叉树的中序序列与后序序列相同：空树或缺右子树的单支树； （3） 二叉树的前序序列与后序序列相同：空树或只有根结点的二叉树。

7．填空题（1）对于一棵具有n 个结点的树，该树中所有结点的度数之和为 n-1 。

数据结构——用C语言描述(第3版)教学课件第6章 树与二叉树

数据结构——用C语言描述(第3版)教学课件第6章 树与二叉树


6.2 二叉树 6.2.1 二叉树的定义与基本操作 6.2.2 二叉树的性质 6.2.3 二叉树的存储结构
6.2.1 二叉树的定义与基本操作 定义：我们把满足以下两个条件的树型结构叫做二 叉树（Binary Tree）： （1）每个结点的度都不大于2； （2）每个结点的孩子结点次序不能任意颠倒。
有序树：在树T中，如果各子树Ti之间是有先后次序的，则称为有序树。 森林：m（m≥0）棵互不相交的树的集合。将一棵非空树的根结点删去，树就变成一 个森林；反之，给森林增加一个统一的根结点，森林就变成一棵树。
同构：对两棵树，通过对结点适当地重命名，就可以使两棵树完全相等（结点对应相 等，对应结点的相关关系也像等），则称这两棵树同构。
二叉树的基本结构由根结点、左子树和右子树组成
如图示
LChild Data RChild
Data
LChild RChild
用L、D、R分别表示遍历左子树、访问根结点、遍 历右子树，那么对二叉树的遍历顺序就可以有：
(1) 访问根，遍历左子树，遍历右子树(记做DLR)。 (2) 访问根，遍历右子树，遍历左子树(记做DRL)。 (3) 遍历左子树，访问根，遍历右子树(记做LDR)。 (4) 遍历左子树，遍历右子树，访问根 (记做LRD)。 (5) 遍历右子树，访问根，遍历左子树 (记做RDL)。 (6) 遍历右子树，遍历左子树，访问根 (记做RLD)。
(8) NextSibling（Tree，x）： 树Tree存在，x是Tree中的某个结点。若x不 是其双亲的最后一个孩子结点，则返回x后面的下一个兄弟结点，否则 返回“空”。
基本操作:
(9) InsertChild（Tree，p，Child）： 树Tree存在，p指向Tree 中某个结点，非空树Child与Tree不相交。将Child插入Tree中， 做p所指向结点的子树。
数据结构 第六章 树和二叉树

数据结构 第六章 树和二叉树


F
G
H
M
I
J
结点F，G为堂兄弟 结点A是结点F，G的祖先
5
树的基本操作
树的应用很广，应用不同基本操作也不同。下面列举了树的一些基本操作： 1）InitTree(&T); 2）DestroyTree(&T); 3）CreateTree(&T, definition); 4）ClearTree(&T); 5）TreeEmpty(T); 6）TreeDepth(T); 7） Root(T); 8） Value(T, &cur_e); 9） Assign(T, cur_e, value); 10）Paret(T, cur_e); 11）LeftChild(T, cur_e); 12）RightSibling(T, cur_e); 13）InsertChild(&T, &p, i, c); 14）DeleteChild(&T,&p, i); 15）TraverseTree(T, Visit( ));
1
2 4 8 9 10 5 11 12 6 13 14 3 7 15 4 6 2
1
3
5 7
证明：设二叉树中度为1的结点个数为n1 根据二叉树的定义可知，该二叉树的结点数n=n0+n1+n2
又因为在二叉树中，度为0的结点没有孩子，度为1的结点有1 个孩子，度为2的结点有2个结孩子，故该二叉树的孩子结点 数为 n0*0+n1*1+n2*2(分支数） 而一棵二叉树中，除根结点外所有都为孩子结点，故该二叉 树的结点数应为孩子结点数加1即：n=n0*0+n1*1+n2*2+1
文件夹1
文件夹n

第六章 树与二叉树

44
森林的遍历
(4) 广度优先遍历(层次序 遍历) ：
数据结构
若森林F为空，返回； 否则 依次遍历各棵树的根 结点； 依次遍历各棵树根结 点的所有子女； 依次遍历这些子女结 森林的二叉树表示 点的子女结点。
45
二叉树的计数 由二叉树的前序序列和中序序列可唯 一地确定一棵二叉树。例, 前序序列 { ABHFDECKG } 和中序序列 { HBDFAEKCG }, 构造二叉树过程如 下：
三个结点构成的不同的二叉树
8
用二 叉 树 表达实际问题
例2 双人比赛的所有可能的结局
开始
甲
开局连赢两局 或五局三胜
乙
甲
甲 甲 乙
乙
乙 甲 乙 甲 甲 乙
甲
乙 甲
乙
乙
甲
乙甲
乙
甲
乙 甲 乙
二叉树的性质
数据结构
性质1 若二叉树的层次从1开始, 则在二叉树的 第 i 层最多有 2i －1个结点。(i 1) [证明用数学归纳法] 性质2 高度为k的二叉树最多有 2k-1个结点。 (k 0) [证明用求等比级数前k项和的公式]
前序遍历二叉树算法的框架是 若二叉树为空，则空操作； 否则 – 访问根结点 (V)； – 前序遍历左子树 (L)； – 前序遍历右子树 (R)。
遍历结果 -+a*b-cd/ef
27
数据结构
后序遍历 (Postorder Traversal)
后序遍历二叉树算法的框架是 若二叉树为空，则空操作； 否则 – 后序遍历左子树 (L)； – 后序遍历右子树 (R)； – 访问根结点 (V)。
数据结构
36
左子女-右兄弟表示法 第一种解决方案

数据结构详细教案——树与二叉树

数据结构教案第六章树与二叉树目录6.1树的定义和基本术语 (1)6.2二叉树 (2)6.2.1 二叉树的定义 (2)6.2.2 二叉树的性质 (4)6.2.3 二叉树的存储结构 (5)6.3树和森林 (6)6.4二叉树的先|中|后序遍历算法 (7)6.5先|后|中序遍历的应用扩展 (9)6.5.1 基于先序遍历的二叉树(二叉链)的创建 (9)6.5.2 统计二叉树中叶子结点的数目 (9)6.5.3 求二叉树的高度 (10)6.5.4 释放二叉树的所有结点空间 (11)6.5.5 删除并释放二叉树中以元素值为x的结点作为根的各子树 (12)6.5.6 求位于二叉树先序序列中第k个位置的结点的值 (12)6.5.7 线索二叉树 (13)6.5.8 树和森林的遍历 (14)6.6二叉树的层次遍历 (16)6.7判断一棵二叉树是否为完全二叉树 (16)6.8哈夫曼树及其应用 (18)6.8.1 最优二叉树(哈夫曼树) (18)6.8.2 哈夫曼编码 (19)6.9遍历二叉树的非递归算法 (19)6.9.1 先序非递归算法 (19)6.9.2 中序非递归算法 (20)6.9.3 后序非递归算法 (21)第6章二叉树和树6.1 树的定义和基本术语1、树的递归定义1）结点数n=0时，是空树2）结点数n>0时有且仅有一个根结点、m个互不相交的有限结点集——m棵子树2、基本术语结点：叶子(终端结点)、根、内部结点（非终端结点、分支结点）；树的规模：结点的度、树的度、结点的层次、树的高度(深度)结点间的关系：双亲(1)—孩子(m)，祖先—子孙，兄弟，堂兄弟兄弟间是否存在次序：无序树、有序树去掉根结点非空树森林引入一个根结点3、树的抽象数据类型定义树特有的操作：查找：双亲、最左的孩子、右兄弟结点的度不定，给出这两种操作可以查找到一个结点的全部孩子插入、删除：孩子遍历：存在一对多的关系，给出一种有规律的方法遍历(有且仅访问一次)树中的结点ADT Tree{数据对象：D={a i | a i∈ElemSet, i=1,2,…,n, n≥0}数据关系：若D为空集，则称为空树；若D仅含一个数据元素，则R为空集，否则R={H}，H是如下二元关系：(1) 在D中存在唯一的称为根的数据元素root，它在关系H下无前驱；(2) 若D-{root}≠Ф，则存在D-{root}的一个划分D1, D2, …, D m (m>0)（D i 表示构成第i棵子树的结点集），对任意j≠k (1≤j, k≤m) 有D j∩D k=Ф，且对任意的i (1≤i≤m)，唯一存在数据元素x i∈D i, 有<root,x i>∈H（H表示结点之间的父子关系）；(3) 对应于D-{root}的划分，H-{<root, x1>,…, <root, x m>}有唯一的一个划分H1, H2, …, H m(m>0)（H i表示第i棵子树中的父子关系），对任意j≠k(1≤j,k≤m)有H j∩H k=Ф，且对任意i(1≤i≤m)，H i是D i上的二元关系，(D i, {H i})是一棵符合本定义的树，称为根root的子树。

第6章树和二叉树(下)-数据结构简明教程(第2版)-微课版-李春葆-清华大学出版社


6.6
【例6.16】 已知先序序列为ABDECFG，中序序列为DBEACGF，
给出构造该二叉树的过程。
解：构造该二叉树的过程如下所示。
根：A 左先序：BDE 右先序：CFG 右中序：DBE 右中序：CGF
二
叉 树
根：B 左先序：D 右先序：E
根：C 左先序：空 右先序：FG
的
右中序：D 右中序：E
右子树中
序序列， 有n-k-1 个结点
的
构 造
若bk前面有k个结点，则左子树有k个结点，右子树有n-k-1 个结点。
可以求出左右子树的中序序列和后序序列。
这样根结点是确定的，左右子树也是确定的，则该二叉树是 确定的。
6.6
【例6.17】 已知一棵二叉树的后序遍历序列为DEBGFCA，
中序遍历序列为DBEACGF，给出构造该二叉树的过程。
间 的
以树的根结点为轴心，将整棵树顺时针转动45度，使之结
转
构层次分明。
换
【例6.18】 将图6.27(a)所示的树转换成二叉树。 解：转换的过程:
A
A
6.7
BC D
二
叉 树
EF
G
与
一棵树
树 之
A
间
的
B
转
换
E
C
相邻兄弟之间 加连线(虚线)
BC D
EF
G
删除与双亲 结点的连线
转换后的二叉树
A BC D
【例6.15】 一棵二叉树的先序遍历序列和中序遍历序列相同，
说明该二叉树的形态。
解：二叉树的先序遍历序列为NLR，中序遍历序列为LNR:
NLR = LNR
二 则L应为空（因为N为空后其L、R没有意义）。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

结束
第 2 页
60 30 15 30 15 60 30 15 5 10 30 15 5 15 10 15 30
结束
5 10
WPL=5*1+10*2+15*3+30*3=160
30 15
WPL=5*3+10*3+15*2+30*1=105
WPL=5*2+10*2+15*2+30*2=120
第 3 页
weight parent lchild rchild
HTNode类型的结构变量
结束
第 18 页
w 100 42 23 11 5 19 8 3 29 14 7 58 29 15 8 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
p 5 29 7 8 14 23 3 11 8 15 19 29 42 58 100
100 60 30 15 5 10
结束
40 30
15
第 5 页
3 哈夫曼树的构造 构造哈夫曼树的步骤： 1．根据给定的n个权值 ，构造n棵只有一个根结点的二叉树， n个权值分 别是这些二叉树根结点的权。设F是由这n棵二叉树构成的集合 2．在F中选取两棵根结点权值最小的树作为左、右子树，构造一颗新的 二叉树，置新二叉树根的权值=左、右子树根结点权值之和； 3．从F中删除这两棵树，并将新树加入F； 4．重复 2、3，直到F中只含一棵树为止；
b: c: d: e: f: g: h: 10 1110 1111 110 00 0111 010
结束
第 17 页
3．哈夫曼编码算法 设用一维数组W存储n个权值， 用静态三叉链表HT存储哈夫曼树
存储哈夫曼树的静态三叉链表类型定义 typedef struct { unsigned int weight; unsigned int parent, lchild, rchild; }HTNode, *HuffmanTree; //动态分配数组存储哈夫曼树
100 42 23 11 5 19 8 3 29 14 7 58 29 15 8 a: b: c: d: e: f: g: h: 0110 10 1110 1111 110 00 0111 010
结束
第 15 页
*哈夫曼树的应用 哈夫曼树的应用 1）报文到电文的译码 a) 从根出发 b) 取一位报文，若取完，译码结束。 c) 若报文=1，向右分支行进一个结点 若报文=0，向左分支行进一个结点 d) 若所得结点不是叶结点，转b) e) 若所得结点是叶结点，则字符即为译码结果，得到一个 字符，转a) 例：报文：111010001100100111 c b f e h g
哈夫曼树
哈夫曼树对应的静态三叉链表
结束
第 19 页
哈夫曼算法 void HuffmanTree(HuffmanTree &HT, int * w, int n){ //w 存放n 个字符的权值（均>0），构造赫夫曼树HT if (n<=1) return; m=2* n-1; HT=(HuffmanTree)malloc(m+1) * sizeof(HTNode); //为哈夫曼树分配存储 //空间 for (p=HT, i=1; i<=n; ++i, ++p, ++w) * p={ * w, 0, 0, 0}; //用给定的n个权// 值 ，构造n棵只有一个根结点的二叉树 for (; i<m; ++i; ++p) { //按构造哈夫曼树的步骤2、3、4，建哈夫曼树 //在HT[1..i-1] 选择parent为0且weight最小的两个结点，其序号分别为s1和 s2。 Select(HT, i-1, s1, s2); HT[s1]. parent =i; HT[s2].parent=i; //HT[i]存放新子树的根结点， HT[i].lchild=s1; HT[i].rchild=s2; HT[i].weight=HT[s1].weight+HT[s2].weight;
结束
第 9 页
采用不等长的编码，并且让字符串中出现频率大的字符的编码尽可 能的短，则电文的（字符串的编码）总长度即可减少，但这时会出现 编码的唯一性问题。 如果：A,B,C,D的编码分别为：0，00，1，01 则：上述电文：000011010 共9位，长度减少。但是译文困难。前面的 连续四个0，可以译成AAAA,BB,ABA。不唯一。 3).前缀 前缀编码 3).前缀编码 任一字符的编码都不是另一个字符编码的前缀。如果我们的不等长 编码是前缀编码，则问题就解决了。 前缀编码可以用二叉树来设计。方法： 1）字符放在叶结点上。 2）树中度为1的结点个数为0。 3）左右分支的编码分别为0，1。 4）从根结点到叶结点的路径上各分支的字符组成的二进制串作为 叶结点的编码。
第 22 页
HT
w
p
lch rch
0 5 0 0 0 1 2 29 0 0 0 5 7 0 0 0 3 8 0 0 0 4 5 14 0 0 0 6 23 0 0 0 3 0 0 0 7 8 11 0 0 0 9 10 11 12 13 14 15 8 棵只有一个结点的二叉树
结束
第 6 页
例：构造以W=（5，15，40，30，10）为权的哈夫曼树。
100 5 15 40 30 10 30 15 5 10 15 40 30 5 15 10 15 60 30 40
60 30 15 5 10 15 40 30 5 15 10 30 15 40
结束
30
第 7 页
6.6.2 哈夫曼编码 1.哈夫曼编码 哈夫曼编码 哈夫曼树除了能求解最优判定问题解，还用于其他一些最优问题的求 解。这里介绍用哈夫曼树求解数据的二进制编码。 在进行数据通讯时，涉及数据编码问题。所谓数据编码就是数据与 二进制字符串的转换。例如：数据压缩、邮局发电报，发送方将原文转 换成二进制字符串，接收方将二进制字符串还原成原文。 原文 ---电文（二进制字符串） ----原文 例 要传输的原文为ABACCDA 设ABCD的编码为 A；00 B；01 C：10 D：11 发送方：将ABACCDA 转换成 00010010101100 接收方：将 00010010101100 还原为 ABACCDA
分数 0-59 60-69 70-79 80-89 90-100 0.15 0.40 0.30 0.10 比例数 0.05
结束
第 4 页
按图的判定过程，转换一个分数所需的比较次数=从根到对应结点的路径 长度。转换10000个分数所需的总比较次数= 10000（0.05 × 1+0.15 × 2+0.4 × 3+0.3 × 4+0.1 × 4） 若将学生成绩在5个等级以上的分布比例看作描述判定过程二叉树叶子结 点权值，（0.05 × 1+0.15 × 2 +0.4 × 3+0.3 × 4+0.1 × 4）正是该二叉树的带 权路径长度。可见要想获得效率较高的转换程序，可构造以分数的分布 比例为权值的哈夫曼树。
结束
第 8 页
1).等长编码 1).等长编码 等长 每个字符都有相同长度的二进制编码。 我们上面的例子是一个等长编码的例子。 *优点：译文容易。 *缺点：报文长。 若某种文字有n个字符，每个字符的编码为k位，则： K=log2(n+1) 例如：英文字母26个，若要等长的给每个字母一个编码，则需要5 位二 进制。 2).不等长编码 2).不等长编码 不等长 每个字符具有长度不同的二进制编码。 在电报通讯的例子中，我们总希望电文长度尽可能的短。在数据 压缩时总希望压缩比尽可能的大。
结束
第 10 页
A :0
A B C
B: 10 C:11 用这种方式得到的编码是前缀编码。
结束
第 11 页
例 某通讯系统只使用8种字符a、b、c、d、e、f、g、h，其使用频率分 别为0.05,0.29,0.07,0.08, 0.14,0.23, 0.03,0.11，利用二叉树设计一种不等长 编码： 1）构造以 a、b、c、d、e、f、g、h为叶子结点的二叉树； 2）将该二叉树所有左分枝标记0，所有右分枝标记1； 3）从根到叶子结点路径上标记作为叶子结点所对应字符的编码；
结束
第 1 页
6.6 哈夫曼树及其应用
6.6.1 哈夫曼树及构造 1 哈夫曼树的概念 哈夫曼树的概念 路径：从一个祖先结点到子孙结点之间的分支构成这两个结点间的路径； 路径长度：路径上的分支数目称为路径长度； 结点的权：根据应用的需要可以给树的结点赋权值； 结点的带权路径长度：从根到该结点的路径长度与该结点权的乘积； 树的带权路径长度=树中所有叶子结点的带权路径之和； 通常记作 WPL= ∑ wi × Li 哈夫曼树：假设有n个权值(w1 , w2 , … , wn )，构造有n个叶子结点的二叉 树，每个叶子结点有一个 wi 作为它的权值。则带权路径长度最小的二叉 树称为哈夫曼树。 哈夫曼树。 哈夫曼树
a: b: c: d: e: f: g: h: 0000 0001 0010 0011 010 011 10 11
结束
g e a b c d f
h
第 12 页
如何得到使二进制 串总长最短编码
应用中每个字符的使用频率是不一样的。显然，为使传输的二进制 串尽可能的短，使用频率高的字符用较短编码，使用频率低的字符用较 长的编码。如何使得电文最短呢？这就希望常用的字符编码尽可能的短。 统计语言各个字符的使用频度Wi，利用哈夫曼树就可以对这种语言 定义出一种最优的编码，使∑WiLi最小（电文最短）。
结束
第 13 页
2．哈夫曼编码 目的：得到使报文最短的前缀码表 途径：构造哈夫曼树 依据：字符的使用频度