立体几何练习题
- 格式:doc
- 大小:2.06 MB
- 文档页数:13

立体几何小题专练1.设,,l m n 是空间三条不同的直线,,αβ是空间两个不重合的平面,给出下列四个命题: ①若l 与m 异面,m ∥n ,则l 与n 异面;②若l ∥α,α∥β,则l ∥β;③若αβ⊥,l α⊥,m β⊥,则l m ⊥;④若m ∥α,m ∥n ,则n ∥α. 其中正确命题的序号有 .(请将你认为正确命题的序号都填上) 2.点P 在正方形ABCD 所在平面外,PA ⊥平面ABCD ,AB PA =,则PB 与AC 所成角的大小是 .3.下列说法中,错误的个数有________个:①平行于同一条直线的两个平面平行. ②平行于同一个平面的两个平面平行.③一个平面与两个平行平面相交,交线平行.④一条直线与两个平行平面中的一个相交,则必与另一个平面相交.A .0个B .1个C .2个D .3个4.如图所示,四棱锥P ﹣ABCD 的底面是边长为a 的正方形,侧棱PA ⊥底面ABCD ,且BE ⊥PC 于E ,PA=a ,,点F 在线段AB 上,并有EF ∥平面PAD .则= .5.设α、β、γ是三个不同的平面,l 、m 、n 是三条不同的直线,则β⊥m 的一个充分条件为 .①l m l ⊥=⊥,,βαβα ; ②αβα⊥⊥⊥m n n ,,;③βγβαγα⊥⊥=,,m ; ④γβγαα⊥⊥⊥,,m .6.如图,PA ⊥圆O 所在的平面,AB 是圆O 的直径,C 是圆O 上的一点,E 、F 分别是点A 在PB 、PC 上的射影,给出下列结论:①AF ⊥PB ;②EF ⊥PB ;③AF ⊥BC ;④AE ⊥平面PBC ;⑤PBC PAC ⊥平面平面.其中正确命题的序号是 .7.底面边长为2,高为1的正三棱锥的表面积为__________.8.已知直三棱柱111ABC A B C -的各项点都在同一球面上,若012,90AB AC AA BAC ===∠=,则该球的体积等于___________.9.在正三棱锥V —ABC 内,有一半球,其底面与正三棱锥的底面重合,且与正三棱锥的三个侧面都相切,若半球的半径为2,则正三棱锥的体积最小时,其高等于__________.10.已知一圆锥的侧面展开图是半径为2的半圆,则该圆锥的体积为 。
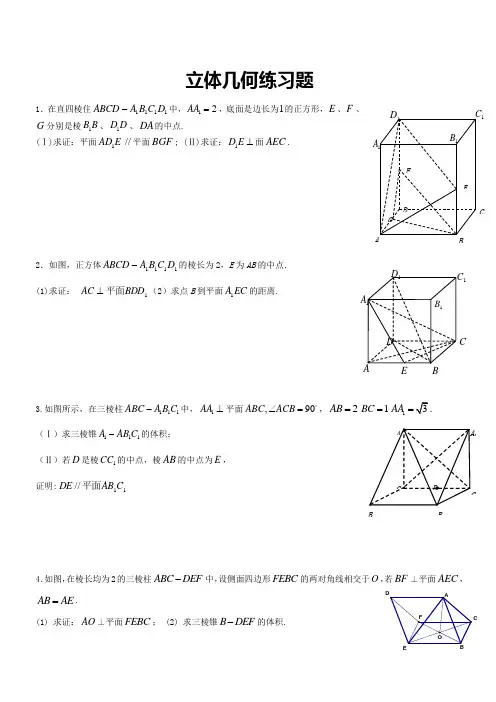
E立体几何练习题1.在直四棱住1111D C B A ABCD -中,12AA =,底面是边长为1的正方形,E 、F 、G 分别是棱B B 1、D D 1、DA 的中点.(Ⅰ)求证:平面E AD 1//平面BGF ; (Ⅱ)求证:1D E ⊥面AEC .2.如图,正方体1111D C B A ABCD -的棱长为2,E 为AB 的中点. (1)求证: 1BDD AC 平面⊥(2)求点B 到平面EC A 1的距离.3.如图所示,在三棱柱111ABC A B C -中,1AA ⊥平面,90ABCACB ∠=,2AB =1BC =1AA =. (Ⅰ)求三棱锥111A AB C -的体积;(Ⅱ)若D 是棱1CC 的中点,棱AB 的中点为E , 证明:11//C AB DE 平面4.如图,在棱长均为2的三棱柱ABC DEF -中,设侧面四边形FEBC 的两对角线相交于O ,若BF ⊥平面AEC ,AB AE =.(1) 求证:AO ⊥平面FEBC ; (2) 求三棱锥B DEF -的体积.FEABD CG 1C 1A1B 1D 1B 1C ED CBA1D 1A5.如图,在体积为1的三棱柱111C B A ABC -中,侧棱⊥1AA 底面ABC ,AB AC ⊥, 11==AA AC ,E 为线段AB 上的动点.(Ⅰ)求证: CA 1C CA 11⊥C 1E ;(2)线段AB 上是否存在一点E ,使四面体E-AB 1C 1的体积为61若存在,请确定点E 的位置;若不存在,请说明理由.6.已知三棱柱ABC —A 1B 1C 1的直观图和三视图如图所示,其主视图BB 1A 1A 和侧视图A 1ACC 1均为矩形,其中AA 1=4。
俯视图ΔA 1B 1C 1中,B 1C 1=4,A 1C 1=3,A 1B 1=5,D 是AB 的中点。
(1)求证:AC ⊥BC 1; (2)求证:AC 1∥平面CDB 1;(3)求异面直线AC 1与B 1C 所成角的余弦值。

立体几何大题专练1、如图,已知PA ⊥矩形ABCD 所在平面,M 、N 分别为AB 、PC 的中点; (1)求证:MNP ABC -,E F ,AC BC //EF PAB PAC ⊥ABC PA PC =90ABC ∠=︒PEF ⊥PBCEF Q E F AC BC //EF AB ∴ ……………………2分 又⊄EF 平面PAB ,⊆AB 平面PAB ,∴ EF ∥平面PAB . ……………………5分(2)PA PC =Q ,E 为AC 的中点,PE AC ∴⊥ ……………………6分 又Q 平面PAC ⊥平面ABCPE ∴⊥面ABC ……………………8分 PE BC ∴⊥……………………9分PAC EBF又因为F 为BC 的中点,//EF AB ∴090,BC EF ABC ⊥∠=∴Q ……………………10分EF PE E =Q IBC ∴⊥面PEF ……………………11分 又BC ⊂Q 面PBC∴面PBC ⊥面PEF ……………………12分3. 如图,在直三棱柱ABC —A 1B 1C 1中,AC=BC ,点D 是AB 的中点。
(1)求证:BC 1PC AB N M ABCD PA 、分别是、所在的平面,矩形⊥PAD MN 平面//CD MN ⊥图,正方形ABCD 所在的平面与三角形AD E所在平面互相垂直,△AEB是等腰直角三角形,且AE=ED 设线段BC 、AE 的中点分别为F 、M ,求证:(1)FM ∥ECD 平面; (2)求二面角E-BD—A的正切值.(1)证明:取AD 的中点N,连结FN,MN,则MN ∥ED ,FN ∥CD∴平面FMN ∥平面ECD. ∵ MF 在平面FMN 内,∴ FM ∥平面ECD ......5分 (2)连接EN, ∵AE=ED ,N 为AD 的中点,NMPDCBA∴ EN⊥AD.又∵面ADE⊥面ABCD,∴EN⊥面ABCD.作NP⊥BD,连接EP,则EP⊥BD,∴∠EPN即二面角E-BD-A的平面角,设AD=a,∵ABCD为正方形,⊿ADE为等腰三角形,∴EN=12a,NP=24a.∴tan∠EPN=2. ......10分7.如图,一个圆锥的底面半径为2cm,高为6cm,其中有一个高为x cm的内接圆柱.(1)试用x表示圆柱的侧面积;(2)当x为何值时,圆柱的侧面积最大.19.(1)解:设所求的圆柱的底面半径为r则有662xr-=,即32xr-=.∴2324)32(22xxxxrxSππππ-=-==圆柱侧.......5分(2)由(1)知当3)32(24=--=ππx时,这个二次函数有最大值为π6所以当圆柱的高为3cm时,它的侧面积最大为26cmπ......10分8.(10分)如图,在三棱锥P ABC-中,⊿PAB是等边三角形,∠PAC=∠PBC=90 o.(1)证明:AB⊥PC;(2)若4PC=,且平面PAC⊥平面PBC,求三棱锥P ABC-体积.解:(1)因为PAB ∆是等边三角形,90PAC PBC ∠=∠=︒, 所以Rt PBC Rt PAC ∆≅∆,可得AC BC =。

高三数学立体几何专项练习题及答案一、选择题1. 下列哪个几何体的所有面都是三角形?A. 正方体B. 圆柱体C. 正六面体D. 球体答案:C2. 一个有8个面的多面体,其中6个面是正方形,另外2个面是等边三角形,它的名字是?A. 正八面体B. 正十二面体C. 正二十面体D. 正二十四面体答案:C3. 空间中任意一点到四个角落连线的垂直距离相等的四棱锥称为?A. 正四棱锥B. 圆锥台C. 四棱锥D. 无法确定答案:C4. 任意多面体的面数与顶点数、棱数的关系是?A. 面数 + 顶点数 = 棱数 + 2B. 面数 + 棱数 = 顶点数 + 2C. 顶点数 + 棱数 = 面数 + 2D. 顶点数 + 面数 = 棱数 + 2答案:A5. 求下列多面体的棱数:(1)正六面体(2)正八面体(3)正十二面体答案:(1)正六面体的棱数为 12(2)正八面体的棱数为 24(3)正十二面体的棱数为 30二、填空题1. 下列说法正确的是:一棱锥没有底面时,它的底面是一个______。
答案:点2. 铅垂线是指从一个多面体的一个顶点到与它相对的棱上所作的垂线,它与该棱垂足的连线相交于该多面体的______上。
答案:中点3. 对正八面体,下列说法不正确的是:_____条对角线与_____两两垂直。
答案:六,相邻面三、计算题1. 一个棱锥的底面是一个边长为6cm的正三角形,其高为8cm。
求棱锥体积。
解答:底面积 S = (1/2) ×底边长 ×高 = (1/2) × 6 × 8 = 24 cm²棱锥体积 V = (1/3) × S ×高 = (1/3) × 24 × 8 = 64 cm³所以,棱锥的体积为64 cm³。
2. 一个正四棱锥的底面是一个边长为10cm的正方形,其高为12cm。
求四棱锥的体积。
解答:底面积 S = 边长² = 10² = 100 cm²四棱锥体积 V = (1/3) × S ×高 = (1/3) × 100 × 12 = 400 cm³所以,四棱锥的体积为400 cm³。

高中数学立体几何经典题型练习题集学校:______姓名:_____班级:______考号:______一.单选题1.正三棱锥的底边长和高都是2,则此正三棱锥的斜高长度为()A.B.C.D.2.在棱长为1的正方体ABCD-A1B1C1D1中,若E,F,G分别为C1D1,AA1,BB1的中点,则空间四边形EFBG在正方体下底面ABCD上的射影面积为()A.1B.C.D.3.一个棱柱是正四棱柱的条件是()A.底面是正方形,有两个侧面是矩形B.底面是正方形,有两个侧面垂直于底面C.底面是菱形,且有一个顶点处的三条棱两两垂直D.每个侧面都是全等矩形的四棱柱4、如图,P是正方体ABCD-A1B1C1D1对角线AC1上一动点,设AP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是()A.B.C.D.5、如图所示,AB是圆O的直径,C是异于A,B两点的圆周上的任意一点,PA垂直于圆O 所在的平面,则△PAB,△PAC,△ABC,△PBC中,直角三角形的个数是()A.1B.2C.3D.46、如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是棱A1B1、BB1、B1C1的中点,则下列结论中:①FG⊥BD;②B1D⊥面EFG;③面EFG∥面ACC1A1;④EF∥面CDD1C1.正确结论的序号是()A.①和②B.③和④C.①和③D.②和④7、三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是()A.B.C.D.8、正方体的直观图如图所示,则其展开图是()A.B.C.D.二.填空题(共__小题)9、如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的中点,并且AC⊥BD,AC=m,BD=n,则四边形EFGH的面积为______.10、如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,给出下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°;⑤直线PD 与平面PAB所成角的余弦值为.其中正确的有______(把所有正确的序号都填上).11.如图所示,三棱锥M,PA⊥底面ABC,∠ABC=90°,则此三棱锥P-ABC中直角三角形有______个.12、如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1,有下述结论(1)AC1⊥BC;(2)=1;(3)二面角F-AC1-C的大小为90°;(4)三棱锥D-ACF的体积为.正确的有______.13.各棱长为a的正三棱柱的六个顶点都在同一个球面上,则此球的表面积为______.14.一四棱锥被平行于底面的平面所截,若截面面积与底面面积之比为1:4,则此截面把一条侧棱分成的两段之比为______.15、如图所示正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F且EF=,给出下列五个结论①AC⊥BE②EF∥平面ABCD③异面直线AE,BF所成的角为60°④A1点到面BEF的距离为定值⑤三棱柱A-BEF的体积为定值其中正确的结论有:______(写出所有正确结论的编号)三.简答题(共__小题)16、如图,立体图形A-BCD的四个面分别为△ABC、△ACD、△ADB和△BCD,E、F、G分别是线段AB、AC、AD上的点,且满足AE:AB=AF:AC=AG:AD,求证:△EFG∽△BCD.17、如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC 的中点,F在棱AC上,且AF=3FC.(1)求三棱锥D-ABC的表面积;(2)求证AC⊥平面DEF;(3)若M为BD的中点,问AC上是否存在一点N,使MN∥平面DEF?若存在,说明点N 的位置;若不存在,试说明理由.参考答案一.单选题(共__小题)1.正三棱锥的底边长和高都是2,则此正三棱锥的斜高长度为()A.B.C.D.答案:D解析:解:在正三棱锥中,顶点P在底面的射影为底面正三角形的中心O,延长A0到E,则E为BC的中点,连结PE,则PE为正三棱锥的斜高.∵正三棱锥的底边长和高都是2,∴AB=PO=2,即AE=,OE=,∴斜高PE==,故选:D.2、在棱长为1的正方体ABCD-A1B1C1D1中,若E,F,G分别为C1D1,AA1,BB1的中点,则空间四边形EFBG在正方体下底面ABCD上的射影面积为()A.1B.C.D.答案:B解析:解:过E点做EH垂直CD于H,连接EH,易得H即为E在平面ABCD上的射影,连接AH,BH,如下图所示则AH,BH,AB分别为FE,EG,FB在平面ABCD上的射影,又由G在平面ABCD上的射影为B,故△ABH即为空间四边形EFBG在正方体下底面ABCD上的射影∵S△ABH=S ABCD=故选B3.一个棱柱是正四棱柱的条件是()A.底面是正方形,有两个侧面是矩形B.底面是正方形,有两个侧面垂直于底面C.底面是菱形,且有一个顶点处的三条棱两两垂直D.每个侧面都是全等矩形的四棱柱答案:C解析:解:上、下底面都是正方形,且侧棱垂直于底面的棱柱叫做正四棱柱.故A和B错在有可能是斜棱柱,D错在上下底面有可能不是正方形,底面是菱形,且有一个顶点处的三条棱两两垂直能保证上、下底面都是正方形,且侧棱垂直于底面.故选C.4、如图,P是正方体ABCD-A1B1C1D1对角线AC1上一动点,设AP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是()A.B.C.D.答案:A解析:解:设正方体的棱长为1,连接AC交BD于O,连PO,则PO是等腰△PBD的高,故△PBD的面积为f(x)=BD×PO,在三角形PAO中,PO==,∴f(x)=××=,画出其图象,如图所示,对照选项,A正确.故选A.5、如图所示,AB是圆O的直径,C是异于A,B两点的圆周上的任意一点,PA垂直于圆O所在的平面,则△PAB,△PAC,△ABC,△PBC中,直角三角形的个数是()A.1B.2C.3D.4答案:D解析:证明:∵AB是圆O的直径∴∠ACB=90°即BC⊥AC,三角形ABC是直角三角形又∵PA⊥圆O所在平面,∴△PAC,△PAB是直角三角形.且BC在这个平面内∴PA⊥BC 因此BC垂直于平面PAC中两条相交直线,∴BC⊥平面PAC,∴△PBC是直角三角形.从而△PAB,△PAC,△ABC,△PBC中,直角三角形的个数是,4.故选D.6、如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是棱A1B1、BB1、B1C1的中点,则下列结论中:①FG⊥BD;②B1D⊥面EFG;③面EFG∥面ACC1A1;④EF∥面CDD1C1.正确结论的序号是()A.①和②B.③和④C.①和③D.②和④答案:D解析:解:如图连接A1C1、A1B、BC1、BD、B1D,因为E、F、G分别是棱A1B1、BB1、B1C1的中点对于①因为FG∥BC1,△BDC1是正三角形,FG⊥BD,不正确.对于②因为平面A1C1B∥平面EFG,并且B1D⊥平面A1C1B,所以B1D⊥面EFG,正确.③面EFG∥面ACC1A1;显然不正确.④EF∥平面CDD1C1内的D1C,所以EF∥面CDD1C1.正确.故选D7、三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是()A.B.C.D.答案:D解析:解:三棱锥P-ABC中,PC⊥面ABC,AB⊂平面ABC,∴PC⊥AB;又AB⊥BC,BC∩PC=C,∴AB⊥平面PBC;又CH⊂平面PBC,∴AB⊥CH,又CH⊥PB,PB∩AB=B,∴CH⊥平面PAB,又DH⊂平面PAB,∴CH⊥DH;又△PAC是等腰直角三角形,且PA=4,D是PA的中点,∴CD=PA=2,设CH=a,DH=b,则a2+b2=CD2=4,∴4=a2+b2≥2ab,即ab≤1,当且仅当a=b=时,“=”成立,此时△CDH的面积最大;在Rt△PBC,设BC=x,则PB===,∴PC•BC=PB•CH,即2•x=•;解得x=,∴CB的长是.故选:D.8、正方体的直观图如图所示,则其展开图是()A.B.C.D.答案:D解析:解:根据题意,可得对于A,展开图中的上下两边的正方形的对边中点连线应该呈左右方向显现,故A的图形不符合题意;对于B,展开图中最右边的“日”字形正方形的对边中点连线应该是上下方向呈现,且应该在含有圆形的正方形的左边放置,故B的图形不符合题意;对于C,展开图中最右边的正方形应该与含有圆形的正方形相邻,故C的图形不符合题意;对于D,沿如图的红线将正方体的侧面剪裁,展开可得如D项图的形状,故D的图形符合题意故选:D二.填空题(共__小题)9、如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的中点,并且AC⊥BD,AC=m,BD=n,则四边形EFGH的面积为______.答案:解析:解:由ABCD是空间四边形,E、F、G、H分别是四边上的中点,并且AC⊥BD,可得四边形EFGH为矩形,且此矩形的长和宽分别为和,故四边形EFGH的面积为=,故答案为:.10、如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,给出下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°;⑤直线PD与平面PAB所成角的余弦值为.其中正确的有______(把所有正确的序号都填上).答案:①④⑤解析:解:对于①、由PA⊥平面ABC,AE⊂平面ABC,得PA⊥AE,又由正六边形的性质得AE⊥AB,PA∩AB=A,得AE⊥平面PAB,又PB⊂平面PAB,∴AE⊥PB,①正确;对于②、又平面PAB⊥平面ABC,所以平面ABC⊥平面PBC不成立,②错;对于③、由正六边形的性质得BC∥AD,又AD⊂平面PAD,∴BC∥平面PAD,∴直线BC∥平面PAE也不成立,③错;对于④、在Rt△PAD中,PA=AD=2AB,∴∠PDA=45°,∴④正确;对于⑤、由于DE∥AB,∴D到平面PAB的距离即为E到平面PAB的距离,即E到直线PA的距离,即EA,EA=AB,在Rt△PAD中,PA=AD=2AB,∴PD=2AB,∴直线PD与平面PAB所成角的正弦值为=,∴直线PD与平面PAB所成角的余弦值为=,∴⑤正确.故答案为:①④⑤.11.如图所示,三棱锥M,PA⊥底面ABC,∠ABC=90°,则此三棱锥P-ABC中直角三角形有______个.答案:4解析:解:由已知PA⊥底面ABC,∠ABC=90°,所以CB⊥PA,CB⊥AB,又PA∩AB=A,所以CB⊥平面PAB,所以CB⊥PB,所以此三棱锥P-ABC中直角三角形有△ABC,△ABP,△ACP,△PBC共有4个.故答案为:4.12、如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1,有下述结论(1)AC1⊥BC;(2)=1;(3)二面角F-AC1-C的大小为90°;(4)三棱锥D-ACF的体积为.正确的有______.答案:(2)(3)(4)解析:解:(1)连接AB1,则∠B1C1A即为BC和AC1所成的角,在三角形AB1C1中,B1C1=2,AB1=2,AC1=2,cos∠B1C1A==,故(1)错;(2)连接AF,C1F,则易得AF=FC1=,又FD⊥AC1,则AD=DC1,故(2)正确;(3)连接CD,则CD⊥AC1,且FD⊥AC1,则∠CDF为二面角F-AC1-C的平面角,CD=,CF=,DF===,即CD2+DF2=CF2,故二面角F-AC1-C的大小为90°,故(3)正确;(4)由于CD⊥AC1,且FD⊥AC1,则AD⊥平面CDF,则V D-ACF=V A-DCF=•AD•S△DCF=×××=.故(4)正确.故答案为:(2)(3)(4)13.各棱长为a的正三棱柱的六个顶点都在同一个球面上,则此球的表面积为______.答案:解析:解:∵正三棱柱的六个顶点都在同一个球面上,所以球心在上下底面中心的连线的中点上,AB=a,OA=R,在△OEA中,OE=,AE=,∵AO2=OE2+AE2,∴,∴球的表面积为4πR2=,故答案为.14.一四棱锥被平行于底面的平面所截,若截面面积与底面面积之比为1:4,则此截面把一条侧棱分成的两段之比为______.答案:1:1解析:解:根据题意,设截得小棱锥的侧棱长为l,原棱锥的侧棱长为L,∵截面与底面相似,且截面面积与底面面积之比为1:4,∴相似比为:==,∴截面把棱锥的一条侧棱分成的两段之比是l:(L-l)=1:1.故答案为:1:1.15、如图所示正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F且EF=,给出下列五个结论①AC⊥BE②EF∥平面ABCD③异面直线AE,BF所成的角为60°④A1点到面BEF的距离为定值⑤三棱柱A-BEF的体积为定值其中正确的结论有:______(写出所有正确结论的编号)答案:①②④⑤解析:解:①AC⊥BE,由题意及图形知,AC⊥面DD1B1B,故可得出AC⊥BE,此命题正确;②EF∥平面ABCD,由正方体ABCD-A1B1C1D1的两个底面平行,EF在其一面上,故EF与平面ABCD无公共点,故有EF∥平面ABCD,此命题正确;③由图知,当F与B1重合时,令上底面顶点为O,则此时两异面直线所成的角是∠A1AO,当E与D1重合时,此时点F与O重合,则两异面直线所成的角是∠OBC1,此二角不相等,故异面直线AE、BF所成的角不为定值,故不正确.④A1点到面DD1B1B距离是定值,所以A1点到面BEF的距离为定值,正确;⑤三棱锥A-BEF的体积为定值,由几何体的性质及图形知,三角形BEF的面积是定值,A点到面DD1B1B距离是定值,故可得三棱锥A-BEF的体积为定值,此命题正确.故答案为:①②④⑤.三.简答题(共__小题)16、如图,立体图形A-BCD的四个面分别为△ABC、△ACD、△ADB和△BCD,E、F、G分别是线段AB、AC、AD上的点,且满足AE:AB=AF:AC=AG:AD,求证:△EFG∽△BCD.答案:证明:在△ABD中,∵AE:AB=AG:AD,∴EG∥BD.同理,GF∥DC,EF∥BC.又∠GEF与∠DBC方向相同.∴∠GEF=∠DBC.同理,∠EGF=∠BDC.∴△EFG∽△BCD.17、如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC.(1)求三棱锥D-ABC的表面积;(2)求证AC⊥平面DEF;(3)若M为BD的中点,问AC上是否存在一点N,使MN∥平面DEF?若存在,说明点N 的位置;若不存在,试说明理由.答案:解:(1)∵AB⊥平面BCD,∴AB⊥BC,AB⊥BD.∵△BCD是正三角形,且AB=BC=a,∴AD=AC=.设G为CD的中点,则CG=,AG=.∴,,.三棱锥D-ABC的表面积为.(2)取AC的中点H,∵AB=BC,∴BH⊥AC.∵AF=3FC,∴F为CH的中点.∵E为BC的中点,∴EF∥BH.则EF⊥AC.∵△BCD是正三角形,∴DE⊥BC.∵AB⊥平面BCD,∴AB⊥DE.∵AB∩BC=B,∴DE⊥平面ABC.∴DE⊥AC.∵DE∩EF=E,∴AC⊥平面DEF.(3)存在这样的点N,当CN=时,MN∥平面DEF.连CM,设CM∩DE=O,连OF.由条件知,O为△BCD的重心,CO=CM.∴当CF=CN时,MN∥OF.∴CN=.。

高中立体几何练习题几何学是数学中非常重要的一个分支,而立体几何则是其中的一个重要部分。
在高中阶段,学生需要掌握各种与立体几何相关的概念和定理,并且能够运用这些知识解决实际问题。
本文将为大家提供一些高中立体几何的练习题,以帮助大家巩固知识和提高解题能力。
练习题一:三棱柱1. 一个三棱柱的底面是一个等边三角形,边长为8cm,高度为10cm。
求该三棱柱的体积和表面积。
2. 一个三棱柱的体积是72cm³,底面边长为6cm。
求该三棱柱的高度和表面积。
练习题二:四棱柱和四棱锥1. 一个正四棱柱的底面是一个边长为4cm的正方形,高度为6cm。
求该四棱柱和与之相似的正四棱锥的体积比值。
2. 一个四棱柱的底面是一个边长为10cm的正方形,高度为8cm。
求该四棱柱和与之相似的四棱锥的表面积比值。
练习题三:球体和圆柱1. 一个半径为4cm的球从中间切割,得到两个半球。
求这两个半球的表面积之和。
2. 一个圆柱的底面半径为3cm,高度为10cm。
在底面上画一个直径,求这个直径与圆柱的侧面交点处的高度和侧面的面积。
练习题四:棱台和棱锥1. 一个棱台的上底是一个边长为6cm的正三角形,下底是一个边长为12cm的正六边形,高度为8cm。
求该棱台的体积和表面积之和。
2. 一个棱台的上底是一个边长为8cm的正方形,下底是一个边长为12cm的正六边形,高度为10cm。
求该棱台的体积和表面积的比值。
以上仅为一些高中立体几何的练习题,希望能够帮助大家巩固知识并提高解题能力。
在解答这些题目时,可以根据已学习的定理和公式进行计算,并注意单位和精度的问题。
同时也要灵活运用几何思维和建模能力,将实际问题转化为几何图形,从而更好地解决问题。
祝各位同学在立体几何学习中取得好成绩!。

高中数学立体几何专项练习题及答案一、选择题1. 下面哪个选项不是描述柱体的特点?A. 体积恒定B. 底面形状不限C. 侧面是矩形D. 顶面和底面平行答案:A2. 如果一个四面体的一个顶点的对边垂直于底面,那么这个四面体是什么类型?A. 正方形四面体B. 倒立四面体C. 锥体D. 正方锥体答案:C3. 以下哪个选项正确描述了一个正方体的特点?A. 全部面都是正方形B. 12 条棱长度相同C. 8 个顶点D. 6 个面都是正方形答案:D4. 若长方体的高度是 6cm,底面积是 5cm²,底面对角线长为 a cm,那么 a 的值为多少?A. √11B. √29C. √31D. √41答案:C二、填空题1. 一个正方体的棱长为 4cm,它的体积是多少?答案:64cm³2. 一个球的表面积是100π cm²,那么它的半径是多少?答案:5cm3. 一个圆柱体的底面半径为 3cm,高度为 8cm,它的体积是多少?答案:72π cm³4. 一个圆锥的底面半径为 6cm,高度为 10cm,它的体积是多少?答案:120π cm³三、计算题1. 一个四棱锥的底面是边长为 5cm 的正方形,高度为 8cm,它的体积是多少?答案:单位为 cm³,计算过程如下:首先计算底面积:5cm * 5cm = 25cm²再计算体积:25cm² * 8cm / 3 = 200cm³2. 一个圆柱体的底面直径为 12cm,高度为 15cm,它的体积是多少?答案:单位为 cm³,计算过程如下:首先计算底面半径:12cm / 2 = 6cm再计算底面积:π * 6cm * 6cm = 36π cm²最后计算体积:36π cm² * 15cm = 540π cm³3. 一个球的直径为 8cm,它的体积是多少?答案:单位为 cm³,计算过程如下:首先计算半径:8cm / 2 = 4cm再计算体积:4/3 * π * 4cm * 4cm * 4cm = 268.08π cm³4. 一个圆锥的底面半径为 10cm,高度为 20cm,它的体积是多少?答案:单位为 cm³,计算过程如下:首先计算底面积:π * 10cm * 10cm = 100π cm²最后计算体积:100π cm² * 20cm / 3 = 2000π cm³四、解答题1. 若一个长方体的长度、宽度、高度分别为 a、b、c,它的表面积为多少?答案:单位为 cm²,计算过程如下:首先计算侧面积:2 * (a * b + a * c + b * c)再计算底面积:a * b最后计算表面积:2 * (a * b + a * c + b * c) + a * b2. 一个四棱锥的底面为边长为 a 的正三角形,高度为 h,求这个四棱锥的体积。
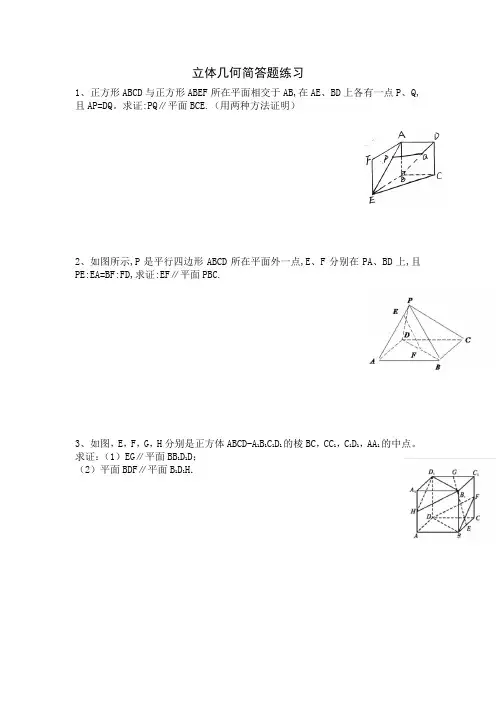
立体几何简答题练习1、正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q,且AP=DQ。
求证:PQ∥平面BCE.(用两种方法证明)2、如图所示,P是平行四边形ABCD所在平面外一点,E、F分别在PA、BD上,且PE:EA=BF:FD,求证:EF∥平面PBC.3、如图,E,F,G,H分别是正方体ABCD-A1B1C1D1的棱BC,CC1,C1D1,AA1的中点。
求证:(1)EG∥平面BB1D1 D;(2)平面BDF∥平面B1D1 H.4、如图所示,已知P 是平行四边形ABCD 所在平面外一点,M 、N 分别为AB 、PC 的中点,平面PAD ∩平面PBC =l. (1)求证:l ∥BC ;(2)MN 与平面PAD 是否平行?试证明你的结论。
5、如图,在四棱锥S-ABCD 中,底面ABCD 是正方形,SA ⊥底面ABCD ,SA=SB ,点M 是SD 的中点,AN ⊥SC ,且交SC 于点N 。
(1)求证:SB ∥平面ACM ;(2)求证:平面SAC ⊥平面AMN ; (3)求二面角D-AC-M 的余弦值。
6、如图,在四棱锥P-ABCD 中,底面ABCD 是边长为2的正方形,侧面PAD ⊥底面ABCD,且PA=PD=22AD,E 、F 分别为PC 、BD 的中点. 求证:(1) 求证:EF ∥平面PAD; (2) 求证:平面PAB ⊥平面PDC;(3) 在线段AB 上是否存在点G,使得二面角C-PD-G 的余弦值为31?说明理由.7、如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点。
(1)求证:C1M∥平面A1ADD1;(2)若CD1垂直于平面ABCD且CD1=3,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值。
8、如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点.(1)证明:PA∥平面EDB;(2)证明:BC⊥DE.9、三棱柱ABC﹣A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.(Ⅰ)求证:MN||平面BCC1B1;(Ⅰ)求证:平面AMN⊥平面A1B1C.10、如图,在三棱锥P﹣ABC中,PA⊥PC,AB=PB,E,F分别是PA,AC的中点.求证:(1)EF∥平面PBC;(2)平面BEF⊥平面PAB.11、如图所示,四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥平面ABCD,点M,N分别是AB,PC的中点,且PA=AD(1)求证:MN∥平面PAD(2)求证:平面PMC⊥平面PCD.12、如图,在直三棱柱ABC﹣A1B1C1中,BC⊥AC,D,E分别是AB,AC的中点.(1)求证:B1C1∥平面A1DE;(2)求证:平面A1DE⊥平面ACC1A1.8、如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.△PAD为正三角形,其所在平面垂直于底面ABCD.若G为AD 边的中点,求证:平面PBG⊥平面PAD;9、如图所示,在四棱柱P-ABCD中,底面ABCD是边长为a菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD。

1.如图,在四棱锥P﹣ABCD中,CB⊥平面PAB,AD∥BC,且PA=PB=AB=BC=2AD=2.(Ⅰ)求证:平面DPC⊥平面BPC;(Ⅱ)求二面角C﹣PD﹣B的余弦值.2.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为菱形,且PA=AD=2,,E、F分别为AD、PC中点.(1)求点F到平面PAB的距离;(2)求证:平面PCE⊥平面PBC;(3)求二面角E﹣PC﹣D的大小.3.《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑;(2)若面DEF与面ABCD所成二面角的大小为,求的值.4.如图所示三棱柱中,平面,四边形为平行四边形,,.(Ⅰ)若,求证:平面;(Ⅱ)若与所成角的余弦值为,求二面角的余弦值.5.在直角梯形中,,现把它沿折起,得到如图所示的几何体,连接,使(1)求证:平面平面;(2)判断在线段上是否存在一点,使得二面角的余弦值为,若存在,确定的位置,若不存在,说明理由.6.如图,四棱锥中,底面为平行四边形,,,底面.(1)证明:平面平面;(2)若二面角的大小为,求与平面所成角的正弦值.7.在三棱锥中,,在底面内作,且(1)求证:平面;(2)如果二面角的大小为,求二面角的余弦值.8.如图,在四棱锥中,底面为正方形,⊥底面,,为棱中点.(1)求证:⊥平面;(2)若为中点,,试确定的值,使二面角的余弦值为.9.如图,在三棱柱中,点在平面内的射影点为的中点.(1)求证:平面;(2)求二面角的正弦值.10.已知多面体如图所示.其中为矩形,为等腰直角三角形,,四边形为梯形,且,,.(1)若为线段的中点,求证:平面. (2)线段上是否存在一点,使得直线与平面所成角的余弦值等于?若存在,请指出点的位置;若不存在,请说明理由.11.在如图所示的几何体中,平面平面,四边形是菱形,四边形是矩形,,,,是的中点.(Ⅰ)求证:平面; (II)在线段上是否存在点,使二面角的大小为?若存在,求出的长;若不存在,请说明理由.12.如图,已知梯形CDEF 与△ADE 所在平面垂直,AD ⊥DE ,CD ⊥DE ,AB ∥CD ∥EF ,AE=2DE=8,AB=3,EF=9.CD=12,连接BC ,BF .(Ⅰ)若G 为AD 边上一点,DG=DA ,求证:EG ∥平面BCF ; (Ⅱ)求二面角E ﹣BF ﹣C 的余弦值.NM DCE B A13.如图三棱柱中,侧面为菱形,.(1)证明:;(2)若,,,求二面角的余弦值.14.如图,在三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=2,A1A=4,A1在底面ABC的射影为BC的中点,D是B1C1的中点.(1)证明:A1D⊥平面A1BC;(2)求二面角A1﹣BD﹣B1的平面角的余弦值.15.如图,在四棱锥中,底面为菱形,为的中点.(Ⅰ)若,求证:平面平面;(Ⅱ)若平面平面,且,点在线段上,试确定点的位置,使二面角大小为,并求出的值.16.已知在边长为4的等边△ABC(如图1所示)中,MN∥BC,E为BC的中点,连接AE交MN于点F,现将△AMN沿MN折起,使得平面AMN⊥平面MNCB(如图2所示).(1)求证:平面ABC⊥平面AEF;(2)若S BCNM=3S△AMN,求直线AB与平面ANC所成角的正弦值.17.如图(1),在五边形中,,,,,是以为斜边的等腰直角三角形.现将沿折起,使平面平面,如图(2),记线段的中点为.(1)求证:平面平面;(2)求平面与平面所成的锐二面角的大小.18.如图,在等腰梯形中,,,,四边形为矩形,平面平面,.(1)求证:平面;(2)点在线段上运动,设平面与平面二面角的平面角为,试求的取值范围.。

立体几何题型一、平行与垂直的证明例1.如图,在四棱锥P —ABCD 中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD =DC ,E 是PC 的中点,作EF ⊥PB 交PB 于点F . (1)证明PA //平面EDB ;(2)证明PB ⊥平面EFD例2.四棱锥S A B C D -中,底面ABCD 为平行四边形,侧面SB C ⊥底面ABCD ,已知45A B C ∠=︒,2A B =,BC =SA SB ==(Ⅰ)证明:SA B C ⊥;(Ⅱ)求直线SD 与平面SBC 所成角的大小. 变式:已知四棱锥P -ABCD 的底面为直角梯形,AB ∥DC ,⊥=∠PA DAB ,90底面ABCD ,且PA =AD =DC =21AB =1,M 是PB 的中点.(Ⅰ)证明:面PAD ⊥面PCD ; (Ⅱ)求AC 与PB 所成的角;(Ⅲ)求面AMC 与面BMC 所成二面角的大小.ACDBCASOE A DCBNM EP题型二、空间角与距离例3.如图,在四棱锥O A B C D -中,底面A B C D 四边长为1的 菱形,4A B C π∠=, OA ABCD ⊥底面, 2O A =,M 为O A 的中点。
(Ⅰ)求异面直线AB 与MD 所成角的大小; (Ⅱ)求点B 到平面OCD 的距离。
例4. 如图,四面体ABCD 中,O 、E 分别BD 、BC 的中点,CA =CB =CD =BD =2 (Ⅰ)求证:AO ⊥平面BCD ;(Ⅱ)求异面直线AB 与CD 所成角的大小; (Ⅲ)求点E 到平面的距离. 变式:如图,正三棱锥O A B C -的三条侧棱O A 、O B 、O C 两两垂直,且长度均为2.E 、F 分别是A B 、A C 的中点,H 是E F 的中点,过E F 的平面与侧棱O A 、O B 、O C 或其延长线分别相交于1A 、1B 、1C ,已知132O A =.(1)求证:11B C ⊥面O A H ; (2)求二面角111O A BC --的大小.1C 1A题型三、探索性问题例5.在四棱锥P-ABCD 中,底面ABCD 是矩形,侧棱PA 垂直于底面,E 、F 分别是AB 、PC 的中点.(1)求证://EF 平面PAD ;(2)当平面PCD 与平面ABCD 成多大二面角时,⊥EF 平面PCD ?变式:如图,在三棱锥A -BCD 中,侧面ABD 、ACD 是全等的直角三角形,AD 是公共的斜边,且AD ,BD =CD =1,另一个侧面是正三角形 (1)求证:AD ⊥BC(2)求二面角B -AC -D 的大小(3)在直线AC 上是否存在一点E ,使ED 与面BCD 成30︒角?若存在,确定E 的位置;若不存在,说明理由.DC题型四、折叠、展开问题例6.已知正方形A B C D E 、F 分别是A B 、C D 的中点,将AD E 沿D E 折起,如图所示,记二面角A D E C --的大小为(0)θθπ<< (1) 证明//B F 平面ADE ;(2)若A C D 为正三角形,试判断点A 在平面B C D E 内的射影G 是否在直线E F 上,证明你的结论,并求角θ的余弦值。

立体几何练习题学校 班级 姓名1.已知正四面体ABCD 中,E 是AB 的中点,则异面直线CE 与BD 所成角的余弦值为( )A .16B .36C .13D .33 2.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )A .814π B .16π C .9π D .274π3.已知直三棱柱1116.34ABC A B C O AB AC -==的个顶点都在球的球面上若,,,AB AC ⊥112AA O =,则球的半径为( )。
A .3172 B .210 C .132D .310 4. 已知三棱锥S-ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC为O 的直径,且SC=2,则此棱锥的体积为( )(A )62 (B )63 (C )32 (D )22 5. 已知正四棱柱ABCD- A 1B 1C 1D 1中 ,AB=2,CC 1=22 E 为CC 1的中点,则直线AC 1与平面BED 的距离为( )A 2 B 3 C 2 D 16. 直三棱柱ABC-A 1B 1C 1中,∠BCA=90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC=CA=CC 1,则BM 与AN 所成的角的余弦值为( ) A. 110 B. 25 C. 3010 D. 227.已知正四棱柱1111ABCD A B C D -中,12,22,AB CC E ==为1CC 的中点,则直线1AC与平面BED 的距离为( )。
A .2 B .3 C .2 D .1 8.如图,四棱锥S —ABCD 的底面为正方形,SD ⊥底面ABCD ,则下列结论中不正确的是( ) A .AC ⊥SB B. AB ∥平面SCD C .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D.AB 与SC 所成的角等于DC 与SA 所成的角9. 已知正三棱锥P-ABC ,点P,A,B,C 都在半径为√3的球面上,若PA,PB,PC 两两垂直,则球心到截面ABC 的距离为 。
第九章立体几何与空间向量第1节简单几何体的结构、三视图和直观图一、选择题1.如图是由哪个平面图形旋转得到的( A )解析:根据面动成体的原理即可解,一个直角三角形绕直角边旋转一周可以得到一个圆锥.一个直角梯形绕着直角腰旋转一周得到圆台.该几何体的上部分是圆锥,下部分是圆台,圆锥的轴截面是直角三角形,圆台的轴截面是直角梯形,所以这个几何图形是由直角三角形和直角梯形围绕直角边所在的直线为轴旋转一周得到.故选A.2.已知三棱柱ABC-A1B1C1的6个顶点都在球O的球面上.若AB=3,AC=4, AB⊥AC,AA1=12,则球O的半径为( C )(A) (B)2 (C) (D)3解析:构建长方体的棱长分别为3,4,12.体对角线长为=13,外接球的半径为,故选C.3.用长为4,宽为2的矩形做侧面围成一个圆柱,此圆柱轴截面面积为( B )(A)8 (B)(C)(D)解析:若以4作为圆柱的高、2作为底面圆的周长,则圆柱轴截面面积为;若以2作为圆柱的高、4作为底面圆的周长,则圆柱轴截面面积为,所以此圆柱轴截面面积为.故选B.4.正四棱锥S-ABCD的底面边长为4,高SE=8,则过点A,B,C,D,S的球的半径为( C )(A)3 (B)4 (C)5 (D)6解析:由正四棱锥及其外接球的对称性,球心O在正四棱锥的高线SE上,球半径R=OS=OB,EB=BD=4.所以在直角三角形OEB中,由勾股定理得,(8-R)2+42=R2,解得R=5,故选C.5.三棱锥P-ABC中,△ABC是底面,PA⊥PB,PA⊥PC,PB⊥PC,且这四个顶点都在半径为2的球面上,PA=2PB,则这个三棱锥的三个侧棱长的和的最大值为( B )(A)16 (B)(C)(D)32解析:因为PA,PB,PC两两垂直,又因为三棱锥P-ABC的四个顶点均在半径为1的球面上,所以以PA,PB,PC为棱的长方体的对角线即为球的一条直径.所以16=PA2+PB2+PC2,因为PA=2PB,则这个三棱锥的三个侧棱长的和PA+PB+PC=3PB+PC,因为5PB2+PC2=16,设PB=4cos α,PC=4sin α,则3PB+PC=cos α+4sin α=sin(α+φ)≤=. 可知其最大值为,选B.6.已知一个四面体其中五条棱的长分别为1,1,1,1,,则此四面体体积的最大值是( B )(A) (B) (C) (D)解析:设四面体为P-ABC,则设PC=X,AB=,其余的各边为1,那么取AB 的中点D,那么连接PD,因此可知,AB垂直于平面PCD,则棱锥的体积可以运用以PCD为底面,高为AD,BD的两个三棱锥体积的和来表示,因此只要求解底面积的最大值即可.由于PD=CD=,那么可知三角形PDC的面积越大,体积越大,可知S△PDC=××sin θ≤=,也就是当PD垂直于CD时,面积最大,因此可得四面体的体积的最大值为××=,选B.二、填空题7.圆柱的侧面展开图是边长为6π和4π的矩形,则圆柱的表面积为.解析:因为圆柱的侧面展开图是边长为6π和4π的矩形,①若6π=2πr,r=3,所以圆柱的表面积为4π×6π+2×πr2=24π2+18π;②若4π=2πr,r=2,所以圆柱的表面积为4π×6π+2×πr2=24π2+8π.答案:24π2+8π或24π2+18π8.一个圆柱和一个圆锥的底面直径和它们的高都与某一个球的直径相等,这时圆柱、圆锥、球的体积之比为.解析:设球的半径为r,则V圆柱=πr2×2r=2πr3,V圆锥=πr2×2r=,V球=πr3,所以V圆柱∶V圆锥∶V球=2πr3∶∶πr3=3∶1∶2.答案:3∶1∶29.将4个半径都是R的球体完全装入底面半径是2R的圆柱形桶中,则桶的最小高度是.解析:由题意知,小球要分两层放置且每层两个,令下层两小球的球心分别是A,B,上层两小球的球心分别是C,D.此时,圆柱底面的半径=两小球半径的和,恰好使小球相外切,且与圆柱母线相切.圆柱的高=上层小球的上方半径+AB与CD间的距离+下层小球的下方半径=2R+AB与CD间的距离.令AB,CD的中点分别为E,F.很明显,四面体ABCD每条棱的长都是2R,容易求出:EC=ED,FA=FB,由EC=ED,CF=DF,得EF⊥CD.由FA=FB,AE=BE,得EF⊥AB.所以EF是AB与CD间的距离,所以圆柱的高=2R+EF.由勾股定理,有CE2+AE2=AC2,CE2=EF2+CF2.两式相减,消去CE,得AE2=AC2-EF2-CF2,所以EF2=AC2-AE2-CF2=(2R)2-R2-R2=2R2,所以EF=R.所以圆柱的高=2r+R=(2+)R.答案:(2+)R10.一个圆锥有三条母线两两垂直,则它的侧面展开图的圆心角大小为.解析:设母线长为l,因圆锥有三条母线两两垂直,则这三条母线可以构成以它们为侧棱、以底面边长为l的正三角形的正三棱锥,故由正弦定理得,圆锥的底面直径2R=,解得R=,因此可知侧面展开图的圆心角大小为π.答案:π11.若圆锥的侧面展开图是圆心角为180°,半径为4的扇形,则这个圆锥的表面积是.解析:因为圆锥的侧面展开图是圆心角为180°,母线长等于4,半径为4的扇形,则这个圆锥的表面积是底面积加上侧面积,扇形面积加上底面面积的和为12π.答案:12π12.若长方体的一个顶点上的三条棱的长分别为3,4,5,从长方体的一条对角线的一个端点出发,沿表面运动到另一个端点,其最短路程是.解析:从长方体的一条对角线的一个端点A出发,沿表面运动到另一个端点B,有三种方案,如图是它们的三种部分侧面展开图,AB路程可能是:最短路程是.答案:三、解答题13.某几何体的一条棱长为,在该几何体的正视图中,这条棱的投影是长为的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,求a+b的最大值.解:如图,把几何体放到长方体中,使得长方体的体对角线刚好为几何体的已知棱,则长方体的体对角线A 1C=,则它的正视图投影长为A 1B=,侧视图投影长为A1D=a,俯视图投影长为A1C1=b,则a2+b2+()2=2·()2,即a2+b2=8,又≤,当且仅当“a=b=2”时等号成立.所以a+b≤4,即a+b的最大值为4.14.某几何体的三视图如图所示.(1)判断该几何体是什么几何体?(2)画出该几何体的直观图.解:(1)该几何体是一个正方体切掉两个圆柱后得到的几何体.(2)直观图如图所示.15.已知正三棱锥V-ABC的正视图和俯视图如图所示.(1)画出该正三棱锥的侧视图和直观图;(2)求出侧视图的面积.解:(1)如图.(2)侧视图中V A===2,则S △VBC=×2×2=6.第2节简单几何体的表面积与体积一、选择题1.如图所示是一个几何体的三视图,则该几何体的体积为( B )(A)16+2π(B)8+2π(C)16+π (D)8+π解析:由图可知该几何体是由两个相同的半圆柱与一个长方体拼接而成,因此V=1×2×4+π×12×2=8+2π.故选B.2.一个三条侧棱两两互相垂直并且侧棱长都为a的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( B )(A)πa2(B)3πa2(C)6πa2(D)πa2解析:由题可知该三棱锥为一个棱长a的正方体的一角,则该三棱锥与该正方体有相同的外接球,又正方体的对角线长为a,则球半径为a,则S=4πr2=4π(a)2=3πa2.故选B.3.一个棱长都为a的直三棱柱的六个顶点全部在同一个球面上,则该球的表面积为( A )(A)πa2(B)2πa2(C)πa2(D)πa2解析:如图,设O1,O2为棱柱两底面的中心,球心O为O1O2的中点.又直三棱柱的棱长为a,可知OO1=a,AO1=a,所以R2=OA2=O+A=,因此该直三棱柱外接球的表面积为S=4πR2=4π×=πa2,故选A.4.某几何体的三视图如图所示,则该几何体的体积为( D )(A) (B)2 (C) (D)解析:由三视图可知,该几何体的直观图为一个竖立的圆锥和一个倒立的圆锥组成,其体积为V=2×π×12×1=,选D.5.某四棱锥的三视图如图所示,则该四棱锥的体积是( C )(A)5 (B)2 (C) (D)解析:由三视图知,该四棱锥的底面是直角梯形,上底长为2,下底长为3,高为,四棱锥的高为h=2,故该四棱锥的底面积S=(2+3)×=,所以该四棱锥的体积V=Sh=××2=.6.已知边长为2的菱形ABCD中,∠A=60°,现沿对角线BD折起,使得二面角A BD C为120°,此时点A,B,C,D在同一个球面上,则该球的表面积为( C )(A)20π(B)24π(C)28π(D)32π解析:如图,分别取BD,AC的中点M,N,连接MN,则容易算得AM=CM=3,MN=,MD=,CN=,由图形的对称性可知球心必在MN的延长线上,设球心为O,半径为R,ON=x,则由题设可得解得x=,则R2=+=7,所以球面面积S=4πR2=28π,故选C.二、填空题7.一个圆柱的轴截面为正方形,则与它同底等高的圆锥的侧面积与该圆柱的侧面积的比为.解析:令正方形的边长为a,则圆柱的侧面积S1=2π××a=πa2,与它同底等高的圆锥的侧面积S2=πrl=π××a=,则与它同底等高的圆锥的侧面积与该圆柱的侧面积的比为.答案:8.球O与直三棱柱ABC-A1B1C1的各个面都相切,若三棱柱的表面积为27,△ABC的周长为6,则球的表面积为.解析:设内切球半径为r,那么直三棱柱的底面内切圆半径为r,棱柱的高为2r,由等面积法,则直三棱柱底面面积S 底=r×6=3r,由等体积法,V三棱柱=S底·2r=r·27,所以9r=6r2,解得r=.其表面积为4π×()2=3π.答案:3π9.已知母线长为6,底面半径为3的圆锥内有一球,球与圆锥的底面及圆锥的所有母线都相切,则球的体积是 .解析:取圆锥的轴截面,则截面是边长为6的正三角形,正三角形的内切圆的圆心即为球心,R=6××,所以R=,所以V=πR3=4π.答案:4π10.棱长为a的正方体ABCD A 1B1C1D1的8个顶点都在球O的表面上,E,F 分别是棱AA1,DD1的中点,则过E,F两点的直线被球O截得的线段长为.解析:设过E,F两点的直线与球O交于M,N,所以△OMN,△OEF均为等腰直角三角形,所以OM=ON=R=a,点O到EF的距离为棱长一半,所以|MN|=2= a.答案: a11.四棱锥P-ABCD的各顶点都在同一球面上,且矩形ABCD的各顶点都在同一个大圆上,球半径为R,则此四棱锥的体积的最大值为.解析:点P到平面ABCD的最大距离为R,设矩形ABCD的长宽分别为x,y,则x2+y2=4R2,四棱锥P ABCD的体积V=xyR≤×=R3,当且仅当x=y=R时,V max=R3.答案:R312.设正四面体ABCD的棱长为a,P是棱AB上的任意一点,且P到平面ACD,BCD的距离分别为d1,d2,则d1+d2= .解析:根据题意,由于正四面体ABCD的棱长为a,各个面的面积为a2,高为a,所以V=×a2×a=×a2×(d1+d2),所以d1+d2= a.答案: a三、解答题13.已知一个几何体的三视图如图所示.(1)求此几何体的表面积;(2)如果点P,Q在正视图中所示位置,P为所在线段中点,Q为顶点,求在几何体表面上,从P点到Q点的最短路径的长.解:(1)由三视图知该几何体是由一个圆锥加一个圆柱组成的,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.S 圆锥侧=(2πa)·(a)=πa2,S圆柱侧=(2πa)·(2a)=4πa2,S圆柱底=πa2,所以S 表=πa2+4πa2+πa2=(+5)πa2.(2)沿P点所在母线剪开圆柱侧面,如图.则PQ===a,所以从P点到Q点在侧面上的最短路径长为a.14.如图,四棱锥P ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明:MN∥平面PAB;(2)求四面体NBCM的体积.(1)证明:由已知得AM=AD=2.如图,取BP的中点T,连接AT,TN,由N为PC中点知TN∥BC,TN=BC=2.所以AM=TN,又AD∥BC,故TN AM,所以四边形AMNT为平行四边形,于是MN∥AT.因为AT⊂平面PAB,MN⊄平面PAB,所以MN∥平面PAB.(2)解:因为PA⊥平面ABCD,N为PC的中点,所以N到平面ABCD的距离为PA.取BC的中点E,连接AE.由AB=AC=3得AE⊥BC,AE==.由AM∥BC得M到BC的距离为,故S △BCM=×4×=2.所以四面体NBCM的体积V N-BCM=×S△BCM×=.15.如图所示,在空间几何体ADE BCF中,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,AD⊥DC,AB=AD=DE=2,EF=4,M是线段AE上的动点.(1)试确定点M的位置,使AC∥平面MDF,并说明理由;(2)在(1)的条件下,平面MDF将几何体ADE-BCF分成两部分,求空间几何体M-DEF与空间几何体ADM BCF的体积之比.解:(1)当M是线段AE的中点时,AC∥平面MDF.理由如下:连接CE交DF于点N,连接MN.因为M,N分别是AE,CE的中点,所以MN∥AC.又因为MN⊂平面MDF,AC⊄平面MDF,所以AC∥平面MDF.(2)将几何体ADE-BCF补成三棱柱ADE-B′CF,如图所示,三棱柱ADE-B′CF的体积为V=S△ADE·CD=×2×2×4=8,则几何体ADE-BCF的体积=-=8-×(×2×2)×2=.因为三棱锥M-DEF的体积=×(×2×4)×1=,所以=-=,所以两几何体的体积之比为∶=1∶4.第3节空间图形的基本关系与公理一、选择题1.设m,n是两条不同的直线,α,β是两个不同的平面( C )(A)若m∥α,n∥α,则m∥n(B)若m∥α,m∥β,则α∥β(C)若m∥n,m⊥α,则n⊥α(D)若m∥α,α⊥β,则m⊥β解析:设直线a⊂α,b⊂α,a∩b=A,因为m⊥α,所以m⊥a,m⊥b.又n∥m,所以n⊥a,n⊥b,所以n⊥α.故选C.2.下列命题中,错误的是( D )(A)平行于同一平面的两个不同平面平行(B)一条直线与两个平行平面中的一个相交,则必与另一个平面相交(C)如果两个平面不垂直,那么其中一个平面内一定不存在直线与另一个平面垂直(D)若直线不平行于平面,则此直线与这个平面内的直线都不平行解析:当直线l在平面α内,即l⊂α时,直线l不平行于平面α,但平面α内存在直线与直线l平行,可知D选项错误,故选D.3.下列四个命题:①若一个平面内的两条直线都与另一个平面平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,为真命题的是( D )(A)①和②(B)②和③(C)③和④(D)②和④解析:①显然错误,因为这两条直线相交才满足条件;②成立;③错误,这两条直线可能平行、相交,也可能异面;④成立,用反证法容易证明.故选D.4.若α,β是两个相交平面,则在下列命题中,真命题的序号为( C )①若直线m⊥α,则在平面β内,一定不存在与直线m平行的直线;②若直线m⊥α,则在平面β内,一定存在无数条直线与直线m垂直;③若直线m⊂α,则在平面β内,不一定存在与直线m垂直的直线;④若直线m⊂α,则在平面β内,一定存在与直线m垂直的直线.(A)①③(B)②③(C)②④(D)①④解析:若α⊥β且直线m⊥α,则在平面β内,一定存在与直线m平行的直线,所以①错误;若直线m⊥α,则在平面β内,一定存在无数条直线与直线m垂直,故②正确;若直线m⊂α,则在平面β内,一定存在与直线m垂直的直线,故③错误,④正确,故选C.5.设不在同一条直线上的A,B,C三点到平面α的距离相等,且A∉α,则( B )(A)α∥平面ABC(B)△ABC中至少有一条边平行于α(C)△ABC中至多有两条边平行于α(D)△ABC中只可能有一条边平行于α解析:因为A∉α,所以A,B,C均不在平面α内.当A,B,C三点在平面α的同侧时,α∥平面ABC,此时△ABC的三条边都平行于α,排除C,D;当A,B,C三点不在平面α的同侧时,易知△ABC中只有一条边平行于α,此时平面α和平面ABC相交,故选B.6.若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的( B )(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件解析:因为l⊥m,m⊥α,所以l∥α或l⊂α.故充分性不成立.若l∥α,m⊥α,一定有l⊥m.故必要性成立.选B.二、填空题7.长方体ABCD-A1B1C1D1的底面是边长为1的正方形,点E在侧棱AA1上(不与A,A1重合),满足∠C1EB=90°,则异面直线BE与C1B1所成的角为,侧棱AA1的长的最小值为.解析:在长方体ABCD-A1B1C1D1中,CB⊥平面ABB1A1,所以∠CBE=90°,又C1B1∥BC,所以异面直线BE与C1B1所成的角为90°.连接BC1,设AA1=x,AE=m(m>0),则有BE2=1+m2,C1E2=(x-m)2+2,C1B2=1+x2,因为∠C1EB=90°,所以C1B2=C1E2+BE2,即1+x2=(x-m)2+2+1+m2,即m2-mx+1=0,所以x=m+≥2,当且仅当m=,即m=1时,“=”成立.答案:90° 28.四边形ABCD中,AB=AD=CD=1,BD=,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A1-BCD,使平面A1BD⊥平面BCD,给出下列结论:(1)A1C⊥BD;(2)∠BA1C=90°;(3)四面体A1-BCD的体积为.其中正确的命题是.(把所有正确命题的序号都填上) 解析:若A1C⊥BD,因为BD⊥CD,A1C∩CD=C,所以BD⊥平面A1CD,所以BD⊥A1D.而由A 1B=AB=1,A1D=AD=1,BD=,得A1B⊥A1D,与BD⊥A1D矛盾,故(1)错.因为CD⊥BD,平面BCD⊥平面A1BD,所以CD⊥平面A1BD,则CD⊥A1B.又A1B⊥A1D,A1D∩CD=D,所以A1B⊥平面A1CD,则A1B⊥A1C,故(2)正确.由(2)知==×·A1D·DC·A1B=,故(3)错.答案:(2)9.在正方体ABCD A 1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线有条.解析:在A1D1上任取一点P,过点P与直线EF作一个平面α,因为CD 与平面α不平行,所以它们相交,设α∩CD=Q,连接PQ,则PQ与EF必然相交.由点P的任意性,知有无数条直线与A1D1,EF,CD都相交.答案:无数10.如图,在直三棱柱ABC-A1B1C1中,底面为直角三角形.∠ACB =90°,AC=6,BC=CC 1=,P是BC1上一动点,则CP+PA1的最小值为.解析:连接A1B,将△A1BC1与△CBC1同时展开形成一个平面四边形A1BCC1,则此时对角线CP+PA1=A1C达到最小,在等腰直角三角形△BCC1中,BC1=2,∠CC1B=45°,在△A 1BC1中,A1B==2,A1C1=6,BC1=2,所以A1+B=A1B2,即∠A1C1B=90°.对于展开形成的四边形A1BCC1,如图,在△A 1C1C中,C1C=,A1C1=6,∠A1C1C=135°,由余弦定理有,CP+PA 1=A1C===5.答案:511. 如图,三棱锥A BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是.解析:如图所示,连接DN,取线段DN的中点K,连接MK,CK.因为M为AD的中点,所以MK∥AN,所以∠KMC为异面直线AN,CM所成的角.因为AB=AC=BD=CD=3,AD=BC=2,N为BC的中点,由勾股定理求得AN=DN=CM=2,所以MK=.在Rt△CKN中,CK==.在△CKM中,由余弦定理,得cos∠KMC===.答案:12.如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE 翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下面四个命题中不正确的是.①BM是定值;②点M在某个球面上运动;③存在某个位置,使DE⊥A1C;④存在某个位置,使MB∥平面A1DE.解析:取DC中点F,连接MF,BF,MF∥A1D且MF=A1D,FB∥ED且FB=ED,所以∠MFB=∠A1DE.由余弦定理可得MB2=MF2+FB2-2MF·FB·cos∠MFB 是定值,所以M是在以B为圆心,MB为半径的球上,可得①②正确;由MF∥A1D与FB∥ED可得平面MBF∥平面A1DE,可得④正确;A1C在平面ABCD中的投影与AC重合,AC与DE不垂直,可得③不正确.答案:③三、解答题13.如图所示,等腰直角三角形ABC中,∠A=90°,BC=,DA⊥AC,DA⊥AB,若DA=1,且E为DA的中点.求异面直线BE与CD所成角的余弦值.解:如图所示,取AC的中点F,连接EF,BF,在△ACD中,E,F分别是AD,AC的中点,所以EF∥CD.所以∠BEF或其补角即为异面直线BE与CD所成的角.在Rt△EAB中,AB=AC=1,AE=AD=,所以BE=.在Rt△EAF中,AF=AC=,AE=,所以EF=.在Rt△BAF中,AB=1,AF=,所以BF=.在等腰三角形EBF中,cos∠FEB===.所以异面直线BE与CD所成角的余弦值为.14.已知正方体ABCD-A1B1C1D1中,E,F分别为D1C1,C1B1的中点,AC∩BD=P,A1C1∩EF=Q.求证:(1)D,B,F,E四点共面;(2)若A1C交平面DBFE于R点,则P,Q,R三点共线.证明:(1)如图所示,因为EF是△D1B1C1的中位线,所以EF∥B1D1.在正方体ABCD-A1B1C1D1中,B1D1∥BD,所以EF∥BD.所以EF,BD确定一个平面.即D,B,F,E四点共面.(2)在正方体ABCD-A1B1C1D1中,设平面A1ACC1确定的平面为α,又设平面BDEF为β.因为Q∈A1C1,所以Q∈α.又Q∈EF,所以Q∈β.则Q是α与β的公共点,同理,P点也是α与β的公共点.所以α∩β=PQ.又A1C∩β=R,所以R∈A1C,则R∈α且∈β.则R∈PQ,故P,Q,R三点共线.15.在长方体ABCD A 1B1C1D1的A1C1面上有一点P(如图所示,其中P点不在对角线B1D1)上.(1)过P点在空间内作一条直线l,使l∥直线BD,应该如何作图?并说明理由;(2)过P点在平面A1C1内作一条直线m,使m与直线BD成α角,其中α∈(0°,90°],这样的直线有几条,应该如何作图?解:(1)连接B1D1,BD,在平面A1C1内过P点作直线l,使l∥直线B1D1,则l即为所求作的直线.因为直线B1D1∥直线BD,l∥直线B1D1,所以l∥直线BD.如图(1).(2)在平面A1C1内作直线m,使直线m与B1D1相交成α角,因为BD∥B1D1,所以直线m与直线BD也成α角,即直线m为所求作的直线,如图(2).由图(2)知m与BD是异面直线,且m与BD所成的角α∈(0,90°].当α=90°时,这样的直线m有且只有一条,当α≠90°时,这样的直线m 有两条.第4节直线、平面平行的判定与性质一、选择题1.若直线l∥平面α,直线a⊂平面α,则l与a的位置关系是( D )(A)l∥a (B)l与a异面(C)l与a相交 (D)l与a没有公共点解析:因为直线平行于平面,那么l与平面内的任何一条直线都没有公共点,因此l与a的位置关系是没有公共点,选D.2.下列条件能推出平面α∥平面β的是( D )(A)存在一条直线a,a∥α,a∥β(B)存在一条直线a,a⊂α,a∥β(C)存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥α(D)存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α解析:因为根据面面平行的判定定理可知,如果存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α,则可以利用线线平行得到面面平行,选D.3.已知直线l,m,平面α,β,则下列命题中:①若α∥β,l⊂α,则l∥β②若α⊥β,l⊥α,则l∥β③若l∥α,m⊂α,则l∥m④若α⊥β,α∩β=l,m⊥l,则m⊥β,其中真命题有( B )(A)0个(B)1个(C)2个(D)3个解析:当两个平面平行时,一个平面上的线与另一个平面平行,故①正确;一条直线垂直于两个垂直平面中的一个平面,那么这条直线平行于或包含于另一个平面,故②不正确;④不正确;③中l,m的关系是不相交,故③不正确,故选B.4.下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( B )(A)①③(B)①④(C)②③(D)②④解析:对图①,构造AB所在的平面,即对角面,可以证明这个对角面与平面MNP平行,由线面平行的定义可得AB∥平面MNP;对图④,通过证明AB∥PN得到AB∥平面MNP;对于②,证MP中点为K,延长BA,KN则相交,所以BA与平面MNP相交,②错;对于③平面MNP与直线AB相交于点B,③错.故选B.5.类比平面几何中的定理“设a,b,c是三条直线,若a⊥c,b⊥c,则a∥b”,得出如下结论:①设a,b,c是空间的三条直线,若a⊥c,b⊥c,则a∥b;②设a,b是两条直线,α是平面,若a⊥α,b⊥α,则a∥b;③设α,β是两个平面,m是直线,若m⊥α,m⊥β,则α∥β;④设α,β,γ是三个平面,若α⊥γ,β⊥γ,则α∥β.其中正确命题的个数是( B )(A)1 (B)2 (C)3 (D)4解析:①错;②垂直于同一个平面的两条直线平行,正确;③垂直于同一条直线的两个平面平行,正确;④错;两个平面也可能相交.6.在空间中,下列命题正确的是( D )(A)平面α内的一条直线a垂直于平面β内的无数条直线,则α⊥β(B)若直线m与平面α内的一条直线平行,则m∥α(C)若平面α⊥β,且α∩β=l,则过α内一点P与l垂直的直线垂直于平面β(D)若直线a与平面α内的无数条直线都垂直,则不能说一定有a⊥α解析:直线a与平面α内的任意直线都垂直,则有a⊥α,所以D正确.二、填空题7.点S在平面ABC外,SB⊥AC,SB=AC=2,E,F分别是SC和AB的中点,则EF= .解析:取BC的中点D,连接ED与FD,因为E,F分别是SC和AB的中点,点D为BC的中点所以ED∥SB,FD∥AC,而SB⊥AC,SB=AC=2,则三角形EDF为等腰直角三角形,则ED=FD=1,即EF=.答案:8.正四棱锥S ABCD的底面边长为2,高为2,E是边BC的中点,动点P 在这个棱锥表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为.解析:由题意知,点P的轨迹为如图所示的三角形EFG,其中G,F为其所在棱的中点,所以EF=BD=,GE=GF=SB=,所以轨迹的周长为+.答案:+9.将边长为2,一个内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,点E,F分别为AC,BD的中点,则下列命题中正确的是.①EF∥AB;②EF⊥BD;③EF有最大值,无最小值;④当四面体ABCD的体积最大时,AC=;⑤AC垂直于截面BDE.解析:因为将边长为2,一个内角为60°的菱形ABCD沿较短对角线BD 折成四面体ABCD,点E,F分别为AC,BD的中点,则可知EF⊥BD,当四面体ABCD的体积最大时,AC=,AC垂直于截面BDE成立.答案:②④⑤10.已知平面α∥平面β,P是α,β外一点,过点P的直线m与α,β分别交于A,C,过点P的直线n与α,β分别交于B,D且PA=6,AC=9,PD=8,则BD的长为.解析:因为平面α∥平面β,所以AB∥CD,①当P在两平面外时,==,所以=,所以BD=.②当P在两平面之间时,=,所以=,所以BD=24,所以BD的长为或24.答案:或2411.给出下列四个命题:①过平面外一点,作与该平面成θ角的直线一定有无穷多条;②一条直线与两个相交平面都平行,则它必与这两个平面的交线平行;③对确定的两条异面直线,过空间任意一点有且只有一个平面与这两条异面直线都平行;④对两条异面的直线,都存在无穷多个平面与这两条直线所成的角相等.其中正确的命题序号为.解析:①中,成90度角的时候,就只有一条,因此错误.②中是线面平行的性质定理,显然成立.③不正确.④中,利用等角定理,可知成立. 答案:②④12.侧棱长为2的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=40°,过A 作截面AEF,则截面△AEF周长的最小值为.解析:沿着侧棱VA把正三棱锥V ABC展开在一个平面内,则设VA的另一边为VA′,则AA′即为截面△AEF周长的最小值,且∠AVA′=3×40=120°.△VAA′中,由余弦定理可得AA′=6.答案:6三、解答题13.已知长方体ABCD-A1B1C1D1中,底面ABCD为正方形,AB=4,AA1=2,点E 在棱C1D1上,且D1E=3.(1)试在棱CD上确定一点E1,使得直线EE1∥平面D1DB,并证明;(2)若动点F在底面ABCD内,且AF=2,请说明点F的轨迹,并探求EF 长度的最小值.解:(1)取CD的四等分点E1,使得DE1=3,则有EE1∥平面D1DB.证明如下:因为D1E∥DE1且D1E=DE1,所以四边形D1EE1D为平行四边形,则D1D∥EE1,因为DD1⊂平面D1DB,EE1⊄平面D1DB,所以EE1∥平面D1DB.(2)因为AF=2,所以点F在平面ABCD内的轨迹是以A为圆心,半径等于2的四分之一圆弧.因为EE1∥DD1,D1D⊥平面ABCD,所以E1E⊥平面ABCD,故EF==.所以当E1F的长度取最小值时,EF的长度最小,此时点F为线段AE1和四分之一圆弧的交点,即E1F=E1A-AF=5-2=3,所以EF==.即EF长度的最小值为.14.在正方体ABCD-A1B1C1D1中,棱长为2,E是棱CD的中点,P是棱AA1的中点,(1)求证:PD∥平面AB1E;(2)求三棱锥B-AB1E的体积.(1)证明:取AB1中点Q,连接PQ,则PQ为中位线,PQ A1B1,而正方体ABCD-A1B1C1D1,E是棱CD的中点,故DE A1B1,所以PQ DE,所以四边形PQED为平行四边形.所以PD∥QE,而QE⊂平面AB1E,PD⊄平面AB1E,故PD∥平面AB1E.(2)解:正方体ABCD-A1B1C1D1中,BB1⊥平面ABE,故BB1为高,BB1=2,因为CD∥AB,所以S△ABE=S△ABC=AB·BC=×2×2=2.故==BB1·S△ABC=.15.如图,在四面体PABC中,PA=PB,CA=CB,D,E,F,G分别是PA,AC,CB,BP的中点.(1)求证:D,E,F,G四点共面;(2)求证:PC⊥AB;(3)若△ABC和△PAB都是等腰直角三角形,且AB=2,PC=,求四面体PABC的体积.(1)证明:依题意DG∥AB,EF∥AB,所以DG∥EF,DG,EF共面,从而D,E,F,G四点共面.(2)证明:取AB中点为O,连接PO,CO.因为PA=PB,CA=CB,所以PO⊥AB,CO⊥AB,因为PO∩CO=O,所以AB⊥平面POC,PC⊂平面POC,所以AB⊥PC.(3)解:因为△ABC和△PAB是等腰直角三角形,所以PO=CO=AB=1,因为PC=,OP2+OC2=PC2,所以OP⊥OC,又PO⊥AB,且AB∩OC=O,所以PO⊥平面ABC,=PO·S△ABC=×1×2×1×=.第5节直线、平面垂直的判定与性质一、选择题1.已知直线l,m和平面α, 则下列命题正确的是( C )(A)若l∥m,m⊂α,则l∥α(B)若l∥α,m⊂α,则l∥m(C)若l⊥α,m⊂α,则l⊥m(D)若l⊥m,l⊥α,则m∥α解析:A项中直线l与平面α可能平行,可能直线在平面内;B项中直线l,m平行或异面;C项中当直线垂直于平面时,直线垂直于平面内任意直线;D项中直线m与平面α平行或直线在平面内.2.在Rt△ABC中,∠ABC=90°,P为△ABC所在平面外一点,PA⊥平面ABC,则四面体P ABC中共有直角三角形个数为( A )(A)4 (B) 3 (C) 2 (D) 1解析:因为PA⊥平面ABC,AB⊥BC,所以PA⊥AB,PA⊥AC,PB⊥CB,所以△ABC,△PBC, △ABP, △APC都是直角三角形,故选A.3.已知直线m,n和平面α,β满足m⊥n,m⊥α,α⊥β,则( C )(A)n⊥β (B)n∥β,或n⊂β(C)n∥α或n⊂α(D)n⊥α解析:由题意画出图形,容易判断选项.由于直线m⊥n,m⊥α,α⊥β,选项A,中线面可能相交,也可能垂直,选项B中,n与β还可能相交,错误,选项D中,直线不能垂直于平面,故结合图象不难得到选项为C.4.正方体的棱长为1,C,D,M分别为三条棱的中点,A,B是顶点,那么点M到截面ABCD的距离是( B )(A)(B)(C)(D)解析:过M作AB的垂线MN交AB于N,连接CN.由于CM⊥AB,MN⊥AB,则AB⊥平面CMN,所以,M到面ABCD的距离h是直角三角形CMN的斜边CN上的高.由于BM=,CM=1,MN=,CN=,则结合=求得h=.故选B.。
高一数学立体几何练习题及答案一、选择题1. 下列哪个图形不是立体图形?A. 立方体B. 圆锥C. 圆柱D. 正方形答案:D2. 已知一个立方体的边长为5cm,求它的表面积和体积分别是多少?A. 表面积:150cm²,体积:125cm³B. 表面积:100cm²,体积:125cm³C. 表面积:150cm²,体积:100cm³D. 表面积:100cm²,体积:100cm³答案:A3. 以下哪个选项可以形成一个正方体?A. 六个相等的长方体B. 一个正方形和一个长方体C. 六个相等的正方形D. 一个正方形和一个正方体答案:C4. 以下哪个图形可以形成一个圆柱?A. 一个正方形和一个长方体B. 一个圆和一个长方体C. 一个长方形和一个长方体D. 一个正方形和一个正方体答案:C5. 以下哪个选项可以形成一个圆锥?A. 一个圆和一个长方体B. 一个圆和一个正方体C. 一个正方形和一个长方体D. 一个正方形和一个正方体答案:B二、填空题1. 已知一个正方体的表面积为96cm²,求它的边长是多少?答案:4cm2. 已知一个圆柱的半径为3cm,高为10cm,求它的表面积和体积分别是多少?答案:表面积:198cm²,体积:90π cm³3. 以下哪个选项可以形成一个长方体?A. 六个相等的正方形B. 一个圆和一个长方形C. 六个相等的长方形D. 一个正方形和一个正方体答案:C三、解答题1. 某长方体的长、宽、高分别为3cm、4cm、5cm,请回答以下问题:(1)它的表面积是多少?(2)它的体积是多少?答案:(1)表面积 = 2(长×宽 + 长×高 + 宽×高)= 2(3×4 + 3×5 + 4×5)= 2(12 + 15 + 20)= 2(47)= 94cm²(2)体积 = 长×宽×高= 3×4×5= 60cm³2. 某圆锥的半径是5cm,高是12cm,请回答以下问题:(1)它的表面积是多少?(2)它的体积是多少?答案:(1)斜面积= π×半径×斜高= π×5×13≈ 204.2cm²(2)体积= (1/3)π×半径²×高= (1/3)π×5²×12≈ 314.2cm³四、解析题某正方体的表面积是96cm²,它的边长是多少?解答:设正方体的边长为x,由表面积的计算公式可得:表面积 = 6x²96 = 6x²16 = x²x = 4所以,该正方体的边长为4cm。
高中立体几何试题及答案一、选择题(每题3分,共15分)1. 空间中,如果直线a与平面α平行,那么直线a与平面α内的任意直线b的位置关系是:A. 平行B. 异面C. 相交D. 垂直2. 一个正方体的棱长为a,那么它的对角线长度为:A. a√2B. a√3C. 2aD. 3a3. 已知一个圆锥的底面半径为r,高为h,圆锥的体积是:A. πr²hB. 1/3πr²hC. 2πr²hD. 3πr²h4. 一个球的半径为R,那么它的表面积是:A. 4πR²B. 2πR²C. πR²D. R²5. 空间中,如果两个平面α和β相交于直线l,那么直线l与平面α和平面β的位置关系是:A. 平行B. 垂直C. 相交D. 包含二、填空题(每题2分,共10分)6. 空间直角坐标系中,点A(2,3,4)到原点O的距离是________。
7. 一个正四面体的每个顶点都与其它三个顶点相连,那么它的边长与高之比为________。
8. 已知一个长方体的长、宽、高分别为l、w、h,那么它的体积是________。
9. 空间中,如果一个点到平面的距离是d,那么这个点到平面上任意一点的距离的最大值是________。
10. 一个圆柱的底面半径为r,高为h,它的侧面积是________。
三、解答题(共75分)11. (15分)已知空间直角坐标系中,点A(1,2,3),B(4,5,6),点C 在平面ABC内,且AC=BC=2,求点C的坐标。
12. (20分)一个圆锥的底面半径为3,高为4,求圆锥的全面积和表面积。
13. (20分)一个长方体的长、宽、高分别为5、3、2,求其外接球的半径。
14. (20分)已知一个球的表面积为4π,求该球的体积。
答案:一、选择题1. A2. B3. B4. A5. C二、填空题6. √(1²+2²+3²)=√147. √3:18. lwh9. d+R10. 2πrh三、解答题11. 点C的坐标可以通过向量运算求得,设C(x,y,z),则向量AC=向量BC,即(1-x,2-y,3-z)=(x-4,5-y,6-z),解得x=3,y=4,z=5,所以点C的坐标为(3,4,5)。
《立体几何》(一)选择题:1.下列说法正确的是 ( ) (A )两平面相交只有一个公共点 (B )两两相交的三条直线共面 (C )不共面的四点中,任何三点不共线 (D )有三个公共点的两平面必重合 2.在空间,下列命题中正确的是 ( ) (A )对边相等的四边形一定是平面图形 (B )四边相等的四边形一定是平面图形(C )有一组对边平行的四边形一定是平面图形 (D )有一组对角相等的四边形一定是平面图形3.过空间一点作三条直线,则这三条直线确定的平面个数是 ( ) (A )1个 (B )2个 (C )3个 (D )1个或3个 4.空间不共线的四点,其中三点共线是这四点共面的 ( ) (A )充分条件 (B )必要条件 (C )充要条件(D )既非充分也非必要条件 5.下列说法正确的是 ( ) (A )过三点确定一个平面 (B )过一条直线和一个点确定一个平面 (C )梯形、平行四边形都是平面图形(D )四边形都是平面图形6.下列命题中正确的是 ( ) (A )空间不同的三点确定一个平面(B )空间两两相交的三条直线确定一个平面(C )空间有三个角为直角的四边形一定是平面图形(D )和同一条直线相交的三条平行直线一定在同一平面内7.“直线上有两点在平面内”是“这条直线在这个平面内”的 ( ) (A )充分条件 (B )必要条件 (C )充要条件 (D )既不充分又不必要 8.下列说法正确的是 ( ) (A )四边形的对角线相交(B )空间有任意四个角是直角的四边形一定是平面图形 (C )两两相交的三条直线一定共面(D )在空间的四点,若无三点共线,则这四点一定不共面。
9.不一定能确定一个平面的是 ( ) (A )直线与直线外一点(B )两条相交直线(C )空间三点(D )两条平行直线10.A 、B 、C 表示不同的点,a 、l 表示不同的直线,α、β表示不同的平面,下列推理不正确的是 ( ) ()A ααα⊂⇒∈∈∈∈l B l B A l A ,,,()B βα∈∈A A ,,AB B B =⇒∈∈βαβα ,直线 ()C αα∉⇒∈⊄A l A l ,()D α∈C B A ,,,β∈C B A ,,且C B A ,,不共线α⇒与β重合 (二)填空题:1.空间三条直线互相平行,但不共面,它们能确定 个平面;三条直线相交于一点,它们最多可确定 个平面。
立体几何测试题(共10篇)立体几何测试题(一): 立体几何问题立体几何试题已知正方体ABCD-A1B1C1D1中,E、F分别为D1C1、C1B1的中点,AC∩BD=P,A1C1∩EF=Q.求证:(1)D、B、F、E四点共面;(2)若A1C交平面DBFE于R点,则P、Q、R三点共线.1.EF平行于B1D1,B1D1平行于BD,所以EF平行于BD,EFBD四点共面2.F,D,A,C1属于平面A1ACC1,且AC1与PQ不平行,所以AC1与PQ相交A1C交平面DBFE于R点,又因为PQ属于平面DBFE,所以AC1与PQ相交于R 所以R属于PQ,PQR共线立体几何测试题(二): 几个书后练习题立体几何1.如果a、b是两条直线,且a‖b,那么a平行于经过b的任何平面.是否正确2.如果a、b是两条直线,且a‖b,那么a平行于经过b的任何平面.为什么不对谢不对,因为a有可能在经过b的面上,不是平行关系立体几何测试题(三): 一道数学基本的立体几何的题目~在正方形ABCD-A"B"C"D"中,P、Q分别为A"B"、BB"的中点.(1)求直线AP与CQ所成的角的大小(2)求直线AP与BD所成的角的大小我还没学过空间向量,1.取DC中点E,连EC,证明EC平行AP,用余弦定理算2.取AB中点F,连接FB,用余弦定理算【立体几何测试题】立体几何测试题(四): 求大量立体几何难题!立体几何综合试题(自己画图)1、已知正三棱柱ABC—A1B1C1中,各棱长都相等,D、E分别为AC1,BB1的中点.(1)求证:DE‖平面A1B1C1;(2)求二面角A1—DE—B1的大小.2、已知直三棱柱ABC—A1B1C1,AB=AC,F为棱BB1上一点,BF∶FB1=2∶1,BF =BC=2a.(I)若D为BC的中点,E为AD上不同于A、D的任意一点,证明EF⊥FC1;(II)试问:若AB=2a,在线段AD上的E点能否使EF与平面BB1C1C成60°角,为什么证明你的结论3、在底面是直角梯形的四棱锥中,AD‖BC,∠ABC=90°,且 ,又PA⊥平面ABCD,AD=3AB=3PA=3a.(I)求二面角P—CD—A的正切值;(II)求点A到平面PBC的距离.4、在直三棱柱ABC—A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BA、BC的中点,G是AA1上一点,且AC1⊥EG.(Ⅰ)确定点G的位置;(Ⅱ)求直线AC1与平面EFG所成角θ的大小.5、已知四棱锥P—ABCD,底面ABCD是菱形,平面ABCD,PD=AD,点E为AB中点,点F为PD中点.(1)证明平面PED⊥平面PAB;(2)求二面角P—AB—F的平面角的余弦值6.在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,点P 在棱CC1上,且CC1=4CP.(Ⅰ)求直线AP与平面BCC1B1所成的角的大小(结果用反三角函数值表示);(Ⅱ)设O点在平面D1AP上的射影是H,求证:D1H⊥AP;(Ⅲ)求点P到平面ABD1的距离.7、在四棱锥中,底面ABCD是正方形,侧棱底面ABCD,,E是PC的中点,作交PB于点F.(I)证明平面;(II)证明平面EFD;(III)求二面角的大小.8、已知在棱长为1的正方体ABCD—A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.(I)试确定点F的位置,使得D1E⊥平面AB1F;(II)当D 1E⊥平面AB1F时,求二面角C1—EF—A的大小(结果用反三角函数值表示).9、直四棱柱ABCD-A1B1C1D1的底面是梯形,AB‖CD,AD⊥DC,CD=2,DD1=AB=1,P、Q分别是CC1、C1D1的中点.点P到直线AD1的距离为⑴求证:AC‖平面BPQ⑵求二面角B-PQ-D的大小10、已知长方体ABCD—A1B1C1D1中,AB=BC=4,AA1=8,E、F分别为AD和CC1的中点,O1为下底面正方形的中心.(Ⅰ)证明:AF⊥平面FD1B1;(Ⅱ)求异面直线EB与O1F所成角的余弦值;这些题应该还可以!你来试试吧!题不要求多就精就可以了!不懂的或不会做的,我来帮你解答!立体几何测试题(五): 立体几何初步练习题已知正方体ABCD-A1B1C1D1中,E,F,M,N分别是棱B1C1,C1D1,A1B1,D1A1的中点,求证(1)MN平行于DEF,(2)平面AMN平行于平面CEF(1)连接B1D1因为MN、EF为三角形A1B1D1、B1C1D1的中位线,所以MN平行于EF因为MN不属于面DEF,EF属于面DEF所以MN平行于面DEF(2)这题题目错了吧,应该是DEF吧立体几何测试题(六): 解析几何基础知识练习题靠!一楼的那么多废话那么多选择题:集合,函数(图像),立体几何,圆锥一、数学命题原则 1.普通高等学校招生数学科的考试,按照“考查基础知识的【立体几何测试题】立体几何测试题(七): 高一必修二立体几何习题1-7的题仓库的房顶呈正四棱锥形,量的地面的边长为2.6m,侧棱长2.1m,先要在房顶上铺一层油毡纸,问:需要油毡纸的面积多少运用海伦公式房顶为4个相同的三角形海伦公式a=2.6 b=2.1 c=2.1 p=a+b+c/2=3.4S=根号下p*(p-a)*(p-b)*(p-c)=2.1444S=2.144*4=8.576平方米立体几何测试题(八): 怎么根据题目画数学的立体几何图形搞懂了题目的要求,就照那意思去画,立体几何记住透视很重要.立体几何测试题(九): 求立体几何判断题的解题方法.①过平面外一点有且仅有一个平面与已知平面垂直②过直线外一点有且仅有一个平面与已知直线平行③过直线外一点有且仅有一条直线与已知直线垂直④过平面外一点有且仅有一条直线与已知平面垂直⑤……等等,诸如此类.见到很多这样的题目,但是却总找不到解题的方法,概念定理也经常记混.本人感激不尽!记一些模型,例如墙角模型什么的这个很重要.遇见不熟悉的题,用书本和笔(手指也可以)比划一下.这种题目主要是找反例!想象力也很重要啦……立体几何测试题(十): 一道高中立体几何的题目.已知长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,O1是底面A1B1C1D1的中心.E 是CO1上的点,设CE等于X,四棱锥E-ABCD的体积为y,求y关于X的函数关系式..图只有自己画一下了,做EF垂直于平面ABCD 垂足为F易得出CEF相似于O1CC1因为C1O1=根号2 CC1=4 得CO1=3根号2CE/CO1=EF/CC1 得出EF=4X/3根号2Y=底面积*EF/3=4*4X/9根号2Y=8根号2*X/9职高立体几何测试题空间立体几何测试题。
立体几何练习题1。
设α、β、γ为两两不重合的平面,l 、m 、n 为两两不重合的直线,给出下列四个命题: 若α⊥γ,β⊥γ,则α∥β;②若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β; ③若α∥β,l ⊂α,则l ∥β;④若α∩β=l ,β∩γ=m ,γ∩α=n ,l ∥γ,则m ∥n . 其中真命题的个数是( ) A .1 B .2 C .3 D .42。
正方体ABCD ﹣A 1B 1C 1D 1中,BD 1与平面ABCD 所成角的余弦值为() A .B .CD .3。
三棱柱ABC ﹣A 1B 1C 1中,AA 1=2且AA 1⊥平面ABC ,△ABC 是 边长为的正三角形,该三棱柱的六个顶点都在一个球面上,则这个球的体积为() A . 8πB .C .D . 8π4.三个平面两两垂直,它们的三条交线交于点O ,空间一点P 到三个平面的距离分别为3、4、5,则OP 长为() A . 5 B . 2 C . 3 D . 55。
如图,四棱锥S ﹣ABCD 的底面为正方形,SD ⊥底面ABCD,则下列结论中不正确的是() A . AC⊥SB B .AB∥平面SCDC . SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D . AB 与SC 所成的角等于DC 与SA 所成的角6.如图,四棱锥P ﹣ABCD 的底面为正方形,PD ⊥底面ABCD ,PD=AD=1,设点CG 到平面PAB 的距离为d 1,点B 到平面PAC 的距离为d 2,则有( ) A . 1<d 1<d 2 B . d 1<d 2<1C . d 1<1<d 2D . d 2<d 1<17。
在锐角的二面角βα--EF ,A EF ∈,AG α⊂, 45=∠GAE ,若AG 与β所成角为30,则二面角βα--EF 为__________。
8。
给出下列四个命题:(1)若平面α上有不共线的三点到平面β的距离相等,则βα//; (2)两条异面直线在同一平面内的射影可能是两条平行直线;(3)两条异面直线中的一条平行于平面α,则另一条必定不平行于平面α; (4)b ,a 为异面直线,则过a 且与b 平行的平面有且仅有一个.EFA Gαβ其中正确命题的序号是_______________________9.已知正方体 1111ABCD A B C D -中,点E 是棱 11A B 的中点,则直线AE 与平而 11BDD B 所成角的正弦值是_________。