西南交通大学2015-2016数理统计考试题

西南交《统计学》在线作业一一、单选题（共 25 道试题，共 50 分。

）1. 根据一个具体样本求出的总体均值95%置信区间( )。

. 以95%的概率包含总体均值. 有5%的可能性包含总体均值. 一定包含总体均值. 要么包含总体均值,要么不包含总体均值正确答案：2. 下列叙述中,错误的是( )。

. 可以从公开发表的资料中获取数据. 最主要的调查类型之一是民意调查,如Gllup的民意调查. 在医疗实验中,参加试验的个人被分成两组:控制组和治疗组. 从调查中获得的数据通常比从实验中获得的数据更加可靠正确答案：3. 某机构十分关心小学生每周看电视的时间。

该机构随即抽取300名小学生家长对他们的孩子每周看电视的时间进行了估计。

结果表明,这些小学生每周看电视的平均时间为15小时,标准差为5。

该机构搜集数据的方式是( )。

. 概率抽样调查. 公开发表的资料. 观察调查. 实验调查正确答案：4. 为了解女性对某种品牌化妆品的购买意愿,调查者在街头随意拦截部分女性进行调查。

这种调查方式是( ). 简单随机抽样. 整群抽样. 方便抽样. 自愿样本正确答案：5. 10家公司的月销售额数据(万元)分布为72,63,54,54,29,26,25,23,23,20。

下列哪些图形不宜用于描述这些数据( )。

. 散点图. 茎叶图. 条形图. 饼图正确答案：6. 假设总体服从均匀分布,从此总体中抽取样本容量为36的样本,则样本均值的抽样分布( )。

. 服从非正态分布. 近似正态分布. 服从均匀分布. 服从χ2分布正确答案：7. 下列不属于描述统计问题的是( )。

. 根据养病信息对总体进行推断. 感兴趣的总体或样本. 图、表或其他数据汇总工具. 对数据模式的识别正确答案：8. 在抽样之前先将总体的元素划分为若干群,然后再以群作为抽样单位从中抽取部分群,再对抽中的各个群中所包含的所有元素进行观察,这样的抽样方式称为( ). 简单随机抽样. 整群抽样. 系统抽样(等距抽样). 分层抽样(类型抽样)正确答案：9. 用简单随机重复抽样方法选取样本单位,如果要使抽样平均误差降低50%,则样本容量需要扩大到原来的( ). 2倍. 3倍. 4倍. 5倍正确答案：10. 在双侧检验中,如果将双侧的面积总和定义为P值,则给定的显著性水平α,拒绝原假设的准则是( )。

西南交通大学研究生2016－2017 学年第(1)学期考试试卷答案课程代码 课程名称 数理统计与多元统计 考试时间 150分钟 1、设总体X (0,1)N :，12n ,,,X X X L 是来自正态的简单随机样本，其中ξ=，321241)3i i n ii nX X η==-=∑∑（试推断统计量ξ和η的分布。

解：=(1)X t n ξ=-:（5分）32321122441)33(3-3)-3ii i i nniii i XnX F n XXn ====-=~∑∑∑∑（，（）（5分）2、设某种元件的使用寿命X 的概率密度为()1(;)0x ex f x x μθμθθμ--⎧≥⎪=⎨⎪<⎩其中00θμ>>，为未知参数，又设12,,,n x x x L 是X 的一组样本观测值，(1)试求参数,μθ的极大似然估计量；(2) 试求参数,μθ的矩估计量.解：1121()1(,,,)1(,,),ni i n nx i i ni L X X X f x ex μθθμθμμθ=--=∑==>∏L 极大似然函数为：（2分）1211ln (,,,)ln (),nn ii i L X X X n x x θμθμμθ==--->∑L （1分）21ln (,)1(),nii i L n x x μθμμθθθ=∂-=+->∂∑（2分）ln (,)0,i L nx θμμμθ∂=>>∂（2分）12(1)(2)(),,...,:...n x x x x x x ≤≤≤的顺序统计值为(1)1ˆmin i i nX X μ≤≤==,()X θ∧１＝Ｘ－,（2分） 1()x uEX xf x dx xedx μθθμθ--+∞+∞-∞===+⎰⎰（2分）22221()2()x uEX x f x dx x edxμθθμθθμ--+∞+∞-∞===++⎰⎰（2分）1222121211212()ˆˆn ii X X n X θθθθθθθθ=⎧+=⎪⎨++=⎪⎩⎧=⎪⎪⎨⎪=⎪⎩∑解方程得矩估计为：－（2分）3.抛一枚硬币，设正面向上的概率为θ，提出如下假设： 0113::24H H θθ==如果检验规则为：将该硬币抛掷5次，若正面向上的次数多余3次，则拒绝0H 。

西南交通大学研究生2015－2016 学年第(1)学期考试试卷课程代码 课程名称 数理统计与多元统计 考试时间 150分钟 题号 一 二 三 四 五 六 七 八 总成绩 得分阅卷教师签字：1．设129,,,XX X L 是来自正态总体X 的简单随机样本，其中1161()6Y X X =++L ，27891()3Y X X X =++,922271()2i i S X Y ==−∑，12)Y Y Z S−=试推断统计量Z 的分布。

（10分）解：因为129,,,X X X L 相互独立且服从正态分布2(,)N μσ，则有26111~(,)66i i Y X N σμ==∑，29271~(,)33i i Y X N σμ==∑----------------------------------（2分）且相互独立， 22212~(0,)(0,)632Y Y N N σσσ−+=，~(0,1)N -----------------------------（3分）又因2S 为样本方差，所以由定理得 2222~(2)S χσ，---------------------------------（2分）且2S 与1Y 与2Y 相互独立，故与12Y Y −也是相互独立的，于是由t 分布定义知12)~(2)Y Y Z t S −==---------------------------------（3分）即统计量Z 服从自由度为2的t 分布。

2. 设某种元件的使用寿命X的概率密度为2()2(;)0x e x f x x θθθθ−−⎧>=⎨≤⎩其中0θ>为未知参数，又设12,,,n x x x L 是X 的一组样本观测值，(1)试求参数θ的极大似然估计量ˆθ极；(2)求极大似然估计 ˆθ极的方差。

（15分）解：(1)由X 的概率密度函数，得似然函数112()112()22()(;)2=22(1,2,,)i nni i i i n nx i i i x x n nni L f x e eex i n θθθθθθ==−−==−−−+==∑∑=>=∏∏L ---------------------------------（2分）取对数得：1ln ()ln 222(1,2,,)ni i i L n x n x i n θθθ==−+>=∑L ---------------------------------（2分）再对θ求导得：ln ()20(1,2,,)i d L n x i n d θθθ=>>=L ---------------------------------（1分）即()L θ是单调增加的，虽然θ越大则()L θ越大，但θ必须满足条件(1,2,,)i x i n θ<=L所以当取θ为12,,,n x x x L 中最小值(1)x 时，()L θ取得满足条件的最大值，所以θ的最大似然估计值为(1)12ˆmin{,,,}nx x x x θ==L ---------------------------------（2分） （2）2()1()0x e x F x x θθθ−−⎧−≥=⎨<⎩---------------------------------（1分） 2()(1)1()1(1())0n x ne x F x F x x θθθ−−⎧−≥=−−=⎨<⎩---------------------------------（1分） 2()(1)(1)()2()0n x dF x ne x f x dxx θθθ−−⎧≥==⎨<⎩--------------------------------（1分）2()(1)122n x EX x ne dx nθθθ+∞−−==+∫--------------------------------（2分）22()2(1)1[]22n x E X x ne dx nθθθθ+∞−−==++∫--------------------------------（2分）22(1)(1)(1)2(21)11[][][]4n D X E X EX n n nθ−=−=+−------------------------------（1分）3. 假设0.50，1.25，0.80，2.00是来自总体X 的简单随机样本值，已知ln Y X =服从正态分布(,1)N μ。

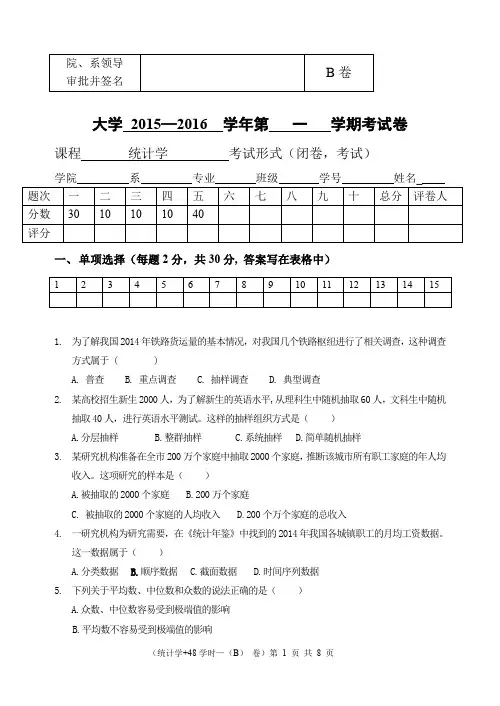
院、系领导B卷审批并签名大学2015—2016 学年第一学期考试卷课程统计学考试形式（闭卷，考试）学院系专业班级学号姓名_题次一二三四五六七八九十总分评卷人分数30 10 10 10 40评分一、单项选择（每题2分，共30分, 答案写在表格中）1 2 3 4 5 6 7 8 9 10 11 12 13 14 151.为了解我国2014年铁路货运量的基本情况，对我国几个铁路枢纽进行了相关调查，这种调查方式属于 ( )A. 普查B. 重点调查C. 抽样调查D. 典型调查2.某高校招生新生2000人，为了解新生的英语水平,从理科生中随机抽取60人，文科生中随机抽取40人，进行英语水平测试。

这样的抽样组织方式是（）A.分层抽样B.整群抽样C.系统抽样D.简单随机抽样3.某研究机构准备在全市200万个家庭中抽取2000个家庭，推断该城市所有职工家庭的年人均收入。

这项研究的样本是（）A.被抽取的2000个家庭B.200万个家庭C. 被抽取的2000个家庭的人均收入D.200个万个家庭的总收入4.一研究机构为研究需要，在《统计年鉴》中找到的2014年我国各城镇职工的月均工资数据。

这一数据属于（）A.分类数据B.顺序数据C.截面数据D.时间序列数据5.下列关于平均数、中位数和众数的说法正确的是（）A.众数、中位数容易受到极端值的影响B.平均数不容易受到极端值的影响C.无论左偏还是右偏分布，一般中位数都在平均数和众数之间D.任何一组数据都存在平均数、中位数和众数6. 在等距组距分组时，最末组是开口组，下限为500，相邻组的组中值为480，则最后组的组中值为（ ）A. 540B. 510C. 580D. 5207. 已知（123,,...x x x ）是来自总体的简单随机样本，在下列样本统计量中，属于总体均值的无偏估计量是（ ） A.22x B. 133x x + C.123x x + D.1233x x x ++8. 在其他条件不变的情况下，置信度（1-α）越大，则区间估计的（ ）A. 抽样推断的精确度越高B. 抽样推断的置信区间越小C. 抽样推断的可靠性越高D.抽样推断的极限误差越小9. 设总体为正态分布，μ，σ是总体均值与方差，其中总体方差已知，记（12325,,...x x x x ）是来自总体的简单随机样本，在对总体均值进行区间估计时，样本均值的抽样分布是（ ）A. N 2(,/25)μσB. N 2(,/25)μσ C. t(24) D. t(25)10. 假设检验中，如果原假设为真，而根据样本所得到的检验结论是拒绝原假设，则（ ）A. 犯了第一类错误B.犯了第二类错误C. 检验结论是正确的D. 备则假设是正确的 11. 检验多个正态总体均值是否相等时，应采用的检验法是（ ）A. Z 检验法B. t 检验法C.2χ检验法 D. F 检验法 12. 一元线性回归方程200 2.9c y x =-，则x 与y 之间的相关系数（ ）A. r=0B. r=1C. 0<r<1D. -1<r<0 13. 在方差分析中，总离差平方和反映（ ）A. 由试验因素变化引起的观测值的差异程度B. 由随机波动引起的观察值的差异程度C. 全部观察值的差异程度D. 组间离差平方和14. 若随机变量X~N (2,μσ)，Z~N (0,1)，则下列等式成立的是（ ）A. Z X μσ-=B. Z X σμ-=C. X Z σμ-=D. X Z μσ-=15. 设随机事件A 、B 及和事件B A 的概率分别是0.4、0.3和0.6，则事件AB 的概率为（ ）A.0.3B.0.4C.0.12D.0.1二、判断（错的打“×”, 对的打“√”, 每题1分，共10分） 1 23 4 5 6 7 8 9 101. 统计量是用来描述样本特征的概括性数字度量，它是根据样本数据计算出来的一些量，是样本的函数。

西南交通大学2015－2016学年第1学期第1次测试卷课程名称 高等数学I 考试时间 60 分钟阅卷教师签字：一. 填空题（每小题5分，共20分）1、已知25lim 232n a bn n →∞++=-，则a = 任意常数 ，b = 6 .2、设常数12a ≠，则21limln (12)nn n na n a→∞⎡⎤-+=⎢⎥-⎣⎦112a - . 3、当0x →时，2()x kx α=与()x β=是等价无穷小量， 则k =34. 4、设2(1)()lim 1n n xf x nx →∞-=+，则()f x 的间断点x = 0.二. 计算和解答题（共80分）1、计算下列极限：（每小题6分，共24分）（1）201sin(sin )limx x x x→； （2）n→∞-； 解：原式=2001sin1lim=lim sin 0x x x x x x x→→=. 解：原式=32n n ==.班 级 学 号 姓 名密封装订线 密封装订线 密封装订线（3）0x →； （4）02lim x x x →⎡⎤⎢⎥⎣⎦.解: 原式= 解：2221x x x⎡⎤-<≤⎢⎥⎣⎦，当0x >时，有x → 222x x x ⎡⎤-<≤⎢⎥⎣⎦；当0x <时，有=012x →=. 222x x x ⎡⎤->≥⎢⎥⎣⎦. 而0lim(2)2x x →-=，故利用夹逼定理知,02lim 2x x x →⎡⎤=⎢⎥⎣⎦.2、确定,αβ的值，使得1sin 0,() ,0x x f x xx αβ⎧≠⎪=⎨⎪=⎩，在0x =处连续.（10分） 解：当0α≤时，01lim sinx x xα→不存在；（5分） 当0α>时，01lim sin0x x xα→=. 故当0α>，0β=时，()f x 在0x =处连续. （5分） 3、讨论函数1sin ,0,()0,0x x f x xx ⎧≠⎪=⎨⎪=⎩在0x =处的连续性与可导性.（11分） 解：001lim ()lim sin0(0)x x f x x f x→→===，因此，()f x 在0x =处连续.（5分）极限00()(0)1lim lim sinx x f x f x x∆→∆→∆-=∆∆不存在，因此，()f x 在0x =处不可导.（6分）4、计算下列函数的导数：（每小题6分，共24分） （1）求22sin sin()y x x =⋅的导数. （2）求arcsin y =.解：（1）2222sin cos sin()sin 2cos()y x x x x x x '=⋅+⋅;(2) 21'1y x =+.（3）求2ln cos y x x x =的导数. （4）求1ln 1ln xy x-=+的导数.解：（3）22cos ln cos sin ln y x x x x x x x x '=⋅+-;(4) 2211(1ln )(1ln )2'(1ln )(1ln )x x x x y x x x -+---==++. 5、设()y f x =在[,)a +∞上连续，且lim ()x f x A →+∞=（A 为有限值）. 证明：()f x 在[,)a +∞上有界.（11分）证明：（注意：本题证明过程的写法不是唯一的，关键在于证明的思路是否正确） 因为lim ()x f x A →+∞=，所以对于1ε=（也可以取其它的数），存在0X >，当x X >时，有|()|1f x A -<，即1()1A f x A -<<+. （4分）又因为()f x 在[,]a X 上连续，所以()f x 在[,]a X 上存在最大值M 和最小值m . （4分）取max{||,||,|1|,|1|}K M m A A =-+，对一切[,)x a ∈+∞，有|()|f x K ≤，即()f x 在[,)a +∞上有界.（3分）。

XX师范大学2015–2016学年第二学期
期末考试试卷（B卷）参考答案
课程名称数理统计课程编号 XXXXXXX 任课教师
题型选择题填空题计算题证明题总分
分值15 15 50 20 100
得分
得分评阅人
一、：选择题（共5题，每题3分，共15 分）
1、样本取自正态分布总体，已知，但= 未知，则下列随机变量中不能作为统计量的是（ C ）
A. ；
B. ；
C. ；
D.
2、设总体，为其子样，，
，则有（ B ）
A．是2的矩估计量B．是2的极大似然估计
量 C．是2的最优无偏估计量D．是的优效估计量
3、在假设检验中，犯第二类错误概率的意义是( C )
A. 原假设H成立，经检验否定H的概率
00
B. 原假设H成立，经检验不否定H的概率
00
C. 备择假设成立，经检验否定的概率
D. 备择假设
H成立，经检验不否定的概率
1
4、设为正态总体的一个样本，表示样本均值，则的置信度为的
置信区间为( C )
A. B.
C. D.
5、关于最小二乘法估计量的性质，下面说法不正确的是（ B ）
A. 是的线性无偏估计量
B. 不是一个统计量
C. 是的极大似然估计量
D. 在的线性估计量中最优。

西南交大09～10第二学期《概率论与数理统计B》期末试题1西南交通大学2021－2021学年第(二)学期考试试卷班级学生人数姓名课程代码2100031课程名称概率论与数理统计B考试时间120分钟密封装订线密封装订线密封装订线题号一二三四五六七八九十总成绩得分批改老师签名考生注意：1．请将班级、学号、姓名填写清楚；2．所有题目的答案写在后面。

一．判断题（对的打“√”，错的打“?”，每题2分，共10分）1.如果a和B是随机事件，那么一定有p（AB）？1.p（ab）。

（2）假设事件a和B 彼此独立，而P（a）？0.1，p（b）？0.2，则a和B不能彼此不兼容（3）让样本x1、X2和X3来自群体n（？，），和那就不知道了221?2?xi?13i是一个统计量.（）4.如果e（x2）？那么一定有p（x×0）？1. ()5. 假设二维随机变量（x，y）的分布函数为f（x，y），那么f（1,2）？1.p（x？1，y？2）。

（）二．选择题（每题3分，共30分）1.如果x和y是任意两个随机变量，cov（x，y）已知吗？0，必须有（）（a）x与y相互独立（b）d(xy)?dxdy（c）e(xy)?exey（d）d(x?y)?dx?dy2．下列各函数中可以作为某个随机变量的分布函数的是（）（a）f(x)?1（b）f(x)?sinx1?x2?1?（c）f(x)??1?x2??1?0x?0x?0?（d）f(x)??1.2x?0? 1x？0x？0 3. 如图所示，构成系统的四个电子元件的可靠性为p，每个元件能否正常工作是相互关联的2134独立的，则系统的可靠性为（）；（a）p4（b）p3?p2（c）p3?2p4（d）2p3?p44．设随机事件a,b互不相容，则必有（）（a） p（a）？1.p（b）（b）p（a？b）？1（c）p（ab）？p（a）p（b）（d）p （ab）？一5．设x1,x2,?,xn为来自正态总体n(0,1)的简单随机样本，x和s2分别为样本均值和样本方差，则（）nxn？t（n？1）（b）？xi2？？2（n？1）（a）si？1（c）x？n（0,1）（d）nx？n （0,1）6．已知x～e()，且y?2x?1，利用切比雪夫不等式估计p(0?y?10)（）（a）?991616（b）?（c）?（d）?25252525127．设随机变量x和y相互独立，且都服从[0,1]区间上的均匀分布，则服从相应区间或区域上的均匀分布的随机变量是（）（a） x2（b）x？y（c）x？Y（d）（x，Y）8。

北 京 交 通 大 学2015~2016学年第一学期概率论与数理统计阶段测验（二）试卷参 考 答 案一．（本题满分10分）设二维随机变量()Y X ,的联合密度函数为()()⎩⎨⎧<<<-=其它0101,y x y c y x f ⑴ 求常数c （5分）；⑵ 求概率{}1<+Y X P （5分）． 解：⑴ 由密度函数的性质：()1,=⎰⎰+∞∞-+∞∞-dxdy y x f ，得()()⎰⎰⎰⎰-==+∞∞-+∞∞-y dx y c dy dxdy y x f 011,1()()6312111210cc dy y y c ydy y c =⎪⎭⎫ ⎝⎛-=-=-=⎰⎰，由此得6=c ． ⑵ {}()⎰⎰<+=<+1,1y x dxdy y x f Y X P()⎰⎰⎰-=-⎪⎪⎭⎫⎝⎛-=-=2101212102616dx y y dy y dx xx y x x ()434121321321=⎪⎭⎫ ⎝⎛-=-=⎰dx x ．二．（本题满分10分）设随机变量Y 服从参数为1=λ的指数分布，定义随机变量k X ，()2,1=k 如下：⎩⎨⎧>≤=k Y kY X k 10 求二维随机变量()21,X X 的联合分布列．解：由题设，得随机变量Y 的密度函数为()⎩⎨⎧≤>=-0x x e y f y． ()()()()111121112,100---∞--=-===≤=≤≤===⎰⎰e e dy e dy yf Y P Y Y P X X P y y ，()()()02,11021=∅=>≤===P Y Y P X X P ，()()()()2121212121112,101-----=-===≤<=≤>===⎰⎰e e edy e dy y f Y P Y Y P X X P y y，()()()()22222122,111-∞+-+∞-+∞=-===>=>>===⎰⎰e e dy e dy yf Y P Y Y P X X P yy ．因此，()21,X X 的联合分布列为三．（本题满分12分）设二维随机变量()Y X ,的联合密度函数为()⎪⎩⎪⎨⎧<<=其它01421,22y x y x y x f ．⑴ 求随机变量X 及Y 各自的边缘密度函数()x f X 与()y f Y （8分）；⑵ 判断随机变量X 与Y 是否相互独立（4分）？ 解：⑴ 当11<<-x 时， ()()()4212212182121421421,22x x y x ydy x dyy x f x f x x X -=⋅===⎰⎰+∞∞-， 所以，随机变量X 的边缘密度函数为()()⎪⎩⎪⎨⎧<<--=其它11182142x x x x f X ．当10<<y 时， ()()2523322724731421421,y y y y y ydy x dx y x f y f yyyyY =⋅=⋅===--+∞∞-⎰⎰， 所以，随机变量Y 的边缘密度函数为()⎪⎩⎪⎨⎧<<=其它102725y yx f X ． ⑵ 因为()()()y f x f y x f Y X ≠,，所以随机变量X 与Y 不独立．四．（本题满分12分）设随机变量X 与Y 相互独立，下表给出()Y X ,的联合分布列及X 与Y 各自的边际分布的某些取值：试计算该表的其它数值． 解：()()()2418161,,12111=-===-====y Y x X P y Y P y Y x X P ， ()()()4161241,1111=======y Y P y Y x X P x X P ，()()()()1218124141,,,2111131=--===-==-====y Y x X P y Y x X P x X P y Y x X P ， ()()()214181,1212=======x X P y Y x X P y Y P ，()()()3141121,1313=======x X P y Y x X P y Y P ，()()43411112=-==-==x X P x X P ，()()()838121,,21222=-===-====y Y x X P y Y P y Y x X P ， ()()()4112131,,31332=-===-====y Y x X P y Y P y Y x X P ．表中其余各值如下表所示：可以验证，对于上述表中各值，X 与Y 相互独立．五．（本题满分12分）将3个球随机地放入4个杯子中．令X 表示杯子中球的最大个数．求：⑴ X 的分布列（6分）；⑵ X 的数学期望()X E 与方差()X D （6分）． 解：⑴ X 的可能取值为3,2,1．且{}8341334===P X P ．{}1614433===X P ．{}{}{}1691618313112=--==-=-==X P X P X P ．所以，随机变量X 的分布列为⑵ ()1616316281=⨯+⨯+⨯=X E ．()1651161316928312222=⨯+⨯+⨯=X E ．因此，()()()()2568716271651222=⎪⎭⎫ ⎝⎛-=-=X E X E X D ． 六．（本题满分10分）记掷n 颗均匀的骰子点数之和为X ，求()X E （5分）与()X var （5分）． 解：以k X 表示掷第k 颗均匀的骰子出现的点数，()n k ,,2,1 =，则随机变量n X X X ,,,21相互独立，而且同分布，∑==nk k X X 1．k X 的分布列为所以，(){}27621616161====⋅=∑∑==k k k k k X P k X E ． (){}691616126122===⋅=∑∑==k k kk k X P k XE所以，()()()()1235273691var 222=⎪⎭⎫ ⎝⎛-=-=k k k X E X E X ．因此，()()n X E X E X E nk nk k n k k 2727111===⎪⎭⎫ ⎝⎛=∑∑∑===．再由n X X X ,,,21 的相互独立性，得()()n X X X nk nk k n k k 12351235var var var 111===⎪⎭⎫ ⎝⎛=∑∑∑===．七．（本题满分14分）一射手进行射击，击中目标的概率为p ()10<<p ，射击直至击中2次目标时为止．令X 表示首次击中目标所需要的射击次数，Y 表示总共所需要的射击次数． ⑴ 求二维随机变量()Y X ,的联合分布律（6分）． ⑵ 求随机变量Y 的边缘分布律（4分）．⑶ 求在n Y =时，X 的条件分布律．并解释此分布律的意义（4分）． 解：⑴ 随机变量Y 的取值为 ,4,3,2；而随机变量X 的取值为1,,2,1-n ，并且 (){}次第次，第二次命中目标在第一次命中目标在第n m P n Y m X P ===, 2211p q p q p q n m n m ----=⋅=， （其中p q -=1） ()1,,2,1;,4,3,2-==n m n ．⑵ ()()()221122111,p q n p q n Y m X P n Y P n n m n n m --=--=-======∑∑，() ,4,3,2=n ． 即随机变量Y 的边缘分布律为()()221p q n n Y P n --== () ,4,3,2=n ．⑶ 由于()()()()111,2222-=-=======--n p q n p q n Y P n Y m X P n Y m X P n n 因此在n Y =时，X 的条件分布律为 ()11-===n n Y m X P ()1,,2,1-=n m 这表明，在n Y =的条件下，X 的条件分布是一个“均匀”分布．它等可能地取值1,,2,1-n ．八．（本题满分10分）设随机变量X 与Y 相互独立，且都服从标准正态分布()1,0N ．令随机变量22Y X Z +=．⑴ 试求随机变量Z 的密度函数()z f Z （6分）．⑵ 试求()Z E （4分）．⑴ 由题意，得()2221x X ex f -=π ()∞<<∞-x ， ()2221y y ey f -=π()∞<<∞-y ．设随机变量22Y X Z +=的分布函数为()z F Z ，则(){}{}z Y X P z Z P z F Z ≤+=≤=22当0≤z 时，(){}()022=∅=≤+=P z Y X P z F Z ；当0>z 时，(){}()()⎰⎰≤+=≤+=zy x YXZdxdy y f x f z Y XP z F 2222⎰⎰≤++-=zy x y x dxdy e 2222221π作极坐标变换θθsin ,cos r y r x ==，则有()⎰⎰⎰--==zr zr Z rdr erdr ed z F 022202221πθπ所以，随机变量22Y X Z +=的分布函数为()⎪⎩⎪⎨⎧≤>=⎰-000022z z rdre z F z rZ所以，随机变量22Y X Z +=的密度函数为()()⎪⎩⎪⎨⎧≤>='=-0022z z zez F z f z Z Z ⑵ ()()⎰⎰⎰∞+-+∞-∞+-∞+∞-+-===2222222dz ezedz e zdz z f z Z E z z z z222212222ππ====⎰⎰+∞∞--+∞-dz e dz ez z ． 九．（本题满分10分）设G 是由X 轴、Y 轴及直线022=-+y x 所围成的三角形区域，二维随机变量()Y X ,在G 内服从均匀分布．① 求X 与Y 的相关系数（6分）；② 计算概率{}X Y P ≥（4分）．（1） 由于区域G 的面积为1，因此()Y X ,的联合密度函数为()()()⎩⎨⎧∉∈=Gy x G y x y x f ,,1,．当10<<x 时，()()()x dy dy y x f x f xX -===⎰⎰-+∞∞-12,220，所以，()()⎩⎨⎧<<-=其它01012x x x f X ．当20<<y 时，()()21,210ydy dx y x f y f yY -===⎰⎰-∞+∞-， 所以，()⎪⎩⎪⎨⎧<<-=其它2021y y y f Y ．()()()3131212121=⎪⎭⎫ ⎝⎛-=-⋅==⎰⎰+∞∞-dx x x dx x xf X E X ， ()()32212=⎪⎭⎫ ⎝⎛-⋅==⎰⎰+∞∞-dy y y dy y yf Y E Y ， ()()()6141312121222=⎪⎭⎫ ⎝⎛-=-⋅==⎰⎰+∞∞-dx x x dx x f x XE X，()()32212222=⎪⎭⎫⎝⎛-⋅==⎰⎰+∞∞-dy y ydy y f y Y E Y，所以，()()()()1813161var 222=⎪⎭⎫ ⎝⎛-=-=X E X E X ，()()()()923232var 222=⎪⎭⎫ ⎝⎛-=-=Y E Y E Y ， ()()⎰⎰⎰⎰⎰--+∞∞-+∞∞-⋅===1220222012,dx y x xydy dxdxdy y x xyf XY E xx，()()6121324122212123102=⎪⎭⎫ ⎝⎛+-=+-=-=⎰⎰dx x x x dx x x ，所以，()()()()181323161,cov -=⨯-=-=Y E X E XY E Y X ．()()()2192181181var var ,cov ,-=-==Y X Y X YX ρ．（2） {}()()()2123232,1121=-=-===≥⎰⎰⎰⎰⎰-≥dx x dy dxdxdy y x f X Y P x xxy ．。

中国农业大学2015 ~2016学年秋季学期概率论与数理统计（C ）课程考试试题（A ）一、 填空题 （每空3分，满分21分）1．已知()0.3P B =，()0.6 P A B =，则()P AB =_______。

2．某人向同一目标独立重复射击，每次射击命中目标的概率为(01)p p <<，则此人3次射击中恰好命中2次目标的概率为_______。

3.设总体X 服从参数为2θ=的指数分布，12,,...n X X X 为总体的一个样本，则当n →∞时，211n i i Y X n ==∑依概率收敛于_______。

4．若X 服从参数为λ的泊松分布，且[(1)(2)]1E X X --=，则λ=_______。

5. 在每次实验中，事件A 发生的概率为0.5，利用切比雪夫不等式估计：在1000次独立实验中事件A 发生的次数在400次到600次之间的概率至少为_______。

6.已知总体~(0,1)X N ，2S 为样本方差，设样本容量为9，则2()D S =_______。

7. 在区间(0, 1)中随机取两个数，则两数之差的绝对值小于0.5的概率为______。

二、选择题 （每题3分，满分15分）1.设有随机事件,,A B C 两两独立，则事件,,A B C 相互独立的充要条件是（ ） （A ）A 与BC 独立 （B ）AB 与 A C 独立 （C ）AB 与AC 独立 （D ） A B 与 A C 独立2．设随机变量X 服从正态分布2(,)N μσ，当2σ增大时，则{}||P X μσ-<的值必将（ ）（A ）减小 （B ）增大 （C ）不变 （D ）增减不定考生诚信承诺1． 本人清楚学校关于考试管理、考场规则、考试作弊处理的规定，并严格遵照执行。

2． 本人承诺在考试过程中没有作弊行为，所做试卷的内容真实可信。

专业：____ ____ 班级：____ ____学号：____ ____姓名：____ ____3．设随机变量X 和Y 的方差存在且不等于0，则表达式()()()D X Y D X D Y +=+是X 和Y （ ）（A ）不相关的充分条件，但不是必要条件 （B ）独立的必要条件，但不是充分条件 （C ）不相关的充分必要条件（D ）独立的充分必要条件4．设12,,...,n X X X 是来自正态总体2(0,)N σ的一个样本，X 与2S 分别是样本均值与样本方差，则下列正确的是（ ）（A ）22~(1)Xχσ（B ）222~(1)S n χσ-（C ）~(1)X t n S - （D ）22~(1,1)S F n nX- 5．设总体X 服从正态分布2(,)N μσ，其中2σ已知，若在置信度不变的情况下增大样本容量n ，总体均值μ的置信区间的长度会（ ） （A ）随之增大（B ）增减不变 （C ）随之减小 （D ）增减不定三．（10分）已知有三个箱子，第一个箱子中有2个红球3个白球，第二个箱子中有1个红球4个白球，第三个箱子中有3个红球。

西南交《统计学》在线作业二一、单选题（共 25 道试题，共 50 分。

）1. 为了顾及某城市愿意乘坐公共汽车上下班的人数所占的比例，在收集数据时，最可能采用的数据搜集方法是（）。

. 普查. 公开发表的资料. 随即抽样. 实验正确答案：2. 一个样本或总体中各个部分的数据与全部数据之比称为（）. 频数. 频率. 频数分布. 累计频数正确答案：3. 根据中心极限定理，在处理样本均值的抽样分布时，可以忽略的信息是（）. 总体标准差. 总体的分布形态. 总体均值. 在应用中心极限定理时，所有的信息都可以忽略正确答案：4. 某大学的一家快餐店记录了过去5年每天的营业额，每天营业额的均值为2500元，标准差为400元。

由于在某些节日的营业额偏高，所以每日营业额的分布是右偏的。

假设从这5年中随机抽取100天，并计算这100天平均营业额，则样本均值的抽样分布是（）. 右偏分布，均值为2500元，标准差为400元. 正态分布，均值为2500元，标准差为40元. 正态分布，均值为250元，标准差为40元. 正态分布，均值为2500元，标准差为400元正确答案：5. 1990年发表的一篇文章讨论了男性和女性M毕业生起薪的差别。

文章称，从前20名商学院毕业的女性M的平均起薪是54749美元，中位数是47543美元，标准差是10250美元。

如果用图示法描述上述数据，则不宜使用的方法是（）. 直方图. 茎叶图. 箱线图. 饼图正确答案：6. 调查时首先选择一组调查单位，对其实施调查之后，再请他们提供另外一些属于研究总体的调查对象，调查人员根据所提供的线索，进行此后的调查。

这种调查方式是（）。

. 系统抽样. 分层抽样. 滚雪球抽样. 判断样本正确答案：7. 对于时间序列数据，用于描述其变化趋势的图形是（）. 条形图. 茎叶图. 直方图. 线图正确答案：8. 下列叙述中，错误的是（）。

. 抽样误差是可以避免的. 非抽样误差是可以避免的. 抽样误差是不可避免的. 抽样误差是可以控制的正确答案：9. 如果一样本因人为故意操纵而出现偏差，这种误差属于（）。

交 通 大 学2015~2016学年第二学期概率论与数理统计期末考试试卷（A 卷）一．（本题满分9分）假设一个人在一年中患感冒的次数X 服从参数为4=λ的Poisson 分布．现有一种预防感冒的新药，它对于22%的人来讲，可将上面的参数λ降为1=λ（称为疗效显著）；对37%的人来讲，可将上面的参数λ降为3=λ（称为疗效一般）；而对于其余的人来讲则是无效的．现有一人服用此药一年，在这一年中，他患了2次感冒，求此药对他是“疗效显著”概率有多大？ 解：设{}此药疗效显著=1A ，{}此药疗效一般=2A ，{}此药无效=3A ， {}次感冒某人一年中患2=B ．由题设，可知如果事件1A 发生，则X 服从参数为1=λ的Poisson 分布；如果事件2A 发生，则X 服从参数为3=λ的Poisson 分布；如果事件3A 发生，则X 服从参数为4=λ的Poisson 分布．因此，由Bayes 公式，我们有 ()()()()()∑==31111k kkA BP A P A B P A P B A P2206.02441.02337.02122.02122.042321212=⨯+⨯+⨯⨯=----ee e e． 二．（本题满分8分）一房间有3扇同样大小的窗户，其中只有一扇是打开的．有一只鸟在房子里飞来飞去，它只能从开着的窗子飞出去．假定这只鸟是没有记忆的，而且鸟飞向各个窗子是随机的．若令X 表示鸟为了飞出房间试飞的次数．求⑴ X 的分布律（4分）．⑴ 这只鸟最多试飞3次就飞出房间的概率（4分）． 解：⑴ X 的取值为 ,3,2,1，并且{}{}313211⋅⎪⎭⎫⎝⎛=-==-k k k P k X P 次试飞飞出房间第次试飞均未飞出房间，前 因此X 的分布律为{}31321⋅⎪⎭⎫⎝⎛==-k k X P () ,3,2,1=k ． ⑵ {}{}27193132313231332=⋅⎪⎭⎫ ⎝⎛+⋅+=≤=X P P 次就飞出房间这只鸟最多试飞． 三．（本题满分10分）设随机变量X 的密度函数为()⎩⎨⎧<<+=其它0102x bx ax x f ， 并且已知()21=X E ，试求方差()X D ． 解：由()1=⎰+∞∞-dx x f 及()()21==⎰+∞∞-dx x xp X E ，得 ()()321102b a dx bx ax dx x f +=+==⎰⎰+∞∞-， ()()432112ba dx bx ax x dx x xf +=+==⎰⎰+∞∞-．由此得线性方程组 ⎪⎩⎪⎨⎧=+=+2143132b a ba ．解此线性方程组，得6,6-==b a ． 所以，()()()1035164166612222=⋅-⋅=-==⎰⎰+∞∞-dx x x x dx x f x XE ，所以，()()()()20121103var 222=⎪⎭⎫ ⎝⎛-=-=X E X E X ．四．（本题满分10分）设随机变量X 与Y 相互独立，()1,0~U X 分布，Y 服从参数1=λ的指数分布．令Y X Z +=，求随机变量Z 的密度函数()z f Z ． 解：由题设，随机变量X 及Y 的密度函数分别为()⎩⎨⎧<<=其它0101x x f X ，()⎩⎨⎧≤>=-000y y e y f y Y ．所以，随机变量Y X Z +=的密度函数为 ()()()()⎰⎰-=-=+∞∞-1dx x z f dx x z f x f z f Y YXZ ．作变换x z u -=，则dx du -=，有 ()()()⎰⎰--=-=zz Yz z Y Z du u f du u f z f 11．① 若0≤z ，在区间[]z z ,1-上，()0≡u f Y ，因此，()0=z f Z ． ② 若10≤<z ，则01≤-z ，因此， ()()()z zuz z Y z YZ e du edu du u f du u f z f -----=+=+=⎰⎰⎰⎰1000101．③ 若1>z ，则01>-z ，有 ()z z z z u zz u Z e e e du e z f -------=-==⎰111．综上所述，随机变量Y X Z +=的密度函数为()⎪⎩⎪⎨⎧>-≤<-≤=---1101001x e e x e z z f z z zZ ． 五．（本题满分15分）设二维随机变量()Y X ,服从二元正态分布，其联合密度函数为()()()()()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-+-------=22222121212122212121ex p 121,σμσσμμσμσπσy y x r x r r y x f ， 其中r ,,,,2121σσμμ均为参数．⑴ 求随机变量X 及Y 的边际密度函数()x f X 及()y f Y （7分）；⑵ 通过观察()y x f ,，()x f X 及()y f Y ，你总结到什么结论？（8分）解：⑴ 对()Y X ,的联合密度函数中的()()()()()⎥⎦⎤⎢⎣⎡-+------22222121212122121σμσσμμσμy y x r x r 进行配方，得 ()()()()()⎥⎦⎤⎢⎣⎡-+------22222121212122121σμσσμμσμy y x r x r ()()()⎥⎥⎦⎤⎢⎢⎣⎡--⎪⎪⎭⎫ ⎝⎛---+---=212122112221212121σμσμσμσμx r x r y x r ()()21122221211212⎪⎪⎭⎫⎝⎛-------=σμσμσμx r y r x ． 所以，()()⎰+∞∞-=dy y x f x f X ,()()⎰∞+∞---⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎪⎭⎫⎝⎛------=dy x r y r erx 2112222221121exp 1212121σμσμσπσσμ． 作变换()⎪⎪⎭⎫ ⎝⎛----=1122211σμσμx r y r u ，则()221r dydu -=σ．因此有()()()()212121212212121212212122121σμσμσμσπππσπσ----∞+∞----=⋅==⎰x x u x X e e du eex f ．即随机变量X 的边际密度函数为()()21212121σμσπ--=x X e x f ，()+∞<<∞-x ．注意到()Y X ,的联合密度函数中的x 与y 的地位对称，得随机变量Y 的边际密度函数为 ()()22212221σμσπ--=y Y e y f ，()+∞<<∞-y ．⑵ 通过观察()y x f ,，()x f X 及()y f Y ，我们总结到以下结论：① 二元正态分布的两个边际分布分别是两个一元正态分布，即()211,~σμN X ，()222,~σμN Y ．② ()X E =1μ，()Y E =2μ，()X var 21=σ，()Y var 22=σ． ③ 二元正态分布的两个边际分布仅与二元正态分布中五个参数r ,,,,2121σσμμ中的四个参数2121,,,σσμμ有关系，而与参数r 没有关系． ④ 如果二维随机变量()11,Y X 服从二元正态分布，密度函数为()()()()()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-+-------=222221************12121ex p 121,σμσσμμσμσπσy y x r x r r y x f ， 二维随机变量()22,Y X 也服从二元正态分布，密度函数为()()()()()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-+-------=222221************12121ex p 121,σμσσμμσμσπσy y x r x r r y x g ， 则()11,Y X 与()22,Y X 不同分布，但是，()2111,~σμN X ，()2112,~σμN X ；()2221,~σμN Y ，()2222,~σμN Y ．即1X 与2X 同分布，1Y 与2Y 同分布．六．（本题满分10分）将一颗均匀的骰子独立地掷10次，令X 表示这10次出现的点数之和，求()X E （5分）与()X D （5分）． 解：设k X 表示第k 次出现的点数，()10,,2,1 =k ． 则1021,,,X X X 相互独立，而且∑==101k k X X ．而k X 的分布列为 ()61==j X P k ，()6,,2,1 =j ． 所以，()()∑∑==⋅==⋅=616161j j k k j j X P j X E2721616161=⨯==∑=j j ， ()10,,2,1 =k ．所以，由数学期望的性质，得()()35102727101101101=⨯===⎪⎭⎫ ⎝⎛=∑∑∑===k k k k k X E X E X E ．()()∑∑==⋅==⋅=612612261j j k kj j X P jXE691916161612=⨯==∑=j j ， ()10,,2,1 =k ．所以，由1021,,,X X X 的相互独立性，及数学期望的性质，得()()345510691691101101101=⨯===⎪⎭⎫ ⎝⎛=∑∑∑===k k k k k X D X D X D ．七．（本题满分10分）设二维随机变量()Y X ,的联合密度函数为()⎩⎨⎧<<<=其它0103,x y x y x p ， 求X 与Y 的协方差()Y X ,cov 及相关系数Y X ,ρ． 解：()()4333,13102====⎰⎰⎰⎰⎰+∞∞-+∞∞-dx x dy x dx dxdy y x xp X E x ， ()()83233,103100====⎰⎰⎰⎰⎰+∞∞-+∞∞-dx x ydy xdx dxdy y x yp Y E x，()()5333,141322====⎰⎰⎰⎰⎰+∞∞-+∞∞-dx x dy x dx dxdy y x p x XE x，()()513,1410222====⎰⎰⎰⎰⎰+∞∞-+∞∞-dx x dy y xdx dxdy y x p y Y E x ，()()103233,1041002====⎰⎰⎰⎰⎰+∞∞-+∞∞-dx x ydy dx x dxdy y x xyp XY E x ，所以有协方差为 ()()()()16038343103,cov =⨯-=-=Y E X E XY E Y X ， ()()()()8034353222=⎪⎭⎫ ⎝⎛-=-=X E X E X D ，()()()()320198351222=⎪⎭⎫ ⎝⎛-=-=Y E Y E Y D ， 因此，有()()()573320198031603,cov ,=⋅==Y D X D Y X Y X ρ． 八．（本题满分8分）某餐厅每天接待400位顾客，假设每位顾客的消费额（单位：元）服从区间()100,20上的均匀分布，并且每位顾客的消费额是相互独立的．试求：⑴ 该餐厅每天的平均营业额；⑴ 用中心极限定理计算，该餐厅每天的营业额在平均营业额760±元内的概率．（附：正态分布的分布函数()x Φ的某些取值：解：⑴ 设i X 表示第i 位顾客的消费额，()400,,2,1 =i ．则有 40021,,,X X X 相互独立，()100,20~U X i ，()400,,2,1 =i ．所以，()60=i X E ，()316001280var 2==i X ． 再设X 表示餐厅每天的营业额，则∑==4001i i X X ．所以，()()240006040040014001=⨯==⎪⎭⎫ ⎝⎛=∑∑==i i i i X E X E X E （元）．⑵ 由独立同分布场合下的中心极限定理，有{}⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⨯≤⨯-≤⨯-=≤-≤-3160040076031600400240003160040076076024000760X P X P()901.019505.021645.123160040076031600400760=-⨯=-Φ=⎪⎪⎪⎪⎭⎫⎝⎛⨯-Φ-⎪⎪⎪⎪⎭⎫ ⎝⎛⨯Φ≈． 九．（本题满分10分）罐中有N 枚硬币，其中θ枚是普通硬币，它掷出正面与反面的概率均为5.0；其余θ-N 枚硬币的两面都是正面．现从罐中随机取出一枚硬币，将它连掷两次并记下其结果，但不去查看它属于哪一种硬币，然后把它放入罐中．如此重复n 次，若掷出0次正面的次数为0n ，1次正面的次数为1n ，2次正面的次数为2n ，（n n n n =++210）．试求参数θ的极大似然估计量L θˆ（提示：令X 表示从罐中取出一枚硬币掷出的正面数，先求X 的分布律）． 解：设X 表示从罐中取出一枚硬币掷出的正面数，则X 取值为2,1,0．并且()N N X P 42121;0θθθ=⋅⋅==，()N N X P 221;1θθθ=⋅==， ()NN N N N N N N X P 434444412121;2θθθθθθ-=-+=⋅-+⋅⋅==． 所以，似然函数为()()()()()()()210;2;1;0nnnX P X P X P L θθθθ====21043424n n n N N N N ⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=θθθ取对数，得()()()()()()()()N N n N n N n L 4ln 34ln 2ln ln 4ln ln ln 210--+-+-=θθθθ． 上式对θ求导数，得()()θθθθθθθ343343ln 1010210----+=--+=N n n n n n N n n n L d d ， 令()0ln =θθL d d ，得似然方程()03431010=----+θθN n n n n n ， 解方程，得解()1034n n n N+=θ，因此参数θ的极大似然估计量为()1034ˆn n nN L +=θ． 十．（本题满分10分） 设总体X 的密度函数为()()⎪⎩⎪⎨⎧<<-=其它0063θθθx x xx f ，其中0>θ是未知参数，()n X X ，， 1是从该总体中抽取的一个样本．⑴. 求未知参数θ的矩估计θˆ； ⑴. 判断θˆ是否为参数θ的无偏估计；⑴. 求方差()θˆD ． 解：⑴. ()()()26032θθθθ=-==⎰⎰+∞∞-dx x x dx x xf X E ，所以，()X E 2=θ ，将()X E 用样本均值∑==ni i X n X 11来替换，得未知参数θ的矩估计为X 2ˆ=θ⑵. 由于()()()()θθθ=⨯====22222ˆX E X E X E E 所以，X 2ˆ=θ是参数θ的无偏估计． ⑶. ()()()()X D nX D X D D 442ˆ===θ，而 ()()()[]22X E X E X D -=()()204622203322θθθθθθ=--=⎪⎭⎫⎝⎛-=⎰⎰+∞∞-dx x x dx x f x所以，()()nn X D n D 52044ˆ22θθθ=⨯== ．。