汇编作业第2章

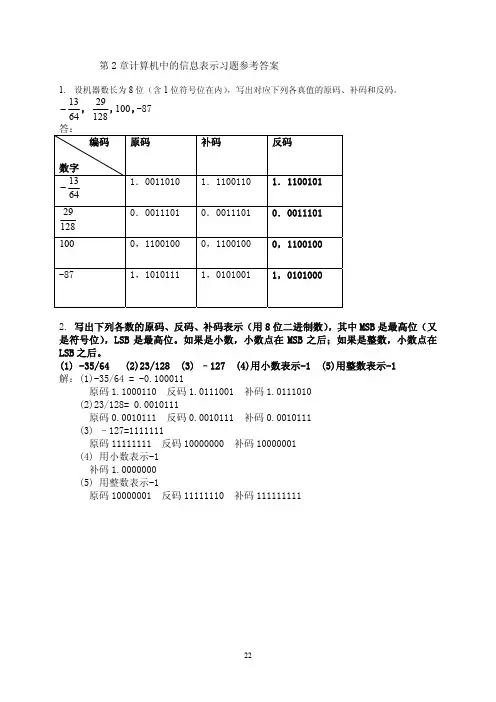
第2章计算机中的信息表示习题参考答案1. 设机器数长为8位（含1位符号位在内），写出对应下列各真值的原码、补码和反码。

6413−, 12829,100,-872. 写出下列各数的原码、反码、补码表示（用8位二进制数），其中MSB 是最高位（又是符号位），LSB 是最高位。

如果是小数，小数点在MSB 之后；如果是整数，小数点在LSB 之后。

(1) -35/64 (2)23/128 (3) –127 (4)用小数表示-1 (5)用整数表示-1 解：(1)-35/64 = -0.100011原码1.1000110 反码1.0111001 补码1.0111010(2)23/128= 0.0010111原码0.0010111 反码0.0010111 补码0.0010111 (3) –127=1111111原码11111111 反码10000000 补码10000001 (4) 用小数表示-1 补码1.0000000 (5) 用整数表示-1原码10000001 反码11111110 补码1111111113. 己知[X]，求[X]和X .补原4. 当十六进制数9B和FF分别表示为原码、补码、反码、移码和无符号数时，所对应的十进制数各为多少（设机器数采用一位符号位）。

答：5. 有一个字长为32位的浮点数，符号位１位，阶码８位，用移码表示，尾数23位，用补码表示；基数为2。

请写出：（1）最大数的二进制表示；（2）最小数的二进制表示； （3）规格化数所能表示数的范围。

解：用IEEE754格式(E的取值范围：1~254，留出全0和全1分别表示0和无穷大)31 30 23 22 20 0S E M(1) 最大数的二进制表示：0 11111110 11111111111111111111111即 2127(2-2-23)(2) 最小数的二进制表示：1 11111110 11111111111111111111111即 - 2127(2-2-23)(3) 规格化数所能表示数的范围：最小的正数：0 00000001 00000000000000000000001 即2-126(1+2-23)绝对最小的负数：1 00000001 00000000000000000000001 即-2-126(1+2-23)所以范围是： -2127(2-2-23)至-2-126(1+2-23) ，2-126(1+2-23)至2127(2-2-23)6. 将下列十进制数表示成IEEE754标准的32位浮点规格化数。

人教版高中数学 教案+学案 综合汇编第2章 函数 第4教时导数的应用习题课（5月8日）教学目标 掌握导数的几何意义，会求多项式函数的单调区间、极值、最值 教学重点 多项式函数的单调区间、极值、最值的求法 教学难点 多项式函数极值点的求法、多项式函数最值的应用 一、课前预习1.设函数)(x f y =在某个区间内有导数，如果在这个区间内＿＿＿＿，则)(x f y =是这个区间内的＿＿＿＿＿；如果在这个区间内＿＿＿，则)(x f y =是这个区间内的＿＿＿＿＿.2.设函数)(x f y =在0x x =及其附近有定义，如果)(0x f 的值比0x 附近所有各点的值都大（小），则称)(0x f 是函数)(x f y =的一个＿＿＿＿＿＿.3.如果)(x f y =在某个区间内有导数，则可以这样求它的极值：（1）求导数＿＿＿＿＿； （2）求方程＿＿＿＿＿＿＿＿的根（可能极值点）； （3）如果在根的左侧附近为＿，右侧附近为＿，则函数)(x f y =在这个根处取得极＿值；如果在根的左侧附近为＿，右侧附近为＿，则函数)(x f y =在这个根处取得极＿值. 4.设)(x f y =是定义在[a ，b]上的函数，)(x f y =在(a ，b)内有导数，可以这样求最值： （1）求出函数在(a ，b)内的可能极值点（即方程0)(/=x f 在(a ，b)内的根n x x x ,,,21 ）； （2）比较函数值)(a f ，)(b f 与)(,),(),(21n x f x f x f ，其中最大的一个为最大值，最小的一个为最小值. 二、举例例1.确定函数31292)(23-+-=x x x x f 的单调区间.例2.设一质点的运动速度是315743)(234++-=t t t t v ，问：从t ＝0到t ＝10这段时间内，运动速度的改变情况怎样？例3.求函数4931)(3+-=x x x f 的极值.例4.设函数x bxaxx f ++=232131)(在1x ＝1与2x ＝2处取得极值，试确定a 和b 的值，并问此时函数在1x 与2x 处是取极大值还是极小值？例5.求函数593)(3+-=x x x f 在[－2,2]上的最大值和最小值.例6.矩形横梁的强度与它断面的高的平方与宽的积成正比例，要将直径为d 的圆木锯成强度最大的横梁，断面的宽和高应为多少？例7.求内接于抛物线21x y -=与x 轴所围图形内的最大矩形的面积.例8.某种产品的总成本C （单位：万元）是产量x （单位：万件）的函数：3202.004.06100)(x x x x C +-+=，试问：当生产水平为x ＝10万件时，从降低单位成本角度看，继续提高产量是否得当？三、巩固练习1.若函数)(x f 在区间[a ，b]内恒有0)(/<x f ，则此函数在[a ，b]上的最小值是＿＿＿＿2.曲线1213141234+--+=x x x x y 的极值点是＿＿＿＿＿＿＿＿＿＿＿＿＿＿3.设函数a ax ax ax x f ---=23)()(在x ＝1处取得极大值－2，则a ＝＿＿＿＿.4.求下列函数的单调区间：（1）1123223+-+=x x x y （2）)2()1(2++=x x y5.求下列函数的极值：（1）642+-=x x y ， （2）59323+--=x x x y ，[－4,4]6.求下列函数的最值：（1）642+-=x x y ，[－3,10] （2）233x x y -=，[－1,4]7.设某企业每季度生产某个产品q 个单位时，总成本函数为cq bqaq q C +-=23)(，（其中a ＞0，b ＞0，c ＞0），求：（1）使平均成本最小的产量（2）最小平均成本及相应的边际成本.8.一个企业生产某种产品，每批生产q 单位时的总成本为q q C +=3)(（单位：百元），可得的总收入为26)(q q q R -=（单位：百元），问：每批生产该产品多少单位时，能使利润最大？最大利润是多少？9.在曲线)0,0(12≥≥-=y x x y 上找一点（00,y x ），过此点作一切线，与x 轴、y 轴构成一个三角形，问：0x 为何值时，此三角形面积最小？10.已知生产某种彩色电视机的总成本函数为73108102.2)(⨯+⨯=q q C ，通过市场调查，可以预计这种彩电的年需求量为p q 50101.35-⨯=，其中p （单位：元）是彩电售价，q （单位：台）是需求量. 试求使利润最大的销售量和销售价格.。

人教版高中数学 教案+学案 综合汇编第2章 函数 第1教时导数的背景（5月4日）教学目标 理解函数的增量与自变量的增量的比的极限的具体意义 教学重点 瞬时速度、切线的斜率、边际成本 教学难点 极限思想 教学过程 一、导入新课 1. 瞬时速度问题1：一个小球自由下落，它在下落3秒时的速度是多少？ 析：大家知道，自由落体的运动公式是221gts =（其中g 是重力加速度）.当时间增量t ∆很小时，从3秒到（3＋t ∆）秒这段时间内，小球下落的快慢变化不大. 因此，可以用这段时间内的平均速度近似地反映小球在下落3秒时的速度.从3秒到（3＋t ∆）秒这段时间内位移的增量：222)(9.44.2939.4)3(9.4)3()3(t t t s t s s ∆+∆=⨯-∆+=-∆+=∆从而，t ts v ∆+=∆∆=--9.44.29.从上式可以看出，t ∆越小，ts ∆∆越接近29.4米/秒；当t ∆无限趋近于0时，ts ∆∆无限趋近于29.4米/秒. 此时我们说，当t ∆趋向于0时，ts ∆∆的极限是29.4.当t ∆趋向于0时，平均速度ts ∆∆的极限就是小球下降3秒时的速度，也叫做瞬时速度.一般地，设物体的运动规律是s ＝s （t ），则物体在t 到（t ＋t ∆）这段时间内的平均速度为tt s t t s ts ∆-∆+=∆∆)()(. 如果t ∆无限趋近于0时，ts ∆∆无限趋近于某个常数a ，就说当t ∆趋向于0时，ts ∆∆的极限为a ，这时a 就是物体在时刻t的瞬时速度. 2. 切线的斜率问题2：P （1,1）是曲线2x y =上的一点，Q 是曲线上点P 附近的一个点，当点Q 沿曲线逐渐向点P 趋近时割线PQ 的斜率的变化情况.析：设点Q 的横坐标为1＋x ∆，则点Q 的纵坐标为（1＋x ∆）2，点Q 对于点P的纵坐标的增量（即函数的增量）22)(21)1(x x x y ∆+∆=-∆+=∆， 所以，割线PQ 的斜率x xx x xy k PQ ∆+=∆∆+∆=∆∆=2)(22.由此可知，当点Q 沿曲线逐渐向点P 接近时，x ∆变得越来越小，PQ k 越来越接近2；当点Q 无限接近于点P 时，即x ∆无限趋近于0时，PQ k 无限趋近于2. 这表明，割线PQ 无限趋近于过点P 且斜率为2的直线. 我们把这条直线叫做曲线在点P 处的切线. 由点斜式，这条切线的方程为：12-=x y .一般地，已知函数)(x f y =的图象是曲线C ，P （00,y x ），Q （y y x x ∆+∆+00,）是曲线C 上的两点，当点Q 沿曲线逐渐向点P 接近时，割线PQ 绕着点P 转动. 当点Q 沿着曲线无限接近点P ，即x ∆趋向于0时，如果割线PQ 无限趋近于一个极限位置PT ，那么直线PT 叫做曲线在点P 处的切线. 此时，割线PQ 的斜率xy k PQ ∆∆=无限趋近于切线PT 的斜率k ，也就是说，当x ∆趋向于0时，割线PQ 的斜率xy k PQ ∆∆=的极限为k.3. 边际成本问题3：设成本为C ，产量为q ，成本与产量的函数关系式为103)(2+=q q C ，我们来研究当q ＝50时，产量变化q ∆对成本的影响.在本问题中，成本的增量为：222)(3300)10503(10)50(3)50()50(q q q C q C C ∆+∆=+⨯-+∆+=-∆+=∆. 产量变化q ∆对成本的影响可用：q qC ∆+=∆∆3300来刻划，q ∆越小，qC ∆∆越接近300；当q ∆无限趋近于0时，qC ∆∆无限趋近于300，我们就说当q ∆趋向于0时，qC ∆∆的极限是300.我们把qC ∆∆的极限300叫做当q ＝50时103)(2+=q q C 的边际成本.一般地，设C 是成本，q 是产量，成本与产量的函数关系式为C ＝C （q ），当产量为0q 时，产量变化q ∆对成本的影响可用增量比qq C q q C qC ∆-∆+=∆∆)()(00刻划. 如果q ∆无限趋近于0时，qC ∆∆无限趋近于常数A ，经济学上称A 为边际成本. 它表明当产量为0q 时，增加单位产量需付出成本A （这是实际付出成本的一个近似值）. 二、小结瞬时速度是平均速度ts ∆∆当t ∆趋近于0时的极限；切线是割线的极限位置，切线的斜率是割线斜率xy ∆∆当x ∆趋近于0时的极限；边际成本是平均成本qC ∆∆当q ∆趋近于0时的极限.三、练习与作业：1. 某物体的运动方程为25)(t t s =（位移单位：m ，时间单位：s ）求它在t ＝2s 时的速度.2. 判断曲线22x y =在点P （1,2）处是否有切线，如果有，求出切线的方程.3. 已知成本C 与产量q 的函数关系式为522+=q C ，求当产量q ＝80时的边际成本.4. 一球沿某一斜面自由滚下，测得滚下的垂直距离h （单位：m ）与时间t （单位：s ）之间的函数关系为2t h =，求t ＝4s 时此球在垂直方向的瞬时速度.5. 判断曲线221x y =在（1，21）处是否有切线，如果有，求出切线的方程.6. 已知成本C 与产量q 的函数关系为742+=q C ，求当产量q ＝30时的边际成本.。

汇编作业第一章作业1.1用降幂法和除法将下列十进制数转换为二进制数和十六进制数：(1) 369 (2) 10000 (3) 4095 (4) 327671.2 将下列二进制数转换为十六进制数和十进制数：(1) 10 1101 (2) 1000 0000 (3) 1111 1111 1111 1111 (4) 1111 11111.3将下列十六进制数转换为二进制数和十进制数：(1) FA (2) 5B (3) FFFE (4) 12341.4 完成下列十六进制数的运算，并转换为十进制数进行校核：(1) 3A+B7 (2) 1234+AF (3) ABCD-FE (4) 7AB×6F1.5下列各数均为十进制数，请用8位二进制补码计算下列各题，并用十六进制数表示其运算结果。

(1) (-85)+76 (2) 85+(-76) (3) 85-76 (4) 85-(-76) (5) (-85)-76 (6)-85-(-76)1.6下列各数为十六进制表示的8位二进制数，请说明当它们分别被看作是用补码表示的带符号数或无符号数时，它们所表示的十进制数是什么？(1) D8 (2) FF1.7 下列各数均为用十六进制表示的8位二进制数，请说明当它们分别被看作是用补码表示的数或字符的ASCII码时，它们所表示的十进制数及字符是什么？(1) 4F (2) 2B (3) 73 (4) 591.8请写出下列字符串的ASCII码值。

For example,This is a number 3692.第二章作业2.1在80x86微机的输入/输出指令中，I/O端口号通常是由DX寄存器提供的，但有时也可以在指令中直接指定00~FFH的端口号。

试问可直接由指令指定的I/O 端口数。

2.2有两个16位字1EE5H和2A3CH分别存放在80x86微机的存储器的000B0H和000B3H单元中，请用图表示出它们在存储器里的存放情况。

人教版高中数学 教案+学案 综合汇编第2章 函数 第10教时极 限 的 概 念（4月27日）教学目的：理解数列和函数极限的概念； 教学重点：会判断一些简单数列和函数的极限； 教学难点：数列和函数极限的理解 教学过程：一、实例引入：例：战国时代哲学家庄周所著的《庄子·天下篇》引用过一句话：“一尺之棰，日取其半，万世不竭。

”也就是说一根长为一尺的木棒，每天截去一半，这样的过程可以无限制地进行下去。

（1）求第n 天剩余的木棒长度n a (尺)，并分析变化趋势；（2）求前n 天截下的木棒的总长度n b (尺)，并分析变化趋势。

观察以上两个数列都具有这样的特点：当项数n 无限增大时，数列的项n a 无限趋近于某个常数A （即A a n -无限趋近于0）。

n a 无限趋近于常数A ，意指“n a 可以任意地靠近A ，希望它有多近就有多近，只要n 充分大，就能达到我们所希望的那么近。

”即“动点n a 到A 的距离A a n -可以任意小。

二、新课讲授1、数列极限的定义：一般地，如果当项数n 无限增大时，无穷数列}{n a 的项n a 无限趋近于．．．．．某个常数A （即A a n -无限趋近于0），那么就说数列}{n a 的极限是A ，记作 A a n n =∞→lim注：①上式读作“当n 趋向于无穷大时，n a 的极限等于A ”。

“n →∞”表示“n 趋向于无穷大”，即n 无限增大的意思。

A a n n =∞→lim 有时也记作当n →∞时，n a →A②引例中的两个数列的极限可分别表示为_____________________，____________________ ③思考：是否所有的无穷数列都有极限？例1：判断下列数列是否有极限，若有，写出极限；若没有，说明理由Oy x（1）1，21，31，…，n 1，… ；（2）21，32，43，…，1+n n ，…；（3）－2，－2，－2，…，－2，…；（4）－0.1，0.01，－0.001，…，n )1.0(-，…； （5）－1,1，－1，…，n )1(-，…；注：几个重要极限： （1）01lim=∞→nn （2）C C n =∞→lim （C 是常数）（3）无穷等比数列}{n q （1<q ）的极限是0，即 ：)1(0lim <=∞→q q nn 2、当∞→x 时函数的极限（1） 画出函数xy 1=的图像，观察当自变量x 取正值且无限增大时，函数值的变化情况：函数值无限趋近于0，这时就说，当x 趋向于正无穷大时，函数xy 1=的极限是0，记作：01lim =+∞→xx一般地，当自变量x 取正值且无限增大时，如果函数 )(x f y =的值无限趋近于一个常数A ，就说当x 趋向于正无穷大时，函数)(x f y =的极限是A ，记作：A x f x =+∞→)(lim也可以记作，当x +∞→时，A x f →)(（2）从图中还可以看出，当自变量x 取负值而x 无限增大时，函数xy 1=的值无限趋近于0，这时就说，当x 趋向于负无穷大时，函数xy 1=的极限是0，记作：01lim =-∞→x x一般地，当自变量x 取负值而x 无限增大时，如果函数)(x f y =的值无限趋近于一个常数A ，就说当x 趋向于负无穷大时，函数)(x f y =的极限是A ，记作：A x f x =-∞→)(lim也可以记作，当x -∞→时，A x f →)(（3）从上面的讨论可以知道，当自变量x 的绝对值无限增大时，函数xy 1=的值都无限趋近于0，这时就说，当x 趋向于无穷大时，函数xy 1=的极限是0，记作01lim =∞→x x一般地，当自变量x 的绝对值无限增大时，如果函数)(x f y =的值无限趋近于一个常数A ，就说当x 趋向于无穷大时，函数)(x f y =的极限是A ，记作：A x f x =∞→)(lim也可以记作，当x ∞→时，A x f →)(特例：对于函数C x f =)(（C 是常数），当自变量x 的绝对值无限增大时，函数C x f =)(的值保持不变，所以当x 趋向于无穷大时，函数C x f =)(的极限就是C ，即 C C x =∞→lim例2：判断下列函数的极限：（1）xx )21(lim +∞→ （2）xx 10lim -∞→（3）21lim xx ∞→ （4）4lim ∞→x三、课堂小结 1、数列的极限2、当x ∞→时函数的极限 四、练习与作业1、判断下列数列是否有极限，若有，写出极限 （1）1，41，91，…，21n，… ；（2）7，7，7，…，7，…； （3） ,2)1(,,81,41,21nn---； （4）2，4，6，8，…，2n ，…； （5）0.1，0.01，0.001，…，n101，…； （6）0，,32,21--…，11-n ，…；（7）,41,31,21-…，11)1(1+-+n n ，…；（8）,51,59,54…，52n ，…；（9）－2, 0，－2，…，1)1(--n,…， 2、判断下列函数的极限：P MNA BCD（1）x x 4.0lim +∞→ （2）xx 2.1lim -∞→（3）)1lim(-∞→x （4）41limx x ∞→ （5）x x )101(lim +∞→ （6）xx )45(lim -∞→（7）11lim 2+∞→x x （8）5lim ∞→x补充：3、如图，在四棱锥P-ABCD 中，底面ABCD 是矩形，PA ⊥平面ABCD ，M 、N 分别是AB 、PC 的中点。

1. 知识点：0202(基于微处理器的计算机系统构成) 在下列的选项中，能够组成计算机系统的是（A）。

选项A）硬件系统和软件系统选项B）CPU、存储器、输入/输出设备选项C）操作系统、各种语言选项D）系统软件和应用软件2. 知识点：01 (基础知识)汇编语言属于（ B）选项A）用户软件选项B）系统软件选项C）高级语言×选项D）机器语言×5知识点：0203(中央处理机)中央处理器CPU是由（D）组成的选项A）运算器选项B）控制器选项C）寄存器组选项D）前三者答案：D6. 知识点：0201(80x86微处理器)IBM PC机的DOS是属于（B ）。

选项A）用户软件选项B）系统软件选项C）系统硬件选项D）一种语言8. 知识点：0203(中央处理机)8086/8088 CPU的寄存器组中，８位的寄存器共有（C ）个选项A）4选项B）6选项C）8选项D）109. 知识点：0203(中央处理机)8086/8088 CPU的寄存器组中，16位的寄存器共有（）个。

选项A）10选项B）12选项C）13选项D）1410. 知识点：0204(存储器)8086/8088 CPU执行算术运算时PSW共有（）个标志位会受影响。

选项A）4选项B）5选项C）6 SF,ZF,CF,OF,PF.AF选项D）711. 知识点：0204(存储器)在程序执行过程中，IP寄存器始终保存的是（）。

选项A）上一条指令的首地址选项B）本条指令的首地址选项C）下一条指令的首地址选项D）需计算有效地址后才能确定地址12. 知识点：0204(存储器)IBM PC机的存储器可分（）个段。

选项A）4选项B）256选项C）512选项D）6553613知识点：0204(存储器)当使用BP作编程地址时，此时使用的是（）段。

选项A）CS选项B）DS选项C）ES选项D）SS17知识点：0204(存储器)存储器的一个字节表示（）位。

选项A）8选项B）16选项C）32选项D）6418知识点：0101(基于微处理器的计算机系统构成)如果某个字变量的数据存放在奇地址单元，则8086/8088 CPU读写该变量时需要（）个读写周期。

汇编语言程序设计第四版【课后习题答案】--囮裑為檤第2章8086的指令系统〔习题2.1〕已知DS＝2000H、BX＝0100H、SI＝0002H，存储单元[20100H]～[20103H]依次存放12 34 56 78H，[21200H]～[21203H]依次存放2A 4C B7 65H，说明下列每条指令执行完后AX寄存器的内容。

（1）mov ax,1200h（2）mov ax,bx（3）mov ax,[1200h]（4）mov ax,[bx]（5）mov ax,[bx+1100h]（6）mov ax,[bx+si]（7）mov ax,[bx][si+1100h]〔解答〕（1）AX＝1200H（2）AX＝0100H（3）AX＝4C2AH ;偏移地址=bx=0100h（4）AX＝3412H ;偏移地址=bx=0100h（5）AX＝4C2AH ;偏移地址=bx+1100h=1200h（6）AX＝7856H ;偏移地址=bx+si=0100h+0002h=0102h（7）AX＝65B7H ;偏移地址=bx+si+1100h=0100h+0002h+1100h=1202h〔习题2.2〕指出下列指令的错误（1）mov cx,dl（2）mov ip,ax（3）mov es,1234h（4）mov es,ds（5）mov al,300（6）mov [sp],ax（7）mov ax,bx+di（8）mov 20h,ah〔解答〕（1）两操作数类型不匹配（2）IP指令指针禁止用户访问（3）立即数不允许传给段寄存器（4）段寄存器之间不允许传送（5）两操作数类型不匹配（6）目的操作数应为[ SI ]（7）源操作数应为[BX+DI]（8）立即数不能作目的操作数〔习题2.3〕已知数字0 ~ 9对应的格雷码依次为：18H、34H、05H、06H、09H、0AH、0CH、11H、12H、14H，它存在于以table为首地址（设为200H）的连续区域中。

汇编语言程序设计第四版【课后习题答案】—-囮裑為檤第2章8086的指令系统〔习题2.1〕已知DS＝2000H、BX＝0100H、SI＝0002H，存储单元[20100H］～[20103H]依次存放12 34 56 78H，［21200H］～[21203H]依次存放2A 4C B7 65H,说明下列每条指令执行完后AX寄存器的内容。

(1) mov ax,1200h(2）mov ax，bx（3）mov ax，[1200h］（4) mov ax,［bx]（5) mov ax，［bx+1100h］(6）mov ax,[bx+si]（7) mov ax，[bx］[si+1100h]〔解答〕（1）AX＝1200H（2）AX＝0100H（3)AX＝4C2AH ；偏移地址=bx=0100h（4）AX＝3412H ;偏移地址=bx=0100h（5）AX＝4C2AH ；偏移地址=bx+1100h=1200h(6）AX＝7856H ;偏移地址=bx+si=0100h+0002h=0102h（7）AX＝65B7H ；偏移地址=bx+si+1100h=0100h+0002h+1100h=1202h〔习题2.2〕指出下列指令的错误（1）mov cx,dl（2）mov ip，ax（3) mov es,1234h（4）mov es，ds(5）mov al，300（6）mov [sp],ax（7）mov ax,bx+di（8）mov 20h，ah〔解答〕（1）两操作数类型不匹配（2)IP指令指针禁止用户访问(3）立即数不允许传给段寄存器（4）段寄存器之间不允许传送(5）两操作数类型不匹配（6）目的操作数应为[ SI ］(7)源操作数应为[BX+DI］（8)立即数不能作目的操作数〔习题2。

3〕已知数字0 ~ 9对应的格雷码依次为：18H、34H、05H、06H、09H、0AH、0CH、11H、12H、14H，它存在于以table为首地址（设为200H)的连续区域中。

第1章作业答案1.1 微处理器、微型计算机和微型计算机系统三者之间有什么不同?把CPU(运算器和控制器)用大规模集成电路技术做在一个芯片上,即为微处理器。

微处理器加上一定数量的存储器和外部设备(或外部设备的接口)构成了微型计算机。

微型计算机与管理、维护计算机硬件以及支持应用的软件相结合就形成了微型计算机系统。

1.2 CPU在内部结构上由哪几部分组成?CPU应该具备哪些主要功能?CPU主要由起运算器作用的算术逻辑单元、起控制器作用的指令寄存器、指令译码器、可编程逻辑阵列和标志寄存器等一些寄存器组成。

其主要功能是进行算术和逻辑运算以及控制计算机按照程序的规定自动运行。

1.3微型计算机采用总线结构有什么优点?采用总线结构,扩大了数据传送的灵活性、减少了连线。

而且总线可以标准化,易于兼容和工业化生产。

1.4数据总线和地址总线在结构上有什么不同之处?如果一个系统的数据和地址合用一套总线或者合用部分总线,那么要靠什么来区分地址和数据?数据总线是双向的(数据既可以读也可以写),而地址总线是单向的。

8086CPU为了减少芯片的引脚数量,采用数据与地址线复用,既作数据总线也作为地址总线。

它们主要靠信号的时序来区分。

通常在读写数据时,总是先输出地址(指定要读或写数据的单元),过一段时间再读或写数据。

第2章作业答案2.1 IA-32结构微处理器直至Pentillm4,有哪几种?80386、30486、Pentium、Pentium Pro、PeruiumII、PentiumIII、Pentium4。

2.6IA-32结构微处理器有哪几种操作模式?IA一32结构支持3种操作模式:保护模式、实地址模式和系统管理模式。

操作模式确定哪些指令和结构特性是可以访问的。

2.8IA-32结构微处理器的地址空间如何形成？由段寄存器确定的段基地址与各种寻址方式确定的有效地址相加形成了线性地址。

若末启用分页机制，线性地址即为物理地址；若启用分页机制，则它把线性地址转为物理地址。

第二章习题及参考答案
1．若采用IEEE754标准的32位短浮点数格式,即0~22位为尾数,23~30位为阶码,第31位为数符.其中阶码偏置为127(即阶码为阶码真值加上127).请将十进制数127.75写成浮点数,列出其二进制代码序列.
参考答案：
解： 127.75＝(1111111.11)
2
＝(1.11111111)
2
26
阶码＝阶码真值+127＝6+127＝133＝(10000101)
2
所求浮点代码为：0，10000101，11111111 0000 0000 0000 000
2.若采用IEEE754标准的32位短浮点数格式,即0~22位为尾数,23~30位为阶码,第31位为数符.其中阶码偏置为127(即阶码为阶码真值加上127).试求出32位浮点代
码(CC9E23AF)
16
的真值（结果可用任何进制的数表示）.
参考答案：
解：将(CC9E23AF)
16
写成二进制代码为：
1,100 1100 1,001 1110 0010 0011 1010 1111
由于数符为1,所以该数为负数。

阶码真值＝（10011001)
2 -（127)
10
＝(26)
10
尾数真值＝（1.001 1110 0010 0011 1010 1111)
2
故该浮点数的真值＝（1.001 1110 0010 0011 1010 1111)
2 ×（226)
10。

`00第一章课外练习题一、单项选择题：1．从键盘输入的字符，在计算机内存储的是它的（A）（A）二进制编码（B）四进制编码（C）八进制编码（D）十六进制编码2．6位无符号二进制数能表示的最大十进制数是（B）。

（A）64 （B）63 （C）32 （D）31 3．十进制数269变换为十六进制数是（C）。

（A）10B （B）10C （C）10D （D）10E 4．8位的微型计算机系统是以16位来表示地址，则该微机系统有（C）个地址空间。

（A）255 （B）65535 （C）65536 （D）1048576 5．8位有符号二进制数能表示的最大十进制数是（D）。

（A）256 （B）255 （C）128 （D）127 6．十六进制数88H，可表示成下面几种形式，请找出错误的表示（D）。

（A）无符号十进制数136 （B）带符号十进制数－120（C）压缩型BCD十进制数88 （D）8位二进制数－8的补码表示7．有一个数值152，它与十六进制数6A相等，那么该数值是（B）。

（A）二进制数（B）八进制数（C）十进制数（D）四进制数8．7位ASCII总共可表示（C）个符号。

（A）256 （B）127 （C）128 （D）255 9．4B的字长是（C）。

（A）8位（B）16位（C）32位（D）64位二、判断题（判断每题正误，对的在题后括号内划“√”，错的划“×”）1．字节通常用英文单词“Bit”来表示（×）。

2．目前广泛使用的Pentium计算机其字长为5个字节（×）。

3．存储器中将8个相邻的二进制位作为一个单位，这种单位称为字节（√）。

4．微型计算机的字长并不一定是字节的整数倍（×）。

三、填空题1．8位有/无符号整数的表示范围写成16进制形式为（80~~7F）/（00~~FF）。

2．己知：计算机中有一个“01100001”编码，如果把它看作是无符号数，它是十进制什么数（97）；如果认为它是BCD，则表示（01100001）BCD；认为它是某个ASCII，则代表（a）字符。

第02章单⽚机指令系统与汇编语⾔程序设计习题解答第02章单⽚机指令系统与汇编语⾔程序设计习题解答⼀、填空题1. MCS-51单⽚机指令系统中有 111 条指令。

2. MCS-51单⽚机指令中，Rn表⽰ R0、R1、R2、R3、R4、R5、R6、R7中的⼀个。

3. MCS-51单⽚机指令中，@表⽰间接寻址。

4. MCS-51单⽚机指令中，$表⽰当前指令的⾸地址。

5. MCS-51单⽚机寻址⽅式有⽴即数、直接地址、寄存器、寄存器间接、变址、相对、位寻址等七种寻址⽅式。

6. 指令MOVC A， @A+PC的功能是将A的内容与PC当前值相加作为程序存储器地址，再将该地址单元的内容传送到A 。

7. 指令JBC CY, LOOP是 3 字节、 2 个机器周期指令。

8. 指令DA A的功能是对A中当前值进⾏⼗进制调整。

9. 调⽤⼦程序时，将PC当前值保存到堆栈。

10. MCS-51单⽚机堆栈操作的基本原则是先进后出。

⼆、简答题1. MCS-51单⽚机指令⼀般由哪⼏个部分组成？各部分的功能是什么？答：MCS-51单⽚机指令⼀般由标号、操作码助记符、操作数、注释四部分组成。

标号是⼀条指令的标志，是可选字段，与操作码之间⽤“:”隔开；设置标号的⽬的是为了⽅便调⽤或转移。

标号的选择应遵从下列规定：标号由1～8个字母或数字组成，也可以使⽤⼀个下划线符号“_”。

第⼀个字符必须是字母。

指令助记符或系统中保留使⽤的字符串不能作为标号。

标号后⾯需要有⼀个冒号。

⼀条语句可以有标号，也可以没有标号，取决于程序中其它语句是否需要访问这条语句。

操作码规定指令的功能，是⼀条指令的必备字段，如果没有操作码，就不能成为指令。

它与操作数之间⽤“空格”隔开。

操作数是指令操作的对象。

分为⽬的操作数和源操作数两类，它们之间⽤“，”分隔。

操作数是可选字段。

⼀条指令可以有0、1、2、3个操作数。

注释是对指令功能的说明解释。

以“；”开始。

2. 程序中，伪指令ORG和END的作⽤是什么？答：ORG⽤于定义汇编语⾔源程序或数据块存储的起始地址。

第1章基础知识检测点1.1(1)1个CPU的寻址能力为8KB，那么它的地址总线的宽度为13。

(2)1KB的存储器有1024个存储单元。

存储单元的编号从0到1023。

(3)1KB的存储器可以存储1024*8个bit，1024个Byte。

(4)1GB、1MB、1KB分别是2^30、2^20、2^10 Byte。

(n^m的意思是n的m次幂)(5)8080、8088、80286、80386的地址总线宽度分别是16根、20根、24根、32根，则它们的寻址能力分别为：64(KB)、1(MB)、16(MB)、4(GB)。

(6)8080、8088、8086、80286、80386的数据总线宽度分别为8根、8根、16根、16根、32根。

则它们一次可以传送的数据为：1(B)、1(B)、2(B)、2(B)、4(B)。

(7)从内存中读取1024字节的数据，8086至少要读512次、80386至少要读256次。

(8)在存储器中，数据和程序以二进制形式存放。

第2章寄存器答案检测点2.1(1) 写出每条汇编指令执行后相关寄存器中的值。

mov ax,62627 AX=F4A3Hmov ah,31H AX=31A3Hmov al,23H AX=3123Hadd ax,ax AX=6246Hmov bx,826CH BX=826CHmov cx,ax CX=6246Hmov ax,bx AX=826CHadd ax,bx AX=04D8Hmov al,bh AX=0482Hmov ah,bl AX=6C82Hadd ah,ah AX=D882Hadd al,6 AX=D888Hadd al,al AX=D810Hmov ax,cx AX=6246H(2) 只能使用目前学过的汇编指令，最多使用4条指令，编程计算2的4次方。

解：mov ax,2add ax,axadd ax,axadd ax,ax检测点2.2(1) 给定段地址为0001H，仅通过变化偏移地址寻址，CPU的寻址范围为00010H到1000FH。