六阶幻方解法

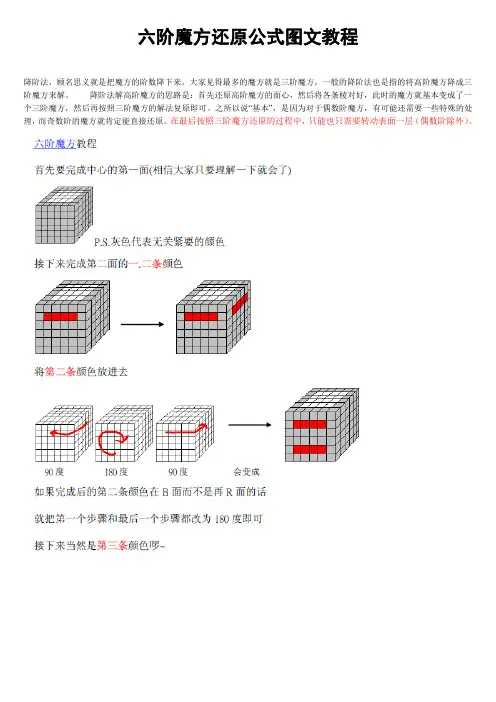
六阶魔方还原公式图文教程
降阶法，顾名思义就是把魔方的阶数降下来。

大家见得最多的魔方就是三阶魔方，一般的降阶法也是指的将高阶魔方降成三阶魔方来解。

降阶法解高阶魔方的思路是：首先还原高阶魔方的面心，然后将各条棱对好，此时的魔方就基本变成了一个三阶魔方，然后再按照三阶魔方的解法复原即可。

之所以说“基本”，是因为对于偶数阶魔方，有可能还需要一些特殊的处理，而奇数阶的魔方就肯定能直接还原。

在最后按照三阶魔方还原的过程中，只能也只需要转动表面一层（偶数阶除外）。

在一种由若干个排列整洁数构成正方形中，图中任意一横行、一纵行及对角线几种数之和都相等，具备这种性质图表，称为“幻方”。

国内古代称为“河图”、“洛书”，又叫“纵横图”。

1、奇数阶幻方——罗伯特法(也有人称之为楼梯法)（如图一：以五阶幻方为例）奇数阶幻方n为奇数(n=3，5，7，9，11……) (n=2×k+1，k=1，2，3，4，5……)奇数阶幻方最典型填法是罗伯特法(也有人称之为楼梯法)。

填写办法是这样：把1(或最小数)放在第一行正中；按如下规律排列剩余n×n-1个数：(1)每一种数放在前一种数右上一格；(2)如果这个数所要放格已经超过了顶行那么就把它放在底行，依然要放在右一列；(3)如果这个数所要放格已经超过了最右列那么就把它放在最左列，依然要放在上一行；(4)如果这个数所要放格已经超过了顶行且超过了最右列，那么就把它放在前一种数下一行同一列格内；(5)如果这个数所要放格已有数填入，解决办法同(4)。

这种写法总是先向“右上”方向，象是在爬楼梯。

口诀：1居首行正中央,依次右上莫相忘上出格时往下放,右出格时往左放.排重便往自下放,右上出格一种样图一 2、单偶数阶幻方()122＋＝m n ——分区调换法（如图二：以六阶幻方为例）① 把()122＋＝m n 阶幻方均提成4个同样小幻方A 、B 、C 、D(如图二)图二（注意A 、B 、C 、D 相对位置不能变化，由于12＋m 为奇数，因此A 、B 、C 、D 均为奇数阶幻方） ② 用持续摆数法在A 中填入21a ——构成幻方，同理，在B 中填入()2221a a ——＋、在C 中填入()22312a a ——＋、在D 中填入()22413a a ——＋均构成幻方（2na ＝）(如图三)图三（由于12＋m 为奇数，因此A 、B 、C 、D 均为奇数阶幻方，必然可以用持续摆数法构造幻方）③ 在A 中间一行上从左侧第二列起取m 个方格，在其他行上则从左侧第一列起取m 个方格，把这些方格中数与D 中相应方格中数字对调(如图四)：图四 不论是几阶幻方，在A 中取数时都要从中间一行左侧第二列开始；由于当6＝n 时，1＝m ，因此本例中只取了一种数）④ 在A 中从最右一列起在各行中取1－m 个方格，把这些方格中数与D 中相应方格中数字对调。

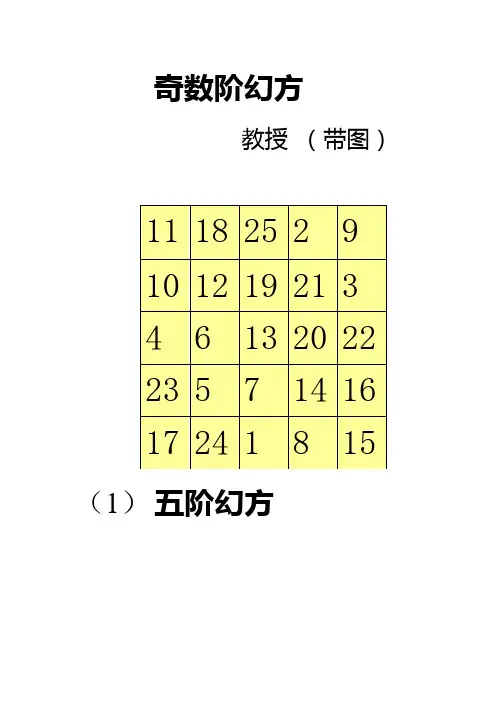
奇数阶幻方教授（带图）（1）五阶幻方（2）七阶幻方（1）幻方简介：幻方（Magic Square）是一种将数字安排在正方形格子中，使每行、列和对角线上的数字和都相等的方法。

幻方也是一种汉族传统游戏。

旧时在官府、学堂多见。

它是将从一到若干个数的自然数排成纵横各为若干个数的正方形，使在同一行、同一列和同一对角线上的几个数的和都相等。

在一个由若干个排列整齐的数组成的正方形中，图中任意一横行、一纵行及对角线的几个数之和都相等，具有这种性质的图表，称为“幻方”。

中国古代称为“河图”、“洛书”，又叫“纵横图”。

幻方也称纵横图、魔方、魔阵，发源于中国古代的洛书——九宫图。

公元前一世纪，西汉宣帝时的博士戴德在他的政治礼仪著作《大戴礼·明堂篇》中就有“二、九、四、七、五、三、六、一、八”的洛书九宫数记载。

2500年前，孔子在他研究《易经》的著作《系词上传》中记载了：“河出图，洛出书，圣人则之。

”最早将数字与洛书相连的记载是2300年前的《庄子·天运》，它认为：“天有六极五常，帝王顺之则治，逆之则凶。

九洛之事，治成德备，监照下土，天下戴之，此谓上皇。

”明代数学家程大位在《算法统宗》中也曾发出“数何肇？其肇自图、书乎？伏羲得之以画卦，大禹得之以序畴，列圣得之以开物”的感叹，大意是说，数起源于远古时代黄河出现的河图与洛水出现的洛书，伏羲依靠河图画出八卦，大禹按照洛书划分九州，并制定治理天下的九类大法，圣人们根据它们演绎出各种治国安邦的良策，对人类社会与自然界的认识也得到步步深化。

《周易本义》中的《洛书》，一个三阶幻方宋杨辉著《续古摘奇算法》中曾叙述三阶幻方构造法：“九子斜排，上下对易，左右相更，四维挺出，戴九履一，左三右七，二四为肩，六八为足”。

（2）解幻方方法：1、奇数阶幻方——罗伯特法(也有人称之为楼梯法)（如图一：以五阶幻方为例）奇数阶幻方n为奇数(n=3，5，7，9，11……) (n=2×k+1，k=1，2，3，4，5……)奇数阶幻方最经典的填法是罗伯特法(也有人称之为楼梯法)。

1～12阶平面幻(魔)方举例
江苏省泗阳县李口中学沈正中
由1到n2（n不小于3）的n2个自然数排成各有n行和n列的n阶方阵，使在同一行、同一列和同一主对角线上的n个数的和（叫幻和）都相等，称这样的正方形方阵叫n阶平面幻方或平面魔方。

平面幻方分为n为奇数、n为4的倍数(即4m的形式）和n为其它偶数(即4m＋2的形式）三种情况。

每阶幻方都有不同的排列方法，下面给出3～12阶平面幻方各阶中的一种排列方法：
1、三阶平面幻方（幻和值为15）
九数填法：九宫内，二四为肩，六八为足，左七右三，戴九
履一，五居中央。

2、四阶平面魔方（幻和值为34）
3、五阶平面魔方（幻和值为65）
4、六阶平面魔方（幻和值为111）
5、七阶平面魔方（幻和值为175）
6、八阶平面魔方（幻和值为260）
7、九阶平面魔方（幻和值为369）
8、十阶平面魔方（幻和值为505）
9、十一阶平面魔方（幻和值为671）
10、十二阶平面魔方（幻和值为870）。

幻方一般地说，在n×n的方格里，既不重复也不遗漏地填上n²个连续的自然数，每个数占一格，并使每行、每列及两条对角线上n个自然数的和都相等，这样排成的数表称为n阶幻方。

这个相等的和叫幻和。

奇数阶幻方奇数阶幻方的方法可以简单概括为方阵斜线对换法：（1）三阶幻方（九宫幻方）：具体可以概括为以下几步：第一步：将1——9九个整数如图1那样排列成方阵；第二步：如图2，画斜线；第三部：如图3，将图2中得到的正方形外四角的数字1、3、7、9，分别向斜线对面数三格，把数字填入空格内，即1和9交换，3和7交换入幻方格内。

便得到了图4的三阶幻方（九宫幻方），横排、数列，对角线上每三个数字的和都为15。

（2）五阶幻方：五阶幻方具体可以概括为以下几步：第一步：将1——25这二十五个整数如图5排列成方阵；第二步：如图6，画斜线；第三部：如图7，将图2中得到的正方形外四角的数字（1、2、6），（4、5、10）；（16、21、22），和（20、24、25）分别向斜线对面数五格，把数字填入空格内，即1 和25交换，2和20交换，6 和24交换，5和21交换，4和16交换，10和22交换填入幻方格内便得到了图8的五阶幻方，横排、数列，对角线上每三个数字的和都为65。

偶数阶幻方偶数阶幻方的方法可以简单概括为方阵对角线数字互换和对面数字互换的方法：比如四阶幻方四阶幻方比较简单，只需要交换对角线上的数字就能使横排、竖列、对角线上的和分别都等于34。

具体步骤为：第一步：将1——16十六个整数如图9排列成方阵；第二步：如图10那样画出对角线和方框；第三步：如图10—图11，将方阵中对角线上的数字1和16，4和13，6和12，以及7和10 对换，便得到了图12的四阶幻方，而六阶幻方就要复杂得多了，不仅仅需要交换对角线上的数字，还需要横排对面交换，竖列对面交换。

反幻方将1～9九个自然数，填在3×3正方形表格内，使其中每一横行、每一竖列及任一条对角线上的三数之和都不等，并且相邻的两个数在图中位置也相邻。

幻方的填写技巧一、N阶幻方的分类：1、奇数阶幻方：当n=2k+1时，称为奇数阶幻方。

2、偶数阶幻方：（1）双偶数幻方：当n=4k=2×2k时，称为双偶数数阶幻方。

（2）单偶数幻方：当n=4k+2=2×(2k+1）时，称为单偶数阶幻方。

二、幻方的填写方法：1、奇数阶幻方：可按照如下方法操作：Merzirac法，有人也叫楼梯法，我管它叫斜步法，即走X+Y斜步（数字按右上方顺序填入），-Y跳步（如果右上方已有数字或出了对角线，则向下移一格继续填写）。

其实斜步法可以向4个方向依次填写数字，即右上、右下、左上、左下4个方向，每种斜步都可有2种跳步，即左（右）跳步、上（下）跳步。

对于X+Y斜步相应的跳步可以为-X，-Y。

【记住，跳步是X+Y斜步的X（或Y）相反方向即可。

如右上方向斜步，跳步就为向左（或向下）一步；左下方向斜步，跳步就为向右（或向上）一步；等等等等】（2）杨辉“阳动阴静”法南宋杨辉不仅精通数学，而且精通易学，在他1275年所著的《续古摘奇算法》中，就对河图和洛书的数学问题进行了详尽的研究。

其中对3阶幻方的排列，找出了一种奇妙的规律：“九子斜排，上下对易，左右相更，四维挺出，戴九履一，左三右七，二四为肩，六八为足”，清代，李光地的《周易折中》把杨辉所概括的这种排列排列原理为“阳动阴静”。

2、双偶数阶幻方：可按照如下方法操作：（一）四阶幻方：（1） （2） 对角线以外的数字关于对角线交点作中心对称对换位置即可。

（3） 完成后的四阶幻方如下：（1）对角线上的数字一律不动；（2）对角线以外的数字关于对角线交点作中心对称对换位置即可。

（3）3、（按奇数阶幻方填法按区域填写）六阶幻方之填法（交换红色字体数字位置，其他数字位置不变）（二）十阶幻方：。

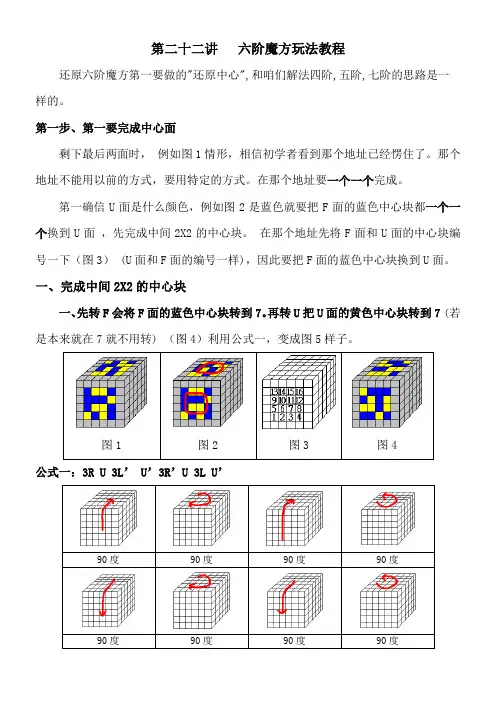
第二十二讲 六阶魔方玩法教程 还原六阶魔方第一要做的"还原中心",和咱们解法四阶,五阶,七阶的思路是一样的。 第一步、第一要完成中心面 剩下最后两面时， 例如图1情形，相信初学者看到那个地址已经愣住了。那个地址不能用以前的方式，要用特定的方式。在那个地址要一个一个完成。 第一确信U面是什么颜色，例如图2是蓝色就要把F面的蓝色中心块都一个一个换到U面 ，先完成中间2X2的中心块。 在那个地址先将F面和U面的中心块编号一下（图3） (U面和F面的编号一样)，因此要把F面的蓝色中心块换到U面。 一、完成中间2X2的中心块 一、先转F会将F面的蓝色中心块转到7。再转U把U面的黄色中心块转到7 (若是本来就在7就不用转) （图4）利用公式一，变成图5样子。

图1 图2 图3 图4 公式一：3R U 3L’ U’3R’U 3L U’

90度 90度 90度 90度 90度 90度 90度 90度 公式说明：

大写字母前加数字代表第几层；小写字母前加数字表示几层一路转动；字母后加2

表示转180°；字母后加“ ' ”表示逆时针。 例如，2R表示右边数第二层顺时转，2r表示右边两层顺时转； 2F表示前面向里第二层顺时转，2f表示前面两层顺时转； 2-3F表示前面向里第二层、第三层同时顺时针转动 4R和4L表示同一层；4F和4B表示同一层 二、再将F面的蓝色中心块转到7 ，U面的黄色中心块转到7（图6），重复一次公式一，中间2X2的中心块就完成了（图7） 。

图5 图6 图7 图8 二、完成F面和U面中心四个角上的块 完成F面和U面上中心四个角上的块。即将1.4.13.16完成（图8），红色圈的块。 先转F将F面的蓝色中心块转到4，再转U把U面的黄色中心块转到4 (若是本来就在4就不用转)，转一次公式二,会变成图9. 公式二：2R U 2L’ U’2R’U 2L U’

90度 90度 90度 90度 90度 90度 90度 90度 那个公式和前面那个公式差不多只是将1.3.5.7步改成转第二层罢了。 图9 图10 图11 图12 重复上面的动作直到1.4.13.16的中心块都正确，如图10. 三、再将F面和U面3.5.12.14.完成 先转F将F面的蓝色中心块转到3 ，再转U把U面的黄色中心块转到3 (若是本来就在3就不用转)，如图11所示。利用公式三，会变成图12. 公式三：3R U 2L’ U’3R’U 2L U’

任意阶幻方填法
飞雪连天著
幻方的填法分为奇阶填法和偶阶填法，其中偶阶又分为单偶［2X（2n+1）如：6阶］和双偶（2X2n )
一、奇阶填法
奇阶填法遵循一个“之”字拐的原则去填，这个需要自己的理解去填。

左图蓝点处为起点处，箭头表示填数顺序方向。

三阶：幻和：15
五阶：幻和：65
七阶：幻和：175
二、单偶填法
单偶填法要必须会奇阶填法。

先将单偶幻方平均分成4个奇阶幻方，然后按规定顺序填好每个奇阶幻方，再进行交换即可。

六阶：红色竖排同位交换。

如5—32，8—35，4—31
幻和：111
十阶：幻和：505
三、双偶填法
双偶填法比单偶简单很多，只须依次把数填好，再进行一些交换即可。

四阶：把红色的按中心对称交换，如2—15，3—14，5—12，9—8
幻和：34
八阶：幻和：260
到此，你可以填好任意阶的幻方了。

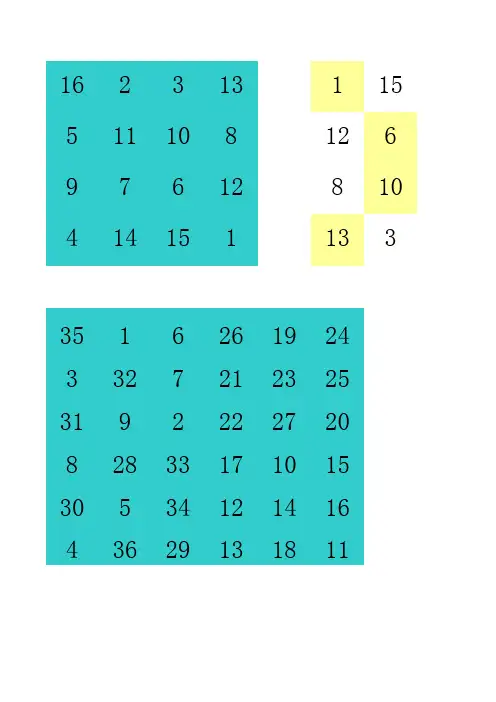
162313115 511108126 97612810 4141511333516261924 3327212325 3192222720 82833171015 30534121416 436291318116423616067 9555412135150 17474620214342 40262737363031 32343529283839 41232244451918 49151452531110 85859546263幻方常规解法汇总没法，组合数学还考幻方构造。

这东西不看解法真不会写，虽然没见有啥用，但还是记录下，免得日后再找。

按目前填写幻方的方奇数阶幻方（罗伯法）奇数阶幻方最经典的填法是罗伯法。

填写的方法是：把1（或最小的数）放在第一行正中；按以下规律排列剩下的(n×n－1)个数：1、每一个数放在前一个数的右上一格；2、如果这个数所要放的格已经超出了顶行那么就把它放在底行，仍然要放在右一列；3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列，仍然要放在上一行；4、如果这个数所要放的格已经超出了顶行且超出了最右列，那么就把它放在前一个数的下一行同一列的格内；5、如果这个数所要放的格已经有数填入，那么就把它放在前一个数的下一行同一列的格内。

例，用该填法获得的5阶幻方：17241815235714164613202210121921311182529双偶数阶幻方（对称交换法）所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方，即4K阶幻方。

在说解法之前我们先说明一个“互补数”定义：就是在 n 阶幻方中双偶数阶幻方的对称交换解法：先看看4阶幻方的填法：将数字从左到右、从上到下按顺序填写：12345678910111213141516内外四个角对角上互补的数相易，（方阵分为两个正方形，外大内小，然后把大正方形的四个对角上的数字对换，小正方形四个对16231351110897612414151对于n=4k阶幻方，我们先把数字按顺序填写。

/*六阶幻方的所有解的程序如下：（5秒之内直接有结果）***************************************m11 m12 m13 m14 m15 m16m21 m22 m23 m24 m25 m26m31 m32 m33 m34 m35 m36m41 m42 m43 m44 m45 m46m51 m52 m53 m54 m55 m56m61 m62 m63 m64 m65 m66****************************************/#include<stdlib.h>#include<stdio.h>#include<time.h>#define exitvoid main(){int t1=clock();intm11,m12,m13,m14,m15,m16,m21,m22,m23,m24,m25,m26,m31,m32,m33,m34,m35, m36,m41,m42,m43,m44,m45,m46,m51,m52,m53,m54,m55,m56,m61,m62,m63,m64, m65,m66,z=0;system("color 1e");//int s=74;//FILE *stream ;//将内容写到testfile.txt或wordfile.doc, "W"是写("r"是读)//if((stream = freopen("wordfile.doc", "w", stdout)) == NULL)//exit(-1);printf("所有六阶幻方如下：\n");for(m12=1;m12<37;m12++)for(m24=1;m24<37;m24++){if(m24==m12)continue;for(m36=1;m36<37;m36++){if(m36==m12||m36==m24)continue;for(m41=1;m41<37;m41++){if(m41==m12||m41==m24||m41==m36)continue;for(m53=1;m53<37;m53++){if(m53==m12||m53==m24||m53==m36||m53==m41)continue;for(m65=1;m65<37;m65++){if(m65==m12||m65==m24||m65==m36||m65==m41||m65==m53)continue;//////for(m64=1;m64<37;m64++){if(m64==m12||m64==m24||m64==m36||m64==m41||m64==m53||m64==m65)contin ue;for(m52=1;m52<37;m52++){if(m52==m12||m52==m24||m52==m36||m52==m41||m52==m53||m52==m64||m52= =m65)continue;for(m31=1;m31<37;m31++){if(m31==m12||m31==m24||m31==m36||m31==m41||m31==m52||m31==m53||m31= =m64||m31==m65)continue;for(m13=1;m13<37;m13++){if(m13==m12||m13==m24||m13==m31||m13==m36||m13==m41||m13==m52||m13= =m53||m13==m64||m13==m65)continue;for(m25=1;m25<37;m25++){if(m25==m12||m25==m13||m25==m24||m25==m31||m25==m36||m25==m41||m25==m52||m25==m53||m25==m64||m25==m65)continue;for(m46=1;m46<37;m46++){if(m46==m12||m46==m13||m46==m24||m46==m25||m46==m31||m46==m36|| m46==m41||m46==m52||m46==m53||m46==m64||m46==m65)continue;//m13=0;m31=0;m25=0;m52=0;m64=0;m46=0;for(m16=1;m16<37;m16++){if(m16==m12||m16==m13||m16==m24||m16==m25||m16==m31||m16==m36|| m16==m41||m16==m46||m16==m52||m16==m53||m16==m64||m16==m65)conti nue;for(m11=1;m11<37;m11++){if(m11==m12||m11==m13||m11==m16||m11==m24||m11==m25||m11==m31||m11== m36||m11==m41||m11==m46||m11==m52||m11==m53||m11==m64||m11==m65||m11+m12+m13+m16<40||m11+m12+m13+m16>108)continue;for(m15=1;m15<37;m15++){if(m15==m11||m15==m12||m15==m13||m15==m16||m15==m24||m15==m25||m15= =m31||m15==m36||m15==m41||m15==m46||m15==m52||m15==m53||m15==m64||m15==m65||m11+m12+m13+m15+m16<75||m11+m12+m13+m15+m16>110)continue;for(m14=1;m14<37;m14++){if(m14==m11||m14==m12||m14==m13||m14==m15||m14==m16||m14==m24||m14= =m25||m14==m31||m14==m36||m14==m41||m14==m46||m14==m52||m14==m53||m14==m64||m14==m65||m11+m12+m13+m14+m15+m16!=111)continue;//m16=0;m11=0;m15=0;m14=0;for(m34=1;m34<37;m34++){if(m34==m11||m34==m12||m34==m13||m34==m14||m34==m15||m34==m16|| m34==m24||m34==m25||m34==m31||m34==m36||m34==m41||m34==m46||m34==m52||m34==m53||m34==m64||m34==m65||m16+m25+m34+m52<40||m16+m25+m34+m52>108||m14+m24+m34+m64<40|| m14+m24+m34+m64>108)continue;for(m61=1;m61<37;m61++){if(m61==m11||m61==m12||m61==m13||m61==m14||m61==m15||m61==m16|| m61==m24||m61==m25||m61==m31||m61==m34||m61==m36||m61==m41||m61==m46||m61==m52||m61==m53||m61==m64||m61==m65||m16+m25+m34+m52+m61<75||m16+m25+m34+m52+m61>110||m11+m31+m4 1+m61<40||m11+m31+m41+m61>108)continue;for(m43=1;m43<37;m43++){if(m43==m11||m43==m12||m43==m13||m43==m14||m43==m15||m43==m16|| m43==m24||m43==m25||m43==m31||m43==m34||m43==m36||m43==m41||m43==m46||m43==m52||m43==m53||m43==m61||m43==m64||m43= =m65||m16+m25+m34+m43+m52+m61!=111||m11+m31+m41+m61<40||m11+m31+m4 1+m61>108)continue;//m34=0;m61=0;m43=0;for(m51=1;m51<37;m51++){if(m51==m11||m51==m12||m51==m13||m51==m14||m51==m15||m51==m16|| m51==m24||m51==m25||m51==m31||m51==m34||m51==m36||m51==m41||m51==m43||m51==m46||m51==m52||m51==m53||m51==m61||m51= =m64||m51==m65||m11+m31+m41+m51+m61<75||m11+m31+m41+m51+m61>110)continue;for(m21=1;m21<37;m21++){if(m21==m11||m21==m12||m21==m13||m21==m14||m21==m15||m21==m16|| m21==m24||m21==m25||m21==m31||m21==m34||m21==m36||m21==m41||m21==m43||m21==m46||m21==m51||m21==m52||m21==m53||m21= =m61||m21==m64||m21==m65||m11+m21+m31+m41+m51+m61!=111)continue;//m21=0;m51=0;for(m66=1;m66<37;m66++){if(m66==m11||m66==m12||m66==m13||m66==m14||m66==m15||m66==m16|| m66==m21||m66==m24||m66==m25||m66==m31||m66==m34||m66==m36||m66==m41||m66==m43||m66==m46||m66==m51||m66==m52||m66==m53||m66= =m61||m66==m64||m66==m65||m16+m36+m46+m66<40||m16+m36+m46+m66>108||m61+m64+m65+m66<40|| m61+m64+m65+m66>108)continue;for(m44=1;m44<37;m44++){if(m44==m11||m44==m12||m44==m13||m44==m14||m44==m15||m44==m16|| m44==m21||m44==m24||m44==m25||m44==m31||m44==m34||m44==m36||m44==m41||m44==m43||m44==m46||m44==m51||m44==m52||m44==m53||m44==m61||m44==m64||m44==m65||m44==m66||m14+m24+m34+m44+m64<75||m14+m24+m34+m44+m64>110||m41+m43+m4 4+m46<40||m41+m43+m44+m46>108)continue;for(m54=1;m54<37;m54++){if(m54==m11||m54==m12||m54==m13||m54==m14||m54==m15||m54==m16|| m54==m21||m54==m24||m54==m25||m54==m31||m54==m34||m54==m36||m54==m41||m54==m43||m54==m44||m54==m46||m54==m51||m54==m52||m54= =m53||m54==m61||m54==m64||m54==m65||m54==m66||m14+m24+m34+m44+m54+m64!=111||m51+m52+m53+m54<40||m51+m52+m 53+m54>108)continue;//m66=0;m54=0;m44=0;for(m55=1;m55<37;m55++){if(m55==m11||m55==m12||m55==m13||m55==m14||m55==m15||m55==m16|| m55==m21||m55==m24||m55==m25||m55==m31||m55==m34||m55==m36||m55==m41||m55==m43||m55==m44||m55==m46||m55==m51||m55==m52||m55= =m53||m55==m54||m55==m61||m55==m64||m55==m65||m55==m66||m15+m25+m55+m65<40||m15+m25+m55+m65>108||m51+m52+m53+m54+m5 5<75||m51+m52+m53+m54+m55>110||m11+m44+m55+m66<40||m11+m44+m55+m66>108)continue;for(m56=1;m56<37;m56++){if(m56==m11||m56==m12||m56==m13||m56==m14||m56==m15||m56==m16|| m56==m21||m56==m24||m56==m25||m56==m31||m56==m34||m56==m36||m56==m41||m56==m43||m56==m44||m56==m46||m56==m51||m56==m52||m56= =m53||m56==m54||m56==m55||m56==m61||m56==m64||m56==m65||m56==m66||m16+m36+m46+m56+m66<75||m16+m36+m46+m56+m66>110||m51+m52+m5 3+m54+m55+m56!=111)continue;for(m26=1;m26<37;m26++){if(m26==m11||m26==m12||m26==m13||m26==m14||m26==m15||m26==m16|| m26==m21||m26==m24||m26==m25||m26==m31||m26==m34||m26==m36||m26==m41||m26==m43||m26==m44||m26==m46||m26==m51||m26==m52||m26==m53||m26==m54||m26==m55||m26==m56||m26==m61||m26==m64||m26==m65||m26==m66||m16+m26+m36+m46+m56+m66!=111||m21+m24+m25+m26<40||m21+m24+m 25+m26>108)continue;//m55=0;m56=0;m26=0;for(m63=1;m63<37;m63++){if(m63==m11||m63==m12||m63==m13||m63==m14||m63==m15||m63==m16|| m63==m21||m63==m24||m63==m25||m63==m26||m63==m31||m63==m34||m63= =m36||m63==m41||m63==m43||m63==m44||m63==m46||m63==m51||m63==m52||m63==m53||m63==m54||m63==m55||m63==m56||m63==m61||m63==m64||m63==m65||m63==m66||m61+m63+m64+m65+m66<75||m61+m63+m64+m65+m66>110||m13+m43+m5 3+m63<40||m13+m43+m53+m63>108)continue;for(m62=1;m62<37;m62++){if(m62==m11||m62==m12||m62==m13||m62==m14||m62==m15||m62==m16|| m62==m21||m62==m24||m62==m25||m62==m26||m62==m31||m62==m34||m62= =m36||m62==m41||m62==m43||m62==m44||m62==m46||m62==m51||m62==m52||m62==m53||m62==m54||m62==m55||m62==m56||m62==m61||m62==m63||m62==m64||m62==m65||m62==m66||m61+m62+m63+m64+m65+m66!=111)continue;//m63=0;m62=0;for(m35=1;m35<37;m35++){if(m35==m11||m35==m12||m35==m13||m35==m14||m35==m15||m35==m16|| m35==m21||m35==m24||m35==m25||m35==m26||m35==m31||m35==m34||m35= =m36||m35==m41||m35==m43||m35==m44||m35==m46||m35==m51||m35==m52||m35==m53||m35==m54||m35==m55||m35==m56||m35==m61||m35==m62||m35==m63||m35==m64||m35==m65||m35==m66||m31+m34+m35+m36<40||m31+m34+m35+m36>108||m15+m25+m35+m55+m6 5<75||m15+m25+m35+m55+m65>110)continue;{if(m45==m11||m45==m12||m45==m13||m45==m14||m45==m15||m45==m16|| m45==m21||m45==m24||m45==m25||m45==m26||m45==m31||m45==m34||m45= =m35||m45==m36||m45==m41||m45==m43||m45==m44||m45==m46||m45==m51||m45==m52||m45==m53||m45==m54||m45==m55||m45==m56||m45==m61||m45==m62||m45==m63||m45==m64||m45==m65||m45==m66||m41+m43+m44+m45+m46<75||m41+m43+m44+m45+m46>110||m15+m25+m3 5+m45+m55+m65!=111)continue;for(m42=1;m42<37;m42++){if(m42==m11||m42==m12||m42==m13||m42==m14||m42==m15||m42==m16|| m42==m21||m42==m24||m42==m25||m42==m26||m42==m31||m42==m34||m42==m35||m42==m36||m42==m41||m42==m43||m42==m44||m42==m45||m42==m46||m42==m51||m42==m52||m42==m53||m42==m54||m42==m55||m42==m56||m42==m61||m42==m62||m42==m63||m42==m64||m42==m65||m42==m66||m41+m42+m43+m44+m45+m46!=111||m12+m42+m52+m62<40||m12+m42+m 52+m62>108)continue;//m42=0;m45=0;m35=0;for(m22=1;m22<37;m22++){if(m22==m11||m22==m12||m22==m13||m22==m14||m22==m15||m22==m16|| m22==m21||m22==m24||m22==m25||m22==m26||m22==m31||m22==m34||m22==m35||m22==m36||m22==m41||m22==m42||m22==m43||m22==m44||m22==m45||m22==m46||m22==m51||m22==m52||m22==m53||m22==m54||m22==m55||m22==m56||m22==m61||m22==m62||m22==m63||m22==m64||m22==m65||m22==m66||m21+m22+m24+m25+m26<75||m21+m22+m24+m25+m26>110||m12+m22+m42+m52+m62<75||m12+m22+m42+m52+m62>110||m11+m22+m44+m55+m66<75||m11+m22+m44+m55+m66>110)continue;for(m32=1;m32<37;m32++){if(m32==m11||m32==m12||m32==m13||m32==m14||m32==m15||m32==m16|| m32==m21||m32==m22||m32==m24||m32==m25||m32==m26||m32==m31||m32==m34||m32==m35||m32==m36||m32==m41||m32==m42||m32==m43||m32==m44||m32==m45||m32==m46||m32==m51||m32==m52||m32==m53||m32==m54||m32==m55||m32==m56||m32==m61||m32==m62||m32==m63||m32==m64||m32==m65||m32==m66||m31+m32+m34+m35+m36<75||m31+m32+m34+m35+m36>110||m12+m22+m32+m42+m52+m62!=111)continue;{if(m33==m11||m33==m12||m33==m13||m33==m14||m33==m15||m33==m16|| m33==m21||m33==m22||m33==m24||m33==m25||m33==m26||m33==m31||m33==m32||m33==m34||m33==m35||m33==m36||m33==m41||m33==m42||m33==m43||m33==m44||m33==m45||m33==m46||m33==m51||m33==m52||m33==m53||m33==m54||m33==m55||m33==m56||m33==m61||m33==m62||m33==m63||m33==m64||m33==m65||m33==m66||m13+m33+m43+m53+m63<75||m13+m33+m43+m53+m63>110||m11+m22+m3 3+m44+m55+m66!=111||m31+m32+m33+m34+m35+m36!=111)continue;for(m23=1;m23<37;m23++){if(m23==m11||m23==m12||m23==m13||m23==m14||m23==m15||m23==m16|| m23==m21||m23==m22||m23==m24||m23==m25||m23==m26||m23==m31||m23==m32||m23==m33||m23==m34||m23==m35||m23==m36||m23==m41||m23==m42||m23==m43||m23==m44||m23==m45||m23==m46||m23==m51||m23==m52||m23==m53||m23==m54||m23==m55||m23==m56||m23==m61||m23==m62||m23==m63||m23==m64||m23==m65||m23==m66||m13+m23+m33+m43+m53+m63!=111||m21+m22+m23+m24+m25+m26!=111)continue;//m22=0;m32=0;m33=0;m23=0;{//int t2=clock();printf("%d\t%d\t%d\t%d\t%d\t%d\n%d\t%d\t%d\t%d\t%d\t%d\n%d\t%d\t%d\t%d\t% d\t%d\n%d\t%d\t%d\t%d\t%d\t%d\n%d\t%d\t%d\t%d\t%d\t%d\n%d\t%d\t%d\t%d\t%d\t%d\n******************************************\tNO：%d\n",m11,m12,m13,m14,m15,m16,m21,m22,m23,m24,m25,m26,m31,m32,m33,m34,m35,m36,m41 ,m42,m43,m44,m45,m46,m51,m52,m53,m54,m55,m56,m61,m62,m63,m64,m65,m66 ,z+1);z++;}//if(z==10)goto A;}}}}} }}}}}} }}}} }}} }} }}} }}} }} }}} }}}}// //A:int t3=clock();printf("写出%d个基本答案，用时%dms。

六阶魔方教程
好的，下面是六阶魔方的教程：
第一步：底层交叉
将所有边块按颜色进行分类，然后选取一个颜色作为底层中心块的颜色。

开始拼接底层交叉，方法是找到底层棱块边上的颜色，将其与对应颜色的底层中心块对齐，然后将边块旋转至其正确位置。

重复上述步骤，直到完成底层交叉。

第二步：底层角块
找到放置在底层的角块，将其放到正确的位置上。

方法是找到角块中没有底层颜色的面，然后将该面与对应的底层中心块面对齐，然后旋转角块至其正确位置。

重复上述步骤，直到完成底层角块。

第三步：中层边块
将中层的边块放到正确的位置上。

方法是找到中层边块与其对应的底层棱块，然后将两个边块旋转至其正确位置。

重复上述步骤，直到完成中层边块。

第四步：顶层十字
将顶层的边块按照颜色分类，然后将顶层中心块调整至正确颜色。

然后找到顶层边块与其对应的顶层中心块，将边块旋转至正确位置。

重复上述步骤，直到完成顶层十字。

第五步：顶层角块
寻找顶层角块并将其放置在正确的位置。

找到顶层三块角块中只有一个面是正确的，然后将该面朝向正确方向后进行相关旋转。

重复上述步骤，直到完成顶层角块。

第六步：顶层边块
找到顶层边块并放置在正确的位置。

方法是找到顶层边块的颜色与其对应的顶层中心块的颜色相同，然后进行旋转操作。

重复上述步骤，直到完成顶层边块。

完成以上六个步骤后，六阶魔方就完成了。